Analytical solutions and application of circular cofferdams considering backseal effects
-
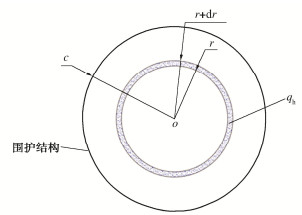
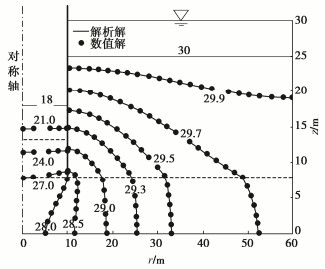
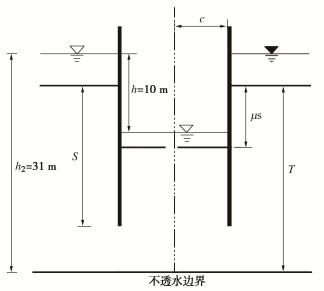
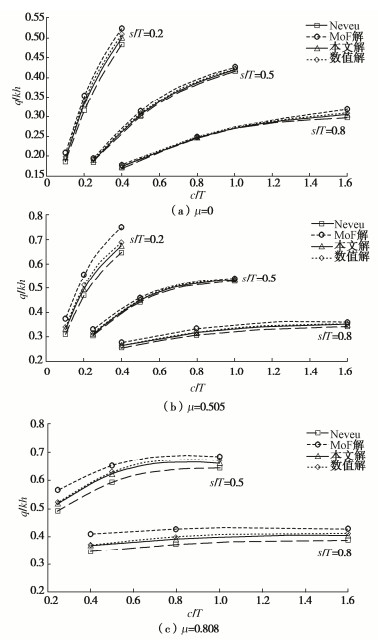
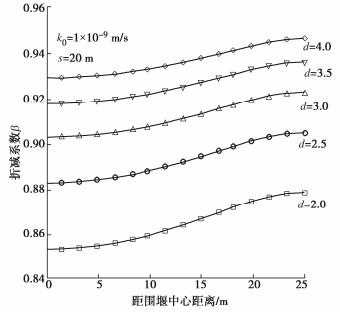
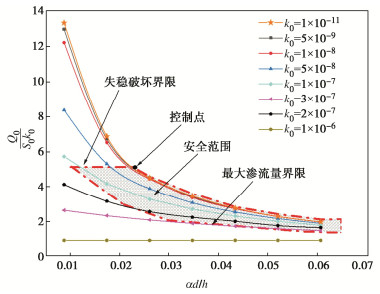
摘要: 将圆形围堰周围渗流场分为4个区域，用分离变量法分别得到柱坐标系下4个区域的水头分布级数解形式，结合区域间的连续条件，并利用贝塞尔函数正交性得到考虑封底效应的圆形围堰稳态渗流场解析解。该解析解能求解成层土情况下围堰涌水量及封底层渗流水压力，并能退化到各向同性土层中围堰未封底情况。通过与数值计算结果以及其他近似法计算结果的对比，证明了该解析解的正确性及有效性。基于解析解，分析了封底层渗流水压力分布规律，结合工程实例探讨了考虑渗流影响的封底层失稳破坏规律。结果表明：渗流作用下封底层所受水压力并非均匀分布，而是呈现中心小四周大的分布形式；封底层渗透系数及厚度会显著影响渗流水压力的大小及分布。Abstract: The seepage fields around a circular cofferdam are divided into four regions, and the fractional variable method is used to obtain the sequence solutions of the water head distribution in the four regions under the cylindrical coordinate system, combined with the continuous conditions between the regions, and the analytical solutions of the steady seepage fields of the circular cofferdam are obtained by using the bessel function orthogonality. The correctness and effectiveness of the analytical solutions are proved by comparison with the numerical results and those by other approximate methods. The analytical solutions can be used to solve the water inflow of the cofferdam and the water pressure of the concrete at the bottom of the cofferdam in the case of double-layer soil, and can be degraded to the case of the cofferdam without the bottom of the isotropic soil. Based on the analytical solutions, the distribution laws of the seepage water pressure of subsealing concrete are analyzed, and the instability failure laws of subsealing concrete considering seepage influences are discussed through an engineering example. The results show that the water pressure on the concrete under seepage is not uniformly distributed, but in the form of being small in the center and large in the periphery. The permeability coefficient and thickness of the concrete at the bottom of the seal significantly affect the magnitude and distribution of the seepage water pressure.
-
0. 引言
注浆是裂隙岩体加固防渗的主要手段，在基础工程设施领域得到了广泛应用[1-2]。深入了解浆液在岩体裂隙中的运移规律对于工程实践具有重要指导意义。
试验是研究注浆扩散机理的重要途径，国内外学者在该领域开展了大量研究工作。Funehag等采用亚克力板制作了单裂隙平板注浆试验装置，研究了宾汉姆浆液黏度、屈服应力和扩散特性[3]。Sui等利用单裂隙模型试验台，通过正交试验研究了动水条件下裂隙宽度、初始水流速度、浆液胶凝时间、注浆量等对注浆堵漏效率的影响[4]。李术才等[5]、刘人太等[6]研制了大尺寸平板裂隙注浆模型试验系统，开展了裂隙岩体动水注浆模型试验研究，对浆液扩散性能和封堵效果进行了定量评价。Wang等[7]设计了一种微裂隙注浆试验系统，采用多种超细水泥浆液，进行不同裂隙开度条件下注浆试验，揭示了注浆压力和注浆量对注浆加固效果的影响。Liang等[8]设计了倾斜裂隙模型试验装置，研究了不同裂隙倾角条件下，注浆对水砂混合物排放控制效果的影响。总体来看，上述研究主要针对水泥、水玻璃等常密度浆液，所得结论不适用于解释具有自膨胀特性的高聚物注浆材料的扩散行为。
近年来，具有自膨胀特性的聚氨酯类高聚物注浆材料及其高压注射技术在国际上发展十分迅速，成为岩土工程领域较为活跃的发展方向之一[9]。高聚物浆液具有反应速度快、膨胀率高、防水抗渗、安全环保等特点，成为综合性能较优的注浆材料，在地下工程水害防治等领域得到广泛应用[10]。为揭示高聚物材料裂隙注浆扩散机理，Hao等[11]和Li等[12]设计了单裂隙平板注浆模型试验装置，测试了不同注浆量条件下高聚物浆液在裂隙中的扩散特性和压力分布。Liang等[13]研究了高聚物浆液在竖向裂隙中的膨胀扩散特性。
一些学者已注意到高聚物浆液反应过程中的高放热现象，石明生等研究了双组分聚氨酯高聚物材料在固化过程中的温度变化规律[14]。郝梅美[15]研究发现，在相同环境温度下，高聚物膨胀速率随浆液预热温度的升高而增大，原因在于提高预热温度能够加快浆液化学反应速度，加速体系升温和物理发泡剂气化，从而使浆液膨胀速率加快。
可以推断，当浆液流动过程中与周围介质之间由于温差发生热传导时将改变浆液温度场分布，进而影响其反应速率和扩散过程。尤其对于裂隙注浆，由于裂隙面延展范围大、开度小，浆液与裂隙壁接触面积大，因温差产生的热传导对浆液温度场及其扩散过程的影响无疑会更加显著。但目前关于温度和热传导效应对高聚物裂隙注浆扩散行为的影响仅限于定性了解，缺乏系统深入的试验研究。
基于这一背景，本文设计了平板裂隙注浆模型试验装置，以一种工程中常用的聚氨酯高聚物浆液为对象，开展了系列注浆试验，测试不同条件下高聚物浆液在平板裂隙中的扩散特性，分析浆液预热温度、环境温度、注浆量等因素对浆液扩散行为的影响，研究高聚物扩散过程浆液温度场变化及分布特征，旨在深化对高聚物裂隙注浆扩散机理的认识，为高聚物注浆工艺设计和施工方案制定提供参考依据。
1. 裂隙注浆试验介绍
1.1 试验装置
试验装置由可视化裂隙注浆平台，温度采集系统，高聚物注浆系统3部分组成，试验装置组成如图 1所示。
裂隙注浆平台由上下两块1.2 m×1.2 m×15 mm尺寸透明亚克力板，加固装置及垫片构成，如图 2所示。在上板表面中心处钻直径10 mm圆孔作为注浆孔。为避免亚克力板在浆液膨胀压力下产生过大变形，在上、下板外侧分别放置4根1.5 m×50 mm×30 mm钢条，利用螺栓将钢条与亚克力板固定，提升亚克力板抵抗变形能力。通过在上、下板间放置长条状垫片形成裂隙空间。为安设温度传感器，以注浆孔为中心，在上板面沿两垂直中轴线方向钻直径2 mm圆孔，相邻两孔间隔10 cm，其中，#1~#15孔钻透板底，#16~#20孔钻深7.5 mm（上板厚度一半）。
温度采集系统如图 3所示，包含温度采集仪和K型热电偶。温度采集仪为慧谱TCP-X多路温度采集仪，能够精确快速、稳定可靠地记录高聚物膨胀扩散过程中的温度变化。把K型热电偶探头插入预先布好的钻孔中，在孔周围涂抹热熔胶将其黏结固定。如图 4所示，#1~#10号探头悬浮于裂隙中，用于测量高聚物浆液温度，#11~#15号探头紧贴亚克力板内侧，用于测量浆液扩散过程中高聚物与亚克力板的接触温度，#16~#20号探头位于亚克力板内部，用于测量亚克力板壁面内温度。
高聚物注浆系统采用重大基础设施检测修复技术国家地方联合工程实验室开发的集成式多功能注浆系统。该系统主要由供料子系统和注射子系统组成，供料子系统将高聚物A，B两种原料按一定比例吸入其内部，利用加热器将两种原料加热至设定的预热温度后通过输料管送入注射子系统中，经注射枪高速混合后高压输出，完成注浆过程。
1.2 试验材料
试验采用的聚氨酯高聚物浆液由A，B两种组分构成，A组分为多亚甲基多苯基多异氰酸酯，B组分主要由多元醇、催化剂、发泡剂等构成。A，B两种组分的质量混合比为1.1∶1，材料配比组成见表 1。高聚物浆液黏度在初凝前基本保持稳定（小于0.8 Pa·s），接近初凝时黏度急剧升高；浆液固化体抗压强度和抗拉强度随材料密度的增大而增大，当材料密度为0.9 g/cm3时，抗压和抗拉强度分别达到36 MPa和13 MPa；浆液固化体具有较好的抗渗性能，渗透系数为1×10-8~1×10-9 cm/s。
表 1 高聚物浆液材料配比Table 1. Proportioning of polymer slurry materials组分 原料 质量分数/% A组分 多亚甲基多苯基多异氰酸酯 100 B组分 硬泡聚醚多元醇体系 35 聚酯多元醇（PS-3152） 15 阻燃剂（磷酸三乙酯） 10 催化剂体系 2 表面活性剂（L6950） 0.5 物理发泡剂 5 化学发泡剂 0.5 其它 32 该浆液的固化过程主要包括两个化学反应——凝胶反应和发泡反应。异氰酸酯和多元醇反应生成聚氨酯的过程被称为凝胶反应，其反应方程式为
(1) 在采用水作为化学发泡剂的情况下，异氰酸酯和水反应生成脲和二氧化碳的反应被称为发泡反应，其反应方程式为
(2) 在高聚物浆液被注入裂隙后，迅速发生化学反应，释放大量热能，一方面促使浆液体系温度不断上升，加速反应进行，另一方面，使浆液中溶解的液态物理发泡剂逐渐气化形成大量微小闭孔气泡悬浮于浆液中，连同发泡反应生成的二氧化碳气体，促使浆液体积膨胀，驱动浆体流动。
1.3 试验过程
首先组装裂隙注浆试验平台，然后连接K型热电偶与温度采集仪，待环境温度达到设定值之后开始注浆试验。利用高聚物注浆系统将预热至设定温度的浆液通过注射枪高压（注浆压力7 MPa）注入裂隙中，此后注浆压力撤去，高聚物浆液依靠其自身的化学反应膨胀，驱动浆液流动扩散，观察高聚物扩散过程，同步记录温度变化。重复上述步骤，依次开展试验，试验各影响因素取值列于表 2中。
表 2 试验各影响因素取值Table 2. Values of influencing factors of tests编号 注浆量/g 浆液预热温度/℃ 环境温度/℃ #1 500 30 20 #2 625 40 30 #3 750 50 — 2. 试验结果分析
2.1 高聚物浆液扩散形态及温度变化和分布特征
图 5所示为裂隙开度7 mm，注浆量500 g，预热温度40℃，环境温度30℃条件下高聚物浆液在裂隙中的扩散过程，高聚物浆液被注入裂隙后开始发生化学反应，浆液以圆饼状向周围迅速膨胀扩散，由最初的透明液态逐渐转变为淡黄色固态。图 6，7分别为对应工况r=10，20 cm测点处浆液温度随时间变化曲线和不同时刻浆液温度沿径向分布情况，可以看到，高聚物浆液温度在反应过程中先快速升高，达到峰值后逐渐降低，温度下降速度低于上升速度；充填区域内的浆液温度分布随时间不断变化，任一时刻，在注浆孔中心处温度最高，沿径向逐渐降低。
![]()
图 6 注浆量500 g，预热温度40℃，环境温度30℃不同测点处高聚物温度随时间变化曲线Figure 6. Variation curves of polymer temperature with time at different measuring points under grouting amount 500 g, preheating temperature 40℃ and ambient temperature 30℃![]()
图 7 注浆量500 g，预热温度40℃，环境温度30℃不同时刻高聚物浆液温度沿径向变化曲线Figure 7. Radial variation curves of polymer temperature with time at different time under grouting amount 500 g, preheating temperature 40℃ and ambient temperature 30℃2.2 预热温度对浆液膨胀扩散过程的影响
裂隙开度7 mm，环境温度30℃，预热温度分别为30℃，40℃和50℃条件下，注浆量为500，625 g时浆液扩散半径随时间的变化如图 8所示，对应工况的浆液最终扩散半径如图 9所示。从图 8可以看出，不同注浆量条件下，浆液扩散过程均表现出相似特征，预热温度越高，浆液扩散速率越快，初凝时间越早，预热温度30℃时的扩散速率和初凝时间显著低于40℃和50℃时的测试结果。当注浆量为500 g，浆液预热温度30℃，40℃，50℃时，其扩散平均速率分别为1.09，2.03，2.31 cm/s，初凝时间分别为22，18，16 s。注浆量625 g，预热温度30℃，40℃，50℃时的平均扩散速率分别为1.04，2.25，2.73 cm/s，分别在24，18，15 s时达到初凝，与500 g时对应预热温度条件下的初凝时间较为接近。
![]()
图 8 不同预热温度条件下高聚物扩散半径随时间变化曲线Figure 8. Variation curves of polymer diffusion radius with time under different preheating temperature conditions![]()
图 9 不同注浆量时高聚物扩散半径-预热温度变化柱状图Figure 9. Histograms of polymer diffusion radius-preheating temperature change under different grouting amounts从图 9中可以发现，预热温度为40℃和50℃时浆液扩散范围较为接近，而预热温度30℃时的浆液最终扩散半径远小于前两者。注浆量500 g时，预热温度30℃，40℃，50℃条件下浆液的最终扩散半径分别为24，36.5，37 cm；注浆量625 g时，3种预热温度条件下浆液最终扩散半径分别为25，40.5，41 cm。分析其原因在于，当预热温度为30℃时，化学反应速率较慢，浆液反应不充分，体系温度较低，物理发泡剂未充分气化，导致体积膨胀倍率较低。从试验结果来看，预热温度40℃以上时浆液反应已较为充分，物理发泡剂充分气化，因此随着温度的继续升高浆液扩散半径不再显著增加。
裂隙开度为7 mm，环境温度为30℃，预热温度为50℃，注浆量分别为500，625 g时高聚物扩散半径及温度随时间变化曲线如图 10所示。可以看到，当注浆量为500 g时，浆液在14 s时达到初凝，此后扩散范围不再增大，但温度仍继续上升，19 s时达到峰值（132℃），之后逐渐下降。注浆量625 g时的试验结果表现出类似特征，表明高聚物浆液化学反应进程与其扩散过程并不同步，浆液化学反应终止时间晚于其初凝时间。
![]()
图 10 不同注浆量时高聚物扩散半径、温度随时间变化曲线Figure 10. Variation curves of polymer diffusion radius and temperature with time under different grouting amounts2.3 预热温度对浆液温度的影响
图 11为注浆量750 g，裂隙开度7 mm，环境温度30℃，预热温度30℃，40℃，50℃条件下，距离注浆孔10，20 cm测点处高聚物浆液温度随时间变化曲线；图 12为预热温度40℃，50℃条件下，t=20，40 s时浆液温度沿径向分布情况。可以看出，不同工况下高聚物温度变化均呈现先升高后下降的趋势。预热温度越高，浆液温度变化速率越快，达到峰值的时刻越早。在10 cm测点处，当预热温度为30℃，40℃，50℃时，浆液温度分别在68，34，20 s达到峰值，峰值温度分别为105℃，129℃，151℃。在温度下降阶段，预热温度30℃工况下浆液温度下降速度慢于其他两种工况，分析其原因可能是由于该工况下浆液扩散范围较小，与裂隙壁接触面积小，因此受热传导效应影响小，使浆液温度下降速率相对较慢。在其它条件相同的情况下，同一时刻预热温度越高，对应测点处浆液温度越高。
![]()
图 11 注浆量750 g不同预热温度、不同位置处浆液温度随时间变化曲线Figure 11. Variation curves of slurry temperature with time at different preheating temperatures and different positions under grouting amount 750 g![]()
图 12 注浆量750 g不同预热温度、不同时刻浆液温度沿径向分布曲线Figure 12. Distribution curves of slurry temperature along radial direction at different preheating temperatures and different time under grouting amount 750 g2.4 环境温度对浆液温度的影响
裂隙开度7 mm，注浆量750 g，预热温度50℃，环境温度20℃和30℃条件下，r=10，20 cm测点处浆液温度随时间变化曲线和t=30，60 s时高聚物温度径向分布情况分别如图 13，14所示。可以看出，环境温度越高，浆液温度上升速率越快，达到峰值的时刻越早，环境温度30℃时的浆液温度和上升速率始终高于环境温度20℃时的试验结果；10 cm测点处，前者浆液温度在20 s时达到峰值151℃，而后者在22 s时才达到峰值133℃；同一时刻注浆孔中心处浆液温度最高，沿径向逐渐降低，在不同位置处，浆液温度随着环境温度的升高而增大。
![]()
图 13 注浆量750 g，预热温度50℃不同环境温度不同位置处浆液温度随时间变化曲线Figure 13. Variation curves of slurry temperature with time at different ambient temperatures and different positions under grouting amount 750 g and preheating temperature 50℃![]()
图 14 注浆量750 g，预热温度50℃不同环境温度不同时刻浆液温度沿径向分布曲线Figure 14. Distribution curves of temperature along radial direction at different ambient temperatures and different time under grouting amount 750 g and preheating temperature 50℃2.5 高聚物浆液与裂隙壁热传导效应
预热温度50℃，环境温度30℃，裂隙开度7 mm，注浆量750 g时，r=10，20 cm测点处高聚物温度、接触面温度及裂隙壁内温度随时间变化曲线及t=30，50 s时以上3类温度的径向分布情况分别如图 15，16所示。从图 15可以看出，高聚物温度与接触面温度随时间变化趋势基本保持同步，先升高然后逐渐降低，几乎同时达到峰值，受热传导作用影响，过峰值后两者温度逐渐下降，但相同位置处接触面温度始终低于高聚物温度。在10 cm测点处，高聚物和接触面峰值温度分别为151℃，93℃，在20 cm测点处，两者的峰值温度分别为129℃，80℃。裂隙壁内温度在初始时刻与环境温度相同，然后随时间缓慢升高，在测试时间范围内始终低于接触面温度。200 s时10 cm测点处温度达到33.8℃，20 cm测点处温度达到32.07℃。其原因在于，在测试时间范围内浆液温度始终高于裂隙壁面温度，受热传导效应影响，裂隙壁内温度逐渐上升。
![]()
图 15 注浆量750 g，预热温度50℃，环境温度30℃时高聚物温度、接触面温度及裂隙壁内温度随时间变化曲线Figure 15. Variation curves of polymer temperature, contact surface temperature and wall temperature with time under grouting amount 750 g, preheating temperature 50℃ and ambient temperature 30℃![]()
图 16 注浆量750 g，预热温度50℃，环境温度30℃时不同时刻高聚物温度、接触面温度及壁面内温度沿径向分布曲线Figure 16. Distribution curves of polymer temperature, contact surface temperature and wall temperature along radial direction under grouting amount 750 g, preheating temperature 50℃ and ambient temperature 30℃从图 16可以看出，裂隙壁内温度始终低于高聚物温度和接触面温度。由于热传导效应，50 s时裂隙壁内不同测点处温度均高于30 s时对应位置测试结果。
2.6 温度和热传导效应对高聚物浆液在裂隙中扩散过程影响机制分析
高聚物浆液被高速混合注入裂隙后，迅速发生化学反应，释放大量热能，促使浆液温度不断上升，使浆液中溶解的液态物理发泡剂达到沸点温度后逐渐气化，连同发泡反应生成的气体，驱动浆液体积快速膨胀并持续扩散。由于温度是影响浆液化学反应速率的重要因素，因此温度变化尤其是浆液预热温度的改变对浆液扩散过程产生较显著影响。
浆液反应过程中温度不断升高与裂隙壁间形成较大温差，因温差产生的热传导使一部分热能通过接触面由浆液传递到裂隙壁内，导致浆液温度减小，改变了温度场分布，降低浆液反应速度和扩散速率。环境温度的变化改变浆液与裂隙壁间的温差，影响两者间热传导效应和温度场变化速率，间接对浆液反应速度和扩散过程产生影响。
3. 结论
（1）浆液预热温度对高聚物扩散过程具有重要影响。相同注浆量条件下，预热温度越高，浆液扩散速率越快，初凝时间越早，浆液扩散半径越大，当预热温度升高至一定值时，浆液扩散范围基本不再变化。
（2）浆液扩散过程与其化学反应进程不完全同步，化学反应终止时间晚于初凝时间。不同注浆量条件下浆液扩散半径、温度随时间变化趋势基本一致，其峰值随着注浆量的增大而增大。
（3）高聚物浆液温度时空演变过程具有明显规律性。不同测点处浆液温度随时间均呈现先升高后下降，变化速率由快到慢的演化特征；在体系温度达到平衡前，注浆孔中心处温度最高，沿径向逐渐递减。
（4）随着预热温度和环境温度的升高，浆液整体温度增大，升温速度加快，峰值温度增高，达到峰值点的时刻变早。与预热温度相比，环境温度对浆液温度变化速率影响相对较小。
（5）受高聚物与裂隙壁温差影响，浆液在裂隙内扩散过程中存在明显热传导效应，使得浆液温度达到峰值后逐渐下降，当两者温度达到平衡前，浆液温度高于接触面温度，接触面温度高于裂隙壁内温度。
围绕温度对高聚物浆液在裂隙中扩散行为影响采用可视化平板裂隙模型开展了初步研究，尚未考虑裂隙壁面粗糙度、起伏度等因素的耦合影响，未来将进一步完善试验装置，使试验工况最大限度逼近真实工程场景，为现场注浆施工提供更有效的指导。
-
![]()
图 5 开挖面涌水量对比结果
Figure 5. Comparison of analytical solutions, MoF and numerical model solutions by Madanayaka
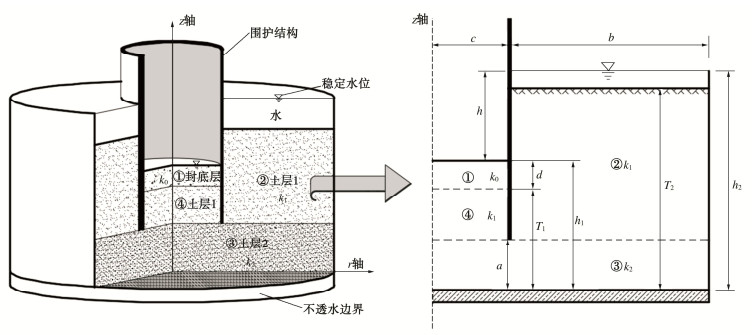
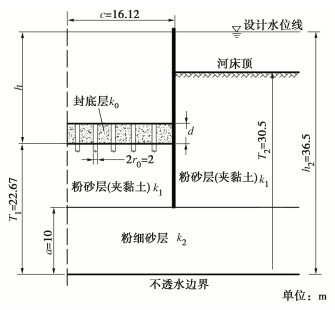
表 1 围堰渗流模型的工程参数
Table 1 Engineering parameters of seepage model for cofferdam
单位: m b c d T1 T2 h1 h2 a 50 10 5 15 25 18 30 5 
下载: 导出CSV
-
[1] MADANAYAKA T A, SIVAKUGAN N. Adaptation of method of fragments to axisymmetric cofferdam seepage problem[J]. International Journal of Geomechanics, 2017, 17(9): 121-129.
[2] MADANAYAKA T A, SIVAKUGAN N. Simple solutions for square and rectangular cofferdam seepage problems[J]. Canadian Geotechnical Journal, 2019, 56(5): 730-745. doi: 10.1139/cgj-2018-0295
[3] BENMEBAREK N, BENSMAINE A, Critical hydraulic head loss inducing cofferdam failure embedded in horizontal sandy ground[J]. Alexandria Engineering Journal, 2015, 51(4): 173-180.
[4] TANAKA T, TACHIMURA R, KUSUMI S, et al. Experimental findings of 3D seepage failure of soil within a cofferdam[J]. Japanese Geotechnical Society Special Publication, 2016, 45(2): 1608-1613.
[5] 薛禹群, 吴吉春. 地下水动力学[M]. 3版. 北京: 地质出版社, 2010. XUE Yuqun, WU Jichun. Groundwater Hydraulics[M]. 3rd ed. Beijing: Geological Publishing House, 2010. (in Chinese)
[6] KAVVADAS M, GIOLAS A, PAPACHARALAMBOUS G. Drainage of supported excavations[J]. Geotechnical & Geological Engineering, 1992, 10(2): 141-157.
[7] BANERJEE S, MULESHKOV A. Analytical solution of steady seepage into double-walled cofferdams[J]. Journal of Engineering Mechanics, 1992, 118(3): 525-539. doi: 10.1061/(ASCE)0733-9399(1992)118:3(525)
[8] BERESLAVSKII E N. The flow of ground waters around a Zhukovskii sheet pile[J]. Journal of Applied Mathematics and Mechanics, 2011, 75(2): 210-217. doi: 10.1016/j.jappmathmech.2011.05.010
[9] NEVEU, G. Axisymmetrical Seepage Flowthrough A Circular Sheet Pile Cofferdam[D]. Montreal: McGill Univ, 1972.
[10] MADANAYAKA T A, SIVAKUGAN N. Validity of the method of fragments for seepage analysis in circular cofferdams[J]. Geotechnical and Geological Engineering, 2020, 38(2): 1547-1565. doi: 10.1007/s10706-019-01111-9
[11] 大卫登可夫R N, 佛兰克O L, 远泓. 漫水地区板桩基坑三向渗流研究[J]. 水利水运科技情报, 1973(增刊3): 50-68. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY1973S3006.htm DAVIDENKOFF R N, FRANKE O L, YUAN Hong. A Study on Three Dimensional Seepage of Sheet Pile Foundation Pit in Overflow Areas[J]. Hydro-Science and Engineering, 1973(S3): 50-68. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY1973S3006.htm
[12] MADANAYAKA T A, SIVAKUGAN N. Approximate equations for the method of fragment[J]. International Journal of Geotechnical Engineering, 2016, 10(3): 297-303. doi: 10.1080/19386362.2016.1144338
[13] 李佩成. 地下水非稳定渗流解析法[M]. 北京: 科学出版社, 1990. LI Peicheng. Analytical Method for Unsteady Seepage of Groundwater[M]. Beijing: Science Press, 1990. (in Chinese)
[14] 张承宗. 数学物理方法与复数特殊函数[M]. 北京: 中国宇航出版社, 2014. ZHANG Chengzong. Anisotropic Mathematical Physics and Complex Special Functions[M]. Beijing: China Astronautic Publishing House, 2014. (in Chinese)
[15] 王竹溪, 郭敦仁. 特殊函数概论[M]. 北京: 北京大学出版社, 2000. WANG Zhuxi, GUO Dunren. Introduction to Special Function[M]. Beijing: Peking University Press, 2000. (in Chinese)
[16] BOUCHELGHOUM F, BENMEBAREK N, Critical hydraulic head loss assessment for a circular sheet pile wall under axisymmetric seepage conditions. [J]. Studia Geotechnica et Mechanica, 2011, 3(4): 3-23.
[17] 李仁民, 刘伟, 陈晓凤. 大直径圆形钢板桩围堰施工技术[J]. 施工技术, 2013, 42(13): 33-37. https://www.cnki.com.cn/Article/CJFDTOTAL-SGJS201313013.htm LI Renmin, LIU Wei, CHEN Xiaofeng. Construction technology of large-diameter circular steel sheet pile cofferdam[J]. Construction Technology, 2013, 42(13): 33-37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SGJS201313013.htm
[18] 曹成勇, 施成华, 彭立敏, 等. 深厚强透水地层基坑深层水平封底隔渗帷幕设计方法及其应用[J]. 中南大学学报(自然科学版), 2020, 51(4): 1012-1021. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202004016.htm CAO Chengyong, SHI Chenghua, PENG Limin, et al. Design method and application of horizontal bottom sealing curtains for deep foundation pits excavated in deep aquifers with high permeability[J]. Journal of Central South University (Science and Technology), 2020, 51(4): 1012-1021. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202004016.htm
-
期刊类型引用(1)
1. 李晓龙，桂云祥，贾赫扬，钟燕辉，张蓓. 温度对高聚物浆液在裂隙中扩散特性影响研究. 土木工程学报. 2025(01): 111-125 . 
百度学术
其他类型引用(1)
-
其他相关附件
计量
- 文章访问数: 342
- HTML全文浏览量: 42
- PDF下载量: 102
- 被引次数: 2
