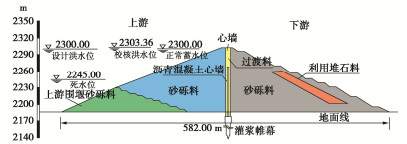
Gradation of filling materials of sand-gravel dams based on multi-dimensional probability distribution
-
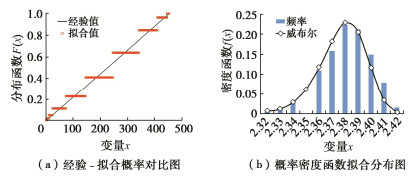
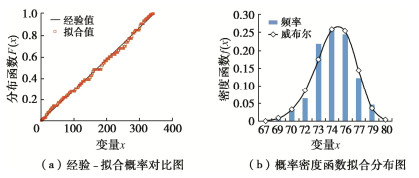
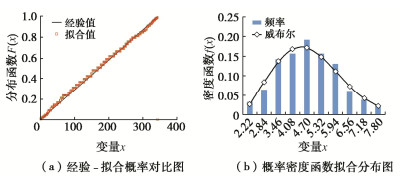
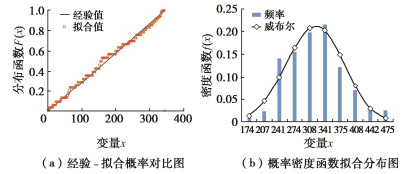
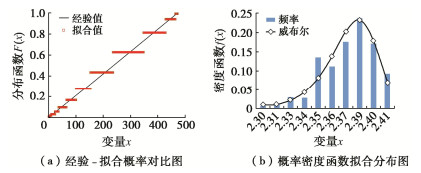
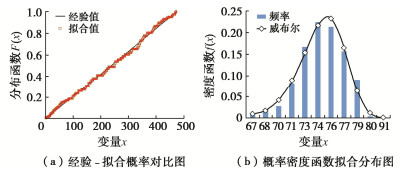
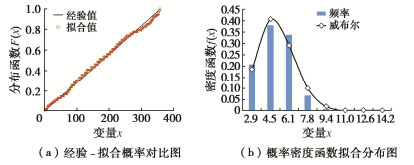
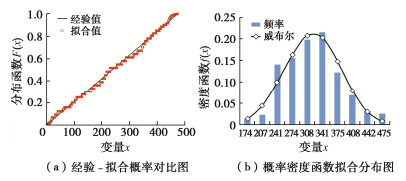
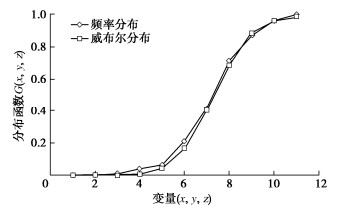
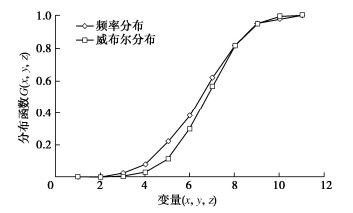
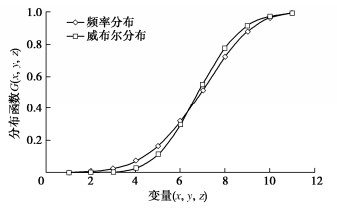
摘要: 砂砾石坝填料的级配和粒径决定颗粒间的接触关系，进而影响其宏观力学响应。基于坝体施工过程中检测得到的两千余组试验数据，结合概率统计方法探索颗粒级配与坝体填料基本物理特征间的关系，分别得出了在砂砾石填料区和过渡料填料区与干密度相关性最密切的3个级配特征参数。进而提出基于一维威布尔概率分布模型的坝体填料试验数据分析方法，对以上3个级配特征参数分别构建一维威布尔分布模型，并得到了在一定保证率条件下的粗粒土级配参数估计值。在此基础上，进一步推导出了三维威布尔分布函数表达式，建立了能够利用3个级配特征参数间的相关关系反映干密度的三维威布尔分布模型，采用K-S检验证明了三维威布尔分布模型用于综合考虑多参数影响的坝体填料分析方法的可靠性。研究结果表明，威布尔分布模型能够较好的适用于大坝填料试验数据的描述及参数估计。Abstract: The gradation and particle size of filling materials of sand-gravel dams determine the inter-particle contact relationship, and further affect the macro-mechanical response. Based on more than 2000 groups of test data detected during dam construction, the relationship between particle gradation and basic physical characteristics of dam materials is explored by using the probability and statistics method, and three gradation characteristic parameters that are most closely related to dry density in sand-gravel materials and transition materials are obtained respectively. Based on the one-dimensional Weibull probability distribution, the test data analysis method for dam materials is proposed. The one-dimensional Weibull distribution model is respectively established for the above three factors, and the estimated value of gradation parameters of coarse-grained soil is obtained under certain assurance rate. The expression for the three-dimensional Weibull distribution function is further derived, and a three-dimensional Weibull distribution model which can reflect the dry density by using the correlation among the three gradation characteristic parameters is established. The K-S tests are used to verify the fitting degree of the model, which proves the reliability that the three-dimensional Weibull distribution model is used for the analysis of dam materials considering the influences of multiple parameters at the same time.
-
0. 引言
随着西部大开发战略、城镇化战略和“一带一路”战略的实施，工程建设中遇到的非饱和土与特殊土的种类和问题急剧增加，研究方法多种多样[1]。横观各向同性非饱和土在国内外广泛分布，例如天然沉积形成的成层地基和机场、大坝等分层填筑的填土工程，都具有横观各向同性特性[2]。郭楠等[3-4]和陈天宇等[5]的一系列横观各向同性岩土材料的试验研究均表明，各向异性的影响不容忽视。研究土的横观各向同性必须综合考虑材料横观各向同性的影响、应力大小和应力方向的影响，主要研究方法包括组构张量法[6]、微观结构张量法[7]和主应力空间坐标旋转法[8]等。
天然地基土和填土大都处于非饱和状态，针对横观各向同性非饱和土的研究目前较少[2-4]，且相关试验结果均是通过常规三轴试验得到的，但是，常规三轴仪的中主应力（σ2）和小主应力（σ3）是相等的，很难反应出土体在复杂应力条件下的应力状态。目前，已有不少学者利用真三轴仪来研究土体的应力应变特性[9]。如方瑾瑾等[10]利用真三轴仪，研究了真三轴压缩条件下非饱和黄土的有效应力屈服变化规律。杨康康等[11]利用真三轴仪对德州地区粉质黏土进行不同围压和中主应力系数b条件下的不排水剪切试验，研究了应力和孔压曲线变化规律、抗剪强度、主应变等。姜景山等[12]应用大型真三轴仪对常规三轴应力状态、平面应变应力状态和真三轴应力状态下粗粒料的力学特性进行了压缩试验研究。但这些研究大都没有考虑基质吸力的影响，且均未考虑土体的横观各向同性特性。
为了研究复杂应力条件下横观各向同性非饱和土体的力学特性，本文采用西安理工大学邵生俊教授研发改装的真三轴仪，对横观各向同性黄土进行研究。西安理工大学研制的新型真三轴仪具有一室四腔、竖向和水平面内正交两向分别呈刚性和柔性加载机构的特征，试样的竖向采用刚性板加载，侧向正交双轴分别采用两组内置于压力腔的液压囊加载[13]。
1. 真三轴条件下横观各向同性非饱和黄土的固结排水剪切试验
1.1 试验方案及过程
试验用土取自延安新区工地现场，为Q3重塑黄土，该土的基本物理性质见表 1[4]。
表 1 土样的基本物理指标Table 1. Physical parameters of soil samples相对质量密度Gs 塑限
wP/%液限wL/% 最大干密度ρdmax/(g·cm-3) 最优含水率wop/% 2.71 17.3 31.1 1.91 12.5 重塑试样按照1.51 g/cm3的干密度、18.6%的含水率进行制样。
试验包括K0预固结及真三轴排水剪切两个阶段。控制试样的吸力为100 kPa，净围压分别为100，200，300 kPa，中主应力参数b值分别为0.25，0.5，0.75，共计9个试样。K0预固结阶段固结稳定的标准如下：在2 h内，试样的竖向位移小于0.01 mm，排水量小于0.01 mL，试验设定剪切速率为0.015 mm/min（该仪器目前所能达到的最小速率），设定轴向应变达到15%为试验结束条件。
试验所用试样为70 mm×70 mm×140 mm的立方体，横观各向同性非饱和土真三轴试样的制样基本过程如下：①配制含水率为18.6%的Q3重塑黄土，按1.51 g/cm3的干密度计算所需湿土的质量，将所需土样平均分为10份放入制样模具中（自行设计加工的内径101 mm，高200 mm的大尺寸制样模具），在压样设备上将重塑黄土按10层均匀压实，各层间接触处必须刮毛；②将制备好的圆柱试样放入图 1所示的大型压力室中，并用侧壁光滑的两瓣模及两个钢环将它固定在大型压力室的底座上，用真三轴仪对试样进行K0预固结，固结过程中试样的轴向荷载控制为200 kPa，两瓣模及两个钢环可严格限制试样的径向位移不变；③K0预固结结束后取出试样，首先将圆柱样大致削成立方体形状，然后在削样器上削成70 mm×70 mm×140 mm的标准真三轴试样；④将削好的试样立即装在真三轴仪上进行试验（见图 2），以免水分散失。
![]()
图 1 大尺寸横观各向同性试样的K0预固结Figure 1. K0-preconsolidation of large-scale transversely isotropic samples横观各向同性非饱和土的真三轴试验对装样要求如下：①试验开始前必须首先饱和陶土板，保证陶土板在试验过程中过水不过气；②将充分饱和后的陶土板立刻放入橡皮膜底部，橡皮膜与陶土板间放有柔性垫片（保证橡皮膜与陶土板之间充分接触，不会发生漏气现象），用螺丝把陶土板紧紧地固定在压力室底座上；③用立方体状的铁皮桶将橡皮膜撑开，轻轻地塞入试样，试样顶端依次放置多孔板（使气压力均匀施加到试样上）、柔性垫片（保证橡皮膜与试样帽之间充分接触，不会发生漏气现象）及试样帽，用螺丝将多孔板、柔性垫片、橡皮膜顶面及试样帽紧紧固定，以免漏气；④安装压力室侧壁，放入柔性液压囊，固定压力室顶盖；⑤安装竖向位移传感器。装样过程需准确、细致且快速，若耗时太长会导致试样吸收底部陶土板的水分，而使得陶土板重新处于非饱和状态，造成较大试验误差[4]。
1.2 试验结果分析
图 3为不同净围压和不同b值条件下偏应力–轴向应变和体应变–轴向应变关系曲线。由图 3可以看出，不同b值下的各应力–应变曲线皆为应变硬化型，且满足双曲线形式。与常规重塑试样一样，当b值一定时，净围压（σ3−ua）越大横观各向同性真三轴试样的硬化趋势越明显，相同净围压下，b值越大试样的偏应力越大，硬化趋势越明显。b=0.5和净围压为300 kPa的试样以及b=0.75和净围压为100，200，300 kPa的试样均未达到剪切破坏标准（轴向应变为15%）就已破坏。这是由于剪切过程中b值越大，σ2方向的应力增长得越快，而柔性液压囊的承受力有限，往往σ2方向的应力达到830 kPa左右甚至更小时，该方向的液压囊便会被水压涨破，σ2迅速较小至0 kPa，试验被迫停止。
![]()
图 3 真三轴固结排水剪切试验q–εa及εv–εa关系曲线Figure 3. q–εa and εv–εa curves of true triaxial consolidated drained shear tests由图 3可知，所有的试样在剪切过程中均处于剪缩状态。除b=0.5的试样，其余试样的体应变–轴向应变关系曲线变化较为规律，净围压越大试样的体应变越大，b=0.75时，净围压对试样体应变的影响更为显著。b=0.5时的3个试样的体应变–轴向应变关系曲线存在交叉现象，轴向应变达到9%之前，各试样的体应变相差不大，曲线几乎重合，轴向应变超过10%后，净围压100 kPa试样的体应变逐渐较小，剪缩趋势略有减弱，净围压300 kPa试样的体应变增长较快，但由于液压囊破坏，未能测得试样破坏时的体应变。相同净围压下，并非b值越大试样的体应变越大。这主要是由试样在σ2，σ3两个方向的体积变化不均匀导致的，当b值较大时试样σ2方向的两个对立面往往被压得凹进去，而σ3方向的两个对立面却被挤得凸出来，不过试样整体还是处于体缩状态。
图 4是同一吸力下（100 kPa），不同净围压和不同b值条件下的含水率–轴向应变关系曲线。由图 4可知，排水剪切过程中，试样含水率的变化较为规律，试样的含水率在剪切过程中不断减小，试样破坏前含水率–轴向应变关系可用直线近似拟合。相同b值下，净围压为100 kPa和200 kPa的试样含水率–轴向应变关系线的斜率相似，均略小于净围压为300 kPa时试样的相应斜率，说明净围压增大有助于试样内水分的排出。但总体上，不同净围压下各曲线斜率相差不大，有可能与剪切速率较快有关，剪切速率较快时，试样中的水分来不及充分排出。
2. 真三轴条件下横观各向同性非饱和黄土的固结不排水剪切试验
应变速率是影响土体强度特性指标的主要因素之一[14-16]，为了研究不同的加载速率对横观各向同性非饱和土体的影响，本节进行了6个真三轴固结不排水剪切试验。试验用土仍为延安新区工地现场的Q3重塑黄土，重塑试样按照1.51 g/cm3的干密度、18.6%的含水率进行制样。控制气压力为100 kPa，净围压为100 kPa，b值分别为0.25，0.5（为保证液压囊不被涨破，气压力、净围压、b值均取较小值），速率分别为0.015，0.03，0.05 mm/min。设定轴向应变达到15%为试验结束条件。
图 5为不同加载速率下试样的偏应力–轴向应变关系曲线和体应变–轴向应变关系曲线。对比图 3（a），（b）可以看出，相同净围压、相同吸力、相同b值条件下，排水剪切试验试样的偏应力均大于不同加载速率下不排水剪切试验试样的偏应力。
![]()
图 5 真三轴不排水试验的q–εa及εv–εa关系曲线Figure 5. q–εa and εv–εa curves of true triaxial undrained tests由图 5可知，不同加载速率下试样的偏应力–轴向应变整体的变化形态较为相似，均表现出应变硬化特性，没有峰值出现。剪切刚开始时，不同加载速率的几条曲线存在交叉现象，剪切过程中，净围压和b值相同时，加载速率为0.015 mm/min的试样偏应力最大，加载速率为0.03 mm/min的试样偏应力最小，加载速率为0.05 mm/min的试样偏应力介于中间。可见加载速率对曲线的基本形态并没有多大影响，但是对试样的刚度有一定影响，这种影响效应也不是单调的，并非加载速率越小，试样的偏应力越大，而是有可能存在临界加载速率。
由图 5还可以看出，剪切过程中各试样均处于剪缩状态。除b=0.25和加载速率为0.03 mm/min的试样外，其余各试样的体应变–轴向应变关系曲线均存在峰值点。b=0.25时，加载速率为0.03 mm/min的试样体缩程度最大，加载速率为0.05 mm/min的试样体缩程度最小，加载速率为0.015 mm/min的试样介于两者之间。b=0.5时，不同加载速率下各试样的体应变不存在单调关系，但剪切破坏时加载速率为0.03 mm/min的试样的体应变最大，其他两试样在剪切破坏时的体应变几乎相等。
图 6为相同净围压、不同加载速率下试样的吸力s与偏应力q之间的关系曲线。由图 6可知，随着偏应力的增大，吸力均逐渐减小。由图 5可知，剪切过程中试样一直处于剪缩状态，由于试样在真三轴剪切过程中体积不断缩小，饱和度随着偏应力的增大而增大，故孔隙水压力增大，吸力不断减小。从图 6可以看出，真三轴条件下试样的初始吸力变化范围为44.2~50.1 kPa。b=0.25时，加载速率为0.015，0.05 mm/min的试样的吸力–偏应力关系曲线发展形态略微相似。加载速率为0.05 mm/min的试样的吸力最大，加载速率分别为0.015，0.03 mm/min的两条曲线相交。b=0.5时，3个加载速率下试样的吸力–偏应力关系曲线整体的变化形态也存在相似之处，偏应力较小时吸力缓慢减小，而后吸力减小速率有所加快。另外，加载速率较快时，孔隙水压力没有足够的时间分布均匀，故不同的加载速率下，试样的吸力变化没有很好的规律性。
综上可见，剪切速率对不排水试验的应力–应变曲线和吸力演化的影响显著，从试验采用的三个剪切速率尚不能选出一个对各方面都影响较小的合适速率，这个问题有待今后进一步研究。
3. 结论
（1）真三轴固结排水剪切试验中各应力–应变曲线皆为硬化型，且满足双曲线形式，当b值一定时，净围压越大试样的硬化趋势越明显，相同净围压下，b值越大试样的硬化趋势越明显；所有的试样在剪切过程中均处于剪缩状态，同一b值下，净围压越大试样的体应变越大；随着剪切的发展试样的含水率不断减小，试样破坏前轴向应变–含水率关系曲线可用直线近似拟合。
（2）真三轴固结不排水剪切试验中，加载速率对应力–应变曲线的基本形态并没有多大影响，但是对试样的刚度有一定影响，这种影响效应也不是单调的，有可能存在临界加载速率。另外，加载速率较快时，孔隙水压力没有足够的时间分布均匀，故不同的加载速率下，试样的吸力变化虽略有相似之处，但没有很好的规律性。
-
![]()
图 1 大石门水利枢纽沥青混凝土心墙坝标准横剖面图
Figure 1. Standard horizontal section of sand-gravel dam with asphalt concrete core wall of Dashimen project
![]()
图 2 上游砂砾填筑料干密度一维威布尔分布拟合
Figure 2. One-dimensional Weibull distribution fitting of dry density in upstream sand-gravel materials
![]()
图 3 上游砂砾填筑料砾石含量一维威布尔分布拟合
Figure 3. One-dimensional Weibull distribution fitting of gravel content in upstream sand-gravel materials
![]()
图 4 上游砂砾填筑料曲率系数一维威布尔分布拟合
Figure 4. One-dimensional Weibull distribution fitting of curvature coefficient in upstream sand-gravel materials
![]()
图 5 上游砂砾填筑料最大粒径一维威布尔分布拟合
Figure 5. One-dimensional Weibull distribution fitting of maximum particle size in upstream sand-gravel materials
![]()
图 6 下游砂砾填筑料干密度一维威布尔分布拟合
Figure 6. One-dimensional Weibull distribution fitting of dry density in downstream sand-gravel materials
![]()
图 7 下游砂砾填筑料砾石含量一维威布尔分布拟合
Figure 7. One-dimensional Weibull distribution fitting of gravel content in downstream sand-gravel materials
![]()
图 8 下游砂砾填筑料曲率系数一维威布尔分布拟合
Figure 8. One-dimensional Weibull distribution fitting of curvature coefficient in downstream sand-gravel materials
![]()
图 9 下游砂砾填筑料最大粒径一维威布尔分布拟合
Figure 9. One-dimensional Weibull distribution fitting of maximum particle size in downstream sand-gravel materials
![]()
图 10 上游砂砾填筑料三维威布尔分布拟合
Figure 10. Three-dimensional Weibull distribution fitting of upstream sand-gravel materials
![]()
图 11 下游砂砾填筑料三维威布尔分布拟合
Figure 11. Three-dimensional Weibull distribution fitting of downstream sand-gravel materials
![]()
图 12 心墙上下游过渡料三维威布尔分布拟合
Figure 12. Three-dimensional Weibull distribution fitting of upstream and downstream transition materials on core wall
![]()
图 13 岸坡过渡料三维威布尔分布拟合
Figure 13. Three-dimensional Weibull distribution fitting of transition materials on bank slope
表 1 试验数据相关性分析
Table 1 Correlation analysis of test data
填料区 相关系数r 砾石含量/% 含泥量(小于0.075 mm)/% 曲率系数Cc 不均匀系数Cu 最大粒径/mm 含水率/% 上游砂砾填筑料 干密度/(g·cm-3) 0.665 -0.028 0.522 -0.004 0.331 -0.123 下游砂砾填筑料 干密度/(g·cm-3) 0.793 0.015 0.441 -0.076 0.473 0.027 心墙上下游过渡料 干密度/(g·cm-3) 0.363 -0.093 0.193 0.003 0.020 -0.036 岸坡过渡料 干密度/(g·cm-3) 0.527 -0.144 0.312 -0.038 -0.025 0.010 
下载: 导出CSV
表 2 上游砂砾填筑料级配威布尔分布模型参数
Table 2 Parameters of Weibull distribution model for gradation of upstream sand-gravel materials
统计指标 样本总数n 位置参数μ 尺度参数σ 形状参数ξ 相关系数r 显著性水平α 临界值D (n，α) Dn 估计值F(N) 干密度/(g·cm-3) 453 2.256 0.124 7.824 0.989 0.05 0.0639 0.0384 2.349 砾石含量/% 345 64.000 10.759 5.691 0.998 0.05 0.0732 0.0534 71.245 曲率系数 345 1.500 3.369 2.314 0.988 0.05 0.0732 0.0259 2.774 最大粒径/mm 345 160.000 159.674 2.856 0.996 0.05 0.0732 0.0564 232.621
下载: 导出CSV
表 3 下游砂砾填筑料级配威布尔分布模型参数
Table 3 Parameters of Weibull distribution model for gradation of downstream sand-gravel materials
统计指标 样本总数n 位置参数μ 尺度参数σ 形状参数ξ 相关系数r 显著性水平α 临界值D (n，α) Dn 估计值F(N) 干密度/(g·cm-3) 473 2.016 0.364 19.533 0.984 0.05 0.0625 0.0437 2.341 砾石含量/% 473 57.967 16.907 7.580 0.997 0.05 0.0625 0.0492 70.532 曲率系数 358 1.231 3.469 2.184 0.994 0.05 0.0719 0.0418 2.507 最大粒径/mm 473 110.434 213.426 3.560 0.993 0.05 0.0625 0.0581 223.851
下载: 导出CSV
表 4 不同填料区三维威布尔分布模型的K-S检验
Table 4 K-S tests of three-dimensional Weibull distribution models in different packing areas
填料区 样本数n 显著性水平α 临界值D (n，α) Dn 上游砂砾填筑料 11 0.05 0.391 0.3093 下游砂砾填筑料 11 0.05 0.391 0.2976 心墙上下游过渡料 11 0.05 0.391 0.3424 岸坡过渡料 11 0.05 0.391 0.3137
下载: 导出CSV
-
[1] 杨玉生, 赵剑明, 王龙, 等. 级配特征对筑坝砂砾料填筑标准的影响[J]. 水利学报, 2019, 50(11): 1374–1383. doi: 10.13243/j.cnki.slxb.20190547 YANG Yu-sheng, ZHAO Jian-ming, WANG Long, et al. Influence of gradation characteristics on filling standard of sand gravel material for dam construction[J]. Journal of Hydraulic Engineering, 2019, 50(11): 1374–1383. (in Chinese) doi: 10.13243/j.cnki.slxb.20190547
[2] 谢定松, 蔡红, 魏迎奇, 等. 覆盖层不良级配砂砾石料渗透稳定特性及影响因素探讨[J]. 水利学报, 2014, 45(增刊2): 77–82. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB2014S2013.htm XIE Ding-song, CAI Hong, WEI Ying-qi, et al. Discussion of seepage stability characteristic of bad graded sand and gravel overlay[J]. Journal of Hydraulic Engineering, 2014, 45(S2): 77–82. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB2014S2013.htm
[3] 李炎隆, 唐旺, 温立峰, 等. 沥青混凝土心墙堆石坝地震变形评价方法及其可靠度分析[J]. 水利学报, 2020, 51(5): 580–588. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202005009.htm LI Yan-long, TANG Wang, WEN Li-feng, et al. Dam seismic deformation evaluation method of asphalt concrete core rockfill dam and its reliability analysis[J]. Journal of Hydraulic Engineering, 2020, 51(5): 580–588. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202005009.htm
[4] 褚福永, 朱俊高. 砂卵砾石料强度及变形大型三轴试验研究[J]. 水力发电学报, 2014, 33(6): 209–214. https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201406032.htm CHU Fu-yong, ZHU Jun-gao. Large-scale triaxial test study of strength and deformation behaviors of sand-grained materials[J]. Journal of Hydroelectric Engineering, 2014, 33(6): 209–214. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SFXB201406032.htm
[5] 任秋兵, 李明超, 杜胜利, 等. 筑坝堆石料抗剪强度间接测定模型与实用计算公式研究[J]. 水利学报, 2019, 50(10): 1200–1213. doi: 10.13243/j.cnki.slxb.20190501 REN Qiu-bing, LI Ming-chao, DU Sheng-li, et al. Mathematical model and practical formula for indirect determination of shear strength of dam rockfill materials[J]. Journal of Hydraulic Engineering, 2019, 50(10): 1200–1213. (in Chinese) doi: 10.13243/j.cnki.slxb.20190501
[6] 张昭, 程靖轩, 刘奉银, 等. 基于颗粒级配参数描述砂土持水及非饱和强度特性的土壤转换函数[J]. 水利学报, 2020, 51(4): 479–491. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202004011.htm ZHANG Zhao, CHENG Jing-xuan, LIU Feng-yin, et al. Pedotransfer functions to describe water retention and unsaturated strength behaviors of sandy soils based on particle size parameters[J]. Journal of Hydraulic Engineering, 2020, 51(4): 479–491. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB202004011.htm
[7] 李罡, 刘映晶, 尹振宇, 等. 粒状材料临界状态的颗粒级配效应[J]. 岩土工程学报, 2014, 36(3): 452–457. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15664.shtml LI Gang, LIU Ying-jing, YIN Zhen-yu, et al. Grading effect on critical state behavior of granular materials[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(3): 452–457. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15664.shtml
[8] 蒋明镜, 郑敏, 王闯, 等. 不同颗粒级配的某火山灰的力学性质试验研究[J]. 岩土力学, 2009, 30(增刊2): 64–66. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2009S2015.htm JIANG Ming-jing, ZHENG Min, WANG Chuang, et al. Experimental investigation on mechanical properties of a volcanic ash with different grain size gradations[J]. Rock and Soil Mechanics, 2009, 30(S2): 64–66. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2009S2015.htm
[9] 朱晟, 钟春欣, 郑希镭, 等. 堆石体的填筑标准与级配优化研究[J]. 岩土工程学报, 2018, 40(1): 108–115. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17259.shtml ZHU Sheng, ZHONG Chun-xin, ZHENG Xi-lei, et al. Filling standards and gradation optimization of rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(1): 108–115. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17259.shtml
[10] 朱晟, 邓石德, 宁志远, 等. 基于分形理论的堆石料级配设计方法[J]. 岩土工程学报, 2017, 39(6): 1151–1155. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16941.shtml ZHU Sheng, DENG Shi-de, NING Zhi-yuan, et al. Gradation design method for rockfill materials based on fractal theory[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(6): 1151–1155. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16941.shtml
[11] 朱俊高, 郭万里, 王元龙, 等. 连续级配土的级配方程及其适用性研究[J]. 岩土工程学报, 2015, 37(10): 1931–1936. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16360.shtml ZHU Jun-gao, GUO Wan-li, WANG Yuan-long, et al. Equation for soil gradation curve and its applicability[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(10): 1931–1936. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16360.shtml
[12] 黄达, 曾彬, 王庆乐. 粗粒土孔隙比及级配参数与渗透系数概率的相关性研究[J]. 水利学报, 2015, 46(8): 900–907. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201508003.htm HUANG Da, ZENG Bin, WANG Qing-le. Study on probabilistic relation between permeability coefficient and void ratio and grain composition of coarse grained soils using Copula theory[J]. Journal of Hydraulic Engineering, 2015, 46(8): 900–907. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201508003.htm
[13] 宫凤强, 李夕兵, 邓建. 小样本岩土参数概率分布的正态信息扩散法推断[J]. 岩石力学与工程学报, 2006, 25(12): 2559–2564. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200612030.htm GONG Feng-qiang, LI Xi-bing, DENG Jian. Probability distribution of small samples of geotechnical parameters using normal information spread method[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(12): 2559–2564. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200612030.htm
[14] 雷刚. Weibull分布寿命数据的参数估计[D]. 武汉: 华中科技大学, 2006. LEI Gang. Parameter Estimation of Lifetime Data in Weibull Distribution[D]. Wuhan: Huazhong University of Science and Technology, 2006. (in Chinese)
[15] WEIBULL W. A statistical distribution function of wide applicability[J]. Journal of Applied Mechanics, 1951, 18(3): 293–297.
[16] KIRCHNER H P, GRUVER R M, SOTTER W A. Fracture stress-mirror size relations for polycrystalline ceramics[J]. Philosophical Magazine, 1976, 33(5): 775–780.
[17] TALREJA R. Estimation of weibull parameters for composite material strength and fatigue life data[J]. ASTM STP, 1981: 291–311.
[18] 蒋仁言. 威布尔模型族: 特性、参数估计和应用[M]. 北京: 科学出版社, 1999. JIANG Ren-yan. Characteristics, Parameter Estimation and Application of Weibull Model Family[M]. Beijing: Science Press, 1999. (in Chinese)
[19] 罗哉, 王艳, 王岚晶, 等. 基于三参数威布尔分布的自动调整臂服役可靠性研究[J]. 计算机测量与控制, 2017, 25(3): 234–236, 247. https://www.cnki.com.cn/Article/CJFDTOTAL-JZCK201703063.htm LUO Zai, WANG Yan, WANG Lan-jing, et al. Service reliability research of automatic brake adjuster based on weibull distribution of three parameters[J]. Computer Measurement & Control, 2017, 25(3): 234–236, 247. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZCK201703063.htm
[20] 金星, 陈景鹏, 文明, 等. 威布尔分布产品参数估计极大似然优化方法[J]. 装备指挥技术学院学报, 2003, 14(5): 46–48. https://www.cnki.com.cn/Article/CJFDTOTAL-XYZH200305012.htm JIN Xing, CHEN Jing-peng, WEN Ming, et al. Optimized maximum likelihood estimation method of parameters estimation for weibull distributed item[J]. Journal of Institute of Command and Technology, 2003, 14(5): 46–48. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XYZH200305012.htm
[21] BANARD A, BOSI-LEVENBACH E C. "Het uitzetten van waarnemingen op waarsechijnlijkdeids-papier" (The Plotting of observations on probability paper)[J]. Statistica Neerlandica, 1953(7): 163–173.
[22] 刘哲, 李琦, 任鲁川, 等. 基于三参量威布尔分布的潜在震源区强震危险性估计[J]. 震灾防御技术, 2017, 12(2): 346–353. https://www.cnki.com.cn/Article/CJFDTOTAL-ZZFY201702011.htm LIU Zhe, LI Qi, REN Lu-chuan, et al. Estimation of the strong earthquake risk in potential seismic source based on 3-parameter weibull distribution[J]. Technology for Earthquake Disaster Prevention, 2017, 12(2): 346–353. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZZFY201702011.htm
[23] 刘子娟, 郑学斌, 郭小军. 应用MS Excel求解三参数威布尔分布函数的参数估计[J]. 机械工程师, 2020(2): 117–119, 124. https://www.cnki.com.cn/Article/CJFDTOTAL-JXGU202002054.htm LIU Zi-juan, ZHENG Xue-bin, GUO Xiao-jun. Parameter estimation of three-parameter weibull distribution function using MS excel[J]. Mechanical Engineer, 2020(2): 117–119, 124. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JXGU202002054.htm
[24] 朱晟, 宁志远, 钟春欣, 等. 考虑级配效应的堆石料颗粒破碎与变形特性研究[J]. 水利学报, 2018, 49(7): 849–857. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201807009.htm ZHU Sheng, NING Zhi-yuan, ZHONG Chun-xin, et al. Study on particle crush and deformation characteristics considering rockfill gradation effect[J]. Journal of Hydraulic Engineering, 2018, 49(7): 849–857. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201807009.htm
[25] 刘德辅, 谢波涛, 伍远康, 等. 台风诱发暴雨降水量的概率预测[J]. 中国海洋大学学报(自然科学版), 2007, 37(6): 1027–1033. https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY200706032.htm LIU De-fu, XIE Bo-tao, WU Yuan-kang, et al. Probability prediction of typhoon-induced rainfall[J]. Periodical of Ocean University of China, 2007, 37(6): 1027–1033. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY200706032.htm
[26] 刘德辅, 姜昊. 台风诱发暴潮极端潮位的预测方法[J]. 中国海洋大学学报(自然科学版), 2009, 39(3): 516–520. https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY200903028.htm LIU De-fu, JIANG Hao. Prediction method of extreme sea level induced by typhoon[J]. Periodical of Ocean University of China, 2009, 39(3): 516–520. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY200903028.htm
[27] 刘德辅, 韩凤亭, 庞亮, 等. 台风作用下核电站海岸防护标准的概率分析[J]. 中国海洋大学学报(自然科学版), 2010, 40(6): 140–146. https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY201006024.htm LIU De-fu, HAN Feng-ting, PANG Liang, et al. Probabilistic approach of coastal defense against typhoon attacks for nuclear power plant[J]. Periodical of Ocean University of China, 2010, 40(6): 140–146. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY201006024.htm
[28] 刘德辅, 王莉萍, 庞亮. 多维复合极值分布理论在极端海况概率预测中的应用[J]. 科学通报, 2006(9): 1112–1116. https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB200609019.htm LIU De-fu, WANG Li-ping, PANG Liang. Application of multidimensional composite extreme value distribution theory in probability prediction of extreme Sea state[J]. Chinese Science Bulletin. 2006(9): 1112–1116. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-KXTB200609019.htm
[29] LIU DF, WANG L P, PANG L Theory of multivariate compound extreme value distribution and its application to extreme sea state prediction[J]. Chinese Science Bulletin, 2006, 51(23): 2926–2930.
[30] LIU D F, PANG L, XIE B T. Typhoon disaster in China: prediction, prevention, and mitigation[J]. Natural Hazards, 2009, 49(3): 421–436.
[31] LIU D F, PANG L, XIE B T, et al. Typhoon disaster zoning and prevention criteria—A double layer nested multi-objective probability model and its application[J]. Science in China Series E: Technological Sciences, 2008, 51(7): 1038–1048.
[32] 史道济, 孙炳堃. 嵌套Logistic模型的矩估计[J]. 系统工程理论与实践, 2001, 21(1): 53–60. https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL200101010.htm SHI Dao-ji, SUN Bing-kun. Moment estimation in a nested logistic model[J]. Systems Engineering-Theory & Practice, 2001, 21(1): 53–60. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XTLL200101010.htm
[33] JUSTEL A, PEÑA D, ZAMAR R. A multivariate Kolmogorov-Smirnov test of goodness of fit[J]. Statistics & Probability Letters, 1997, 35(3): 251–259.
[34] 李申, 赵润东, 宋岳庭, 等. 相关性分析、聚类分析、因子分析的可靠性对比: 以嘎拉勒和躬琼左波两条剖面为例[J]. 地质与勘探, 2018, 54(3): 574–583. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKT201803014.htm LI Shen, ZHAO Run-dong, SONG Yue-ting, et al. Reliability comparison of correlation, clustering and factor analyses for lithogeochemistry: examples of two profiles in galale and gongqiongzuobo, Tibet[J]. Geology and Exploration, 2018, 54(3): 574–583. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZKT201803014.htm
计量
- 文章访问数: 151
- HTML全文浏览量: 26
- PDF下载量: 28
