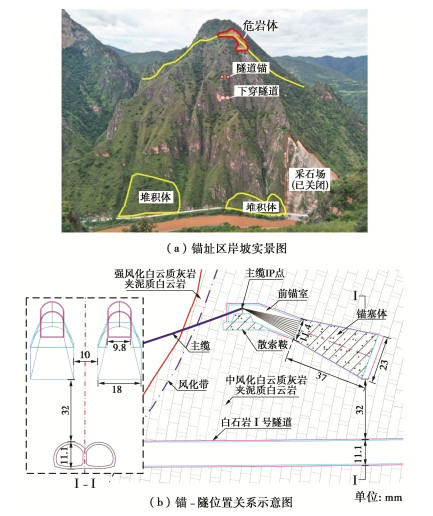
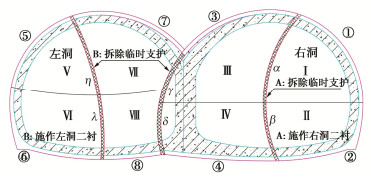
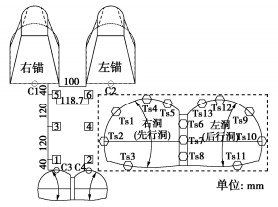
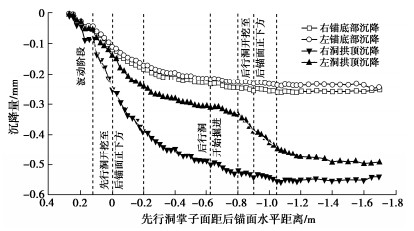
Model tests on interaction between tunnel-type anchorage and underpass tunnel
-
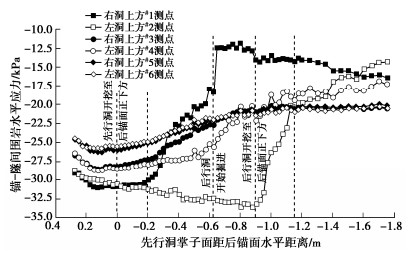
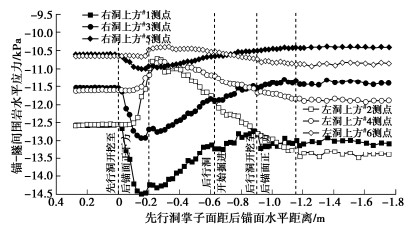
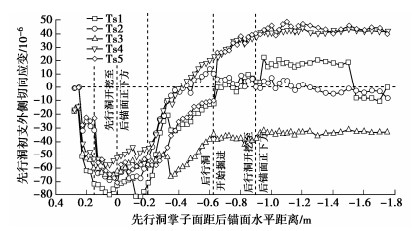
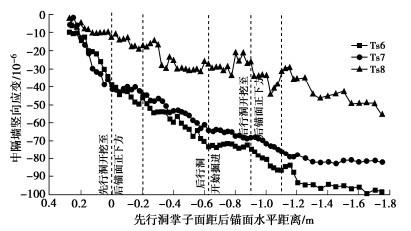
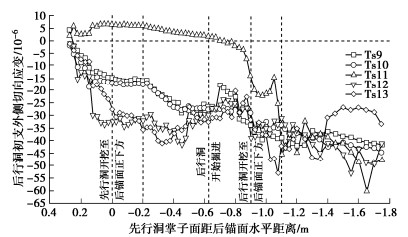
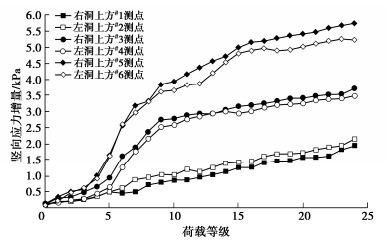
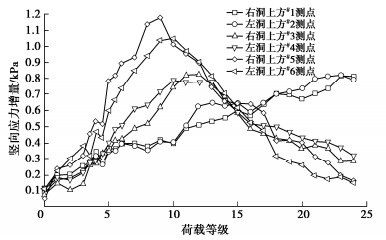
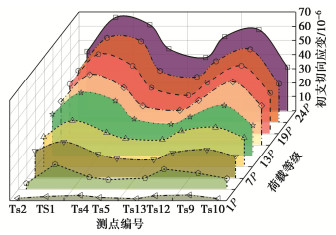
摘要: 为研究下穿隧道近接施工对上部隧道锚力学响应特征的影响及隧道锚承载阶段下穿隧道受力特点，以玉楚高速白石岩Ⅰ号隧道下穿绿汁江大桥楚雄岸隧道锚工程为研究对象，开展了隧道锚与下穿隧道间相互影响规律的1∶100室内模型试验研究。研究表明：①锚塞体沉降主要由下穿隧道先行洞开挖导致，后行洞掘进对锚塞体的扰动不明显。②锚-隧间围岩的应力经历“应力集中—应力转移—趋于稳定”3个发展阶段，围岩水平应力发生急剧变化的时间要早于竖向应力。③隧道开挖过程中初支承载作用明显，随着隧道临时支护的拆除，初支承担的围岩压力逐渐转向中隔墙。④施加主缆拉力的隧道锚会使锚–隧间部分围岩进入塑性状态，并导致下穿隧道拱肩和拱顶处产生较大的拉应力。Abstract: In order to study the influences of approaching construction between underpass tunnel and tunnel-type anchorage on the mechanical characteristics as well as the stress characteristics of the underpass tunnel in the bearing stage of the tunnel-type anchorage, taking the project of Baishiyan tunnel Ⅰ under the tunnel-type anchorage of Lüzhijiang bridge of Yuxi-Chuxiong Expressway as the research object, a 1∶100 scaled model test is carried out. The main conclusions are drawn as follows: (1) The settlement of the anchor plug is mainly caused by the excavation of the advanced tunnel of the multi-arch tunnel, and the disturbance by the following tunnel excavation is not obvious. (2) The stress of the surrounding rock between anchorage and tunnel has experienced three development stages: stress concentration, stress transfer and stabilization. The time of abrupt change of the horizontal stress of the surrounding rock is earlier than that of the vertical stress. (3) The bearing effect of the initial support is obvious during tunnel excavation. With the removal of temporary support, the pressure of the surrounding rock borne by the initial support gradually turns to the middle wall. (4) When the cable tension is applied to anchorage, the surrounding rock between anchorage and tunnel will enter the plastic state, and leading to large tensile stress at the spandrel and vault of the tunnel.
-
0. 引言
在历次地震中,因地基液化导致建筑结构、桥梁、交通设施等构筑物发生严重破坏的记录屡见不鲜,其中因饱和砂土液化引起的土层大变形是造成地下工程结构震害加剧的重要原因之一[1]。地铁作为城市地下空间开发与交通出行的核心基础设施,其抗震安全已成为韧性城市建设和区域防灾工作的重要组成部分。
目前,国内外学者在进行地铁地下结构抗震性能研究时,一般通过原位观测或模型试验的手段定性揭示体系的地震反应规律、解释相互作用机制、推演损伤灾变过程、再现真实震害现象,在此基础上建立能够合理反映其动力相互作用的数值分析模型,进而发展相应的模拟仿真方法,并通过进一步的理论分析、模型试验或现场测试加以验证,以期提出合理的抗震设计、分析及评价方法[2]。然而,受真实震害记录、原位测试条件、足尺试验难度及投入成本等客观因素的制约,模型试验仍是现阶段分析地下结构动力特性的有效方法。振动台模型试验（1g振动台试验和离心机振动台试验）是研究土-地下结构地震动力响应规律的主要手段,通过该技术所进行的试验研究取得了长足进步,其中关于结构外形轮廓相对简单的地铁车站和区间隧道成果最为丰富,Chen等[3]、Kheradi等[4]、Yan等[5]和陈国兴等[6]分别以不同规模的多层多跨框架式地铁车站结构为对象,揭示了复杂场地-地铁车站动力相互作用的地震反应规律和灾变机理；Chian等[7]、Tsinidis等[8]和许成顺等[9]通过构建缩尺比例较大的离心机模型试验,以不同角度探讨了各类地下结构的动力损伤特性及其破坏机制。此外,根据实际工程建设需要,一些外形较为新颖、受力相对复杂的地铁车站结构也陆续引起了学者们的关注,如中庭式[10]、装配式[11]、纵向变截面型[12]等,研究成果为复杂地下结构工程的相互作用问题提供了有力指导。
现有研究表明,地下结构在地震中发生破坏的主要原因是源于周围土体的大变形,结构外形、尺寸的变化不会改变土体变形为主导的作用本质。随着地铁与周边建筑的联系越来越紧密,一种上宽、下窄型的异跨地铁车站日益增多。与此同时,施作地下连续墙是地铁工程建设中基坑维护的常见工序,工程完工后一般将作为永久性构筑物附于车站结构两侧,结构的外部轮廓及其对整体抗侧刚度产生明显改变的附属构筑物都会对主体抗震性能、变形性态、破坏特征及周边地基地震反应规律等产生显著影响[13]。然而,现有关于大型地铁地下结构抗震性能方面的试验研究多将地下车站视为埋置于场地中的单体结构且多为典型多层多跨框架形式,难以考虑地连墙的现实存在及异跨特殊外形对周围场地液化特征及结构地震响应所引起的改变,因而此类具有特殊断面形式的大型复杂地下结构体系动力反应规律还有待进一步探讨。
本文以饱和砂土-地下连续墙-异跨地铁车站结构地震反应特征及地基液化后的失效模式为研究目的,设计并开展了可液化场地中带地连墙异跨地铁车站结构的大型振动台模型试验,介绍了试验方案细节,基于试验结果对不同加载条件下模型体系的地震反应进行分析,研究了该相互作用体系的动力反应规律,研究结论和相关结果对提高此类大型地铁工程建设和抗震设计的认识提供了合理参考。
1. 大型振动台模型试验概况
1.1 试验设备与相似比设计
本次试验在南京工业大学江苏省土木工程与防灾减灾重点实验室开展,采用设备为MTS单向电液伺服加载地震模拟振动台及配套控制系统,振动台加载设备的台面尺寸为3.36 m×4.86 m,最大载重25 t,工作频率范围0.1～50 Hz,水平向峰值加速度±1.0g,最大位移±120 mm。试验采用的矩形框架叠层式剪切模型箱尺寸为3.5 m×2.0 m×1.7 m,较传统刚性箱与柔性箱而言,该模型箱能有效减小模型地基场域的边界效应,降低有限边界带来的地震波反射及散射影响,保证动态数据采集的置信程度。该剪切箱在水平激振方向上的基频为1.515 Hz,阻尼比为4.09%,而地震作用下土体的阻尼比一般为5%～25%。因此,所采用的剪切箱不会给模型土的地震反应带来不良影响[14]。
在进行相似比设计时,通过考虑土-结构耦合的模型体系设计方法分别对模型结构和模型地基进行计算,模型结构选取长度、弹性模量、加速度作为基本物理量,模型地基选取剪切波速、密度、加速度为基本物理量,其他相似指标则根据Bockingham-π定理推导得出,模型地基土的几何相似比是由模型场地和原型场地的剪切波速确定,输入地震动持时宜以模型地基为主,由早期类似试验结果可知模型液化场地的剪切波速约为原型场地的一半。根据已有研究[15],在涉及可液化场地的振动台试验中,地震动持时若严格按照模型地基的时间相似比进行压缩,则将对液化地基在地震荷载下的动力响应产生显著影响,甚至场地有可能不会发生液化,而采用未经压缩的原始地震动持时进行激励输入的试验结果或将更为理想。因此,为保证地基液化效果,本次试验输入地震动采用原始持时记录,模型系统两种介质各物理量间的相似关系及相似比值如表1所示。
表 1 振动台试验体系相似比设计Table 1. Similarity ratios of shaking table test system类型 物理量 相似关系 相似比 模型结构 模型地基 几何特征 长度l Sl 1/30 1/4 惯性矩I SI = Sl4 1.23×10-6 — 位移u Su = Sl 1/30 1/4 材料特征 等效密度ρ Sρ = SE/(SaSl) 7.5 1 质量m Sm = SESl2/Sa 2.77×10-4 — 弹性模量E SE 1/4 — 应力σ Sσ = SεSE 1/4 — 应变ε Sε 1 — 剪切波速Vs Sv — 1/2 剪切模量G SG — 1/4 有效覆土压力σz Sσ = SlSgSρ — 1/4 动力特征 输入振动持时t St = (Sl/Sa)1/2 1/5.4794 1 输入振动加速度a Sa 1 1 频率ω Sω = 1/St 5.4794 2 孔隙水压力u Su = SlSaSρ — 1/4 1.2 模型结构与模型地基制作
本次试验模型结构以地下连续墙-异跨地铁车站体系为原型,根据试验相似比要求并通过对地铁车站节点进行适当简化,缩尺比例为1/30的带地连墙异跨地铁车站模型主体横截面尺寸如图1（a）所示。
![]()
图 1 异跨地铁车站模型结构横截面尺寸及模型结构体系Figure 1. Cross-sectional dimensions of unequal-span subway station and preparation of model structure system微粒混凝土采用的设计配合比为水∶水泥∶石灰∶粗砂＝0.5∶1∶0.58∶5[6],测得其标准养护条件（标准温度20℃±2℃、相对湿度95%以上）下边长70.7 mm立方体28 d龄期抗压强度为7.5 MPa,弹性模量为7.9 GPa；以镀锌钢丝模拟结构中的钢筋,原型结构中选用的钢筋直径为12～32 mm,模型结构中选用的镀锌钢丝直径为0.7～2.0 mm,侧墙和楼板分布钢筋采用定制成品镀锌钢丝网片。分别采用聚苯乙烯泡沫和木板制作形成模型结构内、外模板,之后按照预定流程完成车站结构的浇筑,制作完成的地铁车站主体结构上层宽度为1050 mm,下层宽度为630 mm,结构总高度为446 mm,纵向长度为1430 mm。结构达到养护龄期脱模进行表面处理后,结合模型箱的竖向尺寸,地连墙沿深度方向取值为500 mm,墙体采用20 mm厚有机玻璃板模拟,结构与地连墙之间通过高强结构胶粘接,实现叠合式地连墙构造。地下结构的地震反应主要受制于周围土体的大变形,其本身的惯性力作用并非主导因素,同时,限于模型结构的大缩尺比条件,采用人工质量的完全配重法难以实现[2]。因此,在考虑模型体系配重时,可结合模型结构自身承载能力、尺寸、传感器及配重块空间需求等因素使用欠人工质量模型法在结构各层均匀布置质量块,对结构进行不完全人工配重时每跨沿纵向均布铅块16 kg,总配重质量128 kg。模型内部传感器、照明系统、配重等完成布置后将导线引出,结构两端采用软质PVC塑料透明薄膜进行密封,周边缝隙填充防水胶粘接牢固,模型结构体系的制备过程如图1（b）所示。
可液化场地的振动台试验以令模型场地达到液化为目标,结合模型结构在场地液化过程中的反应特征总结规律,通常以饱和砂土来模拟可液化地基层,并在其上部覆盖一定厚度的黏土来模拟上覆不排水层。本次试验模型地基土分为2层,上层为150 mm厚黏土层,下层为1400 mm厚南京细砂层,试验用土均取自南京本地,土样经人工晒干、去杂、捣碎、过筛去块等步骤后留置备用。模型地基饱和液化砂土层采用水沉法进行制备,每层土制备高度控制在200 mm左右,每层土制备完成后,均用光滑木板将土层表面扫平,再继续装填下一层土；当地基填筑至传感器或结构底板标高时,采用人员吊装的方式布置加速度传感器和安装结构；地连墙嵌入土体部分采用预置木板成槽并辅以人工吊装就位。由于模型车站为上宽下窄型结构,在安置好结构后悬挑跨正下方的砂土层不易填实,可采用人工方法从侧边小心捣入砂土；当砂土层填筑至预定高度时铺设表层黏土层,黏土层填筑完毕后加水漫过地表以使土层充分饱和,模型地基装填结束静置固结2 d后,抽走箱内多余存水方可开始进行试验,模型地基的填筑过程如图2所示。试验前,对模型地基选用填土进行室内试验测定,地基表层粉质黏土的密度为1.68 g/cm3,液限为33.81%,塑限为17.53%；地基下层南京细砂的粒径主要分布范围为0.075～1.0 mm,粒径小于0.075 mm的颗粒含量为0.27%,相对密度为2.66,最大干密度为1.59 g/cm3,根据土工试验规范,本次模型地基砂土密实状态为松散。
1.3 试验测点布置与加载方案
根据此次振动台试验目的,模型地基主要量测指标为场地的加速度、孔隙水压力、水平位移和地表沉降等,在地连墙-异跨地铁车站模型结构上沿轴向共设置3个观测面,其中跨中截面为主观测面,参照模型结构相应截面位置,沿结构纵向在模型地基中共设置2个观测面,其中跨中截面为主观测面,模型地基观测面及测点布置如图3所示。
试验共设置加速度计15只,孔压计14只,土压力计5只,激光位移计3只,电阻应变计64片、光纤光栅测点44个、高清摄像头2部、箱体非接触动态位移标靶8个及高清摄像机1部。传感器编号A代表加速度计、W代表孔压计、P代表土压计、JD代表激光位移计、S代表应变片、G代表光纤光栅、PLT代表非接触动态位移标靶、C代表高清摄像机。
考虑可液化场地地下结构振动台试验中结构的损伤累积过程、输入地震动的影响和模型体系的动力特性变化,本次试验仅选取Taft波作为台面输入地震动。Taft波为1952年美国加利福尼亚地震中具有代表性的加速度记录,其EW向原始峰值加速度约为0.152g,断层距约为41.45 km,强震部分持时约为13 s,主频段范围为0.2～4 Hz,峰值加速度调幅为0.1g时的Taft波加速度时程及傅里叶谱如图4所示。
![]()
图 4 Taft波加速度时程及傅里叶谱Figure 4. Acceleration time-histories and Fourier spectra of Taft motion基于尽量减少激振次数的原则,按照逐级加载的方式以探讨不同强度地震动作用影响,采用输入基岩地震动峰值加速度（PBA）分别取0.05g,0.15g和0.30g,各加载工况之间的时间间隔不小于40 min,以保证模型地基中孔隙水压力的充分消散。为测定模型体系动力特性的改变,试验开始时、结束前分别进行了白噪声扫频,振动台试验的加载方案见表2。
表 2 振动台试验加载工况Table 2. Loading programs of shaking table tests序号 地震动 输入基岩峰值加速度/g 持时/s 1 白噪声 0.05 60 2 Taft波 0.05 54.4 3 Taft波 0.15 54.4 4 Taft波 0.30 54.4 5 白噪声 0.05 60 2. 试验结果分析
2.1 试验宏观现象
不同PBA作用下的模型场地宏观破坏现象如图5所示。当PBA =0.05g时,模型地表在震后出现了一条纵向可见裂缝,其最大开裂宽度约为1.1 cm；当PBA增大至0.15g时,原有裂缝宽度进一步扩大,同时与原有初始裂缝关于中线对称位置及结构端部沿横截面方向均出现可见裂缝,新增纵向、横向裂缝的最大宽度约为1.5 cm和1.2 cm；当PBA进一步增大到0.30g时,车站结构出现了明显的整体上浮,其最大上浮量约为13.2 cm,结构两侧地基出现震陷,地表发生喷砂、冒水现象,在较短时间内涌水浸满结构四周沉陷区域,其中的少量气泡为冒水过程中带出的地基土内残留空气,待地表存水流失后发现模型地表有明显液化痕迹。
2.2 地表震陷与结构上浮
为进一步分析模型体系的竖向位移反应,图6给出了不同加载工况时地表激光位移计记录的场地震陷与结构上浮时程曲线。由图6可知,在0.05g地震动作用下,地基与结构竖向位移变化幅度均小于0.1 cm,结构正上方的两测点JD1、JD2时程曲线吻合较好,其竖向位移值较侧边场地略大且有一定沉降趋势；当PBA = 0.15g时,结构与场地均出现了明显沉降,侧方场地的震陷值显著大于结构位移,其最大震陷值约为2.22 cm,结构竖向沉降位移仅为1.03 cm；在0.30g的Taft波作用下,模型结构上方测点JD1、JD2增长显著且时程规律发展吻合,结构发生了明显上浮且无倾斜现象,模型结构上浮隆起值最终稳定在13.2 cm左右,而侧方地基地表测点JD3结果显示此处发生震陷且在震后稳定在6.37 cm附近,JD3时程曲线最终在105～120 s出现波动,其原因为地表喷砂、冒水致使水位逐渐覆盖地表土层和标靶所致。整体上看,在地震动强度输入等级逐渐增大过程中,模型结构呈现先沉降、后上浮的规律。
![]()
图 6 地表震陷与结构上浮位移反应Figure 6. Vertical displacements of ground surface and subway station2.3 模型地基加速度反应
图7～9分别给出了模型地基不同埋深测点在Taft波作用下的峰值加速度反应、加速度时程记录、和频谱特性曲线,其中测点A1、A7分别位于模型结构正上方和正下方,测点A2～A6位于结构侧边模型地基中同一竖直线上。由图可知,当PBA = 0.05g时,模型地基的加速度反应峰值随土层埋深的减小而逐渐变大,同一水平标高处的测点加速度反应大致相同,模型结构的存在对周围地基各测点加速度反应影响较小；当PBA增大到0.15g和0.30g时,模型结构标高范围内的加速度反应规律变化明显,其中结构上方A1测点的加速度峰值明显小于侧边地基A2,结构下方A7测点的加速度峰值明显大于侧边地基A4,出现该现象的原因应为处于不同液化状态下的模型地基与模型结构相互作用方式对模型体系的动力反应影响明显。同时,车站结构在较强地震作用下发生上浮造成顶部覆土连带顶起并与周围地基逐渐错开,结构抬升导致下方土体逐渐脱空。在0.30g地震动作用下,因地基土的液化,部分测点峰值加速度出现了瞬时尖峰信号,既有实际地震记录中观测到了类似现象[16]。出现上述结果的原因应与强地震作用下浅层土体的循环流动有关,模型地基出现的瞬时卸载现象令土体的剪切刚度在液化时刻急剧上升。此外,模型地基中各测点的主频分量均出现了明显的低频放大、高频抑制效应,在0.05g的Taft波作用下,模型地基土的主频约为7.04 Hz,当PBA增大至0.30g时,模型地基土的主频衰减至1.35 Hz；同时,浅层地基加速度计的低频分量相对更为集中,其幅值也较大,其原因应与场地的孔压发展和刚度退化有关,致使地震波在传播过程中的高频分量被逐渐过滤、低频分量被逐渐放大。
2.4 模型地基动孔压比发展规律
本次试验量测了加载过程中模型地基的孔隙水压力发展过程,除测点W5、W8孔压计信号丢失外,其它孔压计均工作正常。为研究可液化场地中带地连墙异跨地铁车站结构对周围地基液化特性的影响,便于判断地基测点处的液化状态,定义动孔压比
为测点处的孔隙水压力与土体有效自重应力之比。同时,根据试验测点布置定义了模型场地中的4条路径并以编号Path-i表示,其中Path-1、Path-2和Path-3为竖直向路径,通过引入距宽比 （测点至结构侧边水平距离l与结构底部宽度B之比）来表示各路径距结构侧边的远近,则 值分别为2.13,0.79和0.19,代表较远、中等、较近；Path-4为水平向路径,该路径所包含的测点埋深相同,路径定义如图10所示。 图11给出了不同PBA时场地竖直向路径各测点的动孔压比反应时程曲线。整体上看,动孔压比反应随PBA的增大而增加,不同工况地基各测点动孔压比的变化规律基本一致。0.05g加载工况中地基各测点的孔压比幅值基本保持在0.04以内,孔压比反应十分微弱；当加载强度逐渐增加至0.15g和0.30g时,孔压比反应增幅明显,部分测点已达到液化状态,且在震后均有孔隙水压力消散现象,测试结果符合一般液化场地的地震反应规律。此外,各加载工况下模型场地主、次观测面同标高位置处测点（W1与W10、W3与W11）的动孔压比反应时程曲线基本重合,即模型场地孔压发展及分布沿模型结构纵向的变化较小,也说明本次试验所采用的孔压传感链布置方法较传统散点式安装方式更为可靠。距宽比
= 2.13时结构侧方地基Path-1测点的动孔压比反应如图11（a）所示。当PBA较小且场地未发生液化时,模型地基不同深度测点的孔压比幅值随埋深的增加近似呈逐渐减小趋势,土体的有效自重应力越大则液化水平越低；当场地液化程度因强地震动作用而保持在较高水平时,不同深度测点的孔压比反应幅值自上而下呈先增大、后减小的变化规律,其中在测点W2处孔压比反应幅值达到最大,测点W1/W10与W2处的动孔压比水平相当,但W1/W10孔隙水压力较W2的整体发展过程相对滞后,特别是当输入地震动强度达到0.30g模型结构出现明显上浮后,结构下方测点的孔压比发展水平明显减小且小于同深度其他测点幅值。上述规律同样可在距宽比 =0.79,0.19时的Path-2和Path-3路径测点量测结果中观察到,见图11（b）,图11（c）。 ![]()
图 11 模型地基竖直向路径动孔压比反应时程Figure 11. Responses of dynamic pore pressure ratio of model foundation on vertical path出现上述结果的原因应为地下结构的抗侧移刚度明显大于周围土体,导致邻近地下结构的侧向地基剪切变形小于远处地基,进而引起邻近侧向地基的孔压增长幅值减小,该原因与传统矩形地下结构周围的液化规律有一定相似之处,但异跨地铁车站结构的特殊形式导致浅层测点距车站侧墙相对更近,振动积累诱发的地表裂缝及结构侧墙与土体之间所形成的排水通道可能使浅层土体的孔隙水压力消散加快,进而令该测点处的孔压比保持在较低水平,距结构侧壁及地连墙相对更远处的测点则因排水通道不畅致使孔隙水压力难以消散,形成深层孔压比发展较浅层发展程度高、速度快的现象；同时结构上浮导致地连墙之间的土体松散,而两侧地基土体颗粒由于墙体的阻隔作用难以进入补充,进而墙体之间单位体积内的土体颗粒减少,孔隙水压力得到释放。整体上看,输入地震动强度等级越高、土层埋深越大,地基测点孔压比增长到峰值所需的时间越少、发展更为迅速,在强震作用下达到液化状态所需时间也越短,出现孔隙水压力消散的时刻也相对更早,周围地基的动孔压比反应受结构模型体系的影响显著。
图12给出了距宽比
不同的水平向路径Path-4孔压比发展过程曲线。同一标高、距宽比不同测点的孔压比反应区别明显,当PBA = 0.15g,0.30g时,地基测点的动孔压比水平与该处的距宽比值呈正相关,即距宽比 值越大则测点动孔压比水平相对越高,距宽比 值越小则测点的动孔压比水平相对越低,车站结构对邻近土体的液化发展起到了一定的抑制作用,该结果与已有相关数值模拟所得结论一致[17]。 ![]()
图 12 模型地基水平向路径Path-4动孔压比反应时程Figure 12. Responses of dynamic pore pressure ratio of model foundation on Path-43. 结论
通过开展可液化场地中带地连墙的异跨地铁车站结构地震反应振动台模型试验,研究了可液化土-地连墙-异跨地铁地下车站结构周围地基的地震反应特征,揭示了可液化地基中地连墙和地下车站结构对周围基动力反应的影响规律,得到的主要结论如下：
（1）车站结构的存在将明显改变邻近地基的液化分布规律,地下结构较大的抗侧刚度对邻近地基土层的抗剪切变形能力起到了一定提高作用,紧邻结构两侧的地基孔压增长减缓,进而表现为地下车站结构对邻近土体的液化发展起到了一定的抑制作用。
（2）当地震动强度等级较小时,模型地基不同深度测点的动孔压比幅值随埋深增加近似呈逐渐减小趋势,当场地液化程度因强地震动作用而保持在较高水平时,不同深度测点的动孔压比反应幅值自上而下呈先增大、后减小的变化规律；同时,土层埋深越大,地基测点孔压比增长到峰值所需的时间越短、发展更为迅速,在强震作用下达到液化状态所需要的时间也越短。
（3）地下结构侧向地基的液化情况将明显改变土与地下结构动力相互作用体系的加速度反应变化规律,但侧向地基未发生液化和完全液化后的模型地基和地下结构的加速度反应变化规律基本一致,当侧向地基部分液化时,地下结构埋深范围内地基的峰值加速度反应沿深度的变化规律将明显不同。
（4）在输入地震动强度等级逐渐增大过程中,模型结构呈现先沉降、后上浮的规律,其中在强地震动作用下,模型结构发生了明显上浮且无倾斜现象,侧方地基地表发生明显的震陷,其中结构整体上浮是造成地基震陷明显的主要原因。
-
![]()
图 1 隧道锚和下穿隧道位置关系示意图
Figure 1. Location relationship between tunnel-type anchorage and underpass tunnel
![]()
图 6 相似材料直剪试验及单轴压缩试验
Figure 6. Direct shear tests and uniaxial compression tests on similar materials
![]()
图 14 隧道及锚塞体沉降量随隧道开挖进尺的变化情况
Figure 14. Variation of settlement of tunnel and anchor plug with tunnel excavation footage
![]()
图 15 锚-隧间围岩竖向应力随隧道开挖进尺的变化情况
Figure 15. Variation of vertical stress of rock between anchor and tunnel with tunnel excavation footage
![]()
图 16 锚-隧间围岩水平应力随隧道开挖进尺的变化情况
Figure 16. Variation of horizontal stress of rock between anchorage and tunnel with tunnel excavation footage
![]()
图 17 连拱隧道先行洞初支切向应变随隧道开挖进尺的变化情况
Figure 17. Variation of tangential strain of initial support of multi- arch tunnel advanced section with tunnel excavation footage
![]()
图 18 连拱隧道中隔墙竖向应变随隧道开挖进尺的变化情况
Figure 18. Variation of vertical strain of middle wall in multi arch tunnel with tunnel excavation footage
![]()
图 19 连拱隧道后行洞初支切向应变随隧道开挖进尺的变化情况
Figure 19. Variation of tangential strain of the initial support of multi-arch tunnel following section with tunnel excavation footage
![]()
图 20 锚–隧间围岩竖向应力随荷载等级的变化情况
Figure 20. Variation of vertical stress of rock between anchor plug and tunnel with load grade
![]()
图 21 锚–隧间围岩水平应力随荷载等级的变化情况
Figure 21. Variation of horizontal stress of rock between anchor plug and tunnel with load grade
![]()
图 22 隧道初支外侧径向应变–荷载关系曲线
Figure 22. Variation of radial strain outside initial support of tunnel with load
表 1 围岩及混凝土物理力学参数
Table 1 Mechanical parameters of rock and concrete
项目 重度γ/(kN·m-3) 单轴抗压强度p/MPa 弹性模量E/GPa 泊松比μ 黏聚力c/MPa 内摩擦角φ/(°) 中风化白云质灰岩 22 33.0 3.2 0.3 1.18 34.6 锚塞体C40混凝土 25 26.8 32.5 0.2 — — 隧道初支C25喷混 24 16.7 26.0 0.2 — — 隧道中隔墙C30混凝土 25 20.1 30.0 0.2 — — 
下载: 导出CSV
表 2 相似材料物理力学参数
Table 2 Mechanical parameters of similar materials
项目 分类 重度γ/(kN·m-3) 单轴抗压强度p/kPa 弹性模量E/MPa 黏聚力c/kPa 内摩擦角φ/(°) 中风化白云质灰岩 目标值 17.03 255.52 24.78 9.14 34.6 实测值 17.03 234.54 28.53 10.47 41.83 锚塞体C40混凝土 目标值 18.58 205.80 249.57 — — 实测值 18.43 1480.27 281.99 — — 隧道中隔墙C30混凝土 目标值 18.58 154.35 230.37 — — 实测值 15.13 679.11 206.03 — —
下载: 导出CSV
-
[1] 张宜虎, 邬爱清, 周火明, 等. 悬索桥隧道锚承载能力和变形特征研究综述[J]. 岩土力学, 2019, 40(9): 3576–3584. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201909031.htm ZHANG Yi-hu, WU Ai-qing, ZHOU Huo-ming, et al. Review of bearing capacity and deformation characteristics of tunneltype anchorage for suspension bridge[J]. Rock and Soil Mechanics, 2019, 40(9): 3576–3584. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201909031.htm
[2] 刘新荣, 韩亚峰, 景瑞, 等. 隧道锚承载特性、变形破坏特征及典型案例分析[J]. 地下空间与工程学报, 2019, 15(6): 1780–1791. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201906025.htm LIU Xin-rong, HAN Ya-feng, JING Rui, et al. Bearing characteristics, deformation failure characteristics and typical case studies of tunnel-type anchorage[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(6): 1780–1791. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201906025.htm
[3] 王东英, 汤华, 尹小涛, 等. 隧道式锚碇承载机制的室内模型试验探究[J]. 岩石力学与工程学报, 2019, 38(增刊1): 2690–2703. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2019S1010.htm WANG Dong-ying, TANG Hua, YIN Xiao-tao, et al. Study on the bearing mechanism of tunnel-type anchorage based on laboratory model test[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S1): 2690–2703. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2019S1010.htm
[4] 余美万, 张奇华, 喻正富, 等. 基于夹持效应的普立特大桥隧道锚现场模型试验研究[J]. 岩石力学与工程学报, 2015, 34(2): 261–270. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201502006.htm YU Mei-wan, ZHANG Qi-hua, YU Zheng-fu, et al. Field model experiment on clamping effect of tunnel-type anchorage at puli bridge[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 261–270. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201502006.htm
[5] 李栋梁, 刘新荣, 李俊江, 等. 浅埋软岩隧道式锚碇稳定性原位模型试验研究[J]. 岩土工程学报, 2017, 39(11): 2078–2087. doi: 10.11779/CJGE201711016 LI Dong-liang, LIU Xin-rong, LI Jun-jiang, et al. Stability of shallowly buried soft rock tunnel anchorage by in-situ model tests[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(11): 2078–2087. (in Chinese) doi: 10.11779/CJGE201711016
[6] JIANG N, WANG D, FENG J, et al. Bearing mechanism of a tunnel-type anchorage in a railway suspension bridge[J]. Journal of Mountain Science, 2021, 18: 2143–2158 doi: 10.1007/s11629-020-6162-8
[7] 刘新荣, 李栋梁, 吴相超, 等. 泥岩隧道锚承载特性现场模型试验研究[J]. 岩土工程学报, 2017, 39(1): 161–169. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16816.shtml LIU Xin-rong, LI Dong-liang, WU Xiang-chao, et al. Filed model tests on bearing behavior of mudstone tunnel anchorage[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(1): 161–169. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16816.shtml
[8] LIU X R, HAN Y F, LI D L, et al. Anti-pull mechanisms and weak interlayer parameter sensitivity analysis of tunnel-type anchorages in soft rock with underlying weak interlayers[J]. Engineering Geology, 2019, 253: 123–136.
[9] 余美万, 张奇华, 高利萍, 等. 金东大桥隧道锚现场模型试验及承载能力分析[J]. 岩土工程学报, 2021, 43(2): 338–346. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18503.shtml YU Mei-wan, ZHANG Qi-hua, GAO Li-ping, et al. Field model tests and bearing capacity analysis of tunnel anchorage of Jindong Bridge[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(2): 338–346. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18503.shtml
[10] SONG S G, LI S C, LI L P, et al. Model test study on vibration blasting of large cross-section tunnel with small clearance in horizontal stratified surrounding rock[J]. Tunnelling and Underground Space Technology, 2019, 92: 103013.
[11] 刘聪, 李术才, 周宗青, 等. 复杂地层超大断面隧道施工围岩力学特征模型试验[J]. 岩土力学, 2018, 39(9): 3495–3504. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201809048.htm LIU Cong, LI Shu-cai, ZHOU Zong-qing, et al. Model test on mechanical characteristics of surrounding rock during construction process of super-large section tunnel in complex strata[J]. Rock and Soil Mechanics, 2018, 39(9): 3495–3504. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201809048.htm
[12] XU S S, LEI H, LI C, et al. Model test on mechanical characteristics of shallow tunnel excavation failure in gully topography[J]. Engineering Failure Analysis, 2021, 119: 104978.
[13] 李建旺, 冯仕文, 周喻. 隧道下穿采空区施工围岩灾变演化的力学机制[J]. 中南大学学报(自然科学版), 2021, 52(2): 543–554. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202102023.htm LI Jian-wang, FENG Shi-wen, ZHOU Yu. Mechanical mechanism of surrounding rock catastrophe evolution during construction of tunnel under goaf[J]. Journal of Central South University (Science and Technology), 2021, 52(2): 543–554. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD202102023.htm
[14] LI L P, SHANG C S, CHU K W, et al. Large-scale geo-mechanical model tests for stability assessment of super-large cross-section tunnel[J]. Tunnelling and Underground Space Technology, 2021, 109: 103756.
[15] 朱玉, 卫军, 李昊, 等. 悬索桥隧道锚与下方公路隧道相互作用分析[J]. 铁道科学与工程学报, 2005, 1(12): 57–61. https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD200501012.htm ZHU Yu, WEI Jun, LI Hao, et al. Analysis on interaction between tunnel-type anchorage in suspension bridge and highway tunnel[J]. Journal of Railway Science and Engineering, 2005, 1(12): 57–61. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-CSTD200501012.htm
[16] 张奇华, 胡建华, 陈国平, 等. 矮寨大桥基础岩体稳定问题研究[J]. 岩石力学与工程学报, 2012, 31(12): 2420–2430. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201212006.htm ZHANG Qi-hua, HU Jian-hua, CHEN Guo-ping, et al. Study of rock foundation stability of Aizhai bridge[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(12): 2420–2430. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201212006.htm
[17] 云瑞俊, 梅松华, 周湘. 金安金沙江大桥丽江侧隧道锚系统数值分析[J]. 公路, 2020, 65(12): 96–102. https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL202012020.htm YUN Rui-jun, MEI Song-hua, ZHOU Xiang. Numerical analysis of tunnel anchorage system on the Lijiang side of Jinsha river bridge in Jin'an[J]. Highway, 2020, 65(12): 96–102. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GLGL202012020.htm
[18] 王宇华, 谢洪涛, 陈健翔, 等. 价值工程在香丽高速公路虎跳峡金沙江大桥施工成本控制中的应用[J]. 价值工程, 2017, 36(7): 26–28. https://www.cnki.com.cn/Article/CJFDTOTAL-JZGC201707011.htm WANG Yu-hua, XIE Hong-tao, CHEN Jian-xiang, et al. The application of value engineering in construction cost control of Jinsha river bridge in Tiger Leaping gorge on Shangri-La-Lijiang superhighway[J]. Value Engineering, 2017, 36(7): 26–28. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZGC201707011.htm
-
期刊类型引用(22)
1. 曹虎，张广清，李世远，汪文瑞，谢彭旭，孙伟，李帅. 基于断裂过程区的压裂驱油水力裂缝扩展模型及应用. 岩土力学. 2025(03): 798-810 . 
百度学术
2. 何昭宇，王冬明，张太国，范世英. 济南地区土岩二元结构边坡加固设计及稳定性研究. 建筑结构. 2024(04): 73-79+66 . 百度学术
3. 施静怡，吴能森，刘强. 静压桩在成层地基中挤土效应的可视化研究. 河南城建学院学报. 2024(02): 20-26 . 百度学术
4. 刘江涛，李存军，于江华，张彦红，张春彬，孔纲强. 施工顺序对微型钢管桩加固既有基础变形的影响试验研究. 土木与环境工程学报(中英文). 2024(04): 100-108 . 百度学术
5. 高玉峰，王玉杰，张飞，姬建，陈亮，倪钧钧，张卫杰，宋健，杨尚川. 边坡工程与堤坝工程研究进展. 土木工程学报. 2024(08): 97-118 . 百度学术
6. 胡焕校，谢中良，甘本清，卢雨帆，邓超. 透明砂土基本特性及其在注浆模型试验中的应用. 水资源与水工程学报. 2024(04): 179-186 . 百度学术
7. 李梦晨，赵之仲，薛军，姜益顺. 土质边坡滑坡灾害的分级预警判据. 山东交通学院学报. 2024(03): 46-55 . 百度学术
8. 何建新，董旭光，马渊博. 坡顶荷载作用下多级边坡失稳演化机制的透明土试验研究. 西北工程技术学报. 2024(04): 347-355 . 百度学术
9. 刘强，吴能森，黄志波，许旭堂，徐祥. 抗滑桩加固二元结构边坡可视化模型试验. 林业工程学报. 2023(02): 172-179 . 百度学术
10. 赖成联. 基于沉井基础的重力坝坝肩滑坡处理技术. 红水河. 2023(02): 11-15 . 百度学术
11. 周昌，马文超，胡元骏，史光明. 基于透明土的库水位骤降下消落带滑坡-伞型锚体系变形破坏机理. 工程地质学报. 2023(04): 1407-1417 . 百度学术
12. 张立乾，田义斌，闫晶，李兵，孟良. 某场地高边坡和洪水综合治理工程研究. 岩土工程技术. 2023(05): 545-552 . 百度学术
13. 周鹏，柯文斌. 可视化透明土技术在岩土变形测量实验教学中的应用. 教育教学论坛. 2023(50): 9-12 . 百度学术
14. 梁越，代磊，魏琦. 基于透明土和粒子示踪技术的渗流侵蚀试验研究. 岩土工程学报. 2022(06): 1133-1140 . 本站查看
15. 徐志军，王云泰，杜建平，王政权，周洋，王爽. 缩径基桩竖向承载性能的透明土试验研究. 湖南大学学报(自然科学版). 2022(07): 214-221 . 百度学术
16. 卢谅，何兵，肖亮，王宗建，马书文，林浩鑫. 基于透明土的成层土中CPT贯入试验研究. 岩土工程学报. 2022(12): 2215-2224 . 本站查看
17. 胡仕明，杨伟红，李涛，李昕堃. 公路隧道洞口顺层边坡变形规律分析. 岩土工程技术. 2022(06): 477-482 . 百度学术
18. 刘强，吴能森，许旭堂. 基于透明土的黏土边坡土体变形特征试验. 福建工程学院学报. 2022(06): 532-536 . 百度学术
19. 李元松，王玉，朱冬林，闫海涛，戴哲. 边坡稳定性评价方法研究现状与发展趋势. 武汉工程大学学报. 2021(04): 428-435 . 百度学术
20. 周义. 尼日利亚某铁路项目挖方边坡溜坍防护方案研究. 住宅与房地产. 2020(06): 226-227 . 百度学术
21. 翟淑花，孙小华，冒建，程素珍，刘欢欢. 北京山区岩土混合质边坡变形破坏机理分析. 徐州工程学院学报(自然科学版). 2020(04): 24-29 . 百度学术
22. 徐建强，阎宗岭，李海平，马小斐. 黔西岩溶区公路土岩混合边坡致灾模式及调控技术. 公路交通技术. 2019(06): 25-30+42 . 百度学术
其他类型引用(18)
计量
- 文章访问数: 158
- HTML全文浏览量: 24
- PDF下载量: 29
- 被引次数: 40
