Migration of bimolecular reactive solutes considering nonequilibrium sorption
-
摘要: 针对溶质非平衡吸附特征，建立了非平衡吸附条件下双分子反应性溶质一维运移模型，考虑了在对流、弥散、吸附（平衡和非平衡）、反应（氧化反应和自然需氧量反应）耦合作用下的溶质运移过程，选用COMSOL对模型进行数值求解。研究结果表明：①非平衡吸附条件下污染物去除的第一阶段为氧化反应主导的快速修复，第二阶段为非平衡吸附主导的慢速修复；②考虑非平衡吸附可以更加精准刻画污染物拖尾效应；③化学反应速率影响数、平衡吸附比例影响数以及非平衡吸附速率影响数均对污染物的去除效率产生显著影响，且的影响程度与平衡吸附占总吸附比例f相关，佩克莱数Pe影响较小；④在，，较小且Pe较大的情况下，拖尾效应较为严重，必须考虑非平衡吸附。Abstract: A one-dimensional transport model for bimolecular reactive solutes under nonequilibrium sorption is developed for the characteristics of solute nonequilibrium sorption. The transport process of bimolecular reactive solutes under advection, dispersion, sorption (equilibrium and nonequilibrium) and reaction (oxidation and natural oxygen demand) is considered, and the COMSOL Multiphysics is used to solve the model numerically. The most important results are as follows: (1) The first stage of pollutant removal under nonequilibrium sorption conditions is the rapid remediation dominated by oxidation reactions, and the second stage is the slow remediation dominated by nonequilibrium sorption. (2) Considering nonequilibrium sorption can describe the pollutant tailing more accurately. (3) The chemical reaction rate , equilibrium sorption ratio and nonequilibrium sorption rate significantly influence the removal efficiency of pollutants, and the impact of is related to the rate of equilibrium sorption to total sorption f. The effects of the Peclet number are less obvious. (4) In cases of small , , and large Pe, the tailing effects are more serious, and nonequilibrium sorption must be considered.
-
Keywords:
- nonequilibrium sorption /
- two-site model /
- bimolecular reaction /
- solute transport /
- tailing effect
-
0. 引言
中国产业结构升级和城市布局调整过程中产生了大量城市工业污染场地，严重制约了土地资源的安全利用，对污染场地开展管控修复已刻不容缓[1]。原位化学氧化技术具有适用性广、修复周期短、易与其他修复技术联合使用等优点，目前已广泛应用于污染土壤和地下水的修复。
反应性溶质的运移与污染场地氧化修复密切相关，近年来开发的多个反应性溶质运移模型已用于污染场地修复的实际工程中[2]。在这些模型中，一般采用经典对流-弥散-吸附-反应方程描述反应性溶质的运移过程，该方程基于局部平衡假设，认为吸附过程是平衡的，然而该假设成立的前提条件是吸附过程要快于其他溶质运移过程（如对流和弥散）[3]。在一些流速较低的地下水环境中，局部平衡是可以实现的，但是越来越多的室内试验和工程调查表明，局部尺度的浓度达到平衡的时间很长[4]，局部平衡假设的失效会使传统的溶质运移方程高估溶质间的反应程度[2]。另外在修复初期，污染物去除速率较高，而随着修复持续进行，去除速率逐渐降低，污染物浓度也趋向于水平渐近线并难以进一步降低，这种现象即拖尾效应，其本质是污染物在相间的非平衡态迁移，主要归因于污染物非平衡吸附-解吸、土层异质性等。因此，在溶质运移方程中考虑吸附过程的非平衡性对准确模拟溶质运移中的拖尾、回弹等现象有重要意义。
Van Genuchten等[5]基于可动-不动水体概念提出了两点模型，将溶质的吸附分为：①吸附是瞬时，②吸附是有速率限制。Bradford等[6]为了更好描述胶体和微生物的运移，将两点模型扩展为两点动力学模型，即两部分的吸附都是与时间相关的动力过程，并且以不同速率进行。赵颖等[7]建立了双点平衡/动力学吸附溶质运移模型，并指出一阶吸附解吸速率常数和平衡吸附点位所占比例对污染物浓度分布有重要影响。
现有研究主要侧重于非平衡吸附作用对单一溶质运移的影响，而实际的地下水环境中几乎不存在单一溶质运移，不同溶质存在氧化-还原、催化反应等过程，而关于非平衡吸附作用对此类双分子反应性溶质运移影响的研究非常有限，导致吸附非平衡性对氧化修复过程中污染物运移和去除的影响机制尚不明确。
基于非平衡吸附理论，将两点吸附模型与原位化学氧化模型相结合，建立了污染场地中双分子反应性溶质运移数值模型。利用大型有限元数值仿真平台COMSOL Multiphysics进行建模求解，研究了非平衡吸附-解吸作用下溶质的运移规律和污染去除机制。本研究有助于理解药剂和污染物的迁移转化规律，可以为污染场地的修复设计及修复效果评价提供理论依据。
1. 模型建立与求解
1.1 控制方程
（1）两点吸附模型
Batch试验结果表明大多数吸附过程呈现两阶段吸附特征：首先是短时间的快速吸附阶段，随后是较长时间且速率较慢的吸附阶段[8]。大约50%的吸附发生在最初的几分钟或几小时内，其余在几天或几个月内发生。两点平衡/动力学吸附溶质运移模型可以较为准确地描述这种吸附非平衡性，其控制方程为[3]
∂nCi∂t+ρ(∂Se∂t+∂Sk∂t)+∂∂x[n(vCi−D∂Ci∂x)]=Φ ,Se=fKdCi ,∂Sk∂t=α[(1−f)KdCi−Sk] 。} (1) 式中：C为溶质的浓度；下标i为溶质种类；D为溶质运移水动力弥散系数；v为多孔介质中溶质运移平均流速；n为孔隙率；Se，Sk分别为溶质在平衡和非平衡吸附相上的吸附浓度；f为平衡吸附交换点位占总吸附点位的比例；α为一阶吸附解吸速率常数；Kd为分配系数；Φ为源-汇项。
（2）原位化学氧化模型（ISCO）
现有研究中通常将A + B→Product作为双分子氧化反应的基准类型，其中反应物与生成物均为溶质[9]。对于一维饱和多孔介质中的双分子反应，传统的对流-弥散-反应控制方程为[10]
∂nCi∂t+∂∂x[n(vCi−D∂Ci∂x)]=−nkCACB （i=A, B）, (2) ∂nCProduct∂t+∂∂x[n(vCProduct−D∂CProduct∂x)]=nkCACB。 (3) 式中：CA，CB，CProduct分别为药剂液相浓度、污染物液相浓度和生成物液相浓度；k为药剂与污染物的二阶反应速率常数。
现有研究表明，在药剂被输送到目标污染区域后，土壤有机质也会与药剂进行反应，且与污染物存在竞争关系，因此需要考虑自然需氧量（NOD）反应对药剂的消耗。考虑土壤介质对污染物的平衡吸附作用，药剂和污染物对应的控制方程分别为[11]
∂nCA∂t+∂∂x[n(vCA−D∂CA∂x)]=−nkCACB−ρknCANm,∂Nm∂t=−knCANm,} (4) ∂nRCB∂t+∂∂x[n(vCB−D∂CB∂x)]=−nkCACB,R=1+ρKdn。} (5) 式中：Nm为反应NOD；kn为NOD与药剂反应的二阶反应速率常数；R为污染物的线性平衡迟滞因子；ρ为土壤密度。
（3）NS-ISCO模型
为了研究非平衡吸附对双分子反应性溶质运移的影响规律，本文将两点吸附模型与原位化学氧化模型相结合，构建了非平衡吸附-原位化学氧化模型（NS-ISCO）。
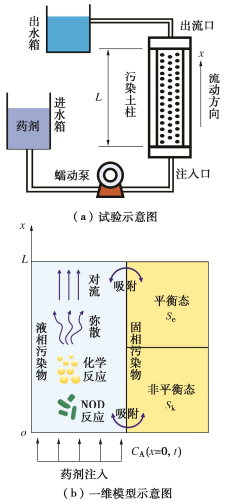
图 1（a）展示了模型对应的试验过程，初始时刻土柱中存在均匀分布的污染物，药剂从注入口（x=0）进入，流经污染土柱后从出流口（x=L）流出。图 1（b）为一维模型示意图，药剂同样从入渗边界进入污染土柱中，考虑液相药剂和液相污染物的一维对流、弥散以及化学氧化反应；考虑污染物固相与液相之间的平衡-非平衡吸附作用；考虑土壤有机质与液相药剂的NOD反应。本模型只考虑液相和吸附相污染物，不考虑NAPL相污染物。建立的双分子反应性溶质一维运移控制方程如下：
![]()
图 1 考虑两点吸附的双分子反应性溶质运移Figure 1. Biomolecular reactive solute transport considering two-site sorptiona）药剂运移方程见式（4）。
b）污染物运移方程
∂(n+ρfKd)CB∂t+ρα[(1−f)KdCB−Sk]+∂∂x[n(vCB−D∂CB∂x)]=−nkCACB ,∂Sk∂t=α[(1−f)KdCB−Sk]。} (6) 1.2 初始条件与边界条件
假定在初始时刻，土柱内药剂浓度为0，污染物浓度为某一固定浓度，即
CA(x,t=0)=0, (7) CB(x,t=0)=C0B。 (8) 式中：CB0为污染物初始浓度。
在入渗边界处（x=0），药剂以恒定浓度注入系统中，而此处并无外部污染物进入，因此将污染物设置为Dirichlet边界条件：
CB(x,t)|x=0=0。 (9) Van Genuchten等[12]认为在这类混合置换试验中，通量形式的边界条件比浓度边界条件更适合，因此药剂的入渗边界条件设置为
(VCA(x,t)−D∂CA(x,t)∂x)|x=0=VCinjA（0＜t≤tinj）,CinjA=0（t＞tinj）。} (10) 式中：CAinj为药剂注入浓度；tinj为药剂注入时间。
出流边界处（x=L）采用Neumann边界条件表示为[13]
∂Ci(x,t)∂x|x=L=0 (i = A, B) 。 (11) 1.3 模型验证
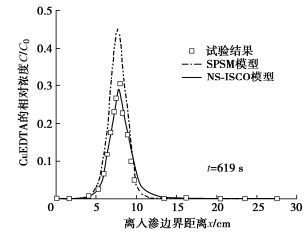
本文采用大型有限元数值仿真平台COMSOL Multiphysics中的物质传递模块建立数值模型并进行求解计算，得到一维土柱中污染物、药剂和生成物的浓度分布。采用双分子反应性溶质运移试验[14]对数值模型进行验证，验证模型中考虑溶质的对流、弥散、吸附（平衡和非平衡）以及反应（氧化反应和NOD反应）过程，验证模型参数取值见表 1，试验选取的双分子反应性溶质为CuSO4和EDTA4-。
表 1 验证模型参数设定Table 1. Adopted parameters for model validation模型参数 取值 孔隙率 n 0.36 [14] 地下水流速度 v/(cm·s-1) 1.21×10-2 [14] 弥散系数 D/(cm2·s-1) 1.75×10-3 [14] 平衡吸附占总吸附的比例 f 0.22 [15] 分配系数 Kd/(m3·kg-1) 4.00×10-4 [15] 一阶吸附解吸速率常数 a/(1·s-1) 1.75×10-4 [15] 药剂与污染物反应速率常数 k/(m3·s-1·mol-1) 2.39×106 [14] 药剂与NOD反应速率 kn/(m3·s-1·mol-1) 1.10×10-5 [11] 药剂注入浓度 CAinj/(mol·m-3) 20 [14] 污染物初始浓度 CB0/(mol·m-3) 20 [14] 图 2为双分子反应性溶质运移试验与数值模型计算得到的生成物浓度分布对比。Gramling等[14]提出了SPSM模型，并将模型结果与试验值进行对比。SPSM模型考虑了溶质对流、弥散和化学反应，但未考虑溶质吸附。对比可以发现本文模型计算结果与试验数据吻合良好，显著优于SPSM模型，验证了本文模型的正确性和优越性，同时也说明忽略溶质吸附会导致数值模拟结果与真实运移情况存在较大偏差。
![]()
图 2 本文模型计算结果与试验数据对比Figure 2. Comparison of results between the proposed model and the experiment2. 非平衡吸附对溶质运移的影响机制
若不考虑吸附的非平衡性，则非平衡吸附-原位氧化（NS-ISCO）模型可退化为原位化学氧化（ISCO）模型，本节通过NS-ISCO与ISCO模型的对比，揭示非平衡吸附对原位氧化过程中关键指标和修复机制的影响，进而说明在原位氧化修复中考虑非平衡吸附的必要性。模型参数见表 2，除平衡吸附占总吸附的比例f和一阶吸附解吸速率常数a有所区别外，其余参数保持一致。本文模拟的工况为将修复药剂高锰酸钾持续注入至含有均匀分布三氯乙烯的污染土柱中，研究修复过程中溶质的运移变化情况。
表 2 NS-ISCO与ISCO模型参数设定Table 2. Adopted parameters for NS-ISCO and ISCO models参数 NS-ISCO模型 ISCO模型 平衡吸附占总吸附的比例 f 0.22 [15] 1 一阶吸附解吸速率常数a/(1·s-1) 1.75×10-4 [15] — 土柱长度 L/m 1 1 分配系数 Kd/(m3·kg-1) 4.00×10-4 [15] 4.00×10-4 [15] 孔隙率 n 0.30 [16] 0.30 [16] 地下水流速度 v/(cm·s-1) 1.21×10-2 [14] 1.21×10-2 [14] 纵向弥散度 αL/cm 0.40 [16] 0.40 [16] 药剂扩散系数 DA/(cm2·s-1) 1.55×10-5 [16] 1.55×10-5 [16] 污染物扩散系数 DB/(cm2·s-1) 7.98×10-4 [16] 7.98×10-4 [16] 药剂与污染物反应速率常数k/(m3·s-1·mol-1) 3.90×10-4 [16] 3.90×10-4 [16] 药剂与NOD反应速率kn/(m3·s-1·mol-1) 3.47×10-7 [11] 3.47×10-7 [11] 2.1 溶质在土柱中的分布规律
为了提高模型可比性，减少由于不同多孔介质体积及流速造成的差异，本文采用无量纲化的孔隙体积（PV）表征溶质运移过程，孔隙体积定义为注入土柱的液体体积与土柱孔隙体积的比值。
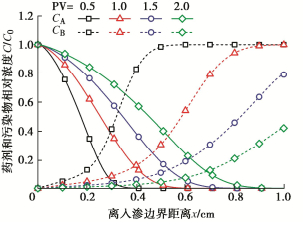
图 3展示了不同PV下药剂与污染物相对浓度分布。随着PV的增大，药剂由入渗边界逐渐被淋溶到下游区域，距离入渗边界更远区域的污染物开始与药剂发生反应。当PV=1.5时，下游污染物浓度开始减小；当PV=2.0时，中上游污染物基本去除，但下游部分仍有较多污染物残留，因此选取合适的药剂注入体积对污染场地的修复效果和成本至关重要。
![]()
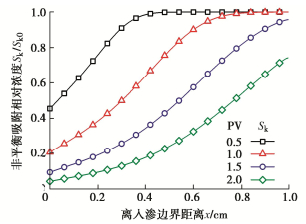
图 3 药剂与污染物在土柱中的相对浓度分布Figure 3. Distribution of relative concentration of reagent and contaminant in soil column图 4展示了不同PV下非平衡吸附相对浓度随土柱长度的变化，曲线的变化趋势与图 3中污染物变化相似，从式（6）也能够发现非平衡吸附浓度与污染物浓度大致呈正相关。当PV=0.5时，图 3中x＜0.1 m部分液相污染物已基本被去除，但是在图 4中其所对应的非平衡吸附相对浓度值仍然较大，表明非平衡吸附是产生污染物浓度拖尾效应的重要原因。
![]()
图 4 注入过程中非平衡吸附相对浓度分布Figure 4. Distribution of relative concentration of nonequilibrium sorption during injection2.2 平衡与非平衡吸附模型中污染物运移规律对比
为了更好说明非平衡吸附对溶质运移的影响，本节从注入过程和注入后这两个阶段分别比较了NS-ISCO模型与ISCO模型中不同相态污染物的变化情况，以探究非平衡吸附对污染物修复机制的影响。
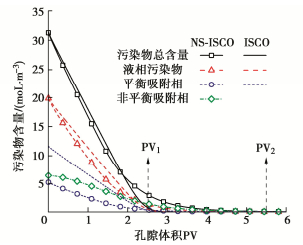
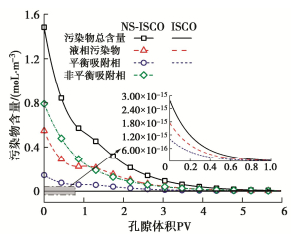
在实际修复工程中往往更加关注污染场地中污染物总量的变化情况，并以此来评价整体修复效果。因此，本节对各相态污染物在土柱中的总体含量进行研究。图 5为两类模型在药剂注入过程中污染物总含量、液相污染物含量、平衡吸附相污染物含量以及非平衡吸附相污染物含量随PV的变化曲线。在ISCO模型中，污染物总含量为液相和平衡吸附相污染物含量之和，在NS-ISCO模型中，污染物总含量为液相、平衡吸附相以及非平衡吸附相污染物含量之和。可以发现对于ISCO模型，随着PV的增加，在氧化反应的作用下土柱中污染物总含量快速降低，当达到PV1时，污染物总含量、液相污染物含量和平衡吸附相污染物含量同时为零，说明此时土柱中的污染物已全部去除，PV1可认为是在平衡吸附条件下完成修复所需的孔隙体积。而对于NS-ISCO模型，当达到PV1时，仅有平衡吸附相污染物含量降为零，此刻土柱中仍存在液相污染物与非平衡吸附相污染物。随后液相和非平衡吸附相缓慢降低，直至孔隙体积达到PV2时，污染物总含量、液相污染物和非平衡吸附相污染物才完全去除，PV2可认为是在非平衡吸附条件下完成修复所需的孔隙体积。
从上述分析可以发现，两类模型对应的污染物含量变化模式有显著区别：①对于ISCO模型，在氧化反应的主导下，总污染量随PV的增加而快速减小，直至修复完成；②对于NS-ISCO模型，呈现两阶段特征：修复前期与平衡吸附类似，是由氧化反应占主导的快速修复阶段（0＜PV＜PV1），该阶段结束后，平衡吸附相污染物基本去除，但场地内仍存在较多污染物；随后氧化反应作用降低，变为由非平衡吸附占主导的慢速修复阶段（PV1＜PV＜PV2），该阶段所需的时间往往大于第一阶段，直至污染物全部去除。
由此可见，考虑非平衡吸附会使污染物在更长时间内保持相对较高的浓度，拖尾效应也会更加严重。这是因为有机化学物质固有的非平衡吸附特性是一个速率受限制的过程，液相与固相的交换相较于平衡吸附更为缓慢，当溶质被吸附到固体基质后，需要更长的时间才能从固相中解吸出来。而当平衡吸附相污染物去除后，非平衡吸附相污染物在后期会作为污染源持久存在。若在实际修复工程中采用平衡吸附假设，往往会高估药剂与污染物的反应程度，且低估场地修复所需药剂的孔隙体积，造成场地修复不彻底。
图 6描述了在注入PV=2.5的药剂后停止注入，随后土柱中污染物含量的变化情况，PV=2.5是本案例中在平衡吸附条件下完成修复所需的孔隙体积。可以发现，当药剂注入停止后，NS-ISCO模型中仍会残留可观数量的污染物，需要3.5个孔隙体积地下水淋洗后才能完全去除。而对于ISCO模型，停止注入后土柱中已基本没有污染物。因此考虑非平衡吸附的运移模型能更加准确地描述原位氧化修复全过程。
![]()
图 6 药剂注入停止后污染物含量时变曲线Figure 6. Temporal variation of pollutant after reagent injection3. 对流作用、氧化反应和非平衡吸附对污染物修复效率的影响
已有研究表明对流作用和氧化反应速率对反应性溶质的运移会产生较大影响[3]，而一阶吸附解吸速率常数和平衡吸附点位所占比例是表征土壤非平衡吸附能力的重要参数。为了减少参数数量，本节采用无量纲分析，通过4个无量纲数研究对流作用、氧化反应和非平衡吸附对修复效率的影响，无量纲参数的定义和取值如表 3所示，其余参数均参考表 2，模拟的工况与第2节相同。选取出流边界污染物相对浓度作为对比指标；参考姜林等[17]提出的场地修复目标，将污染物相对浓度CB/C0=0.01作为修复标准，此时对应的孔隙体积即为修复完成所需的PV值，用PV2表示。在参数分析中仅考虑注入过程。
表 3 无量纲数的定义与取值Table 3. Definition and values of dimensionless numbers无量纲参数 表达式 取值 佩克莱数Pe vLDB 100/1000/10000/100000 化学反应速率影响数˜k kC0BLv 0.5/5/50/500/5000 平衡吸附比例影响数˜f n+fρKdn+ρKd 0.38/0.5/0.7/0.9/1 非平衡吸附速率影响数˜a aρKdLnv 2/20/200/2000/20000 3.1 佩克莱数
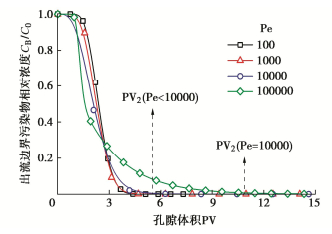
佩克莱数Pe是描述对流与扩散效应相对大小的无量纲数[9]。图 7描述了在不同Pe情况下土柱出流边界处污染物的浓度分布，可以发现Pe等于100/1000/10000对应的分布曲线较为接近，可以认为此时污染物的运移与去除主要受氧化反应影响，而当Pe为10000时，流速较快，此时对流作用主导污染物的运移，氧化反应作用减弱。
![]()
图 7 佩克莱数对污染物浓度分布曲线的影响Figure 7. Effects of Peclet number on distribution curve of contaminant concentration另外，图 7中可以看出当PV较小时，Pe为100000情况下污染物修复效率要快于其他3种情况，但是当PV > 3后，其修复效率快速减小，对应的PV2也大于其他情况。这是由于当流速过快时，贮存在固体基质中的吸附态污染物解吸速率相较于流速而言过于缓慢，因此在前期修复阶段液相污染物浓度较小，修复效率较高。而当PV增大后，非平衡吸附逐渐占据主导，固体基质中吸附态污染物在长时间内缓慢释放，造成其后期污染物浓度高于其他情况。
3.2 化学反应速率影响数
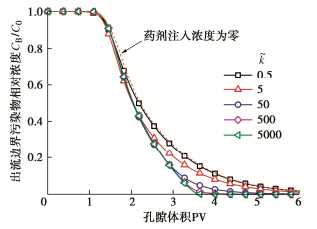
化学反应速率影响数˜k是描述氧化反应与对流效应相对大小的无量纲数。图 8展示了在不同化学反应速率影响数˜k条件下的浓度分布曲线，可以发现污染物的去除速率随着˜k的增加而增加，且对应的PV2也会相应减小，这是因为化学反应速率越快，相同时间、相同体积的药剂能够去除的污染物越多。
![]()
图 8 化学反应速率影响数对污染物浓度分布曲线的影响Figure 8. Effects of number of chemical reaction rate on distribution curve of contaminant concentration当˜k为500，5000时对应的污染物分布曲线较为接近，说明当˜k > 500后，对修复效率的影响较小，难以再提升修复效率，因此在实际修复工程中并不需要过分追求反应速率过高的修复药剂，反应速率对修复效率的影响存在一定阈值。图 8中的虚线表示药剂注入浓度为零时对应的污染物浓度分布曲线，在这种情况下模型中污染物的去除主要依靠地下水的淋洗作用，该曲线与˜k为0.5时的曲线基本重合，说明当˜k较小时，修复药剂对污染物的去除效果有限。
3.3 平衡吸附比例影响数
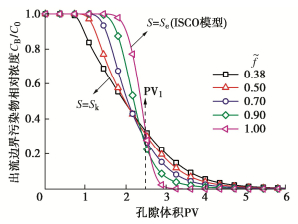
平衡吸附比例影响数˜f是描述平衡吸附与总吸附相对大小的无量纲数[5]，当平衡吸附点位所占比例f=0时，土柱中各点位均为非平衡吸附，此时˜f最小，为0.38；当f=1时，土柱中各点位均为平衡吸附，此时˜f最大，为1，而NS-ISCO模型也退化为ISCO模型。
图 9展示了5种不同˜f情况下的污染物浓度分布曲线，可以发现曲线近似呈现中心对称特征，而对称点所对应的PV值与图 5中的PV1接近。随着˜f的增大，污染物开始变化所需的起始PV值逐渐增加，但越晚开始变化的曲线对应的污染物去除速率却越快，且达到修复完成所需的PV2值越小。这主要是因为˜f的增大导致平衡吸附比例增加，由于平衡吸附相解吸速率较快，因此在修复前期有更多液相污染物生成，导致修复所需的药剂量增加，所以污染物开始减小所需的PV值也相应增加。从2.2节可知，当PV大于PV1后，非平衡吸附将占主导作用，因此在修复后期，˜f越小，非平衡吸附比例越高，更多的污染物会从吸附相解吸到液相，对应的PV2也相应增加。
![]()
图 9 平衡吸附比例影响数对污染物浓度分布曲线的影响Figure 9. Effects of number of equilibrium sorption ratio on distribution curve of contaminant concentration3.4 非平衡吸附速率影响数
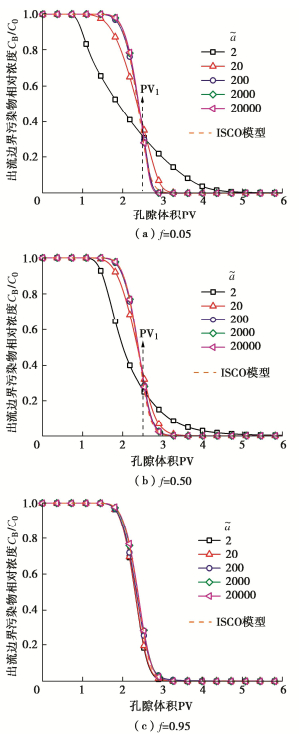
非平衡吸附速率影响数˜a是描述非平衡吸附与对流效应相对大小的无量纲数。赵颖等[7]指出˜a对污染物浓度分布的影响程度与平衡吸附点位所占比例f相关，因此图 10选取了f为0.05，0.50，0.95等3种不同吸附比例，研究在不同f条件下˜a对污染物浓度分布曲线的影响。
![]()
图 10 非平衡吸附速率影响数对污染物浓度分布曲线的影响Figure 10. Effects of number of non-equilibrium sorption rate on distribution curve of contaminant concentration对比图 10（a），（b）可以看出，曲线的变化趋势与图 9相似，˜a增大表明非平衡吸附速率越快，也就越接近平衡吸附，这也造成非平衡吸附所起到的作用越小，这与˜f增大对非平衡吸附作用产生的削弱作用是相似的，因此˜f，˜a对污染物分布曲线产生影响的内在机理也相似。在图 10中还加入了ISCO模型进行对比，从图 10（a）, （b）可以发现，当˜a > 200时，浓度分布曲线基本与ISCO模型对应的曲线重合，说明当˜a > 200时，此时的非平衡吸附过程足够快，可认为接近平衡吸附过程。
图 10还可以看出，随着f的增加不同˜a对应的浓度分布曲线之间的差异也在减小，当f=0.95时，˜a对浓度曲线的分布已几乎不产生影响，因为此时土柱中各点位基本为平衡吸附，不管˜a如何变化，非平衡吸附能起到的作用很小。因此˜a对污染物去除效率的影响程度与f的取值密切相关。
4. 非平衡吸附作用对污染物拖尾效应的量化分析
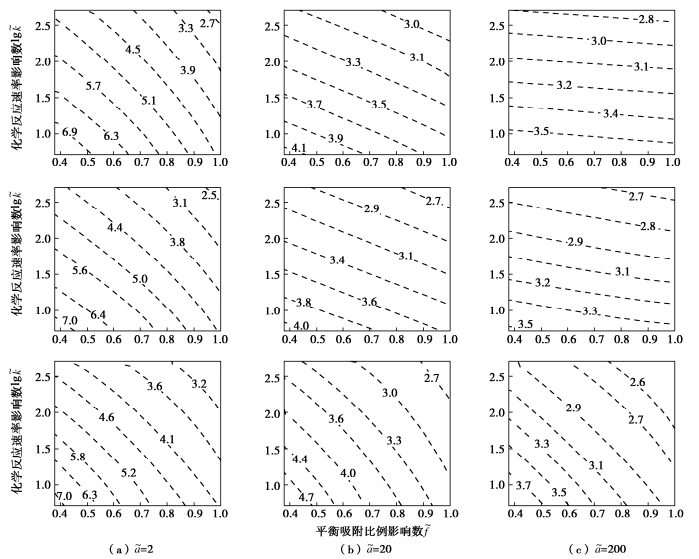
根据上文分析可知，污染物的去除效率与4个无量纲数Pe，˜k，˜a，˜f密切相关，而从3.4节可以发现，不同参数之间的耦合作用也会对模拟结果产生较大影响。因此本节对4个无量纲参数进行耦合分析，并统计出不同参数条件下达到污染物修复目标值（CB/C0=0.01）对应的PV2值（图 11）。
![]()
图 11 不同参数组合下污染物修复目标值对应的孔隙体积Figure 11. Pore volumes corresponding to target value of pollutant remediation for different combinations of parameters由3.3节中分析可知，˜f=1对应仅考虑平衡吸附的ISCO模型，从图 11中可以看出，NS-ISCO模型计算出的PV2均要高于ISCO模型，这也说明考虑非平衡吸附会加剧浓度拖尾效应，使修复所需的孔隙体积增加，当然这也更加接近反应性溶质的真实运移情况。尤其是在˜k，˜a，˜f较小且Pe较大的条件下，此时拖尾效应更加显著，例如Pe=10000，˜k =5（lg˜k=0.7），˜a=2，˜f=0.4所对应的PV2=7.0，而相同参数下的ISCO模型对应的PV2=2.5，前者为后者的2.8倍。但是在˜k，˜a，˜f均较大的情况下，两个模型对应的PV2较为接近。
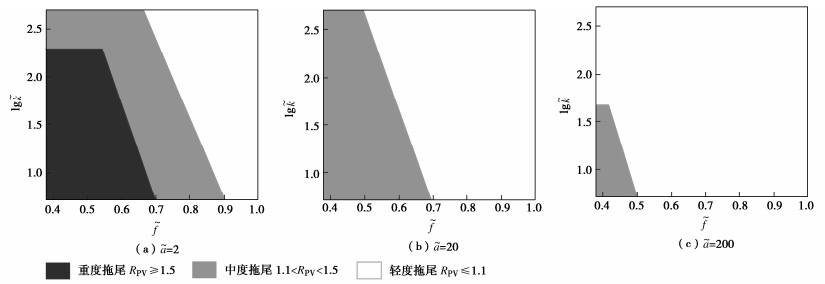
图 11表明在某些参数组合情况下，NS-ISCO模型相较于ISCO模型会产生较为严重的拖尾效应，此时若不考虑非平衡吸附，模型计算结果会与实际情况相差较大。但在某些参数组合下，NS-ISCO模型与ISCO模型结果较为接近，可以不考虑非平衡吸附的影响。为了定量描述不同参数组合下非平衡吸附对浓度拖尾效应的影响，探明是否需要考虑非平衡吸附的判别条件，本节提出孔隙体积比（RPV）的概念，定义为非平衡与平衡吸附模型达到污染物修复目标值对应的PV比值，
RPV=PV2PV1。 (12) 当Rpv≥1.5时，可以认为非平衡吸附显著加剧了拖尾效应；当1.1＜Rpv＜1.5时，非平衡吸附造成了中度拖尾；当Rpv≤1.1，非平衡吸附造成了轻度拖尾，在此情况下，NS-ISCO模型与ISCO模型结果相差较小，可以选择不考虑非平衡吸附的影响。
图 12展示了不同参数组合下拖尾程度的分布范围，由于不同Pe值对应的拖尾程度类似，因此图中并没有考虑Pe的影响。图 12显示重度拖尾主要分布在˜k，˜a，˜f均较小的区域，这也与前文的分析相吻合，在这种参数组合下，非平衡吸附作用不可忽视。当˜a=20时，有接近65%区域属于轻度拖尾，当˜a增大到200时，轻度拖尾的区域扩大至85%以上，再次说明了˜a是影响土壤非平衡吸附能力的重要参数。本节所总结的不同参数组合对拖尾效应的影响程度可以为污染场地的分类、评价和修复提供参考。当场地修复参数组合对应重度和中度拖尾情况时，需对修复场地开展长期现场监测，并可利用缓释等技术延长药剂在污染场地的停留时间，减少拖尾现象。而对于轻度拖尾场地，采用常规修复手段即可满足要求。
5. 结论
（1）对于平衡吸附，污染物含量在氧化反应的主导下，随着PV的增加而快速减小，直至修复完成；对于非平衡吸附，污染物含量变化呈现两阶段特征：第一阶段与平衡吸附相似，第二阶段为非平衡吸附占主导的慢速修复阶段。
（2）采用平衡吸附假设会明显高估溶质间的反应程度，并低估污染修复完成所需的药剂量。考虑非平衡吸附能合理描述溶质固有的非平衡吸附特征，准确刻画由于吸附能力差异导致的污染物拖尾效应。
（3）化学反应速率影响数˜k、平衡吸附比例影响数˜f以及非平衡吸附速率影响数˜a均对污染物的去除效率产生显著影响，且˜a对污染物去除效率影响程度与平衡吸附占总吸附的比例f相关，佩克莱数Pe影响相对较小。
（4）在˜k，˜a，˜f较小且Pe较大的情况下，拖尾效应较为严重，此时必须考虑非平衡吸附；但在˜k，˜a，˜f均较大的情况下，平衡与非平衡吸附模型结果较为接近，可以不考虑非平衡吸附的影响。
-
![]()
图 1 考虑两点吸附的双分子反应性溶质运移
Figure 1. Biomolecular reactive solute transport considering two-site sorption
![]()
图 2 本文模型计算结果与试验数据对比
Figure 2. Comparison of results between the proposed model and the experiment
![]()
图 3 药剂与污染物在土柱中的相对浓度分布
Figure 3. Distribution of relative concentration of reagent and contaminant in soil column
![]()
图 4 注入过程中非平衡吸附相对浓度分布
Figure 4. Distribution of relative concentration of nonequilibrium sorption during injection
![]()
图 6 药剂注入停止后污染物含量时变曲线
Figure 6. Temporal variation of pollutant after reagent injection
![]()
图 7 佩克莱数对污染物浓度分布曲线的影响
Figure 7. Effects of Peclet number on distribution curve of contaminant concentration
![]()
图 8 化学反应速率影响数对污染物浓度分布曲线的影响
Figure 8. Effects of number of chemical reaction rate on distribution curve of contaminant concentration
![]()
图 9 平衡吸附比例影响数对污染物浓度分布曲线的影响
Figure 9. Effects of number of equilibrium sorption ratio on distribution curve of contaminant concentration
![]()
图 10 非平衡吸附速率影响数对污染物浓度分布曲线的影响
Figure 10. Effects of number of non-equilibrium sorption rate on distribution curve of contaminant concentration
![]()
图 11 不同参数组合下污染物修复目标值对应的孔隙体积
Figure 11. Pore volumes corresponding to target value of pollutant remediation for different combinations of parameters
表 1 验证模型参数设定
Table 1 Adopted parameters for model validation
模型参数 取值 孔隙率 n 0.36 [14] 地下水流速度 v/(cm·s-1) 1.21×10-2 [14] 弥散系数 D/(cm2·s-1) 1.75×10-3 [14] 平衡吸附占总吸附的比例 f 0.22 [15] 分配系数 Kd/(m3·kg-1) 4.00×10-4 [15] 一阶吸附解吸速率常数 a/(1·s-1) 1.75×10-4 [15] 药剂与污染物反应速率常数 k/(m3·s-1·mol-1) 2.39×106 [14] 药剂与NOD反应速率 kn/(m3·s-1·mol-1) 1.10×10-5 [11] 药剂注入浓度 CAinj/(mol·m-3) 20 [14] 污染物初始浓度 CB0/(mol·m-3) 20 [14] 
下载: 导出CSV
表 2 NS-ISCO与ISCO模型参数设定
Table 2 Adopted parameters for NS-ISCO and ISCO models
参数 NS-ISCO模型 ISCO模型 平衡吸附占总吸附的比例 f 0.22 [15] 1 一阶吸附解吸速率常数a/(1·s-1) 1.75×10-4 [15] — 土柱长度 L/m 1 1 分配系数 Kd/(m3·kg-1) 4.00×10-4 [15] 4.00×10-4 [15] 孔隙率 n 0.30 [16] 0.30 [16] 地下水流速度 v/(cm·s-1) 1.21×10-2 [14] 1.21×10-2 [14] 纵向弥散度 αL/cm 0.40 [16] 0.40 [16] 药剂扩散系数 DA/(cm2·s-1) 1.55×10-5 [16] 1.55×10-5 [16] 污染物扩散系数 DB/(cm2·s-1) 7.98×10-4 [16] 7.98×10-4 [16] 药剂与污染物反应速率常数k/(m3·s-1·mol-1) 3.90×10-4 [16] 3.90×10-4 [16] 药剂与NOD反应速率kn/(m3·s-1·mol-1) 3.47×10-7 [11] 3.47×10-7 [11]
下载: 导出CSV
表 3 无量纲数的定义与取值
Table 3 Definition and values of dimensionless numbers
无量纲参数 表达式 取值 佩克莱数Pe 100/1000/10000/100000 化学反应速率影响数 0.5/5/50/500/5000 平衡吸附比例影响数 0.38/0.5/0.7/0.9/1 非平衡吸附速率影响数 2/20/200/2000/20000
下载: 导出CSV
-
[1] 查甫生, 刘晶晶, 许龙, 等. 水泥固化重金属污染土干湿循环特性试验研究[J]. 岩土工程学报, 2013, 35(7): 1246-1252. http://www.cgejournal.com/cn/article/id/15114 ZHA Fusheng, LIU Jingjing, XU Long, et al. Cyclic wetting and drying tests on heavy metal contaminated soils solidified/stabilized by cement[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(7): 1246-1252. (in Chinese) http://www.cgejournal.com/cn/article/id/15114
[2] SANCHEZ-VILA X, FERNÀNDEZ-GARCIA D, GUADAGNINI A. Interpretation of column experiments of transport of solutes undergoing an irreversible bimolecular reaction using a continuum approximation[J]. Water Resources Research, 2010, 46(12): W12510.
[3] LEE L S, RAO P S C, BRUSSEAU M L, et al. Nonequilibrium sorption of organic contaminants during flow through columns of aquifer materials[J]. Environmental Toxicology and Chemistry, 1988, 7(10): 779-793. doi: 10.1002/etc.5620071001
[4] JOHNSON G R, GUPTA K, PUTZ D K, et al. The effect of local-scale physical heterogeneity and nonlinear, rate-limited sorption/desorption on contaminant transport in porous media[J]. Journal of Contaminant Hydrology, 2003, 64(1/2): 35-58.
[5] VAN GENUCHTEN M T, WAGENET R J. Two-site/two- region models for pesticide transport and degradation: theoretical development and analytical solutions[J]. Soil Science Society of America Journal, 1989, 53(5): 1303-1310. doi: 10.2136/sssaj1989.03615995005300050001x
[6] BRADFORD S A, BETTAHAR M, SIMUNEK J, et al. Straining and attachment of colloids in physically heterogeneous porous media[J]. Vadose Zone Journal, 2004, 3(2): 384-394. doi: 10.2136/vzj2004.0384
[7] 赵颖, 梁冰, 薛强, 等. 土壤水环境中污染物运移双点吸附解吸动力学模型[J]. 岩土力学, 2007, 28(12): 2574-2578. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200712020.htm ZHAO Ying, LIANG Bing, XUE Qiang, et al. Kinetic model of contaminant transport in soil-water system considering two-site absorption-desorption[J]. Rock and Soil Mechanics, 2007, 28(12): 2574-2578. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200712020.htm
[8] WU S C, GSCHWEND P M. Sorption kinetics of hydrophobic organic compounds to natural sediments and soils[J]. Environmental Science & Technology, 1986, 20(7): 717-725.
[9] VALOCCHI A J, BOLSTER D, WERTH C J. Mixing-limited reactions in porous media[J]. Transport in Porous Media, 2019, 130(1): 157-182. doi: 10.1007/s11242-018-1204-1
[10] JOSE S C, CIRPKA O A. Measurement of mixing-controlled reactive transport in homogeneous porous media and its prediction from conservative tracer test data[J]. Environmental Science & Technology, 2004, 38(7): 2089-2096.
[11] CHA K Y, CRIMI M, URYNOWICZ M A, et al. Kinetics of permanganate consumption by natural oxidant demand in aquifer solids[J]. Environmental Engineering Science, 2012, 29(7): 646-653. doi: 10.1089/ees.2011.0211
[12] VAN GENUCHTEN M T, PARKER J C. Boundary conditions for displacement experiments through short laboratory soil columns[J]. Soil Science Society of America Journal, 1984, 48(4): 703-708. doi: 10.2136/sssaj1984.03615995004800040002x
[13] 张文杰, 赵培, 贾文强. 一维对流-扩散试验各种边界条件及其统一形式解析解[J]. 岩土力学, 2015, 36(10): 2759-2764. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201510003.htm ZHANG Wenjie, ZHAO Pei, JIA Wenqiang. Boundary conditions of one-dimensional convection- diffusion column tests and unified analytical solution[J]. Rock and Soil Mechanics, 2015, 36(10): 2759-2764. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201510003.htm
[14] GRAMLING C M, HARVEY C F, MEIGS L C. Reactive transport in porous media: A comparison of model prediction with laboratory visualization[J]. Environmental Science & Technology, 2002, 36(11): 2508-2514.
[15] PUTZ D K. Effect of Contact Time on Transport and Removal of Trichloroethene[D]. Tucson: University of Arizona, 1997.
[16] WEST M R, KUEPER B H. Numerical simulation of DNAPL source zone remediation with in situ chemical oxidation (ISCO)[J]. Advances in Water Resources, 2012, 44: 126-139. doi: 10.1016/j.advwatres.2012.05.001
[17] 姜林, 钟茂生, 梁竞, 等. 层次化健康风险评估方法在苯污染场地的应用及效益评估[J]. 环境科学, 2013, 34(3): 1034-1043. https://www.cnki.com.cn/Article/CJFDTOTAL-HJKZ201303035.htm JIANG Lin, ZHONG Maosheng, LIANG Jing, et al. Application and benefit evaluation of tiered health risk assessment approach on site contaminated by benzene[J]. Environmental Science, 2013, 34(3): 1034-1043. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HJKZ201303035.htm
-
期刊类型引用(2)
1. 柴春镜，冯政君，吴海滨，史晓凯，张俊杰，宋慧平. 煤矸石基多孔基质对土壤溶质运移的影响. 无机盐工业. 2024(09): 107-116 . 
百度学术
2. 黄孔月，张淇翔，冯启言，周来，朱雪强. 生物炭载纳米零价铁活化过硫酸盐降解土壤中的萘. 环境污染与防治. 2024(10): 1429-1437 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 299
- HTML全文浏览量: 33
- PDF下载量: 90
- 被引次数: 3
