Fluid-solid coupling model for discontinuous deformation analysis of unsaturated transient seepage
-
摘要: DDA由于处理块体大变形、大位移问题能力较强,因此被广泛应用在岩体数值模拟当中。但该方法在模拟渗流场,尤其是瞬态渗流场方面目前鲜有研究。根据立方定律建立DDA稳态渗流模型,将非饱和二维Richards方程离散化处理,推导DDA瞬态整体渗流矩阵。将水头矩阵以外荷载形式作用在块体上,建立瞬态非饱和渗流流固耦合DDA计算模型。通过对土柱入渗、砂槽入渗试验和危岩体工程案例进行数值模拟,验证了该模型的正确性,为DDA处理非饱和瞬态流固耦合问题提供新方法。
-
关键词:
- DDA /
- Richards方程 /
- 瞬态渗流 /
- 非饱和 /
- 流固耦合
Abstract: The discontinuous deformation analysis (DDA) is widely used in numerical simulation of rock mass due to its capability to deal with large deformation and large displacement of a block. However, this method is rarely studied in simulating seepage field, especially transient seepage. Based on the steady-state seepage model established according to the cubic law, the unsaturated two-dimensional Richards equation is discretized and the transient global seepage matrix conforming to the DDA scheme is derived. The DDA transient unsaturated seepage fluid-solid coupling model for the DDA is established by acting the water head matrix as the external load form on the block. The correctness of the model is verified through the numerical simulation of soil column infiltration, sand tank infiltration tests and dangerous rock mass engineering cases, which provides a new method for the DDA to deal with the transient unsaturated fluid-solid coupling problem.-
Keywords:
- DDA /
- Richards equation /
- transient seepage /
- partial saturation /
- liquid-solid coupling
-
0. 引言
DDA(discontinuous deformation analysis)即非连续变形分析,是一种基于非连续介质力学的数值分析方法。该方法以块体作为基本对象进行分析,块体边界可表示实际岩体裂隙,将各块体的位移视作基本未知量,通过块体间的接触关系将独立块体组合成一个块体系统,在处理块体大变形、大位移问题上具有一定的优势。因此DDA被广泛地应用在岩体这一块体离散介质的研究当中。众多学者将DDA应用于边坡稳定、岩体锚固、矿山开挖、地震等众多工程问题当中[1-6]。
原始DDA程序主要考虑块体应力应变场,难以直接应用到岩体渗流问题模拟当中。考虑复杂渗流场-应力应变场耦合最终建立能够真实模拟岩体赋存条件的DDA模型将大幅提高该算法的模拟精度和实用性,成为国内外学者关注的热点[7]。例如,张国新等[8]基于能量原理将水压荷载加入到原始DDA程序中,分析了水位变化条件下岩质边坡的倾倒变形机理。虞松等[9]提出了一种矩阵搜索方法,识别并删除DDA生成的裂隙岩体中的不连通裂隙,以生成更精确的裂隙水通网络,并对地下油库水封条件开挖的工程案例进行模拟,发现考虑流固耦合所获得的裂隙水压相对较小而涌水量则有所增加。王知深[10]在DDARF基础上推导达西-非达西流裂隙岩体渗流场和应力场控制方程,并建立DDARF平台裂隙岩体渗流应力耦合模型,将其应用在碳酸盐岩水力压裂过程分析中。江巍等[11]采用DDA对藕塘滑坡进行了失稳模式分析,采用块体在饱和状态下的强度参数来进行降雨工况的模拟,但在分析过程中没能考虑流固耦合的影响。Hu等[12]利用离散裂隙网络模型模拟页岩的自然裂隙,结合DDA提出复杂水力裂隙网络耦合流体力学模型,并将其应用在页岩气压裂开采设计中。Morgan等[13]利用有限体积裂隙网络模型模拟裂缝中的可压缩流体,研究了在内部有开口加压的格里菲斯裂缝在无渗漏无补给条件下压强和裂缝开度的变化,通过与半解析解进行对比验证了算法的正确性,并对高黏性压裂液在不渗透介质中的传播进行了数值分析。
上述研究成果对于DDA流固耦合的处理多是基于饱和稳态渗流理论。在实际工程中降雨入渗、库水位变化等工程案例均属于非饱和瞬态渗流问题,而目前运用DDA处理这一类问题通常是将降雨工况下材料强度参数进行折减,用饱和强度参数进行模拟,该方法并不能反映降雨入渗过程。针对这一问题,本文对DDA进行二次开发,推导DDA瞬态整体渗流矩阵,并将其加入到总体平衡方程中,实现DDA非饱和瞬态渗流流固耦合计算,通过土柱入渗、砂槽入渗试验验证该计算方法的正确性,为实际工程提供新的数值模拟手段和借鉴参考。
1. DDA稳态渗流计算
DDA以岩块和裂隙组成的岩体作为研究对象,由于岩块渗透能力较弱,岩体渗流通常只考虑裂隙渗流。采用立方定律来描述岩体单裂隙渗流:
q=ge312μJ。 (1) 式中:e为岩体裂隙开度;q为岩体裂隙流量;μ为流体的动力黏滞系数;J为光滑平板两端的水力梯度。
在实际工程当中,岩体裂隙具有一定的起伏和粗糙度。裂隙的起伏和粗糙度会使流体在裂隙中的流线变长,因此在相同情况下单位时间内通过粗糙裂隙的渗流量也会小于光滑裂隙。为了使计算结果更接近于真实值,引入粗糙度修正系数C,可得
q=ge312CμJ。 (2) 根据相关的水力学试验,粗糙度修正系数C可由岩体裂隙内表面凹凸粗糙程度Δ与裂隙开度e计算得到[14]
C=1+(Δe)1.5。 (3) 为将其写入DDA程序当中,将其改写成类似于DDA平衡方程的系数矩阵和未知数矩阵乘积的形式,即
q=TΔH, (4) 式中,T为岩体裂隙的导流系数。
对于岩体裂隙网络中的某一节点,其总流量为各条单裂隙流量对该节点流量的影响之和。对一个由n个节点组成的岩体模型来说,其整体渗流方程可写为
[T11T12…T1nT21T22…T2n⋮⋮⋱⋮Tn1Tn2…Tnn]{H1H2⋮Hn}={Q1Q2⋮Qn}。 (5) 式中:裂隙导流系数矩阵T的对角线元素Tii为与节点i相连接的所有裂隙的导流系数之和;Tij为由节点i和节点j组成裂隙的导流系数的相反数;水头矩阵H中的Hi为节点i对应的水头;流量矩阵Q中的Qi为节点i对应的总流量,由连接该点的所有裂隙流量叠加得到,且以流体流入该点为负流出该点为正。
在渗流的模拟过程当中,为了求解式(5)还需要在迭代前给出边界条件,即流量边界和水头边界。当某一节点的水头为已知量时,在迭代时将该点导流系数矩阵T的对角线元素Tii设置为1,其余元素Tij设置为0,以保证水头不变。当某一节点的流量为已知量时,将流量矩阵Q中对应的元素Qi设为已知量即可[15]。
2. DDA瞬态渗流计算
2.1 瞬态整体渗流矩阵推导
为了运用DDA进行瞬态渗流场模拟,将用体积含水量表示的二维非饱和Richards方程引入到DDA程序当中:
∂∂x(Dx(θ)∂θ∂x)+∂∂y(Dy(θ)∂θ∂y)=∂θ∂t。 (6) 式中:θ为体积含水量,Dx(θ),Dy(θ)分别为x方向和y方向上的水力扩散系数。
推导符合DDA形式的瞬态整体渗流矩阵,需要将二维Richards方程进行离散化处理。DDA中的块体边界代表了岩体中的裂隙,具有实际的物理意义,因此直接用DDA中块体划分形成的网格作为基础,将Dx(θ)∂θ∂x视为整体采用中心差分将式(6)中的第一项偏导数离散化,可得
∂∂x(Dx(θ)∂θ∂x)=D(θj+1i+12hx)∂θj+1i+12hx∂x−D(θj+1i−12hx)∂θj+1i−12hx∂xΔx。 (7) 式中:θ的上标j+1为时间差分,表示在第j+1时间步对应的体积含水量,下标i+12hx为空间差分,表示对第i个节点在x方向上取1/2个空间步长对应的体积含水量;Δx为x方向上两个节点的间距。
对式(7)中的偏微分式继续离散化处理,可得
D(θj+1i+12hx)∂θj+1i+12hx∂x=D(θj+1i+12hx)θj+1i+hx−θj+1iΔx ,D(θj+1i−12hx)∂θj+1i−12hx∂x=D(θj+1i−12hx)θj+1i−θj+1i−hxΔx 。} (8) 对于y方向,也有类似于式(8)的计算结果,只需要将空间差分的下标和节点间距分别记为y方向上的对应值即可。
对式(6)的等式右侧同样进行离散化处理,有
∂θ∂t=θj+1i−θjiΔt。 (9) 由于差分在渗流模拟过程中具有一定的滞后性,因此对于水力扩散系数D(θ)可以近似的用第j时步的计算结果去表达第j+1时步[16]。为了简化算式表达进行如下处理:
αxji=D(θji+12hx)Δx2 ,βxji=D(θji−12hx)Δx2 ,αyji=D(θji+12hy)Δy2 ,βyji=D(θji−12hy)Δy2 。} (10) 对式(7)~(10)进行整理可以得对某一节点体积含水量离散形式的表达式:
θj+1i−θjiΔt=αxjiθj+1i+hx+βxjiθj+1i−hx+αyjiθj+1i+hy+βyjiθj+1i−hy−(αxji+βxji+αyji+βyji)θj+1i。 (11) 式中:Δt为瞬态渗流的时间步长,上标为j表示本时步的体积含水量,均为已知量;j+1表示下一时步的体积含水量,通过本时步的状态求解;下标i+hx表示在x方向上与第i个节点间隔hx的下一个节点对应的体积含水量。
由此可知式(11)中每节点在x方向和y方向上均有两个相邻节点连接,对应了采用较为规则的四边形网格划分的情况。在DDA中块体可以是任意形状,因此网格的划分也会随之变得不规则,对网格中某一点i来说,其体积含水量仍然受到与之相连的其他节点的影响,将式(11)整理成矩阵形式,可得
[A11A12…A1nA21A22…A2n⋮⋮⋱⋮An1An2…Ann]{θj+11θj+12⋮θj+1n}={B1B2⋮Bn}。 (12) 与式(5)相似,式(12)的系数矩阵A是一个只在相邻节点连接的位置上有对应数值的稀疏矩阵。其中,非对角元素Aij表示由i,j两点构成裂隙对应的系数,即式(10)中的4个代数式之一;对角元素Aii表示在第i行中所有非对角元素Aij的和再加上时间步长Δt的倒数;而等式右侧的常数矩阵B为每一个节点本时步的体积含水量θ与时间步长Δt的比值。由此可知,对于系数矩阵A由于有时间项的存在,其每一行的对角线元素都大于该行非对角线元素的总和,是具有严格对角占优特点的矩阵。为了保证其收敛性,采用Gauss-Seidel迭代法求解。
对式(12)进行求解需要已知初始条件下每个节点的体积含水量,以及计算模型的边界条件。对DDA模型先进行稳态渗流计算,以稳态渗流的结果作为瞬态渗流的初始条件。对体积含水量已知的边界,将对角线元素Aii设为1,非对角线元素Aij设为0即可。
得到节点体积含水量后,通过下式转化成有效饱和度:
Se=θ−θrθs−θr。 (13) 式中:Se为有效饱和度;θs为饱和体积含水量;θr为残余体积含水量。
根据Van Genuchten[17]模型和Mualem模型[18]来表示有效饱和度和相对渗透系数、裂隙压力间的关系:
Pc=(Se−1m−1)1nα, (14) Tr=Se12[1−(1−Se1m)m]2。 (15) 式中:m,n,α均为土水特征曲线经验拟合参数,m可由m=1−1n计算得到;Pc为压力水头;Tr为相对渗透系数,加入到导流系数矩阵T中。
2.2 流固耦合计算
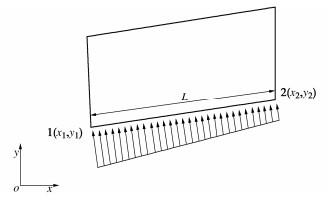
将渗流场计算得到的水头矩阵块体外荷载加入到DDA总体平衡方程中。假设有一块体i,该块体由点1和点2组成的边界受到水压力的作用。将水压力视作在两点之间呈梯形分布的荷载,如图 1所示。
点1上的水压力h分别向x,y方向分解,并规定与坐标轴同向为正,与坐标轴反向为负。
fx1=−h1sinα ,fy1=h1cosα 。} (16) 式中,α角为在点1处块体边界线与水平线的夹角。
对于点2上的水压力沿x,y方向分解可得到相似的结果。类似于DDA的体积力荷载子矩阵,点1和点2的水压力对块体i产生的势能为
Πi=−l12∫0(fxsus+fysvs)ds。 (17) 式中:l12为点1到点2的距离;s为在该裂隙长度方向上选取的某一微元段;us和vs为该微元段在x,y方向上的平移分量。
对式(17)进行势能最小化处理:
- \frac{{\partial {\Pi _i}(0)}}{{\partial {d_{ri}}}} = {\boldsymbol T_i}^{\text{T}}({x_1},{y_1})\left[ E \right] + {\boldsymbol T_i}^{\text{T}}({x_2},{y_2})\left[ G \right] (18) 式中: {\boldsymbol T_i}^{\text{T}} (x1, y1)和TiT(x2, y2)分别为点1和点2的位移转换矩阵,[E]和[G]由下式表示:
\begin{array}{l}\left[E\right]=\left(\begin{array}{cc}-\frac{{l}_{12}}{3}\mathrm{sin}\alpha & -\frac{{l}_{12}}{6}\mathrm{sin}\alpha \\ \frac{{l}_{12}}{3}\mathrm{cos}\alpha & \frac{{l}_{12}}{6}\mathrm{cos}\alpha \end{array}\right)\left\{\begin{array}{c}{p}_{1}\\ {p}_{2}\end{array}\right\}\text{ }\text{,}\\ \left[G\right]=\left(\begin{array}{cc}-\frac{{l}_{12}}{6}\mathrm{sin}\alpha & -\frac{{l}_{12}}{3}\mathrm{sin}\alpha \\ \frac{{l}_{12}}{6}\mathrm{cos}\alpha & \frac{{l}_{12}}{3}\mathrm{cos}\alpha \end{array}\right)\left\{\begin{array}{c}{p}_{1}\\ {p}_{2}\end{array}\right\}\text{ }。\end{array} (19) 式(18)的计算结果为一个6×1的子矩阵,将其加入到DDA总体平衡方程的荷载项Fi中,即式(20)的右侧:
\left[\begin{array}{cccc}{K}_{11}& {K}_{12}& \dots & {K}_{1n}\\ {K}_{21}& {K}_{22}& \dots & {K}_{2n}\\ ⋮& ⋮& ⋮& ⋮\\ {K}_{n1}& {K}_{n2}& \dots & {K}_{nn}\end{array}\right]\left\{\begin{array}{c}{D}_{1}\\ {D}_{2}\\ ⋮\\ {D}_{n}\end{array}\right\}=\left\{\begin{array}{c}{F}_{1}\\ {F}_{2}\\ ⋮\\ {F}_{n}\end{array}\right\}\text{ }。 (20) 式中,Kij为6×6的子矩阵,用于描述块体之间的相互作用,Di和Fi为6×1的子矩阵用以描述块体上的位移和荷载。
通过式(18)可以将渗流场计算的结果作为外荷载施加到应力应变场计算中,实现渗流场对应力应变场的影响。外荷载的施加则会改变下一时步岩体裂隙的开度,反向施加影响于渗流场,进而实现渗流场与应变场的双向耦合。
3. 算例验证
3.1 土柱入渗
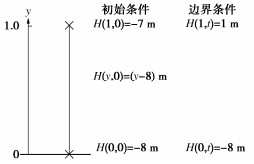
该算例选取长1 m土柱计算水体从其顶部入渗的压力水头分布[19]。在模型顶部初始施加-7 m的水头,底部施加-8 m的水头。当降雨开始后模型底部水头不发生变化,顶部施加1 m的水头作为边界条件,如图 2所示。
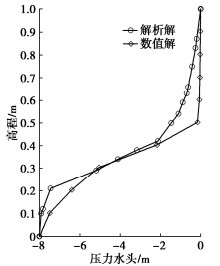
该模型的具体计算参数如表 1所示,将46800 s的压力水头数值解与解析解进行对比。
表 1 模型参数Table 1. Model parameters初始裂隙开度/mm θr θs α/m-1 n Δt/s 0.111 0.363 0.168 1 1.53 180 如图 3所示,数值解与解析解的压力水头均呈现随高程下降而逐渐降低的趋势,且模型上下两端压力水头随高程变化较慢而模型中部压力水头随高程变化较快,这是由于模型上下两端设置了固定水头作为边界条件,而模型中部受边界条件影响较小。与解析解相比,数值解模型顶部压力水头上升较快,原因可能为当块体体积含水量接近饱和体积含水量时,压力水头会近似处理成饱和状态压力水头,从而导致压力水头上升较快。数值解与解析解的压力水头具有相似的变化规律,验证了该数值方法的正确性。
3.2 砂槽入渗试验
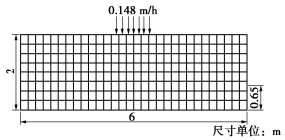
该算例采用砂槽入渗试验对程序的正确性进行验证,该试验常用于检验饱和-非饱和非稳定渗流算法的性能[20]。试验区域为一个高2 m宽6 m的矩形区域。边界条件为两侧边界自由排水、底部边界不透水、上部边界降雨。地下水位在0.65 m处,在试验开始后,对该试验区域中心1 m的范围内均匀施加0.148 m/h的降雨强度,降雨时长为8 h。初始裂隙宽度为0.0003 m,饱和渗透系数为9.72×10-5 m/s,其数值模型如图 4所示。
由于该模型是完全对称的,因此截取模型的右半段进行分析。完成建模后按照表 2参数对模型进行赋值并计算。
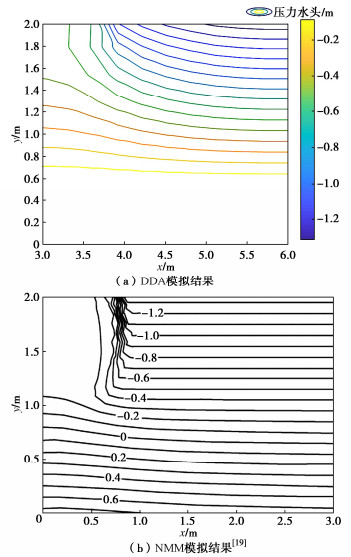
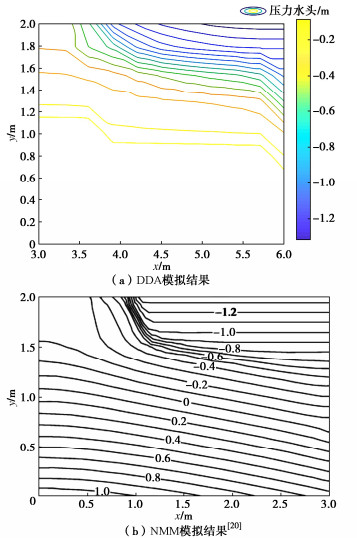
表 2 模型参数[19]Table 2. Model parameters初始裂隙开度/mm θr θs α/m-1 n Δt/s 1.29 0.01 0.3 3.3 4.1 3600 降雨开始2 h后的压力水头等值线如图 5所示。
由于在模型的左上角施加降雨边界,在该边界条件下的地层压力水头较大,随着右侧边界条件变为自由边界,压力水头迅速下降。符合在降雨区域地层饱和度上升负孔隙水压消散,在未降雨区域地层状态与初始状态接近这一规律。整体模型压力水头等值线呈左高右低的趋势,且随着深度降低等值线越发趋于平缓。符合浅表地层受降雨影响较大,体积含水量上升,压力水头上升,而深处地层受到影响较小的规律。与NMM的计算结果主要在降雨边界附近存在差异,其主要原因是NMM可以通过数学片对块体进一步细分,而DDA只在块体的边界有计算点。因此DDA模拟结果的等值线分布相NMM要更为稀疏,但总体分布规律与NMM相似。该模型主要研究降雨引起地下水位的变化,对于地下水位以下部分未进行插值。
降雨开始8 h后的压力水头等值线如图 6所示。随着降雨的进行,模型的压力水头整体呈上升趋势,尤其是在降雨边界处,由2 h的-0.49 m上升到了-0.36 m。地下水位线也随降雨进行而有所升高,且呈现左高右低的趋势,符合离降雨边界较近处饱和度上升较快的规律。等值线出现偏折是由于受到边界条件影响,在降雨边界和自由边界的分界处产生计算数值上的突变。DDA计算结果压力水头的分布规律与NMM计算结果相似。选取试验区域中央截面,分析地下水位随时间上升的规律如图 7所示。
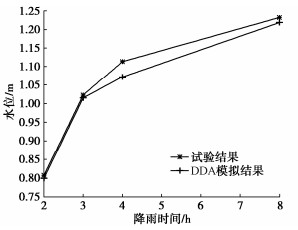
图 7将Vuaclin的室内试验结果和DDA数值模拟的结果进行对比。DDA数值模拟水位线上升的高度稍小于室内试验得到的结果,与试验结果相比最大误差出现在降雨4 h后,为3.74%。因此可以认为数值模拟结果与室内试验结果较为接近,进而认为该程序可以应用在非饱和瞬态渗流相关的模拟当中。
4. 工程案例
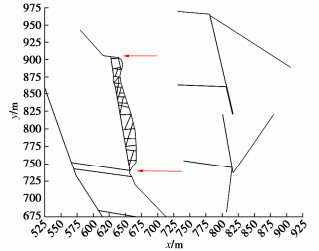
将改进后的DDA程序应用到重庆市巫山县三溪乡大梯子岩危岩体中。根据工程地质剖面图建立如图 8所示的计算模型。模型的力学参数如表 3所示。
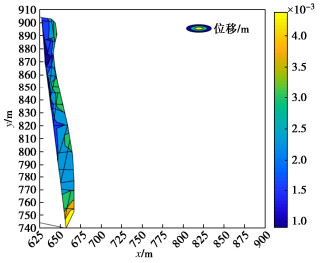
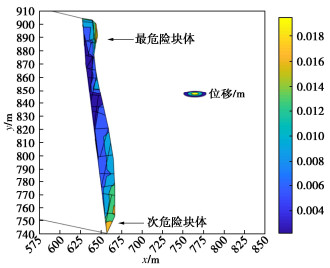
表 3 模型力学参数Table 3. Mechanical parameters for model材料 密度/(kg·m-3) 弹性模量/GPa 泊松比 抗拉强度/MPa 黏聚力/MPa 摩擦角/(°) 危岩体 2400 40 0.3 10 10 35 基岩 2400 50 0.25 20 50 50 在自然工况下对危岩体进行数值计算,结果如图 9所示。如图 9所示,在自然工况下,位移最大值点出现在危岩体的底部,其值为4.35 mm。可能由于差异风化导致危岩体底部出现凹腔,在上部自重等荷载的作用下导致危岩体在底部产生较大位移。其此时危岩体的整体稳定性系数为1.2127,危岩体整体处于相对稳定状态。
对于危岩体的非饱和渗流采用Van Genuchten模型描述,具体取值如表 4所示。
表 4 渗流参数Table 4. Seepage parameters初始裂隙开度/mm Δt/s n α/m-1 {\theta _{\text{s}}} {\theta _{\text{r}}} 0.3 1800 2 0.1 0.39 0.05 根据当地降雨统计数据模拟20 h强度为7.07 mm/h的较长时间持续降雨,得到结果如图 10所示。
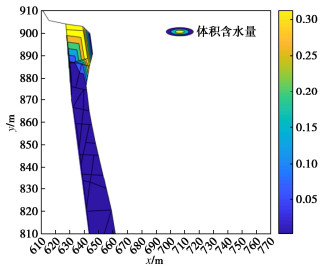
经过20 h降雨作用后,危岩体顶部体积含水量接近饱和体积含水量,产生饱和度大于0.95的暂态饱和区[21],而危岩体下部体积含水量则几乎不受到降雨的影响。由于降雨边界只在该模型顶部设置,因此底部节点的体积含水量受到降雨影响小,降雨从危岩体顶部入渗且无法渗透整个危岩体。危岩体右侧降雨入渗深度相对于左侧较深:一方面由于危岩体顶部有一定坡度,右侧高度低于左侧更有利于雨水入渗;另一方面,降雨入渗计算网格与切割岩体裂隙网格相同,岩体右侧裂隙长度较左侧更短,因此在相同的降雨条件下,危岩体右侧体积含水量更容易受到影响。而岩体顶部最右侧临空块体由于没有联通的裂隙对其进行切割,属于孤立块体,因此不在降雨入渗计算网格当中。危岩体的总位移云图如图 11所示。
危岩体最大位移为2.6 cm,出现在模型顶部的临空块体,发生较大位移的区域位于危岩体底部,其位移为1.8 cm。与自然工况相比,危岩体的位移有明显增长。危岩体顶部受到降雨影响,块体的强度有一定弱化,且顶部受到降雨形成的水头压力使其产生较大的位移。底部块体由于顶部块体的重力和变形增大,也产生了较大的位移。此时危岩体的整体稳定性系数为0.6304,危岩体整体处于不稳定状态。危岩体顶部和底部块体出现裂缝扩展、错动等大变形现象,如图 12所示。
该模拟结果符合工程实际规律,且能用于描述块体大变形过程,验证了本文提出的方法在工程应用中的可行性。
5. 结论
针对DDA难以进行瞬态渗流场模拟这一问题对其进行二次开发,将渗流场计算引入到原始DDA当中,形成一种流固耦合的DDA方法并通过相关经典算例和工程案例进行验证。提出了一种可以反映降雨入渗过程的DDA方法,为实际工程提供新的数值模拟手段,得到以下2点结论。
(1)对土柱入渗和砂槽入渗的模拟结果表明,本文建立的非饱和瞬态流固耦合计算模型与试验结果和NMM计算模型相比具有较好的一致性。能够对降雨造成的地下水位抬升、负压水头消散等变化过程进行模拟,拓展了DDA的适用范围。
(2)对大梯子岩危岩体的模拟结果表明,降雨导致危岩体顶部出现暂态饱和区,造成岩体强度参数弱化以及裂隙水压力上升,从而产生较大的位移。在顶部块体的重力和位移作用下,危岩体底部块体产生相对较大的位移,危岩体整体处于欠稳定状态。在危岩体治理中应做好排水措施,防止降雨造成危岩体失稳崩塌。
-
表 1 模型参数
Table 1 Model parameters
初始裂隙开度/mm θr θs α/m-1 n Δt/s 0.111 0.363 0.168 1 1.53 180 表 2 模型参数[19]
Table 2 Model parameters
初始裂隙开度/mm θr θs α/m-1 n Δt/s 1.29 0.01 0.3 3.3 4.1 3600 表 3 模型力学参数
Table 3 Mechanical parameters for model
材料 密度/(kg·m-3) 弹性模量/GPa 泊松比 抗拉强度/MPa 黏聚力/MPa 摩擦角/(°) 危岩体 2400 40 0.3 10 10 35 基岩 2400 50 0.25 20 50 50 表 4 渗流参数
Table 4 Seepage parameters
初始裂隙开度/mm Δt/s n α/m-1 0.3 1800 2 0.1 0.39 0.05 -
[1] 张开雨, 刘丰, 夏开文. 模拟脆性材料动态裂纹扩展的非连续变形分析方法[J]. 岩土工程学报, 2022, 44(1): 125-133. doi: 10.11779/CJGE202201012 ZHANG Kaiyu, LIU Feng, XIA Kaiwen. Numerical study on dynamic crack propagation of brittle materials by discontinuous deformation analysis[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(1): 125-133. (in Chinese) doi: 10.11779/CJGE202201012
[2] 张洪. 一种增广拉格朗日优化方案及其非连续变形分析实现[J]. 岩土工程学报, 2019, 41(2): 361-367. doi: 10.11779/CJGE201902015 ZHANG Hong. An optimized augmented Lagrangian method and its implementation in discontinuous deformation analysis(DDA) [J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 361-367. (in Chinese) doi: 10.11779/CJGE201902015
[3] XU D D, LU B, CHENG Y H, et al. A continuous-discontinuous deformation analysis method for simulating the progressive failure process of riverbanks[J]. Engineering Analysis With Boundary Elements, 2022, 143: 137-151. doi: 10.1016/j.enganabound.2022.06.012
[4] MA K, LIU G Y, GUO L J, et al. Deformation and stability of a discontinuity-controlled rock slope at Dagangshan hydropower station using three-dimensional discontinuous deformation analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 130: 104313. doi: 10.1016/j.ijrmms.2020.104313
[5] WU J H, DO T N, CHEN C H, et al. New geometric restriction for the displacement–constraint points in discontinuous deformation analysis[J]. International Journal of Geomechanics, 2017, 17(5): E4016002.1-E4016002.18.
[6] XIA M Y, CHEN G Q, YU P C, et al. Improvement of DDA with a new unified tensile fracture model for rock fragmentation and its application on dynamic seismic landslides[J]. Rock Mechanics and Rock Engineering, 2021, 54(3): 1055-1075. doi: 10.1007/s00603-020-02307-9
[7] 刘泉声, 蒋亚龙, 何军. 非连续变形分析的精度改进方法及研究趋势[J]. 岩土力学, 2017, 38(6): 1746-1761. LIU Quansheng, JIANG Yalong, HE Jun. Precision improvement methods and research trends of discontinuous deformation analysis[J]. Rock and Soil Mechanics, 2017, 38(6): 1746-1761. (in Chinese)
[8] 张国新, 雷峥琦, 程恒. 水对岩质边坡倾倒变形影响的DDA模拟[J]. 中国水利水电科学研究院学报, 2016, 14(3): 161-170. ZHANG Guoxin, LEI Zhengqi, CHENG Heng. DDA simulation of impact of water on toppling deformation of rock slope[J]. Journal of China Institute of Water Resources and Hydropower Research, 2016, 14(3): 161-170. (in Chinese)
[9] 虞松, 朱维申, 张云鹏. 基于DDA方法一种流-固耦合模型的建立及裂隙体渗流场分析和应用[J]. 岩土力学, 2015, 36(2): 555-560. YU Song, ZHU Weishen, ZHANG Yunpeng. Coupled hydro-mechanical model based DDA method for seepage analysis of fractured rock mass and its application[J]. Rock and Soil Mechanics, 2015, 36(2): 555-560. (in Chinese)
[10] 王知深. 岩石水压致裂的机理研究及非连续变形分析计算[D]. 济南: 山东大学, 2019. WANG Zhishen. Study on Mechanism and Discontinuous Deformation Analysis of Hydraulic Fracturing of Rock[D]. Jinan: Shandong University, 2019. (in Chinese)
[11] 江巍, 陈玮, 孙冠华, 等. 基于DDA方法的藕塘滑坡失稳模式分析[J]. 防灾减灾工程学报, 2016, 36(4): 551-558, 608. JIANG Wei, CHEN Wei, SUN Guanhua, et al. Research on failure mode of outang landslide using DDA method[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(4): 551-558, 608. (in Chinese)
[12] HU Y Z, LI X A, ZHANG Z B, et al. Numerical modeling of complex hydraulic fracture networks based on the discontinuous deformation analysis (DDA) method[J]. Energy Exploration & Exploitation, 2021, 39(5): 1640-1665.
[13] MORGAN W E, ARAL M M. An implicitly coupled hydro-geomechanical model for hydraulic fracture simulation with the discontinuous deformation analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 73: 82-94. doi: 10.1016/j.ijrmms.2014.09.021
[14] 郑春梅. 基于DDA的裂隙岩体水力耦合研究[D]. 济南: 山东大学, 2010. ZHENG Chunmei. Study on Hydro-Mechanical Coupling of Fractured Rock Mass Based on DDA[D]. Jinan: Shandong University, 2010. (in Chinese)
[15] 雷峥琦. 水库蓄水诱发岸坡蠕变的DDA分析[D]. 北京: 中国水利水电科学研究院, 2018. LEI Zhengqi. DDA Analysis on Creep Deformation of Slope Triggered by Reservoir impoundment[D]. Beijing: China Institute of Water Resources and Hydropower Research, 2018. (in Chinese)
[16] 王睿, 周宏伟, 卓壮, 等. 非饱和土空间分数阶渗流模型的有限差分方法研究[J]. 岩土工程学报, 2020, 42(9): 1759-1764. doi: 10.11779/CJGE202009021 WANG Rui, ZHOU Hongwei, ZHUO Zhuang, et al. Finite difference method for space-fractional seepage process in unsaturated soil[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(9): 1759-1764. (in Chinese) doi: 10.11779/CJGE202009021
[17] VAN GENUCHTEN M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. doi: 10.2136/sssaj1980.03615995004400050002x
[18] MUALEM Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research, 1976, 12(3): 513-522. doi: 10.1029/WR012i003p00513
[19] 陈远强, 杨永涛, 郑宏, 等. 饱和-非饱和渗流的数值流形法研究与应用[J]. 岩土工程学报, 2019, 41(2): 338-347. doi: 10.11779/CJGE201902012 CHEN Yuanqiang, YANG Yongtao, ZHENG Hong, et al. Saturated-unsaturated seepage by numerical manifold method[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(2): 338-347. (in Chinese) doi: 10.11779/CJGE201902012
[20] VAUCLIN M, KHANJI D, VACHAUD G. Experimental and numerical study of a transient, two-dimensional unsaturated-saturated water table recharge problem[J]. Water Resources Research, 1979, 15(5): 1089-1101. doi: 10.1029/WR015i005p01089
[21] 谢强, 田大浪, 刘金辉, 等. 土质边坡的饱和-非饱和渗流分析及特殊应力修正[J]. 岩土力学, 2019, 40(3): 879-892. XIE Qiang, TIAN Dalang, LIU Jinhui, et al. Simulation of seepage flow on soil slope and special stress-correction technique[J]. Rock and Soil Mechanics, 2019, 40(3): 879-892. (in Chinese)
-
期刊类型引用(2)
1. 邱军领,贾玎,赖金星,唐琨杰,强磊. 含裂隙土质隧道降雨入渗双通道渗流模型. 岩土工程学报. 2025(03): 548-558 .  本站查看
本站查看
2. 张小东,路喆津,刘敏,杨峰,赵炼恒. 强降雨作用下引入分形理论的浅层边坡入渗及稳定性分析. 哈尔滨工业大学学报. 2024(11): 140-150 .  百度学术
百度学术
其他类型引用(3)



 下载:
下载: