Prediction of thermal conductivity of soils based on artificial intelligence algorithm
-
摘要: 导热系数是土体热力学特征的基本参数，也是岩土工程热工计算的重要参数之一。它受土体骨架、矿物成分和饱和度等因素的影响。对土体导热系数的影响因素进行分析，采用各种先进的人工智能算法来研究土体的传热机理，并建立预测模型。预测模型通过相关系数R2、均方根误差RMSE、绝对平均误差MAE和方差比VAF进行检验，对误差进行统计分析，并对预测模型的稳健性进行分析，预测模型与传统的经验关系模型进行对比分析。结果表明：人工神经网络（ANN）模型、基于自适应神经网络的模糊推理系统（ANFIS）模型和支持向量机（SVM）模型都准确的预测出土体的导热系数，相关系数R2大于0.9，均方根误差RMSE小于0.2 (W·m-1·K-1)，绝对平均误差MAE小于0.13 (W·m-1·K-1)，方差比VAF大于90%。提出的预测模型精度显著高于传统经验关系模型。根据误差统计和稳健性分析结果，建议土体导热系数的预测计算优先使用ANN模型和SVM模型。Abstract: The thermal conductivity is the basic geotechnical thermodynamic parameter, and it is also one of the important parameters in the design of thermal geotechnical structures. It is affected by the factors such as soil skeleton mineral composition, and degree of saturation. The influencing factors for the thermal conductivity of soils are analyzed. Various advanced artificial intelligence algorithms are used to investigate the heat transfer mechanism of soils, and to establish prediction models. The correlation coefficient (R2), root mean square error (RMSE), mean absolute error (MAE) and variance ratio (VAF) are calculated to analyze the prediction error and robustness of these prediction models. By comparing withthe traditional empirical relationship model, the results show that the artificial neural network (ANN) model, the adaptive neural network-based fuzzy inference system (ANFIS) model and the support vector machine (SVM) model all predict the thermal conductivity of soils acceptably. The R2 is greater than 0.9, the RMSE is less than 0.2 (W·m-1·K-1), the MAE is less than 0.13 (W·m-1·K-1), and the VAF is greater than 88% for all these prediction models. The accuracy of the proposed prediction models is significantly higher than that of the traditional empirical relationship model. According to the results of error statistics and robustness analysis, the ANN and SVM models are recommended in the prediction of the thermal conductivity of soils.
-
0. 引言
随着工业化和城市化的加速发展，人们对化石能源的消耗和全球变暖趋势加剧，对新能源的开发和利用变得日益重要[1]。准确测定岩土材料的导热系数是岩土工程温度场分析和能源桩设计的重要内容，土体导热系数是一个复杂的性质，主要取决于土体的类型、饱和度、粒径分布和颗粒堆积密度等因素[2]。导热系数是土体热力学特性的重要指标之一，能够直接反映热能在土体介质中的传递特性[3]。
近年来，很多学者对土体热传导特性进行大量研究，并提出大量的预测模型。Kersten等[4]采用单根线柱热源径向加热的热传导测试方法对19种不同类型土体的导热系数进行测试，分析了含水率和干密度对导热系数的影响，得出了基于含水率和干密度预测土体导热系数的经验公式；Cote等[5]和Johansen[6]对650多个土样的导热系数测试结果进行分析，并在Johansen[4]提出的归一化模型的基础上建立了广义的归一化模型；Erzin等[7]基于人工神经网络模型建立了预测土体导热系数的单个预测模型和广义预测模型，得出人工神经网络模型在预测土体导热系数方面的有效性。综上所述，预测土体导热系数的主要是通过经验关系模型、理论计算模型和人工神经网络模型，经验关系模型由于考虑的因素较少，计算精度较低。理论计算模型在计算土体导热系数时，所涉及的参数较多，计算过程复杂，难以在实际工程中应用。人工神经网络模型可以考虑的影响因素较多，在预测土体导热系数时精度较高。
为建立预测土体导热系数预测模型，首先对土体导热系数的主要影响因素进行分析，然后利用人工智能算法对土体导热系数进行预测，对预测结果进行检验，并与传统经验关系模型进行对比，验证人工智能算法的有效性和稳健性。
1. 土体导热特性
土体导热系数是表征土体热物理性质的重要指标，与众多因素密切相关，如土颗粒矿物成分、饱和度、粒径分布和孔隙率等，其中矿物成分是决定土颗粒导热性能的关键因素[8]。导热系数能够直接反映热能在土体介质中的传递特性。因此，为了研究土体的传热机理，本文主要介绍土体饱和度、矿物成分、颗粒分布和温度等参数对热传导的影响。
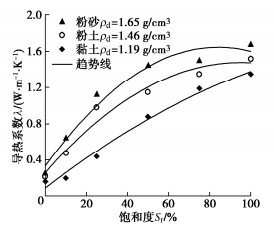
为研究饱和度对土体导热系数的影响，根据Tarnawski等[9-11]对40种土体导热系数实测数据，选择黏土、粉土和粉砂的测试结果来研究饱和度对导热系数的影响，如图 1所示。从图 1可以看出，当土体饱和度增加时，导热系数也随之增加，饱和度增加会提高土体中的含水率，含水率的增加会使土颗粒表面形成水膜，颗粒之间形成水桥，而空气的占比会减小，由于水的导热系数明显大于空气的导热系数，热量通过颗粒表面水膜及其水桥传递增加，使土体导热系数增加[12]。土体饱和度的增加会提高颗粒间的接触面积，热量通过颗粒与颗粒间的传递增加，使土体的导热系数增大。
在影响土体导热系数的因素中，固相的矿物组成成分对固体颗粒导热系数的影响非常重要[13]，土体的固体颗粒主要由原生矿物和次生矿物组成，而这些矿物的导热系数不同，固体颗粒矿物的组成成分不同会影响土体的导热系数。在土体的矿物组成中，石英的导热系数为7.69 (W·m-1·K-1)，而其他矿物的导热系数通常在1.25~4.00 (W·m-1·K-1)，石英的导热系数明显高于其他矿物，石英含量高的土体其导热系数也较大[14]。从图 1可以看出，粉砂的导热系数明显高于黏土的导热系数，因为粉砂的石英含量高于黏土的石英含量，所以石英含量高的土体导热系数较大。因此，土体固体颗粒的导热系数取决于矿物的类型和比例，尤其是石英的含量。
对土体导热系数的影响还包括颗粒分布、颗粒粒径大小、颗粒形状、各向异性和温度等因素。颗粒分布会影响土体的级配，级配的变化会影响颗粒与颗粒间的接触面积，从而影响土体的导热系数。在相同干密度下，颗粒粒径越小，颗粒间的接触点越多，而热量通过固体颗粒内部传递热量要快于颗粒间的传播，在相同情况下，颗粒粒径越小，导热系数越低，从图 1可以看出黏土的颗粒粒径最小，在相同情况下其导热系数最小；颗粒形状会影响颗粒与颗粒间接触的面积，从而影响热量的传播。Macaulay等[15]对澳大利亚粉砂岩导热系数测试，得出导热系数随层理方向角增加而增加，但层理方向角增加到40°后，其导热系随层理方向角的增加而数趋于平稳。温度的变化会影响分子的热运动，Xu等[16]得出膨润土的导热系数随温度升高而增大，当温度为90℃时，其导热系数为5℃时的（1.2~1.5）倍；当温度为5~60℃时，导热系数随温度的变化相对较小；当温度高于60℃时，导热系数显著增加。
2. 土体导热系数数据库
本文使用的数据来源于40种加拿大田间土[9-11]。其中22种为细粒土（含砂量 < 40%），18种为粗粒土（含砂量 > 40%）。根据前述土体导热系数影响因素的分析，选择干密度、饱和度、黏粒含量、粉粒含量和砂粒含量作为预测模型的输入参数，土体导热系数作为模型的输出参数。表 1列出了预测模型输入参数和输出参数的边界值。
表 1 预测模型输入参数的输出参数的边界值Table 1. Boundary values of input parameters and output parameters of prediction model类型 参数项 最小值 最大值 输入参数 干密度ρd/(g·cm-3) 0.999 1.728 饱和度Sr/% 0 100 黏粒含量c/% 0 42 粉粒含量si/% 0 83.4 砂粒含量sa/% 0 100 输出参数 导热系数λ/(W·m-1·K-1) 0.1 3.2 3. 计算模型
随着人工智能算法在岩土工程领域快速发展，使用这些算法对岩土工程参数进行计算，将节约工程造价及时间。基于这一目的，通过人工神经网络模型（ANN模型）、基于自适应神经网络的模糊推理系统（ANFIS模型）和支持向量机模型（SVM模型）对土体的导热系数λ进行计算。
3.1 人工神经网络模型
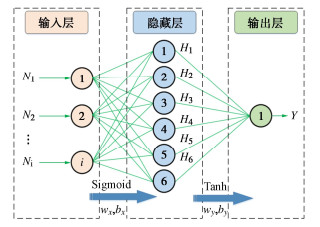
人工神经网络模型是基于模仿人类大脑的结构和功能的信息处理系统[17]。目前已经开发出很多神经网络算法，如Levenberg-Marqurdt算法、共轭梯度算法、贝叶斯正则化算法[17-19]。神经网络模型由输入层、隐藏层和输出层组成，层与层之间通过激活函数f(x)进行转换，激活函数f(x)通常为Sigmoid函数、双曲线正切函数（Tanh）和校正线性函数（Relu）。图 2是一个典型的神经网络结构，其中N1，N2和Ni是输入参数，Y是输出参数。使用下列过程对人工神经网络建模：
将输入数据和输出数据在0到1之间进行归一化。归一化计算式为[7]
xnorm=x−xminxmax−xmin， (1) 式中，xnorm为标准化值，x为实际值，xmax为最大值，xmin为最小值。输入参数Ni在隐藏层的Sigmoid激活函数的计算式为
Sk=sigmoid(N∑i=1wxNi+bx)， (2) sigmoid=(11+e−x)， (3) 式中，Sk，wx和bx分别为隐藏层节点的计算值、权重参数和偏差因子。输出层节点的计算式为
Yn=M∑j=1wySk+by， (4) 式中，wy为权重参数，bx为输出层偏差因子。输出层数据的反归一化：
Y=Yn[xmax−xmin]+xmin。 (5) 本文使用的神经网络模型是基于贝叶斯正则化算法建立的预测模型，贝叶斯正则化算法使用岭回归将非线性回归转换为统计问题[19]。这种方法的优点是在验证过程中不需要使用交叉验证技术，这可以简化模型训练，节约模型的计算时间。
3.2 基于自适应神经网络的模糊推理系统
基于自适应神经网络的模糊推理系统（ANFIS）是将模糊系统和神经网络相结合而构成的网络，采用BP算法和最小二乘估计法的混合算法进行学习，考虑了基于一阶Sugeno模型的两种模糊If-then后置规则。
规则一，如果x=A1和y=B1，则
f1=p1x+q1y+r1。 (6) 规则二，如果x=A2和y=B2，则
f2=p2x+q2y+r2。 (7) 式中x和y为输入参数；Ai和Bi为模糊集；fi为模糊规则指定的模糊区域内的输出值；pi，qi和ri为训练过程中确定的参数。本文使用减法聚类算法训练ANFIS模型，这种算法可以自动估计聚类数目及其位置[20]。
3.3 支持向量机模型
支持向量机模型（SVM）是一种机械学习方法，其理论是建立一个最优分类超平面，将线性不可分问题转换成线性可分问题[21]。训练样本为{xi，yi}，i=1到m，其中xi∈R，yi∈R，R为实数域。以φ(xi)表示映射到高维空间中的样本，构造得到的函数表达式为
yi=Wφ(xi)+b， (8) 式中，W为可调权值向量，b为偏置值。
寻找最优的分类超平面亦即寻找最优的W和b。引入松弛变量ξ和ξ∗，依据结构风险最小化准则，采用ε-SVR模型建立带有约束条件的模型优化函数：
foptimization=minW,b,ξi,ξ∗i[12WTW+Cm∑i=1(ξi+ξ∗i)]， (9) 约束条件为
yi−WTφ(xi)+b⩽ (10) 式中，C为惩罚函数， \varepsilon 为损失函数。
使用二次规划优化算法SMO（sequential minimal optimization）构造得到关于x的预测函数 f(x) ：
f(x) = \sum\limits_{i = 1}^m {(a_i^* - {a_i})} \varphi {({x_i})^{\text{T}}}\varphi ({x_i}) + b \text{，} (11) 式中， f(x) 为代表土体导热系数， a_i^* 为 {a_i} 的伴随矩阵，m为样本数目。
3.4 蒙特卡罗模拟
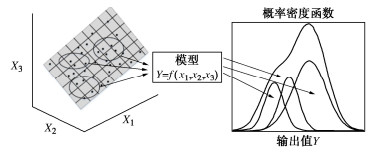
在复杂的岩土工程中使用人工智能算法时，蒙特卡罗方法常用于分析计算模型输入参数存在可变性时的鲁棒性[22]。图 3显示了蒙特卡罗方法的基本原理。它的原理是随机输入参数来多次重现输出结果[23]。输入参数的随机波动可以在输出解上传播，这意味着输出的概率密度函数是由所有输入参数的统计信息构成的。输出的概率分布定量分析对于表征模型的稳健性是非常有效的。在本文中，使用蒙特卡罗方法分析预测模型的稳健性，并对结果进行统计分析。
4. 预测模型的建立与性能检验
4.1 预测模型的建立
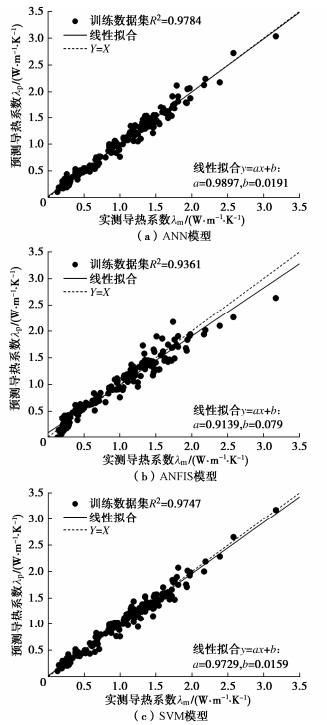
使用了人工智能算法建立预测土体导热系数的预测模型。根据第一节对土体导热系数影响因素的分析，所有计算模型的输入参数为干密度、饱和度、黏粒含量、粉粒含量和砂粒含量，输出参数为土体的导热系数。将数据分为两个部分，训练部分使用70%的数据，测试部分使用30%的数据。人工神经网络模型隐藏层神经元的数量从1开始增加，通过训练得出最佳隐藏层和隐藏层神经元数。SVM模型是由三次多项式核函数构建的，选择盒约束的正则化常数c为0.112，SVM模型的ε参数为0.0111。预测模型（训练集）对土体导热系数λ的计算结果与实测结果如图 4所示。
![]()
图 4 预测模型训练数据集预测值与实测值比较Figure 4. Comparison between predicted and measured values in training data set of prediction model从图 4可以看出，每个智能计算模型在训练数据集中都准确的计算出土体的导热系数，为了得到预测结果与实测结果的相关性，对预测值与实测值进行线性拟合，拟合结果如图 4所示。预测模型训练效果最好的是ANN模型，相关系数R2=0.9784；然后是SVM模型的训练效果较好，相关系数R2=0.9747；训练效果最差的是ANFIS模型，相关系数R2=0.9361。线性拟合结果表明ANN模型和SVM模型的线性拟合最靠近Y=X等值线，也说明ANN模型和SVM模型的预测精度高。
4.2 预测模型的性能检验
为了量化计算模型的质量，采用了相关系数R2、均方根误差RMSE、平均绝对误差MAE和方差比VAF来检验计算模型的性能[17, 24]。均方根误差RMSE、平均绝对误差MAE和方差比VAF的计算公式如下所示：
{\text{RMSE}} = \sqrt {\frac{1}{{N - M}}\sum\limits_1^N {{{({y_0} - {y_{\text{p}}})}^2}} } \text{，} (12) {\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {{y_0} - {y_{\text{p}}}} \right|} \text{，} (13) {\text{VAF}} = \left[ {1 - \frac{{{var} ({y_0} - {y_{\text{p}}})}}{{{var} ({y_0})}}} \right] \times 100 \text{，} (14) 式中， {y_0} 为实测值， {y_{\text{p}}} 为预测值，N为样本的编号，M为回归过程的评估参数，var为方差。如果VAF为100%且RMSE为0，则该模型被视为优秀。表 2给出了各预测模型的性能指标值。预测模型对土体导热系数λ的预测值与实测值对比如图 5所示。
表 2 预测模型性能指标Table 2. Performance indexes of prediction models模型代号 数据集 R2 RMSE
/(W·m-1·K-1)MAE
/(W·m-1·K-1)VAF
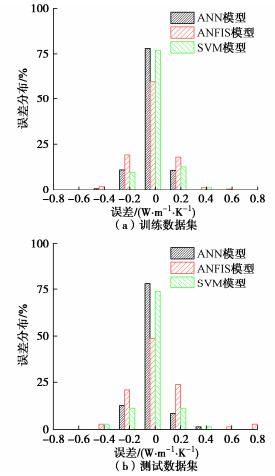
/%ANN 训练数据集 0.9784 0.0874 0.0673 97.84 测试集 0.9746 0.0985 0.0701 97.45 ANFIS 训练数据集 0.9361 0.1391 0.1096 94.50 测试集 0.9078 0.1958 0.1262 90.17 SVM 训练数据集 0.9747 0.0941 0.0725 97.47 测试集 0.9649 0.1147 0.0767 96.48 ![]()
图 5 预测模型测试数据集预测值与实测值比较Figure 5. Comparison between predicted and measured values of test data set of prediction model从表 2和图 5可以看出，每个预测模型对土体导热系数 \lambda 的预测精度都很高。预测模型预测精度最高的是ANN模型，SVM模型的预测精度略低于ANN模型；预测精度最低的是ANFIS模型，从图 5（b）中可以看出，预测值与实测值偏差较大，数据较离散。线性拟合方程结果表明ANN模型和SVM模型的预测精度高。为了分析计算模型预测值与实测值之间的误差，预测模型的误差分布如图 6所示。
从图 6可以看出，在训练数据集和测试数据集，每个智能计算模型的误差分布主要集中在-0.3~0.3 (W·m-1·K-1)，每个智能计算模型的计算误差都很小；ANN模型误差分布达到最高峰值，并靠近零；其次分别是SVM模型和ANFIS模型。然而，从表 2可以看出，在测试测试数据集，ANN模型在均方根误差RMSE方面表现最好，均方根误差RMSE=0.0985 (W·m-1·K-1)，而SVM模型和ANFIS模型的均方根误差RMSE分别为0.1958 (W·m-1·K-1)和0.1147 (W·m-1·K-1)；上述分析结果表明，ANN模型在预测土体的导热系数 \lambda 方面的性能最好，ANN模型的权重和偏差基于贝叶斯正则化优化使模型的性能更好，ANFIS模型和SVM模型也很好的预测了土体的导热系数 \lambda 。
4.3 预测模型的稳健性分析
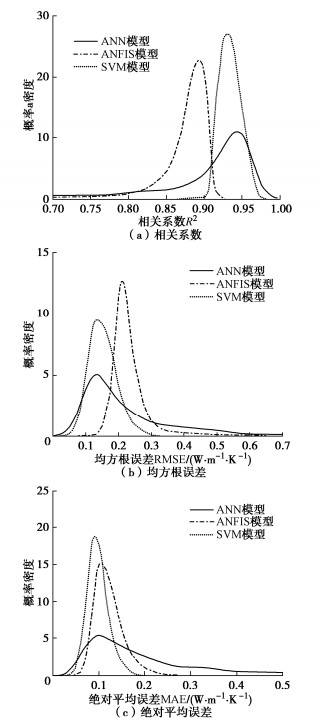
为了评估智能计算模型的稳健性，将用于训练的70%的数据进行随机组合，作为新的输入数据集，生成了300个蒙特卡罗模拟。统计每个预测模型计算值与实测值之间的偏差，每个预测模型获得了300个相关系数R2、均方根误差RMSE和绝对平均误差MAE，计算了关系数R2和均方根误差RMSE的概率分布，以得出智能计算模型在可变输入参数下的性能。蒙特卡罗模拟的相关系数R2、均方根误差RMSE和绝对平均误差MAE概率分布如图 7所示。模拟结果统计如表 3所示。
![]()
图 7 蒙特卡罗模拟检验参数概率分布Figure 7. Probability distribution of parameters by Monte Carlo simulation tests表 3 蒙特卡罗模拟结果统计Table 3. Statistics of simulated results by Monte Carlo method检验参数 预测模型 D25 D50 D75 平均值 R2 ANN 0.8926 0.9512 0.9723 0.9132 ANFIS 0.8731 0.8951 0.9056 0.8761 SVM 0.9362 0.9459 0.9552 0.9449 RMSE ANN 0.0838 0.1338 0.2518 0.1898 ANFIS 0.1935 0.2105 0.2405 0.2285 SVM 0.1093 0.1333 0.1623 0.1373 MAE ANN 0.0432 0.0952 0.1832 0.1322 ANFIS 0.1234 0.1394 0.1614 0.1464 SVM 0.0839 0.0959 0.1109 0.0989 从图 7（a）和表 3可以看出，在相关系数R2概率分布图中可以看出，ANN模型的相关系数R2分布最靠近1，其次分别是SVM模型和ANFIS模型，其中SVM模型的相关系数R2主要分布在0.9至0.97范围内。从图 7（b）和表 3可以看出，在均方根误差RMSE的概率分布图中ANN模型的概率分布最靠近0，其次是SVM模型和ANFIS模型，分布结果跟相关系数R2的概率分布结果相同。从图 7（c）和表 3可以看出，在绝对平均误差MAE的概率分布图中SVM模型的概率分布最靠近0，其次是ANN模型和ANFIS模型。ANN模型、ANFIS模型和SVM模型相关系数R2和均方根误差RMSE的分位数值和平均值如表 3所示。在300次蒙特卡罗模拟中，对相关系数R2、均方根误差RMSE和绝对平均误差MAE的统计研究表明，SVM模型的稳健性最好，其次分别是ANN模型和ANFIS模型。
5. 预测模型性能评价
目前，计算土体导热系数主要是理论计算模型和经验关系模型，理论计算模型计算土体导热系数时，涉及的参数及要求较多，难以有效计算土体导热系数；经验关系模型计算土体导热系数时，具有计算过程简单、易操作等优点，在工程设计中普遍使用此方法。为了评价智能计算模型预测土体导热系数的性能，本文选取Johansen[6]模型、Cote[5]模型和Lu[25]模型计算土体的导热系数。
Johansen模型是Johansen[6]基于归一化热传导系数概念提出的经验关系模型，该模型能对冻结和未冻结土的导热系数进行计算，经验关系式为
\lambda = ({\lambda _{{\text{sat}}}} - {\lambda _{{\text{dry}}}}){K_{\text{e}}} + {\lambda _{{\text{dry}}}} \text{，} (15) 式中， {\lambda _{{\text{sat}}}} 为饱和土体热导率， {\lambda _{{\text{dry}}}} 为干土热导率，Ke为土体的归一化热导率，当 {S_{\text{r}}} > 0.05时，Ke对于粗土的计算式为
{K_{\text{e}}} = 0.7\log {S_{\text{r}}} + 1 \text{，} (16) 式中， {S_{\text{r}}} 为饱和度。当 {S_{\text{r}}} > 0.1时，Ke对于粗土的计算式为
{K_{\text{e}}} = \log {S_{\text{r}}} + 1 \text{，} (17) Johansen通过改进De Vries[26]热导系数计算模型，提出了干土的导热系数计算公式：
{\lambda _{{\text{dry}}}} = \frac{{0.137{\rho _{\text{d}}} + 64.7}}{{2650 - 0.947{\rho _{\text{d}}}}} \text{，} (18) 式中， {\rho _{\text{d}}} 为干密度。在饱和土导热系数计算方面，Sass等[27]提出的公式被普遍运用，其计算式为
{\lambda _{{\text{sat}}}} = \lambda _{{\text{water}}}^n\lambda _{{\text{solid}}}^{1 - n} \text{，} (19) 式中， \lambda _{{\text{water}}}^{} ， \lambda _{{\text{solid}}}^{} 分别为水和土固体颗粒的导热系数，n为孔隙率。
Cote模型是Cote等[5]根据Johansen[6]提出的归一化热导系数计算模型的基础上，建立了广义的归一化预测模型：
\lambda = ({\lambda _{{\text{sat}}}} - {\lambda _{{\text{dry}}}}){K_{\text{e}}} + {\lambda _{{\text{dry}}}} \text{，} (20) 式中，Ke为土体的归一化热导率。但Ke和 {\lambda _{{\text{dry}}}} 的计算公式已经被修改，
{K_{\text{e}}}{\text{ = }}\frac{{\kappa {S_{\text{r}}}}}{{1 + (\kappa - 1){S_{\text{r}}}}} \text{，} (21) {\lambda _{{\text{dry}}}} = \chi ({10^{ - \eta n}}) \text{，} (22) 式中，κ为经验参数，用于表达土体种类和冻结或未冻结对Ke的影响，χ和η为考虑土的种类和颗粒形状对干土热导系数影响的参数。
Lu模型是Lu等[25]对12种不同土性的天然土在各种含水率条件进行了大量导热系数测试，通过试验数据拟合，得到了更为简单的干土导热系数和孔隙率的线性关系，并在Johansen提出的归一化热导系数计算模型的基础上，提出了如下经验公式：
\lambda {\text{ = }}\left[ {\lambda _{{\text{water}}}^n\lambda _{{\text{solid}}}^{1 - n} - (b - an)} \right]\exp [\alpha (1 - S_{\text{r}}^{\alpha - 1.33})] + (b - an) \text{，} (23) 式中，a和b为确定干土热传导系数的参数，建议分别取a=0.56和b=0.51，α反映土种类对Kersten变量的影响，针对粗粒土和细粒土分别取0.96和0.27。
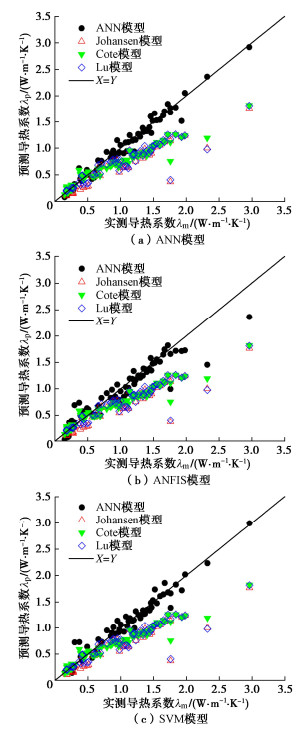
智能计算模型对土体预测所得结果λ与通过使用Johansen模型、Cote模型和Lu模型预测得到的λ值进行比较如图 8所示，智能计算模型和经验关系模型的性能检测如表 4所示。
![]()
图 8 预测模型与经验关系模型对比Figure 8. Comparison between prediction model and empirical relationship model表 4 预测模型的性能指标对比Table 4. Comparison among performance indexes of prediction models预测模型 R2 RMSE
/(W·m-1·K-1)MAE
/(W·m-1·K-1)VAF
/%ANN 0.9746 0.0985 0.0701 97.45 ANFIS 0.9078 0.1958 0.1262 90.17 SVM 0.9649 0.1147 0.0767 96.48 Johansen model 0.6464 0.4251 0.3631 75.05 Cote model 0.7744 0.3841 0.2805 78.34 Lu model 0.6432 0.4075 0.3335 71.49 从图 8可以看出，ANN模型、ANFIS模型和SVM模型都准确的预测了土体的导热系数，其预测值与实测值偏差较小；Johansen模型、Cote模型和Lu模型都明显低估了土体的导热系数，当λ < 1 (W·m-1·K-1)时，Cote模型和Lu模型的预测结果与实际值偏差较小，Johansen模型的预测结果比实测值偏小，但偏离值较小；当λ > 1 (W·m-1·K-1)时，Johansen模型、Cote模型和Lu模型的预测值明显低于实测值，且预测数据较离散，预测精度较低。
从表 4可以看出，ANN模型、ANFIS模型和SVM模型的相关系数R2 > 0.9，RMSE < 0.2 (W·m-1·K-1)，MAE < 0.13 (W·m-1·K-1)，VAF > 90%；Johansen模型、Cote模型和Lu模型的相关系数R2 < 0.78，RMSE > 0.38 (W·m-1·K-1)，MAE > 0.28 (W·m-1·K-1)，VAF < 79%；经验关系模型的性能明显低于ANN模型、ANFIS模型和SVM模型。
上述结果分析表明，预测模型对土体进行预测时，预测精度最高的是ANN模型和SVM模型，其次是ANFIS模型，预测精度最低的是经验关系模型。对于土体导热系数进行计算，建议选择ANN模型或SVM模型进行估算。
6. 结论
基于ANN模型、ANFIS模型和SVM模型对土体的导热系数进行计算研究，对预测模型的误差和稳健性进行分析，主要得出以下结论：
（1）对土体导热系数的影响因素进行分析，确定干密度、饱和度、黏粒含量、粉粒含量和砂粒含量作为预测模型的输入参数。
（2）建立预测土体导热系数的ANN模型、ANFIS模型和SVM模型，模型的计算结果表明，3个预测模型的预测结果精度较高。其中ANN模型的预测精度最高，SVM模型的预测精度略低于ANN模型，ANFIS模型的预测精度最低。基于蒙特卡洛模拟对预测模型的稳健性进行分析，预测模型稳健性最好的是SVM模型。
（3）将ANN模型、ANFIS模型和SVM模型的预测结果和传统经验关系模型的预测结果进行对比，ANN模型、ANFIS模型和SVM模型的预测精度明显高于传统经验关系模型；传统经验关系模型仅以含水率、干密度和土体类别作为计算依据，其预测结果与实际值偏差较大，难以满足工程设计要求。
-
![]()
图 4 预测模型训练数据集预测值与实测值比较
Figure 4. Comparison between predicted and measured values in training data set of prediction model
![]()
图 5 预测模型测试数据集预测值与实测值比较
Figure 5. Comparison between predicted and measured values of test data set of prediction model
![]()
图 7 蒙特卡罗模拟检验参数概率分布
Figure 7. Probability distribution of parameters by Monte Carlo simulation tests
![]()
图 8 预测模型与经验关系模型对比
Figure 8. Comparison between prediction model and empirical relationship model
表 1 预测模型输入参数的输出参数的边界值
Table 1 Boundary values of input parameters and output parameters of prediction model
类型 参数项 最小值 最大值 输入参数 干密度ρd/(g·cm-3) 0.999 1.728 饱和度Sr/% 0 100 黏粒含量c/% 0 42 粉粒含量si/% 0 83.4 砂粒含量sa/% 0 100 输出参数 导热系数λ/(W·m-1·K-1) 0.1 3.2 
下载: 导出CSV
表 2 预测模型性能指标
Table 2 Performance indexes of prediction models
模型代号 数据集 R2 RMSE
/(W·m-1·K-1)MAE
/(W·m-1·K-1)VAF
/%ANN 训练数据集 0.9784 0.0874 0.0673 97.84 测试集 0.9746 0.0985 0.0701 97.45 ANFIS 训练数据集 0.9361 0.1391 0.1096 94.50 测试集 0.9078 0.1958 0.1262 90.17 SVM 训练数据集 0.9747 0.0941 0.0725 97.47 测试集 0.9649 0.1147 0.0767 96.48
下载: 导出CSV
表 3 蒙特卡罗模拟结果统计
Table 3 Statistics of simulated results by Monte Carlo method
检验参数 预测模型 D25 D50 D75 平均值 R2 ANN 0.8926 0.9512 0.9723 0.9132 ANFIS 0.8731 0.8951 0.9056 0.8761 SVM 0.9362 0.9459 0.9552 0.9449 RMSE ANN 0.0838 0.1338 0.2518 0.1898 ANFIS 0.1935 0.2105 0.2405 0.2285 SVM 0.1093 0.1333 0.1623 0.1373 MAE ANN 0.0432 0.0952 0.1832 0.1322 ANFIS 0.1234 0.1394 0.1614 0.1464 SVM 0.0839 0.0959 0.1109 0.0989
下载: 导出CSV
表 4 预测模型的性能指标对比
Table 4 Comparison among performance indexes of prediction models
预测模型 R2 RMSE
/(W·m-1·K-1)MAE
/(W·m-1·K-1)VAF
/%ANN 0.9746 0.0985 0.0701 97.45 ANFIS 0.9078 0.1958 0.1262 90.17 SVM 0.9649 0.1147 0.0767 96.48 Johansen model 0.6464 0.4251 0.3631 75.05 Cote model 0.7744 0.3841 0.2805 78.34 Lu model 0.6432 0.4075 0.3335 71.49
下载: 导出CSV
-
[1] 桂树强, 程晓辉. 能源桩换热过程中结构响应原位试验研究[J]. 岩土工程学报, 2014, 36(6): 1087–1094. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15748.shtml GUI Shu-qiang, CHENG Xiao-hui. In-situ tests on structural responses of energy piles during heat exchanging process[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(6): 1087–1094. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract15748.shtml
[2] ZOU H F, ZHANG N, PUPPALA A J. Improving a thermal conductivity model of unsaturated soils based on multivariate distribution analysis[J]. Acta Geotechnica, 2019, 14(6): 2007–2029. doi: 10.1007/s11440-019-00837-3
[3] 徐婕, 朱合华, 闫治国. 淤泥质黏土火灾高温下导热系数的试验研究[J]. 岩土工程学报, 2012, 34(11): 2108–2113. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14902.shtml XU Jie, ZHU He-hua, YAN Zhi-guo. Experimental studies on coefficient of thermal conductivity of silty clay[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(11): 2108–2113. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14902.shtml
[4] KERSTEN M S. Laboratory Research for the Determination of the Thermal Properties of Soils[R]. Minneapolis, USA: University of Minnesota Engineering Experiment Station, 1949.
[5] CÔTÉ J, KONRAD J M. A generalized thermal conductivity model for soils and construction materials[J]. Canadian Geotechnical Journal, 2005, 42(2): 443–458. doi: 10.1139/t04-106
[6] JOHANSEN O. Thermal Conductivity of Soils[R]. Trondheim: Defense Technical Information Center, 1975.
[7] ERZIN Y, RAO B H, SINGH D N. Artificial neural network models for predicting soil thermal resistivity[J]. International Journal of Thermal Sciences, 2008, 47(10): 1347–1358. doi: 10.1016/j.ijthermalsci.2007.11.001
[8] 张涛, 刘松玉, 蔡国军, 等. 木质素改良粉土热学与力学特性相关性试验研究[J]. 岩土工程学报, 2015, 37(10): 1876–1885. doi: 10.11779/CJGE201510016 ZHANG Tao, LIU Song-yu, CAI Guo-jun, et al. Experimental study on relationship between thermal and mechanical properties of treated silt by lignin[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(10): 1876–1885. (in Chinese) doi: 10.11779/CJGE201510016
[9] TARNAWSKI V R, MCCOMBIE M L, LEONG W H, et al. Canadian field soils II: modeling of quartz occurrence[J]. International Journal of Thermophysics, 2012, 33(5): 843–863. doi: 10.1007/s10765-012-1184-2
[10] TARNAWSKI V R, MOMOSE T, MCCOMBIE M L, et al. Canadian field soils III: thermal-conductivity data and modeling[J]. International Journal of Thermophysics, 2015, 36(1): 119–156. doi: 10.1007/s10765-014-1793-z
[11] TARNAWSKI V R, LEONG W H. Advanced geometric mean model for predicting thermal conductivity of unsaturated soils[J]. International Journal of Thermophysics, 2016, 37(2): 1–42.
[12] 刘路路, 蔡国军, 刘晓燕, 等. 基于热探针测试的橡胶-砂颗粒轻质混合填料导热系数影响因素研究[J]. 土木工程学报, 2019, 52(增刊1): 31–35. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2019S1005.htm LIU Lu-lu, CAI Guo-jun, LIU Xiao-yan, et al. Influence factors of thermal conductivity of rubber-sand lightweight mixture based on thermal probe test[J]. China Civil Engineering Journal, 2019, 52(S1): 31–35. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2019S1005.htm
[13] CHEN S X. Thermal conductivity of sands[J]. Heat and Mass Transfer, 2008, 44(10): 1241–1246. doi: 10.1007/s00231-007-0357-1
[14] HORAI K I, SIMMONS G. Thermal conductivity of rock-forming minerals[J]. Earth and Planetary Science Letters, 1969, 6(5): 359–368.
[15] MACAULAY B D, BOUAZZA A, SINGH R M, et al. Thermal conductivity of soils and rocks from the Melbourne (Australia) region[J]. Engineering Geology, 2013, 164: 131–138.
[16] XU Y S, SUN D A, ZENG Z T, et al. Temperature dependence of apparent thermal conductivity of compacted bentonites as buffer material for high-level radioactive waste repository[J]. Applied Clay Science, 2019, 174: 10–14.
[17] 王才进, 张涛, 骆俊晖, 等. 神经网络反馈分析方法预测土体热阻系数研究[J]. 岩土工程学报, 2019, 41(增刊2): 109–112. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17860.shtml WANG Cai-jin, ZHANG Tao, LUO Jun-hui, et al. Utilization of neural network feedback method to prediction of thermal resistivity of soils[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S2): 109–112. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17860.shtml
[18] MØLLER M F. A scaled conjugate gradient algorithm for fast supervised learning[J]. Neural Networks, 1993, 6(4): 525–533.
[19] BURDEN F, WINKLER D. Bayesian regularization of neural networks[J]. Methods in Molecular Biology (Clifton, N J), 2008, 458(3): 25–44.
[20] FATTAHI H. Indirect estimation of deformation modulus of an in situ rock mass: an ANFIS model based on grid partitioning, fuzzy c-means clustering and subtractive clustering[J]. Geosciences Journal, 2016, 20(5): 681–690.
[21] 倪沙沙, 迟世春. 基于粒子群支持向量机的高心墙堆石坝渗透系数反演[J]. 岩土工程学报, 2017, 39(4): 727–734. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16887.shtml NI Sha-sha, CHI Shi-chun. Back analysis of permeability coefficient of high core rockfill dam based on particle swarm optimization and support vector machine[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(4): 727–734. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract16887.shtml
[22] PHAM B T, LE L M, LE T T, et al. Development of advanced artificial intelligence models for daily rainfall prediction[J]. Atmospheric Research, 2020, 237: 104845.
[23] SOIZE C. Stochastic Models of Uncertainties in Computational Mechanics[M]. Reston V A: American Society of Civil Engineers, 2012.
[24] ABEDINI M, GHASEMIAN B, SHIRZADI A, et al. A novel hybrid approach of Bayesian Logistic Regression and its ensembles for landslide susceptibility assessment[J]. Geocarto International, 2019, 34(13): 1427–1457.
[25] LU S, REN T S, GONG Y S, et al. An improved model for predicting soil thermal conductivity from water content at room temperature[J]. Soil Science Society of America Journal, 2007, 71(1): 8–14.
[26] DE VRIES D A. Thermal Properties of Soils[M]// Physics of the Plant Environment. VAN WIJK W R. New York: John Wiley & Sons, 1963: 210–235.
[27] SASS J H, LACHENBRUCH A H, MUNROE R J. Thermal conductivity of rocks from measurements on fragments and its application to heat-flow determinations[J]. Journal of Geophysical Research Atmospheres, 1971, 76(14): 3391–3401.
-
期刊类型引用(11)
1. 崔纪飞，柏林，饶平平，康陈俊杰，张锟. 基于人工智能算法的氯盐侵蚀混凝土预测模型. 硅酸盐通报. 2024(02): 439-447 . 
百度学术
2. 段文魁，王来发，晁华俊，明锋. 冻结过程中土体导热系数预测模型. 中国农村水利水电. 2024(05): 47-52 . 百度学术
3. 唐少容，殷磊，杨强，柯德秀. 微胶囊相变材料改良粉砂土的导热系数及预测模型. 中国粉体技术. 2024(03): 112-123 . 百度学术
4. 姚兆明，王洵，齐健. 土体导热系数智能方法预测及影响因素敏感性分析. 工程热物理学报. 2024(05): 1440-1449 . 百度学术
5. 邓志兴，谢康，李泰灃，王武斌，郝哲睿，李佳珅. 基于粗颗粒嵌锁点高铁级配碎石振动压实质量控制新方法. 岩土力学. 2024(06): 1835-1849 . 百度学术
6. 李林，左林龙，胡涛涛，宋博恺. 基于孔压静力触探试验测试数据的原位固结系数物理信息神经网络反演方法. 岩土力学. 2024(10): 2889-2899 . 百度学术
7. 王红旗，李栋伟，钟石明，贾志文，王泽成，陈鑫，秦子鹏. 石灰改良红黏土导热系数影响因素及模型预测. 科学技术与工程. 2023(05): 2084-2092 . 百度学术
8. 王才进，武猛，蔡国军，赵泽宁，刘松玉. 基于多元分布模型预测土体热阻系数. 岩石力学与工程学报. 2023(S1): 3674-3686 . 百度学术
9. 王健翔，任瑞琪. 电学等效的稳态平板导热系数测试实验装置. 电子制作. 2023(11): 105-109 . 百度学术
10. 王才进，武猛，杨洋，蔡国军，刘松玉，何欢，常建新. 基于生物地理优化的人工神经网络模型预测软土的固结系数. 岩土力学. 2023(10): 3022-3030 . 百度学术
11. 徐明，康雅晶，马斯斯，张鹤. 基于贝叶斯优化的XGBoost模型预测路基回弹模量. 公路交通科技. 2023(11): 51-60 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 297
- HTML全文浏览量: 53
- PDF下载量: 83
- 被引次数: 12
