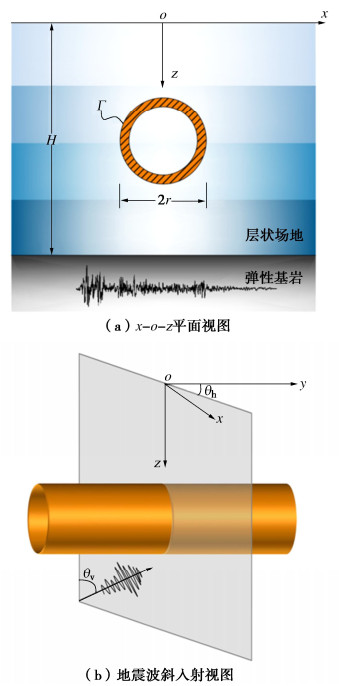
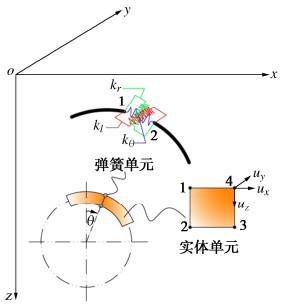
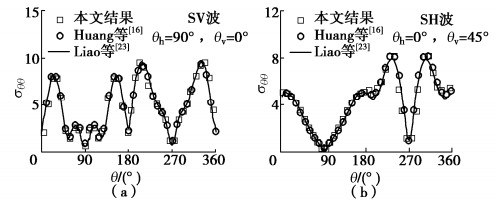
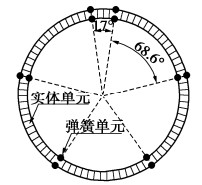
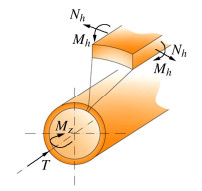
Seismic responses of underground tunnels subjected to obliquely incident seismic waves by 2.5D FE-BE coupling method
-
摘要: 针对地震波斜入射导致的非一致地震激励结构地震响应问题，提出了地下隧道三维地震响应分析的一个2.5维有限元–边界元（FE-BE）耦合分析方法，该耦合方法具有分析效率高和计算精度高的优势。利用有限元模拟隧道结构，并引入弹簧单元考虑衬砌管片接头的影响；半无限土域利用基于场地三维动力刚度矩阵和移动斜线荷载格林函数的边界元方法模拟。通过与文献结果比较验证了耦合方法的正确性。利用该2.5维FE-BE方法，以某盾构隧道为例，研究了斜入射地震波作用下隧道结构的三维地震响应，着重分析了管片接头对隧道衬砌地震变形和内力的影响，并讨论了通过对隧道衬砌整体刚度进行折减（等效均质圆环模型）来考虑管片接头影响的方法的适用性。研究表明，管片接头对隧道地震响应有重要影响，随接头刚度减小隧道衬砌变形呈增大趋势，但衬砌内力显著减小；而且，对于管片接头刚度较大的情况，等效均质圆环模型可以在一定程度上反映管片接头对隧道结构地震响应的影响，但可能导致隧道纵向弯矩的低估。Abstract: A 2.5D finite element-boundary element (FE-BE) coupling method is proposed for the 3D seismic responses of an underground tunnel subjected to obliquely incident seismic waves. The tunnel linings are discretized with finite elements and the effects of the segment joints are simulated by spring elements, while the unbounded soil is modelled by the boundary element method based on the 3D dynamic stiffness matrix of a layered half-space and the Green's functions for moving distributed loads. The proposed 2.5D FE-BE coupling method is of high computation efficiency and accuracy, and its correctness is verified by comparing with the benchmark results in the literature. The 2.5D FE-BE coupling method is used to study the seismic responses of a shield tunnel, with an emphasis on the effects of the segment joints on the deformations and internal forces of the tunnel linings. Moreover, the applicability of the equivalent homogeneous lining model, which approximately considers the effects of segment joints by reducing the bending rigidity of the tunnel linings, is examined. It is shown that compared with a homogeneous tunnel, the shield tunnel can accommodate larger deformations while generate smaller internal forces. Furthermore, for the case of joints with large stiffness, the equivalent homogeneous model for linings can account for the effects of the segment joints to a certain degree, but it may lead to underestimation of the longitudinal bending moment of the tunnel linings.
-
0. 引言
随着城市化进程的推进,基坑工程向更深、更复杂的趋势发展,为了保证周边环境安全,基坑变形的现场监测和预报已成为基坑工程的重要内容。传统的理论分析、数值模拟等方法虽然理论上可以实现变形的预测,但是岩土工程的变形机理复杂,涉及的影响因素众多,这类方法无法全面考虑[1]。
近年来,基于数据分析的时间序列建模方法被逐渐应用于岩土工程领域。其中灰色预测模型对样本数据量要求低,但对于非线性序列的预测效果较差[2]；人工神经网络具有较强的非线性映射能力,但存在网络结构难以确定、容易陷入局部最优、样本数据量要求高等缺点[3]；遗传算法、粒子群算法等优化算法与人工神经网络结合的组合模型改善了神经网络的性能,但仍然存在数据量要求高、泛化能力差的问题[4]。现有方法在预测时都以单测点的监测数据作为输入变量,只关注数据在时间维度上的关联性,而忽略了邻近监测点之间空间维度上的关联性。实际工程会设置大量的监测点,如何充分利用多个监测点的监测数据以提高预测精度是值得进一步研究的问题。针对上述不足,本文提出运用卷积神经网络与长短期记忆神经网络（CNN-LSTM）结合的组合模型,考虑监测数据在时间维度和空间维度上的关联性,对基坑工程多维序列进行预测。该方法在上海云岭超深基坑工程的地表沉降实际监测数据预测中取得了令人满意的效果。
1. CNN-LSTM模型
1.1 卷积神经网络（CNN）
卷积神经网络（convolutional neural networks）是一类包含卷积运算的前馈神经网络。CNN通过对数据的卷积和池化操作,提取数据之间的相互关系,可以用少量参数表达数据的空间特征,具有优秀的高维特征提取能力,被广泛用于图像处理、计算机视觉等问题。CNN网络的核心结构如图1所示。卷积层通过设置卷积核,对输入数据按式（1）进行离散卷积运算,提取输入数据的空间特征。池化层通过对卷积核内的数据进行取最大值、取平均值等操作,实现数据的降采样,即去除杂余信息,保留关键特征。
yi,j=σ(Wk⊗xi,j+bk), (1) Wk⊗xi,j=a−1∑m=0b−1∑n=0wm,n×xi+m,j+n, (2) 式中 xij为卷积层的输入数据；yij为卷积层的输出数据；为离散卷积运算；Wk和bk分别为第k个卷积核的权重系数和偏置参数；
σ 为神经元的激活函数；a,b为卷积核的尺寸参数。1.2 长短期记忆神经网络（LSTM）
LSTM神经网络（long short-term memory neural network）是循环神经网络RNN（recurrent neural network）的一种变体。LSTM神经网络通过设置特殊的“门”结构,可以有选择性地记忆长短期信息,解决了RNN结构的长时间依赖问题,在时序数据的预测问题上表现优异。LSTM单元结构如图2所示。
1.3 CNN-LSTM模型
卷积神经网络CNN与循环神经网络LSTM结合的CNN-LSTM神经网络结构如图3所示。CNN部分以多个监测点的标准化后的历史数据构成的多维时间序列Xt,n作为输入数据。Xt,n是一个二维矩阵,一行表示某一时刻n个监测点的监测值,一列表示某一监测点在时间步长t内的监测值。将该序列输入CNN部分后,进行卷积运算,提取空间特征,输出多个由空间特征组成一维序列。LSTM部分以CNN网络输出的一维序列作为输入数据。LSTM对序列进行回归预测,输出多个空间特征的预测值。最后通过全连接层整合空间特征预测值,输出监测数据的预测值。
2. 工程实例验证
2.1 工程概况
云岭竖井基坑是上海苏州河深隧工程的一部分。竖井基坑为圆形,深度约60 m,支护结构为1500 mm地下连续墙。基坑位于上海软土地区,且基坑开挖深度范围内的深层土体力学特性尚不明确,给基坑周边地表沉降的计算带来了困难。为了实时地进行动态化施工反馈,在基坑周边布置了大量监测点。基坑周边对称布置DB-1、DB-2、DB-3和DB-4四条测线,其中DB-4的监测点在施工中被破坏,监测数据不完整。
本文选取其余三条测线的第一个测点（DB1-1、DB2-1、DB3-1）从2020年7月27日至2020年12月28日,共计155组数据,前135组数据用于训练模型,后20组数据用于验证模型的精度。
2.2 监测数据建模预测
现在以DB1-1测点的监测数据作为预测目标,详细描述如何利用CNN-LSTM模型进行时序预测。
（1）数据预处理
现场采集的数据受各种因素的干扰,包含大量噪声[5]。为避免拟合噪声,在导入模型训练前,对原始数据进行降噪处理。降噪后数据如图4所示。此外,不同监测点的监测数据在绝对值上相差较大,为了避免模型训练时的梯度方向被某一监测点的数据控制,本文按式（3）标准化数据,标准化后的数据符合均值为0,方差为1的正态分布。
x′t,i=xt,i−μiσi, (3) 式中,μi,σi为第i个测点全部监测数据的均值和方差。
（2）CNN-LSTM模型构建
本文基于Python的Keras库构建CNN-LSTM模型。第一层为卷积层,卷积核个数为80,即提取80个空间特征,卷积核尺寸为1×3；第二层为LSTM层,LSTM层的神经元个数对网络的性能影响最大,因此取初始值80,在训练过程中优化；第三层为Dense层。需要指出的是由于本文选取的数据集在空间维度上只有3个监测点,数据规模不大,不设置池化层可以取得更好的效果。
（3）训练样本构造与模型训练
本文采用“5+1”的样本构造模式,即以3个测点前5天的监测数据作为输入数据,输入数据为5×3的二维矩阵,第6天DB1-1测点的监测数据作为输出数据。训练集共135组监测数据构造130组训练样本。训练优化器选择Adam,迭代次数epoch取100次,损失函数为均方误差MSE,模型收敛。
（4）监测值预测
最后利用训练完毕的模型对最后20组数据进行滚动预测。考虑到前期数据的降噪预处理,本文同时对噪声采用统计学模型ARMA进行分析、预测后,与CNN-LSTM的输出结果合并,作为最终预测值。为了验证CNN-LSTM模型的预测效果,本文同时单独采用LSTM模型进行预测,两种方法的结果和预测相对误差对比如图5,6所示。对DB2-1、DB3-1测点采用同样方法的预测结果和误差如图7～10所示。
图5和图6表明,CNN-LSTM组合模型的预测结果与单一LSTM模型相比,在所有观测时间点上都更接近实测值,但是两种模型预测结果的趋势仍然与实测值有明显不同,这是由于噪声的预测模型难以拟合本例的数据。采用CNN-LSTM模型时,预测结果的相对误差介于0.01%～3.44%之间,平均值为2.00%,而LSTM模型相对误差介于0.02%～4.36%,平均值为2.84%,说明前者预测精度更高,效果更为理想。
图7～10表明,DB2-1测点和DB3-1测点的预测结果与DB1-1测点基本一致,CNN-LSTM模型的预测结果更接近实测值。采用CNN-LSTM模型,DB2-1测点、DB3-1测点的预测平均相对误差分别为0.93%、1.35%,而采用LSTM模型的平均相对误差分别为1.84%和1.69%,综合来看,CNN-LSTM模型取得了更好的效果。
需要指出的是,CNN-LSTM的精度优化得益于测点之间的空间关联度,选择测点时可综合测点的几何分布和历史监测曲线两方面判断。本例测点对称分布于基坑周边,且历史监测曲线的趋势也具有一致性。
3. 结论
本文在已有岩土工程时间序列预测方法的基础上,提出可以考虑监测数据空间关联性的CNN-LSTM组合模型。通过基于上海云岭竖井超深基坑工程现场地表沉降监测数据的工程实例验证,得出以下结论：
（1）多个监测点的监测数据构成一个多维时间序列,不同监测点数据之间的空间关联特征可以用CNN网络中的卷积运算提取。
（2）CNN-LSTM模型采用CNN网络提取多维时间序列的空间特征,LSTM网络多空间特征序列进行回归预测。工程实例表明,该模型在预测精度上相较于基于单测点数据的LSTM模型具有更高的精度。
（3）本文预测的多维时间序列的均为地表沉降,即同一类监测数据。工程现场的不同监测项目之间,理论上也可采用CNN-LSTM模型建模预测,如何将该模型推广到任意监测项目组成的多维时间序列是值得深入研究的问题。
-
![]()
![]()
图 6 SH斜入射波（θh = 0°，θv = 45°）隧道衬砌纵向弯矩幅值
Figure 6. Amplitudes of longitudinal bending moment of tunnel linings for SH waves with θh = 0° and θv = 45°
![]()
图 7 SH斜入射波（θh = 45°，θv = 45°）隧道衬砌纵向轴力幅值
Figure 7. Amplitudes of longitudinal axial force of tunnel linings for SH waves with θh = 45° and θv = 45°
![]()
图 9 隧道衬砌纵向弯矩时程
Figure 9. Time histories of longitudinal bending moment of tunnel linings
![]()
图 10 衬砌直径变形率最大时刻的隧道变形图
Figure 10. Transverse deformations of tunnel linings at moments of maximum diametral deformation ratios
![]()
图 11 隧道横向地震内力峰值包络图
Figure 11. Envelopes of peak transverse internal forces of tunnel linings
![]()
图 12 管片接头对隧道横向地震内力峰值的影响
Figure 12. Effects of segment joints on peak transverse internal forces of tunnel linings
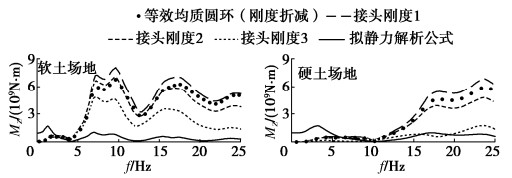
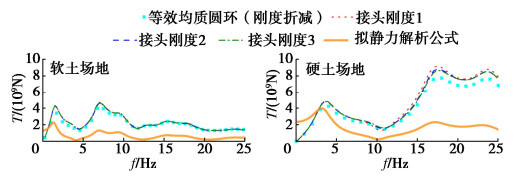
表 1 管片接头刚度
Table 1 Stiffnesses of segment joints
(MN/m) 分类 轴向刚度 径向刚度 纵向刚度 接头刚度1 2000 4200 4200 接头刚度2 500 1050 1050 接头刚度3 125 262.5 262.5 
下载: 导出CSV
表 2 软土场地和硬土场地参数
Table 2 Parameters of soft and stiff soil sites
场地 H/m Gs/MPa ρs/(kg·m-3) cs/(m·s-1) νs ζs 软土层 30 55.5 1990 167 0.4 0.05 基岩 ∞ 515.0 2060 500 0.4 0.02 硬土层 30 308.9 1990 394 0.4 0.05 基岩 ∞ 2878.1 2060 1182 0.4 0.02
下载: 导出CSV
表 3 不同接头刚度隧道的最大直径变形率
Table 3 Maximum diametral deformation ratios of tunnel linings for different joint stiffnesses
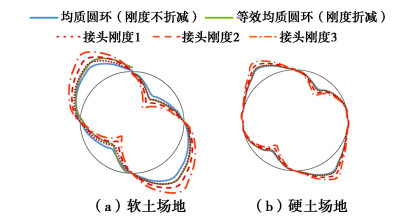
(‰) 分类 软土场地 硬土场地 均质圆环（刚度不折减） 0.35 0.12 等效均质圆环（刚度折减） 0.36 (1.03) 0.12 (1.00) 接头刚度1 0.36 (1.03) 0.12 (1.00) 接头刚度2 0.40 (1.14) 0.13 (1.08) 接头刚度3 0.44 (1.26) 0.14 (1.17) 注：括号内数值为不同接头刚度隧道最大直径变形率与均质圆环隧道结果的比值。
下载: 导出CSV
-
[1] 杜修力, 陈维, 李亮, 等. 斜入射条件下地下结构时域地震反应分析初探[J]. 震灾防御技术, 2007, 2(3): 290–296. doi: 10.3969/j.issn.1673-5722.2007.03.009 DU Xiu-li, CHEN Wei, LI Liang, et al. Preliminary study of time-domain seismic response for underground structures to obliquely incident seismic waves[J]. Technology for Earthquake Disaster Prevention, 2007, 2(3): 290–296. (in Chinese) doi: 10.3969/j.issn.1673-5722.2007.03.009
[2] 禹海涛, 袁勇. 长大隧道地震响应分析与试验方法新进展[J]. 中国公路学报, 2018, 31(10): 19–35. doi: 10.3969/j.issn.1001-7372.2018.10.003 YU Hai-tao, YUAN Yong. Review on seismic response analysis and test methods for long and large tunnels[J]. China Journal of Highway and Transport, 2018, 31(10): 19–35. (in Chinese) doi: 10.3969/j.issn.1001-7372.2018.10.003
[3] 刘晶波, 王艳, 赵冬冬. 地震波斜入射时地铁盾构隧道的动力反应分析[C]//第四届全国防震减灾工程学术研讨会论文集. 福州, 2009: 318–322. LIU Jing-bo, WANG Yan, ZHAO Dong-dong. The dynamic response of subway shield tunnel under oblique seismic waves[C]//Proceedings of the 4th National Symposium on Earthquake Prevention and Disaster Mitigation Engineering. Fuzhou, 2009: 318–322. (in Chinese)
[4] 傅方, 赵成刚, 李伟华, 等. SV波斜入射下局部地形对隧道地震响应的影响[J]. 北京交通大学学报, 2012, 36(6): 79–84. doi: 10.3969/j.issn.1673-0291.2012.06.015 FU Fang, ZHAO Cheng-gang, LI Wei-hua, et al. Influence of local topographic on seismic response of tunnels subjected to obliquely incident SV waves[J]. Journal of Beijing Jiaotong University, 2012, 36(6): 79–84. (in Chinese) doi: 10.3969/j.issn.1673-0291.2012.06.015
[5] 路德春, 李云, 马超, 等. 斜入射地震作用下地铁车站结构抗震性能分析[J]. 北京工业大学学报, 2016, 42(1): 87–94. https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD201601014.htm LU De-chun, LI Yun, MA Chao, et al. Analysis of the three-dimensional seismic performance of underground[J]. Journal of Beijing University of Technology, 2016, 42(1): 87–94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BJGD201601014.htm
[6] 耿萍, 陈昌健, 王琦, 等. 地震P波对圆形隧道最不利入射角研究[J]. 现代隧道技术, 2018, 55(增刊2): 579–587. https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD2018S2075.htm GENG Ping, CHEN Chang-jian, WANG Qi, et al. Research on the most unfavorable incident angle of primary wave to circular tunnel[J]. Modern Tunnelling Technology, 2018, 55(S2): 579–587. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XDSD2018S2075.htm
[7] ST JOHN C M, ZAHRAH T F. Aseismic design of underground structures[J]. Tunnelling and Underground Space Technology, 1987, 2(2): 165–197. doi: 10.1016/0886-7798(87)90011-3
[8] 小泉淳. 盾构隧道的抗震研究及算例[M]. 张稳军, 袁大军, 译. 北京: 中国建筑工业出版社, 2009. KOIZUMI A. Seismic Research and Examples of Shield Tunnels[M]. ZHANG Wen-jun, YUAN Da-jun, trans. Beijing: China Architecture & Building Press, 2009. (in Chinese)
[9] ANASTASOPOULOS I, GEROLYMOS N, DROSOS V, et al. Nonlinear response of deep immersed tunnel to strong seismic shaking[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2007, 133(9): 1067–1090. doi: 10.1061/(ASCE)1090-0241(2007)133:9(1067)
[10] ZHANG J, HE C, GENG P, et al. Improved longitudinal seismic deformation method of shield tunnels based on the iteration of the nonlinear stiffness of ring joints[J]. Sustainable Cities and Society, 2019, 45: 105–116. doi: 10.1016/j.scs.2018.11.019
[11] MIAO Y, YAO E L, RUAN B, et al. Seismic response of shield tunnel subjected to spatially varying earthquake ground motions[J]. Tunnelling and Underground Space Technology, 2018, 77: 216–226. doi: 10.1016/j.tust.2018.04.006
[12] 陈国兴, 孙瑞瑞, 赵丁凤, 等. 海底盾构隧道纵向地震反应特征的子模型分析[J]. 岩土工程学报, 2019, 41(11): 1983–1991. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201911003.htm CHEN Guo-xing, SUN Rui-rui, ZHAO Ding-feng, et al. Longitudinal seismic response characteristics of seabed shield tunnels using submodeling analysis[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(11): 1983–1991. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201911003.htm
[13] 赵宝友, 马震岳, 梁冰, 等. 考虑地震动行波效应的大型岩体地下洞室动力非线性反应分析[J]. 岩石力学与工程学报, 2010, 29(S1): 3370–3377. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1114.htm ZHAO Bao-you, MA Zhen-yue, LIANG Bing, et al. Dynamic nonlinear response of a large underground rock cavern subjected to seismic motion considering wave passage effect[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(S1): 3370–3377. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2010S1114.htm
[14] FABOZZI S, BILOTTA E, YU H, et al. Effects of the asynchronism of ground motion on the longitudinal behaviour of a circular tunnel[J]. Tunnelling and Underground Space Technology, 2018, 82: 529–541. doi: 10.1016/j.tust.2018.09.005
[15] LI P, SONG E X. Three-dimensional numerical analysis for the longitudinal seismic response of tunnels under an asynchronous wave input[J]. Computers and Geotechnics, 2015, 63: 229–243. doi: 10.1016/j.compgeo.2014.10.003
[16] HUANG J Q, DU X L, ZHAO M, et al. Impact of incident angles of earthquake shear (S) waves on 3-D non-linear seismic responses of long lined tunnels[J]. Engineering Geology, 2017, 222: 168–185. doi: 10.1016/j.enggeo.2017.03.017
[17] 王国波, 巴峰, 孙富学, 等. 非一致激励下长大盾构隧道结构地震响应分析[J]. 岩土工程学报, 2020, 42(7): 1228–1237. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202007010.htm WANG Guo-bo, BA Feng, SUN Fu-xue, et al. Seismic response analysis of long shield tunnels under non-uniform excitation[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(7): 1228–1237. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202007010.htm
[18] FRANÇOIS S, SCHEVENELS M, GALVÍN P, et al. A 2.5D coupled FE-BE methodology for the dynamic interaction between longitudinally invariant structures and a layered halfspace[J]. Computer Methods in Applied Mechanics and Engineering, 2010, 199(23/24): 1536–1548. https://www.sciencedirect.com/science/article/pii/S0045782510000022
[19] ZHOU S H, HE C, GUO P J, et al. Dynamic response of a segmented tunnel in saturated soil using a 2.5-D FE-BE methodology[J]. Soil Dynamics and Earthquake Engineering, 2019, 120: 386–397. https://www.sciencedirect.com/science/article/pii/S0267726118311321
[20] LIN K C, HUNG H H, YANG J P, et al. Seismic analysis of underground tunnels by the 2.5D finite/infinite element approach[J]. Soil Dynamics and Earthquake Engineering, 2016, 85: 31–43. https://www.sciencedirect.com/science/article/pii/S0267726116000592
[21] 梁建文, 巴振宁. 三维层状场地的精确动力刚度矩阵及格林函数[J]. 地震工程与工程振动, 2007, 27(5): 7–17. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200705002.htm LIANG Jian-wen, BA Zhen-ning. Exact dynamic stiffness matrices of 3-D layered site and its Green's functions[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(5): 7–17. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200705002.htm
[22] BA Z N, LIANG J W. 2.5D scattering of incident plane SV waves by a canyon in layered half-space[J]. Earthquake Engineering and Engineering Vibration, 2010, 9(4): 587–595. doi: 10.1007/s11803-010-0040-2
[23] LIAO W I, YEH C S, TENG T J. Scattering of elastic waves by a buried tunnel under obliquely incident waves using T matrix[J]. Journal of Mechanics, 2011, 24(4): 405–418. https://www.cambridge.org/core/journals/journal-of-mechanics/article/scattering-of-elastic-waves-by-a-buried-tunnel-under-obliquely-incident-waves-using-t-matrix/865C93FD600B2695AAF6EB1F8CF4B966
[24] DO N A, DIAS D, ORESTE P, et al. 2D numerical investigation of segmental tunnel lining under seismic loading[J]. Soil Dynamics and Earthquake Engineering, 2015, 72: 66–76. https://www.sciencedirect.com/science/article/pii/S0267726115000184
[25] 地下结构抗震设计标准: GB/T 51336—2018[S]. 北京: 中国建筑工业出版社, 2018. Standard for Seismic Design of Underground Structures: GB/T 51336—2018[S]. Beijing: China Architecture & Building Press, 2018. (in Chinese)
-
期刊类型引用(3)
1. 符传邦，吴育麒，吴月磊. 水泥搅拌桩各项参数对软土路基沉降的影响. 市政技术. 2023(02): 73-77 . 
百度学术
2. 赵楠. 地铁隧道基底围岩动三轴试验研究. 资源信息与工程. 2022(02): 116-120 . 百度学术
3. 魏丽，柴寿喜，张琳，李瑶. 冻融作用下三类纤维加筋固化土的抗压抗拉性能. 岩土力学. 2022(12): 3241-3248+3280 . 百度学术
其他类型引用(3)
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
- 被引次数: 6
