重金属污染淤泥一维大变形电渗固结–离子迁移耦合模型

周亚东; 翟鑫东; 杨文庆

doi:10.11779/CJGE202210008

重金属污染淤泥一维大变形电渗固结–离子迁移耦合模型 English Version

周亚东^{1, 2,},
翟鑫东¹,
杨文庆¹

1.
天津城建大学天津市软土特性与工程环境重点实验室, 天津 300384
2.
同济大学土木工程学院, 上海 200092

基金项目:

国家自然科学基金项目 51608351

天津市自然科学基金项目 18JCYBJC22600

天津市科技计划项目 21YDTPJC00030

天津市研究生科研创新项目 2020YJSS082

详细信息

作者简介:
周亚东(1985—)，男，博士，副教授，主要从事软土地基处理、环境岩土等方面的研究工作。E-mail: zyd476300@126.com

中图分类号: TU431
计量
- 文章访问数: 118
- HTML全文浏览量: 27
- PDF下载量: 25
出版历程
- 收稿日期: 2021-10-07
- 网络出版日期: 2022-12-11
- 刊出日期: 2022-09-30

One-dimensional coupled model for large-deformation electroosmotic consolidation and heavy metal ion migration of silt

1.
Key Laboratory of Soft Soils and Engineering Environment of Tianjin Province, Tianjin Chengjian University, Tianjin 300384, China
2.
College of Civil Engineering, Tongji University, Shanghai 200092, China

摘要

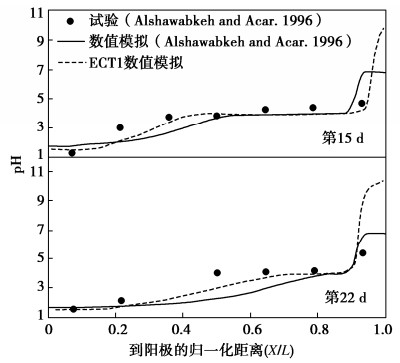
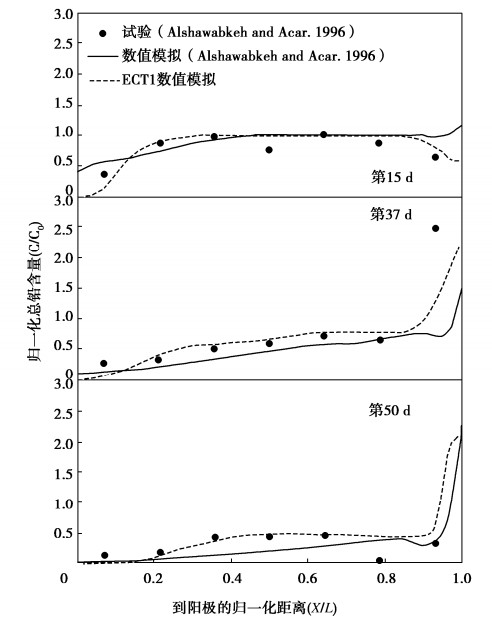
摘要: 电动处理技术在淤泥高效脱水和重金属污染物同步去除方面潜力巨大。基于分段线性差分法，将电渗固结和溶质迁移理论相结合，建立了一维大变形电渗固结-重金属离子迁移耦合模型ECT1。该模型可以模拟电场、渗流场和化学场的耦合作用，可以考虑电动处理过程中土性参数的非线性变化，以及吸附/解吸、中和/电离、沉淀/溶解等多种化学反应。分别采用Alshawabkeh污染土电动修复试验及数值模拟、高含水率重金属污染土电动处理试验，验证分析了ECT1模型的可靠性。通过算例分析，进一步阐述了高含水率污染淤泥电动处理过程中重金属迁移与电渗固结的耦合机理。
- 电渗固结 /
- 离子迁移 /
- 重金属 /
- 淤泥 /
- 电动处理
Abstract: Dewatering and metal removal of silt can be obtained by applying electrokinetics. A coupled model for one-dimensional electroosmosis consolidation and ion migration, called ECT1, is proposed. It employs the piecewise linear finite difference method to simulate the ion migration and large-strain consolidation of soils under the coupling action of electric field, seepage field and chemical field, and to account for the nonlinear variation of physical and electro-chemical properties of soils, such as adsorption/desorption, neutralization/ionization, and precipitation/dissolution. The model is verified by Alshawabkeh's electrokinetic remediation experimental results for contaminated soil, numerical solutions and treatment tests on high-moisture content heavy metal-contaminated soil electrokinetic. The proposed model is applied to example studies to elucidate the coupling mechanism of heavy metal migration and consolidation in the electrokinetic treatment of high-moisture content contaminated silt.
- electroosmotic consolidation /
- ion migration /
- heavy metal /
- silt /
- electrokinetic treatment

HTML全文

0. 引言

随着城市化进程的推进,基坑工程向更深、更复杂的趋势发展,为了保证周边环境安全,基坑变形的现场监测和预报已成为基坑工程的重要内容。传统的理论分析、数值模拟等方法虽然理论上可以实现变形的预测,但是岩土工程的变形机理复杂,涉及的影响因素众多,这类方法无法全面考虑^[1]。

近年来,基于数据分析的时间序列建模方法被逐渐应用于岩土工程领域。其中灰色预测模型对样本数据量要求低,但对于非线性序列的预测效果较差^[2]；人工神经网络具有较强的非线性映射能力,但存在网络结构难以确定、容易陷入局部最优、样本数据量要求高等缺点^[3]；遗传算法、粒子群算法等优化算法与人工神经网络结合的组合模型改善了神经网络的性能,但仍然存在数据量要求高、泛化能力差的问题^[4]。现有方法在预测时都以单测点的监测数据作为输入变量,只关注数据在时间维度上的关联性,而忽略了邻近监测点之间空间维度上的关联性。实际工程会设置大量的监测点,如何充分利用多个监测点的监测数据以提高预测精度是值得进一步研究的问题。针对上述不足,本文提出运用卷积神经网络与长短期记忆神经网络（CNN-LSTM）结合的组合模型,考虑监测数据在时间维度和空间维度上的关联性,对基坑工程多维序列进行预测。该方法在上海云岭超深基坑工程的地表沉降实际监测数据预测中取得了令人满意的效果。

1. CNN-LSTM模型

1.1 卷积神经网络（CNN）

卷积神经网络（convolutional neural networks）是一类包含卷积运算的前馈神经网络。CNN通过对数据的卷积和池化操作,提取数据之间的相互关系,可以用少量参数表达数据的空间特征,具有优秀的高维特征提取能力,被广泛用于图像处理、计算机视觉等问题。CNN网络的核心结构如图1所示。卷积层通过设置卷积核,对输入数据按式（1）进行离散卷积运算,提取输入数据的空间特征。池化层通过对卷积核内的数据进行取最大值、取平均值等操作,实现数据的降采样,即去除杂余信息,保留关键特征。

$y_{i, j} = σ (W_{k} \otimes x_{i, j} + b_{k})$ ,

(1)

$W_{k} \otimes x_{i, j} = \sum_{m = 0}^{a - 1} \sum_{n = 0}^{b - 1} w_{m, n} \times x_{i + m, j + n}$ ,

(2)

图 1 CNN网络核心结构示意图

Figure 1. Structure of convolutional neural networks

下载: 全尺寸图片幻灯片

式中 x_ij为卷积层的输入数据；y_ij为卷积层的输出数据；为离散卷积运算；W_k和b_k分别为第k个卷积核的权重系数和偏置参数； $σ$ 为神经元的激活函数；a,b为卷积核的尺寸参数。

1.2 长短期记忆神经网络（LSTM）

LSTM神经网络（long short-term memory neural network）是循环神经网络RNN（recurrent neural network）的一种变体。LSTM神经网络通过设置特殊的“门”结构,可以有选择性地记忆长短期信息,解决了RNN结构的长时间依赖问题,在时序数据的预测问题上表现优异。LSTM单元结构如图2所示。

图 2 LSTM结构示意图

Figure 2. Structure of LSTM

下载: 全尺寸图片幻灯片

1.3 CNN-LSTM模型

卷积神经网络CNN与循环神经网络LSTM结合的CNN-LSTM神经网络结构如图3所示。CNN部分以多个监测点的标准化后的历史数据构成的多维时间序列X_t,n作为输入数据。X_t,n是一个二维矩阵,一行表示某一时刻n个监测点的监测值,一列表示某一监测点在时间步长t内的监测值。将该序列输入CNN部分后,进行卷积运算,提取空间特征,输出多个由空间特征组成一维序列。LSTM部分以CNN网络输出的一维序列作为输入数据。LSTM对序列进行回归预测,输出多个空间特征的预测值。最后通过全连接层整合空间特征预测值,输出监测数据的预测值。

图 3 CNN-LSTM模型结构示意图

Figure 3. Structure of CNN-LSTM model

下载: 全尺寸图片幻灯片

2. 工程实例验证

2.1 工程概况

云岭竖井基坑是上海苏州河深隧工程的一部分。竖井基坑为圆形,深度约60 m,支护结构为1500 mm地下连续墙。基坑位于上海软土地区,且基坑开挖深度范围内的深层土体力学特性尚不明确,给基坑周边地表沉降的计算带来了困难。为了实时地进行动态化施工反馈,在基坑周边布置了大量监测点。基坑周边对称布置DB-1、DB-2、DB-3和DB-4四条测线,其中DB-4的监测点在施工中被破坏,监测数据不完整。

本文选取其余三条测线的第一个测点（DB1-1、DB2-1、DB3-1）从2020年7月27日至2020年12月28日,共计155组数据,前135组数据用于训练模型,后20组数据用于验证模型的精度。

2.2 监测数据建模预测

现在以DB1-1测点的监测数据作为预测目标,详细描述如何利用CNN-LSTM模型进行时序预测。

（1）数据预处理

现场采集的数据受各种因素的干扰,包含大量噪声^[5]。为避免拟合噪声,在导入模型训练前,对原始数据进行降噪处理。降噪后数据如图4所示。此外,不同监测点的监测数据在绝对值上相差较大,为了避免模型训练时的梯度方向被某一监测点的数据控制,本文按式（3）标准化数据,标准化后的数据符合均值为0,方差为1的正态分布。

${x^{'}}_{t, i} = \frac{x_{t, i} - μ_{i}}{σ_{i}}$ ,

(3)

图 4 降噪后数据示意图

Figure 4. Curves of data after noise reduction

下载: 全尺寸图片幻灯片

式中,μ_i,σ_i为第i个测点全部监测数据的均值和方差。

（2）CNN-LSTM模型构建

本文基于Python的Keras库构建CNN-LSTM模型。第一层为卷积层,卷积核个数为80,即提取80个空间特征,卷积核尺寸为1×3；第二层为LSTM层,LSTM层的神经元个数对网络的性能影响最大,因此取初始值80,在训练过程中优化；第三层为Dense层。需要指出的是由于本文选取的数据集在空间维度上只有3个监测点,数据规模不大,不设置池化层可以取得更好的效果。

（3）训练样本构造与模型训练

本文采用“5+1”的样本构造模式,即以3个测点前5天的监测数据作为输入数据,输入数据为5×3的二维矩阵,第6天DB1-1测点的监测数据作为输出数据。训练集共135组监测数据构造130组训练样本。训练优化器选择Adam,迭代次数epoch取100次,损失函数为均方误差MSE,模型收敛。

（4）监测值预测

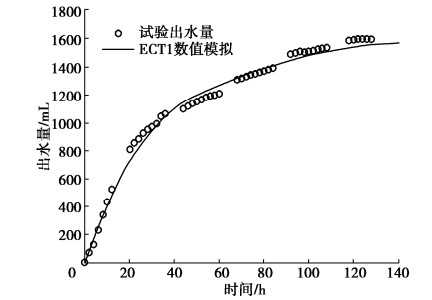
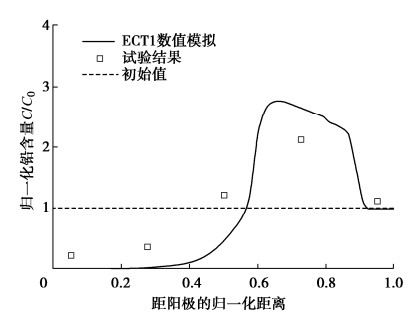
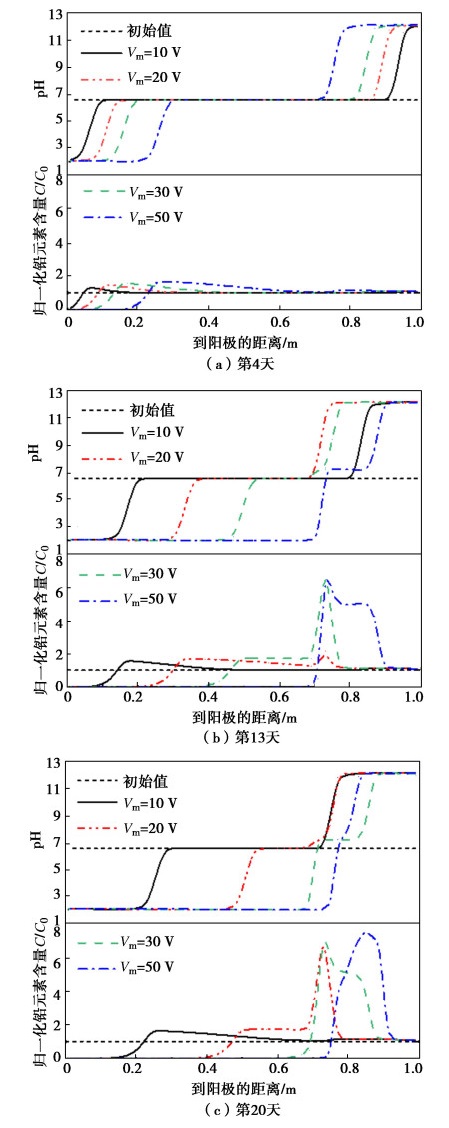
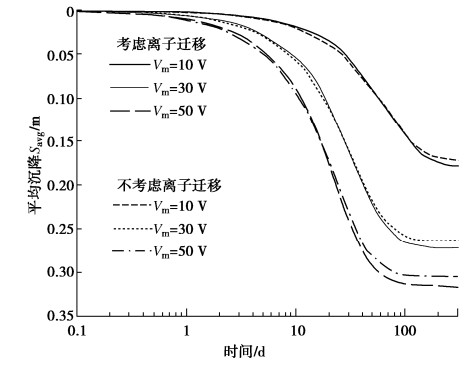
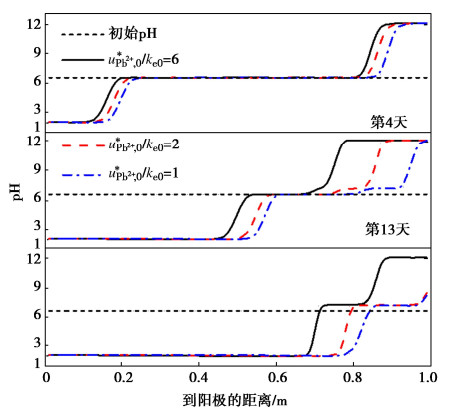
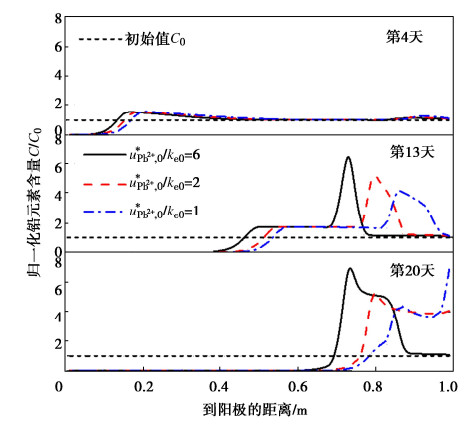
最后利用训练完毕的模型对最后20组数据进行滚动预测。考虑到前期数据的降噪预处理,本文同时对噪声采用统计学模型ARMA进行分析、预测后,与CNN-LSTM的输出结果合并,作为最终预测值。为了验证CNN-LSTM模型的预测效果,本文同时单独采用LSTM模型进行预测,两种方法的结果和预测相对误差对比如图5,6所示。对DB2-1、DB3-1测点采用同样方法的预测结果和误差如图7～10所示。

图 5 DB1-1测点监测值与预测值

Figure 5. Measured and predicted values of DB1-1

下载: 全尺寸图片幻灯片

图 6 DB1-1测点预测相对误差对比

Figure 6. Comparison of prediction relative errors of DB1-1

下载: 全尺寸图片幻灯片

图 7 DB2-1测点监测值与预测值

Figure 7. Measured and predicted values of DB2-1

下载: 全尺寸图片幻灯片

图 8 DB2-1测点预测相对误差对比

Figure 8. Comparison of prediction relative errors of DB2-1

下载: 全尺寸图片幻灯片

图 9 DB3-1测点监测值与预测值

Figure 9. Measured and predicted values of DB3-1

下载: 全尺寸图片幻灯片

图 10 DB3-1测点预测相对误差对比

Figure 10. Comparison of prediction relative errors of DB3-1

下载: 全尺寸图片幻灯片

图5和图6表明,CNN-LSTM组合模型的预测结果与单一LSTM模型相比,在所有观测时间点上都更接近实测值,但是两种模型预测结果的趋势仍然与实测值有明显不同,这是由于噪声的预测模型难以拟合本例的数据。采用CNN-LSTM模型时,预测结果的相对误差介于0.01%～3.44%之间,平均值为2.00%,而LSTM模型相对误差介于0.02%～4.36%,平均值为2.84%,说明前者预测精度更高,效果更为理想。

图7～10表明,DB2-1测点和DB3-1测点的预测结果与DB1-1测点基本一致,CNN-LSTM模型的预测结果更接近实测值。采用CNN-LSTM模型,DB2-1测点、DB3-1测点的预测平均相对误差分别为0.93%、1.35%,而采用LSTM模型的平均相对误差分别为1.84%和1.69%,综合来看,CNN-LSTM模型取得了更好的效果。

需要指出的是,CNN-LSTM的精度优化得益于测点之间的空间关联度,选择测点时可综合测点的几何分布和历史监测曲线两方面判断。本例测点对称分布于基坑周边,且历史监测曲线的趋势也具有一致性。

3. 结论

本文在已有岩土工程时间序列预测方法的基础上,提出可以考虑监测数据空间关联性的CNN-LSTM组合模型。通过基于上海云岭竖井超深基坑工程现场地表沉降监测数据的工程实例验证,得出以下结论：

（1）多个监测点的监测数据构成一个多维时间序列,不同监测点数据之间的空间关联特征可以用CNN网络中的卷积运算提取。

（2）CNN-LSTM模型采用CNN网络提取多维时间序列的空间特征,LSTM网络多空间特征序列进行回归预测。工程实例表明,该模型在预测精度上相较于基于单测点数据的LSTM模型具有更高的精度。

（3）本文预测的多维时间序列的均为地表沉降,即同一类监测数据。工程现场的不同监测项目之间,理论上也可采用CNN-LSTM模型建模预测,如何将该模型推广到任意监测项目组成的多维时间序列是值得深入研究的问题。

图 1 几何模型示意图

Figure 1. Schematic diagram of model geometry

下载: 全尺寸图片幻灯片

图 2 土体pH分布

Figure 2. Distribution of pH value of soils

下载: 全尺寸图片幻灯片

图 3 土体总铅含量分布

Figure 3. Distribution of total lead in soils

下载: 全尺寸图片幻灯片

图 4 试验装置示意图

Figure 4. Schematic diagram of test device

下载: 全尺寸图片幻灯片

图 5 淤泥排水量随时间变化

Figure 5. Change of discharge of soils with time

下载: 全尺寸图片幻灯片

图 6 归一化Pb含量分布

Figure 6. Distribution of normalized total lead in sludge

下载: 全尺寸图片幻灯片

图 7 平均固结度和平均沉降量随时间的变化

Figure 7. Change of average degree of consolidation and average settlement with time

下载: 全尺寸图片幻灯片

图 8 土体局部铅平均残余率随时间的变化

Figure 8. Change of local average residual rate of lead in soils with time

下载: 全尺寸图片幻灯片

图 9 土体pH值与归一化总Pb含量的时空分布

Figure 9. Distribution of pH value and normalized total lead of soils

下载: 全尺寸图片幻灯片

图 10 土体平均沉降随时间的变化

Figure 10. Change of average settlement of soils with time

下载: 全尺寸图片幻灯片

不同 ${u}_{{\text{Pb}}^{2+}，0}^{*}\text{/}{k}_{\text{e0}}$ 条件下土体pH值的时空分布

Distribution of pH value of soils under different ${u}_{{\text{Pb}}^{2+},0}^{*}\text{/}{k}_{\text{e0}}$

下载: 全尺寸图片幻灯片

不同 ${u}_{{\text{Pb}}^{2+}，0}^{*}\text{/}{k}_{\text{e0}}$ 下归一化总Pb含量的时空分布

Distribution of normalized total lead under different ${u}_{{\text{Pb}}^{2+},0}^{*}\text{/}{k}_{\text{e0}}$

下载: 全尺寸图片幻灯片

图 13 不同压缩指数下归一化总Pb含量分布

Figure 13. Distribution of normalized total lead under different compression indices

下载: 全尺寸图片幻灯片

图 14 不同初始pH值下归一化总Pb含量时空分布

Figure 14. Distribution of normalized total lead under different initial pH values

下载: 全尺寸图片幻灯片

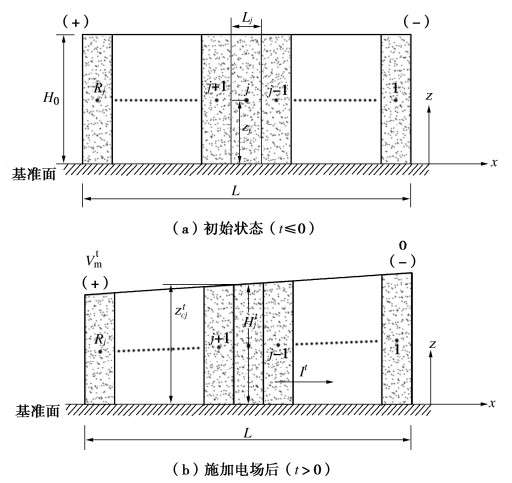
表 1 ECT1排水边界条件

Table 1 Drainage boundary conditions of ECT1

条件	阳极	阴极
不透水	$i_{{\text{e,b}}}^t = i_{{\text{h,b}}}^t = 0$	$i_{{\text{e,1}}}^t = i_{{\text{h,1}}}^t = 0$
透水	$\begin{gathered} i_{e,b}^t = \frac{{2(V_{\text{m}}^t - V_{{R_j}}^t)}}{{{l_0}}} \hfill \\ i_{{\text{h,b}}}^t = \frac{{2({h_{{\text{w2}}}} - h_{t,{R_j}}^t)}}{{{l_0}}} \hfill \\ \end{gathered}$	$\begin{gathered} i_{{\text{e,1}}}^t = \frac{{2V_1^t}}{{{l_0}}} \hfill \\ i_{{\text{h,1}}}^t = \frac{{2(h_{t,1}^t - {h_{{\text{w1}}}})}}{{{l_0}}} \hfill \\ \end{gathered}$
注： $i_{{\text{e,b}}}^t$ 和 $i_{{\text{h,b}}}^t$ 为阳极边界处的电势梯度和水力梯度， $i_{{\text{e,1}}}^t$ 和 $i_{{\text{h,1}}}^t$ 为阴极边界的电势梯度和水力梯度。

下载: 导出CSV

表 2 ECT1离子通量边界条件

Table 2 Species flux boundary conditions of ECT1

离子	阳极	阴极
Me^m+	$J_{{\text{M}}{{\text{e}}^{{\text{m + }}}},{\text{b}}}^t = c_{{\text{M}}{{\text{e}}^{{\text{m + }}}}{\text{,b}}}^tJ_{{\text{w,b}}}^t$	$J_{{\text{M}}{{\text{e}}^{{\text{m + }}}},1}^t = c_{{\text{M}}{{\text{e}}^{{\text{m + }}}},1}^tJ_{{\text{w,1}}}^t$
H⁺	$J_{{{\text{H}}^ + },{\text{b}}}^t = c_{{{\text{H}}^ + },{\text{b}}}^tJ_{{\text{w,b}}}^t + \frac{{R_{{{\text{H}}^ + }}^t}}{{H_{{R_j}}^t}}$	$J_{{{\text{H}}^{\text{ + }}},1}^t = c_{{{\text{H}}^{\text{ + }}},1}^tJ_{w,1}^t$
OH^-	$J_{{\text{O}}{{\text{H}}^ - },{\text{b}}}^t = c_{{\text{O}}{{\text{H}}^ - }{\text{,b}}}^{\text{t}}J_{{\text{w,b}}}^t$	$J_{{\text{O}}{{\text{H}}^ - },1}^t = c_{{\text{O}}{{\text{H}}^ - },1}^tJ_{{\text{w,1}}}^t - \frac{{R_{{\text{O}}{{\text{H}}^ - }}^t}}{{H_1^t}}$
注：下标b代表阳极边界，下标1代表阴极边界。以阳极边界为例， $J_{{\text{M}}{{\text{e}}^{{\text{m + }}}},{\text{b}}}^t$ 和 $c_{{\text{M}}{{\text{e}}^{{\text{m + }}}},{\text{b}}}^t$ 分别为重金属离子Me^m+在阳极边界（阳极电解室）处的通量和浓度，当阳极边界封闭或无该离子补充时， $J_{{\text{M}}{{\text{e}}^{{\text{m + }}}}{\text{,b}}}^t = 0$ 。

下载: 导出CSV

表 3 数值模拟输入参数^[15]

Table 3 Input parameters of numerical simulation

参数	取值
水力渗透系数k_h/(m·s^-1)	6.79×10^-10
电渗系数k_{e, 0}/(m²·s^-1·V^-1)	1×10^-9
压缩系数a_v/(MPa^-1)	2.27×10^-2
初始孔隙比e₀	1.27
干重度 ${\gamma _{\text{d}}}$ /(kg·m^-3)	1800
恒定电流密度I/(A·m^-2)	1.33
模型几何边长L/m	0.7
初始铅浓度 ${c_{{\text{Pb,}}0}}$ /(mg·kg^-1)	5320
初始酸碱性pH₀	4
土样阳离子交换能力CEC/(mEq·100g^-1)	1.06
土样曲折系数 $\tau$	0.44

下载: 导出CSV

表 4 扩散系数与离子迁移率

Table 4 Diffusion coefficient and ion mobility of species

物质种类	扩散系数 ${D_i}$ /(m²·s^-1)	离子电迁移率 ${u_i}$ /(m²·s^-1·V^-1)
${\text{P}}{{\text{b}}^{{\text{2 + }}}}$	9.45×10^-10	7.36×10^-8
${{\text{H}}^{\text{ + }}}$	93.1×10^-10	36.25×10^-8
${\text{O}}{{\text{H}}^ - }$	52.7×10^-10	20.58×10^-8
${\text{NO}}_3^ -$	19.0×10^-10	7.44×10^-8

下载: 导出CSV

表 5 基本物化参数

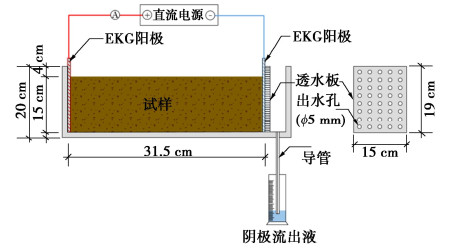
Table 5 Basic physical and chemical parameters of kaolin sample

物化参数	取值
初始含水率	79.2%
相对密度 ${G_{\text{s}}}$	2.65
初始孔隙比e₀	2.1
初始水力渗透系数 ${k_{{\text{h,0}}}}$ /(m·s^-1)	2.1×10^-9
水力渗透指数 ${C_{\text{k}}}$	0.9
初始电渗系数 ${k_{{\text{e,0}}}}$ /(m²·sV^-1)	5.8×10^-9
初始酸碱性pH	8.32
压缩指数 ${C_{\text{c}}}$	0.4
初始铅浓度 ${c_{{\text{Pb,}}0}}$ /(g·kg^-1)	1
阳离子交换能力CEC/(mEq·100g^-1)	2.07
曲折系数 $\tau$	0.45

下载: 导出CSV

表 6 算例输入参数

Table 6 Input parameters of example

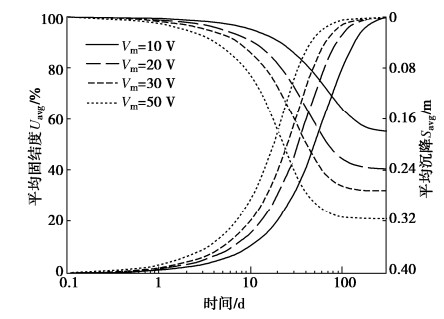
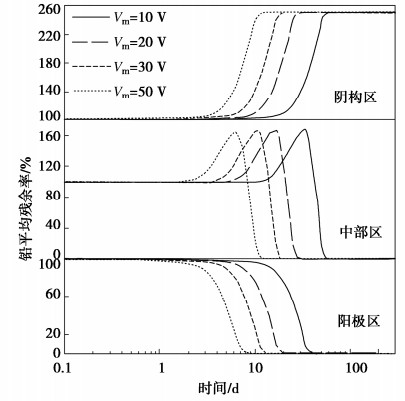
参数	取值
初始水力渗透系数 ${k_{{\text{h,0}}}}$ /(m·s^-1)	2.08×10^-9
水力渗透指数 ${C_{\text{k}}}$	0.99
初始电渗系数 ${k_{{\text{e,0}}}}$ /(m²·sV^-1)	2.35×10^-9
压缩指数 ${C_{\text{c}}}$	0.5
初始孔隙比e₀	1.9
初始孔隙率n₀	0.66
初始相对密度 ${G_{\text{s}}}$	2.62
阳极和阴极间电势差 ${V_{\text{m}}}$ /V	30
模型几何边长L×W×H(m×m×m)	1×1×1
初始铅浓度 ${c_{{\text{Pb,}}0}}$ /(g·kg^-1)	1.9
初始酸碱性pH	6.6
阳离子交换能力CEC/(mEq·100g^-1)	1.7
曲折系数 $\tau$	0.4
集总系数 $\varepsilon$	0.19

下载: 导出CSV

参考文献(24)

[1]	周建, 魏利闯, 詹芳蕾, 等. 生物表面活性剂及其与柠檬酸联合用于污泥重金属电动修复[J]. 湖南大学学报(自然科学版), 2019, 46(6): 109–119. https://www.cnki.com.cn/Article/CJFDTOTAL-HNDX201906016.htm ZHOU Jian, WEI Li-chuang, ZHAN Fang-lei, et al. Electrokinetic repair of heavy metals in sludge by biosurfactant and its combination with citric acid[J]. Journal of Hunan University (Natural Sciences), 2019, 46(6): 109–119. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HNDX201906016.htm
[2]	TUAN P A, SILLANPÄÄ M. Migration of ions and organic matter during electro-dewatering of anaerobic sludge[J]. Journal of Hazardous Materials, 2010, 173(1/2/3): 54–61.
[3]	TANG X Q, LI Q Y, WANG Z H, et al. Improved isolation of cadmium from paddy soil by novel technology based on pore water drainage with graphite-contained electro-kinetic geosynthetics[J]. Environmental Science and Pollution Research International, 2018, 25(14): 14244–14253. doi: 10.1007/s11356-018-1664-4
[4]	ESRIG M I. Pore pressure, consolidation and electrokinetics[J]. Journal of the SMFD, ASCE, 1968, 94(SM4): 899–921.
[5]	HU L, WU W, WU H. Numerical model of electro-osmotic consolidation in clay[J]. Géotechnique, 2012, 62(6): 537–541. doi: 10.1680/geot.11.T.008
[6]	吴辉, 胡黎明. 考虑电导率变化的电渗固结模型[J]. 岩土工程学报, 2013, 35(4): 734–738. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201304020.htm WU Hui, HU Li-ming. Numerical simulation of electro-osmosis consolidation considering variation of electrical conductivity[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(4): 734–738. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201304020.htm
[7]	王军, 符洪涛, 蔡袁强, 等. 线性堆载下软黏土一维电渗固结理论与试验分析[J]. 岩石力学与工程学报, 2014, 33(1): 179–188. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201401021.htm WANG Jun, FU Hong-tao, CAI Yuan-qiang, et al. Analyses of one-dimensional electroosmotic consolidation theory and test of soft clay under linear load[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(1): 179–188. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201401021.htm
[8]	FELDKAMP J R, BELHOMME G M. Large-strain electrokinetic consolidation: theory and experiment in one dimension[J]. Géotechnique, 1990, 40(4): 557–568. doi: 10.1680/geot.1990.40.4.557
[9]	王柳江, 刘斯宏, 王子健, 等. 堆载–电渗联合作用下的一维非线性大变形固结理论[J]. 工程力学, 2013, 30(12): 91–98. doi: 10.6052/j.issn.1000-4750.2012.04.0303 WANG Liu-jiang, LIU Si-hong, WANG Zi-jian, et al. A consolidation theory for one-dimensional large deformation problems under combined action of load and electroosmosis[J]. Engineering Mechanics, 2013, 30(12): 91–98. (in Chinese) doi: 10.6052/j.issn.1000-4750.2012.04.0303
[10]	YUAN J, HICKS M A. Large deformation elastic electro-osmosis consolidation of clays[J]. Computers and Geotechnics, 2013, 54: 60–68. doi: 10.1016/j.compgeo.2013.05.012
[11]	YUAN J, HICKS M A. Numerical simulation of elasto-plastic electro-osmosis consolidation at large strain[J]. Acta Geotechnica, 2016, 11(1): 127–143. doi: 10.1007/s11440-015-0366-z
[12]	ZHOU Y D, DENG A, WANG C. Finite-difference model for one-dimensional electro-osmotic consolidation[J]. Computers and Geotechnics, 2013, 54: 152–165. doi: 10.1016/j.compgeo.2013.06.003
[13]	冯源. 城市污水污泥电动脱水机理试验研究及多场耦合作用理论分析[D]. 杭州: 浙江大学, 2012. FENG Yuan. Experimental Study on Electrokinetic Dewatering Mechanism of Sewage Sludge and Theoretical Analyses of Multi-Field Coupled Phenomenon[D]. Hangzhou: Zhejiang University, 2012. (in Chinese)
[14]	CORAPCIOGLU M Y. Formulation of electro- chemicoosmotic processes in soils[J]. Transport in Porous Media, 1991, 6(4): 435–444.
[15]	ALSHAWABKEH A N, ACAR Y B. Removal of contaminants from soils by electrokinetics: a theoretical treatise[J]. Journal of Environmental Science and Health Part A: Environmental Science and Engineering and Toxicology, 1992, 27(7): 1835–1861. doi: 10.1080/10934529209375828
[16]	ALSHAWABKEH A N, ACAR Y B. Electrokinetic remediation: II theoretical model[J]. Journal of Geotechnical Engineering, 1996, 122(3): 186–196. doi: 10.1061/(ASCE)0733-9410(1996)122:3(186)
[17]	YEUNG A T, DATLA S. Fundamental formulation of electrokinetic extraction of contaminants from soil[J]. Canadian Geotechnical Journal, 1995, 32(4): 569–583. doi: 10.1139/t95-060
[18]	AL-HAMDAN A Z, REDDY K R. Electrokinetic remediation modeling incorporating geochemical effects[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(1): 91–105. doi: 10.1061/(ASCE)1090-0241(2008)134:1(91)
[19]	MASI M, CECCARINI A, IANNELLI R. Multi species reactive transport modelling of electrokinetic remediation of harbour sediments[J]. Journal of Hazardous Materials, 2017, 326: 187–196. doi: 10.1016/j.jhazmat.2016.12.032
[20]	GOODISMAN J. Electrochemistry: Theoretical Foundations, Quantum and Statistical Mechanics, Thermodynamics, the Solid State[M]. New York: Wiley, 1987.
[21]	YEUNG A T, HSU C N, MENON R M. Electrokinetic extraction of lead from kaolinites: I numerical modeling[J]. The Environmentalist, 2011, 31(1): 26–32. doi: 10.1007/s10669-010-9295-4
[22]	KIM S O, KIM J J, KIM K W, et al. Models and experiments on electrokinetic removal of Pb(II) from kaolinite clay[J]. Separation Science and Technology, 2005, 39(8): 1927–1951. doi: 10.1081/SS-120030775
[23]	ACAR Y B, ALSHAWABKEH A N. Electrokinetic remediation I: pilot-scale tests with lead-spiked kaolinite[J]. Journal of Geotechnical Engineering, 1996, 122(3): 173–185. doi: 10.1061/(ASCE)0733-9410(1996)122:3(173)
[24]	YONG R N, WARKENTIN B P, PHADUNGCHEWIT Y, et al. Buffer capacity and lead retention in some clay materials[J]. Water, Air, and Soil Pollution, 1990, 53(1/2): 53–67.

施引文献(6)

期刊类型引用(3)

1.	符传邦，吴育麒，吴月磊. 水泥搅拌桩各项参数对软土路基沉降的影响. 市政技术. 2023(02): 73-77 . 百度学术
2.	赵楠. 地铁隧道基底围岩动三轴试验研究. 资源信息与工程. 2022(02): 116-120 . 百度学术
3.	魏丽，柴寿喜，张琳，李瑶. 冻融作用下三类纤维加筋固化土的抗压抗拉性能. 岩土力学. 2022(12): 3241-3248+3280 . 百度学术