0.   引言

当水库库址分布地层主要有厚度大、透水性较强地层，如粉砂、砂性土或砾石土，缺乏有效隔水层时，则选用库盘土工膜防渗方案可很好地解决场地地层的渗漏问题^[1]，应用成功的例子如胜利水库、夹山子水库、大屯水库^[2]。但也有失败的例子：如山东省淄博市新城水库采用了0.3 mm厚聚乙烯（PE）土工膜防渗方案，运营过程中的库水位下降速度为1.0~1.5 cm/日，截渗沟内水位受库水位影响而变化^[3]，这表明水库仍有渗漏；为此2014年完成了水库扩建，重新采用库盘土工膜防渗，并在膜下设置排气盲沟，运营良好^[4]。袁俊平等^[5]认为土工膜防渗方案的水库渗漏由膜下气胀引发，并分析了引起膜下气胀的影响因素，然后通过现场模型试验，论证了气胀现象产生机制。CAO等^{[2, 6]}数值模拟了山东大屯水库施工、运营过程中的气场，详细分析了围堤填筑施工、库水位下降及地下水位上升等因素对膜下气压的影响，并从理论上分析了膜下排气盲沟设置间距的合理性。

评估膜下排气盲沟设置是否合理的重要指标是膜下土体气压分布状态及对应的气压梯度值。而这些又与膜下土体渗气性及盲沟气阻相关。虽然目前研究土体渗气性的文献很多，但未见有文献研究过盲沟气阻对土体排气效果的影响。Hamamoto等^[7]研究发现渗气系数的控制性因素是试样孔隙大小，与原状土的结构性特征相关联。陈存礼等^[8]利用原状黄土的渗气试验研究了含水率、体积含气率及应力对渗气系数的影响。姚志华等^[9]通过改进的三轴渗气仪测定干密度、含水率和各向异性等因素影响下渗气率变化规律，认为土体渗气性服从Fick定律和Darcy定律的，在较低压力下两者结果差别不大。袁俊平等^[10]通过自行设计加工的气体渗透装置研究了裂隙膨胀土渗气规律。姚志华等^[11]通过现场浸水试验研究了土体从非饱和转变为饱和状态过程中的水、气相互作用，进而认为水分入渗可抑制土排气的作用。显然，影响土体渗气特性因素的室内试验研究成果较多，而现场试验的研究成果少见，更未见数值模拟成果。

为了进一步认识膜下盲沟气阻对土体气场分布规律的影响，依托西夏水库扩容改造工程，开展抽气条件下土体气场分布规律的现场试验数值模拟，结合现场试验测试成果，研究膜下有无盲沟条件下气场分布规律，确定盲沟气阻影响范围，为库盘土工膜防渗水库的膜下盲沟排气设计提供技术支撑。

1.   研究方法

1.1   膜下负压气场的分析方法

土工膜覆盖土体后，隔绝了大气蒸发与降雨对土体含水率的影响，于是膜下土体含水率及饱和度只受地下水位的影响。《公路路基设计规范》（JTG D30—2015）给出地下水以上0.3 m处粉质砾土饱和度为（69%~84%）^[12]。土工膜覆盖土体后，在土工膜下会逐渐形成饱和蒸汽环境，增大土体含水率，提高土体饱和度；在抽气试验的负压状态下，膜下土体的孔隙水上升而使饱和度进一步升高。真空预压时水被抽出来的现象反映了水的运动规律^[13]。因此对于本次试验，地下水位埋深1.0 m，负压状态下膜下土体应能满足较高饱和度的条件，即S_r > 80%。此时，水相占据大孔隙，孔隙气主要是跟随孔隙水一起流动，所以可以将孔隙气、水看成具有可压缩性的混合流体，于是非饱和土可近似看作土骨架与混合流体的两相体^[14]。非饱和土混合流体简化计算方法正是基于此建立的。

1.2   非饱和土混合流体固结计算方法

非饱和土混合流体固结理论是由殷宗泽等^[15]提出的，曹雪山等^[16]以二维饱和土固结程序（BCF）为基础，修改后成功运用于大坝水力劈裂问题、水库膜下气胀问题^{[2, 6]}等，这已表明该方法可行，程序可靠。

（1）混合流体压力

对于饱和度较高的非饱和土，如饱和度大于80%，考虑土体孔隙中的气、水混合流动特征，将孔隙气、水看作具有可压缩性的混合流体，于是建立混合流体的有效应力方程：

式中$\left\{ \sigma \right\}$为总应力；$\left\{ {\sigma '} \right\}$为有效应力；{M}=[1, 1, 0]^T；${u_{\text{m}}}$为混合流体压力，${u_{\text{a}}}$，${u_{\text{w}}}$分别为孔隙气、水压力。$\chi$为有效应力系数，采用Aitchison^[17]经验公式近似计算：

式中，${S_r}$为土体饱和度。式（1）表示总应力由有效应力和混合流体压力分担。

利用有效应力方程、物理方程、几何方程，建立可压缩性的混合流体的连续性方程，并将它与平衡微分方程联立，获得非饱和土固结的混合流体简化方程^[14]：

式中，${k_{\text{m}}}$，${\gamma _{\text{m}}}$，${B_{\text{m}}}$分别为混合流体渗透系数、重度、压缩模量，${\gamma _{\text{m}}} = {S_{\text{r}}}{\gamma _{\text{w}}}$，${\gamma _{\text{w}}}$为水的重度。

修改河海大学岩土所编制的二维饱和土固结程序（BCF）可求解式（4），获得骨架应力、变形及混合流体压力。

（2）水连续性方程

根据非饱和土中单元孔隙水流量变化及孔隙水与孔隙流体的关系，推导出水连续方程^[14]：

式中，${k_{\text{w}}}$为水的渗透系数。

利用已经求出的${u_{\text{m}}}$和水连续方程求出${u_{\text{w}}}$。

（3）孔隙气压力的求解

利用已解得的${u_{\text{m}}}$和${u_{\text{w}}}$，进而求气压力${u_{\text{a}}}$

1.3   模型参数及土工膜单元的处理

（1）非饱和土的水渗透系数${k_{\text{w}}}$

非饱和土中的水渗透系数不仅与饱和状态下土体渗透性，如土体孔隙排列、孔隙大小等相关，还与土体所处的状态，如饱和度相关。因此非饱和土的水渗透系数一般表示为^[15]

式中，${k_{{\text{ws}}}}$为饱和土的渗透系数，${e_0}$，$e$为土体的初始孔隙比和孔隙比。

（2）饱和度变化

根据参考文献[15]的附录（5）可得到

于是将式（6）代入式（8）后得到

考虑到在混合流体压力计算过程中，孔隙水压未知，同时因土体饱和度较高，孔隙水压近似等于混合流体，因此近似取${u_{\text{w}}} = {u_{\text{m}}}$，从而简化非饱和固结计算过程，进而得到

式中，$\Delta {S_{\text{r}}}$为饱和度变化，$\Delta {u_{\text{m}}}$为混合流体压力变化量，${p_{\text{a}}}$为大气压力。

（3）混合流体渗透系数

考虑气渗透系数${k_{\text{a}}}$与饱和度或吸力相关，可得到^[18]

式中${k_{\text{a}}}$为气渗透系数；${S_{\text{e}}}$为有效饱和度；${u_{{\text{sb}}}}$为土性的进气值；$\lambda$为当基质吸力超过土的进气值时，与土中饱和度函数相关的土性参数；${S_{\text{l}}}$为残余饱和度；${S_{{\text{r0}}}}$为初始饱和度；k_d为干燥情况下土体的渗气系数。

鉴于影响非饱和土的水、气渗透系数的因素多，测试难度大^[19]，混合流体的渗透系数测试难度更大，通常采用近似方法确定混合流体的渗透系数^{[15, 20]}。本文根据渗流时流出的混合流体中水和气所占体积与饱和度的关系，由式（13）求得混合流体的渗透系数。

（4）流体体积压缩模量

B_m是反映孔隙流体压缩性的一项重要指标，它不仅与土体初始孔隙比e₀相关，而且与土体所处的状态，如孔压大小、孔隙比值、饱和度等密切相关^[21]。

（5）孔隙比变化

对式（1）微分后，当总应力不变时，即$\Delta \sigma$=0，则

根据压缩试验定义压缩系数，得到

将式（15）代入式（16），得

式中，∆e为孔隙比变化量，${a_{\text{v}}}$为压缩系数。

（6）土工膜单元厚度等效处理方法

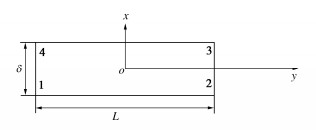
由于土工膜单元的通常厚度远小于宽度，为了避免计算困难，数值计算中往往将其厚度增大。如图 1所示，以x方向为渗流考察方向，通过单元内外侧的流量差∆Q为

图  1  二维单元分析

Figure  1.  Analysis of two-dimensional element

下载: 全尺寸图片 幻灯片

式中，∆p为单元内外两侧压力差，k为单元材料的渗 透系数，∆t为通过单元内侧的流量差∆Q 所持续的时间，δ为单元内外侧的厚度，L为单元宽度。

按介玉新等^[22]提出的等流量换算原则，单元厚度与渗透系数等比例放大；于是因单元厚度$\delta$放大a倍，则单元内外侧流体压力梯度减小a倍，用单元渗透系数增大a倍来弥补。该换算原则符合稳定渗流条件，此时流量与渗流路径长度无关。但本文是非饱和土固结问题，土工膜单元厚度等效原则应满足通过单元内外的流量差不变的要求。如果单元厚度$\delta$放大a倍，单元渗透系数增大a倍只能满足流量相等的条件；而要满足通过单元内外侧的相同流量差∆Q的条件，尚需考虑持续时间也增长a倍，由此要使∆Q，∆t，∆p均不变，渗透系数不仅要克服梯度减小而增大a倍，还应缩短通过时间而增大a倍，所以按流量差不变原则下换算公式为

式中，a为单元厚度的换算倍数，$k'$为换算后单元的渗透系数。式（19）反映流量差不变等效原则下单元渗透系数与厚度的平方成正比例关系。这与太沙基一维固结理论中的排水路径长度对固结时间因素的影响^[21]相一致。

2.   膜下气场的模型的建立与计算

2.1   工程现场背景

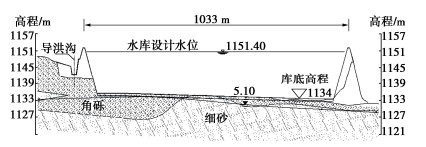
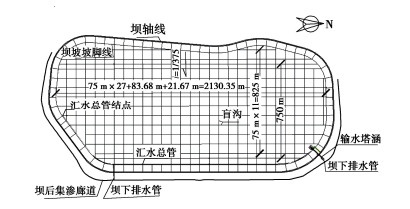
西夏水库扩容改造工程，位于银川市西夏区，蓄水面积约2.09 km²，库容3193万m³，蓄水深度17.55~15.55 m。如图 2所示，库盘地层为厚层、透水性强的角砾土和中透水性的细砂层。角砾土分布在场地近地表，南北坝范围厚度较大，4.40~11.20 m。该层富含粒径20~50 mm的颗粒，粒径大于2 mm以上的占全重60%~80%，中密状态，渗透系数为3.0×10^-4 m/s，变形模量35 MPa。细砂层，在场地内中部广为分布，厚7.0~20.5 m，中密，饱和，含少量角砾，渗透系数为4.0×10^-5 m/s。

图  2  水库场地地质剖面图

Figure  2.  Geological section of reservoir site

下载: 全尺寸图片 幻灯片

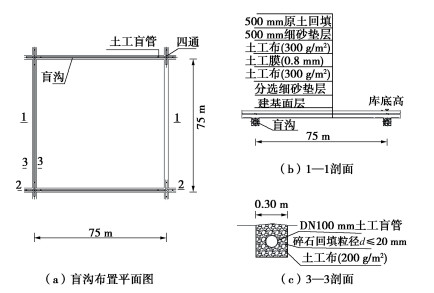
水库库盘采用300 g长丝土工布+0.8 mmPE膜+300 g长丝土工布分离式的防渗结构，膜上覆土保护层厚度不小于0.95 m，膜下布设棋盘式盲沟，间距75 m，如图 3所示。膜下盲沟横截面为0.3 m×0.3 m的矩形，如图 4所示。盲沟内布设一条$\phi$0.1 m土工盲管，截面为蜂窝煤状，外包土工布成品。盲管周边回填卵石，盲沟外包一层0.2 kg/m²的长丝土工布。由于盲沟的填充材料卵砾石渗透系数通常达到0.1~0.2 m/s^[23]，并且中间盲管的空腔还可使盲沟整体渗透系数进一步提高，于是盲沟的渗透系数远高于土体的3个数量级以上。因此通常数值计算中不考虑盲沟渗透性的影响，直接将盲沟内气压取值为大气压^[6]。于是膜下设置盲沟后，土体排气路径长度从水库半幅宽度500多米减小到38 m，大大提高了膜下气体排出的快捷性。

图  3  水库膜下排气排水系统布置图

Figure  3.  Layout of French drain system beneath geomembrane of reservoir

下载: 全尺寸图片 幻灯片

图  4  膜下盲沟设计方案大样图

Figure  4.  Diagram of French drain beneath geomembrane

下载: 全尺寸图片 幻灯片

但实际上，采用库盘土工膜防渗方案后，膜下土体上边界被土工膜封闭，隔离了土体孔隙与大气的联系。膜下土体排气分两步，首先排入盲沟，再由盲沟排至围坝外边界。前步的路径较短，但后步的排气路径相对前步增长1个多数量级；根据流量差不变原则下渗透系数与渗流路径长度的换算倍数的平方成比例（式（19））的关系，渗透系数相当于减小3~4个数量级。

所以即使设置材料渗透性高的盲沟，仍可能存在因盲沟排气路径太长引起的排气不畅的问题。本水库中心位置与围坝外侧的排气路径过长，由盲沟气阻产生库区中心与围堤间的气压差，影响土体内气体顺利排出，增加膜下气胀的可能性。

2.2   计算模型的建立

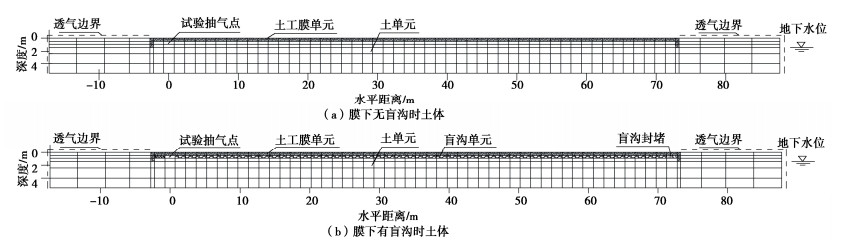
为了确定膜下盲沟气阻对土体排气的影响，评估膜下盲沟设计方案的合理性，依托水库施工开展现场试验的数值研究，以掌握库盘膜下盲沟的气压分布及气压梯度变化规律。如图 4所示，库盘场地被棋盘式盲沟分割成矩形土体单元，形成了膜下有、无盲沟的两种工况类型，如图 4中1—1和2—2断面，相应地有两种地基抽气模型，如图 5所示。图 5（a）对应1—1断面，膜下无盲沟的土体模型，由此可模拟出抽气后土体内气压分布状态；图 5（b）对应2—2断面，膜下有厚度0.3 m盲沟结构的土体模型，由此模拟膜下有盲沟时土体的气压分布状态。场地气压初始状态连通大气。土工膜铺设后形成了不透水不透气的上边界，侧边界处深挖沟1 m将土工膜埋入地下水位以下，地下水位为地面以下1 m处，底边界为地下水位的不透气边界。

图  5  膜下气场的模拟计算模型

Figure  5.  Models for air field beneath geomembrane

下载: 全尺寸图片 幻灯片

2.3   模型参数确定

土体模型计算参数中的c，φ，$\gamma$，k_ws源于《西夏水库设计报告》^[24]；其他E-μ模型参数参考《土工原理》^[21]并结合现场土质取值。土体渗气系数是利用自主研制测试装置，现场取样、室内测定确定的^[25]。测试土水特征曲线时，首先取现场土料样，室内制作与现场土体密度相同的试样；然后按滤纸法测定要求进行风干、标准滤纸平衡吸力、测定试样及滤纸含水率，由滤纸率定曲线得到试样含水率对应吸力值；最后根据土水特征曲线VG模型拟合确定模型参数^[25]。此外，土工膜单元渗透系数的取值是按通过单元流量差不变原则，即单元渗透系数与其厚度换算倍数的平方成比例关系（式（19）），进行换算确定；即土工膜单元的厚度0.0008 m、渗透系数5.0×10^-15 m/s，经等效换算后分别为厚度0.08 m、渗透系数5.0×10^-11 m/s。盲沟内卵砾石的渗透系数根据《工程地质手册》^[23]推荐渗透系数确定，其值比角砾土高出近3个数量级。具体成果如表 1。

表  1  非线性E-μ模型计算参数

Table  1.  Parameters of E-μ model for air field beneath geomembrane

土料	$\gamma$/(kN·m-3)	$\varphi$/(°)	c/kPa	Rf	K	n	G	F	D	Kur	Kws/(m·s-1)	Kd/(m·s-1)	e	Sr0/%	Srl/%	$\lambda$	usb/kPa
角砾土	22.4	30	10	0.93	400	0.6	0.3	0.15	1.5	800	3×10-4	3.22×10-3	0.53	0.90	0.11	4.1	3.1
盲沟	18.0	22	0	0.95	300	0.6	0.3	0.20	1.9	800	0.2	0.2	0.53	0.85	0.11	4.1	0.5
防渗膜	0.036	22	100	0.93	300	0.6	0.3	0.17	1.0	650	5.0×10-11	5.0×10-11	0.064	—	—	—	—

下载: 导出CSV 

| 显示表格

2.4   计算结果与现场试验验证

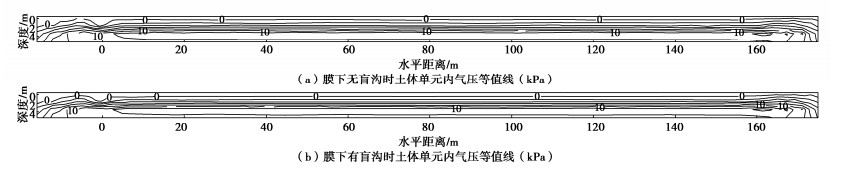
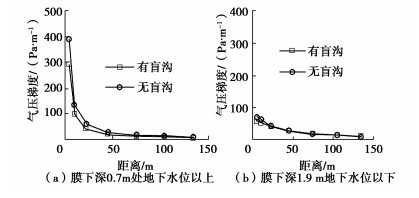
图 6分别展示了抽气作用下膜下有、无盲沟土体的气压分布规律。地下水位埋深为1.0 m，即膜下1.0 m以下土体为饱和，所以孔隙水压力为正值；抽气作用引起的气压急变区范围相对整个试验场地而言不大，在此范围内膜下气压有较大的变化，等值线呈现下凹形，而沿水平方向延伸至远处气压变化微小，为气压稳定区，水平距离大于75 m，这表明抽气作用对膜下孔隙气压的影响趋于稳定。

图  6  抽气范围内膜下气压计算结果

Figure  6.  Calculated results of pore-air pressure beneath geomembrane by field vacuuming tests

下载: 全尺寸图片 幻灯片

在水库场址开展了现场试验，采用水环式真空泵进行抽气，通过渗压计测试膜下抽气点、土体单元及盲沟内气压，获知膜下气压值分布情况，试验结果^[25]统计如表 2所示。

表  2  膜下气压的现场试验值

Table  2.  Pore air pressures beneath geomembranes by in-situ tests

项目	最低值/kPa	最高值/kPa	平均值/kPa	数据量/个	均方差/kPa
TP01	-0.90	-0.46	-0.68	11	0.13
TP02	-0.97	-0.56	-0.76	11	0.13
TP03	-0.80	-0.47	-0.64	11	0.11
TP04	-0.46	-0.23	-0.34	11	0.08
GP01	-2.67	-2.30	-2.49	11	0.12
GP02	-1.02	-0.48	-0.77	11	0.18
GP03	-1.10	-0.43	-0.85	11	0.22
注：TP是埋设于土体中渗压计；GP是埋设于盲沟内的渗压计。GP01是盲沟与真空泵连接部位的渗压计，即为试验场地的抽气点。

下载: 导出CSV 

| 显示表格

抽气点GP01处气压取为现场试验实测均值-2.49 kPa时，对应的膜下无盲沟的土体气压稳定区计算值-0.37 kPa，现场试验实测值的波动范围为（-0.34~-0.76）kPa；膜下有盲沟时气压稳定区计算值-0.87 kPa，现场试验实测值的波动范围（-0.77~-0.85）kPa。由此膜下气压计算值接近于现场试验实测值，且膜下气压分布规律相近，验证了计算方法和参数的合理性。

3.   膜下气场分布规律分析

3.1   膜下气压分布规律

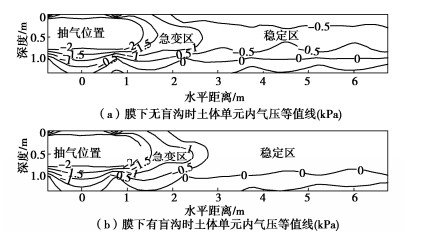
图 7展示了膜下有无盲沟两种工况条件下抽气点附近的气压分布情况；图 8为不同深度处膜下气压与距离的关系；图 9为不同距离处膜下气压与深度的关系。根据膜下气压计算结果，可知：

图  7  膜下抽气点附近的气压计算结果

Figure  7.  Pore-air pressures beneath geomembrane near vacuuming spot

下载: 全尺寸图片 幻灯片

图  8  不同深度处气压与距离的关系

Figure  8.  Relationship between air pressure and distance at different depths

下载: 全尺寸图片 幻灯片

图  9  不同位置处气压与深度的关系

Figure  9.  Relationship between air pressure and depth at different distances

下载: 全尺寸图片 幻灯片

（1）如图 7所示，在膜下地下水位以上，抽气点附近为气压急变区，在2.5 m范围内负压变化显著；远处为气压稳定区。这说明虽然盲沟渗气性高，但不改变膜下气压变化分区，所以盲沟内存在气阻效应。

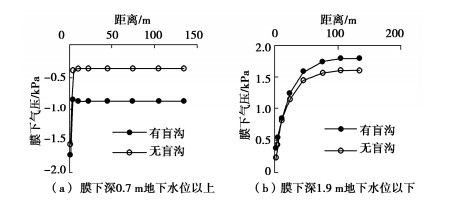
（2）膜下气压分布随距离快速衰减至基本稳定值。如图 8所示，无论膜下有无盲沟，气体负压稳定区水平向距离均大于75 m；沿深度，地下水位以上为孔隙气、水混合区，负压不大但较为稳定，而地下水位以下孔隙压力则为正值，且随距离增加孔隙压力趋向稳定值。这反映了通过显著提高盲沟材料渗透系数（提高3个数量级）后，在膜下形成气体空腔，有利于减小膜下盲沟内气压梯度。

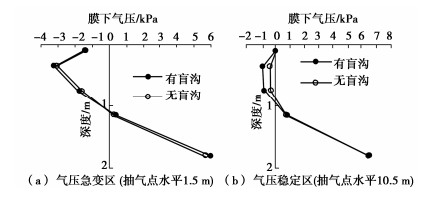
（3）膜下气压变化与深度相关。如图 9所示，不管有无盲沟，膜下深度1.0 m为负压，这与膜下地下水位埋深1.0 m相对应；膜下1.0 m以下为地下水饱和区，水压为正值。

（4）膜下有盲沟时气压低于膜下无盲沟的工况。如图 7~9所示，无论是距离还是深度上，膜下无盲沟时气压值均大于膜下有盲沟工况。这表明盲沟具有较大的渗气性，增大了气体排出效果，所以工程中设置膜下盲沟，并且盲沟材料采用卵石，使其渗透性比土体单元渗透性高出3个数量级，在理论和工程实践上均是合理的。

3.2   膜下气压梯度的分布规律

膜下气压梯度是以抽气点为基准位置，考察位置气压与至抽气点的距离比值。可由下式计算：

式中，${i_{\text{a}}}$为测点的气压梯度，${u_{\text{a}}}$为测点的气压值，${u_{{\text{a0}}}}$为抽气点处的气压值，L为测点至抽气点的距离。

如图 10，11所示，根据膜下气压梯度与距离、深度关系可知：

图  10  不同深度处气压梯度与距离关系

Figure  10.  Relationship between air pressure gradient and distance at different depths

下载: 全尺寸图片 幻灯片

图  11  不同距离处气压梯度与深度关系

Figure  11.  Relationship between air pressure gradient and depth at different distances

下载: 全尺寸图片 幻灯片

（1）膜下气压梯度沿水平距离逐渐减小。图 10显示无论膜下有无盲沟，与抽气处距离愈近，气压梯度变化愈大，例如膜下无盲沟时土中气压梯度衰减幅度最大达到35.5 Pa/m；随着距离增大，气体梯度快速减小，约75 m后气压梯度变化量不足0.2 Pa/m，表明气压梯度基本稳定。

（2）气压改变了土体气压梯度分布状态。图 11显示抽气作用所引起的气压急变区的气压梯度明显大于气压稳定区的，其中膜下深度1.0 m范围内梯度变化显著，而膜下1.0 m以下地下水内气压梯度变化减弱。

（3）膜下盲沟内气压梯度分布规律反映了盲沟气阻的变化。盲沟内气压梯度随距离快速减小，进而达到基本稳定状态。这说明盲沟的气阻效应沿距离、深度也是变化的。相比膜下土体而言，盲沟材料孔隙大、含水率低、渗气性高，所以形成气压梯度小于土体，进而大大减弱了气体在盲沟内传输的阻力。

4.   影响膜下盲沟气阻的因素研究

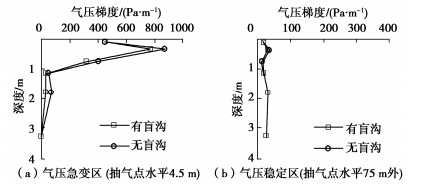
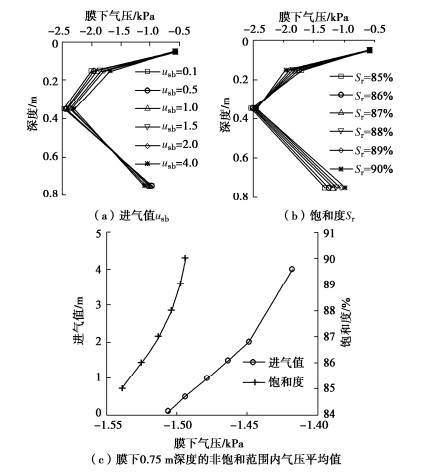
盲沟气阻为盲沟内气体传输过程中遇到的阻力；气阻小的材料渗气性必然高。因此气阻与渗气性高低具有相反的变化规律。尽管研究成果显示土体渗气性的影响因素很多^[7-11]，但基本因素可归纳为两个：进气值与饱和度。进气值是土体脱水过程中允许空气进入时的吸力值。在土体脱水过程中，大孔隙中的水最易流出，进而空气渗透有了通道，所以进气值反映了允许空气流通的土体孔隙特征。Hamamoto等认为土体孔隙是渗气特性的控制因素^[7]，如此则应力状态、干密度^[9]、渗气与渗水系数的相关性均通过孔隙大小、形态的差异及变化来实现改变的。孔隙直径愈大则进气值愈小。图 12展示了盲沟材料的进气值取不同值时对膜下气压的影响。进气值愈小，膜下气压愈低，对应着材料孔隙直径大，相应的盲沟气阻小，这也是盲沟材料采用卵砾石，甚至加通气盲管，增大透气孔径的原因。

图  12  盲沟气阻的影响因素

Figure  12.  Influencing factors of air resistance in French drain

下载: 全尺寸图片 幻灯片

饱和度表征了孔隙中水、气的体积含量，反映了孔隙传输气体时畅通性。土体中气、水均属流体，当土体孔隙渗流过程中通过的流体全为水，则饱和度为100%，渗气性为零；当土体为非饱和状态时，随饱和度降低，渗气快速增加。土体含水率、湿度变化^[9]实质反映了饱和度对渗气性的影响。图 12表明饱和度低，气压小，其影响效应与进气值低时具有相同效果，相应的盲沟气阻小，这与低饱和度的渗气性高的变化规律是一致的^{[9, 11]}。

5.   结论

（1）基于流量差不变的等效原则，提出了单元渗透系数与渗透路径长度换算倍数的平方成比例的变换关系。据此推断出平原水库面积巨大，膜下排气路径太长是形成盲沟气阻的主要原因。

（2）基于现场试验地下水位埋深1.0 m、现场试验中采用真空抽气，增大了膜下土体饱和度，基本满足将孔隙气、水近似看作混合流体的条件。运用非饱和土固结简化方法计算模拟膜下气场分布，现场试验的实测值验证了计算方法和参数的合理性。

（3）无论有无盲沟，膜下气压分布由气压急变区与稳定区组成。气压急变区，即为抽气处附近2.5 m范围内，负压变化显著；气压稳定区气体负压变化不大，负压水平影响距离大于75 m；这说明虽然盲沟孔隙大，渗透高，但气压变化反映了盲沟气阻是客观存在的，在抽气附近表现较为显著。

（4）无论有无盲沟膜下气压梯度在气压急变区变化显著，在气压稳定区变化不明显；地下水位以上孔隙气、水混合区变化剧烈，而地下水位以下变化减弱。气压梯度分布规律反映盲沟气阻的变化。

（5）影响盲沟气阻的主要因素是材料进气值和饱和度。进气值减小、饱和度降低均有利于排气，减小气阻，由此选择卵砾石并加通气盲管，增大透气孔径，同时应充分利用膜下盲沟排水，确保地下水位低于盲沟，这是提高盲沟排气排水效果的有效工程措施。

需要指出，本文通过数值模拟验证了盲沟气阻的存在性，并分析了盲沟气阻的两个主要影响因素；盲沟气阻的其他影响因素尚需作进一步研究。