对《“矢量和法”抗滑稳定计算模型的力学概念错误》一文的回应

郭明伟; 李春光; 刘艳章; 吴振君; 邓琴

doi:10.11779/CJGE202209022

对《“矢量和法”抗滑稳定计算模型的力学概念错误》一文的回应 English Version

1.
中国科学院武汉岩土力学研究所岩土力学与工程国家重点试验室，湖北武汉 430071
2.
武汉科技大学资源与环境工程学院，湖北武汉 430081

详细信息

作者简介:
郭明伟(1981—)，男，河南商丘人，副研究员，主要从事边坡工程、深基础工程及计算岩土力学方面的研究。E-mail：mwguo@whrsm.ac.cn

中图分类号: TU431
计量
- 文章访问数: 173
- HTML全文浏览量: 30
- PDF下载量: 138
出版历程
- 收稿日期: 2022-03-01
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-08-31

Reply to "Mechanical concept errors in anti-sliding stability computational model of vector sum method"

1.
State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China
2.
College of Resource and Environmental Engineering, Wuhan University of Science and Technology, Wuhan 430081, China

摘要

HTML全文

0. 引言

岩石类材料的强度不仅与围压、应力状态等因素有关,还受加载速率的影响。通常应变率越高,强度越大。在分析爆炸冲击、地震等动力荷载作用时,由于应力波的衰减,岩土体各个区域处于不同的应力状态,应变率也存在显著差异,因而需要考虑复杂应力状态下强度的率相关特性。

目前,材料的率效应研究以单轴试验为主,学者针对岩石、混凝土、冻土等材料开展了系列研究。根据是否存在极限峰值强度,单轴动态强度准则可分为J准则和S准则^[1]。对于J准则,随着应变速率的增加,材料的动态强度将无限增大；而S准则认为,当应变率极大时,材料的动态强度也将趋于稳定。Lu等^[2]认为动态强度由真实动态强度和惯性动态强度组成,真实动态强度存在极限值。然而,由于在极高应变率下,试验加载难度极大,可靠数据较少,目前还很难准确测定或预测极限峰值强度。而J准则参数相对较少、易于测定。在材料达到极限峰值强度前,S准则仍可采用J准则近似,因而,目前仍广泛采用J准则。

通常,J准则以对数函数^[3]、指数函数^[1]或幂函数^[4]等形式为主,也有部分学者采用分段函数的形式,但这增加了参数确定和模型使用的难度,函数非连续光滑也使与弹塑性本构理论结合的难度增加。

为了合理考虑岩石类材料在复杂应力状态下的动态强度规律,一些学者采用等效应变率概念^[5-6],将单轴强度拓展至复杂应力状态。此外,王怀亮等采用二次函数作为子午面破坏包络线,在偏平面上采用Willam-Warnke模型,使用特征应力点法对拉压子午面方程进行修正以考虑偏平面上罗德角对动态强度的影响^[7]。杜修力等基于广义非线性强度^[8]框架,结合混凝土材料的非线性单轴、双轴动态强度特性,得出强度参数的率效应公式,由此建立混凝土材料的三轴动态强度准则^[9]。这两种理论均假定静力条件下强度参数与单轴压缩、拉伸强度的关系在动态条件下仍然成立,从而将静力准则外推至考虑应变率效应。由于强度参数均为应变率的函数,这导致强度包线表达式复杂,增加了准则使用的难度。

本文通过整理单轴及多轴动态强度试验数据,分析各个强度参数与应变率效应的相关性,在此基础上建立动态坐标系,提出考虑应变率效应的多轴强度准则。准则中各个参数物理意义明确,模型的建立充分考虑动态强度试验规律,模型特性与试验相符,为强度的率效应提供了新的认识,可以用于预测材料的动态强度特性。

1. 单轴动态强度准则

对于砂土、岩石、混凝土等材料,其强度与加载速率密切相关,受试验条件制约,目前超高应变率下强度的发展规律及机理还没有定论。为了简便起见,本文基于J准则开展研究,即应变率越高,材料强度越高。图1为半对数坐标系下,动态强度典型的试验结果。当应变率较小时,强度保持恒定,此时称为准静态。当应变率超过一定范围后,强度产生突变,强度突变的转折点定义为临界应变率 ${\dot{ε}}_{0}$ 。根据实测数据,强度与应变率在半对数坐标系下为线性关系,其斜率采用静态强度 $σ_{s}$ 无量纲化后,表示为k_εa,描述强度的增长率。

图 1 动态强度随应变率变化规律

Figure 1. Evolution of dynamic strength with strain rate

下载: 全尺寸图片幻灯片

为了简单描述动力强度随应变率变化的规律,对试验结果进行归一化。采用动力增长因子（DIF, dynamic increase factor）作为强度特征量,其定义为动态强度与静态强度的比值；针对应变率,构造无量纲量 $\dot{ε} / {\dot{ε}}_{0} + 1$ ,表征相对应变率。采用无量纲量整理试验数据发现,动力增长因子与相对应变率在半对数坐标系下为线性关系。当应变率较高时, $\dot{ε} / {\dot{ε}}_{0} +$ $1 \to \dot{ε} / {\dot{ε}}_{0}$ ,其斜率趋近于k_εa。由于材料的初始状态为静态,代入相应的条件,直线始终经过点（1,1）,由此,可以采用统一的方程描述岩石类材料由静态到动态的强度特性,

$DIF = \frac{σ_{d}}{σ_{s}} = 1 + k_{εa} l n (\frac{\dot{ε}}{{\dot{ε}}_{0}} + 1)$ ,

(1)

式中, $σ_{d}$ 为动态强度, $\dot{ε}$ 为应变率。

图2为式（1）所得动力增长因子随应变率变化的曲线,当应变率相对较低时,动力增长因子基本为1；而当应变率大于临界应变率时,随着应变率增加,DIF与应变率在半对数坐标系下近似为线性关系。临界应变率不同,曲线上升段起点不同,而曲线基本相互平行,斜率一致。当k_εa不同,动态强度增长速率不同,斜率越大,强度升高越快。在动力作用下,材料单轴拉伸或压缩强度随应变率变化规律一致,式（1）可以较好地描述岩石类材料的单轴动态强度特性。

图 2 参数对动态强度增长因子的影响

Figure 2. Influences of parameters on dynamic increase factor

下载: 全尺寸图片幻灯片

2. 多轴动态强度准则

2.1 统一强度准则

由于缺乏必要的试验基础,目前对材料的动态强度特性还没有清晰的认识,尚不具备通过理论直接建立三维动态强度准则的条件。分析应变率对强度参数的影响规律,是建立动态强度准则是行之有效的方法^[11]。Yao等^[12]提出的统一强度准则适用于描述多种岩土类材料的三维强度特性。该准则仅包含4个相互独立的参数,均具有明确的物理意义,可以方便地通过三轴压缩和拉伸试验确定,便于分析率效应对强度参数的影响规律,因而基于该准则进行多轴动态强度准则的研究。为了反映摩擦效应及静水压力效应,统一强度准则在子午面上采用幂函数作为破坏包线^[12],

$q^{*} = M_{f} {(\frac{\bar{p}}{p_{r}})}^{n} p_{r}$ 。

(2)

式中 q^*为三轴压缩强度；p为平均正应力；p_r为参考应力；n为静水压力效应指数,描述了子午面破坏曲线的弯曲程度；M_f为参考应力p_r处对应的割线斜率,反映了材料的摩擦特性。采用幂函数可以统一描述线性与非线性的强度特性,且通过固定点,方便参数确定。统一强度准则通过坐标平移描述材料的黏聚力效应,坐标平移公式为^[12]

${\bar{σ}}_{i j} = σ_{i j} + σ_{0} δ_{i j}$ 。

(3)

式中 $σ_{i j}$ 为应力张量； $δ_{i j}$ 为Kronecher符号。 ${\bar{σ}}_{i j}$ 为平移后的应力张量, $σ_{0}$ 为等向拉伸强度,对应子午面破坏曲线与p轴的交点坐标。强度包线平移后满足式（2）,强度包线如图3所示。

图 3 子午面强度包线

Figure 3. Strength envelopes on meridian plane

下载: 全尺寸图片幻灯片

在π平面,为了与SMP及Mises准则相结合,当 ${\bar{σ}}_{3}$ ≥0时,定义^[12]

$q^{*} = α \sqrt{{\bar{I}}_{1}^{2} - 3 {\bar{I}}_{2}} + \frac{2 (1 - α) {\bar{I}}_{1}}{3 \sqrt{({\bar{I}}_{1} {\bar{I}}_{2} - {\bar{I}}_{3}) / ({\bar{I}}_{1} {\bar{I}}_{2} - 9 {\bar{I}}_{3})} - 1}$ ,

(4)

式中, ${\bar{I}}_{1}$ , ${\bar{I}}_{2}$ 和 ${\bar{I}}_{3}$ 分别为坐标平移后的主应力不变量。 $α$ 的不同引起同一 $π$ 平面上强度包线由SMP曲边三角形向Mises圆过渡, $α$ 的取值范围为[0,1],当 $α$ =0时,π平面上强度包线为SMP曲边三角形；当 $α$ =1时,π平面上强度包线为Mises圆,如图4所示。

图 4 不同

$α$ 对

$π$ 平面强度包线影响

Figure 4. Strength envelopes on π plane under different α

下载: 全尺寸图片幻灯片

2.2 子午面动态强度特性

文献[13]开展不同应变率条件下混凝土的三轴压缩试验,首先结合该数据分析子午面动态强度特性。根据经验公式,静态等向拉伸强度近似取为0.09f_c^[14],令p_r=f_c,根据统一强度准则,子午面强度在ln(q/p_r)- ln[(p+ $σ_{0}$ )/p_r]坐标系下为线性关系,直线斜率为静水压力系数n,与纵轴的截距为ln(M_f)。图5给出不同应变率条件下的试验结果,各条强度包线基本平行,即应变率对静水压力系数n几乎没有影响。

图 5 双对数坐标系下不同应变率子午面强度试验结果

Figure 5. Strength data on meridian plane under different strain rates in double-log coordinates

下载: 全尺寸图片幻灯片

计算各强度包线与横轴的截距,得到对应的平均正应力,若将应变率10^-5视为静态,计算平均正应力差值Δp,由此可以计算出不同应变率下的动态等向拉伸强度 $σ_{d0}$ ,

$σ_{d0} = σ_{s0} + Δ p$ ,

(5)

整理等效动态等向拉伸强度与应变率的关系,其在半对数空间与单轴强度试验规律一致（图6）,因而可以得到表达式为

$σ_{d0} = σ_{s0} + k_{εa} σ_{s0} l n (\frac{\dot{ε}}{{\dot{ε}}_{0}} + 1)$ ,

(6)

图 6 等向拉伸强度与应变率关系

Figure 6. Evolution of isotropic tensile strength by strain rate

下载: 全尺寸图片幻灯片

式中,k_ε为等向拉伸强度增长率,通常试验均针对单轴拉伸或单轴压缩,根据经验公式,可以将强度值近似转化为等向拉伸强度^[14]。

采用所得的动态等向拉伸强度重新整理试验数据,在ln(q/p_r)-ln[(p+ $σ_{0}$ )/p_r]坐标系下,不同应变率的强度包线均近似归一到同一直线（图7）。由此可得,应变率对静水压力系数及摩擦强度影响较小。这一结论与张建民等^[15]基于砂土所得的试验规律一致,即应变率变化对摩擦角影响不大,不同应变率下强度包线互相平行,应变率增大只引起黏聚力增加。

图 7 双对数空间平移后子午面强度

Figure 7. Strength data on meridian plane in double-log coordinates after translation

下载: 全尺寸图片幻灯片

根据统一强度准则,黏聚力变化可以通过坐标平移考虑,同理,可以采用动态坐标系描述应变率对强度包线的影响,不同应变率下坐标平移公式如下：

${\bar{σ}}_{i j} = σ_{i j} + σ_{d0} δ_{i j}$ ,

(7)

式中, $σ_{d0}$ 为动态等向拉伸强度,可由式（6）得出。

在动态坐标系下,子午面强度可采用式（2）描述,将强度包线转换至真实应力空间,即可得到不同应变率下的子午面强度（图8）。随着应变率的增加,强度包线形状相似,但是逐渐向左平移,强度逐渐升高。而随着平均正应力的升高,强度增长值明显降低,即强度的率敏感性减弱。

图 8 不同应变率下子午面强度包线

Figure 8. Strength envolope on meridian plane under different strain rates

下载: 全尺寸图片幻灯片

在等p条件下,根据式（2）可以得到动态增长因子

$DIF = \frac{q_{d}}{q_{s}} = {[1 + \frac{k_{ε}}{p + σ_{s0}} l n (\dot{ε} / {\dot{ε}}_{0} + 1)]}^{n}$ ,

(8)

由式（8）可以得到,抗剪强度动力增长因子主要受静水压力系数及平均正应力影响。图9给出了强度动力增长因子随应变率及平均正应力演化的规律,随着平均正应力的增加,动力增长因子显著降低,这与Li等^[16]所得的试验规律类似。而随着n值减小,静水压力效应越发显著,率效率越不明显。

图 9 强度动力增长因子随应变率及平均正应力演化规律（n=0.75,k_ε=0.1,σ_s0=1）

Figure 9. Evolution of DIF by strain rate and mean pressure（n=0.75,k_ε=0.1,σ_s0=1）

下载: 全尺寸图片幻灯片

在式（2）中代入单轴压缩应力状态（f_c,0,0）,可以得到单轴压缩强度,结合动态坐标系可以得到不同应变率下的强度特性,其规律与图1（a）中单轴试验规律基本一致（图10）。当超过临界应变率时,DIF与应变率在半对数空间近似为线性,这说明动态强度准则的合理性。随着k_s的变化,其可以描述与单轴准则相同的动态强度特性（图2（b））。

图 10 不同应变率下单轴压缩强度(n=0.94,k_ε=0.1,σ_s0=1.5)

Figure 10. Uniaxial compression strengths under different strain rates (n=0.94,k_ε=0.1,σ_s0=1.5)

下载: 全尺寸图片幻灯片

2.3 多轴动态强度特性

在子午面动态强度的基础上,结合公式（2）,（4）,并假定中主应力参数 $α$ 不随应变率变化,可得动态三维强度准则：

$\begin{matrix} M_{f} {(\frac{\bar{p}}{p_{r}})}^{n} p_{r} = α \sqrt{{\bar{I}}_{1}^{2} - 3 {\bar{I}}_{2}} + \\ \frac{2 (1 - α) {\bar{I}}_{1}}{3 \sqrt{({\bar{I}}_{1} {\bar{I}}_{2} - {\bar{I}}_{3}) / ({\bar{I}}_{1} {\bar{I}}_{2} - 9 {\bar{I}}_{3})} - 1} \end{matrix}$ ,

(9)

式中,坐标平移公式由式（7）定义,拉压应力比 $α$ 可以通过下式计算得出

$α = \frac{M_{e} M_{c} + 3 (M_{e} - M_{c})}{M_{e}^{2}}$ ,

(10)

式中,M_e,M_c分别为三轴拉伸、压缩应力比,对应强度包线在p-q空间的斜率。图11给出不同应率下三轴压缩及拉伸的试验数据^[17],根据实测结果,三轴压缩及拉伸破坏线的斜率几乎不随应变率变化,由式（10）,可以认为 $α$ 不受应变率影响。

图 11 不同应变率三轴压缩与拉伸强度

Figure 11. Triaxial compressive and extensive strengths under different strain rates

下载: 全尺寸图片幻灯片

根据式（9）可以得到不同应变率下的π平面强度包线（图12）。随着应变率增加,π平面强度包线外扩。由于等效破坏应力比减小,理论上,同一π平面的强度包线存在由曲边三角形向圆演变的趋势,在极高应变率下,材料强度特性趋向于金属材料。

图 12 不同应变率π平面强度包线

Figure 12. Strength envelopes on π plane under different strain rates

下载: 全尺寸图片幻灯片

将单轴拉伸应力状态（0,0,-f_t）代入式（9）,可以得到不同应变率下的单轴拉伸强度（图13）,其规律与图2中的试验结果一致,当应变率较低时,单轴拉伸强度动力增长因子趋于1,而当应变率超过临界应变率时,动力增长因子显著增加。为了研究中主应力参数对动力增长因子的影响,图13分别给出不同中主应力参数下的单轴拉伸预测结果,根据统一强度准则,随着中主应力参数 $α$ 的增加,单轴拉伸强度会逐渐提高。然而,不同应变率下动力增长因子却始终保持不变,这也从侧面说明,忽略率效应对 $α$ 的影响,不会显著影响材料单轴或拉伸子午面的动态强度规律。

图 13 不同应变率下单轴拉伸强度

Figure 13. Uniaxial tensile strengths under different strain rates

下载: 全尺寸图片幻灯片

3. 单轴动态强度准则试验验证

根据前人的研究成果,搜集了多种材料的单轴动态强度试验数据（图14）,不同材料强度随应变率变化规律基本一致,通过调整模型中临界应变率、强度增长率等参数,可以较好的拟合各种材料的单轴压缩及拉伸强度特性。

图 14 单轴动态强度试验验证

Figure 14. Validation of uniaxial strength criterion by experiments

下载: 全尺寸图片幻灯片

4. 多轴动态强度准则试验验证

在静态、准静态条件下,统一强度准则已通过砾石、岩石、混凝土等材料的强度试验进行验证^[12]。而在高应变率下开展真三轴试验尚有较大的技术难度,目前率效应试验以双轴压-压或拉压为主。本文将采用混凝土动态试验对强度准则进行验证。图15为三轴压缩试验的预测和实测结果^[13],试验所用试件为100 mm×100 mm×100 mm立方体,试验过程中,侧向压力保持恒定,分别为0,0.25f_c,0.5f_c,0.75f_c,试件竖向加载直至破坏,加载应变率分别为10^-5,10^-4,10^-3,10^-2。理论预测参数为M_f=1.45,n=0.4,p_r=f_c, $σ_{0}$ =0.09f_c,k_ε=0.236, $ε_{0}$ =10^-5。由对比结果可以看出,本文的动态强度准则可以描述应变率对子午面强度包线的影响。

图 15 不同应变率下混凝土三轴压缩试验强度^[13]

Figure 15. Triaxial compressive strengths under different strain rates^[13]

下载: 全尺寸图片幻灯片

图16为双轴压-压试验的预测和实测对比结果,试件采用双轴加载,加载过程中,始终保持2个方向荷载比例不变,应力比分别为1∶0,1∶0.25,1∶0.5,1∶0.75,1∶1。试验过程中,在不同加载应变率下进行试验,使试件破坏。由于应力比不同,各个工况应力罗德角不同,应力比为1∶1时对应三轴拉伸状态。由于混凝土试件强度相同,参数与上文一致,因需要考虑三轴拉伸应力状态,中主应力系数 $α$ 取为0.75,预测结果较好地反映了混凝土双轴压-压强度特性（图16）。

图 16 不同应变率下混凝土双轴压-压强度^[13]

Figure 16. Biaxial compressive strengths under different strain rates^[13]

下载: 全尺寸图片幻灯片

5. 结论

本文结合单轴和多轴动态强度试验数据,基于统一强度准则进行研究,得出以下主要结论：

（1）在半对数坐标系下,单轴强度与无量纲量 $\dot{ε} / {\dot{ε}}_{0} + 1$ 成线性关系,由此可以建立单轴动态强度公式,式中仅包含临界应变率和强度增长率两个物理意义明确且易于确定的参数。

（2）针对子午面动态强度,不同应变率下强度包线在双对数坐标系下近似平行,应变率效应可以归结为对强度包线的平移,即对等向拉伸强度或黏聚力的影响。在半对数坐标系下,等向拉伸强度与无量纲量 $\dot{ε} / {\dot{ε}}_{0} + 1$ 成线性关系,规律与单轴压缩、拉伸试验相似。由此建立动态坐标系,并将统一强度准则扩展至考虑应变率效应。

（3）根据试验规律,应变率变化对中主应力参数几乎没有影响,由此将动态强度准则扩展至3维应力状态。当多轴动态强度准则退化至单轴压缩或拉伸应力状态,可以描述与试验一致的动态单轴强度规律。

（4）采用多轴动态强度准则,可以预测不同应变率下混凝土的双轴试验结果,由于相关试验数据有限,真三轴条件下的动态强度还需要进一步研究验证。

图 1 矢量和法安全系数公式中定义的矢量

Figure 1. Sketch of the vector of the safety factor in the vector sum method

下载: 全尺寸图片幻灯片

图 2 该算例不同方向角

Figure 2. Different sliding angles of the slope example

下载: 全尺寸图片幻灯片

图 3 极限平衡M-P法计算模型

Figure 3. The calculating model of limit equilibrium M-P method

下载: 全尺寸图片幻灯片

图 4 两种方法安全系数对比图

Figure 4. Comparison of safety factors with both methods

下载: 全尺寸图片幻灯片

图 5 矢量和法与M-P法结果相对误差

Figure 5. Relative error of safety factors between the vector sum method and the limit equilibrium M-P method

下载: 全尺寸图片幻灯片

表 1 标准考题EX1C安全系数计算结果汇总表

Table 1 The calculating results of the slope example EX1C

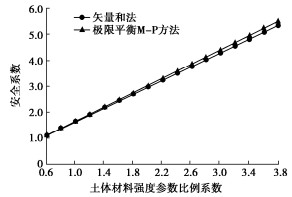
计算方法		安全系数	下滑方向/(°)
极限平衡法	推荐裁判答案Donald	1.3900	—
	SSA(Baker)	1.3900	—
	STAB(陈祖煜)	1.3850	—
	EMU	1.3900	—
	Fredlund	1.4060	—
	平均值	1.3922
孙建生法	孙建生	1.4311	45.533
本文方法	矢量和法	1.3939	23.1938

下载: 导出CSV

参考文献(6)

[1]	孙建生. "矢量和法"抗滑稳定计算模型的力学概念错误[J]. 岩土工程学报, 2021, 43(5): 975–980. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202105028.htm SUN Jian-sheng. Mechanical concept errors in anti-sliding stability computational model of "vector sum method"[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(5): 975–980. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202105028.htm
[2]	李广信, 张丙印, 于玉贞, 等. 土力学[M]. 2版. 北京: 清华大学出版社, 2018. LI Guang-xin, ZHANG Bing-yin, YU Yu-zhen, et al. Soil Mechanics[M]. 2nd ed. Beijing: Tsinghua university Press, 2018. (in Chinese)
[3]	陈祖煜. 土质边坡稳定分析: 原理·方法·程序[M]. 北京: 中国水利水电出版社, 2003. CHEN Zu-yu. Soil Slope Stability Analysis[M]. Beijing: China Water Power Press, 2003. (in Chinese)
[4]	DUNCAN J M. State of the art: limit equilibrium and finite-element analysis of slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1996, 122(7): 577–596. doi: 10.1061/(ASCE)0733-9410(1996)122:7(577)
[5]	GUO M W, LI C G, WANG S L, et al. Vector-sum method for 2D slope stability analysis considering vector characteristics of force[J]. International Journal of Geomechanics, 2019, 19(6): 04019058. doi: 10.1061/(ASCE)GM.1943-5622.0001436
[6]	孙建生. 基于有限元应力载荷宏观刚性滑裂面极限平衡抗滑稳定计算理论[J]. 岩石力学与工程学报, 2018, 37(4): 862–875. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201804009.htm SUN Jian-sheng. Theoretical model of stability calculation of macro-rigid sliding planes with FEM stress load based on limit equilibrium[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(4): 862–875. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201804009.htm

施引文献(8)

期刊类型引用(6)

1.	张雄辉，黄孝福，黄诗渊，刘发贵，聂亮冰，黎子玄. 压剪条件下裂缝开闭对准脆性材料断裂行为的影响机制研究. 中国农村水利水电. 2025(03): 128-135 . 百度学术
2.	梁鹏，李壮，刘俊岭，王聚贤，王骏涛. 三点弯曲试验下花岗岩应变场及损伤演化研究. 地下空间与工程学报. 2023(02): 486-494 . 百度学术
3.	杨旭旭，吴岳，靖洪文. 基于超声波实测的巷道围岩裂缝扩展和强度演变规律研究. 采矿与安全工程学报. 2021(03): 528-537 . 百度学术
4.	张超，杨楚卿，白允. 岩石类脆性材料损伤演化分析及其模型方法研究. 岩土力学. 2021(09): 2344-2354 . 百度学术
5.	何泓易. Hoek-Brown强度准则在隧道围岩卸荷试验中的应用研究. 韶关学院学报. 2021(12): 19-23 . 百度学术
6.	王思，胡晶，张雪东，任晓丹，陈祖煜，张紫涛. 不同水深水下爆炸数值及离心试验研究. 哈尔滨工业大学学报. 2020(06): 78-84 . 百度学术