Design method for internal stability of multi-tiered geosynthetic-reinforced retaining walls based on limit state
-
摘要: 分级台阶设计常用于加筋土高挡墙中，目前相关设计方法滞后于实际工程。基于极限平衡法建立了台阶式加筋挡墙的筋材内力计算方法，用于确定极限状态下筋材内力分布，从而提出了台阶式加筋挡墙内部稳定性设计方法。从安全设计所需的筋材强度和筋材长度两个方面开展参数分析，揭示了台阶宽度、分级级数、分级挡墙高度等因素对挡墙内部稳定设计结果的影响规律。分析结果表明：稳定所需的筋材强度和长度随台阶宽度增加而减小，超过台阶临界宽度后筋材强度不变，直到各级挡墙完全独立筋材长度不变；台阶总宽度固定时，相比简单的放坡方式，台阶分级可以显著减小筋材强度和长度，宽度较大时双级挡墙筋材用量最少；上级挡墙高度稍大于总墙高一半时，双级挡墙稳定所需筋材强度和长度最小。Abstract: The multi-tiered configuration is often used in the geosynthetic-reinforced soil (GRS) high retaining walls. However, the related design methods are currently lagging behind the engineering practice. The analytical approach to calculate the reinforcement loads of GRS retaining walls is established based on the limit equilibrium method, which is used to determine the load distribution of reinforcement in the limit state, and thus the design method for internal stability of multi-tiered GRS retaining walls is proposed. The parameter analysis is carried out in terms of the reinforcement strength and the reinforcement length required for safe design, and the influences of factors such as offset distance, tier number and height of each tier on the internal stability of retaining walls are revealed. The obtained results show that the required strength and length of reinforcement decrease with the increase of the offset distance, and the required reinforcement strength remains unchanged after exceeding the critical offset distance until the reinforcement length of each tier is completely independent. If the total offset distance is constant, the multi-tiered configuration will significantly reduce the reinforcement strength and length compared with the simple step-slope method. In this situation, the two-tiered configuration yields the least length of reinforcement when the offset distance is large. When the upper wall height is slightly higher than half of the total wall height, the required strength and length of the reinforcement in the two-tiered retaining wall are the smallest.
-
Keywords:
- retaining wall /
- reinforced soil /
- limit equilibrium /
- stability analysis /
- tier
-
0. 引言
加筋土技术被广泛应用于挡土结构中，随着挡墙高度增加，需要利用台阶减载作用对挡墙进行分级并设置一定宽度的平台。台阶式加筋土高挡墙安全设计沿用单级加筋挡墙设计思路，主要包括内部稳定性与外部稳定性，其中内部稳定性是加筋设计的核心。
台阶式加筋挡墙内部稳定性分析主要基于土压力理论和极限平衡理论，其中土压力理论是现行规范[1-2]所采用的方法。美国联邦公路局（FHWA）[1]和美国国家混凝土砌体协会（NCMA）[2]规范针对双级挡墙给出了详细的设计参数，考虑台阶减载效应将上级挡墙简化为等效附加垂直应力作用在下级挡墙顶部，进而采用土压力理论确定稳定所需的筋材强度。然而，一些模型试验中的实测结果与理论解有较大误差[3-5]，杨广庆[6]和Mohamed等[7]基于FHWA法对上级挡墙荷载引起的下级挡墙附加垂直应力进行了改进，并与实测结果进行对比验证了其有效性。对于分级台阶超过2级的挡墙，则参照双级挡墙的方法自上而下依次进行设计，但是这种方式只考虑了上一级挡墙产生的附加垂直应力作用，无法考虑下级挡墙以上的所有上级挡墙影响[8-9]。为此，Wright[9]将多级加筋挡墙等效为一定坡度的加筋边坡，根据极限平衡理论确定的加筋边坡稳定所需的筋材强度计算台阶挡墙所需的筋材强度，这样就可以考虑所有的各级挡墙。但是，这种简单的等效边坡方式难以准确反映台阶减载效应，忽视了台阶上可能发生的局部破坏和部分穿过加筋区的复合破坏模式。
台阶式加筋挡墙的设计理论远落后于工程实践，大量现场监测结果[10-12]已经充分表明其变形和力学性状比单级情况更为复杂，有待深入研究。为此，许多学者采用模型试验[13-15]和数值模拟[16-17]探究台阶式加筋挡墙的变形特征、筋材内力分布规律和破坏模式。已有模型试验[2-4]和现场试验[5-6]结果表明：当台阶宽度超过一定值时，加筋挡墙潜在破坏面由直线变为曲线，且形态更接近对数螺旋线。然而，现有设计方法多局限于直线破坏方式，尚未考虑这种转动破坏方式。Leshchinsky等[18]假设加筋土结构可能发生圆弧滑动，基于极限平衡毕肖普法提出加筋土结构筋材内力分析方法，并拓展应用于复杂的台阶式加筋挡墙[19]。在该方法框架下，张飞等[20]开展了台阶式加筋挡墙筋材内力分析，揭示了台阶式挡墙筋材内力分布的影响规律，但是其假定滑动面为直线破坏。为此，本文假设滑动面为对数螺旋线计算台阶式加筋挡墙内力分布，建立基于筋材内力分布的台阶式挡墙内部稳定性设计方法，针对分级台阶布置方式进行参数分析，指导安全设计。
1. 极限状态下台阶式加筋挡墙筋材内力计算方法
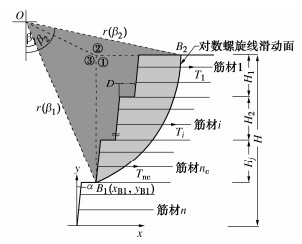
图 1给出了一N级台阶式加筋土挡墙，其中高度H、台阶宽度D、墙面倾角α、加筋间距Sv、筋材层数n、筋材铺设长度L。为了获得台阶式高挡墙各层筋材沿水平铺设方向的加筋力分布，这里采用Leshchinsky等[19]提出的单级挡墙“自上而下”筋材内力计算思路，自挡墙顶部滑动面穿过第1层筋材开始，依次增加滑动面穿过的加筋层数，运用极限平衡理论计算各加筋层所需加筋力分布，直至所有加筋n层结束。
加筋土高挡墙采用台阶布置方式有显著的减载作用，相关模型试验结果[2-4]表明台阶布置下挡墙的潜在破坏面近似对数螺旋线形式。基于极限平衡理论，本文采用对数螺旋线转动破坏方式开展台阶式加筋土挡墙筋材内力分析，同时还有如下5点假设：
（1）填土为均质各向同性，采用莫尔-库仑破坏准则（c和φ分别为黏聚力和内摩擦角）。
（2）认为任意滑动面穿过的所有筋材发挥相同的拉力[7]，作用方向始终为水平方向。
（3）所有可能的滑动面只通过加筋区和墙后填土区，不考虑穿过挡墙底部地基土的深层滑动。
（4）忽略面板和墙趾作用，墙顶荷载换算为等效土柱高度在最上一级台阶中考虑。
（5）认为筋材强度足够，不会发生断裂和剪切破坏，仅发生拔出破坏。
假设滑动面与转动中心O的竖向夹角为β、直径为r，对数螺旋线滑动面在极坐标系表示为
r(β)=Ae−βtanφm。 (1) 式中：A为初始半径；φm为极限状态动用的填土内摩擦角，即tanφm = tanφ/Fs（Fs为设计要求的稳定安全系数）。滑动面滑出点B1和滑入点B2在笛卡尔坐标系为（xB1，yB1），（xB2，yB2），极坐标系的角度为β1，β2。
为了计算挡墙极限稳定状态所需的筋材强度T，以转动中心O的对数螺旋线建立力矩平衡方程，包括土体自身重力W产生的滑动力矩Mw，填土动用黏聚力cm在滑动面上提供的抗滑力矩Mc以及加筋合力∑T提供的抗滑力矩MT。这里需要指出的是，对数螺旋线滑动面上的正应力与抗剪力的摩擦分量的合力通过转动中心，故不产生力矩。因此，力矩平衡方程表示为
MT+Mc=Mw。 (2) 抗滑力矩Mc和MT可以根据下式进行计算：
Mc=cm∫β2β1A2e - 2βtanφmdβ=cmfc， (3) MT=nc∑i=1RcTidi=Tft。 (4) 式中：Rc为筋材覆盖率（这里考虑土工格栅Rc = 100%）；nc为滑动面穿过的加筋层数；di为第i层加筋力Ti水平作用距转动中心O的竖直高度，根据三角关系和几何关系可以获得其表达式：
di=Acosβ1e−β1tanφm+yB1−H+iSv。 (5) 土体自重产生的滑动力矩Mw采用间接法计算，将对数螺旋线组成的扇形B1OB2面积等效土体自重产生的滑动力矩减去阴影部分①，②，③3个区域等效土体自重产生的滑动力矩，这样就可以获得计算表达式：
Mw=MB1OB2−M①−M②−M③ =γ(fw1−fw2−fw3−fw4)。 (6) 式中：γ为填土重度；fw1，fw2，fw3，fw4的计算表达式为
fw1=13∫β2β1A3e - 3βtanφmsinβdβ， (7a) fw2=N−2∑j=1{(N−j)DHj[12(N−j)D+Hjtanα−xB1+Ae−β1tanφmsinβ1]+16Hj3tan2α+12H2jtanα⋅ (Ae−β1tanφmsinβ1−xB1)}+tanα2[A(e−β1tanφmcosβ1−e−β2tanφmcosβ2)−H+HN+HN−1]2[Ae−β1tanφmsinβ1+tanα3(Ae−β1tanφmcosβ1−Ae−β2tanφmcosβ2−H+HN+HN−1)]， (7b) fw3=A36e−β2tanϕmcosβ2(e−2β2tanϕmsin2β2−e−2β1tanϕmsin2β1)， (7c) fw4=A33e−2β1tanϕmsin2β1(e−β1tanϕmcosβ1−e−β2tanϕmcosβ2)。 (7d) 将式（3），（4），（6）代入式（2）可以获得滑动面穿过B2点稳定所需的筋材拉力计算表达式：
T=γ(fw1−fw2−fw3−fw4)−cmfcft。 (8) 对滑动面参数（A，β1，β2）进行优化计算所需筋材拉力T。
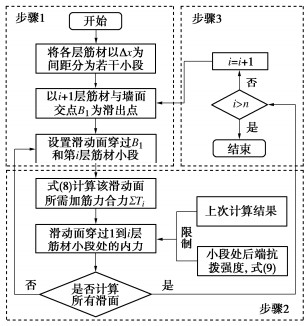
基于上述极限平衡理论就可以“自上而下”逐层计算台阶式挡墙筋材内力分布（图 2），具体步骤如下：
![]()
图 2 台阶式加筋土挡墙筋材内力计算流程Figure 2. Flow chart of tensile loads on reinforcement of tiered GRS walls（1）每层筋材沿水平铺设方向等分为若干小段，首先计算第1层筋材内力，设定滑动面滑出点B1位于下层（第2层）墙面处，从筋材前端至后端依次考虑滑动面穿过第1层各小段位置和B1，采用式（8）对滑动面参数（A，β1，β2）进行优化计算所需筋材拉力T1分布。
（2）当考虑第i层筋材时，滑动面以第i+1加筋层墙面位置或墙趾处为滑出点B1，从筋材前端至后端依次考虑滑动面穿过第i层各小段位置和B1，考虑所有可能的滑动面采用式（8）优化计算得到滑动面穿过i层筋材所需的加筋合力∑Ti，由于这里假设筋材内力均匀发挥为Ti。此时滑动面穿过的其他层筋材，将Ti与该位置前面计算的内力进行比较，以保留较大值为原则不断更新加筋力，需要确保同一滑动面上所需加筋合力∑Ti始终不变。但是，对于筋材后端需要将内力控制在抗拔强度Te-i以内，即
Te−i(xi)=2(L−xi)σiCiRctanφm。 (9) 式中：xi为第i层筋材距墙面的水平距离；Ci为筋土界面系数，Ci = 0.8；σi为第i层筋材上xi位置对应的上覆荷载，即σi = γzi（zi为第i层筋材xi位置竖直向上的覆土厚度）。这样当稳定所需的筋材内力超过Te-i时，则需将多余筋材内力依次往下级筋材进行分配。
（3）重复步骤（2），自上而下逐层计算获得每层筋材所需筋材拉力的分布。
2. 结果对比与验证
基于本文提出的台阶式挡墙筋材内力分析方法可以确定稳定所需筋材强度Tmax及其对应位置作为最危险滑裂面，这里将结合已有文献[8，13]中分析的算例进行计算和结果对比分析，表 1给出了两个算例的模型参数。
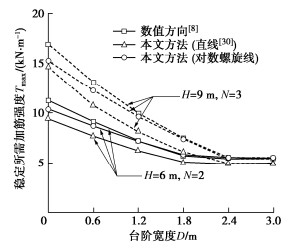
表 1 验证算例的模型参数Table 1. Model parameters for example validationLeshchinsky等[8]采用基于FLAC的有限差分法开展稳定性分析，获得了挡墙安全系数Fs = 1.00时（即极限状态）每层筋材所需的最大拉力Tmax，这里采用同样的安全系数进行内力分析。图 3给出了不同方法计算的双级和三级加筋挡墙结果，同时还给出了基于本文方法采用直线破坏面确定的筋材最大拉力Tmax。结果对比分析可见，本文理论解均小于数值解，随着台阶宽度增加，两者误差逐渐消失、趋于相等。本文所采用的对数螺旋线破坏机制获得的筋材最大拉力Tmax均大于直线破坏机制，表明对数螺旋线更接近最危险破坏方式。
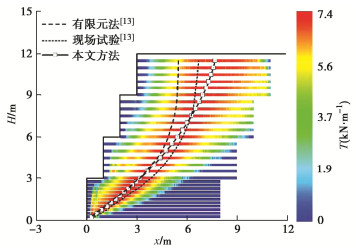
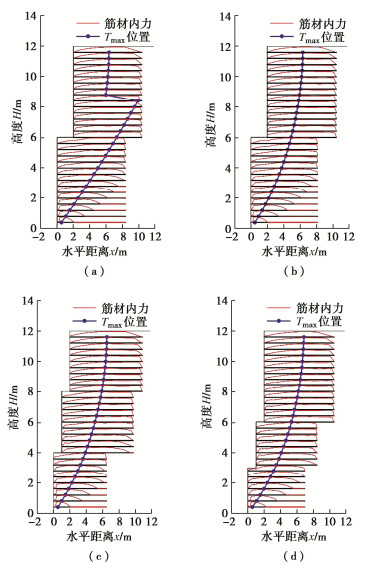
莫介臻等[13]对山区公路的四级加筋挡墙进行现场试验，根据现场测试获得筋材最大拉力Tmax位置推测了潜在滑裂面，同时运用有限元法计算的筋材最大拉力Tmax推测了滑裂面，这里采用本文方法计算各层筋材所需的最大拉力Tmax，将其位置作为最危险滑动面，如图 4所示。从图 4中可以看出3种方法预测的潜在滑动面形状均为曲面形式，相比数值结果本文方法确定的滑动面在墙顶更远离墙面，与现场观测得到的滑动面位置较为接近。因此，上述对比分析进一步验证了本文方法的有效性，可以用于指导安全设计。
3. 台阶式加筋挡墙内部稳定计算
3.1 设计原理与步骤
现有台阶式加筋土挡墙主要采用FHWA方法[1]进行安全设计，考虑台阶减载作用对土压力进行修正，这种方式还存在一定局限性。本文基于筋材内力分布提出台阶式加筋土挡墙安全设计方法，这里主要针对内部稳定性、外部抗滑、抗倾覆稳定性和整体稳定性校核沿用已有规范设计方法。
内部稳定性计算的核心就是确定筋材强度和筋材长度，这里采用前文所述的筋材内力分析方法，具体步骤如下：
（1）根据工程要求确定挡墙高度、台阶设置宽度、分级级数等，假定筋材铺设足够长（计算时默认初始长度为墙高H），采用本文方法确定筋材内力分布及筋材最大拉力Tmax位置。
（2）以不发生筋材后端拔出的复合破坏为判定条件，逐渐缩短筋材长度，若发生复合破坏则保留前一次筋材长度作为该级挡墙设计的筋材长度。
（3）自上级挡墙到下级挡墙依次执行步骤（2），分别确定各级挡墙的筋材长度，同时确定了各层筋材最大拉力Tmax，将Tmax最大值用于确定加筋材料强度。
3.2 分级平台对加筋设计的影响规律
分级平台布置方式是台阶式加筋高挡墙设计的重要环节之一，但是现有设计方法大多根据工程经验来确定。这里运用所提出的设计方法，以双级直立加筋挡墙为例探究分级平台宽度和高度对筋材强度和长度的影响规律，标准模型参数为γ = 18 kN/m3，c = 0 kPa, φ = 34°，α = 0°，Ci = 0.8，Rc=1.0，Sv = 0.6 m，Fs = 1.3。
（1）平台宽度
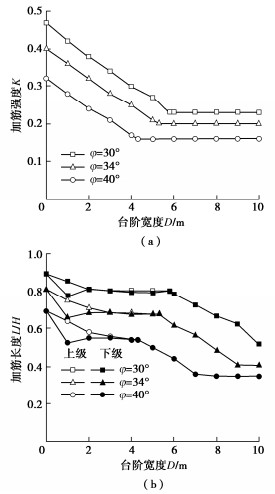
首先考虑加筋填料性质，结合相关规范采用无黏性砂土材料，其内摩擦角φ一般为30°~40°，这里分别选择φ为30°，34°，40°计算不同台阶宽度D下挡墙稳定所需筋材强度和长度，如图 5所示。这里稳定所需的筋材最大拉力以无量纲形式来表示，即K = ∑Tmax/(0.5γH2)。由图中的计算结果可见加筋填土的内摩擦角越小，则稳定所需的筋材强度越大、铺设越长，同时K和L与台阶宽度变化趋势基本一致。筋材强度K随宽度D增加而逐渐降低，当达到某一临界台阶宽度Dcr后上、下级挡墙相互独立，此时不受台阶宽度影响K保持不变。上下级挡墙的筋材长度L则随着D增加整体呈现减少趋势，当D较小时上级筋材长度大于下级情况，随后趋于一致。
![]()
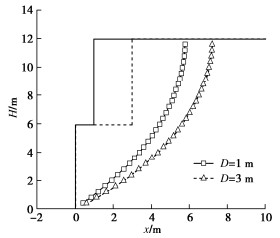
图 5 不同填土内摩擦角下台阶宽度对筋材强度与长度的影响Figure 5. Effects of offset distance on required reinforcement strength and length for various internal friction angles图 6给出了D为1，3 m挡墙的筋材最大拉力Tmax位置，随着宽度增加筋材最大拉力Tmax位置整体远离墙面变深，虽然台阶加宽减少了筋材强度，但下级挡墙筋材长度受滑动面以内的主动区决定，因此呈现先增加直至与上级挡墙筋材相等。此外，从图 5（b）可见在D为2~5 m出现一不变阶段，内摩擦角较小时尤为明显。这是由于此时最危险滑裂面随宽度D增加而加深，致使筋材主动破坏区的长度增加，但是台阶减载效应增加减少所需筋材强度，使得筋材后端抗拔锚固长度减小，这样综合表现为筋材总长度几乎不变。随后台阶宽度再增大使得各级挡墙自上而下依次独立，各级挡墙最危险滑裂面较整体滑裂面较浅，这样所需筋材长度继续减少，直至各级挡墙完全独立保持不变。
![]()
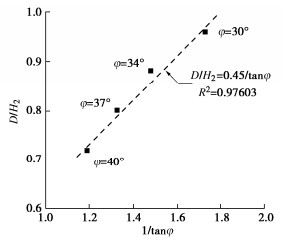
图 6 台阶D为1，3 m标准模型的筋材Tmax位置Figure 6. Location of Tmax for baseline with D of 1 and 3 m从图 5（a）中以筋材最大拉力确定不同内摩擦角对应的台阶临界宽度，Dcr随着填土内摩擦角φ减小而增大。参照Gao等[17]的方式，图 7给出了不同内摩擦角对应的台阶临界宽度与双级挡墙的下级墙高H2的比值，Dcr/H2与1/tanφ近似呈线性关系，但是本文方法确定的临界宽度小于Gao等[17]采用有限差分数值方法分析墙面变形对应的Dcr。表 2给出不同方法确定的临界宽度，规范基于土压力理论确定的Dcr最大。以φ = 34°为例，FHWA确定的Dcr = 1.48H2，与Gao等[17]数值方法确定的Dcr = 1.22H2较为接近，而其他方法获得的Dcr为（0.7~0.8）H2，本文方法计算的Dcr =0.88H2。
![]()
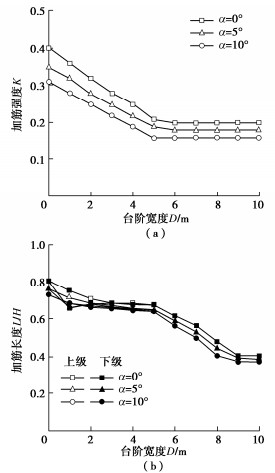
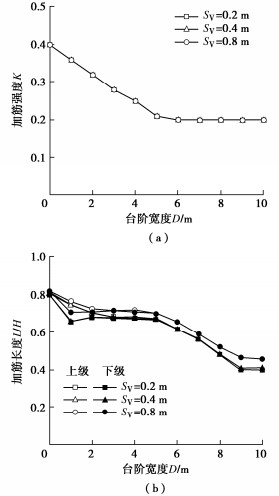
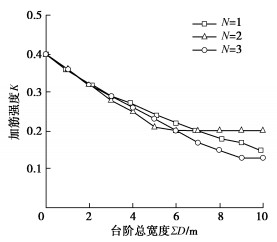
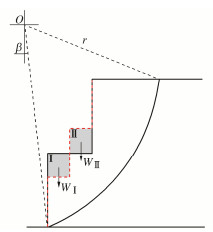
图 7 不同内摩擦角下台阶临界宽度Figure 7. Critical offset distances for various internal friction angles表 2 验证算例的模型参数Table 2. Model parameters for example validation图 8给出了墙面倾角α为0°，5°，10°下台阶宽度对筋材强度与长度的影响，增加墙面倾角能够有效降低所需筋材强度和筋材用量，但不会对台阶减载作用有影响。同时图 9还给出了加筋间距Sv为0.2，0.4，0.8 m下台阶宽度对筋材强度与长度的影响，可见加筋间距对稳定所需筋材总拉力没有影响，但是对筋材长度有一定影响，间距过大会增加筋材长度，总体上依旧不会影响台阶减载作用。图 10给出了挡墙级数N为1，2，3下台阶宽度对筋材强度与长度的影响。其中N = 1时采用等宽度的放坡形式，N为2，3时均为各级等高的直立挡墙。当台阶宽度小于2 m时，挡墙分级对筋材强度K几乎没有影响。继续增加台阶宽度，三级挡墙稳定所需的筋材强度大于双级挡墙。这是由于对于同一个滑裂面三级挡墙的滑动力矩大于双级挡墙。如图 11所示，三级挡墙和双级挡墙的减载空间相同，但是三级挡墙的区域Ⅱ产生的滑动力矩大于双级挡墙的区域Ⅰ。
![]()
图 8 不同墙面倾角下台阶宽度对筋材强度与长度的影响Figure 8. Effects of offset distance on required reinforcement strength and length for various inclination angles![]()
图 9 不同加筋间距下台阶宽度对筋材强度与长度的影响Figure 9. Effects of offset distance on required reinforcement strength and length for various reinforcement spacings![]()
图 10 不同分级数量下台阶宽度对筋材强度的影响Figure 10. Effects of offset distance on required reinforcement.strength for various tier numbers![]()
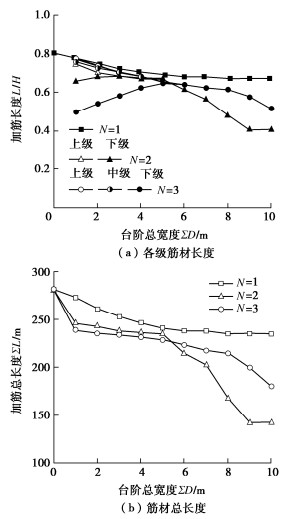
图 11 双级与三级台阶布置对挡墙滑动力矩影响Figure 11. Differences of sliding moment between two- and three-tiered walls图 12给出了不同分级数量下台阶总宽度对稳定所需各级筋材长度和总筋材长度的影响，其中N = 1的单级挡墙采用放坡形式等效考虑双级与三级挡墙的台阶宽度，单级挡墙稳定所需铺设的筋材长度最大，表明分级平台方式可以有效减少筋材铺设长度。同时，发现N为2，3的台阶式挡墙的最下级筋材长度随着台阶宽度增加逐渐与上级筋材相等，然后筋材长度逐渐减少至各级挡墙独立保持不变。当台阶宽度较小时，由于三级挡墙潜在滑动面较双级挡墙更远离墙面，致使三级挡墙的上部筋材长度大于双级挡墙情况。三级挡墙增设一分级平台使得最下级筋材长度大幅减少，从而三级挡墙的加筋总长度少于双级挡墙。当台阶宽度较大时，双级挡墙的上、下级之间独立，稳定所需的总筋材长度大于三级挡墙。
![]()
图 12 不同分级数量下台阶宽度对筋材长度的影响Figure 12. Effects of offset distance on required reinforcement length for various tier numbers（2）分级挡墙高度
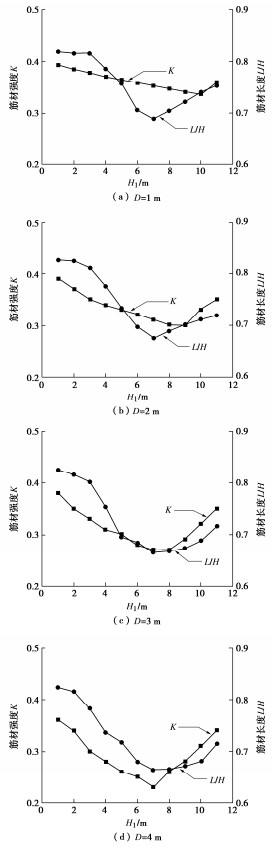
基于相同的标准模型，在上、下级挡墙的总高度始终保持H = H1+H2 = 12 m，图 13给出了不同台阶宽度下双级挡墙的上级挡墙高度H1对筋材强度和筋材长度的影响规律。可见挡墙稳定所需筋材强度和筋材长度均随着上级挡墙高度增加呈现先减小再增大，存在一最小值。筋材强度K未达到最小值时，增加H1会增加平台减载作用而减少K，随后整个挡墙稳定性受上级挡墙影响，其最危险滑裂面主要发生在上级挡墙，这样继续增加H1反而导致K增加。对比四种不同台阶宽度的结果，还发现K最小值对应的临界高度随着台阶宽度增加而减小。由于筋材强度存在最小值，使得稳定所需的筋材长度也存在一最小值，这样采用最小筋材长度对应的H1进行设计是最优的。根据算例分析结果，可以大致发现双级挡墙的上级高度稍大于H/2时筋材用量最少。
![]()
图 13 上级挡墙高度H1对双级挡墙筋材强度与长度的影响Figure 13. Effects of upper wall height H1 on required reinforcement strength and length3.3 不同设计方法结果对比
这里以标准模型为例，采用统一的安全系数Fs = 1.3分别运用FHWA规范[1]和本文方法进行分级平台设计，其中双、三级挡墙的每级台阶宽度分别为2，1 m。表 3给出了各设计方案的各级墙高布置和计算确定的所需筋材总强度、筋材总长度以及各级挡墙的筋材长度和层数，同时表 4还给出4种对应设计方案下，由ReSSA+软件计算的外部稳定性校核结果。相比传统的土压力理论设计方法，本文方法设计的挡墙稳定所需筋材强度和筋材长度都较小，且都满足外部稳定性要求。
表 3 4种不同设计方法计算的筋材总强度和长度Table 3. Total required strengths and lengths of reinforcement calculated by four different design methods设计方法 ∑Tmax-i/
(kN·m)∑Li/m FHWA方法 N = 2
H1 = 6 m531.86 243.6
(8.4 m/层*29层)本文
方法N = 2
H1 = 6 m459.65 242.3
(8.5 m/层*15层+8.2 m/层*14层)N = 3
H1 = 4 m
H2 = H3 = 4 m463.31 235.5
(8.9 m/层*10层+8.8 m/层*10层+6.5 m/层*9层)N = 3
H1 = 6 m
H2 = H3 = 3 m442.25 230.5
(8.6 m/层*15层+7.5 m/层*7层+7.0 m/层*7层)表 4 不同破坏模式的安全校核Table 4. Safety calibration for different failure mechanisms设计方法 抗滑稳定 抗倾覆稳定 整体稳定 FHWA方法 N = 2 1.62 1.43 2.09 本文方法 N = 2 1.61 1.44 2.06 N = 3
H1 = 4 m1.55 1.48 1.80 N = 3
H1 = 6 m1.53 1.50 1.84 图 14给出了4种不同设计方案的筋材内力分布和筋材最大拉力Tmax位置，发现规范设计的加筋挡墙由于上级挡墙铺设筋材长度较短，致使筋材后端抗拔强度不足，部分穿过加筋区的复合破坏使得Tmax位置偏向筋材后端（图 14（a））。本文方法考虑了这种可能发生的复合破坏模式，对筋材长度进行了调整，如双级挡墙中适当增加了上级挡墙筋材长度，这样采用本文方法设计的3种情况对应的最危险滑动面均为加筋区内部破坏（图 14（b）~（d））。因此，采用FHWA方法进行台阶式高挡墙设计需要注意校核复合破坏模式。
![]()
图 14 不同设计方案的挡墙筋材内力分布与Tmax位置Figure 14. Distribution of reinforcement tensile loads on and position of Tmax derived from different design solutions4. 结论
提出了极限状态下台阶式加筋高挡墙筋材内力分析方法，同时考虑内部与复合破坏模式确定了各层筋材内力分布，基于筋材内力计算了台阶式加筋挡墙安全设计的筋材强度和筋材长度，指导内部稳定性设计，获得4点结论。
（1）由于台阶减载效应，挡墙设计安全所需的筋材强度和长度随分级平台宽度增加逐渐减小，至各级挡墙独立后保持不变，筋材最大拉力确定的临界宽度Dcr大致为（0.7~0.8）倍的下级墙高，与已有研究结果相一致。Dcr随着填土内摩擦角减小而增大，不受墙面倾角、加筋间距影响。
（2）当台阶设置总宽度一定时，分级级数会显著影响筋材强度和长度，但均比简单的放坡形式要小。当台阶总宽度较大时，双级挡墙相较于三级挡墙更早发生独立，会大幅减少筋材长度。
（3）在上级挡墙高度稍大于整个墙高的一半时，双级挡墙稳定所需筋材强度和长度达到最小值，此时挡墙的墙高布置达到最优设计。
（4）采用传统的FHWA方法设计的台阶加筋挡墙可能会产生复合破坏，需要对其进行校核，基于本文内力分析的设计方法可以通过增加分级级数和调整各级挡墙高度进行优化。
-
![]()
图 2 台阶式加筋土挡墙筋材内力计算流程
Figure 2. Flow chart of tensile loads on reinforcement of tiered GRS walls
![]()
图 5 不同填土内摩擦角下台阶宽度对筋材强度与长度的影响
Figure 5. Effects of offset distance on required reinforcement strength and length for various internal friction angles
![]()
图 6 台阶D为1，3 m标准模型的筋材Tmax位置
Figure 6. Location of Tmax for baseline with D of 1 and 3 m
![]()
图 7 不同内摩擦角下台阶临界宽度
Figure 7. Critical offset distances for various internal friction angles
![]()
图 8 不同墙面倾角下台阶宽度对筋材强度与长度的影响
Figure 8. Effects of offset distance on required reinforcement strength and length for various inclination angles
![]()
图 9 不同加筋间距下台阶宽度对筋材强度与长度的影响
Figure 9. Effects of offset distance on required reinforcement strength and length for various reinforcement spacings
![]()
图 10 不同分级数量下台阶宽度对筋材强度的影响
Figure 10. Effects of offset distance on required reinforcement.strength for various tier numbers
![]()
图 11 双级与三级台阶布置对挡墙滑动力矩影响
Figure 11. Differences of sliding moment between two- and three-tiered walls
![]()
图 12 不同分级数量下台阶宽度对筋材长度的影响
Figure 12. Effects of offset distance on required reinforcement length for various tier numbers
![]()
图 13 上级挡墙高度H1对双级挡墙筋材强度与长度的影响
Figure 13. Effects of upper wall height H1 on required reinforcement strength and length
![]()
图 14 不同设计方案的挡墙筋材内力分布与Tmax位置
Figure 14. Distribution of reinforcement tensile loads on and position of Tmax derived from different design solutions
表 3 4种不同设计方法计算的筋材总强度和长度
Table 3 Total required strengths and lengths of reinforcement calculated by four different design methods
设计方法 ∑Tmax-i/
(kN·m)∑Li/m FHWA方法 N = 2
H1 = 6 m531.86 243.6
(8.4 m/层*29层)本文
方法N = 2
H1 = 6 m459.65 242.3
(8.5 m/层*15层+8.2 m/层*14层)N = 3
H1 = 4 m
H2 = H3 = 4 m463.31 235.5
(8.9 m/层*10层+8.8 m/层*10层+6.5 m/层*9层)N = 3
H1 = 6 m
H2 = H3 = 3 m442.25 230.5
(8.6 m/层*15层+7.5 m/层*7层+7.0 m/层*7层)
下载: 导出CSV
表 4 不同破坏模式的安全校核
Table 4 Safety calibration for different failure mechanisms
设计方法 抗滑稳定 抗倾覆稳定 整体稳定 FHWA方法 N = 2 1.62 1.43 2.09 本文方法 N = 2 1.61 1.44 2.06 N = 3
H1 = 4 m1.55 1.48 1.80 N = 3
H1 = 6 m1.53 1.50 1.84
下载: 导出CSV
-
[1] Mechanically Stabilized Earth Walls and Reinforced Soil Slopes Design and Construction Guidelines: FHWA-NHI- 10-024[S]. Washington D C: Federal Highway Administration and US, Department of Transportation, 2009.
[2] NCMA. Design Manual for Segmental Retaining Walls[S]. Herndon V A: National Concrete Masonry Association, 2009.
[3] 凌天清. 公路高大加筋土挡墙设计方法的研究[J]. 中国公路学报, 2000, 13(2): 13-15, 19. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200002003.htm LING Tianqing. Research on high reinforced earth retaining wall design methods in highway engineering[J]. China Journal of Highway and Transport, 2000, 13(2): 13-15, 19. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL200002003.htm
[4] YOO C, JUNG H S. Measured behavior of a geosynthetic-reinforced segmental retaining wall in a tiered configuration[J]. Geotextiles and Geomembranes, 2004, 22(5): 359-376. doi: 10.1016/S0266-1144(03)00064-5
[5] MOHAMED S B A, YANG K H, HUNG W Y. Limit equilibrium analyses of geosynthetic-reinforced two-tiered walls: Calibration from centrifuge tests[J]. Geotextiles and Geomembranes, 2013, 41: 1-16. doi: 10.1016/j.geotexmem.2013.08.004
[6] 杨广庆. 台阶式加筋土挡土墙设计方法的研究[J]. 岩石力学与工程学报, 2004, 23(4): 695-698. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200404035.htm YANG Guangqing. Study on design method of tiered reinforced earth retaining wall[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(4): 695-698. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200404035.htm
[7] MOHAMED S B A, YANG K H, HUNG W Y. Finite element analyses of two-tier geosynthetic-reinforced soil walls: comparison involving centrifuge tests and limit equilibrium results[J]. Computers and Geotechnics, 2014, 61: 67-84. doi: 10.1016/j.compgeo.2014.04.010
[8] LESHCHINSKY D, HAN J E. Geosynthetic reinforced multitiered walls[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2004, 130(12): 1225-1235. doi: 10.1061/(ASCE)1090-0241(2004)130:12(1225)
[9] WRIGHT S G. Design Guidelines for Multi-Tiered MSE Walls[S]. FHWA, 2005.
[10] 杨广庆, 蔡英. 多级台阶式加筋土挡土墙试验研究[J]. 岩土工程学报, 2000, 22(2): 254-257. http://www.cgejournal.com/cn/article/id/10491 YANG Guangqing, CAI Ying. Experimental study on multi-step reinforced earth retaining wall[J]. Chinese Journal of Geotechnical Engineering, 2000, 22(2): 254-257. (in Chinese) http://www.cgejournal.com/cn/article/id/10491
[11] 周世良, 何光春, 汪承志, 等. 台阶式加筋土挡墙模型试验研究[J]. 岩土工程学报, 2007, 29(1): 152-156. http://www.cgejournal.com/cn/article/id/12293 ZHOU Shiliang, HE Guangchun, WANG Chengzhi, et al. Study on stepped reinforced soil retaining walls by model tests[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(1): 152-156. (in Chinese) http://www.cgejournal.com/cn/article/id/12293
[12] STUEDLEIN A W, BAILEY M, LINDQUIST D, et al. Design and performance of a 46-m-high MSE wall[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2010, 136(6): 786-796. doi: 10.1061/(ASCE)GT.1943-5606.0000294
[13] 莫介臻, 何光春, 汪承志, 等. 台阶式格栅加筋挡墙现场试验及数值分析[J]. 土木工程学报, 2008, 41(5): 52-58. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200805014.htm MO Jiezhen, HE Guangchun, WANG Chengzhi, et al. Study on a stepped retaining wall with geogrid reinforcement by using site test and numerical analysis[J]. China Civil Engineering Journal, 2008, 41(5): 52-58. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200805014.htm
[14] 杨广庆, 刘伟超, 刘华北, 等. 台阶式加筋土挡墙水平位移模式研究[J]. 岩石力学与工程学报, 2018, 37(增刊1): 3652-3658. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202301016.htm YANG Guangqing, LIU Weichao, LIU Huabei, et al. Horizontal displacement modes of tiered geosynthetic reinforced soil retaining wall[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(S1): 3652-3658. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202301016.htm
[15] YOO C, JANG Y S, PARK I J. Internal stability of geosynthetic-reinforced soil walls in tiered configuration[J]. Geosynthetics International, 2011, 18(2): 74-83.
[16] YOO C. Serviceability state deformation behaviour of two-tiered geosynthetic reinforced soil walls[J]. Geosynthetics International, 2018, 25(1): 12-25.
[17] GAO S, XIAO C Z, HAN J E, et al. Lateral displacements of geosynthetic-reinforced soil walls in a tiered configuration[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2022, 148(9): 04022066.
[18] LESHCHINSKY D, LESHCHINSKY B, LESHCHINSKY O. Limit state design framework for geosynthetic-reinforced soil structures[J]. Geotextiles and Geomembranes, 2017, 45(6): 642-652.
[19] LESHCHINSKY D, LESHCHINSKY O, ZELENKO B, et al. Limit Equilibrium Design Framework for MSE Structures with Extensible Reinforcement[R]. Washington: Federal Highway Administration, Office of Bridge Technology, 2016.
[20] 张飞, 贾世林, 朱玉明, 等. 台阶式加筋挡墙稳定所需加筋力计算方法与影响规律[J]. 岩土力学, 2021, 42(11): 3079-3089. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202111018.htm ZHANG Fei, JIA Shilin, ZHU Yuming, et al. Required strength of geosynthetics in reinforced multi-tiered wall[J]. Rock and Soil Mechanics, 2021, 42(11): 3079-3089. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202111018.htm
-
期刊类型引用(4)
1. 闫清卫. 对拉包裹式土工格栅加筋土路堤拉筋受力分析. 内江师范学院学报. 2025(02): 51-56+86 . 
百度学术
2. 梁小勇，李智广，张森，靳静，邵明杰. 台阶级数对加筋土挡墙地震动力响应影响研究. 河北工业科技. 2024(04): 255-262 . 百度学术
3. 李思汉，王学鹏，蔡晓光，徐洪路，路彤，袁超. 地震作用下复合格宾土工格栅加筋土挡墙筋材受力分析. 铁道科学与工程学报. 2024(12): 5030-5041 . 百度学术
4. 王钰轲，邵琳岚，万愉快，余翔，张蓓，钟燕辉. 基于K-L展开法考虑土体参数空间变异性的土石坝坝坡可靠度分析. 水利学报. 2024(12): 1417-1427 . 百度学术
其他类型引用(2)
-
其他相关附件
计量
- 文章访问数: 352
- HTML全文浏览量: 48
- PDF下载量: 123
- 被引次数: 6
