Static instability criterion and safety factor of tunnels based on loading/unloading response ratio
-
摘要: 为得到隧道的稳定性状态及静力失稳临界点的合理判定方法，将加卸载响应比（LURR）理论引入到隧道受力分析中，解析求解了对称荷载作用下圆形无衬砌隧道的非线性特性及其对应的LURR演化规律，证明了两者的关联性；基于施工及运营隧道不同的荷载特性，提出了基于LURR理论的隧道静力稳定性分析方法，分别分析了施工隧道和运营隧道的稳定性及其LURR变化规律，提出了基于LURR理论的隧道静力失稳判据及其判定机理。研究表明：理论推导得到的隧道变形非线性特性的LURR表达式解析解和有限元解吻合度高；隧道在不同的稳定性阶段，洞周关键点变形的LURR表现出不同的变化规律，根据此变化规律的变化，可划分隧道不同的稳定性阶段；在体系失稳前，隧道局部薄弱区域的LURR增长率会出现异常变化，为隧道失稳前兆判据；基于隧道的极限承载状态，通过各阶段与极限承载阶段的荷载比得到隧道不同阶段的安全系数。提出了隧道静力失稳的LURR判定方法。Abstract: To obtain the method for static instability criterion of tunnels, the loading/unloading response ratio (LURR) theory is introduced into the analysis method. The nonlinear characteristics and the LURR variation laws of unlined circular tunnels under symmetrical loads are analyzed through the analytical method, and the results have proved their relevance. The research approach of LURR method is put forward based on the different loading characteristics of construction and operation tunnels. The critical conditions and the LURR variation laws of tunnels with and without linings are analyzed respectively through the finite element method. The results show that the nonlinear characteristics based on the LURR theory of tunnel deformation calculated by the analytical solution and the finite element solution are similar. The LURR variation laws of tunnel deformation are different in each loading and stability stages of tunnel system, the LURR variation rate in the weak area of the tunnel will be abnormal before its instability, and the abnormal variation trend is the precursor criterion of the instability of the tunnel system. Based on the determination of the ultimate bearing state of the tunnel system by the LURR method, the safety factor of the tunnel system is obtained by using the loading ratio. The static instability method based on the LURR theory of tunnels is proposed.
-
0. 引言
岩石材料在地质构造及矿物成形过程中,矿物晶体结构一般具有较明显的非均质性特点,在成分组成、几何尺寸及力学强度[1]等方面具有较大差异。在外力作用下,岩石矿物可能发生晶体尺度局部应力集中,并导致破坏的发生。岩石破坏后,其宏观裂纹在微观尺度上主要分为两大类：①沿矿物晶体边界发展的晶间裂纹；②矿物晶体内部发展的晶内裂纹（图1）。
近年来,针对岩石微观结构非均质性对宏观力学特性的影响,国内外学者对非均质性岩石进行了较多的试验研究[5-7]。Tugrul等[8]通过试验及数据相关性分析发现,矿物平均晶体尺寸及矿物组成对岩石单轴压缩强度（UCS）有较大的影响；Ündül[9]通过研究矿物组分与岩石强度之间的关系指出,斜长石矿物含量的增加将导致岩石UCS增加。此外,岩石特征应力与微观矿物结构也具有一定的关系。Ündül等[10]研究表明岩石起裂应力
受矿物成分影响较大,随斜长石矿物含量增加, 呈增加的变化趋势。Cowie等[2]对花岗岩特征应力进行统计并拟合发现,云母矿物含量与 及 具有负相关的关系,且随岩石中最小矿物尺寸的增加, 与 的比值呈增加的变化趋势。然而,Eberhardt等[11]对比3种不同粒径花岗岩单轴压缩试验结果指出,岩石中矿物晶体的尺寸对 影响不大,但随矿物晶体尺寸增加, 呈减小的变化趋势。目前,尽管国内外学者对非均质性岩石宏观力学特性进行了较多试验研究,但天然岩石材料微观矿物结构的随机性使得试验结果表现出较大的离散性,故通过试验手段定量化研究非均质岩石宏观力学仍有一定的困难。 Cundall等[12]提出的离散单元法（discrete element method, DEM）可在有效研究岩石宏观力学特性的前提下,从微观尺度对岩石内部裂纹的起裂、扩展及聚合规律进行研究。尽管颗粒流软件（particle flow code, PFC）先后开发的两种团簇模型cluster和clump模型[13-15]可有效克服传统圆盘颗粒所带来的摩擦角及强度值较小问题,但上述模型在研究矿物晶体结构对宏观力学特性影响方面仍具有不足,如cluster模型不能有效控制颗粒簇尺寸,clump模型不能模拟晶体内破裂等；经过多年发展,PFC中矿物晶体模型（PFC-GBM）的提出使得通过岩石内部矿物晶体组成、尺寸等信息进行定量化晶体建模成为了可能,且通过对矿物晶体赋予不同的微观参数即可定量化模拟非均质性岩石宏观力学特性[16-18]。周喻等[19]利用上述模型从细观角度揭示了岩石加载条件下的破裂机制及强度特性。Bewick等[20]研究了非均质岩石直剪条件下宏观力学特性及微裂纹扩展规律。Hofmann等[21]和Peng等[22]研究了花岗岩单轴及三轴压缩条件下岩石内部微裂纹的变化规律。综上,采用GBM对非均质性岩石进行矿物晶体尺度模拟是一种十分有效的方法。
本文结合花岗岩室内试验,采用颗粒流矿物晶体模型（PFC-GBM）对花岗岩矿物晶体结构进行建模,通过对比试验与模拟声发射结果并分析晶体尺度微裂纹发展规律研究了单轴压缩条件下非均质岩石微观力学特性变化规律。同时,改变岩石矿物组成进行了一系列单轴压缩试验模拟,分析并讨论了矿物结构非均质性对岩石宏观力学特性的影响及变化原因。
1. PFC-GBM简介及多尺度断裂机理
1.1 PFC-GBM简介
Potyondy[23]将Voronoi多边形网格引入PFC软件,通过在矿物晶体内赋予平行黏结模型(Parallel bonded model, PBM),矿物晶体间赋予光滑节理模型(Smooth joint model,SJM)可实现非均质岩石内微观矿物晶体建模,其建模流程主要包括以下3个步骤（图2）：①生成大尺寸颗粒以控制矿物晶体尺寸及含量（图2（a））；②连接接触多边形质心形成矿物晶体边界（图2（b）,2（c））；③在晶体边界内填充小尺寸颗粒并进行分组形成矿物晶体模型（图2（d））。
尽管上述方法的提出使得GBM在PFC软件中实现流程化,但并不能定量化控制岩石的矿物结构,尤其晶体组成、尺寸大小。因此,本文采用其他方法对岩石微观结构进行定量化建模,并将模型数据与PFC软件相结合,成功实现定量化研究岩石非均质性对宏观力学特性的影响。
1.2 多尺度断裂机理
根据断裂机理不同,GBM颗粒间接触破坏所产生的晶体尺度裂纹（晶内/晶间裂纹）可进一步分为拉伸裂纹和剪切裂纹。当矿物晶体内颗粒法向拉应力大于拉伸强度时,颗粒间接触将发生拉伸破坏并产生晶内拉伸裂纹；当矿物晶体内颗粒切向剪切应力大于剪切强度时,颗粒间接触将发生剪切破坏并产生晶内剪切裂纹。同理,矿物晶体间拉伸及剪切裂纹断裂原理与上述相同。
2. 花岗岩模型建立及微观参数确定
2.1 花岗岩模型建立
图3为花岗岩室内试验示意图,试样采用尺寸为50 mm×100 mm的标准圆柱试样。单轴压缩试验在中国科学院武汉岩土力学研究所MTS815.04型电液伺服岩石试验系统上进行,轴向加载速率设置为0.001 mm/s。
试验过程中,采用轴向引伸计和环向应变规实时测量岩石的轴向应变及环向应变,同时采用声发射装置对岩石破裂过程中声发射特征参数进行监测与采集。
结合室内试验,本文通过Neper软件对花岗岩非均质结构进行建模。建模流程如图4,主要分为3个步骤,首先在50 mm×100 mm的模型区域内生成直径大小服从均匀分布的圆盘颗粒,颗粒半径最小为0.15 mm,且最大与最小半径的比值为1.66（步骤1）；随后在Neper软件中生成矿物晶体多边形,各矿物晶体尺寸使用软件内相关命令设置为服从正态分布（步骤2）；最后将矿物晶体信息以相应的格式导入PFC软件,根据步骤2所生成的矿物晶体种类将步骤1所生成的颗粒分组以形成GBM模型（步骤3）。
2.2 微观参数确定
结合文献[21, 22, 24, 25]中GBM参数校正方法及模拟效果,模型中矿物晶体力学特性（弹性模量、微观拉伸强度及黏结强度等）设置满足以下关系：石英矿物>长石矿物>云母矿物>其他矿物。另外,由于光滑节理模型并不能较好地模拟实际矿物晶体间凹凸不平的接触面及矿物界面间的内锁问题[26-27],本文采用Li等[16]的方法对矿物晶体内及晶体间接触赋予平行黏结模型（PBM）,且晶体间微观参数采用表2公式进行折减以简化GBM的参数校正过程。使用“试错法”将微观参数进行校正后,得模拟与试验力学特性比对表见表1。
表 2 模型微观参数表Table 2. Micro-parameters of grain-based model参数 石英矿物 长石矿物 云母矿物 其他矿物 矿物晶体间参数 体积含量/% 24 49 24 3 矿物晶体尺寸d/mm 2.43±0.25 3.42±0.25 1.98±0.25 1.17±0.25 颗粒最小半径Rmin/mm 0.15 颗粒半径比Rmax/Rmin 1.66 密度/(kg·m-3) 2650 2600 3050 1650 线性弹性模量E/GPa 51 42 33 24 0.2×2E1E2/(E1+E2) 摩擦系数μ 0.35 0.41 0.33 0.44 0.8 线性刚度比kn/ks 1.1 1.3 1.7 3.7 1.3 平行弹性模量pb_emod/GPa 51 42 33 24 0.2×2E1E2/(E1+E2) 黏结刚度比kn/ks 1.1 1.3 1.7 3.7 1.3 拉伸强度pb_ten/MPa 126±16 105±16 98±13 77±9 21±0 黏结强度pb_coh/MPa 196±42 162±28 146±22 105±0 50±0 摩擦角φ/(°) 19.5 22.4 17.3 23.7 38.6 注： 表中E1,E2分别为晶间两侧矿物颗粒的接触模量值。表 1 宏观力学特性比对表Table 1. Comparison of mechanical properties宏观力学特性 试验结果 模拟结果 误差/% UCSσc/MPa 172 171 0.6 拉伸强度σt/MPa 13.6 14.3 5.1 弹性模量E/GPa 52.4 55.4 5.7 泊松比 0.229 0.228 0.44 峰值应变εp/% 0.36 0.34 5.6 由表可知,使用矿物晶体模型所得宏观力学特性与试验所得结果误差较小,故该模型可在保证有效模拟宏观力学特性的前提下,进一步研究岩石非均质性对宏观力学特性的影响,表2为该模型微观参数表。
3. 矿物晶体模型模拟结果
3.1 应力-应变曲线
图5为花岗岩试验及模拟所得应力-应变曲线。由图5（a）可知,岩石单轴压缩试验力学响应包括以下5个阶段：（Ⅰ）裂纹闭合阶段；（Ⅱ）弹性变形阶段；（Ⅲ）裂纹稳定扩展阶段；（Ⅳ）裂纹不稳定扩展阶段；（Ⅴ）峰后阶段。通过分析裂纹体积应变及试样体积应变的变化关系,可得花岗岩试样特征应力,即闭合应力
、起裂应力 、损伤应力 分别为44.8,71及133.2 MPa。 由于没有考虑材料内部的初始缺陷,模拟结果并不能有效地模拟岩石裂纹闭合阶段,故本文模拟所得力学响应存在4个阶段：（Ⅱ）弹性变形阶段；（Ⅲ）裂纹稳定扩展阶段；（Ⅳ）裂纹不稳定扩展阶段；（Ⅴ）峰后阶段。结合文献[28～30]判断起裂应力及损伤应力的方法,当AE事件率开始变化时,此时所对应的轴向应力可认为是起裂应力
；随着轴向加载的进行,AE事件率开始进入稳定变化段,此时岩石内部微裂纹开始稳定起裂并扩展；当AE事件率变化速率快速变化且在后一段加载过程中波动性较大时,可认为此临界应力为损伤应力 ,此时岩石内部微裂纹开始不稳定扩展及聚合。本文通过上述方法对特征应力进行判断,可得模拟过程中岩石 及 分别为79.2,143.3 MPa。该结果与试验所得特征应力相差在10 MPa以内,差异性较小。 3.2 声发射演化规律
试验过程中,通过对声发射特征参数进行空间定位处理可反演岩石真实破裂过程。模拟过程中,本文借鉴文献[31, 32]中声发射事件的确定方法将一个微裂纹的产生对应于1次声发射事件,通过对岩石内微裂纹空间位置进行监测并记录,可得到岩石的破裂过程。结果表明,模拟与试验所得声发射事件具有相似的变化规律（图6）。当轴向应力达到岩石起裂应力时,试样进入裂纹稳定扩展阶段,此时微裂纹开始起裂且在空间上呈随机分布状态；当轴向应力达到岩石损伤应力时,试样内微裂纹进一步起裂并发生非稳定扩展,此时微裂纹发生聚集成簇的现象；一旦轴向应力超过岩石峰值应力,微裂纹聚集成簇的程度增加进而导致岩石宏观破裂面的产生。从模拟结果可知,岩石发生破坏时其理想声发射空间定位结果应主要聚集在岩石宏观破坏面附近；相比而言,尽管声发射试验受多方面因素影响,如试验环境、岩石非均质结构等,定位的精确性及规律性并不是很完美,但其结果仍可提高对岩石破裂机理的了解。
![]()
图 6 模拟与试验累计声发射规律Figure 6. Accumulative acoustic emission properties of simulation and experiment3.3 晶体尺度裂纹演化规律
图7为岩石加载过程中晶体尺度裂纹演化规律。当轴向应力超过起裂应力后,岩石内部裂纹起裂主要以矿物晶间裂纹为主,且破坏模式大多为拉伸型破坏,这与Kranz[33]发现材料拉伸强度普遍小于剪切强度的结论所一致。随轴向加载的进行,晶内拉伸裂纹数量将超过晶间拉伸裂纹并占主导地位。当试样发生破坏时,晶内裂纹与总裂纹数的占比约为60.95%,拉伸裂纹与总裂纹数的占比约为93.87%。
为验证上述模型模拟所得晶体尺度裂纹发展规律,将试验后花岗岩试样分别进行偏光显微镜及电子显微镜观察。通过在试样表面多处进行观察发现,花岗岩试样受力破坏后所产生的宏观裂纹在矿物晶体尺度主要以不同矿物内部裂纹为主,少部分为矿物晶间裂纹,且该试验结果与文献[34]所得结论一致,故GBM模型可较真实地模拟岩石外力作用下晶体尺度裂纹演化规律。花岗岩代表性微裂纹分析结果如图8所示,图中Qz为石英矿物,Bt为云母矿物,Pl为斜长石,Kf为钾长石。
图9为岩石加载过程中矿物晶体内裂纹演化规律。加载初期,长石矿物晶体内裂纹首先发生起裂,随后石英、云母等矿物内裂纹依次开始起裂并扩展；当试样发生破坏时,矿物内裂纹数量关系如下：长石内裂纹>云母内裂纹>石英内裂纹>其他矿物内裂纹。由于长石矿物在此模型中的含量较高且力学特性相对石英矿物较差,故其内部裂纹最先发生起裂且数量始终占主导地位；相比云母矿物与石英矿物,尽管两者含量相近,但云母矿物相比石英矿物具有较差的力学性质,故岩石发生破坏时,云母内裂纹数量多于石英内裂纹。
在此,为进一步研究矿物晶体裂纹空间演化特征,图9中各加载点（A,B,C,D点）处晶体尺度裂纹分布图如图10所示。由图可知,当轴向应力达到A点时,模型中晶体尺度裂纹主要为矿物晶间裂纹,且裂纹随机分布在模型中；当轴向应力达到B点时,晶体尺度裂纹开始发生聚集现象,此时宏观破裂面开始形成。随着微裂纹的聚集程度加深,岩石宏观破裂面的发展及贯通将导致模型发生破坏。另外,观察宏观破裂面处晶体内裂纹分布发现,长石及云母矿物内裂纹占主导地位,石英矿物内裂纹次之,故在此可推断岩石发生破坏时微裂纹扩展及聚合主要以矿物晶体内裂纹为主,尤其长石及云母矿物内裂纹。
3.4 不同长石矿物含量岩石力学特性
在上述模型基础上,为研究不同矿物组成岩石宏观力学特性,本文在控制石英及其他矿物成分含量不变的条件下,通过Neper软件改变岩石中长石含量w以10%的梯度从20%变化至60%,生成5组不同的GBM模型,且每组模型进行3次共计15次数值模拟。模型如图11所示,黑色多边形为云母矿物,灰色多边形为长石矿物,白色多边形为石英矿物,蓝色多边形为其他矿物。
图12为不同长石含量岩石峰值应力及特征应力变化规律。由图12（a）可知,模拟所得峰值应力整体随长石矿物含量增加呈增加的变化趋势；当长石含量从20%增加至60%时,模拟所得峰值应力从168 MPa变化至178 MPa,但其变化幅度与文献[2]中统计拟合结果相比较小,这可能与模拟及文献[2]中岩石微观结构差异较大具有一定的联系。另外,随长石矿物含量增加,岩石损伤应力呈轻微增加的变化趋势,而起裂应力受长石矿物含量影响较小（图12（b））。
![]()
图 12 不同长石含量模型峰值应力及特征应力变化曲线Figure 12. Curves of peak and characteristic stresses of models with different feldspar contentsÜndül[9]通过试验指出,斜长石矿物与矿物基质含量占比的增加将增大单轴压缩强度,而矿物含量与起裂应力之间并没有较明确的关系,故此模拟所得结果与试验结果相吻合。
现从微观角度对不同长石含量岩石单轴压缩条件下晶体尺度裂纹变化规律进行分析,以进一步研究并讨论峰值应力变化的原因。将上述模型破坏时矿物晶体内裂纹数量取平均值并与总裂纹数进行正则化处理后,得不同长石含量GBM模型矿物晶体内裂纹占比变化规律如图13。
![]()
图 13 不同长石含量模型矿物内裂纹变化规律Figure 13. Variations of intragranular cracks of models with different feldspar contents由图13可知,随长石矿物含量增加,岩石云母矿物内裂纹占比呈递减的变化趋势,而长石矿物内裂纹占比呈递增的变化趋势,石英及其他矿物内裂纹占比则变化不大,故长石矿物含量的升高将导致岩石内部裂纹形式从以云母内裂纹为主转变为以长石内裂纹为主,模型破坏时相应的晶体尺度裂纹分布见图14。随长石矿物含量增加,岩石宏观破裂面处云母内裂纹数量减少,而长石内裂纹数量增加；相比云母矿物而言,长石矿物由于具有更好的力学性质且内部裂纹发生扩展所需要的能量越多,故随着长石含量的增加,岩石内部裂纹形式从以云母内裂纹为主转变为以长石内裂纹为主可能导致岩石峰值应力整体呈增加变化趋势。
![]()
图 14 不同长石含量模型晶体尺度裂纹分布图Figure 14. Distributions of grain-scale cracks of models with different feldspar contents非均质岩石力学特性的数值方法。4. 结论
本文结合花岗岩室内单轴试验并采用矿物晶体模型（GBM）对岩石矿物非均质结构进行了离散元模拟,改变岩石矿物组成研究了岩石微观非均质性对宏观力学特性的影响,并从矿物晶体尺度对其变化原因进行了较为合理的解释。主要结论如下：
（1）矿物晶体模型（GBM）可在考虑岩石矿物晶体结构及强度非均质性的前提下,对其应力-应变曲线、声发射特性进行有效模拟,并可研究矿物晶体尺度微裂纹起裂、扩展及聚合规律,是一种有效研究
（2）岩石单轴压缩过程中,微裂纹起裂首先以晶间裂纹为主,随后以晶内裂纹为主,且主要破坏机理为拉伸型破坏。岩石破坏时,拉伸裂纹及晶内裂纹与总裂纹的占比分别约为93.87%,60.95%。
（3）岩石单轴压缩过程中,长石矿物内裂纹首先起裂,随后云母、石英等矿物内裂纹依次发生起裂并扩展。岩石破坏时,微裂纹聚集将导致宏观破裂面的形成,且宏观破裂面的形成主要与晶体内裂纹扩展及聚合有关。
（4）随长石矿物含量增加,岩石峰值应力及损伤应力整体呈增加的变化趋势,而起裂应力变化并不明显。从矿物晶体尺度裂纹变化规律可推断,岩石峰值应力增大的原因可能与长石内裂纹占比增加、云母内裂纹占比减少有关。
-
![]()
图 4 加卸载响应比解析解与有限元解对比
Figure 4. Comparison of LURR results between analytical solution and finite element solution
![]()
图 6 洞周关键点变形的加卸载响应比结果对比
Figure 6. LURR results of deformation of key points around tunnel
![]()
图 7 浅埋隧道在施工过程中的塑性区变化结果
Figure 7. Plastic zones of shallow tunnel in tunnel construction
![]()
图 8 浅埋隧道在施工过程中的剪切应力变化结果
Figure 8. Shear stresses of shallow tunnel in tunnel construction
![]()
图 9 洞周关键点变形的加卸载响应比结果对比
Figure 9. LURR results of deformation of key points around tunnel
![]()
图 10 深埋隧道在施工过程中的塑性区变化结果
Figure 10. Plastic zones of deep-buried tunnel in tunnel construction
![]()
图 11 深埋隧道在施工过程中的剪切应力变化结果
Figure 11. Shear stresses of deep-buried tunnel in tunnel construction
![]()
图 12 深埋隧道在施工过程中的压应力变化结果
Figure 12. Compressive stresses of deep-buried tunnel in tunnel construction
![]()
图 14 洞周关键点变形的加卸载响应比结果对比
Figure 14. LURR results of deformation of key points around tunnel
![]()
图 15 地表偏压堆载作用下隧道围岩的塑性区变化结果
Figure 15. Plastic zones of surrounding rock of tunnel under surface load
![]()
图 16 地表偏压堆载作用下隧道衬砌的塑性区变化结果
Figure 16. Plastic zones of tunnel linings under surface loads
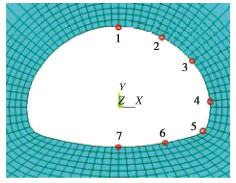
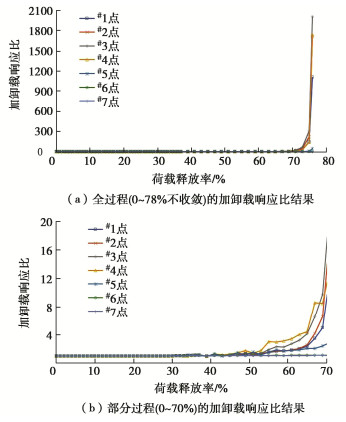
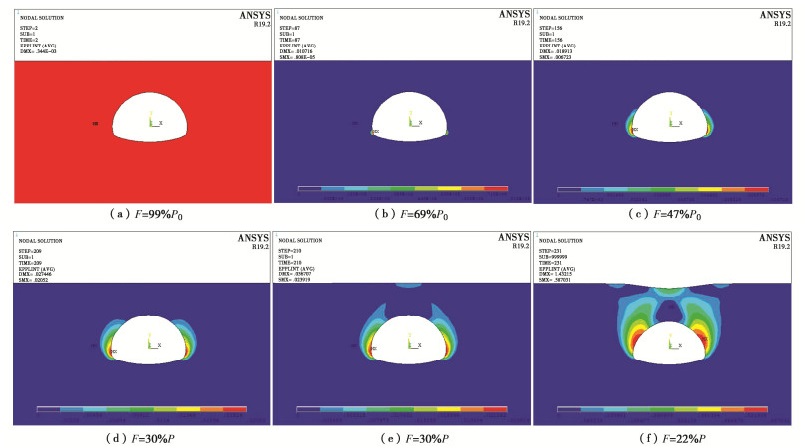
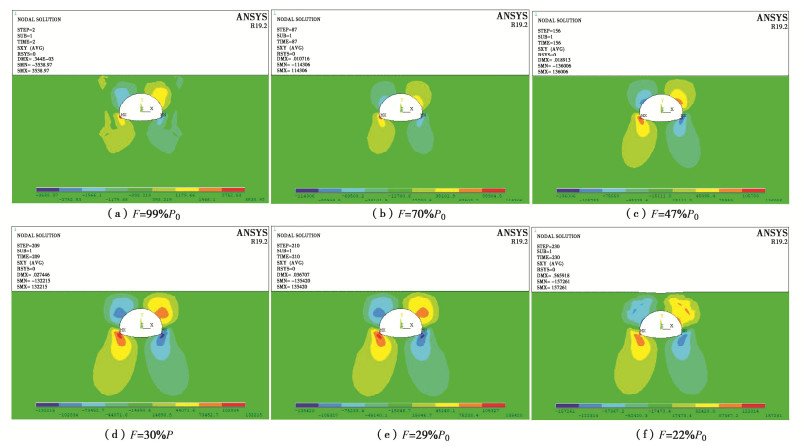
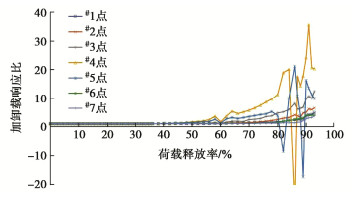
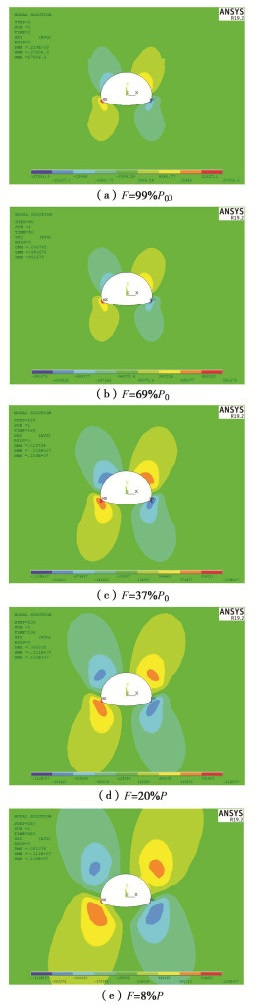
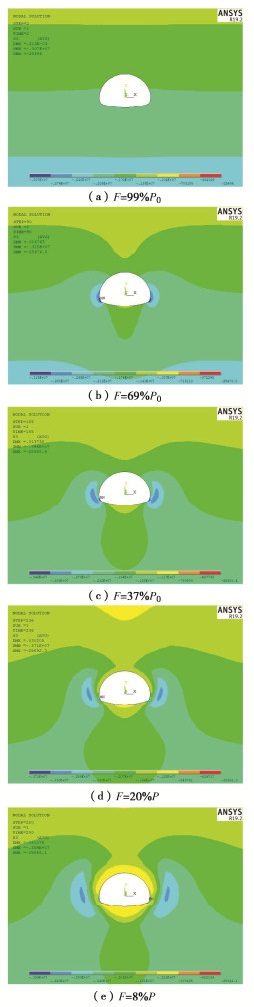
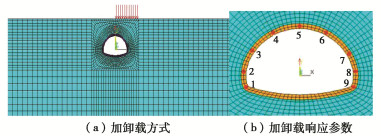
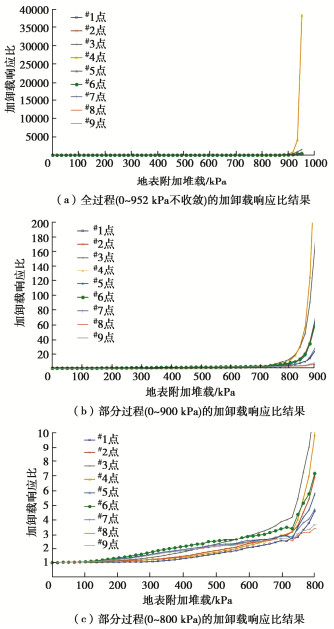
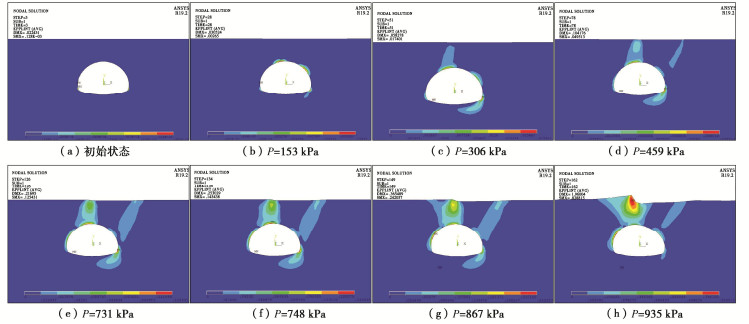
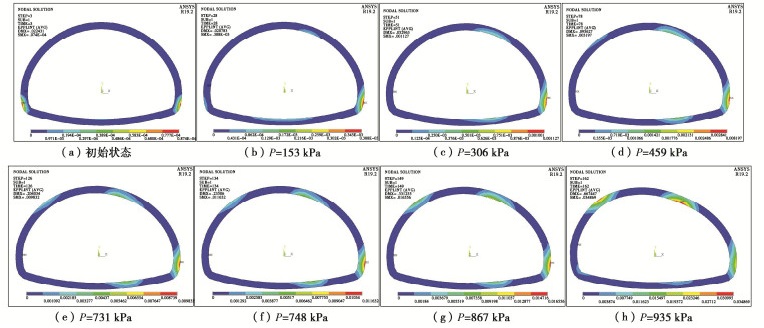
表 1 隧道施工稳定性计算算例
Table 1 Examples of tunnel construction stability
算例号 隧道类型 围岩级别 埋深/m 模型尺寸/(m×m) 算例2 浅埋隧道 Ⅵ级 6.5 167.58×72.83 算例3 深埋隧道 Ⅴ级 96 167.58×162.33 
下载: 导出CSV
表 2 岩土体物理力学参数
Table 2 Mechanical parameters of rock and soil mass
围岩 弹性模量/GPa 重度/(kN·m-3) 泊松比 黏聚力/MPa 内摩擦角/(°) Ⅵ级 0.1 17.0 0.45 0.03 15.0 Ⅴ级 1.0 17.0 0.45 0.15 18.0
下载: 导出CSV
-
[1] 朱永全. 隧道稳定性位移判别准则[J]. 中国铁道科学, 2001, 22(6): 80–83. doi: 10.3321/j.issn:1001-4632.2001.06.016 ZHU Yong-quan. The criterion of predicting tunnel stability by displacement[J]. China Railway Science, 2001, 22(6): 80–83. (in Chinese) doi: 10.3321/j.issn:1001-4632.2001.06.016
[2] 耿晓杰. 深埋条件下隧道稳定性评价方法及应用研究[D]. 北京: 北京科技大学, 2015. GENG Xiao-jie. Research on Stability Evaluation Method and Application of Deep Tunnel[D]. Beijing: University of Science and Technology Beijing, 2015. (in Chinese)
[3] 曹淞宇, 王士民, 刘川昆, 等. 裂缝位置对盾构隧道管片结构破坏形态的影响[J]. 东南大学学报(自然科学版), 2020, 50(1): 120–128. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX202001016.htm CAO Song-yu, WANG Shi-min, LIU Chuan-kun, et al. Influence of crack location on failure mode of shield tunnel lining structure[J]. Journal of Southeast University (Natural Science Edition), 2020, 50(1): 120–128. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX202001016.htm
[4] 漆泰岳, 白永学, 李斌. 复杂断面地铁隧道开挖优化及对建筑物的影响[J]. 西南交通大学学报, 2012, 47(1): 68–77. doi: 10.3969/j.issn.0258-2724.2012.01.012 QI Tai-yue, BAI Yong-xue, LI Bin. Optimization of complex cross-section metro tunnel excavation and its influence on building[J]. Journal of Southwest Jiaotong University, 2012, 47(1): 68–77. (in Chinese) doi: 10.3969/j.issn.0258-2724.2012.01.012
[5] 郑颖人, 赵尚毅. 岩土工程极限分析有限元法及其应用[J]. 土木工程学报, 2005, 38(1): 91–98, 104. doi: 10.3321/j.issn:1000-131X.2005.01.012 ZHENG Ying-ren, ZHAO Shang-yi. Limit state finite element method for geotechnical engineering analysis and its applications[J]. China Civil Engineering Journal, 2005, 38(1): 91–98, 104. (in Chinese) doi: 10.3321/j.issn:1000-131X.2005.01.012
[6] 黄金, 赵淼. 基于贝叶斯网络的隧道围岩失稳风险分析[J]. 西安建筑科技大学学报(自然科学版), 2019, 51(4): 545–550. https://www.cnki.com.cn/Article/CJFDTOTAL-XAJZ201904012.htm HUANG Jin, ZHAO Miao. Risk analysis of tunnel surrounding rock based on Bayesian network[J]. Journal of Xi'an University of Architecture & Technology (Natural Science Edition), 2019, 51(4): 545–550. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-XAJZ201904012.htm
[7] HE S D, LI Y R, AYDIN A. A comparative study of UDEC simulations of an unsupported rock tunnel[J]. Tunnelling and Underground Space Technology, 2018, 72: 242–249. doi: 10.1016/j.tust.2017.11.031
[8] DO T N, WU J H. Simulation of the inclined jointed rock mass behaviors in a mountain tunnel excavation using DDA[J]. Computers and Geotechnics, 2020, 117: 103249. doi: 10.1016/j.compgeo.2019.103249
[9] 袁永才, 李术才, 李利平, 等. 山岭隧道塌方风险评价理论与方法及工程应用[J]. 中南大学学报(自然科学版), 2016, 47(7): 2406–2414. https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201607031.htm YUAN Yong-cai, LI Shu-cai, LI Li-ping, et al. Risk evaluation theory and method of collapse in mountain tunnel and its engineering applications[J]. Journal of Central South University (Science and Technology), 2016, 47(7): 2406–2414. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZNGD201607031.htm
[10] 祝方才, 余继江, 刘丙肖, 等. 基于地应力场加卸载的地下洞室稳定数值模拟研究[J]. 岩土工程学报, 2016, 38(9): 1578–1585. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201609005.htm ZHU Fang-cai, YU Ji-jiang, LIU Bing-xiao, et al. Numerical analysis of stability of underground openings through loading/unloading of in situ stress fields[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(9): 1578–1585. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201609005.htm
[11] 祝方才, 刘丙肖, 李大建. 基于地应力场加卸载的地下洞室稳定模型试验研究[J]. 实验力学, 2016, 31(5): 645–654. https://www.cnki.com.cn/Article/CJFDTOTAL-SYLX201605010.htm ZHU Fang-cai, LIU Bing-xiao, LI Da-jian. Model experimental study of underground cavern stability based on load/unload of in situ stress field[J]. Journal of Experimental Mechanics, 2016, 31(5): 645–654. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SYLX201605010.htm
[12] 石崇, 徐卫亚, 周家文, 等. 动力时程响应的加卸载响应比描述研究[J]. 岩土力学, 2007, 28(增刊1): 743–747. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2007S1150.htm SHI Chong, XU Wei-ya, ZHOU Jia-wen, et al. Dynamic stability research by using load/unload ratio method[J]. Rock and Soil Mechanics, 2007, 28(S1): 743–747. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2007S1150.htm
[13] 杨继华, 盛谦, 朱泽奇, 等. 地下岩体洞室群地震响应的加、卸载响应比分析[J]. 岩土力学, 2012, 33(7): 2127–2132. doi: 10.3969/j.issn.1000-7598.2012.07.032 YANG Ji-hua, SHENG Qian, ZHU Ze-qi, et al. Loading/unloading response ratio study of seismic response on underground rock cavern group[J]. Rock and Soil Mechanics, 2012, 33(7): 2127–2132. (in Chinese) doi: 10.3969/j.issn.1000-7598.2012.07.032
[14] 尹祥础. 加卸载响应比理论及其应用[M]. 北京: 科学出版社, 2015. YIN Xiang-chu. Load/unload Response Ratio Theory and its Application[M]. Beijing: Science Press, 2015. (in Chinese)
[15] 于学馥, 郑颖人. 地下工程围岩稳定分析[M]. 北京: 煤炭工业出版社, 1983. YU Xue-fu, ZHEN Ying-ren. Stability Analysis of Surrounding Rock in Underground Works[M]. Beijing: China Coal Industry Publishing House, 1983. (in Chinese)
计量
- 文章访问数: 146
- HTML全文浏览量: 26
- PDF下载量: 45
