Large-displacement landslides based on affine velocity matrix-improved material point method
-
摘要: 为克服物质点法的数值噪声问题，将仿射质点网格法的动量映射格式应用于经典物质点法，即在动量映射过程中额外维护一个仿射速度矩阵，进而构建出由仿射速度矩阵和物质点的速度矢量共同表示的速度场。通过理论推导证明了仿射速度矩阵是速度梯度的一阶近似，进而利用仿射速度矩阵极大地简化了旋率、变形率的求解过程和单时间步内的计算流程，使计算效率成倍提高。采用可GPU并行计算的Taichi编程语言进行算法编程，使求解效率提高数百倍。通过模拟沙柱自然成堆和铝棒堆积体模型试验分别验证了改进算法克服数值噪声的有效性、数值准确性和程序的计算效率；基于典型形状边坡的滑坡模拟，验证了算法和程序在滑坡分析中的适用性及优势。
-
关键词:
- 物质点法 /
- 仿射质点网格法 /
- Taichi编程语言 /
- 滑坡
Abstract: In order to overcome the numerical noise problem of the material point method, the momentum mapping scheme of the affine particle-in-cell method is applied to the classical material point method, that is, in the process of momentum mapping, an additional affine velocity matrix is maintained, and then the velocity field represented by the affine velocity matrix and velocity vector of material point is constructed. It is proved that the affine velocity matrix is the first-order approximation of velocity gradient. The affine velocity matrix greatly simplifies the solving process of spin rate and rate of deformation as well as the computation process in a single time step, so that the computational efficiency is doubled. The Taichi programming language, which can be used for GPU parallel computing, is used for algorithm programming, which improves the solution efficiency hundreds of times. The effectiveness of the improved algorithm to overcome numerical noise, the numerical accuracy and the computational efficiency of the program are verified by simulating the natural stacking of sand columns and the stacking of aluminum rods. By simulating the landslide of a typical shape slope, the applicability and advantages of the algorithm and program in landslide analysis are verified. -
0. 引言
滑坡是最为常见的地质灾害，2006—2019年间，每年滑坡灾害的发生数量占全国地质灾害总数量的60%~80%，造成了十分惨重的人员伤亡和经济损失[1]。滑坡运动是一种典型的动力问题，并且往往伴随有大变形产生，对滑坡问题进行准确的模拟分析一直是岩土工程领域的研究重点。
根据所采用的运动描述方法的不同，数值模拟方法可以分为拉格朗日格式、欧拉格式和混合格式，物质点法（material point method, MPM）是一种混合格式的方法[2]。该方法主要有以下4点优势[3]：可用于伴随有大变形产生的大规模失效分析；与有限元相似，实现起来非常直观；可以引入历史相关的本构模型；边界条件的施加由于背景网格的存在而更加直观。
经典物质点法由流体隐式质点法（fluid implicit particle，FLIP）[4]发展而来，物质点与网格节点之间的动量映射格式也与之相同。FLIP格式下，动量信息由网格节点映射回物质点时，映射的量为动量增量而非网格节点的动量[5]，该动量映射格式存在较大的数值不稳定性；Jiang等[6]改进了质点网格法（particle-in- cell, PIC）[7]，提出仿射质点网格法（affine particle-in- cell method，APIC），具有良好的数值稳定性。将APIC动量映射格式应用于物质点法，以克服经典物质点法的数值不稳定问题；在此基础上，将仿射速度矩阵作为速度梯度的一阶近似，改进算法，极大地简化了旋率、变形率的求解过程以及单时间步内的计算流程；程序实现采用Hu等[8-9]开发的计算机图形学领域的高性能语言——Taichi，使计算效率大大提高。通过模拟沙柱自然成堆和铝棒堆积体模型试验，从稳定性、数值精度以及计算效率三方面探讨改进的物质点法的优势，基于典型形状边坡的滑坡模拟，验证算法和程序在滑坡分析中的适用性及优势。
1. 经典物质点法基本理论
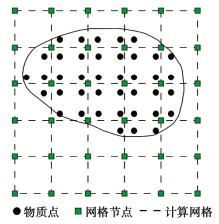
物质点法采用质点和网格两套体系来描述被模拟对象，如图 1。物质点携带了所有的信息，居主要地位，并且作为空间中控制方程的积分点，但并不代表真实的物理粒子；网格则居次要地位，主要用于求解控制方程，物质点和网格节点之间的信息映射则完全由形函数控制[10]。
1.1 控制方程
物质点法固有的满足质量守恒，在该研究中不考虑热交换，故能量也是守恒的，所以仅通过求解动量方程即可确定材料的状态[11]。基于更新拉格朗日格式，连续体运动的动量方程为
$$ \rho {\ddot u_i} = {\sigma _{ij, j}} + \rho {b_i} \text{，} $$ (1) 式中，$ \rho $表示材料当前的质量密度，${u_i}$表示位移，$ {\sigma _{ij}} $表示Cauchy应力，$ {b_i} $表示单位质量的体积力，如重力，本文中所有公式的记法均满足爱因斯坦求和约定。
边界条件为
$$ \left\{ \begin{array}{l}({n}_{j}{\sigma }_{ij})|{{\mathit{\Gamma}} }_{\text{t}}={\overline{t_{i}}}\text{ }\text{，}\hfill \\ {v}_{i}|{{\mathit{\Gamma}} }_{\text{u}}={\overline{v}}_{i}\text{ }\text{，} \end{array} \right. $$ (2) 式中，$ {{\mathit{\Gamma}} _{\text{t}}} $和$ {{\mathit{\Gamma}} _{\text{u}}} $分别表示给定的面力边界和位移边界，$ {n_j} $为边界$ {{\mathit{\Gamma}} _{\text{t}}} $的外法线单位向量，$ {\bar {t_i}} $为作用在边界$ {{\mathit{\Gamma}} _{\text{t}}} $上的面力，$ {\bar v_i} $为位移边界$ {{\mathit{\Gamma}} _{\text{u}}} $的速度。
式（1）可以通过其弱形式在区域Ω中求解：
$$ \int_{\mathit{\Omega}} \rho {\ddot u_i}\delta {u_i}{\text{d}}V + \int_{\mathit{\Omega}} \rho \sigma _{ij}^s\delta {u_{i, j}}{\text{d}}V -\\ \int_{\mathit{\Omega}} \rho {b_i}\delta {u_i}{\text{d}}V - \int_{{{\mathit{\Gamma}} _t}} \rho \bar t_i^s\delta {u_i}{\text{d}}A = 0 \text{，} $$ (3) 式中，$ \delta {u_i} $表示在边界$ {{\mathit{\Gamma}} _{\text{u}}} $上等于0的虚位移；$\sigma _{ij}^s = $ ${\sigma _{ij}}/\rho $表示比应力；$ {\bar {t_i}}^s = {\bar {t_i}}/\rho $表示边界面力。
1.2 离散化
如图 1，区域${\mathit{\Omega}} $被离散为黑色的物质点，连续体的密度被近似为
$$ \rho ({x_i}) = \sum\nolimits_p {{m_p}} \delta ({x_i} - {x_{ip}}) \text{，} $$ (4) 式中，$ \delta $是Dirac delta函数，${m_p}$表示物质点p的质量，$ {x_{ip}} $是物质点p的坐标，代入式（3），将其转化为对物质点求和的形式：
$$ \sum\nolimits_p {{m_p}} {\ddot u_{ip}}\delta {u_{ip}} + \sum\nolimits_p {{m_p}} \sigma _{ijp}^s\delta {u_{ip}} -\\ \sum\nolimits_p {{m_p}} {b_{ip}}\delta {u_{ip}} - \sum\nolimits_p {{m_p}} {\bar {t_i}}{p}^s{h^{ - 1}}\delta {u_{ip}} = 0 \text{，} $$ (5) 式中，下标$p$表示${x_{ip}}$位置处的物质点所携带的物理量，h是假想的边界层厚度，是为了将式（3）中左端的最后一项转化为体积分而引入的。
物质点法的每个计算步内，物质点和背景网格一直是固连在一起的，因此可以通过建立在背景网格节点上的形函数${N_I}({x_i})$插值实现物质点和背景网格节点之间的信息映射，本文采用的形函数为二阶B样条形函数。以带下标I的量表示背景网格节点I上的物理量。
物质点$p$的位移${u_{ip}}$和虚位移$\delta {u_{ip}}$可表示为
$$ {u_{ip}} = {N_{Ip}}{u_{iI}}\text{，} $$ (6) $$ \delta {u_{ip}} = {N_{Ip}}\delta {u_{iI}}\text{，} $$ (7) 根据式（6），（7），以及背景网格节点虚位移$\delta {u_{iI}}$的任意性，可将背景网格节点的运动方程表示为
$$ {\dot p_{iI}} = f_{iI}^{{\text{int}}} + f_{iI}^{{\text{ext}}}, \quad {x_I} \notin {{\mathit{\Gamma}} _{\text{u}}}\text{，} $$ (8) 式中，${p_{iI}} = {\mathit{\boldsymbol{m}}_I}{\dot u_{iI}}$，表示背景网格节点I在$i$方向的动量，${\mathit{\boldsymbol{m}}_I}$表示集中质量矩阵，
$$ f_{iI}^{{\text{int}}} = - \sum\nolimits_p {{N_{Ip, j}}} {\sigma _{ijp}}\frac{{{m_p}}}{{{\rho _p}}} \text{，} $$ (9) $$ f_{iI}^{{\text{ext}}} = \sum\nolimits_p {{N_{Ip}}{m_p}{b_{ip}}} + \sum\nolimits_p {{N_{Ip}}\frac{{{m_p}}}{{{\rho _p}}}{{\bar t_i}{p}}{h^{ - 1}}} \text{，} $$ (10) 式（9），（10）分别表示节点I在$i$方向的内力和外力。
1.3 计算流程
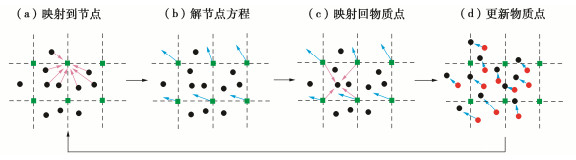
计算流程图如图 2所示，在每个时间步开始，重置背景网格并将物质点的信息映射至网格节点，如图 2（a）；网格节点将收集到的物质点信息用于求解控制方程，本构方程在粒子上进行求解，如图 2（b）；之后，把在网格节点上求得的信息映射回物质点，如图 2（c）；最后，更新物质点，丢弃已变形的网格，如图 2（d）。物质点法不会遇到由网格畸变导致的计算不能进行下去的问题，所以非常适合于做大变形问题的模拟分析。
2. 基于APIC的MPM改进
2.1 MPM-APIC和改进的MPM-APIC方法的原理
APIC方法的原理[6]是：以二维为例，物质点有两个自由度，而它周围的网格节点的自由度却远大于此，因此当网格节点的动量映射回物质点时，必然导致动量不守恒，所以额外为每个物质点定义一个仿射速度矩阵${\mathit{\boldsymbol{C}}_{ijp}}$，
$$ {\mathit{\boldsymbol{C}}_{ijp}} = {B_{ijp}}{({\mathit{\boldsymbol{D}}_{ijp}})^{ - 1}}\text{，} $$ (11) $$ {B_{ijp}} = \sum\nolimits_I {{N_{Ip}}{v_{iI}}{{({x_{jI}} - {x_{jp}})}^{\text{T}}}} \text{，} $$ (12) $$ {\mathit{\boldsymbol{D}}_{ijp}} = \sum\nolimits_I {{N_{Ip}}({x_{jI}} - {x_{jp}}){{({x_{iI}} - {x_{ip}})}^{\text{T}}}} \text{，} $$ (13) 其中，$ {\mathit{\boldsymbol{D}}_{ijp}} $表示仿射运动的惯性矩阵，当使用二阶B样条形函数时，$ {\mathit{\boldsymbol{D}}_{ijp}} = \Delta {x^2}{I_{ij}}/4 $，$ \Delta x $为背景网格间距，$ {I_{ij}} $表示单位矩阵，$ {B_{ijp}} $表示角动量信息[6]。
假设$ {\mathit{\boldsymbol{C}}_{ijp}} = \left[ \begin{gathered} {C_{00}}, \hfill \\ {C_{10}}, \hfill \\ \end{gathered} \right.\left. \begin{gathered} {C_{01}} \hfill \\ {C_{11}} \hfill \\ \end{gathered} \right] $，其中，${C_{00}}$和${C_{11}}$分别代表水平和竖向的拉伸运动，${C_{01}}$和${C_{10}}$分别代表顺时针和逆时针的剪切运动。每个物质点附近的局部速度场由其仿射速度矩阵和速度向量共同表示，从而可以准确地将网格节点的动量映射至物质点，使动量保持守恒，并具有较高的数值稳定性。
APIC的动量映射算法为
$$ m_I^n = \sum\nolimits_p {{m_p}N_{Ip}^n} \text{，} $$ (14) $$ P_{iI}^n = \sum\nolimits_p {{N_{Ip}}{m_p}(v_{ip}^n + C_{ijp}^n(x_{jI}^n - x_{jp}^n))} \text{，} $$ (15) $$ v_{ip}^{n + 1} = \sum\nolimits_I {N_{Ip}^nv_{iI}^{n + 1}} \text{，} $$ (16) $$ \mathit{\boldsymbol{C}}_{ijp}^{n + 1} = \frac{4}{{\Delta {x^2}}}\sum\nolimits_I {{N_{Ip}}v_{iI}^{n + 1}(x_{jI}^n - x_{jp}^n)} \text{，} $$ (17) 式（14），（15）表示从物质点到网格节点的映射，在网格节点上通过求解动量方程将$v_{iI}^n$更新至$ v_{iI}^{n + 1} $，式（16），（17）表示从网格节点到物质点的映射。本文中，将使用APIC动量映射的MPM记作MPM-APIC。
由式（15）可得，任意一节点$ {x_{iI}} $附近的物质点在任意时刻的速度$\tilde v_{ip}^n$可表示为
$$ \tilde v_{ip}^n = v_{ip}^n + \mathit{\boldsymbol{C}}_{ijp}^n(x_{jI}^n - x_{jp}^n)\text{，} $$ (18) 分析式（18）可得，使用APIC进行动量映射时等价于使用移动最小二乘法对$\tilde v_{ip}^n$进行拟合，且基函数为线性基函数，根据式（18）求速度梯度$ \tilde v_{ip, j}^n $，
$$ \tilde v_{ip, j}^n = \frac{{\partial \tilde v_{ip}^n}}{{\partial {x_j}}} = C_{ijp}^n 。 $$ (19) 根据式（18），（19）可得，仿射速度矩阵${\mathit{\boldsymbol{C}}_{ijp}}$即为速度梯度的一阶近似，据此改进MPM，即使用仿射速度矩阵${\mathit{\boldsymbol{C}}_{ijp}}$求解物质点的应变增量和旋量增量，省去在求解速度梯度时的浮点数运算，并且简化MPM的计算流程，详见2.2节。
2.2 时间积分方案
计算域${\mathit{\Omega}} $是随时间变化的，所以式（8）在每个时间步都必须成立，使用中心差分法求解，
$$ p_{iI}^{n + 1/2} = p_{iI}^{n - 1/2} + f_{iI}^n\Delta t \text{，} $$ (20) 式中，$\Delta t$表示时间步长的增量，在本文中为定值，$f_{iI}^n = $$f_{iI}^{{\text{int}}} + f_{iI}^{{\text{ext}}}$。本文使用时间步开始时的动量更新应力，即USF（update-stress-first）格式[12]，该格式具有良好的能量守恒特性。本构模型为：线弹性段，采用各向同性线弹性本构模型，出现塑性变形直至失稳出现大变形阶段，采用Drucker-Prager屈服准则对弹性应力进行校正。
（1）MPM-APIC的实现步骤
第一步，遍历网格节点，将网格节点的动量、质量和节点力置为0，建立新的背景网格。
第二步，遍历物质点，根据式（14），（15）将物质点的质量和动量映射到背景网格。
第三步，遍历网格节点，通过节点动量和质量求解节点速度，并根据具体问题施加边界条件。
$$ v_{iI}^{n - 1/2} = \frac{{p_{iI}^{n - 1/2}}}{{\mathit{\boldsymbol{m}}_I^n}} 。 $$ (21) 第四步，遍历物质点，根据速度梯度求解物质点的应变率$\dot \varepsilon _{ijp}^{n - 1/2}$和旋率${\mathit{\Omega}} _{ijp}^{n - 1/2}$，更新物质点的密度和应力：
$$ \dot \varepsilon _{ijp}^{n - 1/2} = \sum\nolimits_I {\frac{1}{2}(N_{Ip, j}^nv_{iI}^{n - 1/2} + N_{Ip, i}^{n - 1/2}v_{jI}^{n - 1/2})} \text{，} $$ (22) $$ {\mathit{\Omega}} _{ijp}^{n - 1/2} = \sum\nolimits_I {\frac{1}{2}(N_{Ip, j}^nv_{iI}^{n - 1/2} - N_{Ip, i}^{n - 1/2}v_{jI}^{n - 1/2})} \text{，} $$ (23) $$ \rho _p^{n + 1} = \rho _p^n/(1 + \dot \varepsilon _{ijp}^{n - 1/2}\Delta t) \text{，} $$ (24) 利用弹性本构模型计算出弹性试探应力：
$$ \tilde \sigma _{ijp}^n = \sigma _{ijp}^{n - 1} + \dot \sigma _{ijp}^{n - 1/2}\Delta t \text{，} $$ (25) 应力率计算方式为
$$ {\dot \sigma _{ij}} = \sigma _{ij}^\nabla + {\sigma _{ik}}{{\mathit{\Omega}} _{jk}} + {\sigma _{jk}}{{\mathit{\Omega}} _{ik}} \text{，} $$ (26) $$ \sigma _{ij}^\nabla = C_{ijkl}^{\sigma J}{\dot \varepsilon _{kl}} \text{，} $$ (27) 式中，$\sigma _{ij}^\nabla $为焦曼应力率，$\mathit{\boldsymbol{C}}_{ijkl}^{\sigma J}$为弹性刚度张量。采用返回映射算法[5]，将试探应力带入到D-P准则，将超过屈服面的应力拉回到屈服面，得到真实应力$\sigma _{ijp}^n$，然后由式（9），（10）计算网格节点的内力和外力。
第五步，遍历网格节点，根据式（20）更新节点动量。
第六步；遍历物质点，根据式（16），（17）将背景网格节点的速度映射回物质点并更新仿射速度矩阵，最后更新物质点的位置：
$$ x_{ip}^{n + 1} = x_{ip}^n + \Delta {t^{n + 1/2}}v_{ip}^{n + 1/2} 。 $$ (28) 从以上步骤可以见得，在一个计算步中，对物质点和网格节点进行了三次遍历，调用了三次形函数，两次形函数导数。
（2）改进的MPM-APIC的实现步骤
第一步，遍历网格节点，将网格节点的动量、质量和节点力置为0，建立新的背景网格。
第二步，遍历物质点，根据式（14），（15）将物质点的质量和动量映射至背景网格，利用仿射速度矩阵${\mathit{\boldsymbol{C}}_{ijp}}$求解应变率$\dot \varepsilon _{ijp}^{n - 1/2}$和旋率${\mathit{\Omega}} _{ijp}^{n - 1/2}$：
$$ \dot \varepsilon _{ijp}^{n - 1/2} = \frac{1}{2}(\mathit{\boldsymbol{C}}_{ijp}^{n - 1/2} + {(\mathit{\boldsymbol{C}}_{ijp}^{n - 1/2})^{\text{T}}}) \text{，} $$ (29) $$ {\mathit{\Omega}} _{ijp}^{n - 1/2} = \frac{1}{2}(\mathit{\boldsymbol{C}}_{ijp}^{n - 1/2} - {(\mathit{\boldsymbol{C}}_{ijp}^{n - 1/2})^{\text{T}}}) \text{，} $$ (30) 进而利用式（24）~（27）以及Drucker-Prager准则更新物质点的密度和应力，进而根据式（9），（10）计算网格节点的内力和外力。
第三步，遍历网格节点，根据式（21）求解节点速度，根据式（20）更新节点动量，施加边界条件。
第四步，遍历物质点，根据式（16），（17）和（28）将背景网格的速度映射回物质点，并更新物质点的仿射速度矩阵和位置。
对比MPM-APIC的实现步骤可得，改进的MPM-APIC在一个计算流程中只有4个步骤，减少了对物质点和网格节点的遍历次数，并且省去了由网格节点速度插值求解物质点速度梯度的步骤，大大的简化了算法。在程序中，改进的MPM不仅减少了浮点数运算的次数，还减少了对浮点数进行访问和存储的次数，从而使计算效率提高一倍以上。
2.3 算法实现
本文使用Taichi作为开发语言，Taichi是Hu等[9]为计算机图形学应用而开发的高性能领域特定语言，其主要优势有生产力强、性能高（可GPU并行）、数据结构先进等。采用函数式编程的开发策略，实现步骤如下：
（1）变量定义：利用Taichi的数据结构，将物理量定义成计算效率高、易于访问和存储的变量。
（2）定义Drucker-Prager屈服函数：利用Taichi将D-P准则编写为可在GPU并行执行的函数。
（3）定义计算子步函数：利用Taichi将1.3节所示计算流程编写为可在GPU并行执行的循环体，对每物质点和网格节点进行计算更新。
（4）定义初始化函数：包括物质点的初始位置、初始速度、初始应力场等。
（5）定义主函数：设定计算步，调用以上函数进行计算。
（6）利用第三方库对计算结果进行后处理。
2.4 数值稳定性验证
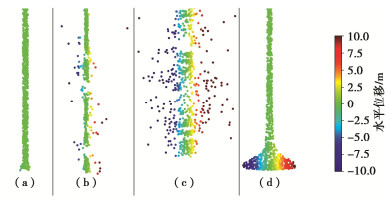
分别用经典MPM和改进的MPM-APIC模拟砂柱自然成堆[13-14]这一现象，直观的说明改进算法的稳定性优势。两个数值试验中材料的参数相同，见表 1，物质点个数相同，均为2000个，时间步长相等，均为0.02 ms，背景网格单元边长为1 m，设定总的运行时间步${T_{\text{s}}} = 24000$，边界条件相同，模拟结果如图 3，4所示。
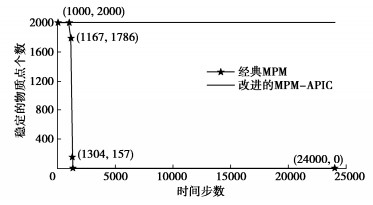
表 1 砂柱材料参数Table 1. Material parameters of sand column$ \rho $/(kg·m-3) E/MPa $\nu $ $c$/kPa $ \varphi $/(°) $\psi $/(°) 2000 20 0.3 0 19.8 0 图 3（a）表示时间步${T_{\text{s}}} = 1000$，两种模拟均可正常进行，随着时间步向前推进，经典MPM的模拟在物质点没有碰到地面就出现一系列水平位移，这是不符合物理规律的，将这些物质点视作不稳定的物质点，如图 3（b），（c）所示，对应的时间步${T_{\text{s}}}$分别为1167，1304；改进的MPM-APIC模拟这一现象时，所有的物质点都是稳定的，如图 3（d）所示。
由图 4可知，改进的MPM-APIC模拟的整个过程都是稳定的；利用经典MPM模拟时，仅稳定运行了1000步，为总时间步的1/24，时间步超过1000步时，稳定的物质点个数快速下降，时间步等于1304时，稳定的物质点个数仅剩157，时间步大于1304时，所有的物质点飞出背景网格区域，模拟无法继续进行。在此基础上，又做了进一步的探究，把时间步长增加至20 ms，改进的MPM-APIC依然可以稳定运行，其数值稳定性优势得到进一步验证。
2.5 数值准确性和效率验证
（1）试验简介
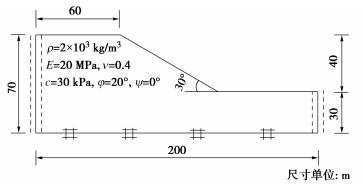
Bui等[15]在实验室内用直径为1~1.5 mm，长为50 mm的干燥铝棒模拟了平面应变条件下边坡的二维失效过程，具体布置如图 5，材料参数与文献[15]相同，铝棒的初始构型为200 mm×100 mm的长方形结构，试验开始时，将右侧的挡板迅速拉开，铝棒在重力的作用下开始自由滑动，最终构型如图 6。
（2）运动过程模拟
背景网格采用边长为2 mm规则四边形单元，每个单元中有4个物质点，每个物质点之间的距离为1 mm，共计20000个，边界条件依据文献[15]进行设置，左边为对称边界条件，底部为摩擦边界条件，摩擦角$\delta $取为铝棒的摩擦角，即$\delta = \phi $，时间步长为20 μs。初始应力由${K_0}$[16-17]法计算生成，${K_0} = 1 - \sin (\phi )$，分别使用MPM-APIC和改进的MPM-APIC进行模拟。
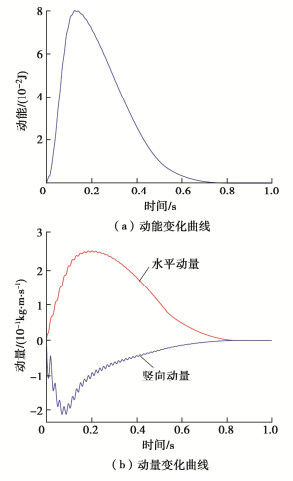
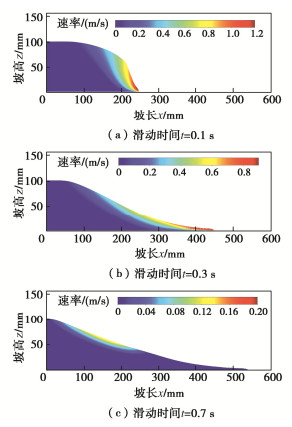
模拟过程中，铝棒的动能和动量变化曲线见图 7，图 8表示典型时刻堆积体的速率云图。由动能变化曲线可知，滑坡持续时间约0.8 s，体系的动能在0.16 s左右达到最大，最大速率为1.5 m/s，对应的动量变化曲线如图 7（b），水平动量和竖向动量呈现出不同的变化趋势。在开始阶段，竖向动量的增长速度远大于水平向，这是由于采用${K_0}$法计算初始应力场时，没有考虑到竖向沉降，导致竖向沉降在模拟开始的瞬间产生，竖向的动量也因此增长迅速，并且先于水平向动量达到极值；在动量逐渐减小的阶段，水平向动量减小的速度小于竖向，但二者均在同一时刻变为0，堆积体也重新归于稳定状态。
![]()
图 7 堆积体失效阶段动能和动量变化曲线Figure 7. Variation curves of kinetic energy and momentum of accumulation body in failure phase根据动能和动量的变化曲线可将滑坡分为：加速滑动阶段、减速滑动阶段和稳定阶段。加速滑动阶段持续时间最短，仅0.18 s左右，最大速率为$1.3{\text{ m/s}}$；减速滑动阶段持续时间最长，约0.6 s；在稳定阶段，$t = 0.7{\text{ s}}$时，坡脚速率降为$0$，坡体上部仍处在滑动状态，但速率非常小，最大约$0.15{\text{ m/s}}$，$t = 0.8{\text{ s}}$时，堆积体速率降为$0$，堆积体归于稳定。
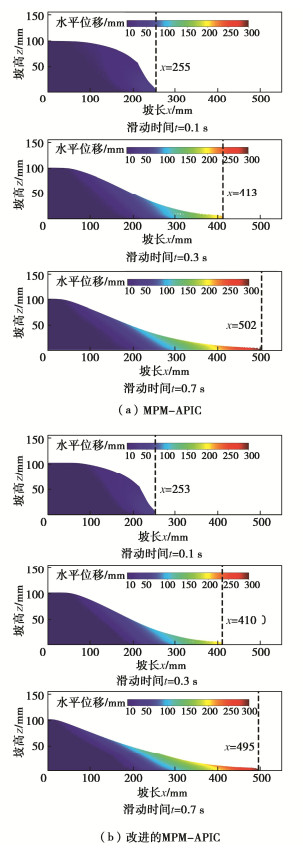
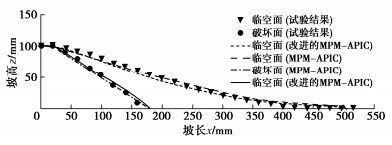
典型计算时刻铝棒堆积体的失稳形态与水平位移云图见图 9，图 10表示模拟得到的堆积体的最终构型与试验所得最终构型的对比，模拟得到破坏面曲线为等效塑性应变分界线。
![]()
图 9 失稳形态与水平位移云图Figure 9. Cloud chart of instability shape and horizontal displacement由图 9可知，在相同时刻，MPM-APIC和改进的MPM-APIC得到的模拟结果基本一致，并且与文献[18]一致，由图 10可知，在形貌上，二者又与试验结果相同，最大水平位移略小于试验结果，这是由于最前端的铝棒在地面上发生滚动导致的，排除掉这个因素的影响，可认为模拟结果与试验结果一致，充分证明了改进的算法的精度之高。
（3）计算效率对比
为说明本文中的程序在计算效率上的优势，将所用到的两个程序的计算耗时与Fortran语言编写的MPM程序进行对比，Fortran程序所运行的设备为3.0GHzCPU和3.2G内存计算机[5]，对比结果见表 2。
表 2 程序运行时间对比Table 2. Comparison of program running time程序 运行时间/s 时间比 物质点个数 MPM-APIC
(Taichi)28.66 1/62 20000 改进的MPM-APIC
(Taichi)13.18 1/130 20000 MPM（Fortran） 1791 3200 注：时间比由本文的程序运行时间除以MPM（Fortran）的运行时间得到。 由表 2可得，利用Taichi编写的物质点法程序，物质点个数为Fortran语言编写的MPM程序的6.25倍的情况下，MPM-APIC的计算效率为MPM（Fortran）的62倍，而改进的MPM-APIC的计算效率则达到MPM（Fortran）的130倍，暂不考虑计算机硬件的发展（本文的两个程序均在4.10GHzCPU、16G内存和RTX3060显卡的计算机上运行），对于同等计算量的MPM模拟，利用Taichi编写的程序计算效率可达Fortran语言的380倍以上，采用本文提出的改进的MPM-APIC方法，则计算效率可达800倍以上。
3. 边坡滑坡模拟
为了验证改进算法及程序在滑坡分析中的适用性，本文采用文献[17]的典型滑坡算例及计算参数进行对比验证。
3.1 边坡模型
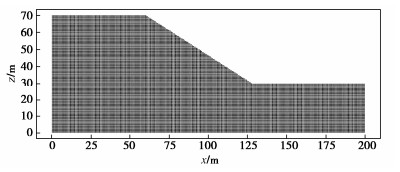
边坡模型和土体材料参数如图 11，模型底部和两侧的边界条件分别是固定边界条件、对称边界条件。物质点离散如图 12，背景网格单元的尺寸为1 m×1 m，每个网格内布置有4个物质点，相邻物质点的间距为0.5 m。
3.2 初始应力场
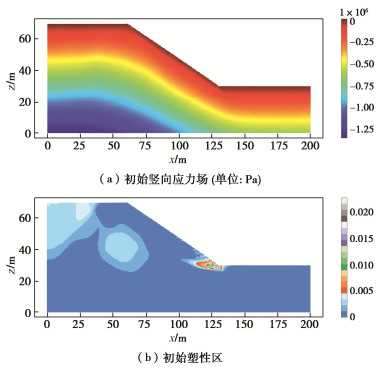
将重力线性加载，在10 s加载完成，得到稳定的初始竖向应力场和初始塑性区分布，如图 13所示，此时，施加运动阻尼，将所有节点的速度重置为0。模拟所得的结果与文献[17]的结果吻合的很好，最大竖向应力为1345 kPa，与文献中的结果相等，塑性区的大小和分布亦与之相同。
3.3 滑坡过程
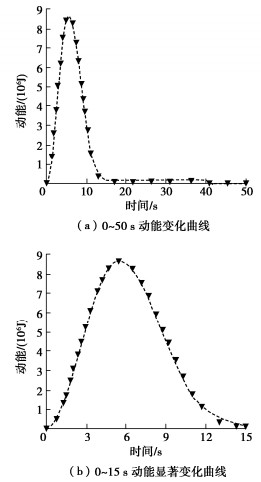
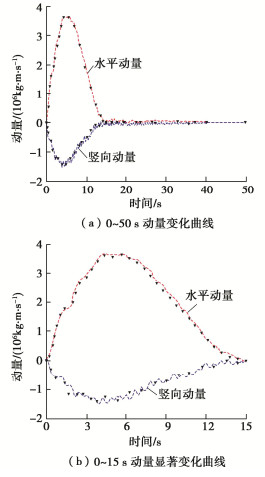
在边坡的初始状态求解完成之后，将土体的黏聚力$c$置为0来模拟暴雨诱发的滑坡。该阶段计算总时长为50 s，在40 s时，引入阻尼，使体系的动能归于0，达到稳定状态，时间步长取10-4 s，计算耗时240.3 s，计算平台与前文相同。滑坡阶段的动能和动量变化曲线如图 14，15。
图中，黑色的倒三角形代表的数据是文献[17]的结果，可以看出，改进的MPM-APIC程序完整的模拟了滑坡的整个过程，能够将滑坡的加速滑动、减速滑动以及稳定阶段3个阶段准确的模拟出来。动能在5.5 s左右达到最大，坡面土体的最大滑动速率对应的时刻稍微滞后于最大动能出现的时刻，约在6.4 s，最大值约等于8 m/s，与文献[17]的结果基本符合。
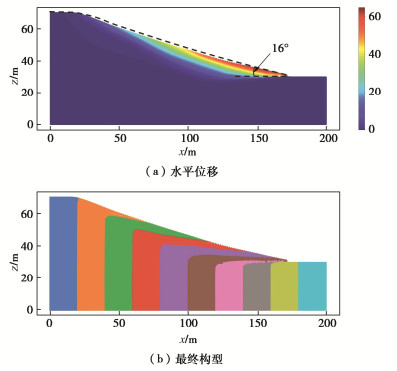
T = 15 s时，坡面基本停止滑动，仅在坡顶极小范围内有较大的速度，最大约1.5 m/s，此时的滑坡构型如图 16所示，水平位移云图如图 16（a）所示，黑色虚线是文献[17]的结果，轮廓与之基本吻合，坡脚为16°，小于土体的内摩擦角，最大水平位移为63.6 m，约是坡高的1.5倍；最终构型如图 16（b）所示，以上结果均与文献[17]吻合，该结果充分证明了改进的MPM-APIC在实际岩土工程问题中的适用性以及准确性。
4. 结论
本文将APIC的动量映射格式应用于经典MPM，通过推导，将仿射速度矩阵作为速度的梯度，简化物质点法，提出改进的MPM-APIC方法；利用高性能的Taichi编写可在GPU并行执行的物质点法程序。利用数值试验的方法验证其数值稳定性；利用数值试验与模型试验对比的方法验证其准确性和计算效率；基于对典型形状滑坡的全过程模拟验证其在实际岩土工程适用性及准确性，得出以下结论：
（1）2.4节中的算例表明，改进的MPM具有较高的数值稳定性，即使时间步长增加至20 ms，模拟依然能够稳定进行，这为大规模的高速运动滑坡灾害模拟分析提供了更高的可靠性和计算效率。
（2）MPM-APIC和改进的MPM-APIC均可准确的模拟出铝棒堆积体失稳破坏的全过程，且模拟结果与试验结果吻合地很好，证明改进的MPM的数值精度是可靠的。
（3）相较于Fortran语言，采用Taichi编程语言可将MPM算法的计算效率提高380倍，改进的MPM-APIC算法的则达到800倍以上，克服了物质点法计算耗时大的问题，为物质点法的程序实现提供了新的思路。
（4）对典型形状边坡的滑坡模拟表明：改进的MPM-APIC可以在短时间内准确模拟出滑坡的全过程，证明了改进算法和程序在实际岩土工程问题中的适用性及优势，在将程序打包为面向对象的程序之后，将会大大提高程序易用性和后续开发的便捷性。
-
![]()
图 7 堆积体失效阶段动能和动量变化曲线
Figure 7. Variation curves of kinetic energy and momentum of accumulation body in failure phase
![]()
图 9 失稳形态与水平位移云图
Figure 9. Cloud chart of instability shape and horizontal displacement
表 1 砂柱材料参数
Table 1 Material parameters of sand column
/(kg·m-3) E/MPa /kPa /(°) /(°) 2000 20 0.3 0 19.8 0 
下载: 导出CSV
表 2 程序运行时间对比
Table 2 Comparison of program running time
程序 运行时间/s 时间比 物质点个数 MPM-APIC
(Taichi)28.66 1/62 20000 改进的MPM-APIC
(Taichi)13.18 1/130 20000 MPM（Fortran） 1791 3200 注：时间比由本文的程序运行时间除以MPM（Fortran）的运行时间得到。
下载: 导出CSV
-
[1] 中国地质环境监测院地质灾害调查与监测室. 地质灾害调查与监测案例[EB/OL]. 中国地质环境信息网. Geological Disaster Investigation and Monitoring Office, Institute of Geological and Environmental Monitoring. Geological Disaster Investigation and Monitoring Cases[EB/OL]. China Geological Environment Information Site. (in Chinese)
[2] SULSKY D, CHEN Z, SCHREYER H L. A particle method for history-dependent materials[J]. Computer Methods in Applied Mechanics and Engineering, 1994, 118(1/2): 179–196.
[3] SOGA K, ALONSO E, YERRO A, et al. Trends in large-deformation analysis of landslide mass movements with particular emphasis on the material point method[J]. Géotechnique, 2016, 66(3): 248–273. doi: 10.1680/jgeot.15.LM.005
[4] BRACKBILL J U, KOTHE D B, RUPPEL H M. FLIP: a low-dissipation, particle-in-cell method for fluid flow[J]. Computer Physics Communications, 1988, 48(1): 25–38. doi: 10.1016/0010-4655(88)90020-3
[5] 张雄, 廉艳平, 刘岩. 物质点法[M]. 北京: 清华大学出版社, 2013. ZHANG Xiong, LIAN Yan-ping, LIU Yan. Material Point Method[M]. Beijing: Tsinghua University Press, 2013. (in Chinese)
[6] JIANG C, SCHROEDER C, SELLE A, et al. The affine particle-in-cell method[J]. ACM Transactions on Graphics, 2015, 34(4): 1–10. http://www.onacademic.com/detail/journal_1000038155784010_1b19.html
[7] HARLOW F H. Particle-in-cell computing method for fluid dynamics[J]. Methods Comput Phys, 1964, 3: 319–343. http://www.researchgate.net/publication/247939887_The_Particle-in-Cell_computing_method_for_fluid_dynamics
[8] HU Y M, FANG Y, GE Z H, et al. A moving least squares material point method with displacement discontinuity and two-way rigid body coupling[J]. ACM Transactions on Graphics, 2018, 37(4): 1–14. http://www.seas.upenn.edu/~cffjiang/research/mlsmpm/hu2018mlsmpm-tech.pdf
[9] HU Y, LI T M, Anderson L, et al. Taichi: a language for high-performance computation on spatially sparse data structures[J]. ACM Transactions on Graphics, 2019, 38(6): 1–16. http://www.researchgate.net/publication/337118128_Taichi_a_language_for_high-performance_computation_on_spatially_sparse_data_structures
[10] MAST C M. Modeling Landslide-Induced Flow Interactions with Structures Using the Material Point Method[D]. Washington: University of Washington, 2013.
[11] JIANG Y, LI M, JIANG C, et al. A hybrid material-point spheropolygon-element method for solid and granular material interaction[J]. International Journal for Numerical Methods in Engineering, 2020, 121(14): 3021–3067. doi: 10.1002/nme.6345
[12] BARDENHAGEN S G. Energy conservation error in the material point method for solid mechanics[J]. Journal of Computational Physics, 2002, 180(1): 383–403. doi: 10.1006/jcph.2002.7103
[13] KlÁR G, GAST T, PRADHANA A, et al. Drucker-Prager elastoplasticity for sand animation[J]. ACM Transactions on Graphics (TOG), 2016, 35(4): 1–12. http://web.cecs.pdx.edu/~fliu/seminar/flyer-teran.pdf
[14] MAST C M, ARDUINO P, MACKENZIE-HELNWEIN P, et al. Simulating granular column collapse using the material point method[J]. Acta Geotechnica, 2015, 10(1): 101–116. doi: 10.1007/s11440-014-0309-0
[15] BUI H H, FUKAGAWA R, SAKO K, et al. Lagrangian meshfree particles method (SPH) for large deformation and failure flows of geomaterial using elastic-plastic soil constitutive model[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2008, 32(12): 1537–1570. doi: 10.1002/nag.688
[16] 孙玉进. 岩土大变形问题的物质点法研究[D]. 北京: 清华大学, 2017. SUN Yu-jin. Research on Geotechnical Problems Involving Extremely Large Deformation Using the Material Point Method[D]. Beijing: Tsinghua University, 2017. (in Chinese)
[17] 孙玉进, 宋二祥. 大位移滑坡形态的物质点法模拟[J]. 岩土工程学报, 2015, 37(7): 1218–1225. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201507008.htm SUN Yu-jin, SONG Er-xiang. Simulation of large-displacement landslide by material point method[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1218–1225. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201507008.htm
[18] 吴方东, 张巍, 史卜涛, 等. 堆载诱发型土质滑坡运动特征物质点法模拟[J]. 水文地质工程地质, 2017, 44(6): 126–134. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201706020.htm WU Fang-dong, ZHANG Wei, SHI Bu-tao, et al. Run-out characteristic simulation of a surcharge-induced soil landslide using the material point method[J]. Hydrogeology & Engineering Geology, 2017, 44(6): 126–134. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201706020.htm
-
期刊类型引用(3)
1. 王曼灵，李树忱，周慧颖，王修伟，彭科峰，袁超. 基于改进对流粒子域插值物质点法的隧道大变形分析. 岩土工程学报. 2024(08): 1632-1643 . 
本站查看
2. 魏星，程世涛，谢相焱，陈睿. 考虑强度速率衰减效应的地震滑坡SPH-FEM模拟. 岩土工程学报. 2024(08): 1753-1761 . 本站查看
3. 吴锐，孙政，岳臣龙，何静怡，周晓敏. 基于蒙特卡洛物质点法的土质滑坡全过程风险定量评估. 力学与实践. 2023(04): 805-817 . 百度学术
其他类型引用(3)
计量
- 文章访问数: 234
- HTML全文浏览量: 46
- PDF下载量: 60
- 被引次数: 6
