循环交通荷载作用下饱和重塑黄土变形特性研究

翁效林; 胡继波; 贾阳; 周尚琪

doi:10.11779/CJGE202209006

循环交通荷载作用下饱和重塑黄土变形特性研究 English Version

1.
长安大学特殊地区公路工程教育部重点实验室, 陕西西安 710064
2.
河南省荥阳市住房和城乡建设局, 河南荥阳 450100

基金项目:

国家自然科学基金面上项目 51378004

详细信息

作者简介:
翁效林(1980—)，男，博士，教授，主要从事特殊土性状及地下工程研究。E-mail: 49768532@qq.com

通讯作者:
胡继波, E-mail: hujibo@chd.edu.cn

中图分类号: TU433
计量
- 文章访问数: 162
- HTML全文浏览量: 35
- PDF下载量: 75
出版历程
- 收稿日期: 2020-12-24
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-08-31

Deformation characteristics of saturated remolded loess under cyclic traffic loads

1.
Key Laboratory of Highway Engineering for Special Regions, Ministry of Education, Chang'an University, Xi'an 710064, China
2.
Housing and Urban-Rural Development Bureau of Xingyang City, Henan Province, Xingyang 450100, China

摘要

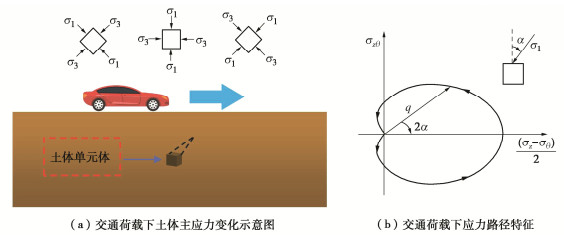
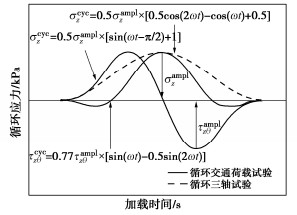
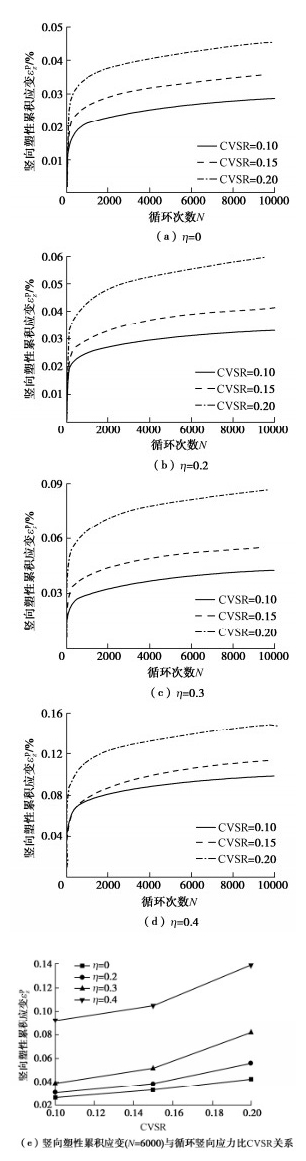
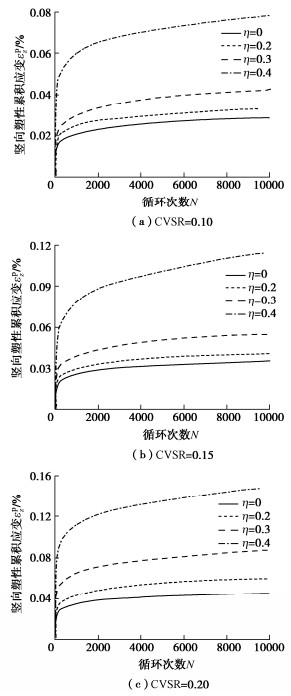
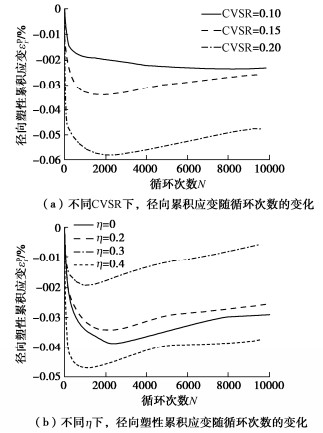
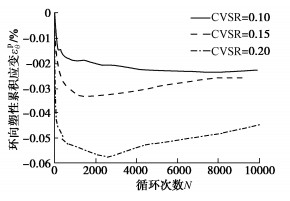
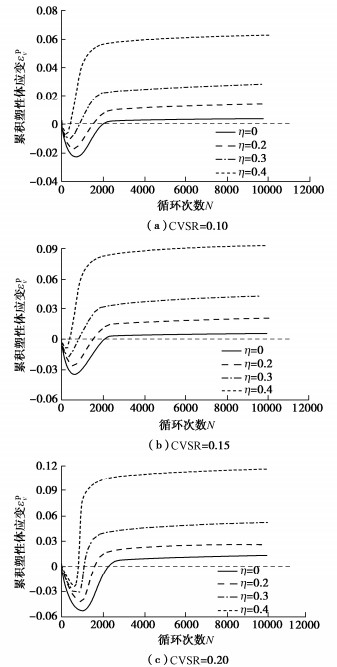
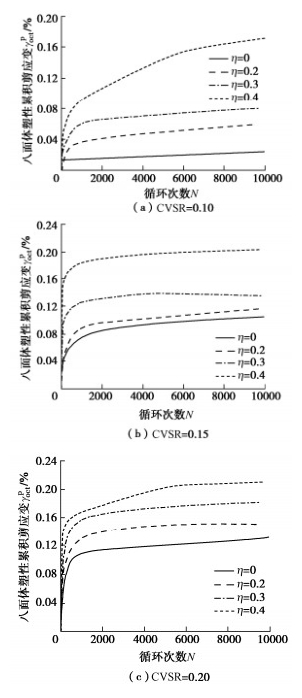
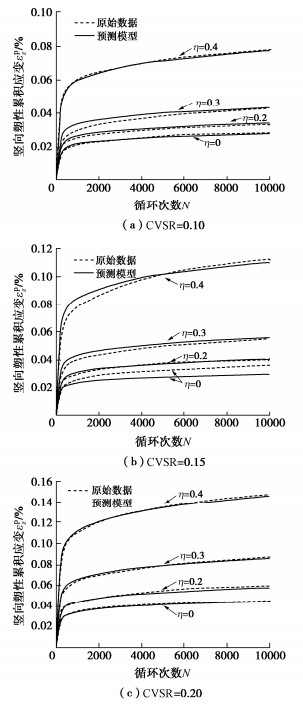
摘要: 为研究主应力轴旋转作用下饱和重塑黄土的变形规律，借助空心圆柱扭剪仪开展了排水状态下饱和重塑黄土的循环三轴试验和循环交通荷载试验，主要研究了主应力轴旋转对饱和重塑黄土的竖向塑性累积应变、径向塑性累积应变以及八面体塑性累积剪应变的影响。试验结果表明：①主应力轴旋转会使土体产生塑性累积变形；土样的竖向塑性累积变形和八面体塑性累积剪应变随循环次数增加呈对数型增长趋势，且循环竖向应力比和循环扭剪应力比与其呈正相关；径向塑性累积应变初期主要表现为拉应变形式，随荷载作用次数的增加，其值逐渐减小并向相反方向累积。②主应力轴旋转会加速相应的竖向塑性累积应变，在其他条件一定时，循环交通荷载作用下试样的变形量是循环三轴试验的数倍。③重塑黄土在交通荷载作用下竖向变形远远小于原状软黏土，作为路基填筑材料具有一定的优越性。④对现有的竖向塑性累积应变计算模型进行了修正，得到了饱和重塑黄土沉降变形的显式预测模型，并对该模型的有效性进行了分析验证。
- 主应力轴旋转 /
- 循环交通荷载试验 /
- 饱和重塑黄土 /
- 累积应变 /
- 沉降预测模型
Abstract: To study the deformation laws of saturated remolded loess under the rotation of principal stress axis, the cyclic triaxial tests and cyclic traffic load tests on the saturated remolded loess under drainage are carried out by using the hollow cylinder torsional shear apparatus, and the effects of the rotation of the principal stress axis on the vertical plastic cumulative strain, radial plastic cumulative strain and octahedral plastic cumulative shear strain of the saturated remolded loess are mainly studied. The experimental results show that: (1) The rotation of the principal stress axis will cause the plastic cumulative deformation of soil. The vertical plastic cumulative deformation and octahedral plastic cumulative shear strain of soil exhibit a logarithmic growth trend with the increase of the cyclic times, and the cyclic vertical stress ratio and cyclic torsional shear stress ratio are positively correlated with them. At the initial stage of the plastic cumulative strain, it is mainly in the form of tensile strain. With the increase of load times, its value gradually decreases and accumulates in the opposite direction. (2) The rotation of the principal stress axis will accelerate the corresponding vertical plastic accumulated strain. When other conditions are certain, the deformation of the samples under cyclic traffic loads is several times that of cyclic triaxial tests. (3) The vertical deformation of the remolded loess under traffic loads is far less than that of undisturbed soft clay, which has certain advantages as the subgrade filling materials. (4) The existing vertical plastic cumulative strain model is modified, and an explicit prediction model for the settlement deformation of saturated remolded loess is obtained, and the validity of the model is analyzed and verified.
- principal stress rotation /
- cyclic traffic load test /
- saturated remolded loess /
- accumulated plastic strain /
- settlement prediction model

HTML全文

0. 引言

粗粒土是一种常见的筑坝材料。粗粒土剪切过程中的颗粒破碎现象明显^[1],这是引起堆石坝发生变形的重要原因之一。随着中国超高坝的建设,越来越多的学者开始关注高应力作用下粗粒土颗粒的破碎特性^[2-5]。但是,由于试验条件的限制,宏观试验只能根据破碎前后的级配曲线演化来推断颗粒破碎程度。与宏观试验相比,近年来日益成熟的离散元法（discrete element method,简称DEM）数值模拟为从细观层面对粗粒土颗粒破碎进行研究提供了新途径^[6-10]。

在DEM数值模拟中,颗粒强度和弹性力学参数是模拟颗粒破碎以及颗粒—颗粒、颗粒—边界相互作用的重要材料特性,是影响数值模拟结果的关键因素之一。目前主流的细观参数标定方法,通常是先假定一组细观参数,通过对参数及其组合的调整使数值试样的宏观力学表现不断逼近土体的真实行为,直到数值试验与室内试验得到的宏观力学性质曲线基本接近时,认为该组细观参数已具备一定合理性,可以用于后续的数值计算中。这种依托于使用者经验的“试错法”需进行多次尝试并有一定的盲目性。考虑到DEM数值模拟建立在细观颗粒间相互作用的基础上,通过物理力学试验获得颗粒强度和弹性力学参数的真实分布规律,可以为DEM数值模拟的细观参数标定提供规律性方面的参考和支撑。

粗粒土的DEM数值模拟中需要考虑的细观参数主要是颗粒强度和弹性模量,关于它们的研究主要集中在两个方面。一是颗粒参数的离散性。以颗粒强度为例,比如McDowell等^[11-12]提出用Weibull分布来描述颗粒强度的分布特点,但是迟世春等^[13]对石灰岩颗粒进行相同试验之后却发现用该分布拟合颗粒强度离散性的效果不佳；另外还有张明等^[14]提出用对数正态分布来描述颗粒强度的随机性在实际应用上更为合理,米晓飞等^[15]用Logistic函数对颗粒强度的随机分布特点进行了描述。上述关于颗粒参数离散性分布特征的研究都是在确定某一特定分布函数后对试验结果进行拟合,对于结果缺少在不同分布类型之间的对比选优。二是颗粒参数的尺寸效应。目前对于颗粒强度的尺寸效应研究很多,结果表明粗粒土颗粒强度与颗粒尺寸之间存在着较强的相关性,这种相关性通常用幂函数关系来表示^[12-13,16]；而对于颗粒弹性模量的尺寸效应研究不多。总体来说,国内外学者对于粗粒土颗粒强度的研究已取得较为丰富的成果；虽然关于粒状材料的弹性力学参数的研究案例并不少^[17-21],但是对于粗粒土颗粒的弹性力学参数进行研究的先例却不多；目前,对于粗粒土颗粒的研究主要集中在粒径60 mm以下的小尺寸范围,得到的尺寸效应模型能否适用于更大的粒径范围也值得探究。

本文基于20～120 mm的粗粒土颗粒单轴压缩试验结果,确定颗粒强度和弹性模量,用统计学中的K-S检验法从Weibull分布、Lognormal分布和Logistic分布中分别比选出它们的最优分布类型,给出它们各自的尺寸效应经验模型。然后采用240 mm粗粒土颗粒的试验结果对提出的尺寸效应经验模型进行验证。最后对颗粒刚度的特点进行了初步讨论。

1. 试验材料和方法

本试验采用爆破开采得到的大连石灰岩颗粒,按照粒径大小依次记为①～⑧组,粒径分别为20～24 mm、24～28 mm、28～32 mm、32～36 mm、36～40 mm以及60 mm、120 mm和240 mm。其中,①～⑤组颗粒由常规筛分得到,⑥～⑧组颗粒用特制的圆孔筛（直径分别为60±5,120±5,240±5 mm）挑选得到。为了减少颗粒形状对参数的影响,选取的颗粒几何形状相似,并剔除针状、扁平状等特殊颗粒。

由于石灰岩颗粒不是完全规则的球形,其尺寸仅用筛孔大小难以准确描述。试验时是将颗粒稳定放置在下刚性板上,并且进行多次试放,找到竖直高度最短的稳定放置状态,定义此时的高度为短轴H,并以此稳定状态进行轴向加载；在与H垂直的横截面中,取最大径为长轴L,与L垂直方向上的最大径为中轴W。此处的L、W和H互相垂直,并且满足 $L \geq W \geq H$ 。颗粒尺寸用算术平均径 $d_{a}$ 来衡量,各组颗粒的特征粒径用该组颗粒的算术平均径的均值表示,颗粒形状用球度S_p来描述：

$d_{a} = (L + W + H) / 3$ ,

(1)

$S_{p} = {(L \cdot W \cdot H)}^{1 / 3} / L \times 100 %$ 。

(2)

本文选择的石灰岩颗粒样本的各项基本物理参数详见表1。由于本文试验中各组颗粒样本的球度接近,可以认为形状对各组的影响是相同的。

表 1 石灰岩颗粒的基本物理参数

Table 1. Basic physical parameters of limestone particles

编号	粒组/mm	个数	算数平均径d_a/mm	球度S_p/%	质量m/g
①	20~24	82	22.13±1.97	74.07±7.53	11.24±2.90
②	24~28	78	25.83±2.03	76.54±7.49	18.10±3.72
③	28~32	76	30.17±2.25	74.34±6.99	26.50±5.99
④	32~36	77	33.81±2.43	75.70±7.49	37.26±7.89
⑤	36~40	76	37.32±2.88	75.99±7.13	48.57±9.81
⑥	60	35	53.89±4.48	77.98±6.68	183.52±31.40
⑦	120	38	120.99±8.31	77.30±6.25	2532.56±2928.13
⑧	240	20	225.35±16.42	78.80±5.07	13357.50±1884.72
注：表中格式为“均值±标准差”。

下载: 导出CSV

| 显示表格

由于本文试验所用石灰岩颗粒的粒径范围大,为保证试验顺利进行,①～⑤组颗粒使用图1（a）所示装置进行单轴压缩试验,⑥～⑧组颗粒使用图1（b）所示装置进行单轴压缩试验。上述两种装置的试验原理相同,加载方式可以采用位移控制或力控制,试验过程相当于上、下两个平行的刚性平面挤压颗粒直至破碎。这两种装置只有最大加载能力和刚性平面最大间距存在区别。

图 1 试验装置示意图

Figure 1. Schematic diagram of test instrument

下载: 全尺寸图片幻灯片

试验前将颗粒在烘箱内连续干燥6 h以上。将颗粒置于两刚性板间,通过控制位移施加轴向荷载,加载速率取0.5 mm/min,试验过程中自动记录荷载和位移。当观察到颗粒发生主体破坏后便停止加载,主体破坏是指颗粒产生贯穿型裂缝或分裂为几块。颗粒破碎前后的情况如图2所示,其荷载–位移曲线如图3所示。由于颗粒形状的不规则性会引起颗粒与刚性板之间的接触点附近产生应力集中,造成颗粒的局部压裂或者棱角破碎,反映在荷载–位移曲线上为荷载突然跌落,曲线呈现锯齿状。

图 2 颗粒破碎前后的照片

Figure 2. Photos of a particle before and after breakage

下载: 全尺寸图片幻灯片

图 3 石灰岩颗粒的荷载–位移曲线

Figure 3. Force-displacement curve of limestone particles

下载: 全尺寸图片幻灯片

2. 颗粒强度和弹性模量的确定

2.1 颗粒强度指标的确定

石灰岩颗粒强度指标由下式计算^[22]：

$σ_{c} = \frac{F_{f}}{d^{2}}$ ,

(3)

式中, $σ_{c}$ 为颗粒强度指标, $F_{f}$ 为颗粒破坏荷载,d为颗粒粒径,此处取每个颗粒的实际受力长度,即两刚性板之间的距离。

2.2 颗粒弹性模量的确定

文献[23]介绍了一种建立在固体力学中计算接触应力的赫兹理论的基础之上,用于计算质地相对坚硬且均匀的粒状材料弹性模量的方法。该方法所使用的试验手段和材料变形过程都与本文的试验研究极为相似,两刚性板的挤压是导致颗粒材料发生变形直至最后破坏的驱动力,所以本文采用该方法对石灰岩颗粒的弹性模量进行了计算。

上述方法将受到两刚性板挤压的不规则颗粒（如图4所示）的荷载–位移关系用下式表示：

图 4 不规则颗粒受压示意

Figure 4. Diagram of compression on an irregular particle

下载: 全尺寸图片幻灯片

$F = \frac{E}{0.338 K (1 - ν^{2})} \cdot s^{3 / 2}$ 。

(4)

式中 $F$ 为轴向荷载； $s$ 为轴向荷载 $F$ 作用下的变形量； $ν$ 为泊松比,本文根据文献[24]中对各类岩石泊松比的汇总,假设石灰岩的泊松比 $ν = 0.25$ ； $E$ 为颗粒弹性模量；K为和颗粒接触点曲率有关的参数,引入该参数是因为颗粒表面粗糙导致接触点附近并非绝对光滑且连续,

$K = {[K_{U} {(\frac{1}{R_{U}} + \frac{1}{{R^{'}}_{U}})}^{1 / 3} + K_{L} {(\frac{1}{R_{L}} + \frac{1}{{R^{'}}_{L}})}^{1 / 3}]}^{3 / 2}$ 。

(5)

式中 ${R^{'}}_{U}$ , $R_{U}$ 分别为颗粒与上刚性板接触点处的最大和最小曲率半径； ${R^{'}}_{L}$ , $R_{L}$ 分别为颗粒与下刚性板接触点处的最大和最小曲率半径； $K_{U}$ , $K_{L}$ 为主曲率半径决定的常数,通过计算 $\cos θ$ ,可以从表2中对应查取, $θ$ 为颗粒表面与刚性板接触点处接触主平面的夹角（°）,根据赫兹接触理论有 $K_{U}$ 和 $K_{L}$ 分别对应的 $\cos θ$ 表达式为

表 2 不同的θ对应的K_U（K_L）值（节选）^[23]

Table 2. Values of K_U (K_L) for various values of θ (excerpts)^[23]

θ/(°)	50	55	60	…	80	85	90
cos θ	0.6428	0.5736	0.5000	…	0.1736	0.0872	0.0
K_U(K_L)	1.198	1.235	1.267	…	1.342	1.349	1.351

下载: 导出CSV

| 显示表格

$\begin{array}{l} K_{U} ： & \cos θ = (1 / R_{U} - 1 / {R^{'}}_{U}) / (1 / R_{U} + 1 / {R^{'}}_{U}) & , \\ K_{L} ： & \cos θ = (1 / R_{L} - 1 / {R^{'}}_{L}) / (1 / R_{L} + 1 / {R^{'}}_{L}) & 。 \end{array}}$

(6)

具体结合本文试验,石灰岩颗粒在自重下处于自稳定状态。可以认为颗粒与下刚性板之间近似面面接触,与上刚性板之间近似点面接触。这种情况下,颗粒与下刚性板接触点处的曲率 ${R^{'}}_{L} = R_{L} = \infty$ 。此时可以将式（4）具体写成

$F = \frac{E}{0.338 (1 - ν^{2}) {[K_{U} {(1 / R_{U} + 1 / {R^{'}}_{U})}^{1 / 3}]}^{3 / 2}} \cdot s^{3 / 2}$ ,

(7)

式中, ${R^{'}}_{U}$ , $R_{U}$ 由颗粒的L,W和H计算^[18]：

${R^{'}}_{U} = (L^{2} / 4 + H^{2}) / (2 H)$ ,

(8)

$R_{U} = (W^{2} / 4 + H^{2}) / (2 H)$ ,

(9)

继续将式（7）简写为

$F = C_{H} \cdot s^{3 / 2}$ ,

(10)

式中, $C_{H}$ 可以由颗粒破坏前的荷载–位移曲线拟合得到。因而,颗粒弹性模量E如下所示：

$E = 0.338 C_{H} (1 - ν^{2}) {[K_{U} {(\frac{1}{R_{U}} + \frac{1}{{R^{'}}_{U}})}^{1 / 3}]}^{3 / 2}$ 。

(11)

3. 数理统计和分析

3.1 参数的数理统计方法

本文首先采用格布拉斯准则^[25]检测样本中的异常值。设 $X = (X_{1}, X_{2}, \dots, X_{n})$ 是待检测数据,如果最值 $X_{i}$ 满足下式则为异常值,应予剔除。

$\frac{| X_{i} - \bar{X} |}{S} \geq G (N, α)$ 。

(12)

式中 $\bar{X}$ 和 $S$ 分别为样本均值和标准差； $G$ 为格拉布斯临界值,根据样本容量 $N$ 和显著性水平 $α$ 查表^[25]得到。在剔除某一异常值后,应继续对余下的样本点进行检测,直到没有异常值为止。

然后根据已有研究经验^[11-17],本文尝试用Weibull分布、Lognormal分布和Logistic分布对颗粒强度 $σ_{c}$ 和弹性模量E分别进行统计。

最后对于每个参数,使用K-S检验法^[26]定量地判断假设的概率分布类型是否合适,并从中确定最优分布形式。该方法通过将选定的分布类型的理论累积概率与观察到的经验累积概率进行比较,找出它们之间最大的差值,并参照抽样分布,给出这一差异是否处于偶然。如果两者较为接近,则表明实际样本的分布类型与假设的理论分布类型拟合程度很高。所有的统计分析均在显著性水平 $α = 0.05$ 的条件下进行,即置信度为95%。

3.2 参数的最优分布类型

采用式（3）,（11）对各粒组的颗粒强度 $σ_{c}$ 和弹性模量E进行整理,绘制参数统计直方图,并采用K-S检验法分别对3种假设分布类型进行了检验。其中,28～32 mm粒组的参数统计直方图和最优概率密度曲线如图5所示,限于篇幅,其他粒组略。各粒组的K-S检验结果详见表3,结果表明：①参数 $σ_{c}$ 和E对于Weibull分布、Lognormal分布和Logistic分布都可接受；②对参数 $σ_{c}$ 和E可以直接判定最优分布类型是Lognormal分布。

图 5 石灰岩颗粒参数统计直方图和最优概率密度曲线

Figure 5. Statistical histograms and optimal probability density functions of parameters for limestone particles

下载: 全尺寸图片幻灯片

表 3 石灰岩颗粒强度和弹性模量分布类型的K-S检验

Table 3. K-S test results of distribution types for strength and elastic modulus of limestone particles

编号	粒组/mm	颗粒强度					弹性模量
编号	粒组/mm	均值/MPa	分布形式	K-S值	判断	最优分布	均值/MPa	分布形式	K-S值	判断	最优分布
①	20~24	13.108	Weibull	0.085	满足	Lognormal	1005.193	Weibull	0.097	满足	Lognormal
			Lognormal	0.055	满足			Lognormal	0.073	满足
			Logistic	0.068	满足			Logistic	0.103	满足
②	24~28	12.389	Weibull	0.092	满足	Lognormal	1113.994	Weibull	0.095	满足	Lognormal
			Lognormal	0.062	满足			Lognormal	0.089	满足
			Logistic	0.096	满足			Logistic	0.092	满足
③	28~32	11.977	Weibull	0.078	满足	Lognormal	928.598	Weibull	0.073	满足	Lognormal
			Lognormal	0.056	满足			Lognormal	0.072	满足
			Logistic	0.089	满足			Logistic	0.085	满足
④	32~36	11.673	Weibull	0.128	满足	Lognormal	839.674	Weibull	0.100	满足	Lognormal
			Lognormal	0.112	满足			Lognormal	0.067	满足
			Logistic	0.126	满足			Logistic	0.084	满足
⑤	36~40	10.438	Weibull	0.084	满足	Lognormal	801.380	Weibull	0.102	满足	Lognormal
			Lognormal	0.040	满足			Lognormal	0.084	满足
			Logistic	0.077	满足			Logistic	0.126	满足
⑥	60	6.442	Weibull	0.113	满足	Lognormal	544.306	Weibull	0.135	满足	Lognormal
			Lognormal	0.079	满足			Lognormal	0.096	满足
			Logistic	0.089	满足			Logistic	0.138	满足
⑦	120	5.242	Weibull	0.103	满足	Lognormal	422.451	Weibull	0.169	满足	Lognormal
			Lognormal	0.048	满足			Lognormal	0.107	满足
			Logistic	0.076	满足			Logistic	0.143	满足
⑧	240	3.394	Weibull	0.117	满足	Lognormal	281.528	Weibull	0.125	满足	Lognormal
			Lognormal	0.084	满足			Lognormal	0.119	满足
			Logistic	0.126	满足			Logistic	0.121	满足

下载: 导出CSV

| 显示表格

3.3 参数的尺寸效应模型

为进一步研究颗粒强度和弹性模量与粒径的相关性,选择参数均值作为其代表值绘制于图6中。由图6可知这两个参数与颗粒尺寸之间存在着明显的非线性相关性。为了能够简单明了地描述这一关系,采用式（13）的幂函数表达式对这一关系进行了拟合,并且将拟合结果作为参数的尺寸效应经验模型,拟合结果详见表4。

图 6 石灰岩颗粒参数的尺寸效应曲线

Figure 6. Curves of size effect of parameters for limestone particles

下载: 全尺寸图片幻灯片

表 4 参数的尺寸效应模型

Table 4. Models for size effect of parameters

参数名称	代表值含义及符号	尺寸效应模型	r²	预测误差/%
颗粒强度	均值 $σ_{0}$	$σ_{0} =89 .71 {\bar{d}}_{a}^{- 0.606}$	0.92	0.58
弹性模量	均值 $E_{0}$	$E_{0} = 7351 {\bar{d}}_{a}^{- 0.615}$	0.91	6.61

下载: 导出CSV

| 显示表格

$y = λ {\bar{d}}_{a}^{n}$ 。

(13)

式中 $y$ 为待研究参数代表值； ${\bar{d}}_{a}$ 为颗粒算数平均径的均值； $λ$ 和 $n$ 为拟合参数。为了验证本文所给的参数尺寸效应经验模型是否准确,对240 mm的颗粒试验结果进行了预测,颗粒强度 $σ_{c}$ 、弹性模量E的预测值和试验值之间的相对误差分别为0.58%,6.61%,在可接受范围内。这表明,本文所给出的参数尺寸效应经验模型能够适用于更大的颗粒尺寸范围。尺寸效应经验模型的n值小于0说明大连石灰岩的颗粒强度和弹性模量的均值和颗粒尺寸之间呈负相关。该结果和前人统计结果一致^[12-13,17],同时弥补了对大尺寸不规则颗粒单轴压缩试验结果进行统计分析的空白。

4. 讨论

前文讨论了颗粒强度和弹性模量的随机分布规律和尺寸效应模型,除了上述两个参数外,颗粒刚度也是DEM数值模拟中需要考虑的重要参数之一。对于刚度的认识有两种：①认为刚度是线性的；②认为刚度是非线性的。而目前多把颗粒刚度看作是线性的。为了分析线性刚度和非线性刚度哪个更加符合实际情况,这里对石灰岩颗粒在破坏点之前的荷载—位移曲线进行了线性拟合（ $F = k s$ ）和非线性拟合（ $F = C_{H} s^{3 / 2}$ ）结果的对比,如图7所示。通过对每个颗粒线性拟合和非线性拟合结果的 $r^{2}$ 进行比较,发现本文试验有81.74%的颗粒用非线性拟合比线性拟合效果更好。这说明,在石灰岩颗粒受单轴压缩过程中,颗粒刚度用非线性来描述更加符合实际。

图 7 石灰岩颗粒荷载–位移曲线的线性拟合和非线性拟合结果对比

Figure 7. Comparison between linear fitting and nonlinear fitting results of load-displacement curves for limestone particles

下载: 全尺寸图片幻灯片

5. 结论

本文通过大量大连石灰岩颗粒单轴压缩试验,获得了颗粒强度和弹性模量的随机分布特征和尺寸效应经验模型,并对颗粒刚度的特点进行了初步讨论。这些统计结果反映了粗粒土颗粒在受力变形过程中的力学规律。建议在进行粗粒土DEM数值模拟时,对这些规律加以考虑。

（1）不仅粗粒土颗粒强度具有离散性,而且颗粒弹性模量同样具有离散性,该情况说明粗粒土颗粒在力学特性上表现出固有的离散性。

（2）大连石灰岩颗粒强度和弹性模量的最优概率分布类型是Lognormal分布。

（3）大连石灰岩颗粒强度和弹性模量的均值均与颗粒尺寸之间呈负相关,用幂函数拟合效果较好。可见,粗粒土颗粒强度和弹性模量都具有明显的尺寸效应。

（4）在石灰岩颗粒单轴压缩过程中,颗粒刚度用非线性来描述更加符合实际。

图 1 交通荷载作用下土体应力变化示意图

Figure 1. Schematic diagram of change of soil stress under traffic loads

下载: 全尺寸图片幻灯片

图 2 GDS空心圆柱扭剪仪

Figure 2. GDS hollow cylinder torsional shear instrument

下载: 全尺寸图片幻灯片

图 3 加载波形图

Figure 3. Diagram of loading waveform

下载: 全尺寸图片幻灯片

图 4 竖向塑性累积应变随竖向循环应力比变化

Figure 4. Variation of vertical plastic accumulated strain with cyclic vertical stress ratio

下载: 全尺寸图片幻灯片

图 5 竖向塑性累积应变随循环扭剪应力比变化

Figure 5. Variation of vertical accumulated strain with cyclic torsional shear ratio

下载: 全尺寸图片幻灯片

图 6 径向累积应变随CVSR和η的变化

Figure 6. Variation of radial accumulated strain with CVSR and η

下载: 全尺寸图片幻灯片

图 7 环向塑性累积应变随CVSR的变化

Figure 7. Variation of radial accumulated strain with CVSR

下载: 全尺寸图片幻灯片

图 8 累积塑性体应变随循环扭剪应力比变化

Figure 8. Variation of cumulative plastic volumetric strain with cyclic torsional shear ratio

下载: 全尺寸图片幻灯片

图 9 八面体塑性累积剪应变随循环扭剪应力比变化

Figure 9. Variation of vertical accumulated strain with cyclic torsional shear ratio

下载: 全尺寸图片幻灯片

图 10 不同应变形式的终值对比结果

Figure 10. Comparative results of final values in different strain forms

下载: 全尺寸图片幻灯片

图 11 重塑黄土与原状软黏土变形对比

Figure 11. Comparison of deformation between remolded loess and undisturbed soft clay

下载: 全尺寸图片幻灯片

图 12 试样竖向塑性累积应变与循环次数曲线

Figure 12. Curves of vertical plastic cumulative strain and cycle times of samples

下载: 全尺寸图片幻灯片

图 13 计算模型与试验数据比对图

Figure 13. Comparison between calculated results and experimental data

下载: 全尺寸图片幻灯片

表 1 土样物理指标

Table 1 Physical parameters of soil samples

含水率 /%	密度 /(g·cm^-3)	干密度 /(g·cm^-3)	相对质量密度	液限 /%	塑限 /%
14.2	2.07	1.83	2.71	13.8	18.9

下载: 导出CSV

表 2 试验方案

Table 2 Test programs

系列编号	试样编号	$\sigma _z^{{\text{ampl}}}$ /kPa	CVSR	$\tau _{z\theta }^{{\text{ampl}}}$ /kPa	η
Ⅰ	A1	20	0.10	0	0
	A2	30	0.15	0	0
	A3	40	0.20	0	0
Ⅱ	B1	20	0.10	4	0.2
	B2	20	0.10	6	0.3
	B3	20	0.10	8	0.4
	C1	30	0.15	6	0.2
	C2	30	0.15	9	0.3
	C3	30	0.15	12	0.4
	D1	40	0.20	8	0.2
	D2	40	0.20	12	0.3
	D3	40	0.20	16	0.4

下载: 导出CSV

参考文献(23)

[1]	LI J, SHAO S J, SHAO S. Collapsible characteristics of loess tunnel site and their effects on tunnel structure[J]. Tunnelling and Underground Space Technology, 2019, 83: 509–519. doi: 10.1016/j.tust.2018.08.035
[2]	WENG X L, SUN Y F, ZHANG Y W, et al. Physical modeling of wetting-induced collapse of shield tunneling in loess strata[J]. Tunnelling and Underground Space Technology, 2019, 90: 208–219. doi: 10.1016/j.tust.2019.05.004
[3]	王星博, 于洪钦, 王财平, 等. 西部寒区高速铁路路基沉降整治措施研究[J]. 路基工程, 2017(5): 53–58. https://www.cnki.com.cn/Article/CJFDTOTAL-LJGC201705012.htm WANG Xing-bo, YU Hong-qin, WANG Cai-ping, et al. Study on control measures for subgrade settlement of high-speed railway in cold regions of Western China[J]. Subgrade Engineering, 2017(5): 53–58. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LJGC201705012.htm
[4]	谷天峰. 郑西客运专线黄土地基振(震)陷研究[D]. 西安: 西北大学, 2007. GU Tian-feng. Study on Loess Seismic Subsidence and Dynamic Settlement of Roadbed of Zhengzhou-Xi'an Passenger Express Railway[D]. Xi'an: Northwest University, 2007. (in Chinese)
[5]	ZDRAVKOVIĆ L, POTTS D M, HIGHT D W. The effect of strength anisotropy on the behaviour of embankments on soft ground[J]. Géotechnique, 2002, 52(6): 447–457. doi: 10.1680/geot.2002.52.6.447
[6]	SIVATHAYALAN S, VAID Y P. Influence of generalized initial state and principal stress rotation on the undrained response of sands[J]. Canadian Geotechnical Journal, 2002, 39(1): 63–76. doi: 10.1139/t01-078
[7]	TOWHATA I, ISHIHARA K. Undrained strength of sand undergoing cyclic rotation of principal stress axes[J]. Soils and Foundations, 1985, 25(2): 135–147. doi: 10.3208/sandf1972.25.2_135
[8]	VAID Y P, A S Y, HOU E H, et al. Generalized stress-path-dependent soil behaviour with a new hollow cylinder torsional apparatus[J]. Canadian Geotechnical Journal, 1990, 27(5): 601–616. doi: 10.1139/t90-075
[9]	熊焕, 郭林, 蔡袁强. 交通荷载应力路径下砂土地基变形特性研究[J]. 岩土工程学报, 2016, 38(4): 662–669. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201604012.htm XIONG Huan, GUO Lin, CAI Yuan-qiang. Deformation behaviors of sandy subgrade soil under traffic load-induced stress path[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 662–669. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201604012.htm
[10]	钱建固, 杜子博. 纯主应力轴旋转下饱和软黏土的循环弱化及非共轴性[J]. 岩土工程学报, 2016, 38(8): 1381–1390. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201608004.htm QIAN Jian-gu, DU Zi-bo. Cyclic degradation and non-coaxiality of saturated soft clay subjected to pure rotation of principal stress axis[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(8): 1381–1390. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201608004.htm
[11]	沈扬, 周建, 张金良, 等. 考虑主应力方向变化的原状黏土强度及超静孔压特性研究[J]. 岩土工程学报, 2007, 29(6): 843–847. doi: 10.3321/j.issn:1000-4548.2007.06.009 SHEN Yang, ZHOU Jian, ZHANG Jin-liang, et al. Research on strength and pore pressure of intact clay considering variation of principal stress direction[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(6): 843–847. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.06.009
[12]	王钰轲, 万永帅, 方宏远, 等. 圆形应力路径下软黏土的动力特性试验研究[J]. 岩土力学, 2020, 41(5): 1643–1652. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202005023.htm WANG Yu-ke, WAN Yong-shuai, FANG Hong-yuan, et al. Experimental study of cyclic behavior of soft clay under circle stress paths[J]. Rock and Soil Mechanics, 2020, 41(5): 1643–1652. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202005023.htm
[13]	刘家顺, 张向东, 孙嘉宝, 等. 主应力轴旋转下K₀固结饱和粉质黏土孔压及变形特性试验研究[J]. 岩土力学, 2018, 39(8): 2787–2794, 2804. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201808010.htm LIU Jia-shun, ZHANG Xiang-dong, SUN Jia-bao, et al. Experimental study on the pore pressure and deformation of saturated silty clay under K₀ consolidation and principal stress axis rotation[J]. Rock and Soil Mechanics, 2018, 39(8): 2787–2794, 2804. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201808010.htm
[14]	扈萍, 魏超, 杨令强, 等. 主应力轴往复循环旋转下砂土的变形特性研究[J]. 地下空间与工程学报, 2018, 14(4): 955–961. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201804011.htm HU Ping, WEI Chao, YANG Ling-qiang, et al. Deformation behavior of sands under reciprocating cyclic principal stress rotation[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(4): 955–961. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201804011.htm
[15]	PRASANNA R, SINTHUJAN N, SIVATHAYALAN S. Effects of initial direction and subsequent rotation of principal stresses on liquefaction potential of loose sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(3): 04019130. doi: 10.1061/(ASCE)GT.1943-5606.0002182
[16]	YANG Z X, LI X S, YANG J. Undrained anisotropy and rotational shear in granular soil[J]. Géotechnique, 2007, 57(4): 371–384. doi: 10.1680/geot.2007.57.4.371
[17]	贾阳. 循环交通荷载下饱和重塑黄土应变及动力特性研究[D]. 西安: 长安大学, 2019. JIA Yang. Study on Strain and Dynamic Characteristics of Saturated Remoulded Loess under Cyclic Traffic Load[D]. Xi'an: Changan University, 2019. (in Chinese)
[18]	谌文武, 刘伟, 王娟, 等. 黄土饱和度与B值关系试验研究[J]. 岩土力学, 2019, 40(3): 834–842. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903002.htm CHEN Wen-wu, LIU Wei, WANG Juan, et al. Relationship between saturation degree and B value for loess[J]. Rock and Soil Mechanics, 2019, 40(3): 834–842. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201903002.htm
[19]	ASTM. Standard Test Method for Load Controlled Cyclic Triaxial Strength of Soil[S]. 2013.
[20]	HIGHT D W, GENS A, SYMES M J. The development of a new hollow cylinder apparatus for investigating the effects of principal stress rotation in soils[J]. Géotechnique, 1983, 33(4): 355–383. doi: 10.1680/geot.1983.33.4.355
[21]	CAI Y Q, GU C, WANG J, et al. One-way cyclic triaxial behavior of saturated clay: comparison between constant and variable confining pressure[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(5): 797–809. doi: 10.1061/(ASCE)GT.1943-5606.0000760
[22]	郭林. 复杂应力路径下饱和软黏土静动力特性试验研究[D]. 杭州: 浙江大学, 2013. GUO Lin. Experimental Study on the Static and Cyclic Behavior of Saturated Soft Clay under Complex Stress Path[D]. Hangzhou: Zhejiang University, 2013. (in Chinese)
[23]	MONISMITH C L, OGAWA N, FREEME C R. Permanent deformation characteristics of subgrade soils due to repeated loading[J]. Transportation Research Record, 1975(537): 1–17. http://www.researchgate.net/publication/279902408_PERMANENT_DEFORMATION_CHARACTERISTICS_OF_SUBGRADE_SOILS_DUE_TO_REPEATED_LOADING

施引文献(12)

期刊类型引用(4)

1.	罗仁宇，李奇志，祖公博，黄云进，杨耿超，姚清河. 基于卷积神经网络的超分辨率格子Boltzmann方法研究. 力学学报. 2024(12): 3612-3624 . 百度学术
2.	侯娟，滕宇阳，李昊，刘磊. 多孔介质曲折度对膨润土衬垫渗透性能的影响. 湖南大学学报(自然科学版). 2022(01): 155-164 . 百度学术
3.	陈经明，周泽超，陈茜茜，李寻，罗跃. 酸法地浸采铀多井系统中渗透系数时空演化模拟. 有色金属科学与工程. 2022(03): 106-116 . 百度学术
4.	吴志平，刘波平，王康，李石滨，胡毕炜，胡必伟，游杰. 基于高性能计算的离散介质冲击过程. 计算机与现代化. 2022(10): 41-46 . 百度学术