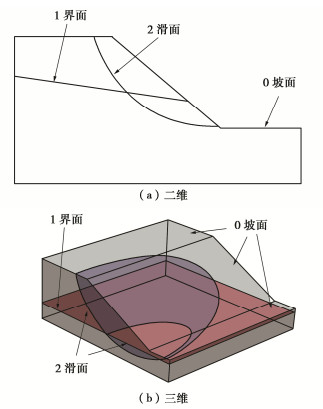
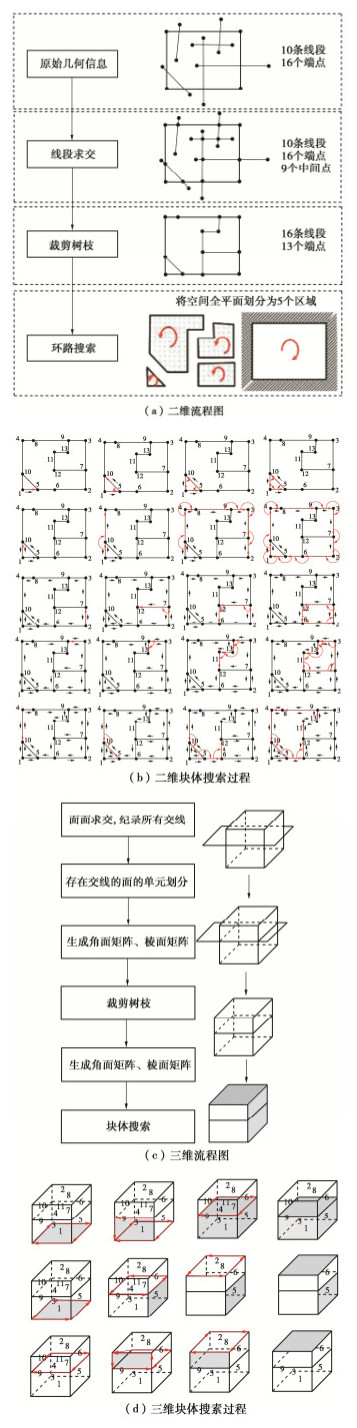
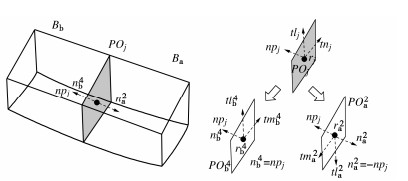
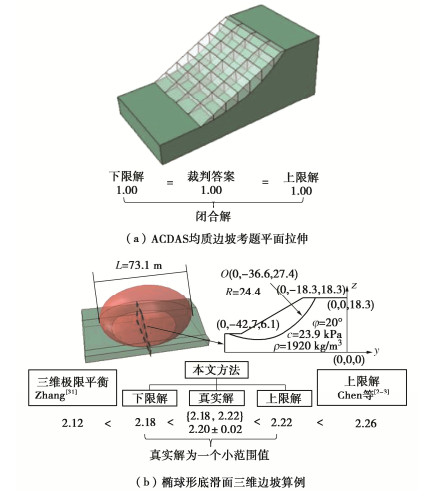
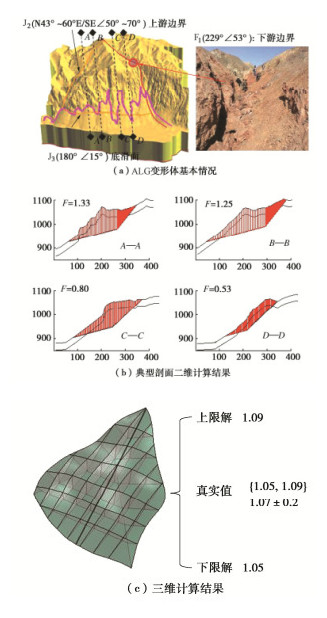
Limit analysis method for slope stability based on discretization of rigid blocks
-
摘要: 针对边坡稳定分析这一岩土力学的经典问题,放弃通过极限平衡等式方程和引入假定来直接求解边坡安全系数的传统思路,在建立边坡极限状态机构一般性构建方法的基础上,依据塑性力学上下限定理,以界面力或速度为主要变量,以应力许可静力场或运动许可位移场的基本要求为约束条件,在不引入任何假定的前提下,将求解边坡安全系数的问题转化为求解安全系数上限、下限解的优化数学问题,通过上下限值逐渐逼近安全系数,形成了完整统一的边坡稳定极限分析方法体系。该方法体系由于没有引入任何假定,不仅使边坡稳定分析方法具备了更为严密的理论基础,而且可方便地推广到三维领域。通过6个代表性算例验证了该方法计算结果的准确性、可靠性以及工程应用的合理性、可行性。Abstract: The classic slope stability analysis problem is solved by abandoning the traditional and direct solutions for safety factors of slopes, such as the limit equilibrium equation and the introduction of assumptions. Instead, the general construction method for constructing a slope limit state mechanism is adopted, and the plastic (upper and lower) limit theorems are taken into account. Moreover, taking the interfacial forces and velocities as the main variables and the basic requirements for statically admissible stress field or kinematically admissible displacement field as the constraints, and on the precondition that all assumptions are omitted, the solution for the safety factor problem of slopes is converted into an upper- and lower-bound optimization problem. Furthermore, a complete and united limit analysis method for slope stability is established by gradually shifting the upper- and lower-limit values toward the real solution for the safety factor. To conclude, the proposed method can provide a robust theoretical basis for slope stability analysis due to the omission of assumptions and address the bottleneck resulting from the method of expanding the 2D slope stability analysis to its 3D form. The accuracy and realiability of the calculated results as well as the rationality and feasibility of its engineering applications are validated through 6 representative examples.
-
Keywords:
- slope stability /
- limit analysis /
- upper and lower bound theorem /
- optimization model /
- solution
-
0. 引言
花岗岩残积土是近地表花岗岩经过长时间物理、化学风化后形成的未经搬运的土体[1],广泛分布在中国东南沿海地区,占闽、粤两省总陆地面积的30%~40%,是这些地区基础建设中经常遇到的一种特殊土[2]。花岗岩残积土组构特点介于砂性土和黏性土之间,力学特性比一般黏性土或砂性土更复杂[3]。残积土的变形和强度指标很容易受扰动的影响,通过室内土工试验获得的指标与真实力学状态存在一定差异,在进行设计参数选取时,取值往往偏于保守,影响了工程的经济性[4-7]。花岗岩残积土内部裂隙发育各异,颗粒组成也有明显差异,在钻探取样、运输和制样过程中容易受到扰动而引起结构性破坏,采用室内试验确定其真实的力学参数难度较大,故对相关地层开展原位试验具有重要意义[8]。
土体的力学本构模型研究是土力学的一项重要课题[9]。近几十年来,诸多本构模型被引入土力学的研究中。例如:莫尔–库仑强度破坏准则[10]、Druker-Prager屈服准则[11]、Duncan-Chang双曲线模型[12]、弹塑性Cam-clay模型及其改进的UH系列模型[13-14]、由黄文熙提出的弹塑性模型[15]以及由沈珠江构建的理想脆弹塑性模型[16]等。Duncan等提出的邓肯–张双曲线模型材料常数少,物理意义明确,在岩土工程中得到了广泛应用[17]。土力学中的参数反演分析是基于实测的应力应变关系反求其力学模型参数的方法。目前,采用原位试验进行本构模型参数反演分析的研究成果还比较罕见。其中,李广信[18]采用原位旁压测试技术进行了推求了邓肯–张双曲线模型的参数;刘小生等[19]联合室内试验、旁压试验和现场载荷试验对双曲线模型进行了反演分析。上述方法由于无法直接从原位应力–应变关系的角度求解模型参数,存在诸多的假定和经验公式。目前获取邓肯–张模型参数的常规方法仍然是室内三轴剪切试验[20]。孔内剪切试验(borehole shear test,简称BST)是一种新型原位测试手段,可以对钻孔内不同深度土层直接进行剪切试验[21]。近年来,国内外学者对于BST测试已经开展了一系列实践研究,BST在土体力学参数的确定中得到了诸多应用[22-24],但利用BST结果反演土体本构模型参数的研究还未见报道。
残积土工程性质的空间变异性较为明显,其干密度、渗透性、孔隙度、微结构、变形模量、抗剪强度和应力–应变关系等各项物理力学性质,均与风化层的埋深有重要关系[25-27]。采用BST测试探究残积土在不同风化程度下的力学行为变异规律有助于加深花岗岩风化层工程特性的认识和理解。此外,土体的应力–应变关系综合反映了其强度和变形特性,通过引入本构理论建立BST应力–应变关系模型,可以为风化程度影响下的力学行为演化特点提供进一步参考。因此,通过BST确定广义邓肯–张本构模型参数,建立反映风化程度影响的应力–应变关系模型,对花岗岩残积土力学行为的研究具有重要意义。
本文以厦门市某地铁站基坑工程为背景,在花岗岩残积土地层中开展多组原位孔内剪切试验,基于测试结果反演了广义邓肯–张模型参数,并评价了物理风化程度对修正模型的影响,最后与实测结果进行对比以验证模型的合理性。
1. 场地地质条件与试验方法
1.1 残积土基本物理性质指标
原位孔内剪切试验和现场取样的场地位于厦门市地铁一号线沿线的一处典型残积土基坑地层。整平场地后通过钻探1个鉴别孔确定土层分布规律,获取了杂填土、残积土、全风化岩、强风化岩的厚度,本场地的残积土分布在地下3.5~20 m。采用钻探取样法沿深度方向自上而下地对残积土地层进行连续取样,直到取至强风化岩层。试样取出后用不锈钢样盒承装,用密封胶带包裹后立即封腊,运至实验室。对取回的试样开展基本物理性质的测试。
土体基本物理性质指标如表1所示,随深度增加,土体的天然密度和砾粒含量有增加趋势,渗透系数有减小的趋势。由图1(a)所示的XRD衍射图谱发现厦门花岗岩残积土内除含有大量石英颗粒外,母岩的矿物成分基本风化为高岭石与伊利石,另含有微量的赤铁矿,其中,石英含量为53.6%,高岭石含量为38.5%,伊利石含量为5.2%,赤铁矿含量为2.5%。花岗岩残积土在不同深度处的颗粒级配结果如图1(b)所示,可以看出该场地残积土的级配曲线呈明显的阶梯状,粗粒和黏粒含量较多,中间粒径含量较少,根据颗粒级配特点认为残积土是一种介于黏性土和砂性土性质之间的中间土[28]。由现场钻探的结果,场地地下水位在-3.2 m左右,认为被测残积土为饱和土,从含水率分布特征也可以看出土体的含水率差异不大。
表 1 土的基本物理力学性质指标Table 1. Basic physical and mechanical properties of soil埋深/m 相对密度Gs 天然密度ρ/(g·cm-3) 孔隙比e0 含水率/% 液限/% 塑限/% 塑性指数 渗透系数/(10-6m·s-1) 砾粒含量G/% 3.8 2.73 1.75 0.74 26.7 48.3 27.2 21.1 7.12 17.3 5.6 2.72 1.75 0.77 26.4 44.8 25.5 19.3 5.17 16.5 7.0 2.71 1.78 0.78 27.0 47.9 24.5 23.4 5.32 19.0 8.0 2.73 1.81 0.75 30.4 50.2 24.2 26.0 5.01 18.9 9.2 2.73 1.75 0.84 26.7 48.5 27.1 21.1 5.12 19.9 10.0 2.72 1.75 0.77 26.4 44.8 25.5 19.3 4.97 19.4 11.0 2.71 1.77 0.80 28.1 45.2 25.2 20.0 4.50 20.5 12.2 2.71 1.78 0.78 27.0 48.2 24.1 24.1 3.92 20.7 13.2 2.73 1.81 0.75 30.4 50.1 24.2 25.9 4.01 22.5 15.0 2.73 1.75 0.84 26.7 48.4 27.3 21.1 3.42 23.8 16.2 2.72 1.75 0.77 26.4 44.3 25.5 18.8 3.17 24.6 18.2 2.71 1,78 0.78 27.0 48.0 24.5 23.5 3.32 24.5 1.2 风化程度指标
在复杂的成土过程中,受控于气候主导下的温度与降水变化,母岩经过漫长时间的风化作用后在地表广泛堆积成残积土。随着母岩矿物的不断发生物理、化学反应,成土体系内的颗粒组成也会随之改变[29]。母岩经历的风化作用越剧烈,则残积土的黏土化程度越高,土颗粒越细,在颗粒组成上表现为粗颗粒含量随物理风化程度提高而下降的现象[30]。在同一场地的地层中,风化程度总是由深至浅地逐渐提高[31]。作为残积土粒径分布特征的重要参数,砾粒含量G随土体深度增加保持上升趋势。因此,砾粒含量G的大小在一定程度上反映了花岗岩残积土的物理风化程度。
1.3 原位孔内剪切试验
试验采用的仪器为美国生产的Iowa原位孔内剪切测试仪,示意图如图2所示。仪器主要由剪切探头、剪切盘、压力表、压力控制箱以及压力气源等部分组成。BST试验具有操作方便,可重复性高,适用性广和无须取样等优点。使用BST剪切仪进行测试对土体的扰动大大降低,测试结果更加接近土体的本真力学属性。虽然BST结果反映了探头与土之间界面的强度特征,但参照十字板剪切试验的方法及原理,可以近似地认为BST试验测得的结果可以表征土体的强度特性[32]。
试验前,首先利用钻机钻取直径为76 mm的孔。然后在钻孔的地表位置安装好底座,将探头放置在预定深度。测试点分布在4~18 m的地层中,每组剪切各进行25,50,100和200 kPa 4组法向应力的固结作用。剪切时,先施加气压使得两个独立不锈钢剪切盘受压张开后对土体进行法向固结15 min;固结完成后匀速转动摇杆向上提拉探头对孔壁土体进行剪切,同时读取压力表的读数;待压力表读数基本稳定后卸除法向和轴向的压力,将探头向下移动10 cm后进行下一次剪切的法向固结。试验中为了满足剪切时的排水条件,剪切速率保持在0.5 mm/min左右。
已知被测残积土均在地下水位线以下,为饱和土,故不考虑饱和度对土体性质的影响。由于剪切探头与孔壁土体接触的土样长度l为50 mm,由此可以获得变形过程中的广义剪应变
ε ,如下所示:ε=δvl, (1) 式中,
δv 为竖向剪切位移(mm),l为土体剪切段的长度(mm)。2. BST试验结果
2.1 应力应变曲线
由BST试验得到了4~18 m深度范围内的残积土广义剪应力
τ 与广义剪应变ε 的关系曲线,结果如图3所示。当土体埋深相同时,剪切强度值随固结压力的上升而增加,且不同法向固结应力作用下的τ –ε 曲线均呈弱硬化变形特征。具体变现为:在剪应力加载的初期,残积土应力–应变关系近似处于线弹性变形,剪应力随剪应变增大呈直线上升;进入非线性变形阶段后,剪应力随应变增加的上升斜率逐渐减小,直至趋于稳定。另外,花岗岩残积土的应力–应变关系曲线受土体深度的影响非常显著。同一固结压力下的剪应力随深度增加而明显提高。2.2 抗剪强度参数
按照莫尔–库仑强度破坏准则,以剪切强度
τf 为纵坐标,以法向应力σn 为横坐标绘制花岗岩残积土的强度包络线,结果如图4所示。可以看出不同深度下的土体强度包络线近似保持线性增长趋势,其相关系数均达到了0.93以上。通过回归分析可以计算不同深度处下花岗岩残积土的抗剪强度参数,即内摩擦角和黏聚力指标。根据图4所示的剪切强度与法向应力的关系,经计算得到了基于BST测试的花岗岩残积土内摩擦角
φ 和黏聚力c 。下面分析风化程度对抗剪强度参数的影响,以砾粒含量G为横坐标,分别以黏聚力c 和内摩擦角φ 分别作为纵坐标,建立强度参数和风化程度指标的关系,结果如图5所示。不同颜色标记数据点反映了土体的埋深,标记颜色与深度的关系如图例所示。从如图5(a),(b)可以看出,花岗岩残积土的黏聚力、内摩擦角与砾粒含量均符合线性函数特征,且c 随G增加呈上升趋势,φ 随G增加呈下降趋势。可以看出随着花岗岩残积土的深度的增加,砾粒含量下降,即物理风化程度逐渐降低,从而导致内摩擦角呈线性减小趋势,黏聚力呈线性上升趋势。究其原因,物理风化程度上升一方面改变了土颗粒之间的接触关系,砾粒颗粒间的咬合摩擦力减小,使内摩擦角减小;另一方面,黏土矿物含量的增加促进黏粒间化学键强度发挥作用,使得黏聚力增大。3. 基于BST的广义邓肯-张模型
3.1 广义邓肯-张模型的适用性验证
(1)广义邓肯–张模型介绍
邓肯–张模型是一种能够通过改进以灵活反映不同测试条件、荷载和边界条件等因素影响的土体本构模型[33]。在土力学本构模型研究中,传统邓肯–张模型参数采用三轴剪切试验结果确定。三轴试验是一种有侧限的压缩,侧向固结压力在剪切过程中始终保持不变。BST也是在一定法向应力作用下的剪切变形过程,与三轴试验在受力模式和边界条件有相似的地方。基于以上分析,本文借鉴前人采用三轴试验结果分析邓肯–张模型的方法,采用比拟的思路获取了基于BST结果的广义邓肯–张模型参数。求取模型参数时,采用BST试验的法向应力
σn 取代三轴试验中的围压σ3 ;采用广义剪应变ε 取代轴向应变ε1 ,采用剪应力τ与取代偏应力q。另外,由于孔内剪切试验没有进行侧向变形的量测,对切线泊松比的验证是近似的。然而根据李广信的研究[18],大部分工程问题接近于平面应变问题,在确定本构模型参数时,建议用平面应变试验得到的指标代替三轴试验的指标。BST本质上是一种平面应变问题,无法测量侧向应变的缺陷对模型参数的影响不大。根据邓肯–张模型,土体在剪切过程中的广义剪应力和应变符合如下所示的关系:
τ=εa+bε, (2) 式中,τ为剪应力,
ε 为剪切沿孔壁轴线方向的应变,a为初始切线模量Ei的倒数,b为极限剪切强度τult的倒数。由初始切线模量与法向压力之间的指数关系,得到土体初始切线模量Ei的表达式如下:Ei=Kpa(σnpa)n, (3) 式中,K和n为计算初始切线模量的拟合常数,pa为大气压力,取101.3 kPa,
σn 为法向应力。前人在式(3)的基础上提出了土体在剪切过程中的切线模量表达式如下所示。此公式可以用于计算基于的邓肯–张本构模型的BST试验应力–应变关系。
Et=Kpa(σnpa)n(1−τRfτf)2, (4) 式中,Et为切线模量,Rf为破坏比。
Rf=τfτult, (5) 式中,τf为土体的破坏强度,τult为土体的极限剪切强度,在数值上等于公式(2)中b值的倒数,Rf的值一般介于0.5~1。
根据莫尔–库仑强度准则,可由抗剪强度参数,即黏聚力和内摩擦角指标求取土体的破坏强度
τf ,表达式如下:τf=2ccosφ+2σnsinφ1−sinφ。 (6) 为了验证基于邓肯–张模型的切线模量表达式在描述孔内剪切试验结果中的适用性,就必须先验证其推导过程中所采用公式与假定的合理性,即验证公式(2)与(3)的合理性。首先将式(2)转换为下式:
ετ=1Ei+ετult, (7) 则由式(7)的线性拟合关系式可以获得
Ei 和τult 的值。对式(3)的两边取对数得
lg(Eipa)=lgK+n⋅lg(σnpa)。 (8) 因此,通过将邓肯–张模型适用性条件转化为对
ετ –ε 与lg(EiPa) –lg(σnPa) 之间线性关系的验证[33]。(2)
ετ –ε 关系验证下面以4,7,9,12,15和18 m深度处的结果为例,根据应力–位移曲线获取不同深度处花岗岩残积土的
ετ –ε 关系曲线,结果如图6所示。从图中可以看出,不同固结压力下的花岗岩残积土在剪切过程中ετ 与ε 近似呈现线性关系,表明应力τ 与应变ε 之间符合双曲线关系。(3)
lg(Eipa) –lg(σnpa) 关系验证由式(7)获得了不同固结压力下的初始切线模量
Ei ,由图7可以看出lg(Eipa) –lg(σnpa) 之间的线性关系良好,说明采用BST确定的Ei满足邓肯–张模型的适用性条件。3.2 邓肯-张模型参数分析
通过对试验数据进行处理,计算了花岗岩残积土邓肯–张模型的5个参数(c,φ,K,n和Rf),结果如表2所示。为了分析物理风化程度对模型参数的影响规律,采用砾粒含量G作为自变量,分别以K,n和Rf作为因变量,进行回归分析,结果如图8所示。发现花岗岩残积土的广义邓肯–张模型参数随砾粒含量变化均呈一定规律性,其中参数K与G保持正相关的线性关系;参数n与G保持二次函数的关系,随砾粒含量上升,参数n先增加后减小;参数Rf与G保持负相关的线性关系。因此,以砾粒含量为影响因子计算的5个待定参数可以根据相关函数表达式进行合理的预测。
表 2 广义邓肯-张模型参数Table 2. Parameters of generalized Duncan-Chang model深度/m 模型参数 c /kPaφ /(°)K n Rf 4 18.2 25.1 3.19 0.356 0.913 5 23.1 23.6 3.36 0.347 0.909 6 19.7 24.4 3.34 0.382 0.918 7 28.5 27.0 3.51 0.374 0.871 8 28.0 29.4 3.55 0.392 0.882 9 27.1 28.1 3.60 0.399 0.832 10 26.5 31.8 3.54 0.397 0.795 11 26.0 32.1 3.62 0.409 0.813 12 25.0 33.8 3.60 0.382 0.795 13 23.4 33.2 3.65 0.418 0.773 14 22.9 33.6 3.70 0.372 0.752 15 21.6 36.3 3.69 0.371 0.785 16 20.9 38.1 3.72 0.355 0.781 17 18.8 43.2 3.78 0.375 0.752 18 18.1 41.9 3.82 0.384 0.756 3.3 实测结果与模型计算结果的对比
在广义邓肯–张本构的模型参数后,土体的应力–应变关系可以表示为
τ=ε1Ei+ε⋅Rfτf。 (9) 下面对花岗岩残积土BST试验的实测数据与邓肯–张模型的拟合曲线进行对比分析,结果如图9所示。可以看出采用广义邓肯–张模型计算的应力–应变曲线与BST测试结果较为吻合,相对误差较小。就拟合结果而言,利用BST结果有有效地反演土体广义邓肯–张本构模型参数,同时可以反映物理风化程度对其力学行为的影响。由于孔内剪切试验更能准确地反映土体原位力学特性,其得到的结果对实际工程参数选取具有很好的参考价值。
4. 结论
(1)由原位孔内剪切试验结果发现在不同法向压力下,花岗岩残积土应力–应变关系曲线均呈现应变硬化型。土体的剪切强度随法向应力增加而上升,用线性方程可以对两者的关系进行拟合。随土层深度增加,土体剪切强度明显提高。
(2)通过对BST得到的力学参数进行回归分析,发现随着砾粒含量G的上升,广义邓肯–张模型参数中的黏聚力c和参数K呈直线型下降;内摩擦角和应力破坏比Rf呈直线型上升;参数n先增加后减小,且与G保持二次函数关系,说明物理风化程度对广义邓肯–张模型参数有显著影响。
(3)以砾粒含量为影响因子建立了基于BST结果的广义邓肯–张本构模型,得到的原位应力–应变关系的拟合曲线与实测数据具有较好的吻合度,验证了采用广义邓肯–张模型反映残积土力学行为的有效性。
(4)基于BST的广义邓肯–张模型研究不仅加深了对残积土力学行为的认识,也扩大了邓肯–张模型在土力学中的适用范围,为土体原位力学本构关系的研究奠定了基础。
-
表 1 ALG变形体主要材料工程力学特性参数
Table 1 Parameters of ALG deformation body
F1 J2 J3 岩石 c
/kPa
/(°)c
/kPa
/(°)c
/kPa
/(°)c
/kPa
/(°)
/(kg·m-3)20 16.7 70 25.6 70 25.6 175 32 2500 -
[1] 周健, 崔积弘, 贾敏才, 等. 静力触探试验的离散元数值模拟研究[J]. 岩土工程学报, 2007, 29(11): 1604–1610. doi: 10.3321/j.issn:1000-4548.2007.11.002 ZHOU Jian, CUI Ji-hong, JIA Min-cai, et al. Numerical simulation of cone penetration test by discrete element method[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1604–1610. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.11.002
[2] CHEN Z Y, WANG X G, HABERFIELD C, et al. A three-dimensional slope stability analysis method using the upper bound theorem part I: theory and methods[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 369–378. doi: 10.1016/S1365-1609(01)00012-0
[3] CHEN Z Y, WANG J, WANG Y J, et al. A three-dimensional slope stability analysis method using the upper bound theorem Part II: numerical approaches, applications and extensions[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 379–397. doi: 10.1016/S1365-1609(01)00013-2
[4] 陈祖煜, 弥宏亮, 汪小刚. 边坡稳定三维分析的极限平衡方法[J]. 岩土工程学报, 2001, 23(5): 525–529. doi: 10.3321/j.issn:1000-4548.2001.05.001 CHEN Zu-yu, MI Hong-liang, WANG Xiao-gang. A three-dimensional limit equilibrium method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 525–529. (in Chinese) doi: 10.3321/j.issn:1000-4548.2001.05.001
[5] JANBU N. Application of composite slip surface for stability analysis[C]// Proceedings of Europan Conference on Stability of Earth Slopes, Stockholm, Sweden, 1954.
[6] BISHOP A W. The use of the slip circle in the stability analysis of slopes[J]. Géotechnique, 1955, 5(1): 7–17. doi: 10.1680/geot.1955.5.1.7
[7] MORGENSTERN N R, PRICE V E. The analysis of the stability of general slip surfaces[J]. Géotechnique, 1965, 15(1): 79–93. doi: 10.1680/geot.1965.15.1.79
[8] SPENCER E. A method of analysis of the stability of embankments assuming parallel inter-slice forces[J]. Géotechnique, 1967, 17(1): 11–26. doi: 10.1680/geot.1967.17.1.11
[9] HOEK E, BRAY J W. Rock slope engineering[M]. London: The Institution of Mining and Metallurgy, 1977.
[10] SARMA S K. Stability analysis of embankments and slopes[J]. Journal of the Geotechnical Engineering Division, 1979, 105(12): 1511–1524. doi: 10.1061/AJGEB6.0000903
[11] WANG X G, LIN X C, LI X, et al. 3D slope stability analysis method based on Pan's maximum principle[J]. Landslides, 2020, 17(5): 1163–1176. doi: 10.1007/s10346-019-01303-7
[12] WANG X G, LIN X C, LI X, et al. 3D slope stability analysis method based on Pan's maximum principle[J]. Landslides, 2020, 17(5): 1163–1176. doi: 10.1007/s10346-019-01303-7
[13] 冯树仁, 丰定祥, 葛修润, 等. 边坡稳定性的三维极限平衡分析方法及应用[J]. 岩土工程学报, 1999, 21(6): 657–661. doi: 10.3321/j.issn:1000-4548.1999.06.005 FENG Shu-ren, FENG Ding-xiang, GE Xiu-run, et al. 3D limit equilibrium method for slope stability and its application[J]. Chinese Journal of Geotechnical Engineering, 1999, 21(6): 657–661. (in Chinese) doi: 10.3321/j.issn:1000-4548.1999.06.005
[14] 郑榕明, 朱禄娟, 谷兆祺. 非对称旋转破坏的三维Bishop边坡稳定算法[J]. 岩土工程学报, 2002, 24(6): 706–709. doi: 10.3321/j.issn:1000-4548.2002.06.007 CHENG Yung-ming, ZHU Lu-juan, GU Zhao-qi. Rotational failure of 3D non-symmetric slope predicted by Bishop's method[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(6): 706–709. (in Chinese) doi: 10.3321/j.issn:1000-4548.2002.06.007
[15] 张均锋, 王思莹, 祈涛. 边坡稳定分析的三维Spencer法[J]. 岩石力学与工程学报, 2005, 24(19): 3434–3439. doi: 10.3321/j.issn:1000-6915.2005.19.005 ZHANG Jun-feng, WANG Si-ying, QI Tao. Three-dimensional spencer method for slope stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(19): 3434–3439. (in Chinese) doi: 10.3321/j.issn:1000-6915.2005.19.005
[16] 李同录, 王艳霞, 邓宏科. 一种改进的三维边坡稳定性分析方法[J]. 岩土工程学报, 2003, 25(5): 611–614. doi: 10.3321/j.issn:1000-4548.2003.05.020 LI Tong-lu, WANG Yan-xia, DENG Hong-ke. An improved method for three-dimensional slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(5): 611–614. (in Chinese) doi: 10.3321/j.issn:1000-4548.2003.05.020
[17] 朱大勇, 钱七虎. 三维边坡严格与准严格极限平衡解答及工程应用[J]. 岩石力学与工程学报, 2007, 26(8): 1513–1528. doi: 10.3321/j.issn:1000-6915.2007.08.001 ZHU Da-yong, QIAN Qi-hu. Rigorous and quasi-rigorous limit equilibrium solutions of 3D slope stability and application to engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(8): 1513–1528. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.08.001
[18] 郑宏. 严格三维极限平衡法[J]. 岩石力学与工程学报, 2007, 26(8): 1529–1537. doi: 10.3321/j.issn:1000-6915.2007.08.002 ZHENG Hong. A rigorous three-dimensional limit equilibrium method[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(8): 1529–1537. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.08.002
[19] 陈昌富, 朱剑锋. 基于Morgenstern-Price法边坡三维稳定性分析[J]. 岩石力学与工程学报, 2010, 29(7): 1473–1480. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201007025.htm CHEN Chang-fu, ZHU Jian-feng. A three-dimensional slope stability analysis procedure based on Morgenstern-Price method[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(7): 1473–1480. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201007025.htm
[20] 郭明伟, 葛修润, 李春光, 等. 边坡和坝基抗滑稳定分析的三维矢量和法及其工程应用[J]. 岩石力学与工程学报, 2010, 29(1): 8–20. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201001001.htm GUO Ming-wei, GE Xiu-run, LI Chun-guang, et al. Three-dimensional vector sum method employed in slope and dam foundation stability analyses and its applications to practical engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1): 8–20. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201001001.htm
[21] 凌道盛, 戚顺超, 陈锋, 等. 一种基于Morgenstern-Price法假定的三维边坡稳定性分析法[J]. 岩石力学与工程学报, 2013, 32(1): 107–116. doi: 10.3969/j.issn.1000-6915.2013.01.016 LING Dao-sheng, QI Shun-chao, CHEN Feng, et al. A limit equilibrium method based on Morgenstern-Price method for 3D slope stability analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(1): 107–116. (in Chinese) doi: 10.3969/j.issn.1000-6915.2013.01.016
[22] MCCOOK D K. Limit analysis and soil plasticity[J]. Soil Science Society of America Journal, 1976, 40: 4. doi: 10.2136/sssaj1976.03615995004000040002x
[23] LE C V, NGUYEN-XUAN H, NGUYEN-DANG H. Upper and lower bound limit analysis of plates using FEM and second-order cone programming[J]. Computers & Structures, 2010, 88(1/2): 65–73. http://www.onacademic.com/detail/journal_1000034067936510_8d83.html
[24] SLOAN S W, KLEEMAN P W. Upper bound limit analysis using discontinuous velocity fields[J]. Computer Methods in Applied Mechanics and Engineering, 1995, 127(1/2/3/4): 293–314. http://www.researchgate.net/profile/Scott_Sloan/publication/222487057_Upper_bound_limit_analysis_using_discontinuous_velocity_fields/links/53d72b280cf228d363ead982
[25] LYAMIN A V, SLOAN S W. Upper bound limit analysis using linear finite elements and nonlinear programming[C]// Civil-Comp Proceedings, Finite Elements: Techniques and Developments. Stirlingshire, UK: Civil-Comp Press, 2002: 61–77.
[26] YIN J, CHEN J, LEE C. Upper limit analysis of stability of rock and soil slopes using rigid finite elements[J]. Chinese Journal of Rock Mechanics & Engineering, 2004, 23(6): 898–905.
[27] LIU F T, ZHAO J D. Upper bound limit analysis using radial point interpolation meshless method and nonlinear programming[J]. International Journal of Mechanical Sciences, 2013, 70: 26–38. doi: 10.1016/j.ijmecsci.2013.01.017
[28] YU S B, ZHANG X, SLOAN S W. A 3D upper bound limit analysis using radial point interpolation meshless method and second-order cone programming[J]. International Journal for Numerical Methods in Engineering, 2016, 108(13): 1686–1704. doi: 10.1002/nme.5273
[29] YUAN S, DU J N. Effective stress-based upper bound limit analysis of unsaturated soils using the weak form quadrature element method[J]. Computers and Geotechnics, 2018, 98: 172–180. doi: 10.1016/j.compgeo.2018.02.008
[30] HUANG M S, FAN X P, WANG H R. Three-dimensional upper bound stability analysis of slopes with weak interlayer based on rotational-translational mechanisms[J]. Engineering Geology, 2017, 223: 82–91. doi: 10.1016/j.enggeo.2017.04.017
[31] ZHANG X. Three-dimensional stability analysis of concave slopes in plan view[J]. Journal of Geotechnical Engineering, 1988, 114(6): 658–671. doi: 10.1061/(ASCE)0733-9410(1988)114:6(658)
-
期刊类型引用(9)
1. 周创兵,姜清辉,姚池,位伟,胡冉. 水利水电工程高陡边坡变形与稳定性研究进展及挑战. 水力发电学报. 2025(01): 1-17 .  百度学术
百度学术
2. 郑颖人,张金良,尹德文,邵颖,苏凯,吴昊,张智沛. 基于下限模型的临界滑动面理论与数值解法. 岩土工程学报. 2025(02): 438-442 .  本站查看
本站查看
3. 叶欣玲,司富生,胡华,鲁蕊. 里底水电站库区巴迪滑坡蓄水前后稳定性评价. 西北水电. 2024(02): 19-25 .  百度学术
百度学术
4. 楼晓明,孙逸玮,张蓟. 软土地基沟渠开挖诱发远处围堰失稳的实例分析. 水利水电技术(中英文). 2024(S1): 151-159 .  百度学术
百度学术
5. 卢树盛,向能武,孙云志. 高边坡勘察新技术在水利工程中的应用现状、挑战与展望. 中国水利. 2024(14): 44-50 .  百度学术
百度学术
6. 鲁松林. 基于简化Janbu法的夹炭质泥岩软弱层的溶蚀峰丛斜坡边坡稳定性分析. 价值工程. 2024(24): 125-127 .  百度学术
百度学术
7. 邱锐,乐巧丽. 基于PLAXIS强度折减法的应变软化边坡稳定性分析. 科技与创新. 2024(18): 104-105+109 .  百度学术
百度学术
8. 童新建,赵世航,刘传新. 基于流固耦合理论的航道边坡稳定性分析. 黑龙江科技大学学报. 2024(05): 722-728 .  百度学术
百度学术
9. 葛虎胜,刘峰,苏怀斌,王宇,廖九波,方庆红. 高陡边坡开挖卸荷位移演变规律及边坡稳定性研究. 矿业研究与开发. 2023(06): 83-88 .  百度学术
百度学术
其他类型引用(6)



 下载:
下载: