SV波空间斜入射下沥青混凝土心墙响应特性及抗拉破坏评价研究

王飞; 宋志强; 刘云贺; 李闯

doi:10.11779/CJGE20220804

SV波空间斜入射下沥青混凝土心墙响应特性及抗拉破坏评价研究 English Version

王飞^{1, 2,},
宋志强^1, ,,
刘云贺¹,
李闯¹

1.
西安理工大学省部共建西北旱区生态水利国家重点实验室, 陕西西安 710048
2.
西华大学能源与动力工程学院, 四川成都 610039

基金项目:

国家自然科学基金重点项目 52039008

国家自然科学基金面上项目 51779208

陕西省自然科学基础研究计划项目 2022JM-276

陕西省教育厅青年创新团队科研计划项目 22JP052

详细信息

作者简介:
王飞(1993—)，男，博士，讲师，主要从事水工结构抗震安全方面的研究。E-mail: feiwang201268@163.com

通讯作者:
宋志强, E-mail: zqsong@xaut.edu.cn

中图分类号: TV312
计量
- 文章访问数: 243
- HTML全文浏览量: 38
- PDF下载量: 59
出版历程
- 收稿日期: 2022-06-26
- 网络出版日期: 2023-02-26

Response characteristics and tensile failure evaluation of asphalt concrete core wall under spatial oblique incidence of SV waves

WANG Fei^{1, 2,},
SONG Zhiqiang^1, ,,
LIU Yunhe¹,
LI Chuang¹

1.
State Key Laboratory of Eco-hydraulics in Northwest Arid Region, Xi'an University of Technology, Xi'an 710048, China
2.
School of Energy and Power Engineering, Xihua University, Chengdu 610039, China

摘要

摘要: 地震波空间斜入射下沥青混凝土心墙响应和动态抗拉破坏研究存在较大不足。考虑SV波入射方位角和斜入射角的空间任意性，基于波场叠加原理构建了地基边界上非一致自由场，建立了SV波空间斜入射波动输入方法。基于试验结果建立了沥青混凝土瞬时抗拉强度随应变速率变化的经验公式，提出了依据瞬时拉应力和瞬时抗拉强度判别心墙单元抗拉破坏的新方法。分析了入射方位角、斜入射角对沥青混凝土心墙加速度、应力空间分布的影响规律，揭示了空间斜入射相对垂直入射造成心墙局部拉应力激增导致心墙破坏机理，论证了传统静态强度判别方法相对本文方法对心墙破坏判别的误差，明确了不同入射方式下心墙抗拉破坏区分布特征。结果表明：与垂直入射相比，空间斜入射下心墙水流向、坝轴向和竖向加速度最大增加54%，9.2倍和5.2倍，心墙拉应力最大增加14.2倍，忽略空间斜入射，会严重低估心墙加速度和应力响应。入射方向越偏向坝轴向且斜入射角越大，心墙迎波侧更容易发生拉裂破坏；传统静态强度判别方法，会造成心墙较大的拉裂破坏判别误差。
- 沥青混凝土心墙土石坝 /
- 空间斜入射 /
- 加速度 /
- 应力 /
- 抗拉破坏
Abstract: The existing researches on response and dynamic tensile failure of asphalt concrete core wall under spatial oblique incidence of seismic waves have great shortcomings. By considering the arbitrariness of SV-wave incident azimuth and oblique incident angles and constructing the non-uniform free field on foundation boundary based on the wave field superposition principle, an input method for spatial oblique incidence of SV waves is established. Then, an empirical formula for the change in instantaneous tensile strength of asphalt concrete with strain rate is established based on the test results. A new method for the safety evaluation of core wall based on instantaneous tensile stress and strength is proposed. Finally, the influences of incident azimuth and oblique incident angles on the acceleration and stress distributions of core wall are analyzed. The damage mechanism of core wall caused by tensile stress surge caused by spatial oblique incidence is revealed. Using the proposed method, the error of the traditional static strength judgment method for core wall damage is demonstrated. The distribution characteristics of tensile failure zone of core wall under different incident modes are clarified. The results show that compared with those under vertical incidence, the acceleration of core wall in water flow, dam axis and vertical directions can be increased by 54%, 9.2 times and 5.2 times at most under spatial oblique incidence. The tensile stress of core wall can be increased by a maximum of 14.2 times at most. Neglecting the spatial oblique incidence severely underestimates the accelerations and stresses of core wall. The more the incident direction deviates to dam axis direction and the larger the oblique incident angle, the more easily the tensile failure at the wave-facing side of core wall occurs. The traditional static strength judgment method leads to a large error of tensile failure of core wall.
- asphalt concrete core wall embankment dam /
- spatial oblique incidence /
- acceleration /
- stress /
- tensile failure

HTML全文

0. 引言

沥青混凝土心墙土石坝防渗性能优、抗震性能好、适应变形能力强，在中国水能资源丰富的西部地区广泛修建。许多沥青混凝土心墙坝正在建设或规划中^[1]，如西藏帕孜和新疆尼雅等百米级以上高坝。西部地区强震频发，大坝选址难以避让，给沥青混凝土心墙坝的抗震安全带来严峻挑战。

沥青混凝土心墙坝地震响应计算大多假定地震波垂直入射，而在近断层区域场址，地震波往往倾斜入射^[2]。此外，汶川地震中，地震波从大坝右岸向左岸传播，导致紫坪铺面板堆石坝发生左侧面板比右侧面板更严重的挤压和位错破坏^[3-4]，可见，地震波入射方向具有三维空间性及任意性^[5]。地震波入射方向与地表法线的夹角-斜入射角，以及地震波相对河谷的入射方位是影响大坝地震响应的两个主要因素。Seiphoori等^[6]研究了P波、SV波和SH波入射方向与坝轴向一致，不同入射角下面板堆石坝地震响应。姚虞等^[7]分析了P波、SV波入射方向与坝轴向垂直，SH波入射方向与坝轴向一致时，斜入射下面板堆石坝地震响应。李明超等^[8]假定地震波入射方向与水流向一致，研究了斜入射角对混凝土重力坝地震响应的影响。上述研究结果均表明：与垂直入射相比，斜入射会显著增加大坝某些响应，对大坝存在不利影响。上述研究忽略了入射方向与坝轴线斜交，地震波空间斜入射考虑的不够全面，不能全面反映大坝的薄弱部位，亟需研究地震波空间斜入射对沥青混凝土心墙坝地震响应和安全的影响。

沥青混凝土心墙作为沥青混凝土心墙坝的防渗体，其抗震安全至关重要。Feizi-Khankandi等^[9]从峰值应变的角度分析了心墙抗拉安全性，认为地震会引起心墙上部发生开裂。朱晟^[10]通过动应力和应力水平等指标，分析了龙头石沥青混凝土心墙坝的抗震性能。上述研究忽略了应变速率对强度和峰值应变的影响。Ning等^[11]近期开展的试验研究表明，荷载应变速率越高，沥青混凝土拉伸和压缩强度越大，不同应变速率下沥青混凝土强度明显不同。在结构层面，现有研究并未考虑应变速率对沥青混凝土心墙动态抗拉和抗压强度的影响，若按静态强度对心墙抗拉和抗压性能进行评价，将高估心墙破坏程度，因此有必要考虑应变速率对沥青混凝土心墙抗拉破坏的影响。

针对地震波斜入射下沥青混凝土心墙动态抗拉破坏评价等方法的不足，本文开展SV波空间斜入射下沥青混凝土心墙坝响应及安全评价研究。考虑地震波入射方位角和斜入射角的任意性，建立了SV波空间斜入射波动输入方法；考虑沥青混凝土拉伸强度随应变率变化，提出依据瞬时拉应力和瞬时抗拉强度判别心墙单元抗拉破坏的新方法。以实际沥青混凝土心墙坝为研究对象，揭示了空间斜入射相对垂直入射造成心墙局部拉应力激增导致心墙破坏机理，明确了不同入射方式下心墙抗拉破坏区分布特征。

1. SV波空间斜入射波动输入方法

黏弹性人工边界结合等效结点荷载的地震波动输入方法精度较高，广泛应用于坝基地震动输入^{[8, 12]}。本节首先构建SV波空间斜入射下弹性半空间自由场，自由场转化为黏弹性边界上等效结点荷载，实现SV波任意入射方位角和斜入射角的波动输入。

1.1 弹性半空间自由场构建

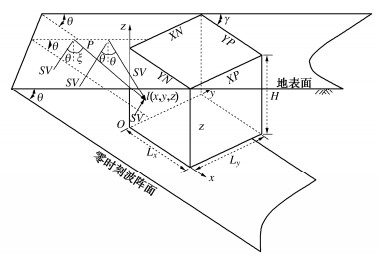
为SV波空间斜入射示意图，入射方向与x轴之间夹角为 $\gamma$ ，入射方向与z轴之间夹角为θ。入射SV波 $f_{{\text{SV}}}^{\text{i}}(t)$ 在自由表面发生波型转换，产生反射角为θ的SV波 $f_{{\text{SV}}}^{\text{r}}(t)$ 和反射角为 $\zeta$ 的P波 $f_{\text{P}}^{\text{r}}(t)$ 。

图 1 SV波空间斜入射示意图

Figure 1. Schematic diagram of spatial oblique incidence of SV waves

下载: 全尺寸图片幻灯片

采用波场分离技术，将自由波场分解为入射波场和反射波场，根据地震波叠加原理计算不同边界上结点自由场。点 $l(x,y,z)$ 处自由场位移为

$\left.\begin{array}{l} \begin{array}{l}{u}_{x}(t)=[{f}_{\text{SV}}^{\text{i}}(t-\Delta {t}_{1})-{B}_{1}{f}_{\text{SV}}^{\text{r}}(t-\Delta {t}_{2})]\mathrm{cos}\theta \mathrm{cos}\gamma -\\ \;\;\;\;\;\;\;\;\;\;\;\;{B}_{2}{f}_{\text{P}}^{\text{r}}(t-\Delta {t}_{3})\mathrm{sin}\zeta \mathrm{cos}\gamma \text{ }，\end{array}\\ \begin{array}{l}{u}_{y}(t)=[{f}_{\text{SV}}^{\text{i}}(t-\Delta {t}_{1})-{B}_{1}{f}_{\text{SV}}^{\text{r}}(t-\Delta {t}_{2})]\mathrm{cos}\theta \mathrm{sin}\gamma -\\ \;\;\;\;\;\;\;\;\;\;\;\;{B}_{2}{f}_{\text{P}}^{\text{r}}(t-\Delta {t}_{3})\mathrm{sin}\zeta \mathrm{sin}\gamma \text{ }，\end{array}\\ \begin{array}{l}{u}_{z}(t)=-[{f}_{\text{SV}}^{\text{i}}(t-\Delta {t}_{1})+{B}_{1}{f}_{\text{SV}}^{\text{r}}(t-\Delta {t}_{2})]\mathrm{sin}\theta +\\ \;\;\;\;\;\;\;\;\;\;\;\;{B}_{2}{f}_{\text{P}}^{\text{r}}(t-\Delta {t}_{3})\mathrm{cos}\zeta \text{ }。\end{array} \end{array}\right\}$

(1)

式中：SV和P分别表示SV波和P波；i和r表示入射和反射；∆t₁，∆t₂和∆t₃分别为入射SV波、反射SV波和反射P波自零时刻波阵面至点 $l(x,y,z)$ 的时间延迟，按几何方法计算；B₁和B₂分别为反射SV波和反射P波振幅与入射SV波振幅之比，计算公式见文献[13]。其它边界面节点自由场位移同式（1），只需替换各自的时间延迟。

1.2 波动输入方法

等效结点荷载计算公式如下^[14]：

$\boldsymbol{F}_{\mathrm{B}}^{\mathrm{F}}=\left(\boldsymbol{K} \boldsymbol{u}_{\mathrm{B}}^{\mathrm{F}}+\boldsymbol{C} \dot{\boldsymbol{u}}_{\mathrm{B}}^{\mathrm{F}}+\boldsymbol{\sigma}_{\mathrm{B}}^{\mathrm{F}} \boldsymbol{n}\right) A_{\mathrm{B}} \quad 。$

(2)

式中： $\boldsymbol{K}$ 和C分别为人工边界上刚度和阻尼系数矩阵，矩阵中元素依据应力人工边界取值^[15]； $\boldsymbol{u}_{\text{B}}^{\text{F}}$ 和 $\dot{\boldsymbol{u}}_{\mathrm{B}}^{\mathrm{F}}$ 分别为自由场位移和速度矢量； $\boldsymbol{\sigma}_{\mathrm{B}}^{\mathrm{F}}$ 为自由场应力张量；n为边界面外法线余弦向量；A_B为边界结点影响面积。

1.1节求解了自由场位移，自由场速度通过位移求导获得。根据连续介质力学中位移-应变和应变-应力关系求解各类型波应力项，将应力项沿坐标轴方向分解，叠加各类型波引起的应力分量，获得任意点处自由场总应力分量。XN面自由场应力分量如下：

$\left.\begin{array}{l} \begin{array}{l}{\sigma }_{x}(t)=\frac{G\mathrm{sin}2\theta {\mathrm{cos}}^{2}\gamma [{\dot{f}}_{\text{SV}}^{\text{i}}(t-\Delta {t}_{1})-{B}_{1}{\dot{f}}_{\text{SV}}^{\text{r}}(t-\Delta {t}_{2})]}{{c}_{\text{S}}}-\\\;\;\;\;\;\;\;\;\;\;\;\;\frac{(\lambda +2G{\mathrm{sin}}^{2}\zeta {\mathrm{cos}}^{2}\gamma ){B}_{2}{\dot{f}}_{\text{P}}^{\text{r}}(t-\Delta {t}_{3})}{{c}_{\text{P}}}\text{ }\text{，}\end{array}\\ \begin{array}{l}{\sigma }_{y}(t)=\frac{G\mathrm{sin}2\theta \mathrm{cos}2\gamma [{\dot{f}}_{\text{SV}}^{\text{i}}(t-\Delta {t}_{1})-{B}_{1}{\dot{f}}_{\text{SV}}^{\text{r}}(t-\Delta {t}_{2})]}{2{c}_{\text{S}}}-\\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{G{\mathrm{sin}}^{2}\zeta \mathrm{sin}2\gamma {B}_{2}{\dot{f}}_{\text{P}}^{\text{r}}(t-\Delta {t}_{3})}{{c}_{\text{P}}}\text{ }\text{，}\end{array}\\ \begin{array}{l}{\sigma }_{z}(t)=\frac{G\mathrm{cos}2\theta \mathrm{cos}\gamma [{\dot{f}}_{\text{SV}}^{\text{i}}(t-\Delta {t}_{1})+{B}_{1}{\dot{f}}_{\text{SV}}^{\text{r}}(t-\Delta {t}_{2})]}{{c}_{\text{S}}}+\\ \;\;\;\;\;\;\;\;\;\;\;\;\frac{G\mathrm{sin}2\zeta \mathrm{cos}\gamma {B}_{2}{\dot{f}}_{\text{P}}^{\text{r}}(t-\Delta {t}_{3})}{{c}_{\text{P}}}\text{ }。\end{array} \end{array}\right\}$

(3)

式中： $\dot f_{{\text{SV}}}^{\text{i}}(t - \Delta {t_1})$ ， $\dot f_{{\text{SV}}}^{\text{r}}(t - \Delta {t_2})$ 和 $\dot f_{\text{P}}^{\text{r}}(t - \Delta {t_3})$ 分别为入射SV波、反射SV波和反射P波在XN面上引起的速度；G和 $\lambda$ 分别为介质弹性模量和拉梅常数。其它边界面上自由场应力采用相同计算方法。将自由场位移、速度和应力代入式（2），获得SV波任意入射方位角 $\gamma$ 和斜入射角θ下边界面结点上等效结点荷载。

1.3 波动输入数值验证

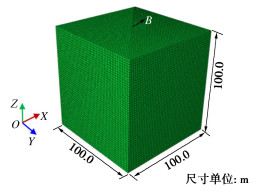
以图 2中100 m×100 m×100 m的有限域为数值算例，图 3中单位脉冲荷载为激励。通过Python实现SV波空间斜入射下边界上等效结点力、阻尼和弹性系数的计算与施加，完成SV波空间斜入射波动输入。

图 2 有限域模型

Figure 2. Finite element model

下载: 全尺寸图片幻灯片

图 3 入射波位移时程

Figure 3. Time histories of displacement of incident waves

下载: 全尺寸图片幻灯片

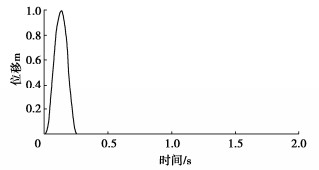
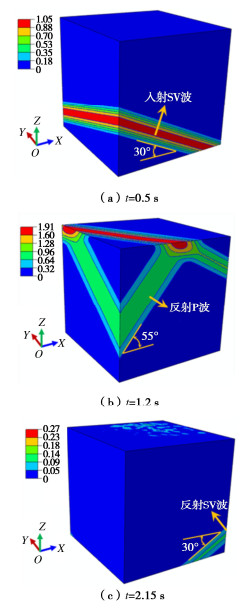
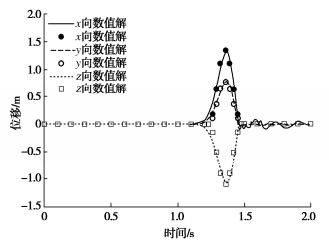
图 4为γ=30°，θ=30°入射方式下地震波在半空间中传播过程，为 $\gamma$ =30°，θ=30°入射方式下表面中心点B（50 m，50 m，100 m）位移时程，并与解析解对比。

图 4 γ=30°，θ=30°下半空间内地震波传播过程

Figure 4. Propagation process of seismic waves in half-space under γ=30°, θ=30°

下载: 全尺寸图片幻灯片

图 5 γ=30°，θ=30°时点B位移时程

Figure 5. Time histories of displacement at point B when γ=30°, θ=30°

下载: 全尺寸图片幻灯片

图 4表明，数值结果很好地反映地震波在半空间内传播过程，能够模拟地震波波型转换、地震波入射方位角和斜入射角，并且在相同高程处，地震动呈现空间非一致性。图 5表明，中心点B各方向数值位移与理论解拟合良好。验证了本文建立的SV波空间斜入射波动输入方法的正确性，并且计算精度较高。

2. 沥青混凝土心墙抗拉破坏判别方法

地震作用下沥青混凝土心墙单元应力、应变速率均随时间变化，不同应变速率对应的抗拉强度不同，心墙单元抗拉强度随时间变化。因而，不能采用最大拉应力与抗拉强度对比的方法判别抗拉破坏，理由是如果单元最大拉应力发生时刻应变速率也较大，对应的抗拉强度较大，单元可能并不发生拉裂破坏。地震过程中每一时刻均考虑单元应变速率对抗拉强度的影响较符合实际情况，通过比较瞬时拉应力和瞬时抗拉强度判别单元抗拉破坏。

依据Ning等^[11]开展的沥青混凝土动态拉伸试验，表 1整理了不同温度和不同应变速率的抗拉强度，其中1×10^-5 s^-1为准静态应变速率。西部高山峡谷地区年平均气温一般较低，如：雅砻江流域1991年—2020年的年平均气温仅为7.3℃，金沙江流域1960年—2016年的年平均气温仅为9.2℃^[16]。因此，选用15℃的抗拉强度作为西部沥青混凝土心墙抗拉破坏的判别标准是合适且偏严格的。

表 1 水工沥青混凝土抗拉强度^[11]

Table 1. Tensile strengths of asphalt concrete (单位: MPa)

温度/℃	应变速率/s^-1
温度/℃	10^-5	10^-4	10^-3	10^-2
5	-1.29	-2.50	-4.24	-5.10
10	-0.65	-1.92	-3.63	-4.53
15	-0.34	-0.93	-2.42	-3.34
20	—	-0.31	-1.03	-2.72

下载: 导出CSV

| 显示表格

采用数学回归法和时温等效原理建立了15℃条件下率相关水工沥青混凝土抗拉强度经验公式：

$f_{\mathrm{t}}[\dot{\varepsilon}(t)]=\left\{\begin{array}{ll} -11.42\left[10^{0.0834(\lg \dot{\varepsilon}(t)-0.647)}-0.3\right] & \dot{\varepsilon}(t) \geqslant 1 \times 10^{-5} \mathrm{~s}^{-1} \\ 0.34 & \dot{\varepsilon}(t)<1 \times 10^{-5} \mathrm{~s}^{-1} \end{array}\right. \text { 。 }$

(4)

式中： ${f_{\text{t}}}[\dot \varepsilon (t)]$ 为瞬时抗拉强度； $\dot \varepsilon (t)$ 为瞬时应变速率。

沥青混凝土心墙抗拉破坏判别方法：在任意时刻，利用坐标变换矩阵将笛卡尔坐标系中应变速率张量转换到主应变空间，依据主应变空间的小应变速率按式（4）确定沥青混凝土抗拉强度时程，若单元拉应力首次超过该时刻抗拉强度则单元发生拉裂破坏。对于地震初始和结束阶段，单元应变速率小于1×10^-5 s^-1的情况，取应变速率为1×10^-5 s^-1对应的抗拉强度。

3. 沥青混凝土心墙土石坝心墙响应特性及抗拉破坏分析

3.1 工程概况与有限元模型

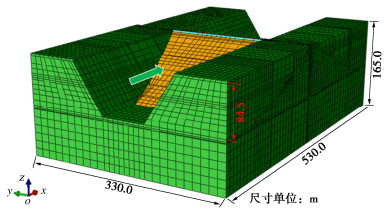
以西南地区某沥青混凝土心墙土石坝为研究对象，图 6为沥青混凝土心墙坝有限元模型，建基面高程为848.00 m，正常蓄水位高程为929.50 m，最大坝高为84.50 m，坝顶宽9.0 m，坝顶长170.0 m。心墙高83.5 m，心墙顶部厚度为0.6 m，底部厚度为1.1 m，心墙底部与混凝土基座连接，大坝上游坡比为1∶2.2，下游坡比为1.2.0。河谷左、右岸坡度均为1∶1.5。在大坝左、右岸方向、上、下游方向和深度方向均延伸1倍坝高。

图 6 地基-沥青混凝土心墙坝三维有限元模型

Figure 6. Three-dimensional finite element model for foundation- asphalt concrete core embankment dam

下载: 全尺寸图片幻灯片

静力计算中土石料、过渡料和沥青混凝土本构关系采用邓肯-张E-B模型。动力计算中，土石料、过渡料和沥青混凝土非线性通过等效线性化方法反映，应力-应变关系采用沈珠江改进的黏弹性模型^[17]，动力计算参数如表 2所示。静动力计算中，混凝土基座和基岩为线弹性，混凝土与基岩密度分别为2450，2700 kg/m³，弹性模量分别为28，8 GPa，泊松比分别为0.167，0.24。

表 2 动力计算参数

Table 2. Dynamic parameters

材料	k₁	k₂	n	λ_max	μ
堆石Ⅰ区	20.0	2270	0.273	0.220	0.350
堆石Ⅱ区	25.9	1694	0.380	0.245	0.350
过渡料	28.3	1832	0.375	0.220	0.328
沥青混凝土	15.7	1979.4	0.400	0.345	0.345

下载: 导出CSV

| 显示表格

本文研究SV波16种空间斜入射方式下沥青混凝土心墙响应，其中入射方位角γ表示入射方向与水流向夹角，取值分别为0°，30°，60°，90°；斜入射角θ为入射方向与水平地表法线夹角，取值分别为0°，15°，30°和35°。

3.2 $\gamma$ 角和θ角对心墙加速度峰值分布规律的影响

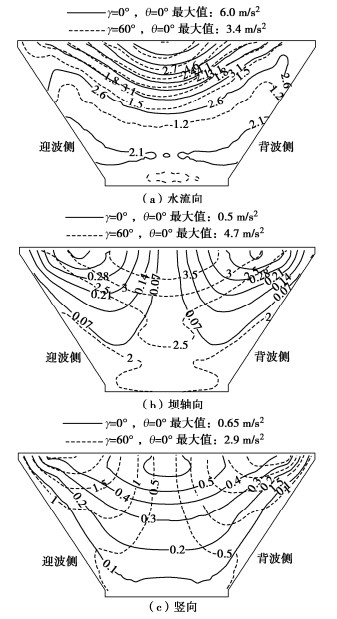
为SV波 $\gamma$ =0°，θ=0°和 $\gamma$ =60°，θ=0°两种入射方式下沥青混凝土心墙加速度峰值等值线分布。表明，在 $\gamma$ =0°，θ=0°入射方式下，加速度峰值关于心墙中心线对称。水流向和竖向加速度峰值从底部往顶部逐渐增大，最大值出现在顶部中心；坝轴向加速度峰值从中部往两侧逐渐增大，最大值出现在两侧顶部，距心墙顶中心1/4坝顶长度位置。

图 7

$\gamma$ =0°,

$\theta$ =0°和

$\gamma$ =60°,

$\theta$ =0°时心墙加速度分布

Figure 7. Distribution of acceleration of core wall when

$\gamma$ =0°,

$\theta$ =0° and

$\gamma$ =60°,

$\theta$ =0°

下载: 全尺寸图片幻灯片

在 $\gamma$ =60°，θ=0°入射时，水流向加速度峰值有偏向背波侧的趋势，坝轴向加速度峰值从底部往顶部逐渐增大，最大值出现在心墙顶中心，竖向加速度从中部往两侧逐渐增大，最大值出现在两侧顶部。与 $\gamma$ =0°，θ=0°入射方式相比， $\gamma$ =60°，θ=0°入射时，水流向加速度最大值减小了43.3%，坝轴向和竖向加速度最大值分别增加了8.4倍和3.5倍。

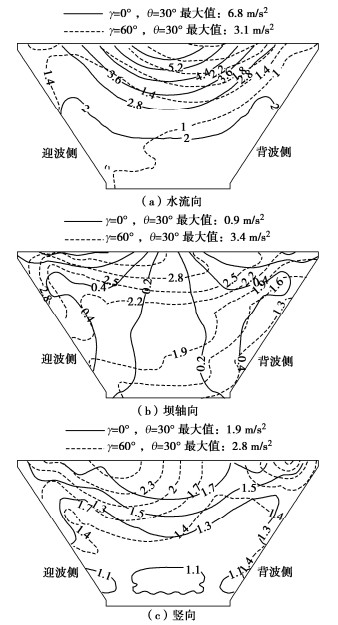
为 $\gamma$ =0°，θ=30°和 $\gamma$ =60°，θ=30°入射方式下心墙加速度峰值等值线。表明，当 $\gamma$ =0°，θ=30°时，加速度峰值关于中心线对称。当 $\gamma$ =60°，θ=30°时，入射方向与水流向夹角 $\gamma$ 较大，迎波侧河谷表面透射波和背波侧河谷表面散射波均指向心墙背波侧顶部，背波侧顶部类似于能量汇聚点，引起水流向加速度峰值倾向背波侧，造成水流向最大加速度位于背波侧顶部。入射方向与地表法线夹角θ较小，地震波从迎波侧开始激励，导致坝轴向和竖向最大加速度出现在迎波侧顶部。两种入射方式下，心墙加速度数值存在明显差异，与 $\gamma$ =0°，θ=30°入射方式相比， $\gamma$ =60°，θ=30°入射方式下水流向最大加速度减小了54.4%，坝轴向和竖向最大加速度分别增加了2.8倍和47.3%。

图 8

$\gamma$ =0°,

$\theta$ =30°和

$\gamma$ =60°,

$\theta$ =30°时心墙加速度分布

Figure 8. Distribution of acceleration of core wall when

$\gamma$ =0°,

$\theta$ =30° and

$\gamma$ =60°,

$\theta$ =30°

下载: 全尺寸图片幻灯片

图 7中γ=0°，θ=0°和中 $\gamma$ =0°，θ=30°的加速度峰值分布对比表明，入射方向沿水流向，θ变化不改变加速度分布特征，各向加速度峰值关于中心线对称。中 $\gamma$ =60°，θ=0°和中 $\gamma$ =60°，θ=30°的加速度峰值分布对比表明，入射方向与水流向斜交或垂直，θ变化会改变心墙加速度分布规律和数值，心墙各向加速度峰值呈现出向背波侧倾斜的分布特征。

3.3 γ角和 $\theta$ 角对心墙最大加速度的影响

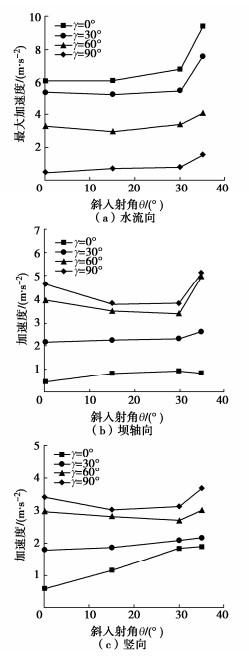
图 9为心墙最大加速度随入射方位角γ和入射角θ的变化。图 9表明，入射方位角γ不变时，最大加速度与斜入射角θ的关系不遵循自由表面地震动强度与斜入射角θ的关系。这种关系受到两方面的干扰：一是河谷地形效应，另一方面是坝体土石料和心墙动力非线性特性。而是表现为水流向最大加速度随斜入射角θ增大而增大，坝轴向和竖向最大加速度在 $\gamma$ = 0°和 $\gamma$ =30°时随斜入射角θ增大而增大，在 $\gamma$ =60°和 $\gamma$ =90°时随斜入射角θ增大而先减小后增大。

图 9 心墙最大加速度随γ和θ角的变化

Figure 9. Variation in maximum acceleration of core wall with angles γ and θ

下载: 全尺寸图片幻灯片

入射方位角 $\gamma$ 对心墙加速度的影响大于河谷散射效应以及坝体和心墙动力非线性的影响，因此水流向和坝轴向最大加速度与入射方位角 $\gamma$ 的关系遵循自由表面地震强度与角 $\gamma$ 的关系。斜入射角θ相同时，水流向最大加速度随入射方位角 $\gamma$ 增大而减小，坝轴向和竖向最大加速度随入射方位角 $\gamma$ 增大而增大。

空间斜入射方式下，不同空间点入射波和反射波叠加方式不同，加上河谷地形高差对地震波的散射和绕射效应，造成河谷表面地震动具有明显的空间非一致性（不均匀性），相比垂直入射，顺坝轴向斜入射引起的河谷表面地震动不均匀性对坝体坝轴向和竖向加速度的影响最显著。当 $\gamma$ =90°，θ=35°（顺坝轴向斜入射）时，坝轴向和竖向加速度达到最大值，分别为5.1，3.71 m/s²，分别比垂直入射增大了9.2倍和5.2倍，分别比 $\gamma$ =0°，θ=35°（顺水流向斜入射）增大了5.4倍和0.9倍。SV波顺坝轴向入射无法引起顺水流向的地震激励，因此SV波顺坝轴向入射下顺水流向加速度较小。当 $\gamma$ =0°，θ=35°时，水流向加速度达到最大值，为9.4 m/s²，比垂直入射增加了54%。

水工建筑物抗震设计标准^[18]指出，垂直入射下设计烈度为Ⅶ度、Ⅷ度和Ⅸ度时，土石坝顶加速度放大系数分别取3.0、2.5和2.0。本文设计地震动峰值加速度为0.22g，介于Ⅷ度和Ⅸ度对应的地震动峰值加速度，本文垂直入射下心墙顶部加速度放大系数为2.2，在2.0~2.5，与规范相符合。而 $\gamma$ =0°，θ=30°空间斜入射方式下顶部放大系数为3.2，比Ⅷ度对应的放大系数2.5大28%，比垂直入射方式的放大系数2.2大45%，超出规范范围，应该予以深入关注。

3.4 沥青混凝土心墙应力

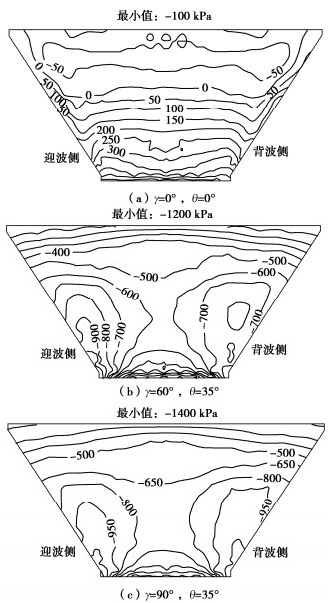
为典型入射方式下心墙小主应力分布。表明，在垂直入射方式（ $\gamma$ =0°，θ=0°）下，心墙下部受压，上部受拉。随入射方位角γ和斜入射角θ增大，下部受压区减小，压应力数值减小，上部受拉区增大，拉应力数值增大。 $\gamma$ 角较小时，最大拉应力发生在心墙顶部附近， $\gamma$ 角较大时，最大拉应力发生在心墙两侧与河谷和基座连接的角点位置，且在迎波侧和背波侧下部均有较大的拉应力区。

图 10 心墙小主应力分布

Figure 10. Distribution of minimum principal stress of core wall

下载: 全尺寸图片幻灯片

当 $\gamma$ =90°，θ=35°时，心墙小主应力均为拉应力，在所有入射方式中拉应力最大1，为-1.4 MPa；在该入射方式下，心墙顶部拉应力相对底部较小，但与 $\gamma$ =0°，θ=0°的垂直入射结果相比，心墙顶部拉应力仍然增加了4.0倍。

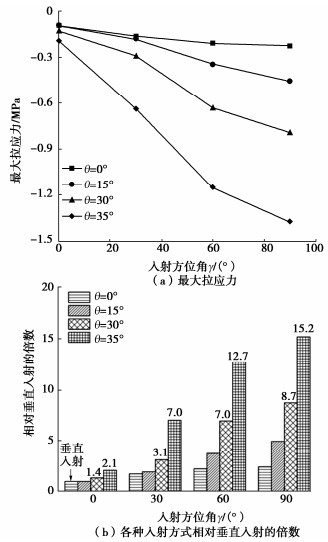
图 11为不同入射方式下心墙最大拉应力以及相对垂直入射结果的增大倍数。图 11表明，垂直入射方式下，最大拉应力为-0.09 MPa，处于较低水平，发生拉伸破坏的可能性低。

图 11 不同入射方式下心墙最大拉应力

Figure 11. Maximum tensile stresses of core wall under different incident modes

下载: 全尺寸图片幻灯片

斜入射方式下，最大拉应力均与入射方位角 $\gamma$ 和斜入射角θ呈正相关，在 $\gamma$ =60°，θ=30°； $\gamma$ =60°，θ=35°； $\gamma$ =90°，θ=30°和 $\gamma$ =90°，θ=35° 4种入射方式下，心墙最大拉应力有显著的增加：当γ=90°，θ=30°（顺坝轴向斜入射）时，最大拉应力比垂直入射增加了7.73倍；当 $\gamma$ =90°，θ=35°（顺坝轴向斜入射）时，最大拉应力比垂直入射增加了14.2倍。顺坝轴向斜入射，河谷迎波侧散射效应和背波侧绕射效应，河谷表面地震动呈现明显的迎波侧大、背波侧小的不均匀分布，河谷两侧不协调运动明显，导致顺坝轴向斜入射下心墙拉应力相对垂直入射有明显的增大。

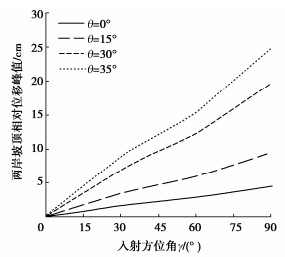
图 12为两岸坡顶坝轴向相对位移峰值随入射方位角γ和斜入射角θ的变化规律。图 12表明，入射方位角γ和斜入射角θ越大，河谷两侧坝轴向相对位移越大，心墙在坝轴向受到拉伸力越大，引起小主应力矢量方向几乎与坝轴线方向一致，造成心墙沿坝轴线方向拉应力显著增加。

图 12 两岸谷顶相对位移峰值

Figure 12. Relative peak displacements of tops at both sides of canyon

下载: 全尺寸图片幻灯片

3.5 沥青混凝土心墙抗拉破坏判别

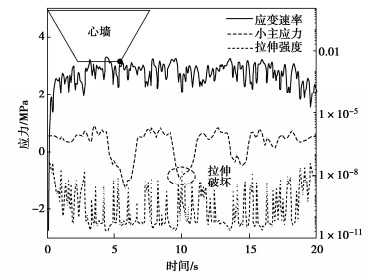
3.4节中结果表明，在SV波所有入射方式中， $\gamma$ =90°，θ=35°入射方式下心墙拉应力最大，因此针对该工况结果开展沥青混凝土心墙抗拉破坏判别分析。根据第2节中提出的沥青混凝土单元抗拉破坏判别方法，图 13给出了背波侧底部角点位置单元应变速率、抗拉强度和小主应力时程曲线。

图 13 γ=90°，θ=35°入射方式下单元应变速率、拉伸强度和小主应力时程

Figure 13. Time histories of element strain rate, tensile strength and minimum principal stress under incident mode of γ=90°, θ=35°

下载: 全尺寸图片幻灯片

图 13表明，地震初始和即将结束时段单元应变速率、抗拉强度较小，接近拟静力状态，主震时段应变速率增大，应变速率在10^-5~10^-2 s^-1范围内，对应的抗拉强度在1~2.5 MPa。背波侧底部角点位置拉应力在10 s左右超过该时刻下的抗拉强度，发生拉裂破坏。顶部中心位置拉应力较小，不会发生拉裂破坏。

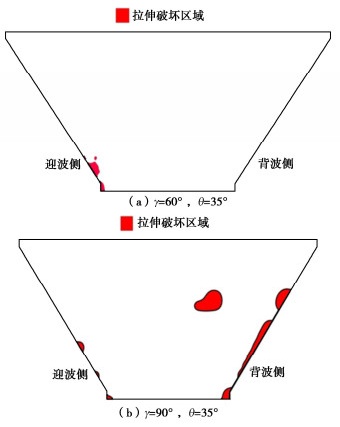
SV波所有入射方式中，在 $\gamma$ =60°，θ=35°和 $\gamma$ =90°，θ=35°两种入射方式下心墙会发生局部拉裂破坏，破坏区域分布如所示。表明， $\gamma$ =60°，θ=35°入射方式下心墙迎波侧与河谷、混凝土基座连接区域发生开裂破坏； $\gamma$ =90°，θ=35°入射方式，心墙背波侧和迎波侧与河谷连接区域发生开裂破坏，其中背波侧破坏区域比迎波侧更大，主要原因是：地震波从河谷迎波侧向背波侧传播，迎波侧河谷表面透射波在背波侧发生散射，地震动能量在背波侧聚集，背波侧拉伸变形增大，造成拉应力增大，单元发生拉裂破坏。

图 14 心墙局部拉裂破坏区

Figure 14. Partial tensile failure area of core wall

下载: 全尺寸图片幻灯片

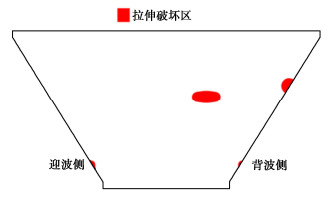
为分析沥青混凝土心墙所处环境温度对心墙开裂破坏区的影响，为 $\gamma$ =90°，θ=35°入射方式下温度为10℃时心墙开裂破坏情况。图 15表明，与温度为15℃相比，心墙开裂破坏区有明显的缩小，开裂破坏区主要集中在背波侧。开裂区缩小的原因是温度降低，沥青混凝土的拉伸强度增大^[11]。

图 15 γ=90°，θ=35°下温度为10℃时心墙开裂破坏区

Figure 15. Tensile failure area of core wall under temperature of 10℃, γ=90°, θ=35°

下载: 全尺寸图片幻灯片

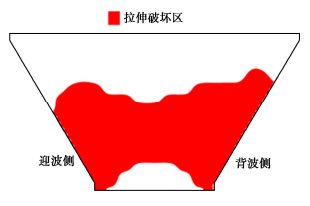
传统混凝土类结构抗拉破坏按应力需求能力比（DCR）结合超应力累计持时判别结构破坏^[19]。DCR为结构最大拉应力与混凝土静态抗拉强度比值。若DCR=2，超应力累计持时超过0 s，判别为严重损伤破坏，否则为低-中等破坏。为了对比传统地震破坏评价方法与本文方法下心墙拉裂破坏程度的差异，图 16为γ=90°，θ=35°入射方式下，传统评价方法判别心墙开裂破坏情况。图 16表明，DCR=2且超应力累计持时超过0.0 s时，在心墙中部发生大范围的开裂破坏。

图 16 传统评价方法下心墙破坏区

Figure 16. Failure area of core wall by traditional evaluation method

下载: 全尺寸图片幻灯片

与本文提出的抗拉破坏判别方法相比，传统地震破坏判别方法获得的心墙开裂破坏区域更大，属于超严重损伤破坏，这种判别方法会高估心墙开裂破坏程度。因此本文建立的沥青混凝土抗拉破坏判别方法更能反映心墙抗拉薄弱部位和破坏区。

4. 结论

本文考虑了入射方位角和斜入射角的任意性，建立了SV波空间斜入射波动输入方法；提出了依据瞬时拉应力和瞬时抗拉强度判别单元抗拉破坏的心墙安全评价新方法。分析了入射方位角、斜入射角对沥青混凝土心墙加速度、应力空间分布的影响规律；揭示了空间斜入射造成心墙局部拉应力激增导致心墙破坏机理；论证了传统静态强度判别方法相对本文提出方法对心墙破坏判别的误差；明确了不同入射方式下心墙抗拉薄弱区分布特征。得到以下4点结论。

（1）入射方位对心墙加速度空间分布有显著影响，入射方向与坝轴向斜交或一致，加速度呈现迎波侧大、背波侧小的分布特征，最大加速度偏向迎波侧或背波侧顶部。与垂直入射相比，空间斜入射下水流向、坝轴向和竖向最大加速度分别增大54%，9.2倍和5.2倍。忽略空间斜入射影响，可能会严重低估沥青混凝土心墙地震响应，抗震设计时应予以格外关注。

（2）与垂直入射相比，空间斜入射下心墙最大拉应力出现位置由上部中心转向迎波侧或背波侧底部。入射方位角 $\gamma$ 和斜入射角θ越大，河谷坝轴向非协调运动越明显，导致心墙拉应力增大，尤其在入射方向与坝轴向一致且斜入射角为35°时，最大拉应力激增，增加了14.0倍。

（3）在SV波所有入射方式中，入射方向与水流向夹角为60°且斜入射角为35°以及入射方向与坝轴向一致且斜入射角为35°的入射方式下，心墙迎波侧和背波侧发生局部拉裂破坏，在入射方向与坝轴向一致且斜入射角为35°入射方式下，背波侧散射效应导致迎波侧拉伸破坏更严重，对于沥青混凝土心墙坝，应重视SV波入射方向与坝轴向一致的斜入射方式。

（4）采用传统抗拉破坏评价方法，心墙拉裂破坏区会显著增大，明显与实际情况不符，有较大误差。考虑应变速率对抗拉强度的影响，依据瞬时拉应力和抗拉强度判别沥青混凝土心墙的拉裂破坏十分必要。

图 1 SV波空间斜入射示意图

Figure 1. Schematic diagram of spatial oblique incidence of SV waves

下载: 全尺寸图片幻灯片

图 2 有限域模型

Figure 2. Finite element model

下载: 全尺寸图片幻灯片

图 3 入射波位移时程

Figure 3. Time histories of displacement of incident waves

下载: 全尺寸图片幻灯片

图 4 γ=30°，θ=30°下半空间内地震波传播过程

Figure 4. Propagation process of seismic waves in half-space under γ=30°, θ=30°

下载: 全尺寸图片幻灯片

图 5 γ=30°，θ=30°时点B位移时程

Figure 5. Time histories of displacement at point B when γ=30°, θ=30°

下载: 全尺寸图片幻灯片

图 6 地基-沥青混凝土心墙坝三维有限元模型

Figure 6. Three-dimensional finite element model for foundation- asphalt concrete core embankment dam

下载: 全尺寸图片幻灯片

$\gamma$ =0°, $\theta$ =0°和 $\gamma$ =60°, $\theta$ =0°时心墙加速度分布

Distribution of acceleration of core wall when $\gamma$ =0°, $\theta$ =0° and $\gamma$ =60°, $\theta$ =0°

下载: 全尺寸图片幻灯片

$\gamma$ =0°, $\theta$ =30°和 $\gamma$ =60°, $\theta$ =30°时心墙加速度分布

Distribution of acceleration of core wall when $\gamma$ =0°, $\theta$ =30° and $\gamma$ =60°, $\theta$ =30°

下载: 全尺寸图片幻灯片

图 9 心墙最大加速度随γ和θ角的变化

Figure 9. Variation in maximum acceleration of core wall with angles γ and θ

下载: 全尺寸图片幻灯片

图 10 心墙小主应力分布

Figure 10. Distribution of minimum principal stress of core wall

下载: 全尺寸图片幻灯片

图 11 不同入射方式下心墙最大拉应力

Figure 11. Maximum tensile stresses of core wall under different incident modes

下载: 全尺寸图片幻灯片

图 12 两岸谷顶相对位移峰值

Figure 12. Relative peak displacements of tops at both sides of canyon

下载: 全尺寸图片幻灯片

图 13 γ=90°，θ=35°入射方式下单元应变速率、拉伸强度和小主应力时程

Figure 13. Time histories of element strain rate, tensile strength and minimum principal stress under incident mode of γ=90°, θ=35°

下载: 全尺寸图片幻灯片

图 14 心墙局部拉裂破坏区

Figure 14. Partial tensile failure area of core wall

下载: 全尺寸图片幻灯片

图 15 γ=90°，θ=35°下温度为10℃时心墙开裂破坏区

Figure 15. Tensile failure area of core wall under temperature of 10℃, γ=90°, θ=35°

下载: 全尺寸图片幻灯片

图 16 传统评价方法下心墙破坏区

Figure 16. Failure area of core wall by traditional evaluation method

下载: 全尺寸图片幻灯片

表 1 水工沥青混凝土抗拉强度^[11]

Table 1 Tensile strengths of asphalt concrete (单位: MPa)

温度/℃	应变速率/s^-1
温度/℃	10^-5	10^-4	10^-3	10^-2
5	-1.29	-2.50	-4.24	-5.10
10	-0.65	-1.92	-3.63	-4.53
15	-0.34	-0.93	-2.42	-3.34
20	—	-0.31	-1.03	-2.72

下载: 导出CSV

表 2 动力计算参数

Table 2 Dynamic parameters

材料	k₁	k₂	n	λ_max	μ
堆石Ⅰ区	20.0	2270	0.273	0.220	0.350
堆石Ⅱ区	25.9	1694	0.380	0.245	0.350
过渡料	28.3	1832	0.375	0.220	0.328
沥青混凝土	15.7	1979.4	0.400	0.345	0.345

下载: 导出CSV

参考文献(19)

[1]	WANG W B, FENG S, ZHANG Y B. Investigation of interface between asphalt core and gravel transition zone in embankment dams[J]. Construction Building and Materials, 2018, 185: 148-155. doi: 10.1016/j.conbuildmat.2018.07.078
[2]	朱俊, 李小军, 梁建文. 地震波斜入射地下隧道地震响应: 2.5维FE-BE耦合模拟[J]. 岩土工程学报, 2022, 44(10): 1846-1854. doi: 10.11779/CJGE202210010 ZHU Jun, LI Xiaojun, LIANG Jianwen. Seismic responses of underground tunnels subjected to obliquely incident seismic waves by 2.5D FE-BE coupling method[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(10): 1846-1854. (in Chinese) doi: 10.11779/CJGE202210010
[3]	陈生水, 霍家平, 章为民. "5.12"汶川地震对紫坪铺混凝土面板坝的影响及原因分析[J]. 岩土工程学报, 2008, 30(6): 795-801. http://www.cgejournal.com/cn/article/id/12873 CHEN Shengshui, HUO Jiaping, ZHANG Weimin. Analysis of effects of "5.12" Wenchuan earthquake on zipingpu concrete face rock-fill dam[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(6): 795-801. (in Chinese) http://www.cgejournal.com/cn/article/id/12873
[4]	ZHANG J M, YANG Z Y, GAO X Z, et al. Geotechnical aspects and seismic damage of the 156-m-high Zipingpu concrete-faced rockfill dam following the Ms 8.0 Wenchuan earthquake[J]. Soil Dynamics and Earthquake Engineering, 2015, 76: 145-156. doi: 10.1016/j.soildyn.2015.03.014
[5]	TAKAHIRO S. Estimation of earthquake motion incident angle at rock site[C]// Proceedings of 12th World Conference Earthquake Engineering. New Zealand, 2002: 0956.
[6]	SEIPHOORI A, MOHSEN HAERI S, KARIMI M. Three-dimensional nonlinear seismic analysis of concrete faced rockfill dams subjected to scattered P, SV, and SH waves considering the dam–foundation interaction effects[J]. Soil Dynamics and Earthquake Engineering, 2011, 31(5/6): 792-804.
[7]	姚虞, 王睿, 刘天云, 等. 高面板坝地震动非一致输入响应规律[J]. 岩土力学, 2018, 39(6): 2259-2266. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806042.htm YAO Yu, WANG Rui, LIU Tianyun, et al. Seismic response of high concrete face rockfill dams subject to non-uniform input motion[J]. Rock and Soil Mechanics, 2018, 39(6): 2259-2266. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201806042.htm
[8]	李明超, 张佳文, 张梦溪, 等. 地震波斜入射下混凝土重力坝的塑性损伤响应分析[J]. 水利学报, 2019, 50(11): 1326-1338, 1349. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201911005.htm LI Mingchao, ZHANG Jiawen, ZHANG Mengxi, et al. Plastic Damage response analysis of concrete gravity dam due to obliquely incident seismic waves[J]. Journal of Hydraulic Engineering, 2019, 50(11): 1326-1338, 1349. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201911005.htm
[9]	FEIZI-KHANKANDI S, GHALANDARZADEH A, MIRGHASEMI A, et al. Seismic analysis of the garmrood embankment dam with asphaltic concrete core[J]. Soils and Foundations, 2009, 49(2): 153-166. doi: 10.3208/sandf.49.153
[10]	朱晟. 沥青混凝土心墙堆石坝三维地震反应分析[J]. 岩土力学, 2008, 29(11): 2933-2938. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200811009.htm ZHU Sheng. 3-D seismic response analysis of rockfill dam with asphalt concrete core[J]. Rock and Soil Mechanics, 2008, 29(11): 2933-2938. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200811009.htm
[11]	NING Z Y, LIU Y H, WANG W B, DONG Jing, MENG Xiao. Experimental study on effect of temperature on direct tensile behavior of hydraulic asphalt concrete at different strain rates[J]. Journal of Materials in Civil Engineering ASCE, 2022, 34(7): 04022143. doi: 10.1061/(ASCE)MT.1943-5533.0004295
[12]	杜修力, 赵密. 基于黏弹性边界的拱坝地震反应分析方法[J]. 水利学报, 2006, 37(9): 1063-1069. doi: 10.3321/j.issn:0559-9350.2006.09.006 DU Xiuli, ZHAO Mi. Analysis method for seismic response of arch dams in time domain based on viscous-spring artificial boundary condition[J]. Journal of Hydraulic Engineering, 2006, 37(9): 1063-1069. (in Chinese) doi: 10.3321/j.issn:0559-9350.2006.09.006
[13]	FAN G, ZHANG L M, LI X Y, et al. Dynamic response of rock slopes to oblique incident SV waves[J]. Engineering Geology, 2018, 247: 94-103. doi: 10.1016/j.enggeo.2018.10.022
[14]	何建涛, 马怀发, 张伯艳, 等. 黏弹性人工边界地震动输入方法及实现[J]. 水利学报, 2010, 41(8): 960-969. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201008014.htm HE Jiantao, MA Huaifa, ZHANG Boyan, et al. Method and realization of seismic motion input of viscous-spring boundary[J]. Journal of Hydraulic Engineering, 2010, 41(8): 960-969. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201008014.htm
[15]	杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件[J]. 力学学报, 2006, 38(1): 49-56. https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB200601007.htm DU Xiuli, ZHAO Mi, WANG Jinting. A stress artificial boundary in fea for near-field wave problem[J]. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(1): 49-56. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-LXXB200601007.htm
[16]	史雯雨, 杨胜勇, 李增永, 等. 近57年金沙江流域气温变化特征及未来趋势预估[J]. 水土保持研究, 2021, 28(1): 211-217. https://www.cnki.com.cn/Article/CJFDTOTAL-STBY202101030.htm SHI Wenyu, YANG Shengyong, LI Zengyong, et al. Variation characteristics and the future trend estimation of temperature in chinsha river basin over the past 57 years[J]. Research of Soil and Water Conservation, 2021, 28(1): 211-217. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-STBY202101030.htm
[17]	沈珠江, 徐刚. 堆石料的动力变形特性[J]. 水利水运科学研究, 1996(2): 143-150. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY602.006.htm SHEN Zhujiang, XU Gang. Deformation behavior of rock materials under cyclic loading[J]. Journal of Nanjing Hydraulic Research Institute, 1996(2): 143-150. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSY602.006.htm
[18]	水工建筑物抗震设计标准: GB51247—2018[S]. 北京: 中国计划出版社. Standard for Seismic Design of Hydraulic Structures: GB51247—2018[S]. Beijing: China Planning Press. (in Chinese)
[19]	沈怀至, 张楚汉, 寇立夯. 基于功能的混凝土重力坝地震破坏评价模型[J]. 清华大学学报, 2007, 47(12): 2114-2118. https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB200712006.htm SHEN Huaizhi, ZHANG Chuhan, KOU Lihang. Performance-based seismic damage assessment model for concrete gravity dams[J]. Journal of Tsinghua University (Science and Technology), 2007, 47(12): 2114-2118. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QHXB200712006.htm