Three-dimensional seismic stability of unsaturated soil slopes using pseudo-dynamic approach
-
摘要: 边坡在地震作用下极易失稳破坏且通常伴随明显的三维破坏特征,增加边坡阶数并结合抗滑桩等加固措施可有效提高边坡的动稳定性,广泛用于滑坡灾害防治中。基于极限分析上限原理并结合拟动力法,将塑性变形理论扩展至非饱和土中,改进已提出的半解析水平片分法,计算具有非线性分布特征的非饱和土重力、地震惯性力和抗滑桩侧阻力所做外功率和表观黏聚力的功率耗散率,与解析解对比,验证了该方法的合理性。通过算例分析,探究了非饱和土边坡的地震响应规律,揭示了吸力对边坡地震稳定性及抗滑桩加固效果的强化作用。结果表明:吸力对边坡稳定性的贡献可达15%~30%,且与地震动特性密切相关,地震波达到峰值时,吸力效应得到显著加强;水平加速度系数和土体剪切模量对边坡地震稳定性影响较大;地震作用下边坡将出现明显的“浅层”滑动现象。Abstract: The seismic excitation remains the main factor in triggering the slope failures that present three-dimensional (3D) features universally. The slopes combined with anti-slide piles are the effective reinforcement techniques in improving the slope stability and are widely employed in slope failure preventions. Based on the upper bound limit analysis theorem and the pseudo-dynamic approach, the plasticity deformation theory is extended to unsaturated soils, and a modified horizontal slice method is proposed to calculate the work rates of unsaturated soil gravity, seismic inertial forces and pile lateral resistance forces as well as the energy dissipation rate of apparent cohesion that are all characterized with nonlinear distribution features. The semi-analytical method is validated through comparisons with the analytical solutions. A series of parametric analyses are conducted regarding the seismic responses of unsaturated soil slopes. The improvements in seismic slope stability due to soil suction are studied systematically. The results show that the slope safety is underestimated by 15% ~ 30% when the soil suction is not considered in the analyses. The suction effects depend on the seismic excitations and are enhanced significantly when the seismic wave approaches the peak. The horizontal acceleration coefficient and soil shear modulus both have a great influence on the slope stability. The critical slip surface becomes much shallower under excitation conditions.
-
Keywords:
- unsaturated soil slope /
- limit analysis /
- pseudo-dynamic approach /
- matric suction /
- 3D effect
-
0. 引言
潜水面上升可能诱发边坡失稳,艾伯凡矿灾[1](Aberfan Disaster)、沃楚西特水坝[2](Wachusett Dam)等就属于这一破坏模式。Brand[3]建议研究边坡的破坏机理时,应该考虑边坡内土体单元的应力应变响应。边坡内潜水面上升的应力路径可以简化为等剪应力排水路径[3-6]。针对等剪应力排水路径下土体的力学响应,研究者们进行了一系列工作[2, 6-7]。Chu等[2]通过试验证明了等剪应力排水路径下土体的非稳定态与边坡失稳存在相关性。Lashkari等[7]利用离散元数值模拟等剪应力排水路径,发现松砂和密砂的非稳定态存在区别。此外,研究者还发现各向异性对等剪应力排水路径的非稳定态存在显著影响。Fanni等[8]通过试验发现大主应力方向从垂直于沉积面旋转到45°时,非稳定态的应力比不断减小,指出在评估边坡稳定时不能忽略各向异性的影响。
一些研究者也在利用本构模型模拟该应力路径。Lashkari等[7]采用了各向异性临界状态塑性本构模型[9]模拟了不同孔隙比和剪应力值下的等剪应力排水试验,表明了模型具有模拟该应力路径的能力。但本构模型能否模拟各向异性条件下的等剪应力排水试验,目前仍然未知。
各向异性对砂土的力学响应有显著影响[10-16]。如何用本构模型描述饱和砂土的力学响应是目前的研究热点之一。为总结各向异性对于砂土力学响应影响的规律,研究者们进行了大量物理试验和离散元数值试验。物理试验方面如Yoshimine等[17]和Nakata等[18]研究了不同加载方向和中主应力系数对丰浦砂应力应变关系的影响,发现当大主应力平行于沉积面、中主应力系数为1时,土样表现出更强的剪缩特性,更易发生静态液化。离散元数值试验方面如Fu等[19]再现了直剪试验,研究各向异性砂土的峰值强度。这些试验为本构模型的建立和验证提供了基础和依据,各类模型通过模拟试验证明了自身的有效性[20-23]。如Wang等[22]通过离散元数值试验总结各向异性对塑性模量和剪胀的影响,在CycLiq本构模型[24]的基础上加入了组构各向异性,并通过离散元试验和物理试验对新模型进行了验证。
本文利用Wang等[22]提出的各向异性CycLiq本构模型,对Fanni等[8]进行的一系列定轴不排水试验与定轴等剪应力排水试验进行了模拟,验证了该模型对于各向异性砂土在不同主应力方向下、不同应力路径力学响应的模拟能力,并研究了初始组构强度对于模型模拟定轴等剪应力排水试验结果的影响。
1. 各向异性CycLiq模型
1.1 本构模型
基于排水与不排水循环扭剪试验现象研究,张建民等[25-26]将砂土的体应变εv分解为有效球应力变化引起的弹性体应变εvc和剪切引起的塑性体应变εvd,又将剪切引起的塑性体应变εvd进一步划分为可逆性剪切体应变εvd, re与不可逆性剪切体应变εv, ir。在此基础上,王刚等[27]和Wang等[24]建立了一个能够模拟饱和砂土液化前后应力应变响应的弹塑性循环本构模型,并在模型中引入了状态变量,使得模型能够统一描述砂土在不同状态下的静动力响应。为考虑各向异性,Wang等[22]基于试验和离散元数值模拟总结的规律,对模型进行了改进,引入了组构张量,在塑性模量与剪胀率的计算中引入了各向异性的影响,使得模型能够描述不同主应力方向下的响应。
CycLiq模型的应力应变关系可以用下式来描述:
˙ε=p˙r2G+(r2G+I3K)˙p+(n+D3I)⟨L⟩。 (1) 式中:p为有效球应力;r为偏应力张量s与球应力p之比;G和K为弹性剪切模量和体积模量;I为单位张量;n为塑性偏应变流动方向与加载方向;D为剪胀率;L为塑性加载指数。参数上加(·)表示增量;〈〉为Macaulay计算符,当x > 0时,〈x〉= x,当x ≤ 0时,〈x〉= 0。
弹性剪切模量和体积模量采用Richart等[28]提出的线性弹性模量公式,在此不再赘述。塑性加载指数L通过下式计算:
L=p˙r:nH。 (2) 式中:H为塑性模量。
砂土临界状态采用Been等[29]提出的状态变量Ψ =e−ec,但ec与p的关系采用了与Wang等[22]所使用的指数关系[30]不同的对数关系:
ec=Γ−λeln(p)。 (3) 这一改动是因为Fanni等[8]给出了本文模拟试样临界状态下试样的e-p曲线,并采用式(3)的对数关系进行了拟合,且e-p曲线的对数关系被广泛采用,许多模型采用了这种关系[31-32],因此对模型中的公式进行了替换。不过需要指出的是,在液化状态时,对数关系不再适用,因此砂土的动力本构模型大都采用指数关系[33-34]。本文中不涉及液化内容,因此可以选取对数关系进行模拟。
为了考虑各向异性的影响,Wang等[22]在模型中引入了组构张量Fn,并考虑了组构张量对于塑性模量与剪胀率的影响。组构张量Fn的演化采用了如下公式:
dFn=⟨L⟩c[n−(1+D)Fn]。 (4) 式中:c为模量参数,代表组构张量演化的速率。通过总结离散元数值试验的规律,Wang等[22]发现组构张量的模||Fn||与组构张量和加载方向的联合不变量An =Fn: n之差||Fn||-An可以作为一个良好的指标,以反映塑性模量和剪胀率随加载角度的变化。以水平沉积的试样在三轴压缩中的加载角度为0°,随着加载角度的增加,指标||Fn||-An不断增大,同时塑性模量不断减小,剪胀率从不断增加。因此,将||Fn||-An引入到了塑性模量与剪胀率的计算公式中:
C=exp[−Δ1(‖Fn‖−An)1/122], (5) H=23hg(θ)Gexp(−npΨ)⋅(Mexp(−npΨ)Mmˉρρ−1C), (6) Dir=dir+Δ2(‖Fn‖−An)dirDir, iso。 (7) 式中:h,Δ1,Δ2,M,dir,np为模型参数;g(θ)为形状函数,这里采用的是Zhang等[35]建议的函数;Mm为历史最大应力比;Dir, iso为各向同性条件下的不可逆剪胀率,详细公式可见Wang等[24]。
1.2 参数标定
Fanni等[8]试验中采用的砂为一种细硅砂,颗粒相对质量密度为2.64,平均粒径D50为0.21 mm,均匀系数Cu为2.3,颗粒呈圆形至亚圆形。因缺乏相关试验,大部分参数参照了Wang等[22]标定的丰浦砂参数,仅对部分可确定的临界状态参数(np,Γ,λe)进行了重新标定。标定结果如表 1所示。
其中,Γ和λe由Fanni等[8]根据试验拟合得到,在更换了Wang等[22]模型中ec与p的关系式后可直接使用。图 1展示了np的标定方法,以Fanni等[8]进行的一组定轴等剪应力排水试验(中主应力系数b = 0.2,加载角度α = 30°)结果参照进行标定。图中点代表试验所得试样到达非稳定态时的有效球应力与孔隙比,虚线和实线分别为np = 6和12时的模拟结果。可以看到当其他参数不变时,np值越大,模拟得到的非稳定态时有效球应力随孔隙比变化越快,曲线更加陡峭。这是由于等剪应力排水路径中的非稳定态代表试样处于峰值应力比状态,而峰值应力比可由Mexp(-npΨ)决定。
除了表 1中列出的模型参数外,初始组构强度,即初始组构张量的模||Fnin||,也是一个重要的参数。它代表了试样在试验开始时的各向异性程度,||Fnin||越大,试样的各向异性越强。不同的制样方式制得的试样往往有着不同的各向异性程度[36],因此需要取不同的初始组构强度。本次模拟中涉及两种不同的制样方式,湿装夯实法(moist tamped, MT)和干砂雨法(dry pluviated, DP),其中干砂雨法得到的试样孔隙比要小于湿装夯实法,结合Yang等[37]、叶斌等[38]通过物理试验与离散元模拟均发现干砂雨法的各向异性强于湿装夯实法,可以推测干砂雨法在制样中,由于受到重力影响,土颗粒的排列具有定向性,而湿装夯实法在制样中,土颗粒更倾向于随机排列,导致其各向异性相对较弱。最终,湿装夯实法制得的试样初始组构强度||Fnin||取为0.5,干砂雨法制得的试样初始组构强度||Fnin||取为0.7。
2. 不同主应力方向下模型的响应
2.1 定轴不排水剪切试验
Fanni等[8]进行了一系列空心圆柱定轴不排水剪切试验。试验中,初始有效球应力均为171 kPa,大小主应力之差均为64 kPa,中主应力系数b分别为0,0.2,0.5,大主应力与沉积方向的夹角α分别为0°,22.5°,30°和45°,两种制样方法,即湿装夯实法和干砂雨法,各5组试验,如图 2,3所示。其中,湿装夯实法所得试样孔隙比在0.761~0.785,干砂雨法所得试样孔隙比在0.674~0.697。采用表 1中的模型参数对试验进行模拟,模拟结果如图 2,3所示。图 2(a),(b)中横纵坐标为Fanni等[8]给出的八面体剪应变和八面体偏应力,图 3同理。
表 1 各向异性CycLiq模型参数Table 1. Model parameters of anisotropic CycLiq modelGo κ h dre, 1 dre, 2 dir α γd, r np nd M λe Γ Δ1 Δ2 c 100 0.008 4.0 0.7 30 0.3 30 0.05 12 2 1.2 0.008 0.761 1.35 0.8 5 图 2展示了湿装夯实法试样定轴不排水试验结果与模拟。湿装夯实法得到的试样均为松砂,各试验和模拟均出现静态液化。总体上来看,随着b和α的增加,试验与模拟中试样的峰值偏应力均不断减小。从图 2(a),(c)中可以看出,试验中b = 0.2的3组曲线极为接近,甚至α = 30°的偏应力要高于α = 22.5°,这主要是试验中不同试样的孔隙比相差较大造成的,在模拟中该现象并不明显。此外,b = 0.5的模拟结果在加载初期剪应力出现了明显的减小,这主要是由于本构模型中组构对塑性模量的影响描述不够准确,在大孔隙比下放大了组构对塑性模量的影响。
图 3展示了干砂雨法试样定轴不排水试验结果与模拟。相比于湿装夯实法,干砂雨法得到的试样孔隙比更小,可认为密砂。各组模拟的曲线与试验结果均有较好的吻合。对于b = 0.2的3组试验和模拟,α = 22.5°时均表现出明显的剪胀,而在α = 45°时则表现出强烈的剪缩。对于b = 0,α = 0°和b = 0.2,α = 22.5°两组试验,试验和模拟的曲线在图 3(a),(b)均出现了交叉,这是由于两者的孔隙比相差较大,在孔隙比、中主应力系数、主应力方向三者的共同作用下出现了图中的效果。
2.2 定轴等剪应力排水试验
在定轴不排水剪切试验的基础上,Fanni等[8]进行了一系列定轴等剪应力排水试验,以探究各向异性对等剪应力排水应力路径的影响。试验中采用了湿装夯实法(MT)和干砂雨法(DP)两种制样方法,初始有效球应力均为171 kPa,大小主应力之差均为64 kPa,中主应力系数b分别为0,0.2,主应力与沉积方向的夹角α分别为0°,22.5°和45°。每个夹角均用不同的孔隙比进行试验,对于湿装夯实法,b = 0,α = 0°组采用了6个不同的孔隙比,b = 0.2,α = 22.5°组采用了4个,b = 0.2,α = 45°组采用了10个;对于干砂雨法, b = 0.2,α = 22.5°组1个,b = 0.2,α = 45°组2个。采用表 1中的模型参数进行模拟,模拟中保持偏应力不变,当有效球应力无法再减小时,即试样达到峰值应力比时,认为此时试样处于非稳定态,模拟结束。
图 4给出了湿装夯实法试样在不同b和α下的定轴等剪应力排水试验结果与模拟。图中圆代表初始状态,三角形代表试样达到非稳定态,即处于峰值应力比状态。当相同b和α时,非稳定态的有效球应力p随孔隙比e的增加而增加,3组中模拟与试验均吻合较好。当孔隙比e不变、α增加时,模拟与试验得到的有效球应力均增加。
图 5给出了干砂雨法试样在不同b和α下的定轴等剪应力排水试验结果与模拟。b = 0.2,α = 45°组试验与模拟结果相近,规律也与湿装夯实法中一致;模拟结果在定量上与试验结果存在差距,推测这是由于模型参数或者初始组构强度不准确导致的。当α增加时,模拟与试验得到的有效球应力均增加,这与湿装夯实法中的规律是一致的。
图 6给出了试验和模拟中非稳定态的结果与趋势线。可以看到试验得到的非稳定态在e-p空间内具有良好的线性关系,对模拟得到的非稳定态进行线性回归,得到R2均在0.99以上,表明模型对等剪应力比试验具有良好的模拟能力。对比湿装夯实法的3组试验,可以发现模拟得到的3条趋势线之间的间距要略小于试验所得,这主要受初始组构强度的影响,具体情况在下文中阐释。
为了说明初始组构强度对于定轴等剪应力排水条件下土体响应的影响,在数值模拟中对不同初始组构强度条件进行了分析。图 7中给出了不同初始组构强度对非稳定态模拟结果的影响。从图中可以发现初始组构越强,不同主应力方向下的非稳定态差异越大,即峰值应力比差异越大。式(5),(6)中可以解释这一现象。试样达到峰值应力比时,有塑性模量H = 0。当初始组构强度增加,即||Fn||增加时,指标||Fn||-An = ||Fn||(1 – nF: n)(其中nF指组构张量的方向)的值域[0, 2||Fn||]随之扩大,式(5)所得C的值域也相应扩大。对于定轴试验,初始组构强度增加,导致了不同的b和α计算得到C值之间的差异增加,因H = 0,进而使得式(6)中历史最大峰值应力比Mm(即非稳定态时的应力比)的差异增加,在剪应力q不变的情况下,非稳定态时的球应力p之间的差异也就增加了。这些反映在图 7中即为趋势线之间的间距增加。
3. 结论
本文利用各向异性CycLiq本构模型,模拟了Fanni等[8]进行的定轴不排水试验与定轴等剪应力排水试验,对比试验结果与模拟结果,可以得到以下3点结论。
(1)对于定轴不排水剪切试验,该模型与试验均表现为随着中主应力系数和加载角度的增加,土体剪缩增强,更易发生静态液化。在定量上,模型模拟的应力路径和应力应变曲线与试验也有较好的吻合。
(2)对于定轴等剪应力排水试验,模型与试验均表现为非稳定态时的平均有效应力随孔隙比和加载角度的增加而增加,且相同加载角度的非稳定态在e-p空间内呈线性分布。总体来说,CycLiq模型对各向异性下砂土等剪应力排水响应的模拟效果较好,具有运用到实际工程中的潜力。
(3)不同初始组构强度对于等剪应力排水试验的结果有显著的影响。初始组构强度越高,不同主应力方向作用下的非稳定态时平均有效应力相差越大。
-
表 1 不同方法得到的边坡安全系数
Table 1 FOSs obtained by different methods
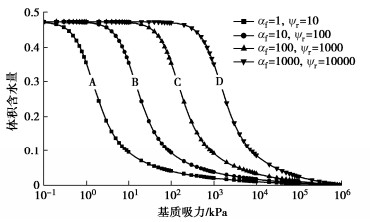
表 2 4种典型非饱和土SWCC曲线参数
Table 2 Parameters for four selected SWCC curves
SWCC No. af/
kPanf mf ψr/
kPaα/
kPa-1θr A 1 2 1 10 2 0.081 B 10 2 1 100 0.2 0.080 C 100 2 1 1000 0.02 0.078 D 1000 2 1 10000 0.002 0.073 -
[1] 郑颖人, 叶海林, 黄润秋, 等. 边坡地震稳定性分析探讨[J]. 地震工程与工程振动, 2010, 30(2): 173-180. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201002028.htm ZHENG Yingren, YE Hailin, HUANG Runqiu, et al. Study on the seismic stability analysis of a slope[J]. Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(2): 173-180. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201002028.htm
[2] 黄润秋. 20世纪以来中国的大型滑坡及其发生机制[J]. 岩石力学与工程学报, 2007, 26(3): 433-454. doi: 10.3321/j.issn:1000-6915.2007.03.001 HUANG Runqiu. Large-scale landslides and their sliding mechanisms in China since the 20th century[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 433-454. (in Chinese) doi: 10.3321/j.issn:1000-6915.2007.03.001
[3] 张江伟, 李小军, 王晓明, 等. 土质边坡地震稳定性状态判定方法研究[J]. 岩土工程学报, 2018, 40(11): 2096-2102. doi: 10.11779/CJGE201811016 ZHANG Jiangwei, LI Xiaojun, WANG Xiaoming, et al. Method for judging seismic stability state of soil slopes[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(11): 2096-2102. (in Chinese) doi: 10.11779/CJGE201811016
[4] NEWMARK N M. Effects of earthquakes on dams and embankments[J]. Géotechnique, 1965, 15(2): 139-160. doi: 10.1680/geot.1965.15.2.139
[5] STEEDMAN R S, ZENG X. The influence of phase on the calculation of pseudo-static earth pressure on a retaining wall[J]. Géotechnique, 1990, 40(1): 103-112. doi: 10.1680/geot.1990.40.1.103
[6] ZENG X, STEEDMAN R S. On the behavior of quay walls in earthquakes[J]. Geotechnique, 1993, 43: 417-431. doi: 10.1680/geot.1993.43.3.417
[7] 宋桂锋, 杜江梅, 柯鉴, 等. 基于拟动力法的顺层岩质边坡稳定性极限分析[J]. 地震工程学报, 2019, 41(4): 931-938. doi: 10.3969/j.issn.1000-0844.2019.04.931 SONG Guifeng, DU Jiangmei, KE Jian, et al. Stability limit analysis of bedding rock slopes based on pseudo-dynamic method[J]. China Earthquake Engineering Journal, 2019, 41(4): 931-938. (in Chinese) doi: 10.3969/j.issn.1000-0844.2019.04.931
[8] 饶平平, 童磊磊, 师昀巍. 基于拟动力法的抗滑桩加固边坡地震稳定性分析[J]. 世界地震工程, 2020, 36(1): 189-196. https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC202001024.htm RAO Pingping, TONG Leilei, SHI Yunwei. Seismic stability analysis of slopes reinforced with anti-slide piles based on pseudo-dynamic method[J]. World Earthquake Engineering, 2020, 36(1): 189-196. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJDC202001024.htm
[9] VANAPALLI S K, FREDLUND D G, PUFAHL D E, et al. Model for the prediction of shear strength with respect to soil suction[J]. Canadian Geotechnical Journal, 1996, 33(3): 379-392. doi: 10.1139/t96-060
[10] FREDLUND D, XING A Q. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521-532. doi: 10.1139/t94-061
[11] LU N, LIKOS W J. Unsaturated Soil Mechanics[M]. New York: John Wiley, 2004.
[12] BISHOP A W. The principle of effective stress[J]. Teknisk Ukeblad, 1959, 39: 859-863.
[13] FREDLUND D G, MORGENSTERN N R, WIDGER R A. The shear strength of unsaturated soils[J]. Canadian Geotechnical Journal, 1978, 15(3): 313-321. doi: 10.1139/t78-029
[14] ZHANG L L, FREDLUND D G, FREDLUND M D, et al. Modeling the unsaturated soil zone in slope stability analysis[J]. Canadian Geotechnical Journal, 2014, 51(12): 1384-1398. doi: 10.1139/cgj-2013-0394
[15] SUN D A, WANG L, LI L. Stability of unsaturated soil slopes with cracks under steady infiltration conditions[J]. International Journal of Geomechanics, 2019, 19(6): 04019044. doi: 10.1061/(ASCE)GM.1943-5622.0001398
[16] WANG L, SUN D A, YAO Y P, et al. Kinematic limit analysis of three-dimensional unsaturated soil slopes reinforced with a row of piles[J]. Computers and Geotechnics, 2020, 120: 103428. doi: 10.1016/j.compgeo.2019.103428
[17] 卢坤林. 基于极限平衡理论的土质边坡空间效应研究及应用[D]. 合肥: 合肥工业大学, 2013. LU Kunlin. Research on the 3D Effect of Homogeneous Slope Stability Analysis Based on the Limit Equilibrium Method and Its Application to Engineering[D]. Hefei: Hefei University of Technology, 2013. (in Chinese)
[18] GIGER M W, KRIZEK R J. Stability analysis of vertical cut with variable corner angle[J]. Soils and Foundations, 1975, 15(2): 63-71. doi: 10.3208/sandf1972.15.2_63
[19] DRESCHER A. Limit plasticity approach to piping in bins[J]. Journal of Applied Mechanics, 1983, 50(3): 549-553. doi: 10.1115/1.3167089
[20] MICHALOWSKI R, DRESCHER A. Three-dimensional stability of slopes and excavations[J]. Géotechnique, 2009, 59(10): 839-850. doi: 10.1680/geot.8.P.136
[21] PARK D, MICHALOWSKI R L. Three-dimensional roof collapse analysis in circular tunnels in rock[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 128(C): 104275.
[22] YANG S Y, WANG Z, WANG J M, et al. 3D seismic stability analysis of bench slope with pile reinforcement[J]. Geotechnical and Geological Engineering, 2022, 40: 1149-1163. doi: 10.1007/s10706-021-01949-y
[23] CHEN W F. Limit Analysis and Soil Plasticity[M]. Amsterdam, New York: Elsevier Scientific Pub Co, 1975.
[24] ITO T, MATSUI T. Methods to estimate lateral force acting on stabilizing piles[J]. Soils and Foundations, 1975, 15(4): 43-59. doi: 10.3208/sandf1972.15.4_43
-
本文视频
其他相关附件




 下载:
下载: