Reinforcement calculation of concrete slab in concrete faced rockfill dams
-
摘要: 混凝土面板应力变形安全是面板堆石坝工程的关键，然而传统面板坝分析方法大多未考虑面板的配筋效应，实际面板配筋方案制定缺乏理论依据。提出了基于限裂理念的混凝土面板配筋计算方法：采用非协调网格计算技术精细模拟混凝土面板应力，采用钢筋埋置单元模拟钢筋加固作用，采用损伤模型模拟混凝土材料损伤开裂行为，通过引入与几何尺寸、钢筋应力相关的裂缝宽度公式实现混凝土面板限裂配筋计算。提出的方法可定量研究面板限裂配筋，为复杂条件下面板坝配筋设计提供理论依据。文中以正在施工建设的大石峡特高面板坝为例，初步研究了该坝的面板配筋方案。Abstract: The stress and deformation safety of the concrete slab is crucial to the concrete faced rockfill dams (CFRDs), however, most of the traditional methods do not consider the effects of the reinforcement in slab, therefore, the calculated results can not provide enough information to the design of slab reinforcement. In this study, a method for calculating the slab reinforcement based on the concept of crack width limit is proposed: the non-coordinated grid computing technology is used to refinedly simulate the stress of the concrete slab, the embedded steel element is used to simulate the reinforcement effects, and the damage model is used to simulate the cracking of the slab concrete. By introducing a formula for crack width related to geometric size and rebar stress, and setting the crack width limit, the reinforcement calculation is realized. The proposed method can be used to quantitatively study the slab reinforcement and provide a theoretical basis for reinforcement design under complex conditions. The Dashixia CFRD under construction is taken as an example and its slab reinforcement design is preliminarily studied.
-
0. 引言
混凝土面板的应力变形安全是面板堆石坝安全保障的核心内容。实践表明，许多面板堆石坝在施工期和运行期均出现过面板裂缝问题。水布垭大坝Ⅰ，Ⅱ，Ⅲ期面板均曾出现过不同程度的裂缝问题，从裂缝发育形态来看，大部分表现为水平向裂缝，修复后水库能够安全运行[1]，图 1为该坝Ⅰ期面板裂缝。蓄水运行十余年的HJD面板坝在2020年汛前低水位检查时发现了面板裂缝，其中，河床坝段裂缝以顺坡向的纵裂缝为主，而两岸坝肩面板裂缝则以水平向裂缝为主，图 2为该坝左岸面板出现的水平裂缝形态。JL面板坝面板脱空严重，面板受力状态差，左岸面板出现了贯穿性裂缝和水平向断裂，严重影响了大坝正常运行，如图 3。
混凝土面板裂缝成因主要有外力引起的结构性裂缝、混凝土干缩裂缝、温度裂缝等，其中结构裂缝的危害最大。配筋是控制面板表面裂缝的主要工程措施，但长期以来面板堆石坝计算中极少考虑钢筋的加固作用，计算结果难以定量辅助面板配筋，实际工程配筋仍以经验为主。新修订的《混凝土面板堆石坝设计规范：NB/T 10871—2021》规定[2]“面板可采用单层双向或双层双向钢筋。面板每层每向配筋率宜为0.3%~0.5%...”，以上规定来源于国内外面板堆石坝工程实践总结，常规堆石坝工程可参照执行，但对于复杂地形地质条件、软岩筑坝、深厚覆盖层上高面板堆石坝工程能否适用尚没有定论。所以，进一步发展考虑面板配筋加固效应的计算方法具有重要工程意义。
在传统的面板堆石坝数值计算方法基础上实现面板配筋计算需进行以下3方面必要改进：①混凝土面板应力的精细模拟，工程案例表明，面板破损、开裂呈明显的局部化特征，稀疏的混凝土面板单元会因为单元“平均效应”低估局部的应力量值，不能准确定位面板的危险区；②钢筋-混凝土单元模型的选择，面板中钢筋数目庞大，选用合理的钢筋-混凝土单元可降低几何建模工作量，增加计算方法的实用性和处理复杂问题的能力；③描述混凝土损伤退化的本构模型，传统的线弹性模型不能反映混凝土材料刚度损伤退化性质，无法模拟混凝土开裂后钢筋的加固效应。
基于以上的实际考虑，本研究分别采用非协调网格计算技术实现混凝土面板精细模拟，采用便捷的钢筋埋置单元模拟钢筋加固作用，采用损伤模型模拟混凝土材料损伤开裂行为。基于自主研制的TOSS3D有限元软件平台，集成实现了以上技术，提出了基于限裂理念的混凝土面板配筋计算方法。本文采用的方法理论清晰、使用简便，具有较好的应用前景，文中以开工建设的大石峡面板坝为例，初步研究了面板配筋方案。
1. 非协调网格计算方法
大型面板堆石坝工程计算模拟中，研究人员应兼顾计算精度和计算效率。实践表明，筑坝堆石体应力变形变化平缓，可设置相对稀疏的计算网格，混凝土面板应力变化梯度大，应布置精细网格[3]。因此，采用非协调网格计算技术实现面板精细网格向堆石体稀疏网格的过渡是一种行之有效的方法。清华大学周墨臻等[4-5]基于非线性接触力学的方法实现多体之间荷载传递，并应用于了天生桥一级面板堆石坝应力变形性状模拟。孔宪京等[6]、邹德高等[7-8]采用多边形比例边界有限元技术实现了面板坝结构跨尺度精细化分析，已应用于数座在建高面板坝工程。
笔者基于位移多点约束法发展了面板坝非协调网格计算技术，实现了对混凝土面板的精细模拟[9]，该方法优势在于基于矩阵变换[3]，无需引入罚函数和迭代求解[10]，提高了计算效率。
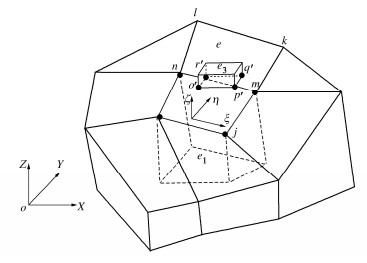
位移多点约束法基本原理如图 4。单元e1，e2为稀疏网格单元，单元e3为密集网格单元，则单元e3的结点o′，p′，q′，r′的3向位移均可由单元e1和e2的结点位移表示，其中结点o′的三向位移uo′，vo′，wo′可由结点i，j，m，n的位移表达，q′的三向位移可由结点m，k，i，n的位移表示。以结点o′为例，若采用等参单元插值方法，其三向位移可表示为
uo′=N1ui+N2uj+N3um+N4un,vo′=N1vi+N2vj+N3vm+N4vn,wo′=N1wi+N2wj+N3wm+N4wn。} (1) 式中：N1∼N4为i，j，m，n平面局部坐标表示的形函数[11]，
N1=14(1−ξ)(1−η)， (2a) N2=14(1+ξ)(1−η)， (2b) N3=14(1+ξ)(1+η)， (2c) N4=14(1−ξ)(1+η)。 (2d) 式中：ξ，η为结点o′在i，j，m，n面上的局部坐标。此时单元结点o′，p′，q′，r′的3向自由度均为“从自由度”，结点i，j，m，n，l，k的3向自由度为“主自由度”。
通过转换矩阵缩聚运算[3]可将密集网格单元e3刚度矩阵、荷载矩阵组装到整体刚度矩阵和荷载列阵，求解平衡方程后，得到结点i，j，m，n位移，再根据式（1）反推出结点o′的位移。
2. 钢筋-混凝土组合模型
有限元法模拟混凝土配筋可分为2类模式。
（1）分离式，把混凝土和钢筋作为不同的单元处理，混凝土和钢筋通过共结点实现相互作用[12]，这种方法优点在于可直接利用现有的程序，缺陷在于前处理复杂，方案调整成本高，对于复杂三维情况甚至难以实现，该方法多见于二维数值模拟和研究探索，在工程实际中未见大规模使用。
（2）组合式，假设钢筋以一个任意角度分布在单元中，并假设混凝土与筋材之间存在良好的胶结，可推导出带钢筋的等参数单元刚度矩阵。该方法中钢筋单元与混凝土单元不共结点，增加了解决三维复杂问题的灵活性。本文计算即采用组合式钢筋混凝土模型。
2.1 钢筋混凝土组合单元
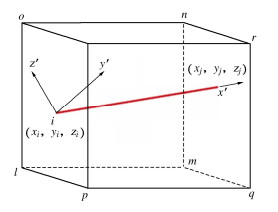
图 5为埋置一根钢筋的混凝土实体单元[11]。令钢筋埋置单元起点坐标为(xi,yi,zi)，终点的坐标为(xj, yj,zj)。则组合单元的应变能由实体单元和筋材单元应变能两部分组成，
\begin{aligned} U_{\mathrm{e}} & =\frac{1}{2} \int\limits_{V^e} \boldsymbol{\varepsilon}^{\mathrm{T}} \boldsymbol{\sigma} \mathrm{d} v+\frac{1}{2} \varepsilon \sigma \\ & =\frac{1}{2}\left(\boldsymbol{a}^{\mathrm{e}}\right)^{\mathrm{T}} \int\limits_{V^{\mathrm{e}}} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{B} \mathrm{d} v \alpha^{\mathrm{e}}+\frac{1}{2}\left(\boldsymbol{a}^{\mathrm{e}}\right)^{\mathrm{T}} \int\limits_{-1}^1 \boldsymbol{B}_{\mathrm{s}}^{\mathrm{T}} A_{\mathrm{s}} E_{\mathrm{s}} \boldsymbol{B}_{\mathrm{s}} h \mathrm{d} \xi 。 \end{aligned} (3) 钢筋埋置单元的刚度矩阵表示为
{\boldsymbol{k = }}{{\boldsymbol{k}}_{\text{r}}}{\boldsymbol{ + }}{{\boldsymbol{k}}_{\text{s}}} 。 (4) 式中： {{\boldsymbol{k}}_{\text{r}}} 为实体单元刚度矩阵，形式与常规有限元一致； {{\boldsymbol{k}}_{\text{s}}} 为钢筋单元刚度矩阵，
{{\boldsymbol{k}}_{\text{s}}} = \int_{ - 1}^1 {{A_{\text{S}}}{E_{\text{S}}}{\boldsymbol{B}}_{\text{s}}^{\text{T}}} {\boldsymbol{B}}_{\text{s}}^{}h{\text{d}}\xi ' 。 (5) 式中：As为钢筋截面积； {E_{\text{S}}} 为钢筋模量。
h = \sqrt {{{\left( {\frac{{\partial x}}{{\partial \xi '}}} \right)}^2} + {{\left( {\frac{{\partial y}}{{\partial \xi '}}} \right)}^2} + {{\left( {\frac{{\partial z}}{{\partial \xi '}}} \right)}^2}} 。 (6) 钢筋应变矩阵Bs可表示为
\left[B_{\mathrm{s}}\right]=\left[\begin{array}{l} l^2 \frac{\partial N_1}{\partial x}+lm \frac{\partial N_1}{\partial y}+ln \frac{\partial N_1}{\partial z} \\ lm \frac{\partial N_1}{\partial x}+m^2 \frac{\partial N_1}{\partial y}+m n \frac{\partial N_1}{\partial z} \\ ln \frac{\partial N_1}{\partial x}+n m \frac{\partial N_1}{\partial y}+n^2 \frac{\partial N_1}{\partial z} \\ \quad\quad\quad\quad\quad \cdots \end{array}\right]^{\mathrm{T}}。 (7) 式中：l，m，n为钢筋的方向余弦。
2.2 钢筋交点与积分点坐标
式（5）所表达的钢筋刚度矩阵在应用于计算之前还有2个关键问题需要解决：①钢筋与混凝土单元交点位置确定；②钢筋高斯积分点局部坐标确定。这2个问题都涉及到局部坐标的逆映射方法[13]，即通过整体坐标求局部坐标。
等参元中任意点p的坐标可表示为
{\left\{ {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right\}_p} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{N}}&{}&{} \\ {}&{\boldsymbol{N}}&{} \\ {}&{}&{\boldsymbol{N}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\boldsymbol{X}} \\ {\boldsymbol{Y}} \\ {\boldsymbol{Z}} \end{array}} \right\} 。 (8) 式中：N为三维等参元形函数矩阵，X，Y，Z为单元结点坐标向量。
式（8）中未知量为局部坐标 \left\{ {\begin{array}{*{20}{c}} {\xi , }&{\eta , }&\zeta \end{array}} \right\} ，可采用牛顿迭代法求解，迭代格式为
\left\{ {\begin{array}{*{20}{c}} \xi \\ \eta \\ \zeta \end{array}} \right\}_p^{n + 1} = \left\{ {\begin{array}{*{20}{c}} \xi \\ \eta \\ \zeta \end{array}} \right\}_p^n + \left\{ {\begin{array}{*{20}{c}} {\Delta \xi } \\ {\Delta \eta } \\ {\Delta \zeta } \end{array}} \right\}_p^{n + 1} \text{，} (9) \left\{ {\begin{array}{*{20}{c}} {\Delta \xi } \\ {\Delta \eta } \\ {\Delta \zeta } \end{array}} \right\}_p^{n + 1} = {\left[ {{\boldsymbol{J}}_n^{\text{T}}} \right]^{ - 1}}\left\{ {{{\left\{ {\begin{array}{*{20}{c}} x \\ y \\ z \end{array}} \right\}}_p} - \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{N}}^n}}&{}&{} \\ {}&{{{\boldsymbol{N}}^n}}&{} \\ {}&{}&{{{\boldsymbol{N}}^n}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\boldsymbol{X}} \\ {\boldsymbol{Y}} \\ {\boldsymbol{Z}} \end{array}} \right\}} \right\} 。 (10) 式中： {\boldsymbol{J}} 为雅克比矩阵。
基于以上解法，钢筋与混凝土单元交点位置确定方法如下：对于任意一个混凝土单元，求解单元各表面所在空间平面方程与钢筋空间直线方程的交点，如果交点存在，则通过交点整体坐标按式（9）求局部坐标，如果局部坐标满足判别式（11），则交点是有效的，将得到的交点局部坐标代入式（8）得到交点的整体坐标。
- 1 \leqslant \begin{array}{*{20}{c}} {\xi , }&{\eta , }&\zeta \end{array} \leqslant 1 。 (11) 需要注意，式（5）中钢筋的积分点坐标需要从钢筋单元一维局部坐标换算至混凝土单元三维局部坐标系。具体方法如下：通过钢筋单元一维局部坐标系下积分点坐标 \xi^{\prime} 、钢筋单元起点整体坐标 ({x_j}, {y_j}, {z_j}) 、终点整体坐标 ({x_j}, {y_j}, {z_j}) 可得到钢筋积分点的整体坐标 ({x_p}, {y_p}, {z_p}) ，然后根据式（9）求该积分点对应的实体单元内部局部坐标 \{ {\xi _p}, {\eta _p}, {\zeta _p}\} 。
3. 混凝土损伤模型
当混凝土受力状态未达到峰值强度时，采用线弹性模型是基本合适的，一旦应力到达到峰值强度，其后加载过程会出现明显的刚度退化，线弹性模型已不再适用。近些年，已有不少学者尝试将损伤模型[14-15]、黏聚力模型[12]等引入混凝土面板计算。本文采用《混凝土结构设计规范：GB50010—2010》推荐的混凝土损伤模型[16]。
混凝土应力应变关系表示为
\sigma = {\text{(}}1 - {d_{{\text{t/c}}}}{\text{)}}{E_{\text{c}}}\varepsilon 。 (12) 式中： \sigma 为应力状态； \varepsilon 为应变； {E_{\text{c}}} 为初始变形模量； {d_{{\text{t/c}}}} 为拉/压损伤演化参数。
受拉情况下，损伤演化参数定义为
d_{\mathrm{t}}=\left\{\begin{array}{ll} 1-\rho_{\mathrm{t}}\left[1.2-0.2 x^5\right] & (x \leqslant 1) \\ 1-\frac{\rho_t}{\alpha_{\mathrm{t}}(x-1)^{1.7}+x} & (x>1) \end{array}, \right. (13) x = \frac{\varepsilon }{{{\varepsilon _{{\text{tr}}}}}} \text{，} (14) {\rho _t} = \frac{{{f_{{\text{tr}}}}}}{{{E_{\text{c}}} \cdot {\varepsilon _{{\text{tr}}}}}} 。 (15) 式中： {f_{{\text{tr}}}} 为抗拉强度代表值； {\varepsilon _{{\text{tr}}}} 为与抗拉强度代表值 {f_{{\text{tr}}}} 对应的拉应变； {\alpha _{\text{t}}} 为受拉应力应变曲线下降段控制参数。
受压情况下，损伤参数定义如下：
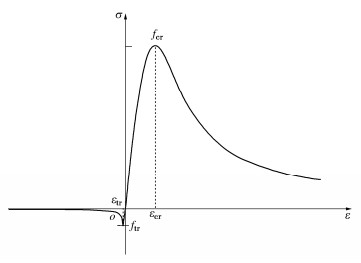
d_{\mathrm{c}}=\left\{\begin{array}{cc} 1-\frac{\rho_{\mathrm{c}} n}{n-1+x^n} & (x \leqslant 1) \\ 1-\frac{\rho_{\mathrm{c}}}{\alpha_{\mathrm{c}}(x-1)^2+x} & (x>1) \end{array}, \right. (16) {\rho _{\text{c}}} = \frac{{{f_{{\text{cr}}}}}}{{{E_{\text{c}}} \cdot {\varepsilon _{{\text{cr}}}}}} \text{，} (17) n = \frac{{{E_{\text{c}}} \cdot {\varepsilon _{{\text{cr}}}}}}{{{E_{\text{c}}} \cdot {\varepsilon _{{\text{cr}}}} - {f_{{\text{cr}}}}}} \text{，} (18) x = \frac{\varepsilon }{{{\varepsilon _{{\text{cr}}}}}} 。 (19) 式中： {f_{{\text{cr}}}} 为抗压强度代表值； {\varepsilon _{{\text{cr}}}} 为与抗压强度代表值 {f_{{\text{cr}}}} 对应的压应变； {\alpha _{\text{c}}} 为受压应力应变曲线下降段控制参数。模型应力应变关系如图 6。
该模型使用简便，参数可根据混凝土标号依规范取定。另外需要指出的是，式（12）给出的是混凝土“割线模量”，堆石坝计算需要采用增量法模拟填筑、蓄水过程，实际应用中还需要取微分得到“切线模量”。
4. 工程案例与数值模型
4.1 工程概况
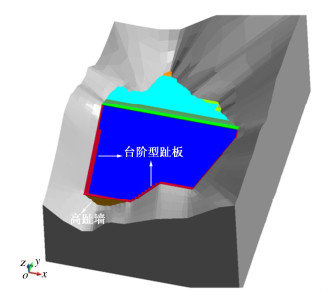
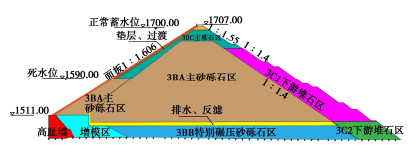
正在施工建设的新疆大石峡面板坝最大坝高247 m，建成后将成为世界第一高面板坝。该坝位于强不对称河谷，左岸极为陡峭，右岸略平缓但存在古河槽覆盖层，为缓解周边缝变形，采用了河床高趾墙、两岸台阶型趾板的特殊防渗体型式，如图 7。大坝材料分区如图 8，坝体主要采用砂砾石料填筑，死水位以上上游坝坡及下游坝坡采用爆破堆石料填筑，以增强坝坡的稳定性和排水能力。坝体填筑、面板浇筑均分为Ⅲ期，从大坝开始填筑至初次满蓄历时78个月，计算模拟至蓄水运行后8 a。
4.2 有限元几何模型
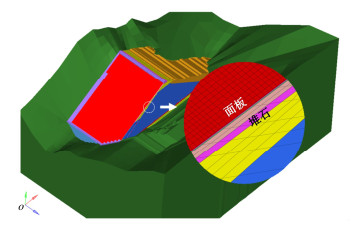
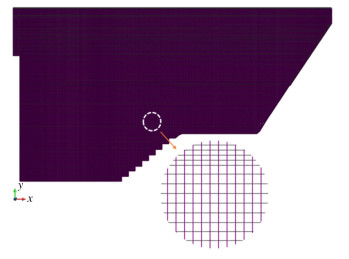
基于非协调网格计算技术建立的大石峡大坝有限元模型如图 9所示，大坝堆石体布置相对稀疏的网格，面板布置精细网格，面板厚度方向分为3层，面板长、宽方向尺寸约为1~2 m。
面板内布设双层双向钢筋，初步计算方案中，水平向和顺坡向钢筋间距均为0.2 m，钢筋直径25 mm，保护层厚度为8 cm。根据2.2节方法建立的钢筋三维模型如图 10。有限元整体几何模型包含结点数4126301个，坝体单元数328183个，钢筋单元数1857092个。
4.3 本构模型和计算参数
筑坝料瞬变模型采用“南水”模型[17]，参数如表 1；筑坝料流变模型采用7参数流变模型[18]，参数如表 2；面板-垫层接触面、止水接缝模拟如文献[19]。混凝土面板和高趾墙均为C30混凝土，高趾墙采用线弹性模型，弹性模量为30 GPa，泊松比0.167。混凝土面板采用损伤模型，参数如表 3，钢筋单元采用线弹性模型，弹性模量200 GPa，屈服强度335 MPa。
表 1 筑坝料“南水”模型参数Table 1. Parameters of "NHRI" model坝体分区 {\rho _{\text{d}}} /(g·cm-3) {\varphi _0} /(°) \Delta \varphi /(°) k n {R_{\text{f}}} cd/% nd Rd 垫层区（2A） 2.31 49.3 5.9 920 0.29 0.67 0.49 0.45 0.65 主砂砾石区（3BA、3BB） 2.27 50.1 6.3 1294 0.32 0.74 0.30 0.67 0.72 主堆石区（3BC、3C2） 2.22 53.2 9.0 1104 0.22 0.65 0.40 0.72 0.64 下游堆石区（3C1） 2.22 52.6 8.7 1044 0.21 0.66 0.46 0.70 0.66 增模区 2.28 69.1 17.9 0.14 3928.7 0.35 0.08 0.44 0.11 表 2 筑坝料流变模型参数Table 2. Parameters of creep model坝体分区 α b /% c/% d /% m1 m2 m3 垫层区（2A） 0.006 0.130 0.028 0.277 0.355 0.600 0.700 主砂砾区（3BA、3BB） 0.0062 0.114 0.025 0.241 0.351 0.578 0.696 主堆石料区（3BC、3C2） 0.0055 0.138 0.030 0.363 0.358 0.629 0.783 下游堆石区（3C1） 0.0054 0.140 0.032 0.365 0.358 0.629 0.783 表 3 混凝土损伤模型参数Table 3. Parameters for damage modelEc/104 MPa fcr/MPa εcr αc ftr/MPa εtr αt 3.0 20.1 1.470×10-3 0.74 2.01 9.5×10-5 1.25 5. 计算结果
工程上，面板表层的应力变形性态更受关注，本文给出的计算结果均为面板表层单元。
5.1 混凝土面板应力变形
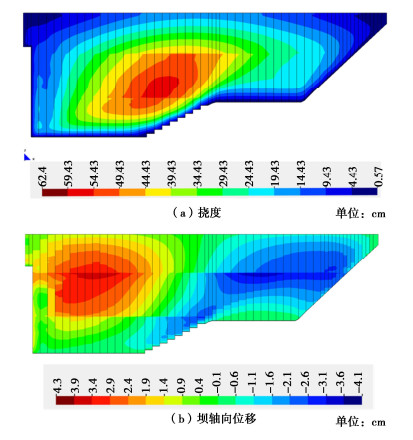
图 11给出了大坝蓄水运行至变形稳定时混凝土面板的变形分布。可以看出，面板坝轴向变形表现为由两岸向河床部位的挤压变形，左岸面板指向右岸方向的位移最大值为4.3 cm，右岸面板指向左岸的最大位移为4.1 cm，由于左岸岸坡更陡峭，左岸面板轴向位移也较右岸大。蓄水运行期面板最大挠度为62.4 cm，基本位于坝体最大断面处。
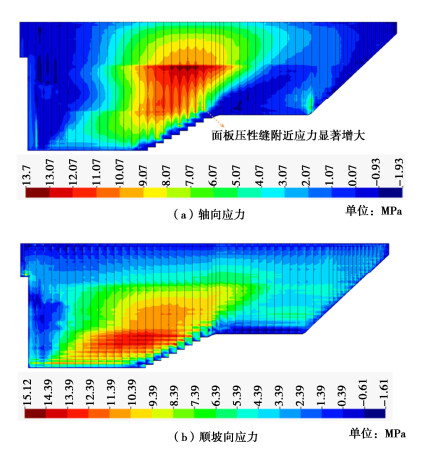
图 12给出了大坝蓄水运行至变形稳定时面板应力分布，可以看出，面板轴向应力在河床坝段表现为受压，最大值为13.70 MPa，两岸岸坡段表现为受拉，最大值为1.93 MPa；面板顺坡向应力绝大部分表现为受压，最大值为15.12 MPa，左岸面板顶部以及右岸台阶型面板底部存在一定的拉应力区，最大值为1.61 MPa。计算采用的面板精细模拟技术可很好反映面板应力分布的局部变化特征，其中轴向应力在河床坝段面板板间缝附近的“挤压”增强效应尤为明显。
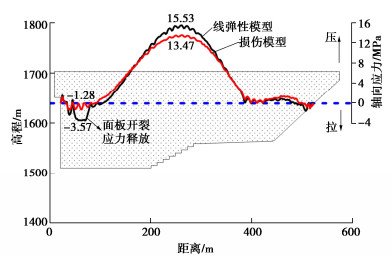
本文混凝土面板采用损伤模型，以高程1640 m处面板轴向应力为例，对比了损伤模型与线弹性模型计算结果的差异，如图 13，很明显看出，线弹性模型计算的左岸面板局部拉应力远高于材料抗拉强度，产生了一定范围的“超应力”区；损伤模型能考虑面板损伤开裂引起的应力重分布过程，计算结果更符合实际。
![]()
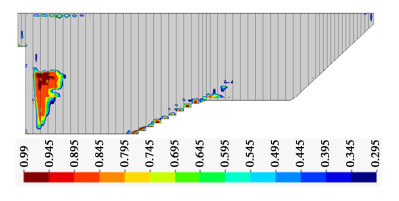
图 13 不同计算模型1640 m高程面板轴向应力比较Figure 13. Comparison of axial stresses at elevation 1640 m by different models本例中，混凝土面板未出现压性破坏（压应力未达到过峰值抗压强度），面板局部区域出现了受拉损伤，图 14给出了受拉损伤参数 {d_{\text{t}}} 的分布，可见，混凝土面板受拉损伤区主要位于左岸#4—#7面板中下部，以及右岸台阶型面板底部。
![]()
图 14 蓄水运行期面板受拉损伤参数dt分布Figure 14. Tensile damage factor dt of slab during operation period5.2 钢筋应力和裂缝宽度
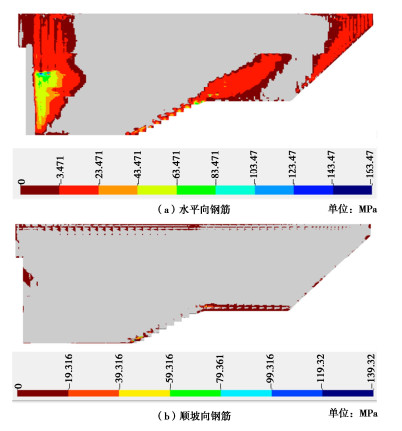
计算结果表明，钢筋的拉、压应力远未达到其屈服强度，图 15给出了水平向和顺坡向钢筋受拉应力分布，可以看出，水平向钢筋拉应力最大值为163.47 MPa位于左岸#4面板，1608 m高程处，顺坡向钢筋拉应力最大值139.32 MPa，出现在右岸台阶型#17面板1517 m高程处。
近些年，国内外众多学者开展了钢筋混凝土裂缝宽度研究，提出了众多的裂缝宽度计算方法[20]，本文采用丁旭柳等[21]提出的基于钢筋应力和配筋几何参数的混凝土裂缝宽度公式，
{W_{\max }} = 0.0145 \cdot {\sigma _{\text{s}}} \cdot \sqrt[3]{{d \cdot A}} \times {10^{ - 3}} 。 (20) 式中： {\sigma _{\text{s}}} 为钢筋应力；A=2dr；d为保护层厚度，本文取80 mm，r为钢筋间距。
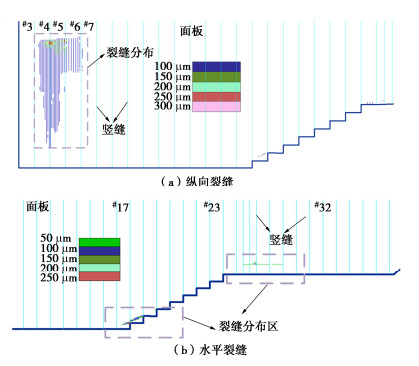
式（20）可便捷地与数值结果结合计算裂缝宽度，被美国钢筋混凝土建筑规范所采纳，在中国水工建筑物限裂设计中也得到了较好应用[21-22]。图 16为本文基于裂缝宽度公式得到的面板纵向、水平向裂缝分布与宽度，可以看出，左岸面板纵向裂缝从范围和最大宽度两方面都对工程安全危害较大，应引起足够重视，右岸台阶型面板底部也存在小范围的水平裂缝。
5.3 面板限裂要求和配筋补强
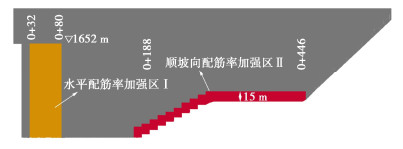
《混凝土面板堆石坝设计规范：NB/T 10871—2021》指出[2]“根据实践经验，为限制通过裂缝渗水的流速和钙的溶出，裂缝宽度在0.2 mm以上…需要处理”。本文即以0.2 mm作为混凝土面板最大限制裂缝宽度，由图 16，左岸面板纵向裂缝以及右岸台阶面板底部水平裂缝均有宽度超过0.2 mm。根据裂缝分布范围，给出了需进行配筋加强的区域，如图 17，其中加强区Ⅰ位于左岸0+32—0+80剖面、高程1511~1652 m区域，该区增加水平向配筋率限制纵向裂缝；加强区Ⅱ位于右岸0+188—0+446剖面、面板底部以上15 m区域，该区增加顺坡向配筋率限制水平裂缝。
表 4为给出了原配筋方案和加强配筋方案最大裂缝宽度对比，结果表明，Ⅰ区水平向配筋率由0.578%增加至0.783%时，纵向最大裂缝宽度降低至0.2 mm，Ⅱ区顺坡向配筋率由0.578%增加至0.691%时，纵向最大裂缝宽度降低0.18 mm。
表 4 不同配筋方案面板裂缝宽度Table 4. Cracks width under different reinforcements scheme配筋加强区Ⅰ 配筋加强区Ⅱ 水平向配筋率/% 纵向裂缝最大宽度/mm 顺坡向配筋率/% 水平向最大裂缝宽/mm 原方案 0.587 0.32 0.587 0.24 加强方案 0.783 0.20 0.691 0.18 6. 结论
本文通过集成面板坝非协调网格精细计算技术、钢筋混凝土组合单元、混凝土损伤模型提出了基于限裂理念的混凝土面板配筋计算方法，可定量研究面板配筋效应，为复杂条件下面板坝配筋设计提供支撑。
（1）混凝土面板精细模拟技术可较好表达面板应力变化的梯度以及局部性，准确定位面板应力危险区。
（2）钢筋混凝土组合模型物理概念清晰，钢筋与混凝土单元可非共结点作用耦合，适用于复杂三维问题中大规模钢筋群模拟。
（3）混凝土面板采用损伤模型可反映材料损伤开裂引起的应力重分布现象，克服线弹性模拟的不足。
（4）综合有限元数值结果和最大裂缝宽度模型提出了基于限裂理念的面板配筋方法，可为面板配筋设计提供技术支撑。
-
![]()
图 13 不同计算模型1640 m高程面板轴向应力比较
Figure 13. Comparison of axial stresses at elevation 1640 m by different models
![]()
图 14 蓄水运行期面板受拉损伤参数dt分布
Figure 14. Tensile damage factor dt of slab during operation period
表 1 筑坝料“南水”模型参数
Table 1 Parameters of "NHRI" model
坝体分区 /(g·cm-3) /(°) /(°) cd/% nd Rd 垫层区（2A） 2.31 49.3 5.9 920 0.29 0.67 0.49 0.45 0.65 主砂砾石区（3BA、3BB） 2.27 50.1 6.3 1294 0.32 0.74 0.30 0.67 0.72 主堆石区（3BC、3C2） 2.22 53.2 9.0 1104 0.22 0.65 0.40 0.72 0.64 下游堆石区（3C1） 2.22 52.6 8.7 1044 0.21 0.66 0.46 0.70 0.66 增模区 2.28 69.1 17.9 0.14 3928.7 0.35 0.08 0.44 0.11 
下载: 导出CSV
表 2 筑坝料流变模型参数
Table 2 Parameters of creep model
坝体分区 α b /% c/% d /% m1 m2 m3 垫层区（2A） 0.006 0.130 0.028 0.277 0.355 0.600 0.700 主砂砾区（3BA、3BB） 0.0062 0.114 0.025 0.241 0.351 0.578 0.696 主堆石料区（3BC、3C2） 0.0055 0.138 0.030 0.363 0.358 0.629 0.783 下游堆石区（3C1） 0.0054 0.140 0.032 0.365 0.358 0.629 0.783
下载: 导出CSV
表 3 混凝土损伤模型参数
Table 3 Parameters for damage model
Ec/104 MPa fcr/MPa εcr αc ftr/MPa εtr αt 3.0 20.1 1.470×10-3 0.74 2.01 9.5×10-5 1.25
下载: 导出CSV
表 4 不同配筋方案面板裂缝宽度
Table 4 Cracks width under different reinforcements scheme
配筋加强区Ⅰ 配筋加强区Ⅱ 水平向配筋率/% 纵向裂缝最大宽度/mm 顺坡向配筋率/% 水平向最大裂缝宽/mm 原方案 0.587 0.32 0.587 0.24 加强方案 0.783 0.20 0.691 0.18
下载: 导出CSV
-
[1] 罗福海, 张保军, 夏界平. 水布垭面板堆石坝施工期裂缝成因及处理措施[J]. 水利水电快报, 2010, 31(12): 5-8. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSK201012002.htm LUO Fuhai, ZHANG Baojun, XIA Jieping. Causes and treatment measures of cracks in Shuibuya concrete face rockfill dam during construction[J]. Express Water Resources & Hydropower Information, 2010, 31(12): 5-8. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSK201012002.htm
[2] 混凝土面板堆石坝设计规范: N/T 10871—2021[S]. 北京: 中国水利水电出版社, 2022. Code for Design of Concrete Face Rockfill Dams: N/T 10871—2021[S]. Beijing: China Water & Power Press, 2022. (in Chinese)
[3] 钟红, 林皋, 胡志强. 有限元计算中疏密网格过渡方法研究[J]. 计算力学学报, 2007, 24(6): 887-891, 898. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG200706030.htm ZHONG Hong, LIN Gao, HU Zhiqiang. Two methods for transition between coarse and fine finite elements[J]. Chinese Journal of Computational Mechanics, 2007, 24(6): 887-891, 898. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJG200706030.htm
[4] 周墨臻, 张丙印, 王伟. 高面板堆石坝软缝接触计算模型及其数值实现[J]. 岩石力学与工程学报, 2016, 35(增刊1): 2803-2810. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2016S1024.htm ZHOU Mozhen, ZHANG Bingyin, WANG Wei. Algorithm and simulation methods for the soft longitudinal joint of the concrete faces in high concrete-faced rockfill dams[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(S1): 2803-2810. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2016S1024.htm
[5] 周墨臻, 张丙印, 张宗亮, 等. 超高面板堆石坝面板挤压破坏机理及数值模拟方法研究[J]. 岩土工程学报, 2015, 37(8): 1426-1432. doi: 10.11779/CJGE201508010 ZHOU Mozhen, ZHANG Bingyin, ZHANG Zongliang, et al. Mechanisms and simulation methods for extrusion damage of concrete faces of high concrete-faced rockfill dams[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1426-1432. (in Chinese) doi: 10.11779/CJGE201508010
[6] 孔宪京, 陈楷, 邹德高, 等. 一种高效的FE-PSBFE耦合方法及在岩土工程弹塑性分析中的应用[J]. 工程力学, 2018, 35(6): 6-14. https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201806004.htm KONG Xianjing, CHEN Kai, ZOU Degao, et al. An efficient fe-psbfe coupled method and its application to the elasto-plastic analysis of geotechnical engineering structures[J]. Engineering Mechanics, 2018, 35(6): 6-14. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCLX201806004.htm
[7] 邹德高, 刘锁, 陈楷, 等. 基于四叉树网格和多边形比例边界有限元方法的岩土工程非线性静动力分析[J]. 岩土力学, 2017, 38(增刊2): 33-40. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2017S2005.htm ZOU Degao, LIU Suo, CHEN Kai, et al. Nonlinear static and dynamic analysis for geotechnical engineering based on quadtree mesh and polygon scaled boundary finite element method[J]. Rock and Soil Mechanics, 2017, 38(S2): 33-40. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2017S2005.htm
[8] 邹德高, 陈楷, 刘锁, 等. 非线性比例边界有限元在面板坝分析中的应用[J]. 土木与环境工程学报, 2019, 41(3): 11-18. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201903002.htm ZOU Degao, CHEN Kai, LIU Suo, et al. Application of nonlinear scaled boundary polygon element method in analysis of concrete face rockfill dam[J]. Journal of Civil and Environmental Engineering, 2019, 41(3): 11-18. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN201903002.htm
[9] 魏匡民, 陈生水, 李国英, 等. 位移多点约束法在面板堆石坝精细模拟中的应用研究[J]. 岩土工程学报, 2020, 42(4): 616-623. doi: 10.11779/CJGE202004003 WEI Kuangmin, CHEN Shengshui, LI Guoying, et al. Application of displacement multi-point constraint refinement method in simulation of concrete-faced rockfill dams[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(4): 616-623. (in Chinese) doi: 10.11779/CJGE202004003
[10] 王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003. WANG Xucheng. Finite Element Method[M]. Beijing: Tsinghua University Press, 2003. (in Chinese)
[11] 陈国荣. 有限单元法原理及应用[M]. 北京: 科学出版社, 2009. CHEN Guorong. Principle and Application of Finite Element Method[M]. Beijing: Science Press, 2009. (in Chinese)
[12] 孔宪京, 屈永倩, 邹德高, 等. 强震作用下面板堆石坝跨尺度面板开裂演化分析[J]. 岩土工程学报, 2020, 42(6): 989-996. doi: 10.11779/CJGE202006001 KONG Xianjing, QU Yongqian, ZOU Degao, et al. Cross-scale crack evolution analysis for face slab in concrete faced rockfill dams under strong earthquake[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(6): 989-996. (in Chinese) doi: 10.11779/CJGE202006001
[13] 巫昌海, 汪基伟. 混凝土三维钢筋埋置组合式有限单元模型及其网格自动生成[J]. 计算机辅助设计与图形学学报, 2000, 12(10): 761-764. https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF200010011.htm WU Changhai, WANG Jiwei. Three-dimensional embedded finite element model of reinforced concrete and its automatic mesh generation[J]. Jouraal of Computer Aided Design & Computer Graphics, 2000, 12(10): 761-764. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JSJF200010011.htm
[14] XU B, ZOU D G, KONG X J, et al. Dynamic Damage evaluation on the slabs of the concrete faced rockfill dam with the plastic-damage model[J]. Computers and Geotechnics, 2015, 65: 258-265. http://www.onacademic.com/detail/journal_1000037433272510_9a3e.html
[15] CEN W J, WEN L S, ZHANG Z Q, et al. Numerical simulation of seismic damage and cracking of concrete slabs of high concrete face rockfill dams[J]. Water Science and Engineering, 2016, 9(3): 205-211. http://qikan.cqvip.com/Qikan/Article/Detail?id=7000080633
[16] 混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社, 2011. Code for Design of Concrete Structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press, 2011. (in Chinese)
[17] 朱百里, 沈珠江. 计算土力学[M]. 上海: 上海科学技术出版社, 1990. ZHU Baili, SHEN Zhujiang. Computational Soil Mechanics[M]. Shanghai: Shanghai Science and Technology Press, 1990. (in Chinese)
[18] 李国英, 米占宽, 傅华, 等. 混凝土面板堆石坝堆石料流变特性试验研究[J]. 岩土力学, 2004, 25(11): 1712-1716. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200411008.htm LI Guoying, MI Zhankuan, FU Hua, et al. Experimental studies on rheological behaviors for rockfills in concrete faced rockfill dam[J]. Rock and Soil Mechanics, 2004, 25(11): 1712-1716. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200411008.htm
[19] 顾淦臣, 沈长松, 岑威钧. 土石坝地震工程学[M]. 北京: 中国水利水电出版社, 2009. GU Ganchen, SHEN Changsong, CEN Weijun. Earthquake Engineering for Earthrock Dams[M]. Beijing: China Water & Power Press, 2009. (in Chinese)
[20] 高瑞平. 混凝土构件裂缝宽度计算方法研究[D]. 南京: 东南大学, 2008. GAO Ruiping. Study on Calculation Method of Crack Width of Concrete Members[D]. Nanjing: Southeast University, 2008. (in Chinese)
[21] 丁旭柳, 伍鹤皋, 朱忠华. 钢筋混凝土压力隧洞裂缝宽度计算方法的探讨[J]. 武汉大学学报(工学版), 2001, 34(2): 24-27. https://www.cnki.com.cn/Article/CJFDTOTAL-WSDD200102006.htm DING Xuliu, WU Hegao, ZHU Zhonghua. Study on computational method of crack width of reinforced concrete pressure tunnels[J]. Engineering Journal of Wuhan University, 2001, 34(2): 24-27. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-WSDD200102006.htm
[22] 兰伟钦, 肖明. 考虑钢筋滑移效应的高压隧洞衬砌配筋计算方法[J]. 水电与新能源, 2021, 35(4): 66-71. https://www.cnki.com.cn/Article/CJFDTOTAL-HBFD202104016.htm LAN Weiqin, XIAO Ming. On the reinforcement calculation of high-pressure tunnel lining considering the slip effect of reinforcement[J]. Hydropower and New Energy, 2021, 35(4): 66-71. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HBFD202104016.htm
-
期刊类型引用(1)
1. 贾丽娜. 面板堆石坝施工中过渡料的碾压特性研究. 陕西水利. 2024(07): 178-179+183 . 
百度学术
其他类型引用(0)
-
其他相关附件
计量
- 文章访问数: 423
- HTML全文浏览量: 73
- PDF下载量: 89
- 被引次数: 1
