基于颗粒破碎耗能的粗粒料剪胀方程研究

吴二鲁; 朱俊高; 陆阳洋; 钱彬

doi:10.11779/CJGE202205013

基于颗粒破碎耗能的粗粒料剪胀方程研究 English Version

吴二鲁^{1, 2,},
朱俊高^{1, 2, ,},
陆阳洋³,
钱彬³

1.
河海大学岩土力学与堤坝工程教育部重点实验室, 江苏南京 210024
2.
河海大学江苏省岩土工程技术工程研究中心, 江苏南京 210024
3.
南京水利科学研究院岩土工程研究所, 江苏南京 210024

基金项目:

国家自然科学基金委员会雅砻江联合基金项目 U1865104

长江水科学研究联合基金重点支持项目 U2040221

高等学校学科创新引智计划项目（111计划） B13024

详细信息

作者简介:
吴二鲁(1993—)，男，博士，主要从事土体基本性质及本构关系、土石坝工程研究。E-mail: 170804010004@hhu.edu.cn

通讯作者:
朱俊高，E-mail: zhujungao@hhu.edu.cn

中图分类号: TU411
计量
- 文章访问数: 231
- HTML全文浏览量: 33
- PDF下载量: 107
出版历程
- 收稿日期: 2021-07-05
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-04-30

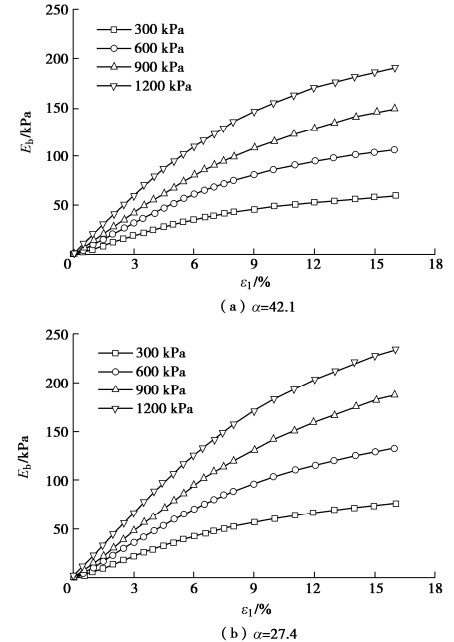
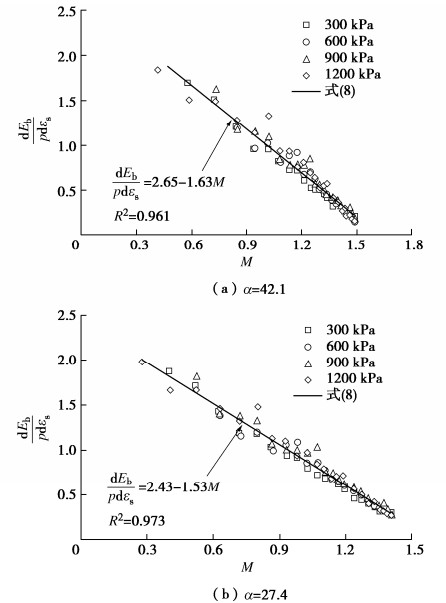
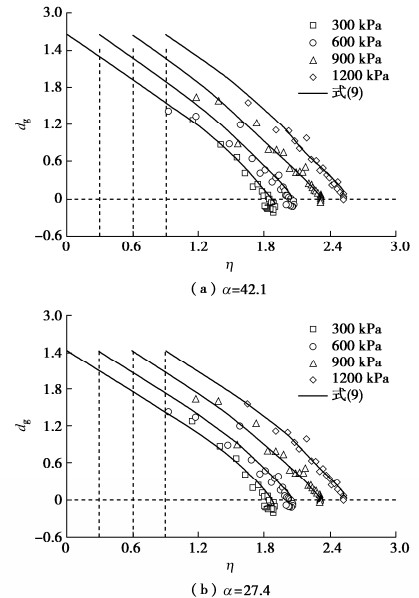
Dilatancy equation for coarse-grained soils incorporating particle breakage energy

WU Er-lu^{1, 2,},
ZHU Jun-gao^{1, 2, ,},
LU Yang-yang³,
QIAN Bin³

1.
Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing 210024, China
2.
Jiangsu Research Center for Geotechnical Engineering Technology, Hohai University, Nanjing 210024, China
3.
Geotechnical Engineering Department, Nanjing Hydraulic Research Institute, Nanjing 210024, China

摘要

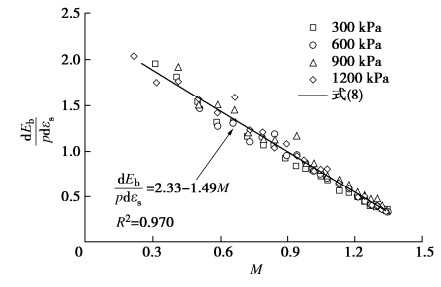
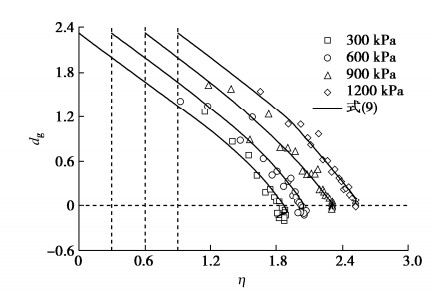
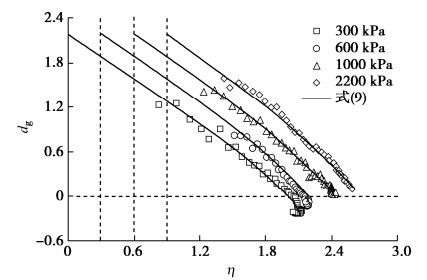
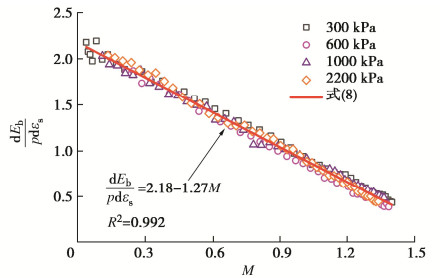
摘要: 粗粒料颗粒破碎和应力变形的内在联系可以用颗粒破碎耗能反映。研究了三轴试验过程中粗粒料的颗粒破碎变化规律，根据此规律对Ueng等提出的考虑颗粒破碎的能量平衡方程中的摩擦系数M进行了修正，以此解决依据该能量平衡方程计算出的颗粒破碎耗能违反热力学定律的问题。在此基础上，发展了一个形式简单且适用于粗粒料的剪胀方程。主要结论如下：①提出的颗粒破碎指标与围压及轴向应变之间的数学关系可以较好地描述三轴试验过程中粗粒料的颗粒破碎变化规律；②通过对能量平衡方程中的摩擦系数进行修正实现了颗粒破碎耗能的合理计算，满足了热力学定律；③试验结果表明，剪胀耗能在总的输入功里占比甚微，在能量平衡方程中可以忽略剪胀耗能；④ ${{{\text{d}}{E_{\text{b}}}} / {p{\text{d}}{\varepsilon _{\text{s}}}}}$ 与M之间存在一个明显的线性关系，将其代入忽略剪胀耗能的能量平衡方程得到了最终的剪胀方程。研究表明，该剪胀方程可以较好地模拟粗粒料的剪胀行为，而且其数学形式简单，可以推出其塑性势函数，为后续考虑颗粒破碎的分数阶本构模型的研究提供了条件。
- 粗粒料 /
- 颗粒破碎 /
- 分数阶 /
- 摩擦系数 /
- 剪胀方程
Abstract: The internal relationship between particle breakage and stress deformation of coarse-grained soils can be reflected by the particle breakage energy. The change law of particle breakage of coarse-grained soils during triaxial tests is studied. According to this law, the fraction coefficient M in the energy balance equation proposed by Ueng and Chen is modified to solve the problem that the particle breakage energy calculated by the energy balance equation violates the thermodynamic law. On this basis, a simple dilatancy equation for coarse-grained soils is developed. The main conclusions are as follows: (1) The proposed mathematical relationship among particle breakage index, confining pressure and axial strain can describe the change law of particle breakage well. (2) The reasonable calculation of particle breakage energy is realized by modifying the fraction coefficient in the energy balance equation, which satisfies the thermodynamic law. (3) The test results show that the ratio of the dilatancy energy to the total input work is very small, so it can be ignored in the energy balance equation. (4) There is an obvious linear relationship between ${{{\text{d}}{E_{\text{b}}}} / {{\text{d}}{\varepsilon _{\text{s}}}}}$ and M, and a dilatancy equation can be developed by substituting this linear relationship into the energy balance equation, and this dilatancy equation can well simulate the dilatancy behaviors of coarse-grained soils, and its mathematical form is simple enough, so that its plastic potential function can be derived, which provides conditions for the subsequent studies on the fraction-order constitutive model considering particle breakage.
- coarse-grained soil /
- particle breakage /
- fractional order /
- friction coefficient /
- dilatancy equation

HTML全文

0. 引言

对于饱和砂土地震液化触发判别问题,应用最广泛的Seed简化判别方法主要建立在包含液化宏观震害现象、地震动加速度记录和场地原位测试指标三要素的地震液化实例数据和液化分界线的基础上^[1-3]。以基于原位剪切波速测试指标的液化实例为例,图1给出了地震液化和非液化实例,以及区分液化与否的分界线^[4]。由于强震液化事件彻底破坏易液化土体原有结构性,导致了消除液化土层既往沉积作用的“时钟重置”效应,使得震后获得的场地原位测试指标与真正控制场地抗液化性能的震前土体工程力学特性不对应。考虑到针对地震液化场地的原位测试一般发生在震后数天或数月甚至更长的时间里,图1中地震液化实例数据的剪切波速和相应的液化分界线可能存在与测试时间相关的系统误差。因此,研究震后易液化场地饱和砂土土层的剪切波速（或其它原位测试指标）随时间的变化规律,对正确认识现有基于原位测试指标的液化判别简化方法的可靠性并对震后测试指标进行合理修正具有重要的科学意义。

图 1 基于剪切波速的地震液化实例数据与分界线

Figure 1. v_s-based field case histories and liquefaction boundary curves

下载: 全尺寸图片幻灯片

土体在自然沉积过程中或者经受外荷载剧烈扰动后,其刚度和强度等工程力学参数在恒定应力状态下随时间变化的现象被称为“时间效应”,且该变化可以通过原位测试指标（例如,SPT、CPT和V_s）体现^[5-7]。例如,Andrus等^[8]通过静力触探与剪切波速的经验关系获得了原位砂土剪切波速和完全扰动后剪切波速的比值MEVR,初步揭示了地质时间尺度上的砂土时间效应（见图2）；周燕国等^[9]结合剪切波速（剪切模量）的Hardin公式^[10]和静力触探测试,提出了砂土时间效应的表征指标A_I,并利用不同地质年代砂土实测数据对其表征能力进行了检验。然而,上述研究主要面向地质沉积年代和土性测试指标的经验关系,关注数万年到数十万年甚至更长的地质时间尺度,并没有考虑地质沉积年代中可能受到的各种扰动（如强震事件）对土体工程力学特性的影响。以图2为例,深色椭圆圈内的数据并不符合图中拟合斜线的趋势,而这个时间范围（10^-1～10² a）正是实际工程服役寿命或者高烈度区强震重现周期的范围。Pavlenko等^[11]研究1995年神户地震中场地刚度演化问题,发现液化使得场地刚度急剧降低,但在震后较长一段时间内无法恢复到地震液化前的值。可见,对于实际工程,震后较短的时间尺度内场地土体的时间效应更具有工程意义,是影响易液化场地在余震中的地震响应和再液化可能性的重要因素。

图 2 土体测量与估算剪切波速比的时变趋势

Figure 2. Time variation of measured to estimated velocity ratio

下载: 全尺寸图片幻灯片

针对上述问题,本文对新西兰基督城的REHS强震台站在2010—2011年间的若干强震记录的尾波进行水平与竖向谱比（HVSR）分析,获得了该台站所在的易液化场地在地震前后小应变剪切刚度随时间的发展规律。在此基础上,提出了综合考虑主固结和次固结作用的震后饱和砂土小应变刚度计算模型,并合理预测了REHS台站场地震后刚度恢复变化过程。

1. 场地条件与强震台站记录分析

HVSR方法通过对强震台站的三向加速度记录进行分析得到场地卓越频率以及场地土层结构分布,相比于其它场地频率分析方法,HVSR方法相对简单,能够基本消除震源和传播路径的影响,得到的场地卓越频率更可靠^[12-13]。场地的卓越频率与场地平均剪切波速的关系可表示为^[14]

$v_{savg} = 4 H f$ 。

(1)

式中, $v_{savg}$ 为场地平均剪切波速,H为场地土层厚度,f为场地卓越频率。

根据弹性理论,土体小应变剪切模量表达为

$G_{\max} = ρ \cdot v_{s}^{2}$ 。

(2)

本文针对新西兰基督城CBD区的REHS台站（见图3）,通过触发液化的强震本身和之后发生余震的加速度记录的尾波信号,获得场地卓越频率,根据式（1）,（2）分析从2010年以来3次强震事件之后场地刚度随时间变化规律。REHS台站所处场地的上覆软弱土层厚度约为20 m,存在较厚的饱和粉质砂土层和洁净砂土层,下卧刚度较大的砂卵石层（见图4）,是较典型的易液化场地^[15]。

图 3 基督城REHS强震台站位置（来源：www.nzgd.org.nz）

Figure 3. REHS strong motion station at Christchurch (source: www.nzgd.org.nz)

下载: 全尺寸图片幻灯片

图 4 REHS台站场地土层信息

Figure 4. Soil profile at REHS station site

下载: 全尺寸图片幻灯片

本文采用Geopsy软件进行HVSR分析,该软件能够多窗口同时计算H/V谱比和上覆土层的卓越频率f,并计算它们的平均值和方差。H/V谱比曲线的峰值对应的频率即为该尾波窗口时间对应的卓越频率。图5是尾波窗口选取和计算结果示意图,其中黑色实线代表所有窗口的平均值,两条虚线分别代表它的上、下限,竖向灰色条状区域代表了平均峰值所在的频率段。采用地震动记录的尾波进行HVSR分析获得场地卓越频率需满足一定的条件,即首先要保证主震后的选取的余震强度足够小,一是为了避免该余震事件对场地刚度恢复过程产生额外的显著影响,二是为了尾波段对应场地土体处于小应变弹性应变响应状态；其次,为保证数据处理结果的可靠性,均要求H/V谱比值大于2.0,而且卓越频率的误差在±0.3 Hz以内。

图 5 地震尾波HVSR谱比分析

Figure 5. HVSR analysis of seismic coda wave

下载: 全尺寸图片幻灯片

2. 震后场地小应变刚度演化规律

图6给出了REHS台站场地2010年至2011年间3次强震后场地卓越频率随时间的发展情况。考虑到每次强震事件之后大部分余震在台站的地震动强度都很小,可以忽略其对震后场地的进一步扰动作用。每张图上方的黑色虚线代表2010年9月3日M_w7.2地震事件之前场地的卓越频率（f_i=2.20 Hz）,由2010年大震之前的小震记录进行HVSR分析得到；右上角红色虚线表示强震事件后场地的稳定值,可视为下次强震前的场地卓越频率初始值。由图6可见,每次强震后场地刚度恢复至相对稳定的状态所需要的时间基本一致（为数天到数十天）,而且场地稳定后的卓越频率均值接近但低于最初的水平（即2.20 Hz）。

图 6 震后场地卓越频率时变规律

Figure 6. Evolution of fundamental frequency of earthquake site

下载: 全尺寸图片幻灯片

由图6（b）可见,20110221 M_w6.2地震事件中场地卓越频率受到强余震地震历史的影响,因此图7仅将图6（a）和（c）的归一化场地卓越频率（f/f_i）随时间发展规律归纳在一起。由图7可见,震后场地刚度恢复速率基本一致,呈现对数形式的增长,这与PENG等^[16-17]的研究发现类似。而基督城场地小应变刚度在震后10～100 d会有显著的恢复。根据Downes等^[18]的研究,2010年距上次基督城发生强震液化的时间间隔接近100 a,可以认为基督城典型易液化场地的新近沉积时间（或液化的重现周期）为100 a左右,所以尽管REHS台站场地的砂土层刚度在液化后的数月内会有较大的恢复,但仍小于震前水平。需要指出的是,在基督城的其它强震台站（如CBGS和CCCC台站）场地也观测到了类似规律^[19]。另外,注意到图7中同一时间对应的频率数据存在一定离散性,原因包括：首先,HVSR方法不能完全消除震源及传播路径的影响；其次,地震动加速度信号（尤其是小震事件）信噪比水平不同；再次,地下水位的季节性升降等环境变化带来的可能影响。

图 7 震后场地归一化卓越频率变化规律

Figure 7. Evolution of normalized fundamental frequency of earthquake site

下载: 全尺寸图片幻灯片

3. 饱和砂土震后小应变刚度计算模型

需要注意,Andrus等^[8]将砂土的MEVR参数用于剪切模量的时间效应修正,这种修正主要反映数十万年甚至更久的由于颗粒胶结引起的时间效应,不能合理反映砂土液化后短期内刚度的变化规律（即孔压消散与次固结引起的时间效应）,而大部分震后实例调查的原位测试均是在这一时间段获得的；其次,这种修正对特定地震和场地数据的依赖性较大,数据十分有限,规律的一般性不强。本节基于饱和砂土的主固结与次固结过程,提出了考虑有效应力变化和砂土颗粒间接触力均质化（包括孔隙比变化）这两个主要因素的震后饱和砂土小应变刚度计算模型。

3.1 主固结影响函数

首先考虑由孔压消散和孔隙变化引起的剪切模量增量,可采用Hardin公式表示土体小应变剪切模量与土体孔隙比及有效应力的关系：

$G_{\max} = A \cdot F (e) {({σ^{'}}_{m})}^{n}$ ,

(3)

式中,G_max为砂土小应变剪切模量,A为结构性参数,F(e)为孔隙比方程, ${σ^{'}}_{m}$ 为平均有效应力,n约等于0.5。

平均固结度U通常定义为

$U = \frac{S_{ct}}{S_{c \infty}}$ ,

(4)

式中,S_ct为地基某时刻的主固结变形,S_c∞为地基的最终主固结变形。

根据太沙基一维固结理论,平均固结度U为

$U = 1 - \sum_{m = 1}^{\infty} \frac{2}{M^{2}} e^{- M^{2} T_{v}}$ 。

(5)

式中,竖向固结时间因子T_v为

$T_{v} = \frac{k_{v} t}{H^{2} γ_{w} m_{v}}$ ,

(6)

式中,k_v为土的竖向渗透系数,t为固结时间,H为土层厚度, $γ_{w}$ 为水的重度,m_v为土体体积压缩模量。

设砂土震后初始孔隙比为e₀,主固结完成后孔隙比为e_c∞,固结中土体孔隙比为e_ct,则由式（4）可以得到土体平均固结度：

$U = \frac{e_{0} - e_{ct}}{e_{0} - e_{c \infty}}$ 。

(7)

超静孔压比与砂土有效应力的关系如下：

$1 - r_{u} (t) = {[\frac{{σ^{'}}_{m, t}}{{σ^{'}}_{m,i}}]}^{2}$ ,

(8)

式中, $r_{u} (t)$ 为t时刻砂土的超静孔压比, ${σ^{'}}_{m, t}$ 为t时刻砂土的有效应力, ${σ^{'}}_{m,i}$ 为砂土的初始最大有效应力。

考虑到在主固结阶段砂土剪切模量增长主要由有效应力增加和孔隙比减小引起的,而结构性变化的影响很小。因此本文假设砂土主固结过程中结构性参数A不变,结合式（3）,（7）,（8）得到砂土震后剪切模量随时间的变化函数如下：

$\frac{G_{pc} (t)}{G_{R}} = \frac{F (e_{0} - U e_{0} + U e_{c \infty})}{F (e_{c \infty})} {[1 - \frac{p_{0}}{σ^{'}} (1 - U)]}^{0.5}$ ,

(9)

式中,G_pc(t)为任意固结时刻的砂土小应变剪切模量,G_R为砂土在参考时间时的小应变剪切模量,一般参考时间t_R大于主固结时间t_p。

3.2 次固结影响函数

砂土次固结过程中,颗粒间接触力均质化（包括孔隙比减小）也是引起砂土刚度随时间增长的一个重要因素^[20-21]。本文采用Howie等^[22]基于室内试验提出的经验公式加以描述：

$\frac{G_{sc} (t)}{G_{R}} = 1 + \frac{Δ G}{G_{R}} \cdot \lg (\frac{t}{t_{R}})$ ,

(10)

式中,t为固结时间,t_R为参考时间,G_sc(t)为任意固结时刻的小应变剪切模量,G_sc,R为在参考时间的小应变剪切模量, $Δ G$ /G_sc,R为剪切模量增长速率,对于特定的土体需根据室内固结试验确定。

3.3 饱和砂土震后小应变刚度计算模型

在震后一定的时间段,砂土剪切模量变化受上述两个因素共同影响,本文假设这两种机理相互独立,结合式（9）,（10）得

$\frac{G (t)}{G_{R}} = 1 + \frac{Δ G_{pc} (t)}{G_{R}} + \frac{Δ G_{sc} (t)}{G_{R}}$ 。

(11)

式（11）结合 $G = ρ v_{s}^{2}$ 和 $v_{s} = 4 H f$ 可得到场地卓越频率随随时间发展的函数：

$\frac{f (t)}{f_{R}} = \sqrt{\frac{G (t)}{G_{R}}}$ 。

(12)

根据现有围绕基督城场地的研究成果,式（12）的参数取值如下：该场地上覆软弱土层厚20 m,主要由砂土和粉土组成,排水条件良好^[15]；根据CPT测试的I_c和渗透系数的经验关系^[23]取土层平均渗透系数k_v=2.5×10^-5 m/s；土层的平均压缩模量由动力触探锤击数与压缩模量的经验关系^[24]得到,取E_s=15.0 MPa；土层初始平均超静孔压比取p₀=0.8。另外,假设震后场地刚度需要经历震前同样的沉积时间才能恢复至2010年9月3日强震液化事件之前的震前值,则参考时间取为t_R=100 a。

根据式（12）计算得到基督城REHS台站场地液化后基频随时间的发展规律如图8中的曲线所示,图中上、下两条边界线代表由于参数取值带来的标准差。由图8可见,该计算模型对图6（a）,（c）中的两次强震数据的预测效果较好,能够考虑震后一定时间内饱和砂土刚度的恢复规律。

图 8 震后刚度发展函数预测效果

Figure 8. Prediction of post-earthquake stiffness function

下载: 全尺寸图片幻灯片

4. 结论

为研究震后饱和砂土场地原位测试指标变化规律及其与震前值的差异,本文针对新西兰基督城的典型易液化场地,开展了从实际场地卓越频率监测分析到砂土小应变刚度计算模型的研究。主要结论如下：

（1）针对基督城系列强震,对REHS强震台站记录信号进行HVSR分析,揭示了震后场地刚度整体呈现指数形式的增长规律。场地小应变刚度会在震后经过数天的快速恢复后进入相对稳定的缓慢上升期。对于震前沉积时间较久的场地,场地刚度在震后短时间内难以恢复到震前水平,现有基于震后原位调查获得的液化实例数据应当根据震后原位测试时间进行适当的修正。

（2）假设震后场地刚度需要经历震前同样的沉积时间才能恢复至震前值,基于主固结与次固结过程提出了具有物理意义的饱和砂土震后小应变刚度计算模型,可估算基督城典型易液化场地在强震后平均小应变刚度随时间的发展规律。该计算模型为将特定场地的震后原位测试指标（如剪切波速）修正到对应的震前值提供了一种有效手段。

注意到本文所揭示的震后场地小应变刚度演化规律和所建议的计算模型及参数主要针对新西兰基督城场地,有必要进一步研究更多的其它地震和场地刚度演化规律,并获取各类易液化场地和土体参数,才能为将液化实例中的震后原位测试指标修正到震前原状土的对应值提供定量依据,提高当前基于液化实例调查的地震液化简化判别方法的准确性。

图 1 破碎指标的实测值与拟合值

Figure 1. Measured and fitting data of particle breakage index

下载: 全尺寸图片幻灯片

图 2 粗粒料C的三轴应力应变曲线

Figure 2. Triaxial stress-strain curves of coarse-grained soil C

下载: 全尺寸图片幻灯片

图 3 粗粒料C的颗粒破碎耗能

Figure 3. Particle breakage energy of coarse-grained soil C

下载: 全尺寸图片幻灯片

图 4 粗粒料C的颗粒破碎耗能

Figure 4. Particle breakage energy of coarse-grained soil C

下载: 全尺寸图片幻灯片

图 5 剪胀耗能与外力做功

Figure 5. Dilatancy energy and external work

下载: 全尺寸图片幻灯片

${{d{E_\text{b}}} / {pd{\varepsilon _\text{s}}}}$ 与M之间的关系

Relationship between ${{\text{d}{E_\text{b}}} / {p\text{d}{\varepsilon _\text{s}}}}$ and M

下载: 全尺寸图片幻灯片

图 7 粗粒料C剪胀比的试验值与预测值

Figure 7. Test data and prediction of dilatancy ratio of coarse-grained soil C

下载: 全尺寸图片幻灯片

图 8 粗粒料D剪胀比的试验值与预测值

Figure 8. Test data and prediction of dilatancy ratio of coarse-grained soil D

下载: 全尺寸图片幻灯片

图 9 粗粒料D的三轴试验数据

Figure 9. Triaxial test data of coarse-grained soil D

下载: 全尺寸图片幻灯片

图 10 粗粒料D的颗粒破碎耗能

Figure 10. Particle breakage energy of coarse-grained soil D

下载: 全尺寸图片幻灯片

${{\text{d}{E_\text{b}}} / {p\text{d}{\varepsilon _\text{s}}}}$ 与M之间的关系

Relationship between ${{\text{d}{E_\text{b}}} / {p\text{d}{\varepsilon _\text{s}}}}$ and M

下载: 全尺寸图片幻灯片

图 12 式（5）表示的曲线

Figure 12. Curves expressed by Eq. (5)

下载: 全尺寸图片幻灯片

图 13 粗粒料C的颗粒破碎耗能

Figure 13. Particle breakage energy of coarse-grained soil C

下载: 全尺寸图片幻灯片

图 14 粗粒料C的颗粒破碎耗能

Figure 14. Particle breakage energy of coarse-grained soil C

下载: 全尺寸图片幻灯片

图 15 粗粒料C剪胀比的实测值与预测值

Figure 15. Measured and predictive data of dilatancy ratio of coarse-grained soil C

下载: 全尺寸图片幻灯片

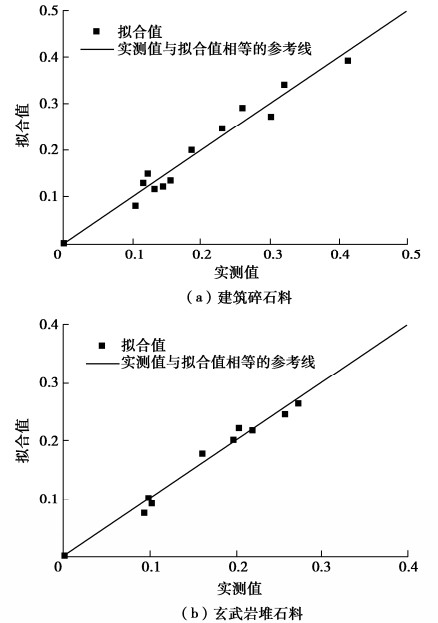
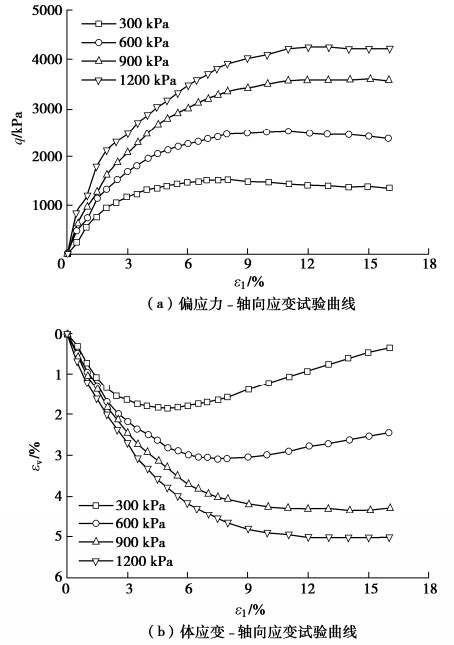
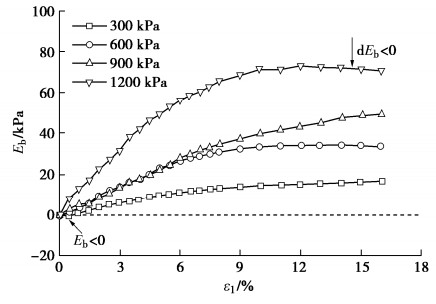
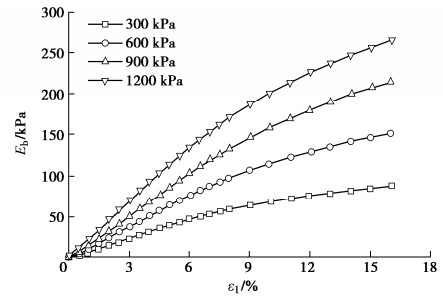
表 1 颗粒破碎试验数据

Table 1 Particle breakage data

粗粒料	围压/kPa	轴向应变/%	破碎指标 ${B_\text{E}}$ /%
建筑碎石料^[14]	200	4.58	10.60
	200	9.72	14.40
	200	12.90	15.60
	500	3.88	11.60
	500	7.96	18.70
	500	14.40	23.10
	1000	3.17	12.20
	1000	9.40	26.00
	1000	15.80	32.00
	1500	2.05	13.20
	1500	6.31	30.20
	1500	17.20	41.40
玄武岩堆石料^[15]	1000	2.16	9.40
	1000	7.84	16.10
	1000	15.10	21.90
	1500	2.41	10.20
	1500	8.24	19.70
	1500	15.60	25.70
	2000	2.47	9.90
	2000	8.61	20.30
	2000	15.10	27.20

下载: 导出CSV

表 2 式（1）的拟合结果

Table 2 Fitting results of Eq. (1)

粗粒料	$\beta$	$\alpha$	$\omega$	决定系数R²
建筑碎石料	0.417	19.5	5.42	0.962
玄武岩堆石料	0.260	21.4	5.18	0.980

下载: 导出CSV

参考文献(23)

[1]	郭庆国. 粗粒土的工程特性及应用[M]. 郑州: 黄河水利出版社, 1998. GUO Qing-guo. Engineering characteristic and pplication of coarse-grained soil[M]. Zhengzhou: Yellow River Conservancy Press, 1998. (in Chinese)
[2]	姚仰平, 刘林, 罗汀. 砂土的UH模型[J]. 岩土工程学报, 2016, 38(12): 2147–2153. doi: 10.11779/CJGE201612002 YAO Yang-ping, LIU Lin, LUO Ting. UH model for sands[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(12): 2147–2153. (in Chinese) doi: 10.11779/CJGE201612002
[3]	YAO Y P, LIU L, LUO T, et al. Unified hardening (UH) model for clays and sands[J]. Computers and Geotechnics, 2019, 110: 326–343. doi: 10.1016/j.compgeo.2019.02.024
[4]	YAO Y P, YAMAMOTO H, WANG N D. Constitutive model considering sand crushing[J]. Soils and Foundations, 2008, 48(4): 603–608. doi: 10.3208/sandf.48.603
[5]	郭万里, 蔡正银, 武颖利, 等. 粗粒土的颗粒破碎耗能及剪胀方程研究[J]. 岩土力学, 2019, 40(12): 4703–4710. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912018.htm GUO Wan-li, CAI Zheng-yin, WU Ying-li, et al. Study on the particle breakage energy and dilatancy of coarse-grained soils[J]. Rock and Soil Mechanics, 2019, 40(12): 4703–4710. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912018.htm
[6]	UENG T S, CHEN T J. Energy aspects of particle breakage in drained shear of sands[J]. Géotechnique, 2000, 50(1): 65–72. doi: 10.1680/geot.2000.50.1.65
[7]	GUO W L, ZHU J G. Particle breakage energy and stress dilatancy in drained shear of rockfills[J]. Géotechnique Letters, 2017, 7(4): 304–308. doi: 10.1680/jgele.17.00099
[8]	米占宽, 李国英, 陈生水. 基于破碎能耗的粗颗粒料本构模型[J]. 岩土工程学报, 2012, 34(10): 1801–1811. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14871.shtml MI Zhan-kuan, LI Guo-ying, CHEN Sheng-shui. Constitutive model for coarse granular materials based on breakage energy[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(10): 1801–1811. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14871.shtml
[9]	王占军, 陈生水, 傅中志. 堆石料的剪胀特性与广义塑性本构模型[J]. 岩土力学, 2015, 36(7): 1931–1938. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201507019.htm WANG Zhan-jun, CHEN Sheng-shui, FU Zhong-zhi. Dilatancy behaviors and generalized plasticity constitutive model of rockfill materials[J]. Rock and Soil Mechanics, 2015, 36(7): 1931–1938. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201507019.htm
[10]	姚仰平, 黄冠, 王乃东, 等. 堆石料的应力–应变特性及其三维破碎本构模型[J]. 工业建筑, 2011, 41(9): 12–17, 104. https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ201109004.htm YAO Yang-ping, HUANG Guan, WANG Nai-dong, et al. Stress-strain characteristic and three-dimensional constitutive model of rockfill considering crushing[J]. Industrial Construction, 2011, 41(9): 12–17, 104. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GYJZ201109004.htm
[11]	贾宇峰, 迟世春, 林皋. 考虑颗粒破碎影响的粗粒土本构模型[J]. 岩土力学, 2009, 30(11): 3261–3266, 3272. doi: 10.3969/j.issn.1000-7598.2009.11.007 JIA Yu-feng, CHI Shi-chun, LIN Gao. Constitutive model for coarse granular aggregates incorporating particle breakage[J]. Rock and Soil Mechanics, 2009, 30(11): 3261–3266, 3272. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.11.007
[12]	陈生水, 傅中志, 韩华强, 等. 一个考虑颗粒破碎的堆石料弹塑性本构模型[J]. 岩土工程学报, 2011, 33(10): 1489–1495. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14194.shtml CHEN Sheng-shui, FU Zhong-zhi, HAN Hua-qiang, et al. An elastoplastic model for rockfill materials considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1489–1495. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract14194.shtml
[13]	张丙印, 贾延安, 张宗亮. 堆石体修正Rowe剪胀方程与南水模型[J]. 岩土工程学报, 2007, 29(10): 1443–1448. doi: 10.3321/j.issn:1000-4548.2007.10.002 ZHANG Bing-yin, JIA Ya-nan, ZHANG Zong-liang. Modified Rowe's dilatancy law of rockfill and Shen Zhujiang's double yield surfaces elastoplastic model[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(10): 1443–1448. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.10.002
[14]	郭万里, 朱俊高, 彭文明. 粗粒土的剪胀方程及广义塑性本构模型研究[J]. 岩土工程学报, 2018, 40(6): 1103–1110. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17386.shtml GUO Wan-li, ZHU Jun-gao, PENG Wen-ming. Dilatancy equation and generalized plastic constitutive model for coarse-grained soils[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(6): 1103–1110. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17386.shtml
[15]	孙逸飞, 高玉峰, 鞠雯. 分数阶塑性力学及其砂土本构模型[J]. 岩土工程学报, 2018, 40(8): 1535–1541. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17490.shtml SUN Yi-fei, GAO Yu-feng, JU Wen. Fractional plasticity and its application in constitutive model for sands[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(8): 1535–1541. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract17490.shtml
[16]	ROWE P W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1962, 269(1339): 500–527.
[17]	郭万里. 粗粒土颗粒破碎演化规律及本构模型研究[D]. 南京: 河海大学, 2018. GUO Wan-li. Particle Breakage Evolution Model of Coarse-Grained Soil and Constitutive Model[D]. Nanjing: Hohai Universiyt, 2018. (in Chinese)
[18]	王峰, 张建清. 考虑颗粒强度尺寸效应的原型堆石料破碎特性研究[J]. 岩土力学, 2020, 41(1): 87–94. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202001011.htm WANG Feng, ZHANG Jian-qing. Study of breakage behaviour of original rockfill materials considering size effect on particle strength[J]. Rock and Soil Mechanics, 2020, 41(1): 87–94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202001011.htm
[19]	吴二鲁, 朱俊高, 黄维, 等. 三轴剪切过程中粗粒料颗粒破碎变化规律研究[J]. 岩土工程学报, 2020, 42(12): 2330–2335. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18383.shtml WU Er-lu, ZHU Jun-gao, HUANG Wei, et al. Evolution law of particle breakage of coarse-grained soil during triaxial shearing[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(12): 2330–2335. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18383.shtml
[20]	PRÉVOST J, HØEG K. Soil mechanics and plasticity analysis of strain softening[J]. Géotechnique, 1975, 25: 279–297. doi: 10.1680/geot.1975.25.2.279
[21]	秦红玉, 刘汉龙, 高玉峰, 等. 粗粒料强度和变形的大型三轴试验研究[J]. 岩土力学, 2004, 25(10): 1575–1580. doi: 10.3969/j.issn.1000-7598.2004.10.013 QIN Hong-yu, LIU Han-long, GAO Yu-feng, et al. Research on strength and deformation behavior of coarse aggregates based on large-scale triaxial tests[J]. Rock and Soil Mechanics, 2004, 25(10): 1575–1580. (in Chinese) doi: 10.3969/j.issn.1000-7598.2004.10.013
[22]	贾宇峰, 迟世春, 杨峻, 等. 粗粒土的破碎耗能计算及影响因素[J]. 岩土力学, 2009, 30(7): 1960–1966. doi: 10.3969/j.issn.1000-7598.2009.07.015 JIA Yu-feng, CHI Shi-chun, YANG Jun, et al. Measurement of breakage energy of coarse granular aggregates[J]. Rock and Soil Mechanics, 2009, 30(7): 1960–1966. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.07.015
[23]	WANG L, ZHU J G, ZHANG Z L, et al. Effects of dry density on shear behavior and particle breakage for slate rockfill material[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(2): 1181–1192. doi: 10.1007/s10064-020-01971-z

施引文献(2)

期刊类型引用(2)

1.	刘志文，王媛，董琪，高山. 不连续界面渗流的堤防防渗膜防渗效果模拟研究. 人民黄河. 2024(06): 48-53+67 . 百度学术
2.	张升，兰鹏，苏晶晶，熊海斌. 基于PINNs算法的地下水渗流模型求解及参数反演. 岩土工程学报. 2023(02): 376-383+443-444 . 本站查看