颗粒特性对材料小应变动力特性的影响

黄志鹏; 魏骁; 潘坤; 杨仲轩

doi:10.11779/CJGE202205012

颗粒特性对材料小应变动力特性的影响 English Version

黄志鹏^1,,
魏骁^1, ,,
潘坤²,
杨仲轩¹

1.
浙江大学建筑工程学院, 浙江杭州 310058
2.
浙江工业大学土木工程学院, 浙江杭州 310014

基金项目:

国家自然科学基金项目 51825803

国家自然科学基金项目 52020105003

高校基本科研业务费专项资金资助项目 2021QNA4021

详细信息

作者简介:
黄志鹏(1995—)，男，硕士研究生，主要从事土动力学方面的研究。E-mail: zphuang@zju.edu.cn

通讯作者:
魏骁，E-mail: weixiaos@zju.edu.cn

中图分类号: TU43
计量
- 文章访问数: 204
- HTML全文浏览量: 26
- PDF下载量: 203
出版历程
- 收稿日期: 2021-07-04
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-04-30

Effects of particle characteristics on small-strain dynamic properties of granular materials

1.
College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China
2.
College of Civil Engineering, Zhejiang University of Technology, Hangzhou 310014, China

摘要

摘要: 土体的小应变剪切模量和阻尼比是表征土体动力学特性的重要参数。针对文献中关于砂土颗粒形状与粒径大小对小应变动力特性的影响仍存在争议，利用能量注入式虚拟质量共振柱，系统测量了特定形状与粒径的聚碳酸酯颗粒试样的小应变剪切模量和阻尼比。试验结果表明，颗粒粒径大小对试样的小应变动力学特性影响不大，而颗粒形状则有显著影响。球形颗粒试样的小应变剪切模量小于椭球颗粒和双球颗粒的试样，而球形颗粒试样的小应变阻尼比大于椭球、双球颗粒试样。椭球和球形颗粒混合试样的小应变剪切模量和阻尼比则处于两种单一颗粒之间。小应变剪切模量与阻尼比均与颗粒综合规则度存在较好的相关性，表明综合规则度可用于表征颗粒形状对材料小应变动力特性的影响。
- 颗粒特性 /
- 小应变 /
- 剪切模量 /
- 阻尼比 /
- 共振柱 /
- 综合规则度
Abstract: The small-strain shear modulus and damping ratio are the important dynamic properties of granular soils. Controversial views exist regarding the effects of particle shape and size on the small-strain dynamic properties. In this study, the small-strain shear modulus and damping ratio are measured systematically for the specimens formed by polycarbonate particles with well-controlled particle shape and size using the energy injecting virtual mass resonant column system. The test results show that the particle size has few effects on the small-strain shear modulus and damping ratio, while the particle shape has significant impacts. The shear modulus of the specimens of spherical particles is smaller than that of the elliptical particles and the clumped particles under otherwise similar conditions, while the damping ratio of the specimens of spherical particles is higher than that of the specimens of the other two particles. For the mixtures of spherical and elliptical particles, the small-strain shear modulus and damping ratio are between those of the specimens of each type of particles. The overall regularity, quantifying the shape of the particles, can be used to characterize the small-strain properties of the specimens.
- particle characteristic /
- small strain /
- shear modulus /
- damping ratio /
- resonant column /
- overall regularity

HTML全文

0. 引言

盐渍土在中国西北部寒旱区有着广泛的分布,其工程性质除了受到本身矿物、结构等因素影响外,更多的是受环境因素的影响和控制。其中,温度的改变会导致盐渍土孔隙中的盐溶液发生水盐相变现象,包括孔隙溶液中液态水结晶/融化和溶解盐析出/溶解等,进而影响土的物理力学性质,引起盐渍土地基的盐胀、冻胀和融陷等现象,从而对建筑物和地面设施产生危害^[1]。盐渍土孔隙溶液的相变行为受到温度、湿度以及孔隙的吸附和毛细作用、溶质的种类与含量等诸多因素的影响^[2-9],使得盐渍土中水盐相变机制成为特殊土力学及其工程性质领域的一个研究热点和难点问题。盐渍土冻结时的特征温度：冻结温度和过冷温度,是孔隙溶液相变在热量维度的宏观表现,是判断土体是否冻结,预测冻结深度和冻胀变形等工程应用中重要的基本物理指标^[10-11],同时对土体中的水分迁移和分凝冰形成有着重要的影响^[12-14]。

许多学者利用室内冻结温度试验,对土体冻结温度与土质、水盐含量及盐的种类等因素的关系进行了系统的研究^[15-23],认为黏性土冻结温度小于砂土冻结温度,塑限对冻结温度有显著影响,土体的冻结温度随含盐量的增加而降低,一定范围内随含水率的增加而增大,随荷载增加而逐渐降低。大量学者利用核磁共振和差热分析技术针对受限于孔隙中水的相变温度进行研究,结果表明孔隙中水的相变温度与冰晶-溶液接触面的曲率和表面张力有关^[24-27],满足Gibbs-Thomson方程,该方程被广泛应用于孔隙分布和孔形貌的测定^[28]。

Wan等^[29]、Xiao等^[30]考虑了盐溶液中水的活度对冻结温度的影响,给出了盐渍土冻结温度的计算公式,揭示了冻结温度随溶液浓度增大而降低的机理。Kozlowski等^[31]根据试验结果给出了以液塑限、含水率和土样质量为参数的土体过冷温度经验公式,但对于盐渍土的过冷温度,还是缺少简单有效的理论计算模型。试验表明当盐渍土冻结前有结晶盐析出时,冻结温度会发生突变^[29],上述冻结温度公式不再适用。对于结晶盐析出对冻结特征温度的影响这一问题,现有的研究缺乏深入的分析与探讨。

本文通过室内试验测定了盐渍土在冻结过程中的过冷温度和冻结温度,基于热力学原理与成核理论,给出了冻结特征温度的计算方法,分析了结晶盐析出对盐渍土冻结过程中特征温度的影响规律。成果对深化认识多孔介质中的水盐相变机理和寒区盐渍土的盐冻胀病害防治具有一定的指导意义。

1. 盐渍土特征温度试验研究

1.1 试验材料

试验用土为兰州地区粉土,土体经纯净水洗盐（6次）、烘干、粉碎、过筛（2 mm）后密封保存,土的物理性质指标见表1。使用无水硫酸钠溶解于蒸馏水中,在室温下（20±2℃）配制成一定浓度的硫酸钠溶液,将其与干燥土体拌和均匀后配制成土样。土样的含水率为溶液中水的质量与干土质量之比,控制为18%。土样中含盐量由溶液浓度控制,本次试验中土体含盐量控制见表2。试样在高3.5 cm,直径3.5 cm的金属容器中压实,干密度为1.75±0.01 g/cm³,该干密度下土样的孔隙分布由压汞试验测定,孔隙分布曲线如图1所示,由压汞试验可知,试样孔径结构为单峰孔隙结构,平均孔径为0.25 μm,孔隙率为35.2%。

表 1 土的物理性质指标

Table 1. Physical properties of soil

土粒相对质量密度	液限w_L/%	塑限w_P/%	塑性指数I_p
2.71	26.8	17.6	9

下载: 导出CSV

| 显示表格

表 2 土样含盐量

Table 2. Salt contents of samples

编号	含盐量/(mol·L^-1)	编号	含盐量/(mol·L^-1)
1	0	9	0.610
2	0.076	10	0.685
3	0.152	11	0.761
4	0.228	12	0.838
5	0.305	13	0.914
6	0.381	14	0.990
7	0.457	15	1.066
8	0.533	16	1.142

下载: 导出CSV

| 显示表格

图 1 重塑土样的孔隙分布

Figure 1. Grain-size distribution curves of remolded samples

下载: 全尺寸图片幻灯片

1.2 试验仪器及测试方法

试验所采用的控温装置为低温冷浴,精度为±0.1℃,测温装置采用中科院寒旱所自制的温度探头,精度为±0.01℃。将温度探头插入金属容器中土样中,容器用隔水膜包裹后放入冷浴,冷浴温度由18℃降至-15℃,过程中试样的降温速率为0.3± 0.05℃/min,期间使用数据采集器DT80每隔5 s采集一次温度数据。

1.3 试验结果

土体冻结时的特征温度包括冻结温度T_f与过冷温度T_s,如图2所示^[10-12]。从图2可以看到,土体冻结曲线分为过冷、上升、稳定和下降4个阶段。过冷阶段中孔隙溶液处于过冷状态,没有冰晶产生,在该阶段的温度最低点为过冷温度,是孔隙溶液中冰晶成核的起始点。在上升阶段,大量冰晶成核,释放潜热,土体温度回升。在稳定阶段晶体生长所释放的潜热与土体与外界热量交换所导致的热量散失相平衡,大量自由水在该阶段冻结,此时土体温度保持稳定,为土体的冻结温度。当大量自由水冻结完成后,吸附水冻结释放的潜热有限,土体温度逐渐下降,该阶段为土体冻结的下降阶段。

图 2 土体冻结曲线示意图

Figure 2. Typical cooling curve of frozen soil

下载: 全尺寸图片幻灯片

图3为试验测得不同含盐量盐渍土的冻结曲线,从曲线上可以读出土体的冻结温度与过冷温度。将不同含盐量土体的冻结特征温度绘制于图4,可以看到,随着含盐量的增大,冻结温度与过冷温度的变化趋势基本一致,分为下降、上升和稳定3个阶段。在下降阶段,随着土体含盐量的增加,特征温度逐渐降低；当含盐量大于0.533 mol/L时,过冷温度和冻结温度随着含盐量的增加而升高,为上升阶段；当含盐量大于等于0.76 mol/L时,土体冻结曲线上的两个特征温度将随着含盐量的增加基本保持不变,为稳定阶段。从图3可以明显观察到,当土体含盐量大于等于0.609 mol/L时,土体冻结前有结晶盐析出放热现象,这说明在土体含盐量为0.533～0.609 mol/L的某一值时,土体冻结前有结晶盐析出。所以冻结前结晶盐析出的临界点为0.533～0.609 mol/L的某一值,由试验无法精确得到,采用上升阶段的起始点,0.533 mol/L作为冻结前结晶盐析出的临界点。认为当土体含盐量小于等于0.533 mol/L时,土体冻结前无结晶盐析出,当土体含盐量大于0.533 mol/L时,土体冻结前开始有结晶盐析出。

图 3 盐渍土冻结曲线

Figure 3. Cooling curves of saline soil

下载: 全尺寸图片幻灯片

图 4 盐渍土冻结特征温度试验值

Figure 4. Experimental results of characteristic temperatures of saline soil

下载: 全尺寸图片幻灯片

由图4可以看到,当含盐量大于0.533 mol/L时,土体冻结温度开始进入上升阶段,这表明土体冻结前的结晶盐析出与土体冻结温度的上升同步发生,由此可以判断,土体冻结前的结晶盐析出是导致土体冻结特征温度升高的原因,Wan等^[29]研究结果也证实了这一点。

2. 盐渍土冻结温度模型

2.1 溶液冻结温度

冰-溶液共存体系中当溶液与冰达到平衡时,二者的化学势相等：

$μ_{i} (T, p_{i}) = μ_{l} (T, p_{l}, a_{w})$ ,

(1)

式中, $μ_{i}$ 和 $μ_{l}$ 分别为冰和溶液的化学势, $p_{i}$ 和 $p_{l}$ 分别为冰和溶液的压力（Pa）, $a_{w}$ 为溶液的活度,T为温度（K）。

当冰晶直径大于1 μm,可忽略冰晶曲率的影响^[32],此时溶液和冰的化学势分别为

$μ_{l} (T, p_{l}, a_{w}) = μ_{l}^{0} (T_{0}, p_{0}) + \int_{p_{0}}^{p_{l}} V_{w} d p - \int_{T_{0}}^{T} S_{w} d T + R T ln a_{w}$ ,

(2)

$μ_{i} (T, p_{i}) = μ_{i}^{0} (T_{0}, p_{0}) + \int_{p_{0}}^{p_{i}} V_{i} d p - \int_{T_{0}}^{T} S_{i} d T$ 。

(3)

式中 $μ_{l}^{0} (T_{0}, p_{0})$ 和 $μ_{i}^{0} (T_{0}, p_{0})$ 分别为溶液和冰在标准态（p₀为标准大气压,T₀=273.15 K）下的化学势；V_w和V_i分别为水和冰的摩尔体积（m³·mol^-1）；S_w和S_i分别为水和冰的摩尔焓（J·mol^-1·K^-1）；R为理想气体常数（J·mol^-1·K^-1）。

在标准态下冰水两相达到平衡时有

$μ_{l}^{0} (T_{0}, p_{0}) = μ_{i}^{0} (T_{0}, p_{0})$ 。

(4)

将式（2）～（4）代入式（1）,可得

$\int_{p_{0}}^{p_{l}} V_{w} d p - \int_{p_{0}}^{p_{i}} V_{i} d p + R T ln a_{w} = \int_{T_{0}}^{T} S_{w} - S_{i} d T$ 。

(5)

当T为冻结温度 $T_{f}$ 时,过冷度 $Δ T = T_{f} - T$ 为0,此时 $p_{0} = p_{i} = p_{l}$ ^{[30, 33]},代入式（5）可得

$T_{f} - T_{0} = \frac{R T ln a_{w}}{Δ S_{m}}$ 。

(6)

式中, $Δ S_{m} = S_{w} - S_{i} = L_{wi} / T$ 为冰水相变时的焓变（J·mol^-1·K^-1）,L_wi = 6010 J·mol^-1为冰水相变潜热。

式（6）表示溶液的冻结温度 $T_{f}$ 还将受到溶液活度的影响。对于盐溶液来说,溶液浓度对冻结温度的影响体现在水的活度 $\ln a_{w}$ 这一项上。

考虑结晶体含有 $v_{M}$ 个电荷数为 $z_{M}$ 的正离子M, $v_{X}$ 个电荷数 $z_{X}$ 的负离子X和 $v_{0}$ 个H₂O,其电离反应为

$M_{v_{M}} X_{v_{X}} \cdot v_{0} H_{2} O ⇌ v_{M} M^{z_{M+}} + v_{X} X^{z_{X -}} + v_{0} H_{2} O$ 。

(7)

对于芒硝晶体 ${Na}_{2} {SO}_{4} \cdot {10H}_{2} O$ , $v_{M} = 2$ , $v_{X} = 1$ , $z_{M} = 1$ , $z_{X} = 2$ , $v_{0} = 10$ 。

溶液中水的活度为^[34]

$ln a_{w} = - ϕ \frac{M_{w}}{1000} v C$ ,

(8)

式中, $v = v_{M} + v_{X}$ ,C为溶液浓度,M_w为水的摩尔质量,取18.0153 g·mol^-1, $ϕ$ 为渗透参数,且有

$(ϕ - 1) = | Z_{M} Z_{X} | f^{ϕ} + 2 C \frac{v_{M} v_{X}}{v} B_{MX}^{ϕ} + 2 C^{2} \frac{{(v_{M} v_{X})}^{\frac{3}{2}}}{v} C_{MX}^{ϕ}$ ,

(9)

$B_{MX}^{ϕ} = β_{MX}^{(0)} + β_{MX}^{(1)} \exp (- α_{1} I^{1 / 2}) + β_{MX}^{(2)} \exp (- α_{2} I^{1 / 2})$ 。

(10)

其中,

$f^{ϕ} = - A_{ϕ} \frac{I^{1 / 2}}{1 + b I^{1 / 2}}, I = \frac{1}{2} \sum_{i} C_{i} z_{i}^{2}$ ,

(11)

式中 $I$ 为溶液的离子强度（mol·kg^-1）； $z_{i}$ 为第 $i$ 种离子的离子价。对于Na₂SO₄溶液,b=1.2 kg^0.5 mol^-0.5,a₁=1.2 kg^0.5·mol^-0.5和a₂=1.2 kg^0.5 mol^-0.5为经验参数, $β_{MX}^{（ 0 ）}$ , $β_{MX}^{（ 1 ）}$ , $β_{MX}^{（ 2 ）}$ 和 $C_{MX}^{ϕ}$ 为离子间相互作用的参数（kg^0.5·mol^-0.5）,取值见表3, $A_{ϕ}$ 为Debye-Hückel参数（kg^0.5·mol^-0.5）,其取值与温度T相关,计算式为^[35]

$A_{ϕ} = 0.13422 (0.0368329 T - 14.627 \ln T - \frac{1530.1474}{T} + 80.40631) 。$

(12)

表 3 溶液参数表

Table 3. Parameters of electrolyte solution

盐种类	$β_{MX}^{（ 0 ）}$	$β_{MX}^{（ 1 ）}$	$β_{MX}^{（ 2 ）}$	$C_{MX}^{ϕ}$
Na₂SO₄	0.1939	1.4285	-0.5954	-0.008222

下载: 导出CSV

| 显示表格

由式（8）可计算得到0℃时Na₂SO₄溶液中水的活度与溶液浓度的关系,如图5所示。图中可以看到,随着溶液浓度的增大,溶液中水的活度不断减小,由式（6）可知,这将导致溶液的冻结温度的降低。图5给出了理论上溶液浓度和溶液中水的活度的关系,而实际上当溶液浓度增加至一定值时,会有盐结晶析出,导致溶液浓度的降低,所以溶液浓度不会无限增大,溶液中水的活度和冻结温度也不会随着溶液中盐的增多而无限减小所以图5所示的关系曲线只适用于溶液中没有盐析出时的情况,盐析出对溶液冻结温度的影响会在第4节进行详细分析。

图 5 Na₂SO₄溶液在0℃时的水分活度

Figure 5. Water activities of Na₂SO₄ solution at 0℃

下载: 全尺寸图片幻灯片

采用逐次逼近的计算方法,图6给出了式（6）的计算结果,并与其他模型的Na₂SO₄溶液冻结温度计算结果进行了对比。可以看到3个公式的计算结果的差异不大,都能较好地反映冻结温度与溶液浓度之间的关系。当T₀与 $T_{f}$ 相差不大,式（6）中的T可近似为T₀,则与文献[30]的计算公式一致。但当T₀与T_f的差值逐渐增大,文献[30]的计算结果与公式（6）的计算结果的差值也逐渐增大。

图 6 不同浓度下硫酸钠溶液冻结温度

Figure 6. Freezing temperatures of Na₂SO₄ solutions with different salt concentrations

下载: 全尺寸图片幻灯片

2.2 孔隙溶液的冻结温度

当孔隙直径小于1 μm时,孔隙中冰晶的化学势受其表面曲率的影响较大,晶体表面曲率的增大导致晶体化学势和溶解度的增大^[36],此时冰的化学势为

$μ_{i} (T, p_{i}) = μ_{i}^{0} (T_{0}, p_{0}) + γ_{sl} V_{i} \frac{d A}{d V} + \int_{p_{0}}^{p_{i}} V_{i} d p - \int_{T_{0}}^{T} S_{i} d T$ 。

(13)

式中, $γ_{sl}$ 为冰与溶液的界面能,A为冰晶表面积,V为冰晶体积。

利用式（13）代替式（3）,经推导可得孔隙中盐溶液冻结温度 $T_{f}$ 的表达式为

$T_{f} - T_{0} = \frac{R T ln a_{w}}{Δ S_{m}} - \frac{γ_{sl} V_{i}}{Δ S_{m}} \frac{d A}{d V}$ 。

(14)

当认为孔中的结晶形状为球形时,其曲率 $d A / d V =$ $2 / r_{p}$ , $r_{p}$ 为球状冰晶的半径且等于孔隙半径,此时式（14）右侧第二项与Gibbs-Thomson方程一致。

土体作为多孔材料,在利用式（14）计算其冻结温度时,需先确定等效孔径 $r_{p}$ 。受孔壁毛细与吸附作用的共同影响,多孔材料的等效孔径不仅与其孔隙分布有关,还受含水率与土颗粒表面性质的影响,所以等效孔径不等于平均孔径,等效孔径需根据试验数据修正或直接拟合得到。Wang等^[8]通过试验数据拟合得到粉质黏土和粉土的等效孔径和平均孔径的关系式,结果表明不同土体的等效孔径和平均孔径的关系式有较大差异。根据冻结温度试验数据对式（14）中的孔隙半径进行拟合,当等效半径为0.11 μm,可得计算值与试验值的可决系数达到最大值0.995,认为本试验所使用兰州黄土的等效半径为0.11 μm。根据式（14）计算得到当溶液浓度增大时,兰州黄土的冻结温度,如图7所示,随着孔中溶液浓度增大,土体冻结温度不断降低。

图 7 不同含盐量下盐渍土冻结温度

Figure 7. Freezing temperatures of saline soil with different salt contents

下载: 全尺寸图片幻灯片

3. 盐渍土过冷温度模型

3.1 过冷度与成核位垒

当土体的温度T低于冻结温度 $T_{f}$ 时,溶液处于过冷状态。过冷度 $Δ T = T_{f} - T$ 是导致冰晶析出的驱动力,当冰晶在土颗粒表面析出时,要克服冰晶与土颗粒表面物质键合能差异和晶格不匹配所导致的成核位垒,这需要一定的过冷度,需要克服的位垒越大,所需要的过冷度越高^[37]。

晶体在催化剂表面的成核为异质成核,由于土颗粒尺寸远大于冰核尺寸,所以土颗粒表面的冰晶成核为平基底上的非均匀成核,根据经典成核理论冰晶的临界半径 $r^{*}$ 为^[37]

$r^{*} = - \frac{2 γ_{sl} V_{s}}{Δ g}$ ,

(15)

$Δ g = - \frac{L_{w} Δ T}{N T_{f}}$ 。

(16)

式中, $V_{s}$ 为单个冰分子的体积, $Δ g$ 为相变驱动力,N为阿伏伽德罗常数。

成核位垒 $Δ G (r^{*})$ 计算公式为

$Δ G (r^{*}) = \frac{16}{3} \frac{π V_{s}^{2} γ^{3}}{Δ g^{2}} f (m)$ ,

(17)

式中, $f (m)$ 为几何因数,当催化剂为平基底时, $f (m) =$ $(2 - 3 m + m^{3}) / 4$ ^[37],m为土颗粒与冰晶的接触角θ的余弦,其值由土颗粒表面物质的物理化学性质决定。若在亚稳流体相F中存在催化剂C,催化剂和流体的界面为平面,有球状晶体胚团S在催化剂C上成核,此时三相交界处的接触角θ,则有

$cos θ = \frac{γ_{SC} - γ_{CF}}{γ_{SF}}$ ,

(18)

其中, $γ_{SC}$ , $γ_{CF}$ 和 $γ_{SF}$ 为界面能,下标S、C和F分别对应于晶体胚团、催化剂和流体。

催化剂表面物质与冰晶的键合能差异越小,晶格越匹配,则 $γ_{SC}$ 越小,催化剂与冰晶的接触角越小。由于接触角0°≤θ ≤ 180°,所以m的取值范围为-1≤m≤1。

3.2 孔隙溶液的过冷温度

当系统过冷度达到一定值时,冰晶才会在土颗粒表面析出,此时的过冷度为临界过冷度。成核率的计算公式为^[38]

$I = 4 π 10^{25} r^{*}^{2} exp(- Δ G (r^{*}) / k T)$ ,

(19)

式中,k为玻尔兹曼常数。

由于成核率与驱动力之间满足指数规律,当溶液过冷度大于临界过冷度时,冰晶成核率从一个接近0的值突然增大,宏观上表现为冰晶突然出现。经典成核理论规定,当成核率I = 1 cm^-3 s^-1时,对应的过冷度为临界过冷度^[37-38],可以得到临界过冷度的计算公式为

$Δ T^{*} = {[\frac{8 π T γ^{3} V_{s}^{2} f (m)}{3 k {(\frac{L_{w}}{N})}^{2} (60.1 + 4.604 lg r^{*})}]}^{\frac{1}{2}}$ 。

(20)

代入接触角余弦m和一个任意给定的晶核临界半径 $r^{*}$ 的初始值可得到临界过冷度,将该值代入式（15）和（16）可得到一个更准确的临界半径 $r^{*}$ ,临界过冷度和临界半径的数值可由该过程逐次逼近得到。最终可以得到孔隙溶液的过冷温度为

$T_{s} = T_{f} - Δ T^{*}$ 。

(21)

土颗粒与冰晶的接触角由土颗粒的表面物理化学系性质决定。根据过冷温度试验数据对式（20）中的接触角余弦m进行拟合,当接触角余弦m=0.935时,计算值与试验值的可决系数达到最大值0.94,认为兰州黄土的接触角余弦m为0.935。由式（21）得到兰州黄土过冷温度的计算值,如图8所示,可以看到计算值与试验值吻合很好,随着溶液浓度的增加,过冷温度不断减小。

图 8 盐渍土过冷温度与含盐量的关系

Figure 8. Relationship between supercooling temperatures and salt contents of saline soil

下载: 全尺寸图片幻灯片

4. 结晶盐析出对特征温度的影响

4.1 结晶盐析出对冻结时溶液浓度的影响

与冰晶成核需要一定的过冷度相似,结晶盐的成核需要一定的过饱和度^[5]。结晶盐与溶液两相平衡时,溶液的浓度为饱和浓度C_s,当溶液浓度C > C_s时,溶液处于过饱和状态,U = C / C_s,称为过饱和度,当过饱和度U > 1,系统中存在驱动结晶盐生长的相变驱动力。由于成核位垒的存在,只有当过饱和度U大于起始过饱和度U_s（U_s > 1）时,才会有结晶盐析出,此时溶液浓度为起始析出浓度C_p。溶液系统中有结晶盐存在后,只要过饱和度U > 1,就会有结晶盐生长,直至过饱和度U ≤ 1,结晶盐生长停止。由于U_s > 1,所以起始析出浓度C_p大于该温度下的饱和浓度C_s。结晶盐析出过程是溶液从过饱和状态向饱和状态转变的过程,该过程中溶液浓度不断降低,直到溶液浓度达到饱和浓度。万旭升^[35]的试验表明,当不同起始浓度的溶液降温至同一温度,若降温过程中各溶液都有结晶盐析出,则当各溶液结晶盐析出完成时,其浓度基本相同且近似等于该温度下的饱和浓度。

在降温过程中,有结晶盐析出时和无盐结晶析出时,溶液浓度的变化路径不同,如图9所示。溶液1的起始浓度 $C_{1}^{*}$ 小于冻结时的析出浓度 $C_{p}^{·}$ ,温度降至过冷温度时,溶液中无结晶盐析出,溶液浓度保持不变。溶液2的起始浓度 $C_{2}^{*}$ 大于冻结时的析出浓度 $C_{p}^{·}$ ,则在冻结发生之前,溶液中有结晶盐析出,当温度降至过冷温度时,溶液浓度按箭头所示路径减小为 $C_{s}^{·}$ ,很明显 $C_{s}^{·}$ 小于 $C_{1}^{*}$ 。所以降温前溶液2的浓度大于溶液1的浓度,由于降温过程中溶液2有结晶盐析出,同时溶液1没有结晶盐析出,导致在冻结发生时,溶液2的浓度反而小于溶液1的浓度。

图 9 降温过程中的溶液浓度

Figure 9. Solution concentrations in cooling process

下载: 全尺寸图片幻灯片

由上述分析可知,结晶盐析出作用导致冻结发生时孔隙溶液浓度的降低。根据试验结果分析可知,试验土样冻结前的起始析出浓度为0.533 mol/L,由芒硝的溶解度计算公式可得稳定阶段孔隙溶液的饱和浓度为0.317 mol/L^[39]。由图3可以看到,当溶液浓度略大于起始析出浓度时,盐析出时刻与冻结发生时刻间隔很短,则溶液冻结发生时,结晶盐未能完全析出,这时的溶液浓度介于起始析出浓度与稳定阶段的饱和浓度之间,如图10所示。可以看到,当溶液起始浓度大于起始析出浓度时,结晶盐析出导致冻结时的溶液浓度的下降。

图 10 冻结时的溶液浓度

Figure 10. Solution concentrations at freezing point

下载: 全尺寸图片幻灯片

4.2 结晶盐析出对冻结温度的影响

当土体含盐量较大时,在冻结前会有盐析出,在计算冻结温度时应考虑盐析出对冻结时溶液浓度的影响。将图10中的冻结时溶液浓度值代入式（14）,计算考虑了盐析出影响的土体冻结温度,见图11。从图11可以看到,冻结时的溶液浓度降低,导致了结晶盐析出时冻结温度的上升,计算值与试验值吻合很好,说明这一分析是合理的。

图 11 盐析出对冻结温度的影响

Figure 11. Influences of salt precipitation on freezing temperatures

下载: 全尺寸图片幻灯片

4.3 盐析出对催化剂接触角的影响

催化剂与晶体的接触角越大则非均匀成核所需的过冷温度越高。若催化剂与晶体键合能接近,晶格匹配则能有效降低接触角。结晶盐与冰晶的接触角要小于土体颗粒与冰晶的接触角。若冻结前土颗粒表面没有结晶盐,则冻结时冰晶只能在土颗粒表面成核。若冻结前土颗粒表面存在结晶盐,则冻结发生时,就会有部分冰晶在结晶盐表面析出。这在宏观上表现为,冻结前随着结晶盐不断析出,土颗粒表面的结晶盐增多,土颗粒与冰晶的接触角不断减小,并最终趋近于结晶盐与冰晶的接触角。根据特征温度稳定阶段的过冷温度值对式（20）中的接触角余弦m进行拟合,当接触角余弦m=0.971时,计算值与试验值的可决系数达到最大值0.977,认为在特征温度稳定阶段,兰州黄土的接触角余弦m为0.971。所以特征温度下降阶段接触角余弦值为0.935,稳定阶段的接触角余弦为0.971,上升阶段的接触角余弦由二者插值得到。

4.4 盐析出对过冷温度的影响

结晶盐析出导致冻结时溶液浓度的降低和冰晶与土颗粒接触角的减小,这两个变化同时对过冷温度产生影响。当认为土体与冰晶接触角为常数,只考虑冻结时溶液浓度的变化,得到的过冷温度计算值如图12中曲线1所示,可以看到冻结时溶液浓度的降低会导致过冷温度的升高。当考虑冻结时溶液浓度和土体与冰晶接触角变化的双重作用,得到的过冷温度如图12中曲线2所示,试验值与曲线2吻合很好,说明结晶盐的析出,导致孔隙溶液浓度降低和土颗粒与冰晶的接触角减小的双重作用,导致了过冷温度的升高。

图 12 盐析出对过冷温度的影响

Figure 12. Influences of salt precipitation on supercooling temperatures

下载: 全尺寸图片幻灯片

5. 结论

本文给出了盐渍土冻结时的过冷温度和冻结温度的理论计算表达式,并通过与试验结果对比,验证了表达式的有效性,同时对盐渍土冻结特征温度的影响因素进行了分析,得到以下3点结论。

（1）随着硫酸钠溶液浓度的增大,特征温度的变化分为下降、上升和稳定3个阶段,上升阶段的起始点为土体冻结前结晶盐析出的含盐量临界点。当土体含盐量小于等于该值,土体冻结前无结晶盐析出,当土体含盐量大于该值,土体冻结前开始有结晶盐析出。

（2）冻结温度随着溶液浓度的增大而降低,当冻结前有结晶盐析出,则冻结时孔隙溶液浓度降低,该作用导致了冻结温度的上升。

（3）结晶盐析出导致孔隙溶液降低和土体与冰晶的接触角减小,是过冷温度的升高的原因。

图 1 本研究所采用的聚碳酸酯颗粒

Figure 1. Poly carbonate particles used in this study

下载: 全尺寸图片幻灯片

图 2 形状参数的定义与计算方法示意图

Figure 2. Schematics of calculation of shape parameters

下载: 全尺寸图片幻灯片

图 3 能量注入式虚拟质量共振柱设备

Figure 3. EIVM resonant column testing system

下载: 全尺寸图片幻灯片

图 4 能量注入式虚拟质量共振柱系统示意图

Figure 4. Schematics of EIVM resonant column system

下载: 全尺寸图片幻灯片

图 5 孔隙比对材料G_max的影响

Figure 5. Effects of void ratio on G_max of test materials

下载: 全尺寸图片幻灯片

图 6 有效应力对材料G_max的影响

Figure 6. Effects of effective stress on G_max of test materials

下载: 全尺寸图片幻灯片

图 7 孔隙比对材料D_min的影响

Figure 7. Effects of void ratio on D_min of test materials

下载: 全尺寸图片幻灯片

图 8 有效应力对材料D_min的影响

Figure 8. Effects of effective stress on D_min of test materials

下载: 全尺寸图片幻灯片

图 9 颗粒特性对材料G_max的影响

Figure 9. Effects of particle characteristics on G_max of materials

下载: 全尺寸图片幻灯片

图 10 颗粒形状对材料G_max的影响

Figure 10. Effects of particle shape on G_max of test materials

下载: 全尺寸图片幻灯片

图 11 颗粒特性对材料D_min的影响

Figure 11. Effects of particle characteristics on D_min of materials

下载: 全尺寸图片幻灯片

图 12 颗粒形状对材料D_min的影响

Figure 12. Effects of particle shape on D_min of test materials

下载: 全尺寸图片幻灯片

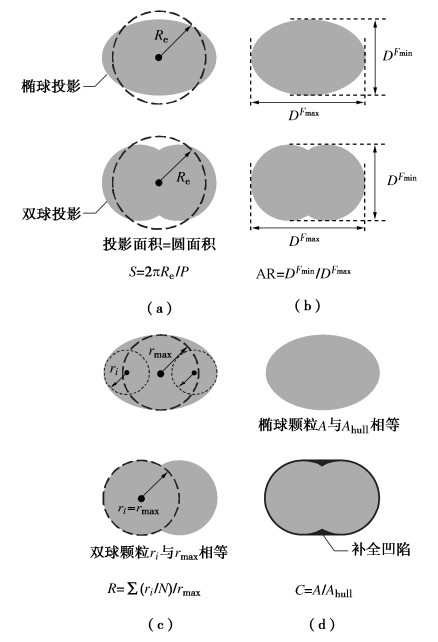
表 1 颗粒形状参数表

Table 1 Shape quantities of particles

颗粒种类	球度S	长细比AR	圆度R	凸度C	综合规则度OR
S2	1.00	1.00	1.00	1.00	1.00
S3	1.00	1.00	1.00	1.00	1.00
El	0.97	0.67	0.67	1.00	0.83
Cl	0.95	0.67	1.00	0.98	0.90
S3︰El =2︰1	0.99	0.89	0.89	1.00	0.94
S3︰El =1︰2	0.98	0.78	0.78	1.00	0.88

下载: 导出CSV

表 2 试验方案表

Table 2 Test schemes

颗粒种类	试样孔隙比	有效应力/kPa
S2	0.580/0.605/0.635/0.665	50/100/200/400
S3	0.580/0.607/0.638/0.667	50/100/200/400
El	0.500/0.550/0.575/0.604	50/100/200/400
Cl	0.500/0.551/0.571/0.603	50/100/200/400
S3︰El =2︰1	0.605	50/100/200/400
S3︰El =1︰2	0.605	50/100/200/400

下载: 导出CSV

表 3 G_max拟合参数表

Table 3 Fitting parameters of G_max

类别	颗粒种类	A/MPa	a	n	R²
a固定	S2	7.16	2.97	0.410	0.998
	S3	7.13	2.97	0.411	0.998
	El	8.72	2.97	0.378	0.998
	Cl	8.35	2.97	0.392	0.998
	S3︰El=2︰1	7.51	2.97	0.396	0.997
	S3︰El=1︰2	8.13	2.97	0.380	0.997
a可变	S2	12.54	2.40	0.409	0.999
	S3	13.20	2.35	0.411	0.999
	El	7.44	3.17	0.378	0.998
	Cl	5.70	3.48	0.393	0.999

下载: 导出CSV

表 4 D_min拟合参数表

Table 4 Fitting parameters of D_min

颗粒种类	D₁	κ	R²
S2	0.0076	0.169	0.677
S3	0.0077	0.178	0.718
El	0.0071	0.192	0.674
Cl	0.0072	0.159	0.573
S3︰El=2︰1	0.0071	0.151	0.962
S3︰El=1︰2	0.0068	0.176	0.997

下载: 导出CSV

参考文献(28)

[1]	ISHIHARA K. Soil Behaviour in Earthquake Geotechnics[M]. New York: Oxford University Press, 1996.
[2]	HARDIN B O, RICHART F E Jr. Elastic wave velocities in granular soils[J]. Journal of the Soil Mechanics and Foundations Division, 1963, 89(1): 33–65. doi: 10.1061/JSFEAQ.0000493
[3]	WICHTMANN T, TRIANTAFYLLIDIS T. Influence of the grain-size distribution curve of quartz sand on the small strain shear modulus gmax[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(10): 1404–1418. doi: 10.1061/(ASCE)GT.1943-5606.0000096
[4]	LIU X, YANG J. Shear wave velocity in sand: effect of grain shape[J]. Géotechnique, 2018, 68(8): 742–748. doi: 10.1680/jgeot.17.T.011
[5]	GU X Q, YANG J, HUANG M S. Laboratory measurements of small strain properties of dry sands by bender element[J]. Soils and Foundations, 2013, 53(5): 735–745. doi: 10.1016/j.sandf.2013.08.011
[6]	SENETAKIS K, ANASTASIADIS A, PITILAKIS K. The small-strain shear modulus and damping ratio of quartz and volcanic sands[J]. Geotechnical Testing Journal, 2012, 35(6): 20120073. doi: 10.1520/GTJ20120073
[7]	IWASAKI T, TATSUOKA F. Effects of grain size and grading on dynamic shear moduli of sands[J]. Soils and Foundations, 1977, 17(3): 19–35. doi: 10.3208/sandf1972.17.3_19
[8]	MENQ F Y. Dynamic Properties of Sandy and Gravelly Soils[D]. Austin: The University of Texas at Austin, 2003.
[9]	SHARIFIPOUR M, DANO C, HICHER P. Wave velocities in assemblies of glass beads using bender-extender elements[C]// Proceedings of 17th ASCE Engineering Mechanics Conference, 2004, Newark.
[10]	HARDIN B O, KALINSKI M E. Estimating the shear modulus of gravelly soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(7): 867–875. doi: 10.1061/(ASCE)1090-0241(2005)131:7(867)
[11]	DUTTA T T, OTSUBO M, KUWANO R, et al. Stress wave velocity in soils: apparent grain-size effect and optimum input frequencies[J]. Géotechnique Letters, 2019, 9(4): 340–347. doi: 10.1680/jgele.18.00219
[12]	YANG J, GU X Q. Shear stiffness of granular material at small strains: does it depend on grain size?[J]. Géotechnique, 2013, 63(2): 165–179. doi: 10.1680/geot.11.P.083
[13]	PATEL A, BARTAKE P, SINGH D. An empirical relationship for determining shear wave velocity in granular materials accounting for grain morphology[J]. Geotechnical Testing Journal, 2009, 32(1): 1–10.
[14]	HARDIN B O. Dynamic versus static shear modulus for dry sand[J]. Materials Research and Standards, 1965, 5(5): 232–235.
[15]	CHO G C, DODDS J, SANTAMARINA J C. Particle shape effects on packing density, stiffness, and strength: natural and crushed sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(5): 591–602. doi: 10.1061/(ASCE)1090-0241(2006)132:5(591)
[16]	PAYAN M, KHOSHGHALB A, SENETAKIS K, et al. Effect of particle shape and validity of G_max models for sand: a critical review and a new expression[J]. Computers and Geotechnics, 2016, 72: 28–41. doi: 10.1016/j.compgeo.2015.11.003
[17]	ALTUHAFI F N, COOP M R, GEORGIANNOU V N. Effect of particle shape on the mechanical behavior of natural sands[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(12): 04016071. doi: 10.1061/(ASCE)GT.1943-5606.0001569
[18]	曾国熙, 顾尧章, 吴建平. 粉煤灰的动剪切模量[J]. 岩土工程学报, 1985, 7(5): 1–9. doi: 10.3321/j.issn:1000-4548.1985.05.001 ZENG Guo-xi, GU Rao-zhang, WU Jian-ping. Dynamic shear moduli of fly ashes[J]. Chinese Journal of Geotechnical Engineering, 1985, 7(5): 1–9. (in Chinese) doi: 10.3321/j.issn:1000-4548.1985.05.001
[19]	SHIN H, SANTAMARINA J C. Role of particle angularity on the mechanical behavior of granular mixtures[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2013, 139(2): 353–355. doi: 10.1061/(ASCE)GT.1943-5606.0000768
[20]	ATHANASSIADIS A G, MISKIN M Z, KAPLAN P, et al. . Particle shape effects on the stress response of granular packings[J]. Soft Matter, 2014, 10(1): 48–59. doi: 10.1039/C3SM52047A
[21]	袁晓铭, 孙锐, 孙静, 等. 常规土类动剪切模量比和阻尼比试验研究[J]. 地震工程与工程振动, 2000, 20(4): 133–139. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200004021.htm YUAN Xiao-ming, SUN Rui, SUN Jing, et al. Laboratory experimental study on dynamic shear modulus ratio and damping ratio of soils[J]. Earthquake Engineering and Engineering Vibration, 2000, 20(4): 133–139. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC200004021.htm
[22]	SHIN B. Laboratory Investigation of the Stiﬀness and Damping Properties of Binary and Gap-Graded Mixtures of Granular Soils[D]. Austin: The University of Texas at Austin, 2019.
[23]	PAYAN M, SENETAKIS K, KHOSHGHALB A, et al. Influence of particle shape on small-strain damping ratio of dry sands[J]. Géotechnique, 2016, 66(7): 610–616. doi: 10.1680/jgeot.15.T.035
[24]	LI X S, YANG W L, SHEN C K, et al. Energy-injecting virtual mass resonant column system[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(5): 428–438. doi: 10.1061/(ASCE)1090-0241(1998)124:5(428)
[25]	YANG Z X, WEN Y X, PAN K. Previbration signature on dynamic properties of dry sand[J]. Journal of Testing and Evaluation, 2019, 47(3): 2167–2192.
[26]	蔡正银, 李相崧. 材料状态对干砂小应变特性的影响[J]. 岩土力学, 2004, 25(1): 10–14. doi: 10.3969/j.issn.1000-7598.2004.01.003 CAI Zheng-yin, LI Xiang-song. Effects of material state on the small strain behavior of dry sand[J]. Rock and Soil Mechanics, 2004, 25(1): 10–14. (in Chinese) doi: 10.3969/j.issn.1000-7598.2004.01.003
[27]	HARDIN B O, BLACK W L. Sand stiffness under various triaxial stresses[J]. Journal of the Soil Mechanics and Foundations Division, 1966, 92(2): 27–42. doi: 10.1061/JSFEAQ.0000865
[28]	LIU X, YANG J, WANG G H, et al. Small-strain shear modulus of volcanic granular soil: an experimental investigation[J]. Soil Dynamics and Earthquake Engineering, 2016, 86: 15–24. doi: 10.1016/j.soildyn.2016.04.005

施引文献(11)

期刊类型引用(8)

1.	杨旭辉，柏谦，贾鹏蛟. 地铁车站小直径管幕-横梁支护参数优化分析. 沈阳工业大学学报. 2025(01): 114-123 . 百度学术
2.	邱建，赵文，路博，孙旭. 新型管幕工法修建地铁车站地层变形特性及参数优化. 东北大学学报(自然科学版). 2024(11): 1645-1655 . 百度学术
3.	崔光耀，宋博涵，何继华，田宇航. 超近接上跨既有隧道施工影响分区及加固措施效果. 长江科学院院报. 2023(06): 114-118+125 . 百度学术
4.	伍凯，毕延哲，杨鑫，储修琼. 超浅覆土小净距上跨运营线路盾构掘进超前管幕支护模拟分析. 路基工程. 2023(04): 130-136 . 百度学术
5.	陈凯. 基于变形控制的密排管幕顶管施工顺序优化分析. 铁道勘察. 2023(05): 149-157 . 百度学术
6.	王子君，赵文，程诚，柏谦. 地铁车站小直径管幕工法开挖变形规律. 东北大学学报(自然科学版). 2022(11): 1630-1637 . 百度学术
7.	袁庆利. 大直径密排管幕的力学分析及在地铁车站中的应用. 吉林水利. 2021(06): 1-10 . 百度学术
8.	张贺. 新型钢管幕力学变形特征及其在地铁车站中的应用. 工程建设. 2021(09): 1-6 . 百度学术