Quality evaluation for measured data of slope displacement based on its spatial distribution
-
摘要: 滑坡灾害预警依赖于边坡位移等监测数据,因此数据质量评估具有重要意义。对边坡剖面位移多点测量数据进行了分析,结果表明边坡在变形破坏过程中一般可划分为不同位移特点的3个区域,同区域各点的位移测量数据具有相关性并且该相关性随着测点间距离的增加而衰减。基于规律认识,设计了边坡区域划分算法,提出一种测点相似度衰减方程,建立了一种边坡位移大数据质量快速评估方法。针对边坡离心模型试验位移测量结果进行分析,验证了方法的有效性。该方法更新迭代时间复杂度较低,能够满足大数据快速处理的要求。Abstract: The landslide hazard warning relies on the monitoring data such as slope displacement. Therefore, data quality assessment is of great significance in practice. The multi-point measured data of slope profile displacement are analyzed. The results show that the slope can generally be divided into three regions with different displacement characteristics during the deformation and failure. The slope displacements of points in the same area are correlated, and the correlation degree decreases as the distance between the measuring points increases. Accordingly, an algorithm for the slope region division is designed. A correlation decay equation for measuring points is proposed, and then thus a method is set up for the rapid assessment on the quality of large data of slope displacement. The slope displacement measured in a centrifuge model test is analyzed to confirm the effectiveness of the proposed method. The method has low complexity of update iteration time and is suitable for fast processing of big data.
-
Keywords:
- slope /
- profile displacement /
- monitoring /
- big data /
- quality assessment
-
0. 引言
滑坡灾害是重要的地质灾害之一,每年造成巨大损失,严重危害人民的生命和财产安全[1-2]。而基于实测数据进行边坡灾害预警预报,是有效预防和减小滑坡灾害的重要途径,这已被工程实践所证明[1]。
随着卫星导航系统、遥感等技术的发展,针对边坡进行大规模全时段监测已经成为可能[3]。然而,通过监测、试验和计算分析得到的数据,总是存在着各种原因导致的误差,需要对监测数据的质量进行甄别。以往对边坡数据误差的识别和数据质量的评估,主要是依赖于经验性的判断进行人工筛选,但该方法缺乏理论依据并且无法处理大批量的数据。在自动化处理方面,常用插值法、小波变换、稳健估计[4-6]等数理统计方法检测数据异常。不过需要指出,边坡的位移等数据通常在时空上不服从常见的概率分布,仅靠常规数理统计或者滤波处理等方法难以取得较好效果。
本文基于边坡离心模型试验图像分析得到的边坡位移多点测量数据,研究了边坡剖面位移的空间分布特性及其规律,在此基础上提出了一种边坡剖面位移数据有效性甄别与质量评估方法。
1. 规律分析
1.1 位移空间分布特性
边坡的破坏是一个渐进的过程。其在很长一段时间内发生微小的变形累积并最终在短时间内发生滑动破坏及较大变形[7]。
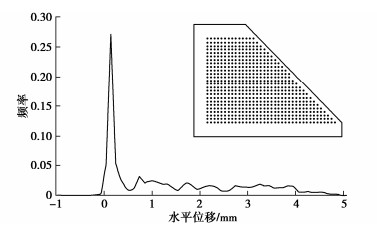
本文基于均质黏性土边坡开挖离心模型试验进行分析[8]。该试验采用的边坡模型高30 cm,坡度为1.5︰1。在60g离心加速度条件下于边坡坡脚处进行开挖,开挖高度9.6 cm。图 1给出了该试验测得的边坡剖面各测点位置及测点位移的频率分布。需要指出,本文中边坡位移、几何尺寸等均基于模型尺寸给出,可根据模型相似律乘以60换算为原型。从图中可以看到,半数以上测量的位移监测数据都分布在零点附近。较大位移的数据在测点数量上占比很小,却对滑坡灾害预警具有重要意义。这表明仅从概率统计的角度考虑位移分布特性进而评估数据质量并不是一种有效的途径。
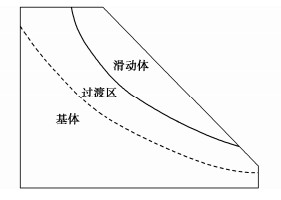
已有研究表明,边坡剖面位移分布具有显著的区域化特征,如图 2所示。边坡在变形破坏过程中一般可划分为3个区域 [8-9],分别表现出不同的位移特点。本文将这3个区域分别称为基体、过渡区和滑动体。基体的位移一般很小,有些点已经达到仪器的测量极限,因此测量数据质量整体偏低。过渡区的位移较为显著且分布梯度较大。滑动体的位移较大,且位移分布梯度较小,表现为整体向下滑动。因此,应针对不同区域分别研究位移测量数据分布特性并得出相关规律性认识。
1.2 位移相关性
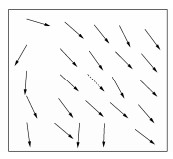
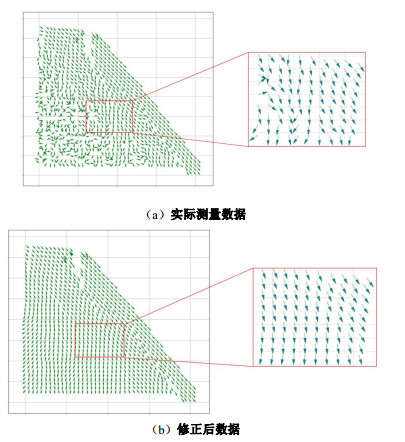
图 3展示了某边坡离心模型试验某区域测量位移结果。可以看出,图中虚线色箭头标识的位移数据与其附近测点位移数据较为接近,当测点距离增加后,其位移数据的差异也随之增加。可以推测,各点的位移测量数据具有一定的相关性,该相关性随着测点间距离的增加而逐渐衰减。这与地理统计学的相近相似原理相符合。有学者基于该认识使用反距离权重插值法对相近的测点进行插值计算[10]。
为了定量研究位移相关性规律,本文提出了相似度的计算公式:
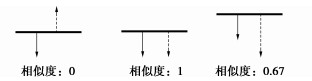
s = 1−|u−v||u|+|v|, (1) 式中,u为监测数据,v为标准数据。该相似度计算公式的特点在于它的取值是在[0, 1]区间,并且两个数据在该维度具有相同方向的位移增量时才具有正相似度。从监测数据与标准数据方向相同开始,随着监测数据不断接近标准数据,相似度会迅速的增大至1,而当监测数据大于标准数据并不断偏离时,相似度会缓慢减少并且以0为极值。图 4展示了3种情况下的数据相似度计算结果,整体比较符合实际的认知。
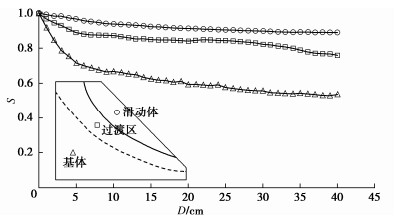
图 5给出了对离心模型试验中各区域典型点的相似度随距离的变化。可以看到,各点的相似度均随着距离的增加而减小。其中,基体区的位移较小,所以该区域的相似度衰减明显比其他区域快。滑动体区的相似度衰减较慢,且数值高于其他区域,这是因为该区域表现为整体运动,其位移相关性较好。
2. 分析方法
首先统一数据编码的格式。将边坡上的测点进行编号后,第i个测点的数据表示为Pi(X,Y,u1,u2, ⋯, ut)。式中,前两个维度X,Y表示该测点的位置信息,后t个维度表示该测点在t个时刻的响应信息。本文所建立方法对测点进行空间区域划分以及数据质量的评估,本质上都是基于这t+2维度的数据进行分类和预测。
2.1 区域划分
常见的对数据进行划分聚类的算法有K-means、层次聚类和GMM高斯混合模型算法等[11]。但是,这些算法对于数据是否包含不同层次的物理信息并不敏感。考虑到边坡位移数据包含了位置信息和时程响应两个层次,最终划分的区域基于测点位移性质进行划分,也需要同时满足空间位置关系的约束。为此,提出了新的算法,分如下两步加以实现。
(1)测点性质的划分
基于层次聚类算法的思想,首先将相似度尽可能高的测点划分为一类,假设两条数据分别为
{Pi(Xi,Yi,u1,u2,⋯,ut)Pj(Xj,Yj,v1,v2,⋯,vt), 计算两条数据相似度的原则是用式(1)先算出每个时程响应数据的相似度,然后以该时刻两条数据平均的位移增量作为权重加权求和,
Sij=t∑k=1(1−|uk−vk||uk|+|vk|)(Δik+Δjk2)t∑k=1(Δik+Δjk2), (2) 式中,Δik,Δjk为测点i与测点j在第k时间段的位移增量,其表达式为(记u0=v0=0)
Δik=|uk−uk-1| ,Δjk=|vk−vk-1| 。} (3) 因为较大位移的数据在边坡灾害预报预警中非常关键,在数据评估中将更加关注较大位移的数据响应信息是否一致。
与层次聚类不同的是,本方法使用的搜寻算法是以距离优先的原则对数据点进行相似度计算,为了使得分类的结果在空间上具有一定的连续性,在计算过程中迭代调整阈值作为数据点划分的依据,如果相似度计算结果大于该阈值时则认定两测点属于同一类,反之则计算下一个点。
(2)空间位置关系的约束
由于数据本身存在监测误差,仅根据时程响应信息进行分类得到的结果在空间分布上往往有如下问题:①异常数据点被分类算法单独划分成一类; ②同一个类别中的点在空间上分布不连续; ③存在过度分类的现象。
针对上述问题,对第一步的划分结果进行聚类操作。如果一个类中测点的个数少于总测点个数的5%,则将这种类定义为“小类”。将所有“小类”中的测点以欧氏距离作为衡量指标,运用K-means算法的思想划分到其他的类中。然后根据进一步的划分结果在适当的运用KNN算法[12]进行空间迭代,消除同一类在空间分布上不连续的现象。最后根据需要输出最大的K类,与此同时要将其它的类视作“小类”用上述相同的方法划分进最大的K类中。
图 6给出了采用本文算法的分区结果。在该算法下将边坡上的测点(图 6(a))分成了3个区域(图 6(b))。基体区用红点标记,过渡区用黄色点标记,滑动体区用绿色点标记。
2.2 相似度衰减方程
基于相关性衰减规律,定义同一区域内数据之间的相似度随距离衰减函数为
S=k(dijH)−α, (4) 式中,S为总体相似度,表示测量数据参考权重的大小,dij为两数据点间的距离,H为边坡高度。参数k的作用是消除数据测量和采集过程中各种因素的影响,需要根据实际情况确定。参数α为一个正实数,其值越大表明相似度衰减得越快。K,α可通过对每个区域进行预处理得到。需要强调的是,该式只是统计意义上距离和相关性之间的函数关系,目的是计算不同参考点之间参考价值的权重。它以距离为衡量标准,赋予有效范围内每一个数据点不同的参考权重。
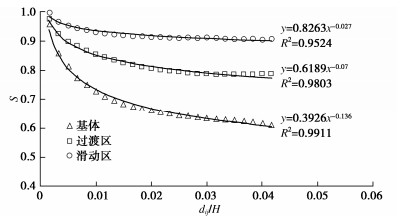
在实际的质量评估中,一般不会用到距离过大的数据点进行分析评估。所以,只需重点关注短距离内的相似度衰减规律。图 7给出了各区域在短距离内相似度的公式拟合结果,并确定了各区域的公式具体参数。
2.3 迭代算法
本文方法的迭代流程如下:
(1)质量参数初始化
在空间测点区域化完成后,将每一个时程响应数据表示为Pi(X,Y,u,v,C(u)C(v))。式中,Pi为这个数据的编号,括号中X,Y为位置信息,u,v为水平和竖直两个方向上这一时刻位移的增量。C(u),C(v)为两个增量的数据质量,都是[0, 1]区间的一个实数,并且初始化为1。
(2)确定参考数据范围
定义一个常数ε,规定在同一区域类别中,某点到该点的距离小于ε,则认为在评估该测点数据质量时可以作为参考数据。如果范围内的参考数据量过少,也可以考虑周围的其他数据,但是需要设定一个数量上界。本文规定最多只参考最近的5个测点作为参考数据。
(3)计算数据标准值
将该时刻选中的所有参考数据基于相似度衰减方程(式(4))进行加权求和,计算出一个最可能的增量值⌢ui与⌢vi:
⌢ui=∑jk(dijH)−α⋅C(uj)⋅uj∑jk(dijH)−α⋅C(uj) ,⌢vi=∑jk(dijH)−α⋅C(vj)⋅vj∑jk(dijH)−α⋅C(vj) ,} (5) 式中,α,k为统计意义上的系数,在不同的区域可以通过对数据进行预处理的方式进行拟合回归得到。例如,图 7给出了一个拟合结果,过渡区的α的取值为0.07,k取值为0.6189。从式(5)可以看出,采用的权重不仅与两点间的距离有关,也与参考点本身的数据质量有关,从而综合考虑了测点位置及数据质量等信息,使得分析结果更为可靠。
(4)更新迭代质量参数
对每条数据的C(u),C(v)参数进行更新迭代:
C(ui)′=lr⋅(1−|ui−⌢ui||ui|+|⌢ui|)+(1−lr)⋅C(ui) ,C(vi)′=lr⋅(1−|vi−⌢vi||vi|+|⌢vi|)+(1−lr)⋅C(vi),} (6) 式中,C(ui)′,C(vi)′为更新后的质量参数,lr为迭代更新中的学习率,一般取10-2。
(5)重复步骤(2)~(4),收敛判断条件为
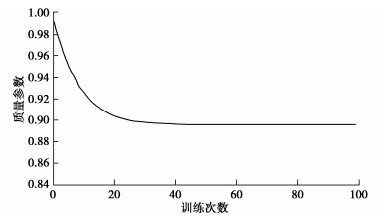
maxi{|C(ui)−C(ui)′|,|C(vi)−C(vi)′|}⩽0.001。 (7) 图 8展示了某数据的质量参数变化曲线。
本算法主要的计算量是在遍历每一个数据点的过程中需要计算该点的有效范围,每次迭代的时间复杂度至多为O(n2)级。如果能够提前存储监测数据点两两之间的距离信息,该迭代算法时间复杂度能够优化至最佳的O(n)级别,能够满足对大数据质量快速评估的需求。
3. 方法有效性验证
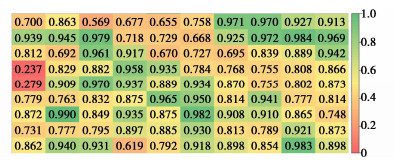
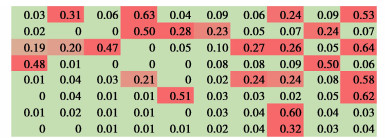
图 9给出了某离心模型试验边坡剖面位移测量数据的分析结果。选取图 9中的一个小区域,给出每条数据的质量评估结果(图 10)。图 10中的数值越大,说明其数据质量越高。为了更好的展示质量评估结果,还分别用不同颜色作为标记。红色结果表示数据质量很低,而绿色将结果表示数据质量很高。
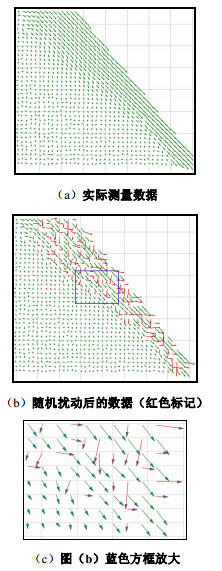
进一步验证本文方法的有效性,采用本文方法进行数据质量评估。在边坡离心模型试验位移测量结果的基础上,人为引入扰动造成部分测点错误的测量结果。图 11(a)给出了边坡位移测量结果。将数据质量大于90%的位移数据中的一半引入噪声干扰,扰动后的数据如图 11(b)红色标记的数据所示。将扰动后的数据重新进行质量评估,就能得到原始数据的质量评估结果和扰动后数据的评估结果之差。为了更好的展示,重点展示图 11(b)中蓝色矩形边框中的数据质量结果(图 11(c))。
规定两次评估结果差距大于一定阈值时即判断该数据为“错误”,反之则判定为“可用”。该阈值本文取0.1。图 12给出了蓝色矩形边框中数据扰动前和扰动后的两次评估质量结果之差的绝对值,其中红色标记的是两次评估结果之差大于阈值0.1的数据。表 1给出了边坡所有数据的甄别结果,一共1009条数据中修改了190条数据,其中仅有4条未成功识别,有8条数据误判,误判的原因是该数据周围被扰动的数据太多。总体来看,本文方法的有效性很高。
表 1 位移数据有效性甄别结果Table 1. Validity screening results for slope displacement类别 真实修改 真实未修改 设别成修改 186 8 识别成未修改 4 811 4. 结论
(1)基于边坡离心模型试验图像分析得到的边坡剖面位移多点测量数据,揭示了边坡剖面位移的空间分布特性及其规律:①边坡剖面在变形破坏过程中一般可划分为3个区域,分别表现出不同的位移特点;②同一区域各点的位移测量数据具有一定的相关性,该相关性随着测点间距离的增加而逐渐衰减。
(2)基于规律认识,提出了一种边坡剖面位移大数据质量快速评估方法,包括:①以监测点的位置和相应时程位移数据作为分类标准,设计出了边坡区域划分算法,既满足了对测点性质的划分,也满足了空间位置的约束条件;②提出了一种位移相似度衰减方程,实现了对边坡剖面位移相关性的定量刻画;③建立了各区域中数据质量参数的迭代算法,其更新迭代时间复杂度较低,能够满足大数据快速处理的要求。
(3)针对边坡离心模型试验剖面位移测量结果进行分析,验证了方法的有效性。
-
表 1 位移数据有效性甄别结果
Table 1 Validity screening results for slope displacement
类别 真实修改 真实未修改 设别成修改 186 8 识别成未修改 4 811 -
[1] 尚岳全, 王清, 蒋军, 等. 地质工程学[M]. 北京: 清华大学出版社, 2006. SHANG Yue-quan, WANG Qing, JIANG Jun, et al. Geological Engineering[M]. Beijing: Tsinghua University Press, 2006. (in Chinese)
[2] 高杰. 激光与CCD技术在边坡远程监测中的应用研究[D]. 杭州: 浙江大学, 2010. GAO Jie. A Research on Laser and CCD Technology Application of Slope Remote Monitoring[D]. Hangzhou: Zhejiang University, 2010. (in Chinese)
[3] 程胜伟, 段继东, 马科研, 等. 基于北斗智慧云监测平台的高边坡变形控制研究[J]. 施工技术, 2019, 48(增刊1): 149–151. https://www.cnki.com.cn/Article/CJFDTOTAL-SGJS2019S1034.htm CHENG Sheng-wei, DUAN Ji-dong, MA Ke-yan, et al. Research on high slope deformation control based on Beidou smart cloud monitoring platform[J]. Construction Technology, 2019, 48(S1): 149–151. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SGJS2019S1034.htm
[4] 田雷, 董德明, 魏强, 等. 3种空间插值方法在道路尘中Pb监测数据统计处理中的应用比较[J]. 吉林大学学报(理学版), 2011, 49(5): 964–968. https://www.cnki.com.cn/Article/CJFDTOTAL-JLDX201105040.htm TIAN Lei, DONG De-ming, WEI Qiang, et al. Comparison of three spatial interpolation methods for statistical processing of lead monitoring data in road dust[J]. Journal of Jilin University (Science Edition), 2011, 49(5): 964–968. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JLDX201105040.htm
[5] 雷孟飞, 周俊华, 汤金毅. 基于小波变换的高边坡变形监测数据误差处理方法[J]. 导航定位学报, 2020, 8(6): 109–113. doi: 10.3969/j.issn.2095-4999.2020.06.016 LEI Meng-fei, ZHOU Jun-hua, TANG Jin-yi. Application of wavelet transform in error elimination of high slope deformation monitoring[J]. Journal of Navigation and Positioning, 2020, 8(6): 109–113. (in Chinese) doi: 10.3969/j.issn.2095-4999.2020.06.016
[6] 陈志江, 杨久东, 张凌云. 稳健估计在地铁沉降监测数据处理中的应用[J]. 华北理工大学学报(自然科学版), 2021, 43(1): 26–31. doi: 10.3969/j.issn.2095-2716.2021.01.005 CHEN Zhi-jiang, YANG Jiu-dong, ZHANG Ling-yun. Application of robust estimation in data processing of subway subsidence monitoring[J]. Journal of North China University of Science and Technology (Natural Science Edition), 2021, 43(1): 26–31. (in Chinese) doi: 10.3969/j.issn.2095-2716.2021.01.005
[7] LUO F Y, ZHANG G. Progressive failure behavior of cohesive soil slopes under water drawdown conditions[J]. Environmental Earth Sciences, 2016, 75(11): 1–12.
[8] ZHAO Y Y, ZHANG G. Centrifuge modeling of soil slopes overlying bedrock under excavation conditions[J]. Soils and Foundations, 2020, 60(4): 886–897. doi: 10.1016/j.sandf.2020.06.009
[9] CHEN T Y, LUO F Y, ZHANG G, et al. Study on deformation and failure of slopes under coupled application of water level change and vertical load[J]. Bulletin of Engineering Geology and the Environment, 2021, 80(1): 353–364. doi: 10.1007/s10064-020-01958-w
[10] 汤国安, 杨昕. ArcGIS地理信息系统空间分析实验教程[M]. 北京: 科学出版社, 2007. TANG Guo-an, YANG Xin. ArcGIS Geographic Information System Spatial Analysis Experiment Tutorial[M]. Beijing: Science Press, 2007. (in Chinese)
[11] 方开泰, 潘恩沛. 聚类分析[M]. 北京: 地质出版社, 1982. FANG Kai-tai, PAN En-pei. Cluster Analysis[M]. Beijing: Geological Publishing House, 1982. (in Chinese)
[12] 闭小梅, 闭瑞华. KNN算法综述[J]. 科技创新导报, 2009(14): 31. doi: 10.3969/j.issn.1674-098X.2009.14.019 BI Xiao-mei, BI Rui-hua. Summary of KNN algorithm[J]. Science and Technology Innovation Herald, 2009(14): 31. (in Chinese) doi: 10.3969/j.issn.1674-098X.2009.14.019
-
期刊类型引用(4)
1. 农花舒. 无人机摄影测量在边坡位移测量中的应用. 中国新技术新产品. 2025(05): 143-145 .  百度学术
百度学术
2. 段帅安,王江锋. 强震区高边坡稳定性及支护方案的数值模拟. 河南科技. 2023(02): 65-69 .  百度学术
百度学术
3. 董星星,高继勋,王晓桐,李松. 空间方向关系表达与推理模型研究综述. 计算机工程. 2023(09): 1-15 .  百度学术
百度学术
4. 徐文胜. 基于有限元模型的城市地下隧道施工边坡支护技术创新研究. 粘接. 2023(10): 158-161 .  百度学术
百度学术
其他类型引用(2)



 下载:
下载: