高级切线模量法及其在地基沉降计算中的应用

杨光华; 李卓勋; 王东英; 李志云; 姜燕

doi:10.11779/CJGE202205001

高级切线模量法及其在地基沉降计算中的应用 English Version

杨光华^{1, 2, 3,},
李卓勋¹,
王东英^{2, 3},
李志云^{2, 3},
姜燕^{2, 3}

1.
华南理工大学土木与交通学院, 广东广州 510640
2.
广东省水利水电科学研究院, 广东广州 510610
3.
广东省岩土工程技术研究中心, 广东广州 510610

基金项目:

国家自然科学基金项目 52078143

详细信息

作者简介:
杨光华(1962—)，男，广东罗定人，博士，教授级高级工程师，博士生导师，主要从事本构理论、基础工程、软土工程及基坑工程等方面的研究、设计及咨询工作。E-mail: 1084242143@qq.com

中图分类号: TU433
计量
- 文章访问数: 308
- HTML全文浏览量: 20
- PDF下载量: 262
出版历程
- 收稿日期: 2021-03-01
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-04-30

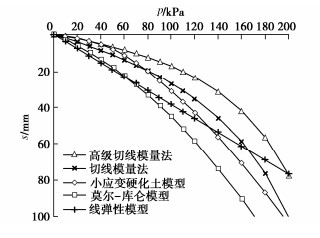
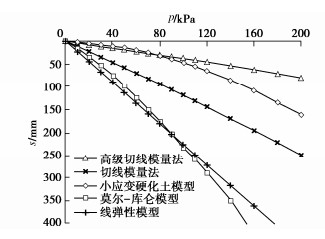
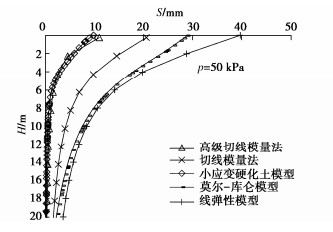
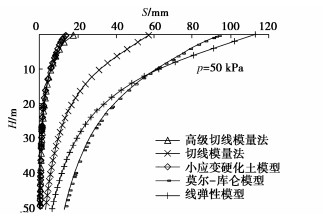
Advanced tangent modulus method and its application to calculation of foundation settlement

YANG Guang-hua^{1, 2, 3,},
LI Zhuo-xun¹,
WANG Dong-ying^{2, 3},
LI Zhi-yun^{2, 3},
JIANG Yan^{2, 3}

1.
Department of Civil Engineering, South China University of Technology, Guangzhou 510640, China
2.
Guangdong Research Institute of Water Resources and Hydropower, Guangzhou 510610, China
3.
The Geotechnical Engineering Technology Center of Guangdong Province, Guangzhou 510610, China

摘要

摘要: 切线模量法方法简单、参数少，易于工程应用，研究表明在计算常规尺寸的基础时具有较好的精度，而对于筏板这样的大尺寸基础时，当计算深度较深时，存在计算沉降偏大的问题。为此提出了考虑初始切线模量沿深度增大的高级切线模量法，通过与实际工程案例和小应变有限元数值计算方法结果比较，高级切线模量法能更符合实际，进一步发展完善了切线模量法。
- 切线模量法 /
- 地基沉降 /
- 有限元 /
- 小应变硬化土模型
Abstract: The tangent modulus method proposed by YANG Guang-hua is simple, with few parameters and easy for engineering application. The researches have shown that it has better accuracy when calculating the foundations with conventional dimensions, but for the large-sized foundations such as rafts, the calculated settlement is too large. For this reason, an advanced tangent modulus method considering the increase of the initial tangent modulus extension depth is proposed. The comparison with the actual engineering case and the calculated results by the finite element method of the small-strain hardening soil model shows that the advanced tangent modulus method can be more realistic. This further develops and improves the tangent modulus method.
- tangent modulus method /
- foundation settlement /
- finite element /
- small-strain hardening soil model

HTML全文

0. 引言

土质心墙坝因其良好的变形协调能力被广泛应用于复杂地形地质条件,中国已投入运行的坝高100 m以上的土质心墙堆石坝数十座,一批200 m级的高土质心墙堆石坝已建成,另有多座300 m级的特高土石坝在建或拟建。近年来,随着筑坝技术的进步,越来越多不良坝址及筑坝料被选用,暴露出的工程问题也越来越多,尤以坝顶裂缝问题较为突出。

坝顶裂缝主要分为平行于坝轴线的纵向裂缝与顺河向的横向裂缝,近年的土石坝设计及施工中,通过在两岸设置高塑性黏土,产生横向裂缝的案例不多,但出现纵向裂缝的工程仍屡见不鲜,引起了广大研究人员的关注,如位于黄河中游干流上的小浪底斜心墙堆石坝（坝高160 m）,在其建成后的第3年发生了坝顶裂缝事故^[1],最大表面缝宽约15 cm,平行坝轴线方向裂缝长627 m,缝深为2.6～3.9 m。大渡河流域的瀑布沟心墙堆石坝（坝高186 m）在初次蓄水后坝顶下游侧出现了一条平行于坝轴线的裂缝^[2],缝长230 m,最大缝宽约5 cm,深度为1.0~2.5 m。

如何模拟坝顶裂缝的产生及扩展过程,从而为相关工程提供预防坝顶裂缝发生的措施成为一个难题。一些学者采用离心模型试验来模拟坝顶裂缝的发生及演化过程,但由于实际工程中坝顶裂缝的表面张开宽度只有几厘米,在离心机的“时空压缩”效应^[3]下,模型中产生的裂缝只有数毫米,常规仪器较难观测到裂缝发展的整个过程。因此,数值方法是研究坝顶裂缝的有效途径。南京水科院最早提出了变形倾度法^[4]来判定土石坝裂缝的发生,依据大量实测数据,临界倾度值一般为1%^[5]。基于此方法,一些学者将倾度法植入常规有限元法^[6-7],通过计算相邻节点间的倾度值来判断裂缝的发生,然而,计算得到的倾度值与网格节点间距有关,且不能模拟裂缝的扩展过程,因此该方法只能作为定性的判据。

目前,模拟裂缝扩展过程的手段主要为：①通过全面加密网格,按照一定的统计分布给不同的材料单元赋予不同的力学参数,以单元的破坏范围描述裂缝的扩展^[8]；②采用弥散裂缝模型^[9],但该方法的计算结果依赖于网格的划分,且裂缝带网格过密会影响计算效率；③采用扩展有限元法^[10-11],其优势在于允许裂纹穿过单元,可以在粗网格上获得精确解答,裂纹扩展时无需重新划分网格。阮滨等^[12]采用扩展有限元对含初始裂缝的均质土坝坝顶扩展路径进行了模拟；吉恩跃等^[13]对简化平面模型进行了扩展有限元模拟,初步探讨了蓄水作用下坝顶裂缝的发生规律,但未考虑筑坝料流变及固结,上述成果表明扩展有限元在坝顶裂缝研究方面是可行的。

本文首先详细介绍了坝顶裂缝的模拟方法,其后采用神经网络遗传算法对瀑布沟心墙堆石坝典型监测点监测数据进行了反演,采用反演得到的模型参数同时分别考虑筑坝料湿化、流变及固结,进行了瀑布沟心墙坝平坝顶裂缝模拟,最后基于计算结果及实测值,对瀑布沟心墙坝坝顶裂缝的产生原因及演化过程进行了详细分析。相关成果可为类似高土质心墙坝工程预防坝顶裂缝的发生提供相关参照。

1. 坝顶裂缝的模拟方法

1.1 位移模式

扩展有限元的基本原理是基于单位分解的思想在常规有限元的框架内引入加强函数以反映位移的不连续性。为方便解释,图1分别给出了含裂缝及不含裂缝的4单元网格,内部圆圈内的数字代表单元号,其它则为节点号。

图 1 平面4单元网格

Figure 1. Plane mesh of 4 elements

下载: 全尺寸图片幻灯片

此处,定义表示位移的向量k和l分别为

$k = \frac{u_{9} + u_{10}}{2}$ ,

(1)

$l = \frac{u_{9} - u_{10}}{2}$ ,

(2)

式中,k介于u₉和u₁₀之间,l为9号和10号节点间位移的一半。

则可得

$u_{9} = k + l$ ,

(3)

$u_{10} = k - l$ 。

(4)

常规有限元位移模式可以表示为

$u (x) = \sum_{i = 1}^{n} N_{i} u_{i}$ ,

(5)

式中,N_i为内部节点i的插值形函数,u_i为节点i的自由度,任意一点插值形函数都应满足 $\sum_{i = 1}^{n} N_{i} (x, y) = 1$ 。

将式（3）,（4）代入式（5）可得

$u^{h} = \sum_{i = 1}^{8} N_{i} u_{i} + k (N_{9} + N_{10}) + l (N_{9} + N_{10}) H (x)$ ,

(6)

式中,H (x)为Heaviside跳跃函数, $H (x) = {\begin{cases} 1 (y > 0) \\ - 1 (y < 0) \end{cases}$ 。

这样,图1（a）带裂缝的位移场即可表示为

$u^{h} = \underset{常规有限元位移}{\underset{︸}{\sum_{i = 1}^{8} N_{i} u_{i} + N_{11} u_{11}}} + \underset{不连续富集函数}{\underset{︸}{l N_{11} H (x)}}$ 。

(7)

上述只是裂纹面的描述,对于裂尖的位移场则引入渐进函数,即裂纹完全穿过单元时,用跳跃函数来加强这些节点,而裂纹尖端周围的节点则由描述裂纹尖端的渐进函数来加强。如图2所示,方形的节点用裂尖渐进函数来描述,圆形的节点由跳跃函数来描述。

图 2 含裂缝单元集示意图

Figure 2. Element set with initial crack

下载: 全尺寸图片幻灯片

将上述不连续的位移场整合推广到统一形式,可表示为

$u = \sum_{i = \in s}^{} N_{I} (x) [u_{I} + \underset{I \in S_{h}}{\underset{︸}{H (x) α_{I}}} + \underset{I \in S_{c}}{\underset{︸}{\sum_{i = 1}^{4} ψ_{i} (x) b_{I}^{i}}}]$ ,

(8)

式中,N_i(x)为常规节点位移形函数,u_I为常规单元节点位移向量, $α_{I}$ 为贯穿单元节点改进自由度,b_I为裂尖单元节点的改进自由度。

Ψ_i为反映裂尖奇异性的渐进函数,可以表示为（针对各向同性材料）

$\begin{matrix} ψ_{i} (x) = [\sqrt{r} \sin (\frac{α}{2}), \sqrt{r} \cos (\frac{α}{2}), \sqrt{r} \sin (\frac{α}{2}) \sin (α), \\ \sqrt{r} \cos (\frac{α}{2}) \sin (α)] \end{matrix}$ ,

(9)

式中,r,θ为以裂尖为原点的极坐标系。

确定位移模式后即可和常规有限元方法一样根据虚功原理推导控制方程,这里不再赘述。

1.2 本构模型

经过大量工程检验,土石坝设计规范中推荐采用邓肯–张（Duncan-Chang）模型^[14]计算其应力变形特性,简单起见,本文采用E– $ν$ 模型,切线弹性模量E_t表示为

$E_{t} = {[1 - \frac{R_{f} (1 - \sin φ) (σ_{1} - σ_{3})}{2 c \cos φ + 2 σ_{3} \sin φ}]}^{2} K \cdot p_{a} {(\frac{σ_{3}}{p_{a}})}^{n}$ ,

(10)

式中,K为切线模量基数,n为弹性模量指数,c为黏聚力, $φ$ 为内摩擦角,R_f为破坏比, $p_{a}$ 为大气压力。

在卸荷状态下堆石料的弹性模量E_ur可表示为

$E_{ur} = K_{ur} p_{a} {(\frac{σ_{3}}{p_{a}})}^{n}$ ,

(11)

式中,K_ur为卸载弹性模量基数,n为指数。

流变曲线随时间呈指数型衰减的规律符合Merchant黏弹性模型,流变变形可以表达为

$ε_{t}^{} = ε_{i}^{} + ε_{f}^{} (1 - e^{- α t})$ ,

(12)

式中, $ε_{f}^{}$ 为最终流变量, $α$ 为流变随时间衰减的指数（第1天的流变量占总流变量之比）。

最终体积流变和最终剪切流变为

$ε_{vf}^{} = b {(\frac{σ_{3}}{p_{a}})}^{m^{1}} + c {(\frac{q}{p_{a}})}^{m^{2}}$ ,

(13)

$γ_{f}^{} = d {(\frac{S}{1 - S_{}})}^{m^{3}}$ 。

(14)

上游堆石料湿化模型采用改进的沈珠江湿化模型,湿化体积应变和剪应变为

$Δ ε_{v}^{w} = a {(\frac{σ_{3}}{p_{a}})}^{c} + b S$ ,

(15)

$Δ ε_{s}^{w} = D_{w} S / (1 - S)$ ,

(16)

式中,a,b,c,D_w为模型参数,S为应力水平。

1.3 断裂准则

从目前的工程实测资料来看,坝顶裂缝多为张拉型浅层裂缝^[15],而浅层处土体应力水平通常较低,产生剪切裂缝可能性不大,因此采用最大主应力或最大主应变准则来判定心墙或坝顶填土张拉裂缝是否发生。鉴于目前的试验测量技术较难准确获得土体拉伸应变,采用抗拉强度作为判定坝顶裂缝发生的条件,可表示为

$f = {\frac{〈 σ_{t \max} 〉}{σ_{t \max}^{a}}}$ 。

(17)

式中 $σ_{t \max}^{a}$ 为临界最大拉应力； $〈 〉$ 为Macaulay,表示在纯压缩应力作用下,材料不会产生初始能量损失。当f >1,即计算小主应力大于土料抗拉强度时,裂缝随即发生。此外,采用断裂能指标^[16]（试样承受拉伸载荷时裂缝扩展单位面积所需要的能量,拉伸应力–应变曲线与横坐标所围面积）来控制裂缝发展程度。

2. 瀑布沟心墙坝工程概况及计算模型

2.1 工程实测资料分析

如图3所示,瀑布沟水电站为砾石土心墙堆石坝,上游坝坡1∶2～1∶2.25,下游坝坡1∶1.8,坝顶宽度14 m,心墙顶高程854.00 m,顶宽4 m,上、下游侧坡度均为1∶0.25,底高程670.00 m,底宽96.0 m,坝高184 m,属于已建成200 m级高土质心墙坝的典型代表。大坝于2007年开始填筑,2009年底填筑至坝顶高程,同时下闸蓄水,于2010年8月26日上午（第一次满蓄）发现坝顶裂缝,裂缝位于坝轴线下游约5.5～6.0 m,发生在坝顶填土内,未深入心墙,裂缝基本平行于坝轴线,长约230 m,最大缝宽约5 cm。

图 3 瀑布沟心墙坝典型剖面及监测点布置图

Figure 3. Typical section and monitoring points of Pubugou earth core rockfill dam (ECRD)

下载: 全尺寸图片幻灯片

图3中“CH”开头代表水管式沉降仪和水平位移计；“VE”代表电磁沉降仪。

依据监测仪器数据^[17],图4,5给出了典型断面堆石体沉降、水平位移随坝体填筑过程和蓄水过程的变化曲线。可以看出坝体沉降随填筑高程的增加而增加,运行期沉降发展较缓,库水位变化对坝体沉降有一定滞后性；坝体水平位移则受库水位影响较大,特别是第一次满蓄过程中,监测点的水平位移最大增加了约0.25 m,占到了总变位的40%。总体来说,瀑布沟坝体沉降符合一般性规律,但下游次堆石区的沉降偏大（最大沉降约2.5 m）,表明其堆石料力学特性一般,蓄水后加上上游坝壳的湿化,有可能存在较大不均匀沉降,从而产生坝顶裂缝。

图 4 典型监测点沉降过程曲线

Figure 4. Settlement process curves of typical monitoring points

下载: 全尺寸图片幻灯片

图 5 典型监测点水平位移过程曲线

Figure 5. Curves of horizontal displacement at typical monitoring points

下载: 全尺寸图片幻灯片

2.2 计算网格

取大坝最大典型断面（0+240）为计算断面,采用平面有限元网格,单元类型为CPE4P（考虑筑坝料固结流变）。因本文重点研究目标为坝顶区域,网格中保留了原设计中路堤等结构,同时为精确模拟坝顶裂缝的扩展长度、路径等,在坝顶高程10 m深度内对原网格进行加密,保持单元基本为规则四边形并设置为富集区（可扩展自由度）,节点间距离为0.25 m,采用沙漏控制提高计算的收敛性。所用平面模型单元数5709个,节点数5811个,网格划分示意图如图6所示。

图 6 瀑布沟典型断面网格剖分示意图

Figure 6. Plane mesh generation of typical section of Pubugou ECRD

下载: 全尺寸图片幻灯片

按照大坝实际的施工顺序及水位变化过程（图6所示）,采用29级分级加载：坝体分21级填筑,水荷载分7级施加,最后1级（保持满蓄状态）模拟大坝10 a后应力变形及坝顶裂缝发展情况。

2.3 计算参数

瀑布沟心墙坝自开建至今积累了大量的实测数据,为最大程度真实模拟大坝施工及运行期的应力变形性状,采用神经网络遗传算法^[17]对典型监测点（见图4,5）监测数据进行反演,因篇幅有限,具体反演过程不再赘述,所得邓肯模型参数和流变参数分别如表1,2所列。

表 1 筑坝料邓肯E-

$ν$ 模型参数列表

Table 1. Parameters of E-

$ν$ of construction materials

坝料	R_f	K	n	G	F	D	K_ur	φ/(°)	Δφ/(°)	c/kPa	ρ/(g·cm^-3)	k/(m·s^-1)
上游主堆石	0.578	1068	0.52	0.390	0.06	5	1923	54	10	0	2300	1×10^-3
下游主堆石	0.578	1068	0.52	0.390	0.06	5	1923	54	10	0	2300	1×10^-3
下游次堆石	0.680	707	0.50	0.381	0.06	5	1230	51	10	0	2200	1×10^-3
下游盖重	0.680	700	0.52	0.320	0.06	5	1400	54	10	0	2300	1×10^-3
心墙掺砾料	0.552	677	0.42	0.394	0.01	8	1108	35	0	1.2	2300	7×10^-8
过渡层	0.520	1045	0.52	0.402	0.08	7	2089	50	6	0	2200	3×10^-4
反滤料	0.520	949	0.54	0.407	0.08	7	1818	48	6	0	2200	8×10^-5
高塑土	0.860	200	0.70	0.380	0.02	2	550	15	0	5	2000	7×10^-8
覆盖层	0.640	780	0.42	0.320	0.08	7	1500	48	6	0	1470	5×10^-4

下载: 导出CSV

| 显示表格

表 2 筑坝料流变模型参数列表

Table 2. Rheological parameters of construction materials

坝料	α/10^-3	B/10^-3	C/10^-3	D/10^-3	m₁	m₂	m₃
上游堆石体	1.337	0.292	0.617	2.423	0.514	0.416	0.427
下游堆石体	1.334	0.229	0.557	1.933	0.408	0.365	0.482
下游次堆石体	1.234	0.388	0.637	2.606	0.848	0.455	0.542
下游盖重	1.234	0.388	0.637	2.606	0.848	0.455	0.542
心墙掺砾料	0.617	0.428	1.532	3.053	0.996	0.679	0.518
过渡层	1.440	0.324	0.609	5.514	0.679	0.409	0.551
反滤料	1.440	0.356	0.613	2.206	0.721	0.420	0.549
覆盖层	1.241	0.434	0.712	2.674	0.848	0.455	0.542

下载: 导出CSV

| 显示表格

上游堆石料的湿化参数：a=0.0000547,b= 1.367,c=0.00341,D_w=0.00265。

瀑布沟心墙坝坝顶下有2 m厚的路堤填土,其下心墙土质为宽级配砾石土,大于5 mm土料含量接近50%,对于其抗拉强度,文献[18]中给出了糯扎渡、两河口和如美心墙料的单向拉伸试验结果,综合参考取其抗拉强度为43 kPa；同时,依据对应的拉伸应力–应变曲线,计算得到断裂能为4.8 N/m。

3. 计算结果分析

3.1 坝体变形分析

总体来说,坝体竣工期及蓄水期的变形符合一般的土石坝应力变形规律。图7给出了竣工期坝体在自重作用下变形云图。从图7可以看出竣工期坝体最大沉降为3.23 m,最大值发生在心墙中下部；下游次堆石区沉降变形较上游略大,此规律与监测数据一致,表明下游堆石质量较差。从坝体施工期水平位移云图可以看出,上游堆石向上游最大顺河向位移为0.60 m,下游堆石向下游最大顺河向位移为0.61 m。

图 7 竣工期坝体变形云图

Figure 7. Deformations of dam during construction period

下载: 全尺寸图片幻灯片

蓄水期由于上游堆石料湿化和渗透体积力的影响,坝体位移发生了较大的变化（图8）。在水压力的作用下,蓄水期堆石料向上游最大顺河向位移减小为0.33 m,下游堆石向下游最大顺河向位移增大为1.17 m；坝体最大沉降为3.27 m（蓄水后上游堆石料改为浮容重）,最大沉降区域向上游移动。

图 8 蓄水期坝体变形云图

Figure 8. Deformations of dam during impoundment period

下载: 全尺寸图片幻灯片

为验证反演参数计算坝体变形的合理性,选取了CH6,CH14两个监测点沉降实测值及计算值进行比较,从图9可以看出,基于实测值的反演参数计算结果能够较为合理的反映坝体的实际变形,此外,由于考虑了施工期筑坝料的流变特性,从坝体运行后10 a沉降曲线可以看出坝体沉降主要发生在施工期及蓄水后前3 a,运行后期坝体沉降很小,符合流变的指数型发展规律。

图 9 典型监测点实测值与计算值比较曲线

Figure 9. Comparison curves between measured and calculated values of typical measuring points

下载: 全尺寸图片幻灯片

3.2 湿化变形分析

图10给出了上游坝壳湿化引起坝体变形云图,可以看出上游堆石料产生的湿化沉降变形最大达到了0.48 m,位于上游坝面4/5处,约占总沉降的14.7%,总体来说,上游坝壳料的湿化变形较大。从湿化变形总矢量图也可以看出,堆石料湿化作用下上游坝壳产生了明显的变形,坝顶上游侧变形最大,不难看出,湿化作用造成了坝顶上下游的不均匀沉降,易导致裂缝的产生。

图 10 上游坝壳湿化变形云图

Figure 10. Wetting deformations of upper rockfills

下载: 全尺寸图片幻灯片

3.3 坝顶应力分析

上节指出,因土心墙坝坝顶应力水平较低,坝顶裂缝体现为张拉裂缝,剪切产生的裂缝多发生在应力水平较高的不同材料接触面部位或位移较大的两岸河谷部位,因此采用坝顶小主应力作为判定坝顶裂缝发生的依据。图11给出了坝顶竣工期及首次满蓄后的坝顶小主应力云图,其中负值表示压应力,反之为拉应力。可以看出竣工后坝顶均为压应力,而首次满蓄后在湿化变形和水压力的共同作用下,坝顶向上游侧偏移,导致在坝顶下游侧（距离坝轴线约4.75 m处）出现了拉应力,且接近了其抗拉强度（43 kPa）,表明此处已具备坝顶裂缝产生的力学条件。

图 11 不同时期坝顶小主应力云图

Figure 11. Minor principal stresses of dam crest in different periods

下载: 全尺寸图片幻灯片

图12为2011年1月28日坝顶区域的主应力迹线,可以看到大主应力基本沿着竖直方向,小主应力沿水平方向,红色虚线区域为拉应力区,在此位置土体水平向受拉伸,且在靠近坝顶表面位置,该水平向拉力大于竖向压力；同时该水平向拉力随着坝顶往下深度逐渐减小,由此可以推测裂缝开口宽度沿深度依次减小,直至闭合,但由于裂缝扩展后的应力会发生调整,因此仅从图12难以预测裂缝扩展的具体深度和张开宽度。

图 12 蓄水期坝顶以下2 m深度范围内主应力迹线

Figure 12. Stress trajectory of dam within 2 m depth below crest during impoundment period

下载: 全尺寸图片幻灯片

3.4 坝顶裂缝产生及扩展过程

图13（a）～（g）为模拟得到的坝顶裂缝产生及扩展过程,坝顶裂缝首次发生在2011年1月30日,距离坝轴线约4.75 m位置处,1个月后裂缝扩展至1.75 m深度（在坝顶填土内,未扩展至心墙）,宽度最大在10 cm以内。瀑布沟心墙堆石坝实际于2010年8月26日上午发现坝顶裂缝,裂缝位于坝轴线下游约5.5～6.0 m,基本平行于坝轴线,裂缝长约230 m,最大缝宽约5 cm,深度约为1～2.5 m,2.5 m深度以下无异常。可以看出计算得到的坝顶产生及发展情况能够较为实际的反映瀑布沟坝顶裂缝的实测结果。存在误差的原因一部分是因为计算所用本构模型的限制及计算参数的误差（主要体现在坝顶材料断裂参数上）,另一方面模型本身为二维模型,且作了一定简化处理。

图 13 瀑布沟心墙坝坝顶裂缝发生及扩展过程

Figure 13. Occurrence and propagation process of crest crack in Pubugou ECRD

下载: 全尺寸图片幻灯片

此外,计算结果表明,首次蓄水产生坝顶裂缝后,后续流变变形已较小,裂缝的发展极大的减小了不均匀沉降差引起的坝顶拉应力,因此计算得到裂缝在此后10 a间未发生实质性扩展。实际上,现场进行开挖回填处理后,未发现有新的裂缝发生,表明坝体变形及裂缝发展已基本稳定。

为分析湿化变形和筑坝料流变对坝顶裂缝形成及发展过程的影响,分别进行了考虑流变不考虑湿化、考虑湿化不考虑流变方案下的坝顶裂缝模拟。计算结果表明考虑流变不考虑湿化方案下大坝施工过程中及蓄水后坝顶均未出现拉应力,因此未发生坝顶裂缝；考虑湿化不考虑流变方案下大坝在第一次蓄水后即发生了坝顶裂缝,但裂缝的扩展深度及张开宽度均比考虑湿化及流变的计算结果小。

图14,15分别为考虑流变和不考虑流变下坝顶裂缝的扩展深度及坝顶表面张开宽度随时间变化曲线。可以看出,不考虑流变时坝顶裂缝扩展深度最大为1.25 m,最大张开宽度为2.7 cm；考虑流变后,由于下游次堆石区流变量较上游大,进一步加剧了上下游的不均匀沉降,因此坝顶裂缝扩展深度达到1.75 m,表面张开宽度也达到4.1 cm。

图 14 坝顶裂缝扩展深度随时间变化曲线

Figure 14. Variation of propagation depth of crest cracks with time

下载: 全尺寸图片幻灯片

图 15 坝顶裂缝张开宽度随时间变化曲线

Figure 15. Variation of opening width of crest cracks with time

下载: 全尺寸图片幻灯片

上述计算分析表明：瀑布沟土心墙坝坝顶张拉裂缝产生的直接原因是由于蓄水后上游堆石料过大的湿化变形,导致坝顶上下游的不均匀变形,使得坝顶达到了其极限抗拉能力,而筑坝料的流变变形,特别是上下游堆石的不一致流变变形,加剧了上下游的不均匀沉降,使得坝顶裂缝进一步扩展。

4. 结论

（1）将扩展有限元基本原理耦合到传统土石坝有限元计算框架内,实现了高土质心墙坝坝顶裂缝发展过程的真实模拟。

（2）模拟得到的坝顶裂缝首次发生在满蓄后,距离坝轴线约4.75 m位置处,1个月内裂缝扩展至1.75 m深度（坝顶填土内,未扩展至心墙）,运行10 a间坝顶裂缝未发生实质性发展,模拟结果与实测值较为接近。

（3）考虑湿化而不考虑流变时坝顶裂缝扩展深度最大为1.25 m,最大张开宽度为2.7 cm；考虑流变后,由于下游次堆石区流变量较上游大,进一步加剧了上下游的不均匀沉降,坝顶裂缝扩展深度达到1.75 m,张开宽度达4.1 cm。

（4）对于瀑布沟心墙坝而言,其上游坝壳的湿化变形作用导致了坝顶上下游的不均匀变形,从而直接诱发了坝顶裂缝的发生,后续流变变形加剧了此不均匀变形,使得坝顶裂缝进一步扩展。

图 1 各模型计算所得p–s曲线

Figure 1. p–s curves calculated by various models

下载: 全尺寸图片幻灯片

图 2 s与s/p拟合曲线

Figure 2. Fitting curves of s and s/p

下载: 全尺寸图片幻灯片

图 3 各方法p–s曲线对比图(1 m×1 m)

Figure 3. Comparison of p–s curves by various methods (1 m×1 m)

下载: 全尺寸图片幻灯片

图 4 各方法H–S曲线对比图(1 m×1 m)

Figure 4. Comparison of H–S curves by various methods (1 m×1 m)

下载: 全尺寸图片幻灯片

图 5 各方法p–s曲线对比图(3 m×3 m)

Figure 5. Comparison of p–s curves by various methods (3 m×3 m)

下载: 全尺寸图片幻灯片

图 6 各方法p–s曲线对比图(6 m×6 m)

Figure 6. Comparison of p–s curves by various methods (6 m×6 m)

下载: 全尺寸图片幻灯片

图 7 各方法p–s曲线对比图(10 m×10 m)

Figure 7. Comparison of p–s curves by various methods (10 m×10 m)

下载: 全尺寸图片幻灯片

图 8 各方法p–s曲线对比图(20 m×20 m)

Figure 8. Comparison of p–s curves by various methods (20 m×20 m)

下载: 全尺寸图片幻灯片

图 9 各方法H–S曲线对比图(3 m×3 m)

Figure 9. Comparison of H–S curves by various methods (3 m×3 m)

下载: 全尺寸图片幻灯片

图 10 各方法H–S曲线对比图(6 m×6 m)

Figure 10. Comparison of H–S curves by various methods (6 m×6 m)

下载: 全尺寸图片幻灯片

图 11 各方法H–S曲线对比图(10 m×10 m)

Figure 11. Comparison of H–S curves by various methods (10 m×10 m)

下载: 全尺寸图片幻灯片

图 12 各方法H–S曲线对比图(20 m×20 m)

Figure 12. Comparison of H–S curves by various methods (20 m×20 m)

下载: 全尺寸图片幻灯片

图 13 压板在不同埋深处的荷载–沉降曲线

Figure 13. Load-settlement curves of plate at different buried depths

下载: 全尺寸图片幻灯片

图 14 不同埋深处的E_t0

Figure 14. E_t0 at different buried depths

下载: 全尺寸图片幻灯片

图 15 E_t0与H拟合图

Figure 15. Fitting of E_t0 and H

下载: 全尺寸图片幻灯片

图 16 E_t0与H拟合图(10 m×10 m)

Figure 16. Fitting of E_t0 and H (10 m×10 m)

下载: 全尺寸图片幻灯片

图 17 E_t0与H拟合图(20 m×20 m)

Figure 17. Fitting of E_t0 and H (20 m×20 m)

下载: 全尺寸图片幻灯片

图 18 p–s曲线对比(1 m×1 m)

Figure 18. Comparison of p–s curves (1 m×1 m)

下载: 全尺寸图片幻灯片

图 19 H–S曲线对比(1 m×1 m)

Figure 19. Comparison of H–S curves (1 m×1 m)

下载: 全尺寸图片幻灯片

图 20 E_t–H曲线对比(1 m×1 m)

Figure 20. Comparison of E_t–H curves (1 m×1 m)

下载: 全尺寸图片幻灯片

图 21 p–s曲线对比(3 m×3 m)

Figure 21. Comparison of p–s curves (3 m×3 m)

下载: 全尺寸图片幻灯片

图 22 p–s曲线对比图(6 m×6 m)

Figure 22. Comparison of p–s curves (6 m×6 m)

下载: 全尺寸图片幻灯片

图 23 p–s曲线对比(10 m×10 m)

Figure 23. Comparison of p–s curves (10 m×10 m)

下载: 全尺寸图片幻灯片

图 24 p–s曲线对比图(20 m×20 m)

Figure 24. Comparison of p–s curves (20 m×20 m)

下载: 全尺寸图片幻灯片

图 25 H–S曲线对比图(3 m×3 m)

Figure 25. H–S curve comparison (3 m×3 m)

下载: 全尺寸图片幻灯片

图 26 H–S曲线对比图(6 m×6 m)

Figure 26. Comparison of H–S curves (6 m×6 m)

下载: 全尺寸图片幻灯片

图 27 H–S曲线对比图(10 m×10 m)

Figure 27. Comparison of H–S curves (10 m×10 m)

下载: 全尺寸图片幻灯片

图 28 H–S曲线对比图(20 m×20 m)

Figure 28. Comparison of H–S curves (20 m×20 m)

下载: 全尺寸图片幻灯片

图 29 E_t–H曲线对比图(3 m×3 m)

Figure 29. Comparison of E_t–H curves (3 m×3 m)

下载: 全尺寸图片幻灯片

图 30 E_t–H曲线对比图(6 m×6 m)

Figure 30. Comparison of E_t–H curves (6 m×6 m)

下载: 全尺寸图片幻灯片

图 31 E_t–H曲线对比图(10 m×10 m)

Figure 31. Comparison of E_t–H curves (10 m×10 m)

下载: 全尺寸图片幻灯片

图 32 E_t–H曲线对比图(20 m×20 m)

Figure 32. Comparison of E_t–H curves (20 m×20 m)

下载: 全尺寸图片幻灯片

图 33 实测p–s曲线

Figure 33. Measured p–s curves

下载: 全尺寸图片幻灯片

图 34 不同充水荷载下H–S曲线

Figure 34. H–S curves under different water-filling loads

下载: 全尺寸图片幻灯片

图 35 有限元模型图

Figure 35. Finite element model diagram

下载: 全尺寸图片幻灯片

图 36 不同方法p–s曲线对比

Figure 36. Comparison of p–s curves of different methods

下载: 全尺寸图片幻灯片

图 37 不同方法H–S曲线对比图

Figure 37. Comparison of H–S curves by various methods

下载: 全尺寸图片幻灯片

图 38 E_t–H曲线对比图

Figure 38. Comparison of E_t–H curves by various methods

下载: 全尺寸图片幻灯片

图 39 地层分布图

Figure 39. Distribution of soil strata

下载: 全尺寸图片幻灯片

图 40 实测H–S曲线

Figure 40. Measured H–S curves

下载: 全尺寸图片幻灯片

图 41 有限元模型图

Figure 41. Diagram of finite element model

下载: 全尺寸图片幻灯片

图 42 不同方法H–S曲线对比图

Figure 42. Comparison of H–S curves by various methods

下载: 全尺寸图片幻灯片

图 43 E_t–H曲线对比图

Figure 43. Comparison of E_t–H curves by various methods

下载: 全尺寸图片幻灯片

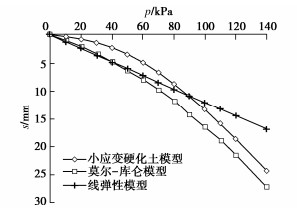
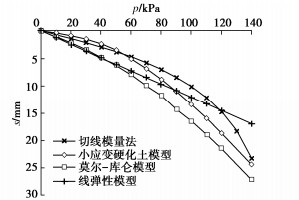
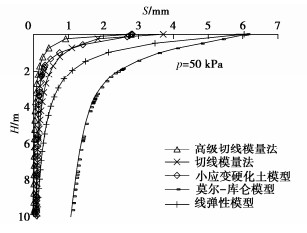
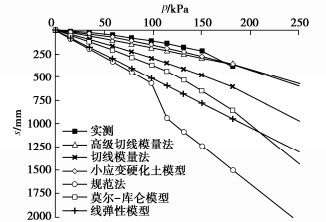
表 1 有限元小应变硬化土模型参数取值

Table 1 Mechanical parameter of soil for small strain hardened model

土层	$\gamma$ /(kN·m^-3)	${\nu _{{\text{ur}}}}$	c/kPa	$\varphi$ /(°)	$K_{\text{0}}^{{\text{nc}}}$	p^ref/kPa	m	$G_{\text{0}}^{{\text{ref}}}$ /MPa	$E_{{\text{oed}}}^{{\text{ref}}}$ /MPa	$E_{{\text{50}}}^{{\text{ref}}}$ /MPa	$E_{{\text{ur}}}^{{\text{ref}}}$ /MPa	${\gamma ^{0.7}}$
伦敦黏土	18.44	0.2	2	24	0.59	100	0.5	40	6.73	8	16	9.68×10^-4

下载: 导出CSV

表 2 莫尔-库仑模型参数取值

Table 2 Mechanical parameters for Mohr Coulomb model

土层	$\gamma$ /(kN·m^-3)	$\nu$	c/kPa	$\varphi$ /(°)	E/MPa
伦敦黏土	18.44	0.3	2	24	7.3

下载: 导出CSV

表 3 线弹性模型参数取值

Table 3 Mechanical parameters for linear elastic model

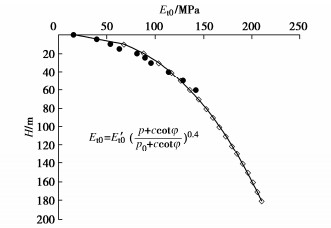
土层	γ/(kN·m^-3)	$\nu$	E/MPa
伦敦黏土	18.44	0.3	7.3

下载: 导出CSV

表 4 1 m×1 m压板E_t0随深度变化情况

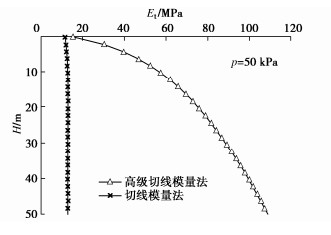
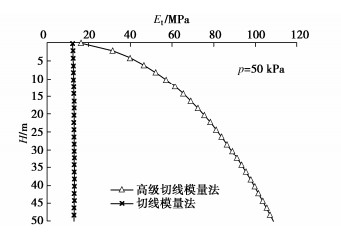
Table 4 Variation of E_t0 of 1 m×1 m plate with buried depth

H/m	K₀	E_t0/MPa	a	b
0	18.25	14.61	0.0548	0.0056
1.0	28.82	23.08	0.0347	0.0022
1.5	32.15	25.75	0.0311	0.0020
2.0	39.84	31.90	0.0251	0.0018
2.5	46.73	37.42	0.0214	0.0014
3.0	48.08	38.50	0.0208	0.0013
4.0	54.95	44.00	0.0182	0.0013
5.0	61.73	49.43	0.0162	0.0009
6.0	64.52	51.66	0.0155	0.0008
7.0	69.93	56.00	0.0143	0.0007

下载: 导出CSV

表 5 土的基本力学参数

Table 5 Mechanical parameters of soil

土体名称	$\gamma$ /(kN·m^-3)	c/kPa	$\varphi$ /(°)	e	E_s1-2/MPa	E₀/MPa
粉质黏土	18.5	18.3	19.5	1.15	7.5	14
淤泥质黏土	17.6	7.5	5.8	1.20	3	4.1
砂质粉土	18.3	10	20	1	7.4	14

下载: 导出CSV

表 6 莫尔-库仑模型参数取值

Table 6 Mechanical parameters for Mohr Coulomb model

土层	$\gamma$ /(kN·m^-3)	$\nu$	c/kPa	$\varphi$ /(°)	E/MPa
粉质黏土	18.5	0.3	18.3	19.5	14
淤泥质黏土	17.6	0.3	7.5	5.8	4.1
砂质粉土	18.3	0.3	10	20	14

下载: 导出CSV

表 7 线弹性模型参数取值

Table 7 Mechanical parameters for linear elastic model

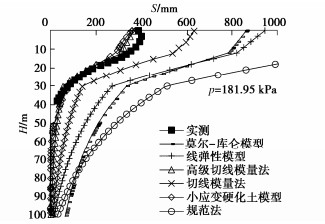
土层	γ/(kN·m^-3)	$\nu$	E/MPa
粉质黏土	18.5	0.3	14
淤泥质黏土	17.6	0.3	4.1
砂质粉土	18.3	0.3	14

下载: 导出CSV

表 8 小应变硬化土模型参数取值

Table 8 Mechanical parameters of soil for small-strain hardening model

土层	$\gamma$ /(kN·m^-3)	ν_ur	c/kPa	ϕ/(°)	$K_{\text{0}}^{{\text{nc}}}$	p^ref/kPa	m	$G_{\text{0}}^{{\text{ref}}}$ /MPa	$E_{{\text{oed}}}^{{\text{ref}}}$ /MPa	$E_{{\text{50}}}^{{\text{ref}}}$ /MPa	$E_{{\text{ur}}}^{{\text{ref}}}$ /MPa	${\gamma ^{0.7}}$
粉质黏土	18.50	0.2	18.3	19.5	0.6662	100	0.8	63.0	14	14.0	42.0	2×10^-4
淤泥质黏土	17.60	0.2	7.5	5.8	0.8989	100	0.8	18.1	4.1	4.1	12.3	2×10^-4
砂质粉土	18.30	0.2	10.0	20.0	0.6580	100	0.5	63.0	14	14.0	42.0	2×10^-4

下载: 导出CSV

表 9 土的基本力学参数

Table 9 Mechanical parameters of soil

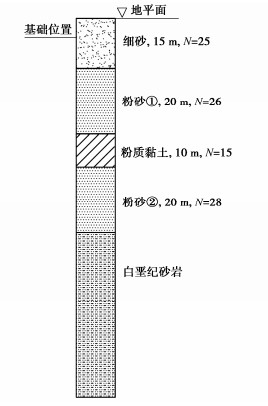
土体名称	$\gamma$ /(kN·m^-3)	c/kPa	$\varphi$ /(°)	E₀/MPa
细砂	18.5	0	37	44.4
粉砂①	18.5	0	38	48.7
粉质黏土	18.5	25	22	27.0
粉砂②	18.5	0	39	67.3
白垩纪砂岩	18.5	150	38	250.0

下载: 导出CSV

表 10 莫尔-库仑模型参数取值

Table 10 Parameters for Mohr Coulomb model

土层	$\gamma$ /(kN·m^-3)	$\nu$	c/kPa	$\varphi$ /(°)	E/MPa
细砂	18.5	0.3	0	37	44.4
粉砂①	18.5	0.3	0	38	48.7
粉质黏土	18.5	0.3	25	22	27.0
粉砂②	18.5	0.3	0	39	67.3
白垩纪砂岩	18.5	0.3	150	38	250.0

下载: 导出CSV

表 11 线弹性模型参数取值

Table 11 Parameters for linear elastic model

土层	γ/(kN·m^-3)	$\nu$	E/MPa
细砂	18.5	0.3	44.4
粉砂①	18.5	0.3	48.7
粉质黏土	18.5	0.3	27.0
粉砂②	18.5	0.3	67.3
白垩纪砂岩	18.5	0.3	250.0

下载: 导出CSV

表 12 小应变硬化土模型参数取值

Table 12 Parameters of soil for small-strain hardening model

土层	$\gamma$ /(kN·m^-3)	${\nu _{{\text{ur}}}}$	c/kPa	$\varphi$ /(°)	$K_{\text{0}}^{{\text{nc}}}$	p^ref/kPa	m	$G_{\text{0}}^{{\text{ref}}}$ /MPa	$E_{{\text{oed}}}^{{\text{ref}}}$ /MPa	$E_{{\text{50}}}^{{\text{ref}}}$ /MPa	$E_{{\text{ur}}}^{{\text{ref}}}$ /MPa	${\gamma ^{0.7}}$
细砂	18.5	0.2	0	37	0.398	100	0.5	199.8	44.4	44.4	133.2	2×10^-4
粉砂①	18.5	0.2	0	38	0.384	100	0.5	438.3	48.7	48.7	146.1	2×10^-4
粉质黏土	18.5	0.2	25	22	0.625	100	0.8	121.5	27.7	27.7	81.0	2×10^-4
粉砂②	18.5	0.2	0	39	0.371	100	0.5	302.8	67.3	67.3	201.9	2×10^-4
白垩纪砂岩	18.5	0.2	150	38	0.384	100	0.5	1125.0	250	250	750.0	2×10^-4

下载: 导出CSV

参考文献(12)

[1]	王海波, 徐明, 宋二祥. 基于硬化土模型的小应变本构模型研究[J]. 岩土力学, 2011, 32(1): 39–43, 136. doi: 10.3969/j.issn.1000-7598.2011.01.007 WANG Hai-bo, XU Ming, SONG Er-xiang. A small strain constitutive model based on hardening soil model[J]. Rock and Soil Mechanics, 2011, 32(1): 39–43, 136. (in Chinese) doi: 10.3969/j.issn.1000-7598.2011.01.007
[2]	建筑地基基础设计规范: GB 50007—2011[S]. 2012. Code for Design of Building Foundation: GB 50007—2011[S]. 2012. (in Chinese)
[3]	杨光华. 地基非线性沉降计算的原状土切线模量法[J]. 岩土工程学报, 2006, 28(11): 1927–1931. doi: 10.3321/j.issn:1000-4548.2006.11.002 YANG Guang-hua. Nonlinear settlement computation of the soil foundation with the undisturbed soil tangent modulus method[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(11): 1927–1931. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.11.002
[4]	杨光华, 王俊辉. 地基非线性沉降计算原状土切线模量法的推广和应用[J]. 岩土力学, 2011, 32(增刊1): 33–37. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S1007.htm YANG Guang-hua, WANG Jun-hui. Application of undisturbed soil tangent modulus method for computing nonlinear settlement of soil foundation[J]. Rock and Soil Mechanics, 2011, 32(S1): 33–37. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S1007.htm
[5]	杨光华. 根据经验地基承载力反算土的强度和变形参数[J]. 广东水利水电, 2002(1): 3–6. https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD200201000.htm YANG Guang-hua. According to the experience of foundation bearing capacity to inverse the strength and deformation parameters of soil[J]. Guangdong Water Resources and Hydropower, 2002(1): 3–6. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GDSD200201000.htm
[6]	杨光华. 深基坑支护结构的实用计算方法及其应用[M]. 北京: 地质出版社, 2004. YANG Guang-hua. Practical Calculation Method of Retaining Structures for Deep Excavations and Its Application[M]. Beijing: Geological Publishing House, 2004. (in Chinese)
[7]	DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(5): 1629–1653. doi: 10.1061/JSFEAQ.0001458
[8]	赵同顺, 周波. 大型油罐地基变形特性的研究[J]. 岩石力学与工程学报, 2004, 23(6): 1037–1043. doi: 10.3321/j.issn:1000-6915.2004.06.028 ZHAO Tong-shun, ZHOU Bo. Deformation behaviors of soft foundation under large oil tank[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(6): 1037–1043. (in Chinese) doi: 10.3321/j.issn:1000-6915.2004.06.028
[9]	赵同顺. 5×10⁴ m³大型油罐岩土工程实录[C]// 第五届全国岩土工程实录交流会岩土工程实录集, 2000, 南京. ZHAO Tong-shun. Geotechnical engineering record of 5×10⁴m³ large oil tank[C]// The 5th National Geotechnical Engineering Record Exchange Conference, 2000, Nanjing. (in Chinese)
[10]	舒武堂, 李国胜, 蒋涛. 武汉地区淤泥质软土、黏性土的压缩模量与变形模量的相关关系[J]. 岩土工程界, 2004, 7(7): 29–30. https://www.cnki.com.cn/Article/CJFDTOTAL-YSJS200407011.htm SHU Wu-tang, LI Guo-sheng, JIANG Tao. The correlativity between the compression model and elastic model for silt and clay in Wuhan[J]. Geotechnical Engineering World, 2004, 7(7): 29–30. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSJS200407011.htm
[11]	C M PLANT G W. The settlement performance of a raft supporting a 27-storey hotel on estuarine deposits in Durban[J]. Civil Engineering = Siviele Ingenieurswese, 1990, 32(6).
[12]	建筑地基基础设计规范: DBJ15—31—2016[S]. 2016. Design Code for Building Foundation: DBJ15—31— 2016[S]. 2016. (in Chinese)

施引文献(29)

期刊类型引用(19)

1.	沈书拯，江巍，欧阳晔，谭亿虹，吴剑，陈勇. 基于三维连续-离散耦合模型的门架式双排抗滑桩受力分析. 防灾减灾工程学报. 2025(01): 84-94 . 百度学术
2.	王洪涛，李建华，殷允腾，张红军，宣兆腾，赵明珠. 承压水作用下岩质地层基坑抗突涌安全厚度研究. 建筑结构学报. 2024(06): 213-223 . 百度学术
3.	马勤. 超挖对软土基坑工程稳定性的影响分析. 现代矿业. 2024(04): 121-123 . 百度学术
4.	张瑞程. 新型斜撑-排桩基坑支护体系工程应用分析. 施工技术(中英文). 2024(12): 162-166 . 百度学术
5.	王强，宋歌，廖利，刘国伟，蔡崇德. 全地下空间枢纽深基坑支护结构变形特征控制. 铁路技术创新. 2024(03): 178-185 . 百度学术
6.	赵升峰，汪敏营，邬喜春，李明东. 不同深度基坑中桩加支撑支护特性研究. 江苏建筑. 2024(06): 112-115+129 . 百度学术
7.	赵玉成，代兆宇，夏瑞萌，娄海成. 雄安新区深基坑双排桩支护的实践与探讨. 粉煤灰综合利用. 2024(06): 79-83+95 . 百度学术
8.	蔡红岩. 供水泵站基坑排桩支护局部失效引发连续破坏机理研究. 陕西水利. 2023(01): 100-102 . 百度学术
9.	曾诚. 基坑局部设置双排桩桩长桩径对连续变形控制效果影响研究. 中国新技术新产品. 2023(07): 81-85 . 百度学术
10.	梁文辉. 深基坑双排桩式围护结构支护施工技术研究. 江西建材. 2023(09): 244-245+248 . 百度学术
11.	黄礼明. 某邻近既有建筑的异形软土基坑变形控制. 福建建筑. 2023(11): 84-88 . 百度学术
12.	徐琳，黄程翔，邵根才，杨璞，李宝山. 软土地区基坑超挖对围护结构变形的影响. 建筑安全. 2023(12): 33-36 . 百度学术
13.	魏焕卫，李传斌，种记鑫，郑晓. 局部超挖对内支撑结构的施工效应. 计算机辅助工程. 2023(04): 56-65 . 百度学术
14.	常强. 双排桩治理边坡的数值模拟研究. 黑龙江水利科技. 2022(04): 37-39+179 . 百度学术
15.	郑刚，程雪松，周海祚，张天奇，于晓旋，刁钰，王若展，衣凡，张文彬，郭伟. 岩土与地下工程结构韧性评价与控制. 土木工程学报. 2022(07): 1-38 . 百度学术
16.	唐小军，袁仕贵. 铁路桥台基坑开挖支护方案及稳定性计算. 中国水运. 2022(08): 146-148 . 百度学术
17.	唐小军，袁仕贵. 铁路桥台基坑开挖支护方案及稳定性计算. 中国水运. 2022(15): 146-148 . 百度学术
18.	孙永梅，程海涛，米春荣，孙贝. 土体超挖对深基坑变形影响分析. 山西建筑. 2021(19): 61-63 . 百度学术
19.	曾锦秀. 基于上限法的边坡双排抗滑桩变形计算方法. 福建工程学院学报. 2021(06): 538-544 . 百度学术