Multi-field coupled model for solid-phase degradable soils and its numerical implementation using finite volume method
-
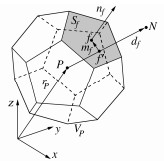
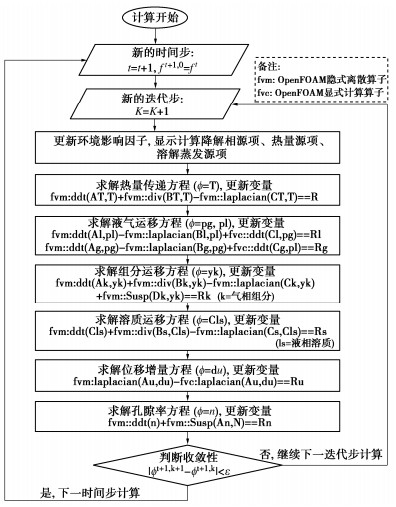
摘要: 固相可降解土体内部作用异常复杂，分析其水–力–热–化多场耦合行为对于解决相关工程问题具有重要意义。基于多孔介质基本理论，从可降解土体固液气三相系统的质量、动量及能量守恒出发，建立了考虑降解相变、液气运移、骨架变形、热量传递等过程的多场耦合理论模型。以液相压力、气相压力、组分质量分数、溶质质量浓度、温度、骨架位移和孔隙率为基本未知量，采用有限体积法对耦合模型控制方程进行数值离散，以顺序耦合的求解思路对耦合模型进行求解，并研发了相应的数值求解器。开展砂柱排水试验、多孔介质中溶质迁移和传热过程、可降解生活垃圾试验的模拟，验证了耦合模型及数值求解器的正确性。模型及程序有助于加深对可降解土体多场耦合模型控制方程建立、本构关系确定以及数值实现的理解，为相关可降解土体多场耦合模型建立奠定基础。Abstract: The internal interaction of solid-phase degradable soils is extremely complex, and analysis of its hydraulic- mechanical-thermal-chemical multi-field coupled behaviors is of great significance for analyzing the related engineering problems. Based on the basic theory of porous media, a multi-field coupled model is developed by incorporating the mass, momentum and energy conservation of the degradable soils characterized by a solid-liquid-gas three-phase system. The coupled model considers the degradation phase transition, liquid-gas migration, skeleton deformation and heat transfer. By selecting the liquid phase pressure, gas phase pressure, mass fraction of gas components, liquid solute concentration, temperature, skeleton displacement and porosity as the basically unknown variables, the finite volume method is used to numerically discretize the governing equations for the established coupled model, and sequentially the solving method is adopted to iteratively solve the coupled model. In addition, the corresponding numerical solver is developed. The simulations of sand column drainage tests, solute migration and heat transfer in porous media, and degradable municipal solid waste experiments are conducted to verify the correctness of the coupled model and the numerical solver. The model and program will help to enhance the understanding of the derivation of the governing equations, the determination of constitutive relations and the numerical implementation for the multi-field coupled model for the degradable soil. It also provides a basis for the development of multi-field coupled model of related degradable soils.
-
0. 引言
在松软饱和地层、城市密集区域、穿越河海段等隧道工程建设中，传统的人工钻爆工法将面临严峻的挑战与巨大的风险，盾构技术的引进为此提供解决方案。随着机械设备与施工技术的不断发展，盾构工法已逐渐推广应用于城市给排水、水资源配置、发电引水、农业灌溉等水利建设工程，国内外已有大量成功案例，见表 1。
表 1 国内外部分单层衬砌盾构输水隧洞工程Table 1. Some single-layer lining shield water conveyance tunnel projects at home and abroad区别于交通隧道，水工隧洞工作条件更为复杂，结构承担管片衬砌的外部水土荷载和内部水压力，使得接缝张开、管片受力等呈现不同的结构承载与变形特点[7-8]。目前，国内外针对地铁、公路等无内压管片衬砌结构的研究已取得丰富的成果[9-11]，而专门针对有内压管片衬砌结构的研究相对薄弱。章青等[12]基于不连续介质变形体的界面应力元理论建立了能模拟管片接头不连续变形的盾构输水隧洞计算模型；赵大洲等[13]依托南水北调西线工程，借助数值仿真手段探讨了围岩变形及内、外水压力对管片衬砌受力变形的影响；佘成学等[14]结合青松电站引水隧洞针对管片衬砌在高内水压力作用下的力学响应展开了数值计算；闫治国等[1]结合青草沙水源地原水工程，针对管片接头开展原型试验；周龙等[15]针对蓄排水盾构隧洞开展了足尺荷载试验及数值分析，揭示了管片衬砌在内压下的变形规律及错缝拼装效应；Zhang等[2]、刘威等[16]分别基于上海苏州河段深层排水调蓄管道系统工程开展室内足尺模型试验及数值计算，研究了隧洞对于内压、埋深、封顶块位置及螺栓预紧力等因素的敏感性。
综上，现有研究主要通过室内模型试验和数值模拟，探讨衬砌结构的承载与变形机理。但受条件制约，室内试验在结构尺寸、内水压力模拟、外部水土荷载施加等方面需要进行简化与等效，难以真实表征管片环在内水压力作用下的力学响应，一定程度上影响了理论分析和数值计算的可靠性。为了弥补上述研究的局限性，本文依托珠江三角洲水资源配置工程，提出一种基于“高压囊体-反力支架-伺服泵机”装置的内压模拟方式，并采用“光纤传感技术”与“振弦式仪器”相结合的测量系统，对华南地区盾构输水隧洞单层衬砌结构开展原位试验研究，揭示了该结构在真实地层条件下承受内压的受力变形规律。在此基础上，采用三维有限元模型对不同围岩条件下单层管片衬砌结构的内压承载变形特性开展进一步的分析，为长距离输水工程衬砌结构选型设计提供参考与借鉴。
1. 输水盾构隧洞结构试验
1.1 试验概况
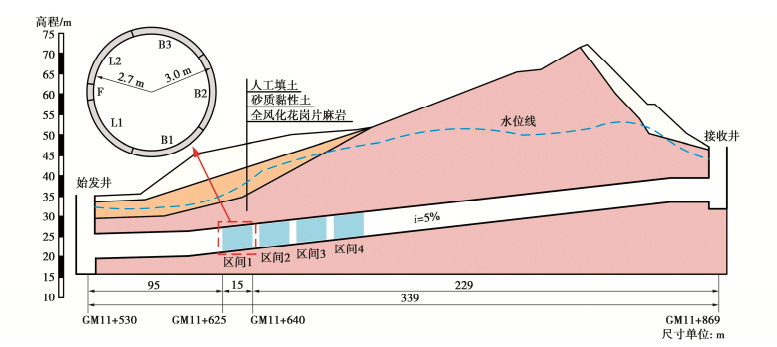
珠江三角洲水资源配置工程是广东省有史以来线路最长、内压最高的跨流域调水工程，最大设计内压达1.5 MPa。输水隧洞将穿越多种地层，沿线涉及泵站、水库、调压塔等水工建筑物，使得各标段隧洞设计内压差异较大。综合考虑工程安全性与经济性，衬砌结构的选型与设计面临诸多难题，需开展原位试验为工程实践提供有效参考。本试验共设置4组盾构区间，每组长度为15 m，衬砌型式分别采用单层管片、钢筋混凝土内衬、分离式及叠合式钢管内衬结构。区间隧洞埋深为19.5~20.0 m，处于全风化花岗片麻岩层，地下水位深度为6.6~13.8 m。本文重点针对区间1的单层管片衬砌结构展开讨论，该区间由10环C55预制钢筋混凝土管片错缝拼接而成，隧洞上覆土层分布及衬砌结构型式见图 1。管片内外侧均设置HRB400环向受力筋(12φ18)，内、外侧钢筋保护层厚度分别为30，40 mm；每环管片由6个分块组成，包括3个标准块(B1~B3)、2个邻接块(L1、L2)和1个封顶块(F)；管片间采用A4-70级M24弯螺栓连接，每道纵缝布置2根环向螺栓；每道环缝等间距布置10根纵向螺栓。
![]()
图 1 试验区间的地质条件及衬砌结构型式Figure 1. Geological conditions and lining structure of in-situ tests1.2 加载方案
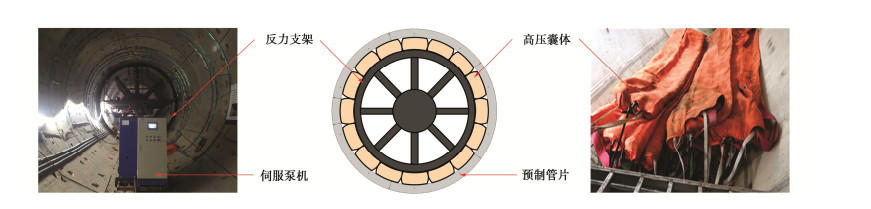
为确保洞内试验安全和加载效率，本试验专门设计了一套“高压囊体-反力支架-伺服泵机”系统模拟内水压力，如图 2所示，即，在衬砌结构内部设置圆筒形反力支架，将16个高压囊体均布于反力支架与预制管片之间，操作液压伺服系统，通过泵机对高压囊体同步注水。囊体不断膨胀并将压力传递于管片内表面，以实现内水压力的模拟。
鉴于试验区间后续将应用于实际工程，需保证结构安全和正常使用，本次试验将最大内压设置为0.30 MPa，以0.02 MPa为梯度逐级加载。
1.3 测量系统
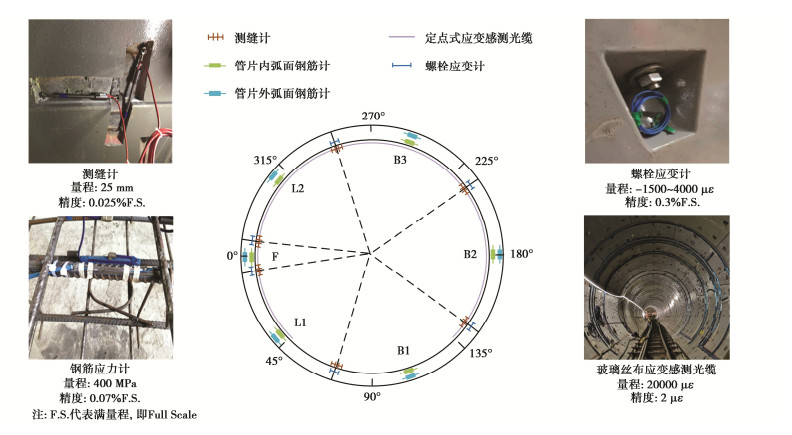
区别于室内模型试验，现场原位试验的操作环境更加复杂，监测难度更大。本试验采用振弦类与光纤类传感器对结构的受力与变形规律进行了监测，以确保测量系统在复杂的地下环境中仍保持较高的精度和效率，监测内容主要包括螺栓应力、纵缝张开量、钢筋应力、混凝土应变等，仪器参数及布置如图 3所示。在原位试验区间内，围岩以全风化花岗片麻岩为主，地层条件相对均匀，未出现断层、破碎带等不利地层，故本文重点考虑衬砌横断面的承载变形特征。
2. 三维地层-结构模型
受限于洞内试验和现场监测的复杂性，原位试验仅针对单一地质条件下的衬砌结构开展较小内压加载测试，难以针对该衬砌结构开展系统研究，因此，本文基于数值仿真技术进一步探讨单层管片衬砌结构在不同内水压力、围岩类型等条件下承载变形机理。
2.1 有限元网格与边界条件
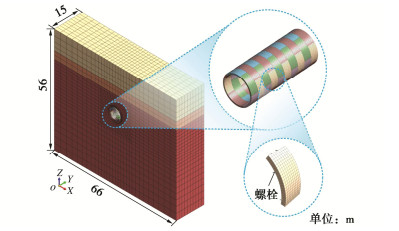
根据区间1的结构型式及地层状况建立有限元模型，如图 4所示。其中，左右及下边界各取5倍隧洞外径，上边界与原位试验区间埋深相同(取20 m)。考虑管片环间的错缝拼装效应(错缝角度为180°)及管片间的连接螺栓，岩土体及管片均采用实体单元，连接螺栓以杆单元形式嵌入管片单元，共计119380个单元和172977个节点。围岩左右边界约束x向位移，前后边界约束y向位移，底部边界约束z向位移。为消除首尾环的边界效应，本次计算取第5环管片作为参考。
2.2 本构关系与接触关系
土体材料采用Drucker-Prager塑性模型，管片采用损伤塑性本构模型，螺栓采用双折线塑性强化模型，塑性加强段弹性模量为弹性段的1/100，主要参数详见表 2。“管片-管片”、“管片-围岩”之间设置面-面接触，即，切向上服从库仑摩擦定律，当切向应力达到临界值后允许发生滑移，摩擦系数取0.5[7]；法向上定义为硬接触，允许接触面之间发生分离。
表 2 主要材料物理力学参数Table 2. Mechanical parameters of materials材料 密度/(g·cm-3) 弹性模量/MPa 泊松比 内摩擦角/(°) 黏聚力/kPa 屈服强度/MPa 极限强度/MPa 抗压强度标准值/MPa 抗拉强度标准值/MPa 人工填土 2.03 40 0.48 12 8 — — — — 砂质黏性土 1.98 120 0.45 19 10 — — — — 全风化花岗片麻岩 1.97 200 0.38 20 50 — — — — A4-70级螺栓 7.85 210000 0.30 — — 450 700 — — HRB400钢筋 7.85 210000 0.30 — — 400 540 — — C55混凝土 2.50 35500 0.20 — — — — 35.5 2.74 2.3 加载方式
通过引入土层饱和状态下的容重，以反映外水作用，其中，外部水位与现场相同。为准确模拟管片衬砌周边围岩的应力分布，在施加管片衬砌之前，对围岩进行地应力平衡获得围岩初始应力；在管片内表面沿高度方向施加不均匀分布的内水压力，增量设为0.05 MPa/步。
3. 不同内压下结构响应
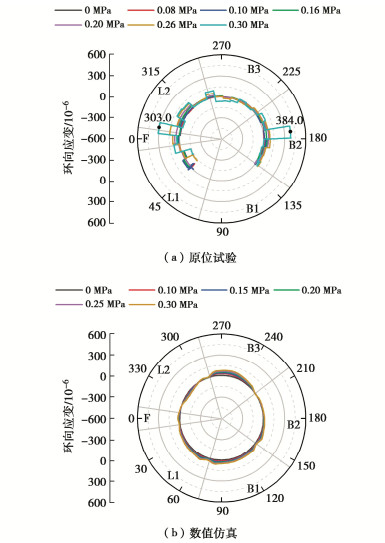
图 5~8为试验监测与数值计算结果，其中，拉应力、拉应变和径向扩张取“+”；压应力、压应变和径向收缩取“-”。结构达到正常使用极限状态时的限值列如表 3。
表 3 结构正常使用极限状态限值[17]Table 3. Values of structural response in normal service limit state结构响应 正常使用极限状态 收敛变形/mm 12 钢筋应力/MPa 400 接缝张开量/mm 2 螺栓应力/MPa 450 3.1 收敛变形
从试验结果(图 5)不难发现，当衬砌无内压时，管片在外部水土压力作用下，呈现竖向收敛、横向扩张的“横椭圆”变形规律。随着内压增加，整体逐渐呈现向外膨胀趋势，且“横椭圆”变形特征更为明显，相关模型试验亦呈现类似变形规律[15-16]。当内压为0.30 MPa时，左、右拱腰的拉应变增量分别为303.0×10-6和384.0×10-6，但考虑到洞内试验测量环境的复杂性，仅依据混凝土环向应变增量无法准确判断局部混凝土是否开裂，有待结合其他监测指标进行综合判断。数值计算结果反映出与试验相似的变形规律，但前者环向应变分布相对监测结果更加均匀。
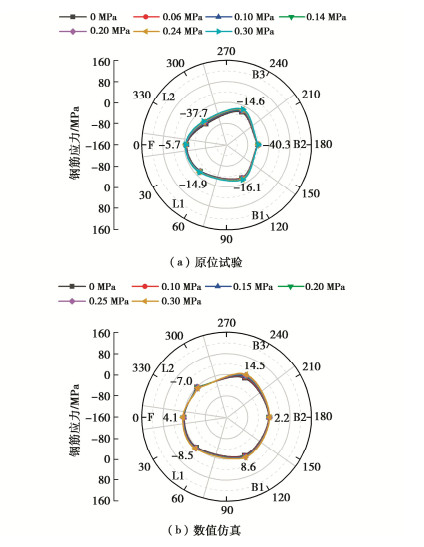
3.2 钢筋应力
如图 6所示，数值计算与试验监测结果具有良好的可比性，随着内压增加，钢筋应力均呈现拉应力增加或压应力减少趋势。当内压为0.30 MPa时，管片钢筋应力皆处于较小水平，局部未出现突变；由此可见，管片内表面混凝土尚未出现开裂现象。
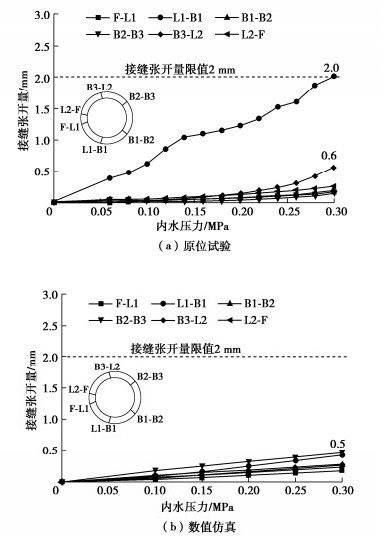
3.3 接缝张开量
由试验和数值结果(图 7)可见，接缝张开量随内压的增加而增大。在试验中，隧洞仰拱处L1-B1接缝变化规律最显著，而其余接缝张开量变化平缓，且量值较小。当内压超过0.20 MPa时，张开量逐步进入快速增长阶段；当内压为0.30 MPa时，L1-B1接缝张开量为2.0 mm，已达到规范限值[17]。对应于前述管片“横椭圆”变形模式，管片衬砌仰拱和拱顶处的接缝张开量大于其余位置。相比于试验，数值计算结果偏小，当内压为0.30 MPa时，最大接缝张开量仅为0.5 mm，且为外侧张开量。值得注意的是，受限于现场测量条件，测缝计只能布设于管片内表面，在内压加载过程中，接缝将产生一定的错台变形，使得测缝计无法准确获取管片外表面的接缝变形情况，影响监测结果。
对于输水隧洞而言，接缝张开或错台等变形必然导致洞内壁糙率增大，从而造成一定水头损失，甚至引发内水外渗。因此，对于采用管片衬砌的水工隧洞，须加强隧洞防渗措施。根据相关工程经验[1, 3, 18]，建议采用预埋铸铁件的手孔接头、设置双排连接螺栓、双层止水等措施约束接缝变形，以增强防渗效果。
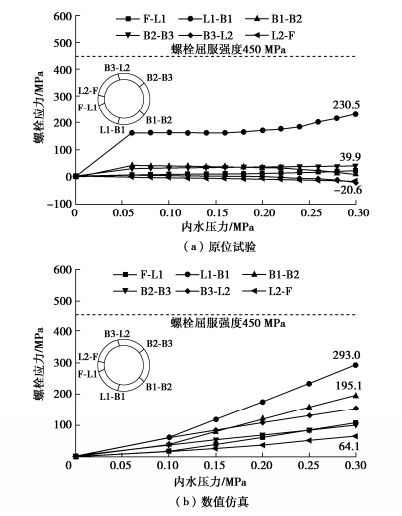
3.4 螺栓应力
螺栓应力与接缝张开量变化趋势基本相对应，见图 8。在原位试验中，L1-B1螺栓应力增长显著，当内压为0.30 MPa时，达到230.5 MPa的拉应力，但螺栓尚未屈服，而其余螺栓应力变化不明显，应力水平偏小。相比于试验，在数值仿真中，所有的螺栓应力均呈现拉应力平稳增大的趋势。数值结果真实表征螺栓整体应力情况，但原位试验通过在螺栓外侧埋置光纤，仅能反映局部应力分布，当管片出现正负弯矩时，螺栓(特别是弯螺栓)内外侧应力差异大，测量结果存在较大误差。
4. 围岩对管片衬砌承载变形特性的影响
考虑到引调水工程沿线地质条件复杂多变，洞身所处的围岩差异较大，而原位试验未能针对多种地层进行深入研究。本文选取III、IV和V类围岩，针对不同围岩条件下，单层管片衬砌结构的力学和变形响应开展数值仿真研究。根据相关规范[17, 19-20]，结合现场工程地质勘测资料，选取上述三类围岩最不利工况作为本次数值计算参数，如表 4所示。“+”和“-”定义同第3节。
表 4 各类围岩物理力学参数Table 4. Mechanical parameters of various surrounding rocks围岩类别 密度/(g·cm-3) 弹性模量/MPa 泊松比 内摩擦角/(°) 黏聚力/kPa III 2.10 3000 0.28 35 200 IV 1.97 200 0.38 20 50 V 1.70 70 0.42 15 10 4.1 收敛变形
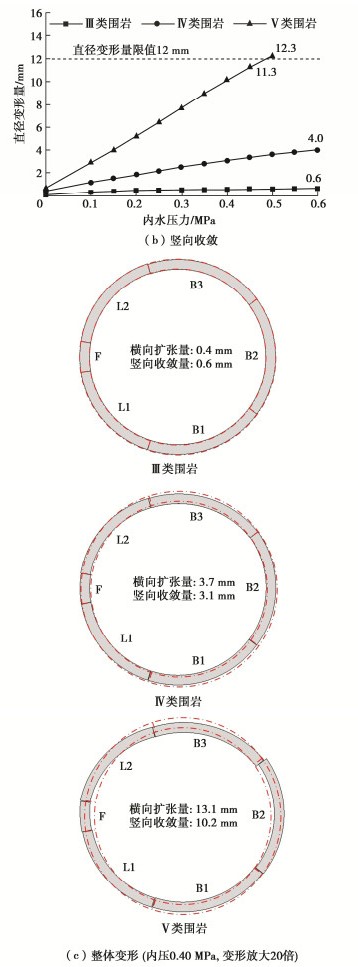
图 9(a)，(b)分别为3种围岩等级下管片衬砌结构的横向扩张量和竖向收敛量随内压发展曲线。在内压与外部水土压力的作用下，3种围岩下的管片衬砌均呈现拱顶及仰拱向内收敛、左右拱腰向外扩张的“横椭圆”变形；内压越大，“横椭圆”变形特征越明显。当内压达0.40 MPa时，V类围岩下的管片衬砌的横向扩张量已达13.1 mm，超过规范限制的2‰隧道外径[17]，竖向收敛量已达10.2 mm，为规范限值的85.0%。如图 9(c)所示，在相同内压下，V类围岩下管片衬砌“横椭圆”变形趋势相比III类、IV类围岩更加明显。当内压为0.60 MPa时，处于IV类围岩下的管片衬砌最大径向变形为横向扩展(5.5 mm)，为规范限值的45.8%；处于III类围岩下的管片衬砌竖向收敛量与横向扩张量的最大值均为0.6 mm，为规范限值的5.0%。
可见，随着围岩力学性能的提高，围岩对衬砌结构的约束变形作用增强，管片衬砌的“横椭圆”变形特征减弱。从管片收敛变形来看，衬砌在V类围岩下承受的内压不宜超过0.35 MPa，综合相应的外部水土压力状况，衬砌可承担的内外压差不宜超过0.15 MPa。
4.2 螺栓应力和接缝张开量
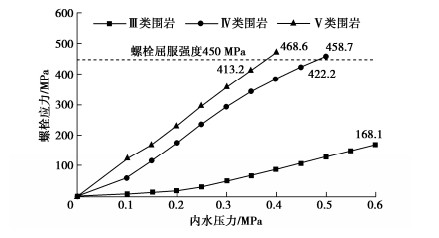
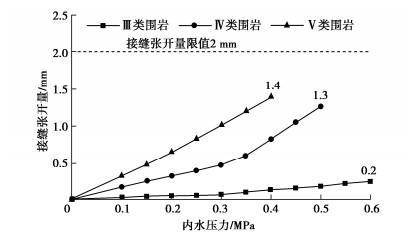
由图 10，11可见，随围岩力学性能的提高，螺栓应力和接缝张开量逐渐减小。在内压作用下，管片螺栓应力与接缝张开量呈现相似的变化规律，其中，前者相对接后者更易达到结构正常使用极限状态。本次数值模拟中，V类与IV类围岩下的螺栓应力随内压增长较快，分别于0.40，0.50 MPa超过屈服强度，对应最大接缝张开量分别为1.4，1.3 mm，尚未达到规范限值；III类围岩下的螺栓应力随内压缓慢增长，当内压为0.60 MPa时，最大螺栓应力为168.1 MPa，最大接缝张开量为0.2 mm，仍具有较大安全储备。因而，从螺栓应力和接缝张开量来看，管片衬砌在V类和IV类围岩下承受的内压不宜超过0.35，0.45 MPa，综合相应的外部水土压力状况，衬砌可承担的内外压差极限分别为0.15，0.25 MPa。
5. 结论
本文针对单层管片衬砌结构开展了原位试验与数值仿真研究，揭示了结构在内水压力作用下的变形规律，并探讨了结构在20 m埋深，3种围岩条件下结构的承载变形特性，得到以下3点结论。
(1) 在内压作用下，管片衬砌结构呈现“横椭圆”变形且向外膨胀趋势，接缝张开量和螺栓应力随内压增加而增大。对于V类围岩，宜综合衬砌收敛变形和螺栓应力判断结构是否达到正常使用极限状态，而对于IV类围岩，螺栓应力为结构达到正常使用极限状态的控制因素。
(2) 随着围岩力学性能的提高，结构在内压作用下结构响应减小，围岩分担内压的效果增强。综合结构承载变形特性及工程经济性的考虑，管片衬砌适用于穿越IV或V类围岩且内外压差较小的水工隧洞。其中，IV类围岩中的内外压差不宜超过0.25 MPa，V类围岩的内外压差不宜超过0.15 MPa；若需承载更高内水压力，建议采用钢筋混凝土或钢管内衬的复合衬砌结构。对于穿越III类及以上类别围岩的水工隧洞，当内外压差达0.40 MPa时，管片衬砌仍具有较大安全储备。
(3) 单层管片衬砌输水隧洞需加强接缝变形控制，接缝张开或错台等变形将增大洞内壁糙率，造成水头损失，同时，容易引发内水外渗，尤其对于砂质软土地层，更应加强防渗措施，以防出现流砂、管涌等破坏现象。建议采用预埋铸铁手孔接头、设置双排连接螺栓、双层止水等措施约束接缝变形，从而达到较好的防渗效果。
-
![]()
图 3 耦合模型顺序迭代耦合求解示意图
Figure 3. Schematic diagram of sequential iterative coupling solution of coupled model
![]()
图 5 Liakopoulos砂柱试验结果与模拟结果
Figure 5. Laboratory and simulated results of Liakopoulos sand column tests
![]()
图 9 CAR1试验模型初始竖向应力分布图
Figure 9. Distribution of initial vertical stress of model for CAR1 tests
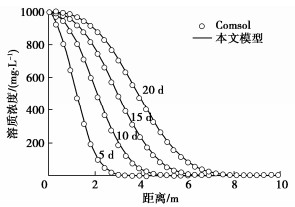
表 1 污染物迁移案例模型参数
Table 1 Model parameters for contaminant transportation case
孔隙率n 饱和度Sl 液相
流速vlr/
(m·s-1)扩散系数Ds l/
(m2·s-1)孔隙弯曲因子τl 质量源
BQs l/
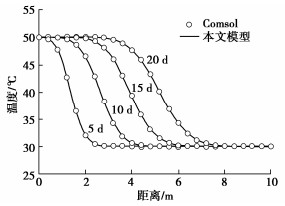
(kg·m-3)0.6 0.4 4.8×10-7 1.2×10-9 0.1576 0 
下载: 导出CSV
表 2 热量传递案例模型参数
Table 2 Model parameters for heat transfer case
孔隙率n 饱和
度Sl固相密度ρs/ (kg·m-3) 液相密度ρl/
(kg·m-3)气相密度ρg/
(kg·m-3)固相单位热容量Hs/
(J·kg-1·K-1)液相单位热容量Hw/ (J·kg-1·K-1) 气相单位热容量Hg/
(J·kg-1·K-1)液相流速vlr/
(m·s-1)气相流速vgr/
(m·s-1)热传导系数Г/
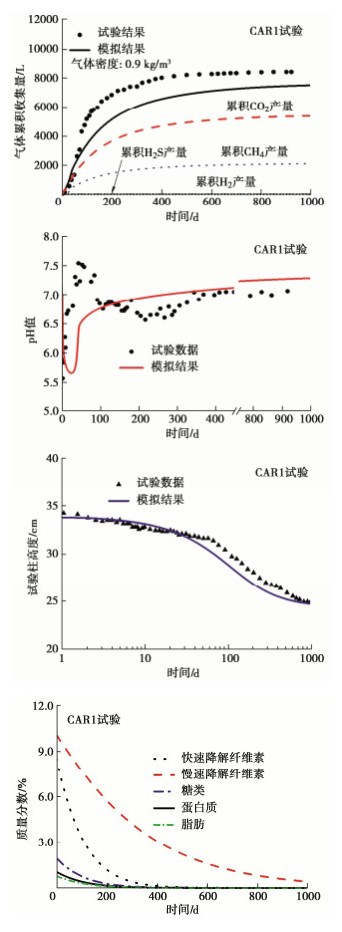
(m·s-1·K-1)参考温度Tr/℃ 0.6 0.4 800 1000 1.29 1300 4200 1514 10-6 10-6 0.436 20
下载: 导出CSV
表 3 CAR1试验中生活垃圾成分表
Table 3 Composition of municipal solid waste in CAR1 experiment
成分 纤维素a 纤维素b 糖类 蛋白质 脂肪 其他 质量/(kg·m-3) 37.37 44.19 8.49 4.59 3.41 339.45 质量分数/% 8.54 10.12 1.94 1.05 0.78 77.57 注：a代表快速降解纤维素，b代表慢速降解纤维素。
下载: 导出CSV
-
[1] 张旭俊. 可降解土体BCHM耦合模型研究[D]. 杭州: 浙江大学, 2015. ZHANG Xujun. Study on Bio-Chemical- Hydro-Mechanical Coupling Model in Degradable Soil[D]. Hangzhou: Zhejiang University, 2015. (in Chinese)
[2] 陈云敏. 环境土工基本理论及工程应用[J]. 岩土工程学报, 2014, 36(1): 1-46. doi: 10.11779/CJGE201401001 CHEN Yunmin. A fundamental theory of environmental geotechnics and its application[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 1-46. (in Chinese) doi: 10.11779/CJGE201401001
[3] 徐晓兵. 基于降解-渗流-压缩耦合模型的填埋场垃圾固液气相互作用分析及工程应用[D]. 杭州: 浙江大学, 2011. XU Xiaobing. Bio-Hydro-Mechanical Coupled Analyses of Solid-liquid-Gas Interactions in Landfilled Municipal Solid Wastes and its Application[D]. Hangzhou: Zhejiang University, 2011. (in Chinese)
[4] 陈云敏, 谢焰, 詹良通. 城市生活垃圾填埋场固液气耦合一维固结模型[J]. 岩土工程学报, 2006, 28(2): 184-190. doi: 10.3321/j.issn:1000-4548.2006.02.008 CHEN Yunmin, XIE Yan, ZHAN Liangtong. One-dimensional consolidation model for landfills considering solid-liquid-gas interaction[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(2): 184-190. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.02.008
[5] 薛强, 刘磊, 梁冰, 等. 垃圾填埋场沉降变形条件下气-水-固耦合动力学模型研究[J]. 岩石力学与工程学报, 2007, 26(增刊1): 3473-3478. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2007S1133.htm XUE Qiang, LIU Lei, LIANG Bing, et al. A gas-hydraulic-solid coupling dynamics model under landfill settlement[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S1): 3473-3478. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2007S1133.htm
[6] 薛强, 赵颖, 刘磊, 等. 垃圾填埋场灾变过程的温度–渗流–应力–化学耦合效应研究[J]. 岩石力学与工程学报, 2011, 30(10): 1970-1988. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201110004.htm XUE Qiang, ZHAO Ying, LIU Lei, et al. Study of thermo-hydro-mechanical-chemical coupling effect of catastrophe process of landfill[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 1970-1988. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201110004.htm
[7] LU S F, FENG S J, ZHENG Q T, et al. A multi-phase, multi-component model for coupled processes in anaerobic landfills: theory, implementation and validation[J]. Géotechnique, 2021, 71(9): 826-842. doi: 10.1680/jgeot.20.P.002
[8] CHEN Y M, XU W J, LING D S, et al. A degradation–consolidation model for the stabilization behavior of landfilled municipal solid waste[J]. Computers and Geotechnics, 2020, 118: 103341. doi: 10.1016/j.compgeo.2019.103341
[9] KUMAR G, REDDY K R, MCDOUGALL J. Numerical modeling of coupled biochemical and thermal behavior of municipal solid waste in landfills[J]. Computers and Geotechnics, 2020, 128: 103836. doi: 10.1016/j.compgeo.2020.103836
[10] LI K, CHEN Y M, XU W J, et al. A thermo-hydro-mechanical-biochemical coupled model for landfilled municipal solid waste[J]. Computers and Geotechnics, 2021, 134: 104090. doi: 10.1016/j.compgeo.2021.104090
[11] LAI Y M, PEI W S, ZHANG M Y, et al. Study on theory model of hydro-thermal–mechanical interaction process in saturated freezing silty soil[J]. International Journal of Heat and Mass Transfer, 2014, 78: 805-819. doi: 10.1016/j.ijheatmasstransfer.2014.07.035
[12] 凌贤长, 罗军, 耿琳, 等. 季节冻土区非饱和膨胀土水-热-变形耦合冻胀模型[J]. 岩土工程学报, 2022, 44(7): 1255-1265. doi: 10.11779/CJGE202207006 LING Xianzhang, LUO Jun, GENG Lin, et al. Coupled hydro-thermo-deformation frost heave model for unsaturated expansive soils in seasonally frozen soil regions[J]. Chinese Journal of Geotechnical Engineering, 2022, 44(7): 1255-1265. (in Chinese) doi: 10.11779/CJGE202207006
[13] DE LA FUENTE M, VAUNAT J, MARÍN-MORENO H. Thermo-hydro-mechanical coupled modeling of methane hydrate-bearing sediments: formulation and application[J]. Energies, 2019, 12(11): 2178. doi: 10.3390/en12112178
[14] GUPTA S, HELMIG R, WOHLMUTH B. Non-isothermal, multi-phase, multi-component flows through deformable methane hydrate reservoirs[J]. Computational Geosciences, 2015, 19(5): 1063-1088. doi: 10.1007/s10596-015-9520-9
[15] REDDY K R, KUMAR G, GIRI R K. Modeling coupled hydro-bio-mechanical processes in bioreactor landfills: framework and validation[J]. International Journal of Geomechanics, 2018, 18(9): 04018102. doi: 10.1061/(ASCE)GM.1943-5622.0001164
[16] LU S F, FENG S J. Coupled bio-hydro-thermo-mechanical interactions of landfilled MSW based on a multi-phase, multi-component numerical model[J]. Computers and Geotechnics, 2022, 144: 104659. doi: 10.1016/j.compgeo.2022.104659
[17] LEWIS R W, SHREFLER B A. The finite element method in the static and dynamic deformation and consolidation of porous media[M]. 2nd ed. New York: John Wiley, 1998.
[18] LU S F, FENG S J. Comprehensive overview of numerical modeling of coupled landfill processes[J]. Waste Management (New York, N Y), 2020, 118: 161-179. doi: 10.1016/j.wasman.2020.08.029
[19] MASON I G. An evaluation of substrate degradation patterns in the composting process. Part 2: temperature-corrected profiles[J]. Waste Management (New York, N Y), 2008, 28(10): 1751-1765. doi: 10.1016/j.wasman.2007.06.019
[20] MCDOUGALL J R, PYRAH I C. Phase relations for decomposable soils[J]. Géotechnique, 2004, 54(7): 487-493. doi: 10.1680/geot.2004.54.7.487
[21] BENTE S. Interaction of Degradation, Deformation and Transport Processes in Municipal Solid Waste Landfills[D]. Braunschweig: Technische Universitat Braunschweig, 2011.
[22] MUALEM Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research, 1976, 12(3): 513-522. doi: 10.1029/WR012i003p00513
[23] WILKE C R, CHANG P. Correlation of diffusion coefficients in dilute solutions[J]. AIChE Journal, 1955, 1(2): 264-270. doi: 10.1002/aic.690010222
[24] CELIA M A, BINNING P. A mass conservative numerical solution for two-phase flow in porous media with application to unsaturated flow[J]. Water Resources Research, 1992, 28(10): 2819-2828. doi: 10.1029/92WR01488
[25] KIM J, TCHELEPI H A, JUANES R. Stability and convergence of sequential methods for coupled flow and geomechanics: fixed-stress and fixed-strain splits[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(13/14/15/16): 1591-1606.
[26] TUKOVIĆ, IVANKOVIĆ A, KARAČ A. Finite-volume stress analysis in multi-material linear elastic body[J]. International Journal for Numerical Methods in Engineering, 2013, 93(4): 400-419. doi: 10.1002/nme.4390
[27] JASAK H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows[D]. London: Imperial College London, 1996.
[28] FENG S J, LU S F, CHEN H X, et al. Three-dimensional modelling of coupled leachate and gas flow in bioreactor landfills[J]. Computers and Geotechnics, 2017, 84: 138-151. doi: 10.1016/j.compgeo.2016.11.024
[29] LU S F, XIONG J H, FENG S J, et al. A finite-volume numerical model for bio-hydro-mechanical behaviors of municipal solid waste in landfills[J]. Computers and Geotechnics, 2019, 109: 204-219. doi: 10.1016/j.compgeo.2019.01.012
[30] JASAK H, JEMCOV A, TUKOVI´C Z. OpenFOAM: A C++ library for complex physics simulations[C]//International Workshop on Coupled Methods in Numerical Dynamics, 2007: 1-20.
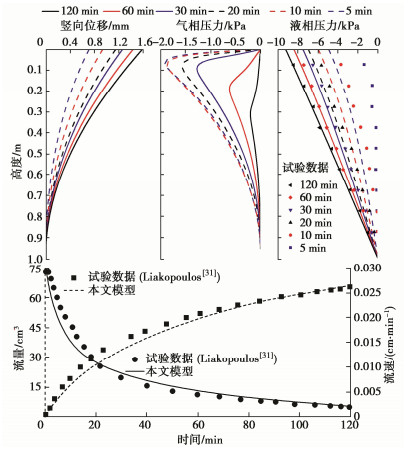
[31] LIAKOPOULOS A. Transient Flow through Unsaturated Porous Media[D]. Berkeley: University of California, 1964.
[32] HU R, CHEN Y F, LIU H H, et al. A coupled two-phase fluid flow and elastoplastic deformation model for unsaturated soils: theory, implementation, and application[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2016, 40(7): 1023-1058. doi: 10.1002/nag.2473
[33] ASADI R, ATAIE-ASHTIANI B. A comparison of finite volume formulations and coupling strategies for two-phase flow in deforming porous media[J]. Computers and Geotechnics, 2015, 67: 17-32. doi: 10.1016/j.compgeo.2015.02.004
[34] IVANOVA L K, RICHARDS D J, SMALLMAN D J. The long-term settlement of landfill waste[J]. Proceedings of the Institution of Civil Engineers-Waste and Resource Management, 2008, 161(3): 121-133. doi: 10.1680/warm.2008.161.3.121
[35] IVANOVA L K, RICHARDS D J, SMALLMAN D J. Assessment of the anaerobic biodegradation potential of MSW[J]. Proceedings of the Institution of Civil Engineers - Waste and Resource Management, 2008, 161(4): 167-180. doi: 10.1680/warm.2008.161.4.167
[36] CHEN Y M, GUO R Y, LI Y C, et al. A degradation model for high kitchen waste content municipal solid waste[J]. Waste Management (New York, N Y), 2016, 58: 376-385. doi: 10.1016/j.wasman.2016.09.005
-
期刊类型引用(2)
1. 吴彦燊，徐博远，刘璐，薄昭，吴琪. 砂-粉混合料不排水剪切相变强度特性试验研究. 人民长江. 2025(01): 187-192 . 
百度学术
2. 王钰轲，蒋睿，郭成超，王复明. 考虑相变状态及温度效应的冻结砂土非关联弹塑性本构模型. 岩石力学与工程学报. 2025(04): 1026-1039 . 百度学术
其他类型引用(0)
-
其他相关附件
计量
- 文章访问数: 340
- HTML全文浏览量: 58
- PDF下载量: 103
- 被引次数: 2
