0.   引言

土工离心模型试验是当今研究岩土工程问题最先进的方法之一，它借助离心机的高速运转实现了模型应力水平与原型完全一致的相似性要求，原型土体和结构的受力变形特性包括破坏性状在理论上都可以在模型中得到逼真再现。然而，任何模型都必须置于模型箱内再置于离心机吊篮平台内，经受离心机高速运转试验，模型箱箱壁的摩擦和法向限位约束必然影响到模型位移变形性状包括大变形破坏性状。

Ovesen^[1]研究了模型箱侧壁竖向摩擦妨碍作用对浅基础承载力试验结果的影响，结果发现当模型浅基础边缘与内壁之间的距离B_b大于2.82D（D为浅基础直径）后，才能避免模型箱侧壁竖向摩擦的影响，否则离心模型试验得到的承载力高出原型真实的承载力，高出范围介于10%~20%。为了验证Ovesen^[1]的上述结论，徐光明等^[2]也开展了同样的研究，得到了类似结果，发现当模型浅基础边缘与内壁之间的距离B_b大于3.0D后，才能完全消除模型箱侧壁竖向摩擦对承载力试验结果的影响，离心模型试验结果不再高估原型真实的承载力。Feld等^[3]则研究了模型箱侧壁竖向摩擦妨碍作用对模型土体竖向自重应力比（自重应力实测值与理论计算值之比）的影响，通过16组砂土离心模型试验研究了孔隙比、箱壁有无泡沫衬垫、离心加速度、土样深度（即模型箱高度或筒深）和模型箱宽度（即筒径）这5个变量的影响，结果分析发现模型箱高度不影响自重应力比，其它4个因素的重要性从最高到最低依次是加速度水平、模型箱宽度、土样孔隙比和有无设置泡沫衬垫，因此，建议离心模型试验尽可能采用大宽度或大直径的模型箱。总而言之，离心模型所模拟的基础等构筑物与模型箱侧壁之间需要留有足够的距离，才能消除模型箱侧壁竖向摩擦的边界约束对模型受力变形性状的影响，可见，采用宽度大的模型箱最为直接有效。

Malushitsky^[4]则研究了模型箱侧壁横向摩擦妨碍作用对模型废料堆破坏舌状滑动面的影响，发现在距离模型箱侧壁8~12 cm范围内的滑动面弯曲明显，而中间滑动面伸出最远并且伸出距离相同，即模型废料堆中间部分发生破坏最为明显，推移距离大于邻近箱壁区域部分发生的推移距离，这中间部分废料堆模型对应的才是平面应变条件，因此，Malushitsky决定用48.8，49.2 cm两种宽度的模型箱进行离心模型试验研究，并且只关注模型不受侧壁横向摩擦影响、滑动面无扭曲的中间部分^[4]。换言之，模型箱侧壁横向摩擦妨碍影响范围大致在距离侧壁8~12 cm范围内。基于这一研究成果，南京水利科学研究院容量为50g·t和60g·t两台中型土工离心机所配置的平面应变模型箱，其宽度均为35 cm^[5]，容量为400g·t大型土工离心机所装备的平面应变模型箱，其宽度为40 cm^[6]。

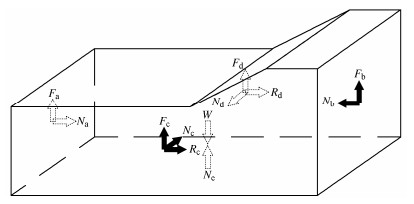
本文采用大型平面应变模型箱进行了一组离心模型试验，尝试再现南方某散货码头堆场地基在试堆载过程中发生的大变形推移破坏现象。先分析长方体平面应变模型箱箱壁对模型土体的约束作用力，它除了顶面和底面，共有4个侧面，即前后2个长侧壁（简称侧壁）和左右端部2个短侧壁（简称端壁），当模型土体与箱壁之间有相对位移或者存在变形趋势，箱壁上就产生阻碍两者相对位移或变形趋势的约束阻碍作用力。前面提及的箱壁竖向摩擦就是阻碍模型土体与箱壁发生竖向相对位移或竖向变形趋势^[1-3]，箱壁横向摩擦就是阻碍模型土体与箱壁发生横向相对位移或横向变形趋势^[4]。图 1为长方体平面应变模型箱内带坡面模型土体受力分析图，这里左右侧面、前后侧面和底面分别用a、b、c、d和e表示，显然在离心机超重力场中的模型土体承受自重W、箱底反力Ne和4个侧壁面上约束力的共同作用下，将发生向下沉降变形和指向左侧的位移变形。

图  1  平面应变模型受力分析图

Figure  1.  Force analysis diagram of plain-strain model

下载: 全尺寸图片 幻灯片

先看模型箱前后两侧壁c和d对模型土体作用的约束力，根据牛顿第三定律，图 1所示模型土体前后侧面在3个方向上受到前后箱壁阻碍其位移变形的作用力，首先是前后箱壁作用的法向约束力N_c和N_d，它们限制模型土体在垂直于前后侧壁方向上位移变形，满足平面应变受力变形条件；其次前后箱壁阻碍模型土体向下位移变形的摩擦阻力F_c和F_d，方向竖向向上；最后是前后箱壁阻碍模型土体横向位移变形的摩擦阻力R_c和R_d，方向水平向右。无论是竖向摩擦力还是横向摩擦力，都是模拟研究平面应变问题不需要的作用力，如前所述，箱壁竖向和横向摩擦阻力的影响范围仅局限于邻近箱壁区域的土体，因此，只要模型箱宽度足够，可以忽略它们对模型土体尤其是中间部分土体位移变形的影响。

再看模型箱左右两端壁a和b对模型土体的作用力，由于模型土体处于平面应变受力状态，在垂直于前后侧壁的方向上没有位移变形，因此，土体与端壁之间在这个方向上就没有横向摩擦阻力，因此，图 1所示模型土体左右侧面仅在两个方向上受到端壁阻碍其位移变形的作用力。首先是两端壁阻碍模型土体向下位移变形的摩擦阻力F_a和F_b，方向竖向向上，其影响范围仅局限于邻近端壁区域的土体；其次是两端壁法向限位约束力N_a和N_b，它们限制模型土体在垂直于端壁方向上的位移变形。如图 1所示，端壁刚性限位约束力N_a和N_b，尤其是与模型土体位移变形方向相反的左端壁法向约束力N_a，换算到原型尺度，在数值上强于原型对应位置平面上的作用力。对于大变形破坏性离心模型试验，平面应变模型箱的端壁法向限位约束力对模型土体位移变形性状特别是对破坏性状的阻碍影响，是值得探索研究的，然而，令人遗憾的是，至今尚无这方面的研究报道。本文采用平面应变模型箱进行大变形破坏性离心模型试验时，设置了两种端部边界约束条件，得到了端部不同限位约束条件下的堆场地基极限承载力和所发生的地基推移破坏状况，就此初步探讨了平面应变模型箱端部限位约束程度对离心模型试验再现大变形破坏性状的影响，同时挖掘了模型与原型大变形破坏性状巨大差异的深层原因。

1.   工程概况

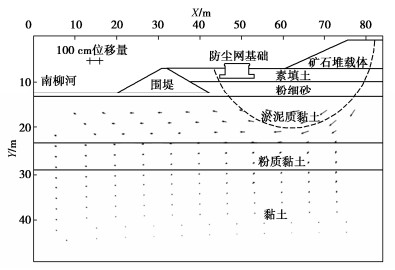
根据该散货码头工程设计资料^[7-9]，散货码头堆场区原场地泥面标高为-0.65~3.76 m，在其上吹填疏浚土至标高5.5 m，再回填砂至标高8.0 m，之后抽真空并联合堆载3 m厚中细砂进行加固处理，卸载时预压荷载约120 kPa。整个散货码头堆场从北至南分别为^#11~^#16堆场，如图 2所示，本工程是位于最南侧的^#16散货堆场，西南侧邻近南柳河，东北侧邻近轨道梁，其长度1271.4 m，宽度54.5 m，堆场面积69291 m²。另外，^#16堆场两侧的地基，则采用水泥搅拌桩复合地基进行加固处理，南柳河围堰和防尘网基础一侧水泥搅拌桩加固宽度为33 m，轨道梁基础一侧水泥搅拌桩加固宽度28.8 m，搅拌桩直径80 cm，间距1.40 m，正方形布置，置换率25.6%，加固深度15 m。该散货堆场所在区域地基土层可分为以下4大层：（1）第四系全新统人工堆填土层(Q4ml)，仅①2素填土；（2）第四系全新统海陆交互相层(Q4mc)，分②1淤泥质黏土、②2粉细砂和②3中粗砂；（3）第四系中更新统土层(Q2)，分③2中粗砂和③4粉质黏土；（4）第四系下更新统地层(Q1)，分④1黏土、④2黏土、④3中粗砂和④5粉细砂。

图  2  ^#16堆场推移区俯视图

Figure  2.  Vertical view of yard No. 16 and cofferdam after restoration

下载: 全尺寸图片 幻灯片

近期^#16堆场在矿石试堆载过程中，临近1#跨河桥的一段长度约148 m堆场地基发生了往南柳河一侧的岸坡推移，往南柳河推移推出宽度0~20 m。图 2是按推移后地形所修筑的永久围堰和反压护坡照片，可见，南柳河围堰岸坡受推移发生了明显的挤出。^#16堆场发生岸坡推移现象后，重新开展了补充勘察^[10]，该区域钻孔ZK9揭示的淤泥质黏土层厚达9.9 m，表明推移区域正是堆场地基淤泥质黏土层厚度最大之处。此处十字板剪试验结果发现淤泥质黏土层的不排水强度平均值约40 kPa，最小值不足30 kPa。该区域标贯击数普遍在2~6击，平均击数约3.9击，根据经验^[11-12]推测的承载力特征值约136 kPa。表 1列出了推移区域地基土层物理力学特性指标，其中淤泥质黏土含水率60.2%，大于液限57.0%，孔隙比1.66，大于1.50，压缩系数1.071 MPa^-1，大于0.5 MPa^-1，其力学特性相当软弱。另外，对^#16堆场两侧水泥搅拌桩进行了质量检测^[13]，判定南柳河围堰和防尘网基础一侧地基中的水泥搅拌桩质量为不合格。^#16堆场修复加固后，设计按一次性达到承载350 kPa的使用要求堆放矿石，已知矿石重度约25 kN/m³，这相当于在堆场表面上要堆放一座底宽54.5 m高度14 m的矿石堆载体。

表  1  地基土层主要物理力学指标

Table  1.  Properties of soil ground

土层	湿密度/(g·cm-3)	含水率/%	孔隙比	液限/%	塑性指数	压缩系数/MPa-1	压缩模量/MPa	凝聚力/kPa	内摩擦角/(°)	不排水强度/kPa
回填土①2	1.91	32.0	0.895	39.4	11.6	—	—	25.1	10.7	—
粉细砂②2	1.85	—	—	—	—	—	—	—	—	—
淤泥质黏土②1	1.63	60.2	1.658	57.0	29.6	1.07	2.69	12.8	13.1	40
粉质黏土层③4	1.84	36.3	1.036	41.0	20.3	0.28	8.99	22.4	15.4	55
黏土层④	1.76	43.9	1.246	49.7	25.3	0.33	7.16	32.6	14.8	67

下载: 导出CSV 

| 显示表格

2.   离心模型试验研究

土工构筑物的自重应力对其应力应变特性影响巨大，能模拟原型自重应力的离心模型试验就成为预测土工构筑物性状、再现破坏现象和验证设计理念的重要手段^[14]。朱维新等^[15]1987年在国内首次开展离心模型试验，研究了深圳五湾码头坍塌，其结果与现场码头后倾坍塌形式一致，从而找出了码头坍塌的原因。为了直观再现该散货码头堆场地基所发生的大变形推移破坏现象，分析掌握滑移破坏的关键因素，为该堆场下一步修复加固提供指导原则，从现场钻取了土样，采用大型平面应变模型箱开展了土工离心模型，设置了两种端部边界约束条件，模拟了矿石堆载体的填筑过程，得到了不同边界约束条件下堆场地基极限承载力和所发生的推移破坏性状。

2.1   模型设计

土工离心模型试验在南京水利科学研究院400g·t大型土工离心机上进行，这台大型土工离心机吊篮平台旋转半径为5.5 m，最大离心加速度为200g，相应最大负荷为20 kN，容量400g·t，所采用的大型平面应变模型箱净空尺寸1200 mm（长）×400 mm（宽）×800 mm（高）^[6]。

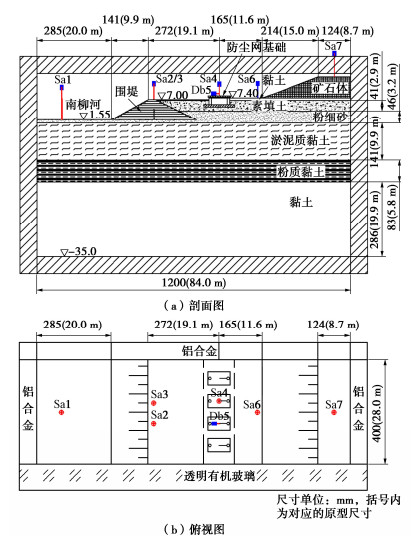
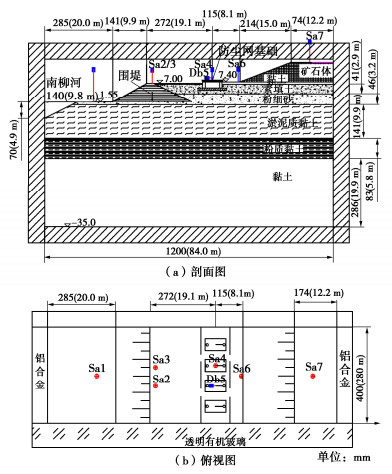
整个离心模型试验布置如图 3所示，试验模拟范围从左向右依次包括一部分南柳河、围堰、防尘网基础、一大半堆载区和其上矿石堆载体。需要指出的是，设计的矿石堆载体原有宽10 m高6 m的下平台和宽8.7 m高14 m的上平台，为节省空间起见，矿石堆载体被简化成梯形状，即仅模拟8.7 m宽14 m高的上平台，但矿石堆载体坡脚、防尘网基础中心和围堰边沿的间距均保持不变，分别为11.6，19.1 m。另外，此处堆场推移前南柳河一侧的地形和围堤护岸构造均参照未出现推移现象处的堆场断面。作为破坏性模型试验，模型布置需要预留足够的滑移长度^[5-6]，故模拟范围从围堰坡脚向南柳河一侧延展预留了20 m的长度空间，约为淤泥质黏土层厚度的两倍，最终这组离心模型的比例尺确定为70，垂直堆场和南柳河方向模拟长度达84 m，顺堆场和南柳河方向模拟长度为28 m，地基土层向下模拟至标高-35.00 m。当模型离心加速度运转到设计加速度70g时，正对8.7 m宽平台的矿石堆载体底部作用于堆场面上的最大竖向荷载就等于350 kPa。

图  3  模型布置（第一次运转）

Figure  3.  Model setup (first running)

下载: 全尺寸图片 幻灯片

2.2   地基土层的制备

对于淤泥质黏土层②1、粉质黏土层③4和黏土层④（合并的④1和④2）三层黏土，按各层原位不排水剪强度平均值作为控制指标，从泥浆沉淀到分级静压固结重塑而成^[16]，而素填土层①2和粉细砂层②2则采用事先配制好含水率的土样控制其密实度，采用分层击实法压密而成。另外，这次模型试验不必考虑南柳河围堤和防尘网基础下的水泥搅拌桩的作用，此处堆场面原有一薄层砂层，模型制备时也代之以黏土料压密填筑。

如图 3所示，所模拟的地基土层由上往下直至标高-35.00 m依次为：①2素填土层，厚度2.9 m，②2粉细砂层，厚度3.2 m，②1淤泥质黏土层，厚度9.9 m，③4粉质黏土层，厚度5.8 m，和④黏土层，厚度19.9 m，模型地基各土层物理力学特性详见表 1。

至于南柳河一侧的充填砂袋围堰，按照模型相似律，模型按比例采用土工滤膜包裹中粗砂，分层填筑压实模拟。另外，原型防尘网基础为混凝土结构，鉴于铝合金与混凝土密度相近，故按比例采用铝合金板块制作了模型防尘网基础结构物，并安放于模型指定位置。另外，南柳河水位受潮汐变化，退潮时河床面基本暴露，此状况对堆场地基和围堰的稳定最为不利，故模型试验时直接模拟南柳河河床面无水暴露情形。

2.3   矿石堆载体的模拟

已知堆放的散装原型矿石料重度为25 kN/m³，通常一个月试堆至14 m，若模型采用原型矿石料填筑，模型矿石堆载体高度为200 mm，为了减小模型矿石堆载体占有空间，降低其填筑高度，模型试验采用重度可达60 kN/m³的铅丸料来模拟原型矿石料进行填筑，这样，模型矿石堆载体高度仅83 mm左右（图 3）。离心机运行时，矿石堆载体作用在堆场表面的荷载值就等于模型矿石堆体高度、重度和离心机速度水平（即离心机速度与自重加速度比值）三者之乘积，已知模型运转到70g条件下，其模型矿石堆载体最大竖向荷载与原型完全一致，为350 kPa，根据这一荷载等效原理^[14]，就可以计算出模型矿石堆载体所需的铅丸质量。

2.4   模型测量

这组离心模型试验重点测量南柳河河床面沉降、围堤顶面沉降、防尘网基础沉降和水平位移、矿石堆载体坡脚前沉降以及矿石堆载体平台顶部沉降，同时重点观察测量矿石堆载体作用下整个堆场地基剖面上发生的位移矢量场。所采用的非接触高精度激光位移传感器，为德国Venglor公司生产，量程50 mm，精度20 μm，同时采用最先进PIV图像分析方法^[17]，拍摄捕捉模型堆场地基剖面试验前后的位移变形情况。通过模型离心机速度提升过程中各测点处沉降和水平位移发展变化的突变转折点，来确定推移区堆场推移前此处地基极限承载力大小，同时通过此处堆场地基剖面在矿石堆载体作用下的位移矢量场，来确定地基土层中各处发生位移方向和大小以及推移破坏发生的区域深度范围。

2.5   试验步骤

（1）模型地基制备，如图 3所示，重塑土样是在模型箱内由下往上逐层制备的，并控制其与原型地基对应土层土体特性对应一致（表 1）。之后将制备好的模型地基置于离心机吊篮平台，启动离心机至设计加速度70g，保持设计加速度持续运行120 min，让整个模型地基恢复自重应力。停机后在模型地基左上部开挖，形成南柳河，并用土工滤膜包裹中粗砂分层填筑，模拟原型的充填砂袋围堰，又在模型指定位置区域安放防尘网基础模型（图 3）。

（2）在模型地基另一侧的堆场区域，按图 3所示形状堆放铅丸体，以模拟矿石堆载体。

（3）安装和调试位移传感器，如图 3所示，在模型表面自左往右安装布置了7只激光位移传感器，分别位于南柳河河床沉降测点Sa1、围堤堤顶沉降测点Sa2和Sa3、防尘网基础沉降测点Sa4和水平位移测点Db5、矿石堆载体坡脚前沿沉降测点Sa6和矿石堆载体顶部沉降测点Sa7。

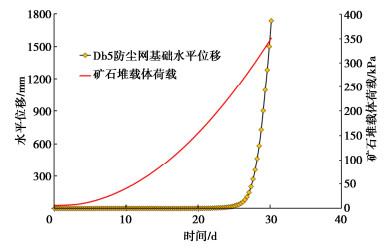
（4）模拟矿石堆载体的填筑，近似匀速升高模型离心加速度，相当于加高矿石堆载体的高度，当达到设计加速度70g时，就相当于原型30 d时矿石堆载体荷载达到设计值350 kPa，如图 4，5所示。

图  4  堆场沉降和矿石堆载体荷载随时间发展变化过程曲线（第一次运转）

Figure  4.  Development curves of settlement of terminal yard and load of ore heap with time (first running)

下载: 全尺寸图片 幻灯片

图  5  防尘网基础水平位移和矿石堆载体荷载随时间发展变化过程曲线（第一次运转）

Figure  5.  Development curves of horizontal displacement of dust screen footing and load of ore heap with time (first running)

下载: 全尺寸图片 幻灯片

（5）停机测量，尽管模型从高速运转状态降速转入停机状态，整个地基土体因应力释放而出现竖向回弹现象，此时模型中所保留的变形为不可恢复的残余变形。由于回弹变形在总变形量中所占的比例总是很小，试验过程中矿石堆载体荷载作用下所发生的变形，特别是地基土层中反映推移破坏迹象的水平位移，大部分被保留下来，因此对停机后的模型加以拍摄和测量，不仅可以发现一些重要的变形特征如裂缝等，而且可以获得模型剖面上的位移矢量图，从而有助于确定滑动破坏面性状和位置。

3.   模型试验结果和分析

下面所介绍的离心模型试验结果和分析中，模型实测结果已经根据离心模型相似率^[14]，将其换算成原型尺度的对应数值，并且这里规定竖向变位即沉降向下为正，又规定水平位移指向南柳河一侧为正。这组离心模型试验共运转了两次，每次提升离心加速度至设计值70g，即模拟原型堆场地基表面30 d内堆载加荷至设计值350 kPa，下面首先介绍第一次运转得到的离心模型试验结果，即模型箱端部限位约束未作调整前的离心模型试验结果。

3.1   第一次运转试验结果和分析

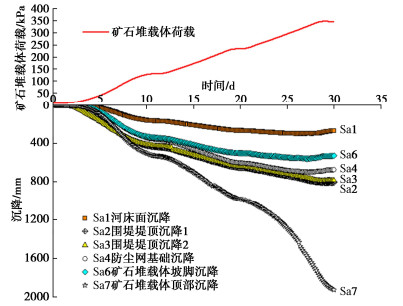
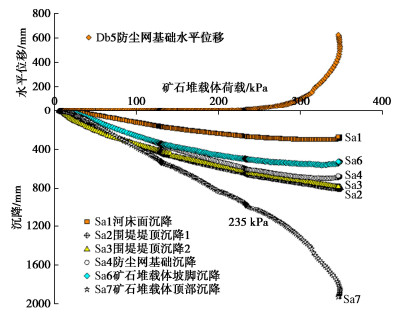
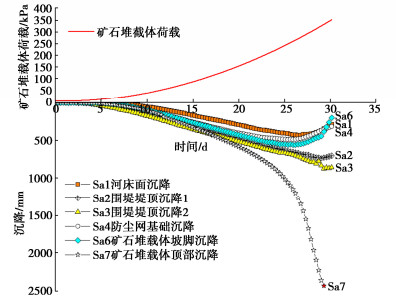
图 4给出了矿石堆载体荷载和堆场各处表面沉降发展变化过程曲线，很显然，矿石堆载体荷载随时间近乎线性升高，期间南柳河河床面沉降测点Sa1、围堤堤顶两沉降测点处Sa2和Sa3、防尘网基础沉降测点Sa4和矿石堆载体前沿沉降测点Sa6这5个测点处的沉降发展规律大体相似：前5 d沉降变形先随时间缓慢增长，之后随时间近乎线性增长，20 d时矿石堆载体荷载约达235 kPa，此后沉降变形随时间增长缓慢下来，并且进一步转为负增长，沉降曲线形状由下凹、平缓最后缓缓上翘，换言之，沉降发展速率随时间减小并转为负值，即由绝对沉降转为相对隆起，表明这些沉降测点所在处的堆场地基已由先前的稳定状态进入另一种状态。至于矿石堆载体顶部沉降测点Sa7，其沉降数值前期近乎随时间线性增大，但20 d后的沉降曲线陡然下转，沉降发展速率越来越大，沉降由线性增长转为骤然飙升，表明矿石堆载体已完全失去稳定。

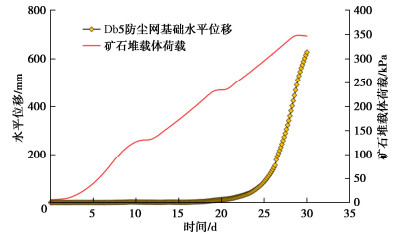
图 5给出了矿石堆载体荷载和防尘网基础水平位移随时间的发展变化过程曲线，前20 d防尘网基础发生的水平位移数值很小，但20 d之后防尘网基础的水平位移曲线越来越上翘近乎陡然上翘，即水平位移发展速率越来越大，不久水平位移超出防尘网基础侧移允许值200 mm，表明防尘网基础由稳定状态转入失稳状态。

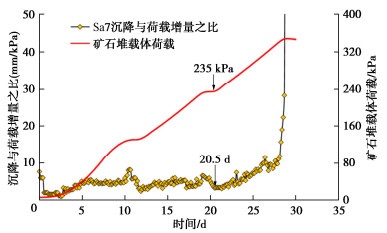
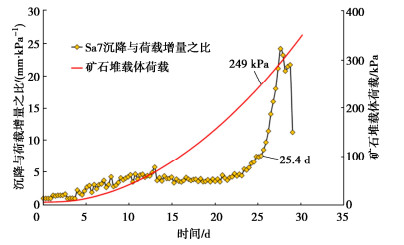
为了进一步确定堆场地基的极限承载力，绘制矿石堆载体顶部沉降测点Sa7的沉降与荷载增量之比和矿石堆载体荷载随时间的发展变化过程曲线（图 6）。从图中测点Sa7沉降与荷载增量之比变化曲线可见，自加载开始至20.5 d期间，该比值上下波动，最大值约8 mm/kPa，之后又变小，在20.5 d时达到一低值，约3.2 mm/kPa。但20.5 d后，比值逐渐增大至11 mm/kPa，最后出现飙升，表明过了20.5 d这个时间节点，矿石堆载体已经失去稳定。矿石堆载体失稳一定是堆场地基沉陷所致，表明地基承载力此时已经达到极限，因此，20.5 d就是矿石堆载体增高过程中的转折点，此时间节点所对应的矿石堆载体荷载值是235 kPa，可近似作为此处堆场地基的极限承载力。

图  6  码头堆场临界承载力的确定（第一次运转）

Figure  6.  Determination of critical bearing capacity of terminal yard ground (first running)

下载: 全尺寸图片 幻灯片

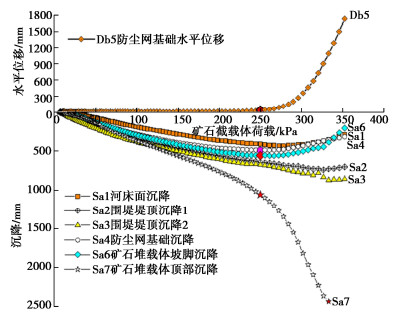
图 7给出了堆场表面上6个测点和防尘网基础水平位移随矿石堆载体荷载变化过程曲线，图 7中曲线类似于现场荷载试验的压力与沉降曲线，从图 7中可以看出，前面确定的极限承载力值点（235 kPa），正是这些承载力曲线的临界转折点荷载值，沉降测点Sa7和水平位移测点Db5两曲线上表现尤为明显。

图  7  堆场沉降和防尘网基础水平位移随矿石堆载体荷载变化过程曲线（第一次运转）

Figure  7.  Development curves of settlement of terminal yard and horizontal displacement of dust screen footing with pressure under ore heap (first running)

下载: 全尺寸图片 幻灯片

已知该区域堆场地基的极限承载力值，按照现有的地基承载力规范，此处堆场地基的承载力特征值仅为112 kPa左右，与前面按标准贯入击数推测的承载力特征值136 kPa相接近，远低于堆场设计使用值350 kPa，因此，对该堆场实施地基加固是非常必需的。

参考文献[6，17]中分析方法，采用试验前后所拍摄的模型剖面图片，开展PIV图像分析处理，获得了图 8所示的堆场地基剖面位移矢量图，需要说明的是，图中位移矢量也已经换算到原型尺度。从图 8中首先看到，堆场地基土层中受矿石堆载体竖向荷载作用位移变形最大的就是淤泥质黏土层，该土层中发生的位移矢量，其长度和方向都非常明显，尤其是位移矢量长度远大于下卧的粉质黏土层和黏土层中发生的位移矢量。

图  8  地基剖面位移矢量图（第一次运转）

Figure  8.  Map of vectors of soil movement and sliding surface (first running)

下载: 全尺寸图片 幻灯片

其次，就淤泥质黏土层而言，矿石堆载体正下方区域的淤泥质黏土发生的位移最可观，最大位移量约100 cm，水平位移和竖向位移分量都很显著，并且竖向位移分量向下；矿石堆载体坡脚正下方区域的淤泥质黏土也发生了相当可观的位移，水平位移分量为主，竖向位移分量很小；防尘网基础至围堤下方区域淤泥质黏土同样发生了明显的位移，仍是水平位移分量为主，但竖向位移分量向上，表明此处的淤泥质黏土层发生了向上的隆起；围堤以外南柳河下方区域淤泥质黏土也发生了位移，基本上是水平位移分量为主。

最后，可以粗略看出，从矿石堆载体到淤泥质黏土层，从右往左已隐约形成了一条圆形滑弧，包括下滑段、平移段和隆起段，如图 8中的虚线所示，而南柳河一侧下方区域淤泥质黏土层土体则继续保持着一定的水平侧移趋势，只因模型箱端壁法向限位约束而不能展示。

概括来说，矿石堆载体正下方区域的淤泥质黏土层发生了明显的沉降，同时伴有一定指向南柳河侧的侧向移动，进而迫使介于矿石堆载体与防尘网基础之间下方区域的淤泥质黏土层向南柳河侧水平位移和向上隆起，一条滑动圆弧已经从右侧矿石堆载体和下卧淤泥质黏土层中形成，从中间防尘网基础附近穿出，而围堰和南柳河下方区域的淤泥质黏土层土体则蓄积着指向南柳河侧的水平位移之势。

3.2   第二次运转试验结果和分析

第一次运转的离心模型试验结果发现，在矿石堆载体升高过程中，堆场地基尤其是淤泥质黏土层发生了沉降变形，并且形成了一条圆形滑弧滑动破坏面，发生的最大位移量近100 cm，但与原型出现的0~20 m的推移距离相比，离心模型试验所再现的推移破坏程度还远远不够，同时看到围堤和南柳河下方区域的淤泥质黏土层土体中积聚着明显的指向南柳河侧的水平侧移之势（图 8）。模型与原型中所发生的推移破坏程度上的差异显然与平面应变模型箱端壁法向限位约束密切关系，若能适当解除模型箱端部限位约束，消除模型堆场地基土体侧移滑动时不该受到的侧向阻力，模型地基中发生的滑移破坏程度有望得到更充分的再现。

基于上述考虑和分析，首先在紧挨模型箱左端壁的南柳河河床上开挖了一条断面为三角形的沟槽，槽宽140 mm，最深70 mm，如图 9所示。该沟槽换算到原型尺度，宽度9.8 m，最深4.9 m，这沟槽底最深处接近淤泥质黏土层中心位置，这样等于解除了一部分模型箱左端壁法向限位约束力对淤泥质黏土滑移土体的拦阻作用。其次拓展模型矿石堆载体作用范围50 mm（图 9），相当于整个原型矿石堆载体向防尘网基础一侧拓宽了3.5 m，矿石堆载体平台宽度由原先8.7 m增加到现在的12.2 m，平台宽度净增3.5 m，换言之，矿石堆载体作用区域比先前增宽了3.5 m，这样一定程度上减小模型箱右端壁竖向摩擦对矿石堆载体竖向荷载传递的阻碍作用，让矿石堆载体荷载作用更充分传递到下卧地基土层上。再次开启离心机进行了第二次运转试验，模拟原型30 d内矿石堆载体加荷至350 kPa，其试验结果和分析如下。

图  9  模型布置（第二次运转）

Figure  9.  Model setup (second running)

下载: 全尺寸图片 幻灯片

图 10是第二次运转试验中矿石堆载体荷载和堆场表面沉降随时间发展变化过程曲线，前10 d整个堆场表面各测点的沉降数值不大，10 d后沉降数值开始明显增大，但约25.4 d，也就是矿石堆载体荷载约249 kPa后，除矿石堆载体顶部测点Sa7外，其它五个测点的沉降曲线陆续发生转折，由下凹转为上翘，即沉降数值不增反减，表明堆场这些测点处位移变形由下沉转为隆起，表明堆场地基由此从稳定状态转入失稳状态。矿石堆载体顶部沉降测点Sa7曲线从25.4 d起转为陡降，沉降发展速率越来越大，沉降量急速增大，超出传感器量程（图 11），由此表明矿石堆载体已经坍塌失稳。

图  10  堆场沉降和矿石堆载体高度随时间发展变化过程曲线（第二次运转）

Figure  10.  Development curves of settlement of terminal yard and load of ore heap with time (second running)

下载: 全尺寸图片 幻灯片

图  11  矿石堆载体高度和防尘网基础水平位移随时间发展变化过程曲线（第二次运转）

Figure  11.  Development curves of horizontal displacement of dust screen footing and load of ore heap with time (second running)

下载: 全尺寸图片 幻灯片

图 11给出了第二次运转试验中矿石堆载体荷载和防尘网基础水平位移随时间发展变化过程曲线，其变化规律与第一次运转试验中的情形类似，前25.4 d防尘网基础水平位移量很小，但25.4 d矿石堆载体荷载约达249 kPa后，防尘网基础水平位移开始陡然增大，水平位移量很快超出防尘网基础侧移允许值200 mm，即防尘网基础出现了不可容许的侧向移位。

同样为了确定堆场地基的极限承载力，绘制了图 12所示的矿石堆载体荷载和顶部沉降测点Sa7的沉降与荷载增量之比随时间发展变化过程曲线。从图 12中沉降与荷载增量之比发展变化曲线可见，25.4 d这个时间节点之后该比值急速增大，即从7.5 mm/kPa快速升至24.3 mm/kPa，表明过了25.4 d这个时间节点，矿石堆载体已经不能保持稳定，完全失去稳定，因此，25.4 d就是矿石堆载体加荷过程中的转折点，此时矿石堆载体荷载值249 kPa即为堆场地基的极限承载力。

图  12  码头堆场临界承载力的确定（第二次运转）

Figure  12.  Determination of critical bearing capacity of terminal yard ground (second running)

下载: 全尺寸图片 幻灯片

图 13是6个表面测点处的沉降和防尘网基础水平位移随矿石堆载体荷载变化过程曲线，从上下两幅图中曲线可以看出，上述确定的地基极限承载力正好对应这些曲线转折点的荷载值，防尘网基础沉降测点Sa4和水平位移测点Db5以及矿石堆载体坡脚坡顶测点Sa6和Sa7四条曲线转折点尤为显著。这样，第二次运转所求得的此处堆场地基的极限承载力为249 kPa，相应的承载力特征值仅仅约为124 kPa，这个承载力特征值与第一次运转所获得的非常接近，表明这组离心模型两次运转试验结果是一致可靠的。

图  13  堆场沉降和防尘网基础水平位移随矿石堆载体荷载变化过程曲线（第二次运转）

Figure  13.  Development curves of settlements of terminal yard and horizontal displacement of dust screen footing with pressure under ore heap (second running)

下载: 全尺寸图片 幻灯片

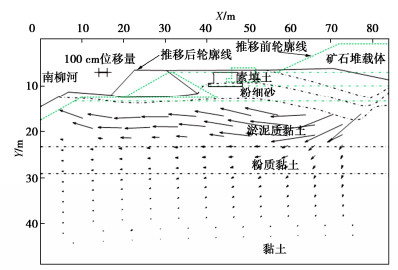
根据第二次运转试验前后的模型剖面图片，开展了PIV图像分析处理，得到了图 14所示的堆场地基剖面位移矢量图，从中可以看到堆场地基尤其是淤泥质黏土层位移量非常显著，伴随着非常明显的滑动推移破坏。从图 14中所示试验前后的堆场表面轮廓线和土层分界面的位置变化就可以看到，经过第二次运转，首先是矿石堆载体和下方的堆场地基面发生了明显的塌陷变形。其次防尘网基础向南柳河一侧发生了显著的侧移，水平位移量超出了200 cm；围堤同样也向南柳河一侧发生了较为显著的侧移，水平位移量更是超出了300 cm。最后南柳河河床发生了明显的侧移和隆起。矿石堆载体下方的堆场地基中的素填土层和粉细砂层分界面以及粉细砂层和淤泥质黏土层分界面，发生了150~300 cm量级凹陷变形，下沉的这两层土体挤占了下卧淤泥质黏土层土体的空间，迫使这层软土向南柳河一侧继续推移。与第一次运转试验结果相比，第二次运转模型试验结果更充分地再现了矿石堆载体和地基土层中所发生的推移破坏现象。

图  14  地基剖面位移矢量图（第二次运转）

Figure  14.  Map of vectors of soil movement and sliding surface (second running)

下载: 全尺寸图片 幻灯片

再看推移破坏形成机制，从右往左分析图 14中淤泥质黏土层的位移变形，矿石堆载体下方的淤泥质黏土层土体发生的位移已经达到400~500 cm量级，其水平位移分量大于竖向位移分量；矿石堆载体坡脚下方区域的淤泥质黏土层土体中发生的位移更是达到550 cm量级，水平位移分量占主导；介于矿石堆载体坡脚和围堤中心之间正下方区域的淤泥质黏土层土体发生的位移量介于350~430 cm量级，水平位移分量为主，但竖向位移分量为负值，即方向向上，表明此区间淤泥质黏土层土体发生向上的隆起；介于围堤中心和南柳河河床之间下卧淤泥质黏土层土体发生的位移量介于250~300 cm量级，位移方向几乎水平，即为明显的侧向推移，但挨近最左侧河床沟槽下卧的淤泥质黏土层土体发生的位移，其竖向位移分量方向向上，即此处既发生了明显的侧移又发生了一定的隆起。总而言之，淤泥质黏土层土体最大位移量已经达到550 cm量级，并且水平位移分量为主；上覆矿石堆载体的巨大竖向荷载作用下，浅表两层土体向下沉降，发生了十分严重的凹陷，挤占了下卧的饱和软弱的淤泥质黏土层空间，进而引发该软土层土体向没有堆载的南柳河一侧位移变形，最终导致堆场地基侧向滑动推移破坏。

3.3   模型箱约束对大变形破坏离心模型试验影响初探

如前所述，该散货码头堆场地基推移破坏发生的区域正是堆场地基淤泥质黏土层厚度最大之处，此处堆场地基承载能力基本上为深厚软弱的淤泥质黏土层承载力所控制。这组离心模型两次运转试验的结果发现此处堆场地基极限承载力分别约235，249 kPa，相应的承载力特征值分别约114，124 kPa，与按标准贯入击数推测的承载力特征值136 kPa相近，因此，离心模型试验很好地预测了原型堆场地基的承载力特征值。

然而这组离心模型两次运转试验所再现的推移破坏状况远不如原型堆场地基发生的推移破坏严重，原型堆场地基中淤泥质黏土层发生的最大位移达20 m量级。模型箱端部法向约束未作解除的第一次运转的离心模型试验，再现的滑移破坏现象中淤泥质黏土发生的最大位移约为100 cm，即1 m量级；模型箱端部法向约束部分解除的第二次运转的离心模型试验，再现的滑移破坏现象中淤泥质黏土发生的最大位移达到550 cm，即5.5 m量级。可见，模型箱端部法向约束部分解除前后两次运转试验再现的推移破坏程度有着显著的不同，换言之，部分解除平面应变模型箱端部法向限位约束能够在更大程度上再现原型堆场地基中发生的推移破坏现象，平面应变模型箱端部法向限位约束的影响是相当显著的。

端部法向限位约束本质上是模型箱长度有限所致，另一个容易被忽略的深层原因，乃是大变形三维破坏问题被简化成二维平面问题模拟所致的。严格地说，原型堆场地基中发生的大变形推移破坏已不是一个平面应变二维问题，而是一个三维问题，原型发生的大变形推移破坏涉及长度148 m的堆场，推移破坏舌状滑动面最前沿的推移距离之所以能够达到20 m，是因为两侧淤泥质黏土层不断地向最前沿舌状滑动面补充土料，如果土料补充一旦被阻隔，舌状前沿就不会继续向南柳河侧推进。若按模型比尺70去模拟这样一个大变形三维破坏现象，所需要模型箱宽度至少需要达到2114 mm，这是难以实现的。而宽度400 mm的平面应变模型箱所模拟的堆场长度是28 m，还不足原型推移破坏长度148 m的五分之一。模型箱前面侧壁对应到原型，就如同两道刚性阻隔墙，它们阻隔了前后两侧淤泥质黏土层土体向中间正在推移滑动土体进行土料补充，舌状前沿向南柳河侧推移的距离必然大大受到抑制。平面应变模型中土体破坏推进过程土料补充不足本质上是模型箱宽度有限所致，这就解释了第二次运转的离心模型试验所展示的推移破坏程度仍不及原型所发生的大变形推移破坏。

总结来说，对于试图再现原型破坏性状的离心模型试验来说，必须充分考虑模型箱箱壁对模型土体存在着横向与竖向摩擦阻碍约束、法向限位约束、和箱壁阻隔。首先前后侧壁面上的摩擦尤其是横向摩擦在邻近箱壁一定范围阻碍破坏土体的位移变形，影响舌状前沿滑动面的形状。其次模型箱左右端壁的法向限位约束更是直接阻碍破坏土体的推进，限制破坏土体的位移变形量。第三，大变形三维破坏问题被简化成二维平面问题模拟，模型箱宽度模拟的长度往往小于原型破坏现象覆盖的长度，前后箱壁截断破坏土体舌状面的土料补充，这在更大程度上抑制破坏土体整体推进，限制了破坏土体推移的位移变形，降低了推移破坏现象的严重程度。

4.   结语

采用大型平面应变模型箱开展了离心模型试验，尝试再现某散货码头堆场地基的大变形推移破坏现象，发现模型箱端部法向约束部分解除前后两次运转试验预测的原型堆场地基的极限承载力值一致，但再现的推移破坏程度有着显著的不同，部分解除端壁法向限位约束有助于再现原型大变形推移破坏程度，端部法向限位约束本质上是模型箱长度有限所致。

即使部分解除模型箱端部法向限位约束，其离心模型试验再现的推移破坏程度仍不及原型，这另一个深层原因是模型箱宽度有限，前后箱壁如同两道墙体，截断了两侧土体向正在推进舌状变形破坏土体的土料补充，这在更大程度上削弱了推移破坏现象的严重程度。

对于试图再现原型大变形破坏性状的离心模型试验来说，必须考虑模型箱箱壁摩擦、箱体长度和宽度有限等三方面的约束影响。模型箱箱壁摩擦会改变了土体前沿舌状滑动面的形状；箱体长度有限构成的法向限位阻碍，直接限制了土体滑动位移量；箱体宽度有限使得模拟的宽度范围往往小于原型，造成土体破坏过程中土料补充不及原型，破坏土体推进的距离和发展的严重程度自然不及原型。