Three-dimensional stability analysis of shied tunnel face adjacent to existing tunnels
-
摘要: 针对近接既有隧道条件下的盾构施工开挖面稳定性问题，采用数值模拟和三维理论分析方法进行深入研究。通过数值模拟手段获取了近接既有隧道的盾构开挖面破坏模式，据此提出了改进的三维旋转破坏理论模型。研究结果表明，近接既有隧道的盾构开挖面破坏模式主要受开挖面与既有隧道的相对水平距离(s/D)影响，当-1 < s/D < 0.5时，开挖面破坏模式呈截面为椭圆的对数螺旋体。提出的对数螺旋体+椭圆柱的三维破坏模型可以反映开挖面失稳扩展沿隧道纵向和横向的非均匀性，因而能够更准确地分析开挖面稳定性。参数分析表明，盾构隧道开挖面极限支护力对土体强度最为敏感，其次是隧道埋深和近接距离。在一定埋深和近接距离范围内(C/D = 2.0~3.0和d/D = 0.5~1.0)，当土体黏聚力不变时，开挖面极限支护力随土体内摩擦角增加呈现先增后减的趋势，内摩擦角临界值约为11°~13°。Abstract: Aiming at the stability of the shield tunnel face adjacent to an existing tunnel, the numerical simulation and three-dimensional theoretical analysis methods are used for in-depth research. The failure modes of the shield tunnel face are obtained through numerical simulation. The results show that the failure mode of shield tunnel face adjacent to the existing tunnel is mainly affected by the distance between the tunnel face and the existing tunnel (s/D), and it looks like a logarithmic spirochete with elliptical section when -1 < s/D < 0.5. The proposed three-dimensional failure model which is composed of logarithmic spiral body and elliptic column can reflect the non-uniformity of the instability expansion along the longitudinal and transverse directions, respectively, hence, the analytical results of the tunnel face stability may be more accurate. The parameter analysis indicates that the limit support pressure of the shield tunnel face is the most sensitive to the strength parameters of soils, followed by the buried depth and adjacent distance. The limit support pressure of the tunnel face increases first and then decreases with the increase of the internal friction angle when the cohesion of soils remains unchanged within a certain buried depth and adjacent distance (C/D = 2.0 ~ 3.0 and d/D = 0.5 ~ 1.0), and the critical value of the internal friction angle is about 11°~13°.
-
Keywords:
- shield tunnel face /
- existing tunnel /
- stability /
- failure mode /
- analytical model
-
0. 引言
维持开挖面稳定性是确保盾构施工安全的关键，在盾构施工中若开挖面支护力等施工参数设置不当，将会诱发开挖面失稳，造成地表的沉降[1]。近年来，中国城市地下工程建设迅速发展，出现了越来越多的新建隧道近接既有隧道施工案例[2]。盾构隧道近接施工的力学行为更加复杂，施工风险更加突出。与常规单一隧道不同，近接施工中的盾构开挖面稳定性分析受既有结构、近接形式和近接距离等因素的影响，因而呈现出多体、多形式、多过程的特点。当前针对近接施工盾构开挖面稳定性分析的研究成果匮乏，理论依据尚不完善，给盾构近接施工带来较大风险。
盾构隧道开挖面稳定性问题已成为地下工程施工安全研究的重点。国内外学者从模型试验、理论分析和数值模拟等方面开展了大量的研究。模型试验是研究盾构开挖面失稳破坏的主要手段之一，基于离心模型试验、大尺寸模型试验和小尺寸透明土模型试验等方法，学者们得到了砂土地层的烟囱状破坏模式[3]和黏土地层的盆状破坏模式[4]。在理论分析方面，学者们基于极限状态分析方法(极限平衡法和极限分析法)提出了二维及三维的失稳破坏模型，包括二维锥形模型[5]、二维对数螺旋线模型[6]、三维对数螺旋体模型[7]、经典三维楔形体模型[8]、各类改进的棱柱体-楔形体模型[9-11]、Torus模型[12]和三维水平球缺形模型[13]等。二维模型和楔形体模型由于过于简化，因而计算结果误差较大，而三维旋转破坏理论考虑了破坏体三维空间形态，并且可用于砂土和黏土地层，因而具有明确的物理意义，准确性高，适用性广。近年来已有研究考虑不同影响因素对三维旋转破坏理论进行了改进，如Zou等[14]考虑土拱效应影响，将对数螺旋线旋转模型在隧道拱顶以上部分修正为半椭球体；Ibrahim等[15]考虑开挖面位于成层土地基，采用分段的对数螺旋形进行修正；Li等[16]考虑渗流的影响，将水头方程引入三维旋转模型。然而，考虑近接既有隧道条件下的盾构开挖面稳定性问题及其相关计算方法还鲜见报道，因而本文基于近接既有隧道条件下开挖面破坏模式，对三维旋转模型的截面形状进行修正，可用于深入分析近接施工的盾构开挖面稳定性。
数值模拟是确定盾构隧道开挖面破坏模式的主要手段之一，主要包括有限元法(FEM)、有限差分法(FDM)和离散元法(DEM)等。有限元法在计算大变形时可能会出现网格畸变导致计算不收敛。离散元法虽然对大变形问题处理较好，但计算效率较低，并且对于足尺模型无法还原土体的真实粒径。有限差分法作为隧道围岩变形计算的常用方法，具有求解速度快，计算精度高和可处理大变形等优势而被广泛应用。
本文基于FLAC3D有限差分软件揭示了近接既有隧道条件下的盾构开挖面破坏模式，构建了考虑水平方向破坏扩展不均匀性的对数螺旋体+椭圆柱的开挖面稳定性三维理论分析模型，给出了考虑土体黏聚力和重度影响系数的开挖面极限支护力表达式。分析了近接距离、隧道埋深和地层参数等因素对近接既有隧道条件下的盾构开挖面极限支护力的影响。
1. FLAC3D数值模拟
1.1 数值模型建立
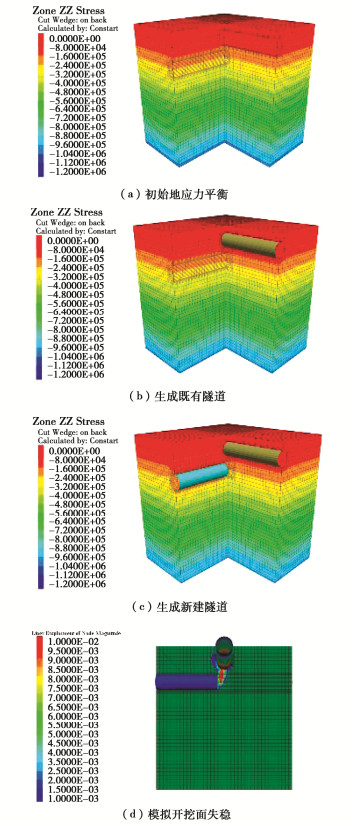
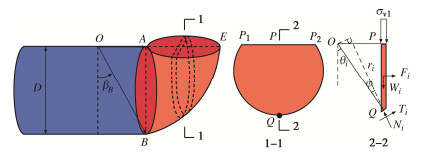
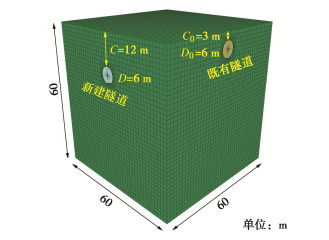
对于单隧道条件，可以建立半模型以节约计算资源，但本文主要考虑近接施工条件，若采用半模型会截断既有隧道，不利于设置边界条件，因此采用全模型进行数值模拟分析。为尽可能地削减边界效应，模型尺寸取为10倍盾构直径(D = 6 m)，如图 1所示。
模型边界条件设置为：地表为自由边界，侧面为固定水平位移边界，底面为固定边界。土体选用基于Mohr–Coulomb准则的弹塑性本构模型。数值模型物理力学参数如表 1所示。不同地层条件下的土体参数根据Mollon等[17]的建议取为4种，分别对应松砂、密砂、软黏和硬黏。土体的弹性模量根据不同土性分类进行取值[18]。隧道结构(新建隧道与既有隧道)均采用衬砌结构单元(Liner)，厚度取为0.35 m。注浆层采用泥浆的相关参数。利用六面体单元划分网格，模型建立完成后，共有79360个单元，83681个节点。
类别 重度γ/(kN·m-3) 弹性模量E/MPa 泊松比$ \nu $ 黏聚力c/kPa 内摩擦角φ/(°) 土体 松砂 17.0 17.5 0.397 0 20 密砂 19.5 65.0 0.263 0 40 软黏 16.0 3.5 0.414 7 17 硬黏 18.0 12.5 0.366 10 25 衬砌 混凝土 25.0 33500 0.20 — — 注浆层 泥浆 12.0 50 0.49 — — 模型生成后，首先施加重力加速度，使模型整体达到初始地应力平衡状态。其次，开挖既有隧道并施加衬砌，并再次进行地应力平衡。随后，开挖新建隧道至既有隧道附近并在开挖面处施加与初始水平地应力持平的支护力。本文针对盾构开挖面失稳破坏这一特定阶段进行研究，因此简化盾构施工过程，采用一次性开挖到位的形式。最后采用逐渐降低支护力的手段模拟开挖面失稳，这是由于在实际工程中，开挖面失稳往往是由于支护力不足导致的，即主动破坏模式。通过逐级降低开挖面支护力(共取20级)，待每级支护力下模型运算至平衡状态或出现塑性流动后方可调整为下一级支护力[19]，直至支护力降为0。具体模拟过程如图 2所示。近接条件下由于设定既有隧道在新建隧道上方，限制了土体的变形发展，因而此时破坏模式的主要影响因素应为隧道间距，而非埋深，故在近接条件下暂不考虑埋深的影响。具体模拟方案如表 2所示。
表 2 数值模拟方案Table 2. Scheme of numerical simulations土体类别 近接形式 新建隧道埋深比C/D 隧道垂直净距比d/D 开挖面水平间距比s/D 松砂 无 1.0，1.5，2.0 — — 密砂 松砂 新建隧道垂直下穿既有隧道 2.0 0.25，0.50，0.75 -1，-0.5，0，0.5 密砂 软黏 硬黏 注：隧道垂直净距比d/D为新建隧道上表面与既有隧道下表面的垂直距离d与新建隧道直径D之比；开挖面水平间距比s/D为新建隧道开挖面与既有隧道中心轴线的水平距离s与新建隧道直径D之比，负值表示盾构尚未穿越既有隧道中心轴线。 在模拟过程中，由于盾构开挖面支护力逐渐降低，开挖面土体产生朝向隧道内部的位移，但位移分布并不均匀，为了统一量化开挖面位移随支护力的变化情况，通过FISH函数获取开挖面各节点位移的平均值，以此作为盾构开挖面的代表性位移。
1.2 数值模型建立
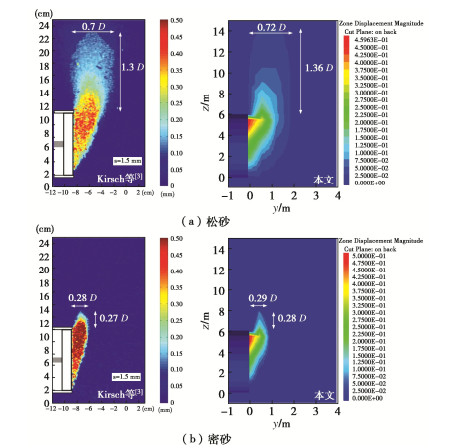
为了验证数值模拟中采用的本构模型和参数的适用性和正确性，选取Kirsch等[3]开展的离心模型试验结果进行对比分析。图 3所示为单隧道条件下，埋深比C/D = 1.5时的变形区域对比。可以看出，离心模型试验中沿开挖面前方和上方的主要变形范围与本文数值模拟结果基本一致，结果相差均在5%以内，因此可以认为数值模型可以较好地还原真实情况。
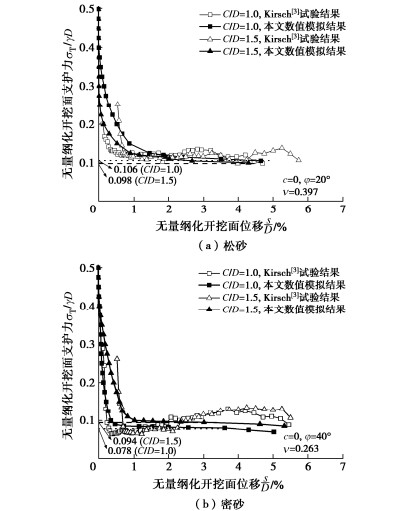
图 4为不同埋深条件下开挖面支护力-位移关系对比结果，其中，虚线为本文单隧道条件下的开挖面极限支护力，取值原则为：当支护力变化不大时，开挖面位移显著增加，认为开挖面发生失稳，此时的支护力即为极限支护力。通过对比可以发现，松砂条件下数值模拟结果和离心试验结果[3]相差不大；而密砂条件下，数值模拟结果未显现出支护力曲线回弹的现象，这是由于离心试验[3]中采用“位移法”(控制开挖面的支护面板以一定速度后退模拟失稳的方法)，初始阶段由于土拱效应使得支护力迅速下降，超过临界位移后，周围土体出现“应变软化”，导致所需支护力回升[20]。而在实际盾构施工中，开挖面失稳的直接原因是支护力的不足，因而采用“力法”(即本文中控制支护力逐级降低的方法)模拟开挖面失稳更加符合实际。
![]()
图 4 无量纲化开挖面支护力–位移关系曲线Figure 4. Relationship between normalized displacement and normalized support force of tunnel face1.3 数值模拟结果
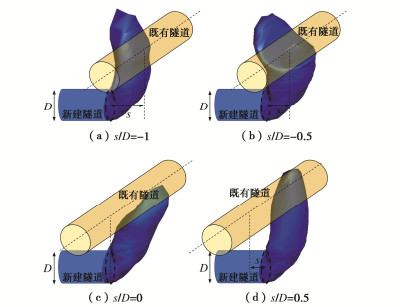
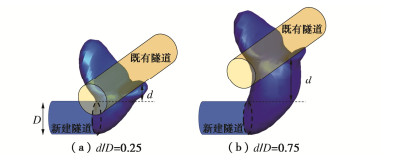
近接条件下(松砂，d/D = 0.5)盾构开挖面失稳变形模式如图 5所示。由于黏性土层失稳滑移时没有明显的剪切带，因此多通过采用位移轮廓线来确定破坏模式的范围[21]。本文参考Li等[22]数值模拟结果，取位移值大于1%盾构直径的区域为破坏模式包络面。由模拟结果可见，随着盾构开挖面接近→穿越→远离既有隧道(s/D逐渐增加)，失稳区呈现出沿开挖方向不对称的特点，这是由于既有隧道与土体刚度差异很大，限制了土体的位移发展。除s/D =-0.5外，其余3种条件下开挖面变形模式均与单隧道情况类似，即由开挖面前方对数螺旋体和上方筒仓状滑动体组合而成。当s/D =-0.5时，开挖面变形呈现出沿既有隧道方向扩展的形态。
![]()
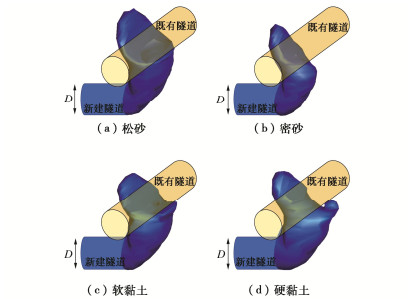
图 5 近接既有隧道条件下开挖面变形模式(不同s/D)Figure 5. Deformation characteristics of shield tunnel face adjacent to an existing tunnel under different s/D不同隧道垂直净距下(松砂，s/D = -0.5)的盾构开挖面失稳模式如图 6所示。垂直净距对破坏模式的影响较小，随着净距的增加，上方破坏影响范围有所增加。不同土性条件下的开挖面失稳模式(d/D = 0.5，s/D = -0.5)如图 7所示，可以发现不同土性中的失稳模式基本一致，只是沿开挖面前方和两侧的扩展范围有所不同：密砂相比松砂向两侧扩展范围更小，黏土相比砂土向前方扩展更大。
![]()
图 6 近接既有隧道条件下开挖面变形模式(不同d/D)Figure 6. Deformation characteristics of shield tunnel face adjacent to an existing tunnel under different d/D![]()
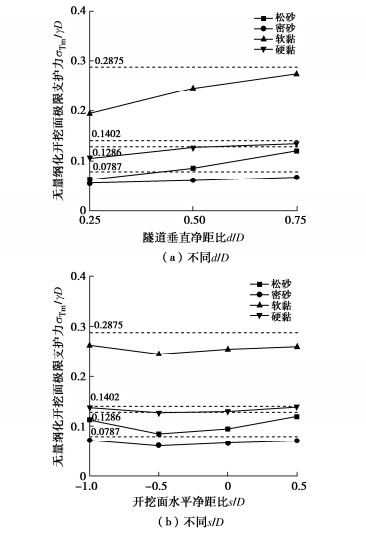
图 7 近接既有隧道条件下开挖面变形模式(不同土性)Figure 7. Deformation characteristics of shield tunnel face adjacent to an existing tunnel under different soil properties近接条件下的开挖面极限支护力如图 8所示。图 8(a)中虚线为相应地层中的单隧道开挖面极限支护力，可以看出既有隧道的存在使开挖面极限支护力有所降低，这是由于既有隧道的刚度远大于土体，在开挖面失稳过程中起到了“支撑”的作用。对于同种地层，随着隧道垂直净距的增加，开挖面极限支护力略有增加，这是由于隧道净距越大，隧道间松动土柱越高，导致松动土压力越大，也就需要更大的支护力。图 8(b)为盾构穿越既有隧道过程中的开挖面极限支护力，可以看出随着开挖面水平间距比s/D逐渐增加，开挖面极限支护力呈现先降低后升高的趋势，在s/D = -0.5时最低，这是由于此时失稳破坏区域与既有隧道的重合区域最大，既有隧道对开挖面前方土体的“支撑”作用最显著，因此所需的极限支护力越低。对于同一工况，软黏土地层的极限支护力最大，这是由于软黏土强度低且破坏范围较大。
![]()
图 8 不同近接距离下开挖面极限支护力Figure 8. Limit support pressures on tunnel face under different adjacent distances2. 三维旋转破坏模型
2.1 理论模型描述
基于数值模拟结果，构建近接既有隧道条件下的开挖面三维旋转破坏模型。对于近接工况，当s/D = -0.5时，开挖面破坏模式受既有隧道的影响最大，因而先依据此工况建立理论模型进行推导。影响开挖面破坏模式的主要因素为隧道净距，但若垂直净距过大，则不符合近接施工条件。因此，为体现近接施工特点，同时参考相关规范中对于近接施工的定义[23]，本文假定隧道垂直净距不大于1倍盾构直径。
根据数值模拟结果，将开挖面破坏模式简化为对数螺旋体+筒仓体，如图 9所示。对于筒仓体部分，为体现沿开挖面前方和两侧扩展范围的差异性，假设其为半长轴、半短轴和高度分别设为a，b和h的椭圆柱；对数螺旋体由对数螺旋线旋转得到，对数螺旋线又称等角螺旋线，曲线上每个点的切向量与对数螺旋线极点至该点所成的向量均成一固定角度[21]，满足
$$ r = {r_0} \cdot \exp \left[ {(\theta - {\theta _0})\tan \varphi } \right] 。 $$ (1) 目前已有一些学者基于对数螺旋体模型开展了盾构开挖面稳定性的相关研究[14, 17]，但其截面被假定为圆形，这在多数情况下与实际不符，且无法与本模型中的上部椭圆体对应，因此本文采用截面为椭圆形的对数螺旋体作为破坏体模型。对数螺旋体具体生成方式为：极角为θ的射线OG与对数螺旋线AH、BE分别相交，以两条对数螺旋线之间线段长度的一半为椭圆半短轴b。假定同一地层中椭圆离心率保持不变，即椭圆长短轴之比不变，设a = kb。则
$$ a = k\frac{{{r_2} - {r_1}}}{2}, {\text{ }}b = \frac{{{r_2} - {r_1}}}{2} 。 $$ (2) 其中，
$$ {r_1} = D\tan {\beta _B} \cdot \exp \left[ {(\theta - {\text{π }}/2)\tan \varphi } \right] \text{，} $$ (3a) $$ {r_2} = D\sec {\beta _B} \cdot \exp \left[ {{\text{(}}\theta - {\beta _B}{\text{)}}\tan \varphi } \right] 。 $$ (3b) 令射线OG与对数螺旋线BE相交于G点，与开挖面中心线AB相交于F点，过F点作平行于x轴的直线F1F2与开挖面圆周分别相交于F1、F2点，截去椭圆F1GF2外侧部分得到椭圆缺形截面，该截面关于FG两侧对称。令极角θ由$ {\beta _B} $增加至π/2，则生成的所有截面叠加即形成对数螺旋体。图 10为近接既有隧道条件下盾构开挖面失稳变形区域的数值模拟结果与理论模型对比，可以看出，所提出的对数螺旋体+筒仓体模型在各个方向上均可较好地拟合实际位移包络面。
2.2 理论模型求解
首先，求解椭圆柱对下部对数螺旋体的土压力。根据图 9所示条分法，并假设土体服从Mohr–Coulomb破坏准则，建立垂直方向受力平衡方程：
$$ {\text{π }}{a_0}{b_0}\gamma {\text{d}}z = {\text{π }}{a_0}{b_0}{\text{d}}{\sigma _{\text{v}}} +\\ \left[ {2{\text{π }}{b_0} + 4({a_0} - {b_0})} \right]{\text{(}}c + K\tan \varphi {\sigma _{\text{v}}}{\text{)d}}z \text{，} $$ (4) $$ \gamma = \sum\limits_{i = 1}^n {{\gamma _i}{h_i}} /({C_0} + {D_0}) 。 $$ (5) 式中：a0，b0分别为椭圆柱的半长轴和半短轴；γ为椭圆柱体上方考虑既有隧道空心影响的土体加权平均重度；γi，hi分别为既有隧道上方各层土体的重度和层厚；c，φ分别为土体黏聚力和内摩擦角；$ K = 1 - \sin \varphi $为土体侧压力系数；$ {\sigma _{\text{v}}} $为竖向土压力。
椭圆柱体上表面压力为既有隧道底部处的土体自重应力，即$ {\sigma _{\text{v}}} $(0) = γ(C0+D0)，其中，C0，D0分别为既有隧道埋深和直径。由式(4)及a = kb可得
$$ {\sigma }_{\text{v}}(z)=\frac{\left[\text{π}k{b}_{0}\gamma -2(\text{π}+2k-2)c\right]\left(1-{\text{e}}^{-\frac{2\left(\text{π}+2k-2\right)K\mathrm{tan}\varphi }{\text{π}k{b}_{0}}z}\right)}{2(\text{π}+2k-2)K\mathrm{tan}\varphi }+\gamma ({C}_{0}+{D}_{0})\text{ }。 $$ (6a) 进而可得椭圆柱体作用在对数螺旋体顶面的竖向力$ {\sigma _{{\text{v1}}}} $(其中柱体高度h取为隧道垂直净距d)：
$$ {\sigma }_{\text{v1}}=\frac{\left[\text{π}k{b}_{0}\gamma -2(\text{π}+2k-2)c\right]\left(1-{\text{e}}^{-\frac{2\left(\text{π}+2k-2\right)K\mathrm{tan}\varphi }{\text{π}k{b}_{0}}d}\right)}{2(\text{π}+2k-2)K\mathrm{tan}\varphi }+\gamma ({C}_{0}+{D}_{0})\text{ }。 $$ (6b) 式中，当$ c \geqslant {\text{π }}k{b_0}\gamma /(2{\text{π }} + 4k - 4) $时，$ {\sigma _{{\text{v1}}}} $取0，b0可由式(2)令θ = π/2得到。
其次，建立对数螺旋体对原点O的力矩平衡方程：
$$ {M_{\text{w}}} + {M_{\text{v}}} - {M_{\text{T}}} - {M_{\text{c}}} = 0 \text{，} $$ (7) 式中：$ {M_{\text{w}}} $为重力力矩；$ {M_{\text{v}}} $为上表面压力$ {\sigma _{{\text{v1}}}} $产生的力矩；$ {M_{\text{T}}} $为开挖面支护力力矩；$ {M_{\text{c}}} $为土体抗力矩。
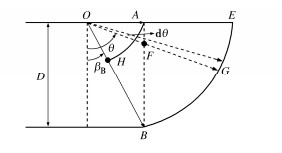
如图 11所示，由于直接计算$ {M_{\text{w}}} $较为复杂，因此采用完整对数螺旋体AHBE重力力矩减去不规则体AHB重力力矩进行计算：
$$ {M_{\text{w}}} = {M_{AHBE}} - {M_{AHB}} 。 $$ (8) 完整对数螺旋体AHBE微元体的重力力矩为
$$ {\text{d}}{M_{AHBE}} = \gamma \cdot {\text{π }}ab\left[ {\frac{1}{2}({r_{\text{1}}} + {r_{\text{2}}}){\text{d}}\theta } \right]({r_2} - b)\sin \theta \text{，} $$ (9) 对式(9)积分得
$$ {M_{AHBE}} = \int_{{\beta _B}}^{\frac{{\text{π }}}{2}} {\gamma \cdot {\text{π }}ab\left[ {\frac{1}{2}({r_{\text{1}}} + {r_{\text{2}}})} \right]({r_2} - b)\sin \theta {\text{d}}\theta } 。 $$ (10) 不规则体AHB可以近似看作底面为正方形的楔形体，根据面积等效原则，其边长为$ \sqrt {\text{π }} D/2 $，则
$$ {M_{AHB}} = \gamma \cdot \frac{1}{2}{\left( {\frac{{\sqrt {\text{π }} D}}{2}} \right)^2}{h_{\text{H}}} \cdot \left( {D\tan {\beta _B} - \frac{{{h_{\text{H}}}}}{3}} \right) \\ {h_{\text{H}}} = D\tan {\beta _B}\left\{ {1 - \exp \left[ {({\beta _B} - {\text{π }}/2)\tan \varphi } \right]} \right\} \text{，} $$ (11) 式中，$ {h_{\text{H}}} $为三角形AHB中底边AB的高。
上表面压力$ {\sigma _{{\text{v1}}}} $产生的力矩$ {M_{\text{V}}} $为
$$ {M_{\text{V}}} = {\text{π }}kb_0^2{\sigma _{{\text{v}}1}}(OE - {b_0}) \text{，} $$ (12) 其中，$ OE = \frac{D}{{\cos {\beta _B}}} \cdot \exp \left[ {\left( {\frac{{\text{π }}}{2} - {\beta _B}} \right)\tan \varphi } \right] $。
开挖面支护力力矩$ {M_{\text{T}}} $为
$$ {M_{\text{T}}} = {\sigma _{\text{T}}}{\text{π }}({D^2}/4)(D/2) 。 $$ (13) 采用条分法计算土体抗力矩$ {M_{\text{c}}} $，如图 12所示。
假设滑动面上土体强度同时得到发挥，且服从Mohr–Coulomb破坏准则：
$$ {\tau _{\text{f}}} = c + \sigma \tan \varphi 。 $$ (14) 将条分单元体近似看作圆缺形，则根据第i个土条的竖直方向受力平衡，有
$$ {\sigma _{{\text{v1}}}}{l_i} \cdot {P_1}{P_2} + {W_i} = {T_i}\sin ({\theta _i} - \varphi ) + {N_i}\cos {\text{(}}{\theta _i} - \varphi {\text{)}} \text{，} $$ (15) $$ {T}_{i}=c{l}_{i}\stackrel{⌢}{{P}_{1}Q{P}_{2}}+{N}_{i}\mathrm{tan}\varphi 。 $$ (16) 其中：$ {l_i} = {r_i}{\text{d}}\theta $；$ {W_i} = \gamma \cdot \Delta {S_i}{l_i}\cos ({\theta _i} - \varphi ) $为第i个土条的重力；Ti，Ni分别为第i个土条的滑动面摩擦力合力和支持力合力。
ΔSi，P1P2和$ \stackrel{⌢}{{P}_{1}Q{P}_{2}} $可根据几何性质进行求解：
$$ \begin{array}{l}\Delta {S}_{i}=\frac{\mathrm{arccos}\left(\frac{{P}_{1}{P}_{2}{}^{2}-4P{Q}^{2}}{{P}_{1}{P}_{2}{}^{2}+4P{Q}^{2}}\right)\cdot \left(PQ+\frac{{P}_{1}{P}_{2}{}^{2}}{4PQ}\right)+{P}_{1}{P}_{2}\left(PQ-\frac{{P}_{1}{P}_{2}{}^{2}}{4PQ}\right)}{4}\text{，}\\ {P}_{1}{P}_{2}=2{a}_{0}\sqrt{1-{\left(\frac{{r}_{i}\mathrm{sin}\theta -D\mathrm{tan}{\beta }_{B}-{b}_{0}}{{b}_{0}}\right)}^{2}}\text{，}\\ PQ={r}_{i}\mathrm{cos}\theta \end{array} \\ \stackrel{⌢}{{P}_{1}Q{P}_{2}}=\mathrm{arccos}\left(\frac{{P}_{1}{P}_{2}{}^{2}-4P{Q}^{2}}{{P}_{1}{P}_{2}{}^{2}+4P{Q}^{2}}\right)\cdot \left(PQ+\frac{{P}_{1}{P}_{2}{}^{2}}{4PQ}\right) 。 $$ (17) 由式(15)~(17)可得
$$ \begin{array}{l}{N}_{i}=\frac{{\sigma }_{\text{v}1}{r}_{i}\mathrm{cos}({\theta }_{i}-\varphi ){P}_{1}{P}_{2}\text{d}\theta +{W}_{i}-c{r}_{i}\stackrel{⌢}{{P}_{1}Q{P}_{2}}\mathrm{sin}({\theta }_{i}-\varphi )\text{d}\theta }{\mathrm{tan}\varphi \mathrm{sin}({\theta }_{i}-\varphi )+\mathrm{cos}({\theta }_{i}-\varphi )}\text{ }\text{，}\\ {T}_{i}=c{l}_{i}+\frac{{\sigma }_{\text{v}1}{r}_{i}\mathrm{cos}({\theta }_{i}-\varphi ){P}_{1}{P}_{2}\text{d}\theta +{W}_{i}-c{r}_{i}\stackrel{⌢}{{P}_{1}Q{P}_{2}}\mathrm{sin}({\theta }_{i}-\varphi )\text{d}\theta }{\mathrm{tan}\varphi \mathrm{sin}({\theta }_{i}-\varphi )+\mathrm{cos}({\theta }_{i}-\varphi )}\mathrm{tan}\varphi 。\end{array} $$ (18) 滑动面上土体抗力的微力矩为
$$ \left. \begin{array}{l} {\rm{d}}{M_{{\rm{cT}}}} = {T_i}{r_i}{\rm{cos}}\varphi ,\\ {M_{{\rm{cN}}}} = {N_i}{r_i}{\rm{sin}}\varphi 。 \end{array} \right\} $$ (19) 则滑动面上土体抗力的总力矩为
$$ {M_{\text{c}}} = {M_{{\text{cT}}}} + {M_{{\text{cN}}}} = \int_{{\beta _B}}^{\frac{{\text{π }}}{2}} {({T_i}{r_i}\cos \varphi + {N_i}{r_i}\sin \varphi )}\\ ={\displaystyle {\int }_{{\beta }_{B}}^{\frac{\text{π}}{2}}\left(c{r}_{i}^{2}\stackrel{⌢}{{P}_{1}Q{P}_{2}}\mathrm{cos}\varphi +\frac{2{N}_{i}{r}_{i}\mathrm{sin}\varphi }{\text{d}\theta }\right)}\text{d}\theta 。 $$ (20) 最后，联立式(7)，(8)，(10)~(18)和(20)，可得
$$ {\sigma _{\text{T}}} = c{N_c} + \gamma D{N_\gamma } 。 $$ (21) 式中：$ {\sigma _{\text{T}}} $为开挖面支护力；$ {N_c} $，$ {N_\gamma } $分别为土体黏聚力和重度对开挖面支护力的影响系数：
$$ \begin{array}{l}{N}_{c}=\frac{8k{b}_{0}^{2}(OE-{b}_{0})\left[\mathrm{exp}\left(-\frac{2(\text{π}+2k-2)K\mathrm{tan}\varphi }{\text{π}k{b}_{0}}d\right)-1\right]}{{D}^{3}K\mathrm{tan}\varphi }-\\ \frac{8}{\text{π}{D}^{3}}{\displaystyle {\int }_{{\beta }_{B}}^{\frac{\text{π}}{2}}\{{r}_{2}^{2}\stackrel{⌢}{{P}_{1}Q{P}_{2}}\mathrm{cos}\varphi +\frac{2\mathrm{sin}\varphi \cdot {r}_{\text{2}}{}^{2}\mathrm{cos}(\theta -\varphi ){P}_{1}{P}_{2}}{K\mathrm{tan}\varphi \left[\mathrm{tan}\varphi \mathrm{sin}(\theta -\varphi )+\mathrm{cos}(\theta -\varphi )\right]}\cdot }\\ \left[\mathrm{exp}\left(-\frac{2(\text{π}+2k-2)K\mathrm{tan}\varphi }{\text{π}k{b}_{0}}d\right)-1\right]-\end{array} \\ \frac{2\mathrm{sin}\varphi \cdot {r}_{\text{2}}{}^{2}\stackrel{⌢}{{P}_{1}Q{P}_{2}}\mathrm{sin}\text{(}\theta -\varphi \text{)}}{\mathrm{tan}\varphi \mathrm{sin}\text{(}\theta -\varphi \text{)}+\mathrm{cos}\text{(}\theta -\varphi \text{)}}\}\text{d}\theta \text{，} $$ (22) $$ {N_\gamma } = \frac{{4\int_{{\beta _B}}^{\frac{{\text{π }}}{2}} {ab({r_{\text{1}}} + {r_{\text{2}}})({r_2} - b)\sin \theta {\text{d}}\theta } }}{{{D^4}}} - \frac{{{h_{\text{H}}} \cdot \left( {D\tan {\beta _{\text{B}}} - \frac{{{h_{\text{H}}}}}{3}} \right)}}{{{D^2}}} +\\ \begin{array}{l} \frac{{8k{b_0}^2(OE - {b_0})({C_0} + {D_0})}}{{{D^4}}} + \hfill \\ \frac{{4{\text{π }}{k^2}{b_0}^3(OE - {b_0})\left[ {1 - \exp \left( { - \frac{{2({\text{π }} + 2k - 2)K\tan \varphi }}{{{\text{π }}k{b_0}}}d} \right)} \right]}}{{{D^4}({\text{π }} + 2k - 2)K\tan \varphi }} - \hfill \\ \frac{8}{{{\text{π }}{D^4}}}\int_{{\beta _B}}^{\frac{{\text{π }}}{2}} {\left\{ \begin{array}{l} \hfill \\ \hfill \\ \hfill \\ \end{array} \right.} \frac{{2\sin \varphi \cdot {r_{\text{2}}}^2\cos (\theta - \varphi )\Delta S}}{{\tan \varphi \sin (\theta - \varphi ) + \cos (\theta - \varphi )}} + \hfill \\ \frac{{2\sin \varphi \cdot {r_{\text{2}}}^2\cos (\theta - \varphi ){P_1}{P_2}}}{{\tan \varphi \sin (\theta - \varphi ) + \cos (\theta - \varphi )}} \cdot \hfill \\ \end{array} \\ \left. {\left( {\frac{{{\text{π }}k{b_0}\left[ {1 - \exp \left( { - \frac{{2({\text{π }} + 2k - 2)K\tan \varphi }}{{{\text{π }}k{b_0}}}d} \right)} \right]}}{{2({\text{π }} + 2k - 2)K\tan \varphi }} + C + {D_0}} \right)} \right\} \text{d}\theta 。 $$ (23) 当s/D为其他值时，可采用线性插值对开挖面极限支护力进行求解，具体为
$$ {\sigma }_{\text{T}}^{*}=\{\begin{array}{l}(0.5-s/D){\sigma }_{\text{Tm}}+(s/D+0.5){\sigma }_{\text{T0}}\text{ (}-0.5 < s/D < 0.5)\\ 2(s/D+1){\sigma }_{\text{Tm}}-2(s/D+0.5){\sigma }_{\text{T0}}\text{ (}-1 < s/D < -0.5)\\ {\sigma }_{\text{T0}}\text{ (}s/D\le -1或s/D\ge 0.5)\end{array}。 $$ (24) 式中：$ \sigma _{\text{T}}^* $为相应s/D处的极限支护力；$ {\sigma _{{\text{Tm}}}} $为近接条件下s/D =-0.5时的极限支护力；$ {\sigma _{{\text{T0}}}} $为相同土性和埋深的单隧道开挖面极限支护力，可令k = 1进行计算。
3. 理论模型验证及参数分析
3.1 理论模型验证
理论模型中自定义参数为两个：OB与垂直面的夹角$ {\beta _B} $及椭圆长短轴之比k。根据村山公式原理[6]，对数螺旋线在盾构底面与水平方向夹角为$ {\text{π }}/4 + \varphi /2 $，则$ {\beta _B} = {\text{π /}}4 - \varphi /2 $。近接条件下k值主要受地层条件和既有隧道影响，可由数值模拟结果得到(松砂：k = 1.8；密砂：k = 1.3；软黏：k = 1.9；硬黏：k = 1.6)。由于式(22)和(23)较为复杂，可代入已知参数至Matlab中进行求解。当隧道埋深较大(通常C/D > 3.0)，则盾构施工引起的土拱效应、渐进性破坏特性与常规埋深隧道完全不同[13]，因此本文暂不考虑大埋深情况。
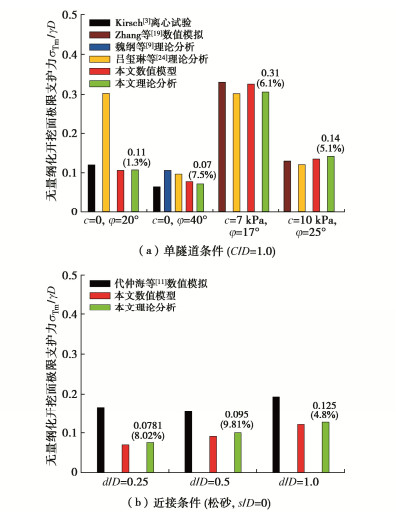
图 13为本文理论分析和数值模拟结果与其他学者的结果对比。单隧道条件下(图 13(a))的理论分析结果与已有试验结果和本文数值模拟结果均符合较好。图 13(b)为松砂地层近接条件下(s/D = 0)的结果对比，可以看出，本文基于三维旋转破坏模型得到的极限支护力与数值模拟结果的偏差在10%以内，表明计算结果较好，且相比于数值模拟繁琐的建模过程可以大大提高不同工况下的计算分析效率。
3.2 理论模型参数分析
在本文理论模型中，参数k体现了近接工况下破坏体横截面的椭圆程度，这一现象是由于土体变形向上方的扩展被既有隧道限制而只能沿水平方向扩展，并且沿既有隧道方向的土体存在与既有隧道“剥离”的趋势，更加容易产生变形，因而与垂直方向的土体变形扩展产生差异。土体c，φ值越高，变形越不易扩展，导致土体更趋于各向同性，因此两个方向的变形范围差异(k值)随土性抗剪强度增加而降低。
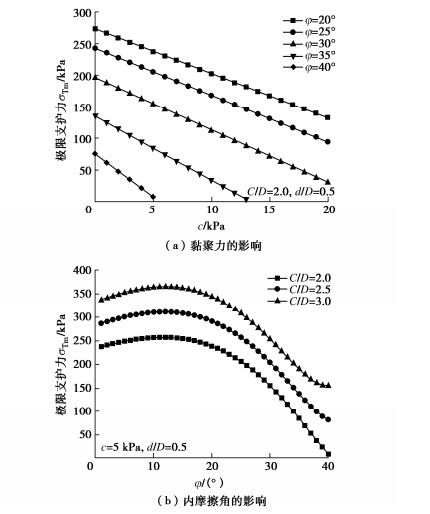
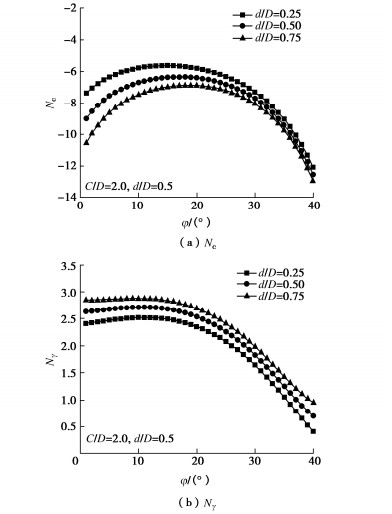
如图 14所示，开挖面极限支护力随黏聚力的增加而线性降低，随土体内摩擦角φ增加呈现出先增加后降低的趋势，随埋深增加近似线性增加。极限支护力影响系数Nc、Nγ与土体内摩擦角的关系如图 15所示。由于土体黏聚力起抗力作用，因而Nc为负数。Nc随土体φ值增加而先增加后降低，随近接距离增加而降低。Nγ随φ值增加先基本不变而后逐渐降低，随近接距离增加而增加。此外，当土体内摩擦角较大(φ > 30°)时，近接距离对Nc的影响很小，这是由于内摩擦角越大，破坏范围越小，邻近的既有隧道的影响越低。
![]()
图 15 极限支护力系数与土体内摩擦角关系Figure 15. Relationship between coefficient of limit support pressure and internal friction angle of soils4. 结论
本文揭示了近接既有隧道条件下的盾构开挖面破坏模式，构建了对数螺旋体+椭圆柱的开挖面失稳三维破坏模型并对主要参数进行了分析，得到以下3点结论。
(1) 近接既有隧道条件下盾构开挖面失稳三维变形区呈现沿隧道纵向和横向不对称的特点。当盾构开挖面与既有隧道轴线距离(s/D)在-1~0.5时，破坏模式呈现螺旋体+筒仓体形态。隧道垂直净距和土性对近接条件下开挖面破坏模式影响不大，但会改变三维方向上破坏扩展范围。
(2) 改进的对数螺旋体+椭圆柱体模型可以反映开挖面失稳扩展沿隧道纵向和横向的非均匀性，因此更加符合近接既有隧道条件下的实际开挖面破坏模式，且可以通过设置参数k使其适用于单隧道条件。基于所提出的破坏模型，推导了可以反映土体黏聚力和重度影响系数的开挖面极限支护力计算公式。
(3) 理论模型中参数k可体现开挖面失稳变形沿隧道纵向和横向扩展的非均匀性。土体强度越高(黏聚力c和内摩擦角φ越大)、隧道埋深越浅、近接距离越小，则开挖面极限支护力越低。开挖面极限支护力影响系数Nc、Nγ随土体内摩擦角φ增加呈现先增加后降低的变化趋势。内摩擦角临界值约为11°~13°。
-
![]()
图 4 无量纲化开挖面支护力–位移关系曲线
Figure 4. Relationship between normalized displacement and normalized support force of tunnel face
![]()
图 5 近接既有隧道条件下开挖面变形模式(不同s/D)
Figure 5. Deformation characteristics of shield tunnel face adjacent to an existing tunnel under different s/D
![]()
图 6 近接既有隧道条件下开挖面变形模式(不同d/D)
Figure 6. Deformation characteristics of shield tunnel face adjacent to an existing tunnel under different d/D
![]()
图 7 近接既有隧道条件下开挖面变形模式(不同土性)
Figure 7. Deformation characteristics of shield tunnel face adjacent to an existing tunnel under different soil properties
![]()
图 8 不同近接距离下开挖面极限支护力
Figure 8. Limit support pressures on tunnel face under different adjacent distances
![]()
图 15 极限支护力系数与土体内摩擦角关系
Figure 15. Relationship between coefficient of limit support pressure and internal friction angle of soils
类别 重度γ/(kN·m-3) 弹性模量E/MPa 泊松比ν 黏聚力c/kPa 内摩擦角φ/(°) 土体 松砂 17.0 17.5 0.397 0 20 密砂 19.5 65.0 0.263 0 40 软黏 16.0 3.5 0.414 7 17 硬黏 18.0 12.5 0.366 10 25 衬砌 混凝土 25.0 33500 0.20 — — 注浆层 泥浆 12.0 50 0.49 — — 
下载: 导出CSV
表 2 数值模拟方案
Table 2 Scheme of numerical simulations
土体类别 近接形式 新建隧道埋深比C/D 隧道垂直净距比d/D 开挖面水平间距比s/D 松砂 无 1.0，1.5，2.0 — — 密砂 松砂 新建隧道垂直下穿既有隧道 2.0 0.25，0.50，0.75 -1，-0.5，0，0.5 密砂 软黏 硬黏 注：隧道垂直净距比d/D为新建隧道上表面与既有隧道下表面的垂直距离d与新建隧道直径D之比；开挖面水平间距比s/D为新建隧道开挖面与既有隧道中心轴线的水平距离s与新建隧道直径D之比，负值表示盾构尚未穿越既有隧道中心轴线。
下载: 导出CSV
-
[1] 陈仁朋, 李君, 陈云敏, 等. 干砂盾构开挖面稳定性模型试验研究[J]. 岩土工程学报, 2011, 33(1): 117-122. http://www.cgejournal.com/cn/article/id/12371 CHEN Renpeng, LI Jun, CHEN Yunmin, et al. Large-scale tests on face stability of shield tunnelling in dry cohesionless soil[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 117-122. (in Chinese) http://www.cgejournal.com/cn/article/id/12371
[2] HU Y, LEI H Y, ZHENG G, et al. Assessing the deformation response of double-track overlapped tunnels using numerical simulation and field monitoring[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2022, 14(2): 436-447. doi: 10.1016/j.jrmge.2021.07.003
[3] KIRSCH A. Experimental investigation of the face stability of shallow tunnels in sand[J]. Acta Geotechnica, 2010, 5(1): 43-62. doi: 10.1007/s11440-010-0110-7
[4] SCHOFIELD A N. Cambridge geotechnical centrifuge operations[J]. Géotechnique, 1980, 30(3): 227-268. doi: 10.1680/geot.1980.30.3.227
[5] LECA E, DORMIEUX L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material[J]. Géotechnique, 1990, 40(4): 581-606. doi: 10.1680/geot.1990.40.4.581
[6] MURAYAMA S, ENDO M, HASHIBA T, et al. Geotechnical aspects for the excavating performance of the shield machines[C]// Proceedings of the 21th Annual Lecture in Meeting of Japan Society of Civil Engineers. Tokyo, 1966.
[7] SUBRIN D, WONG H. Tunnel face stability in frictional material: a new 3D failure mechanism[J]. Comptes Rendus Mecanique, 2002, 330(7): 513–519. (in French)
[8] HORN N. Horizontal earth pressure on the vertical surfaces of the tunnel tubes[C]// Proceedings of National Conference of the Hungarian Civil Engineering Industry. Budapest, 1961.
[9] 魏纲, 贺峰. 砂性土中顶管开挖面最小支护压力的计算[J]. 地下空间与工程学报, 2007, 3(5): 903-908. doi: 10.3969/j.issn.1673-0836.2007.05.024 WEI Gang, HE Feng. Calculation of minimal support pressure acting on shield face during pipe jacking in sandy soil[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(5): 903-908. (in Chinese) doi: 10.3969/j.issn.1673-0836.2007.05.024
[10] 胡雯婷, 吕玺琳, 黄茂松. 盾构隧道开挖面极限支护压力三维极限平衡解[J]. 地下空间与工程学报, 2011, 7(5): 853-856, 862. doi: 10.3969/j.issn.1673-0836.2011.05.006 HU Wenting, LÜ Xilin, HUANG Maosong. Three-dimensional limit equilibrium solution of the support pressure on the shield tunnel face[J]. Chinese Journal of Underground Space and Engineering, 2011, 7(5): 853-856, 862. (in Chinese) doi: 10.3969/j.issn.1673-0836.2011.05.006
[11] 代仲海, 胡再强. 穿越紧邻隧道时盾构开挖面稳定性分析[J]. 中国公路学报, 2020, 33(1): 145-152. doi: 10.3969/j.issn.1001-7372.2020.01.015 DAI Zhonghai, HU Zaiqiang. Stability analysis of excavation face during shield passing through adjacent tunnels[J]. China Journal of Highway and Transport, 2020, 33(1): 145-152. (in Chinese) doi: 10.3969/j.issn.1001-7372.2020.01.015
[12] TANG X W, LIU W, ALBERS B, et al. Upper bound analysis of tunnel face stability in layered soils[J]. Acta Geotechnica, 2014, 9(4): 661-671. doi: 10.1007/s11440-013-0256-1
[13] 张孟喜, 戴治恒, 张晓清, 等. 考虑主应力轴偏转的深埋盾构隧道开挖面主动极限支护压力计算方法[J]. 岩石力学与工程学报, 2021, 40(11): 2366-2376. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202111019.htm ZHANG Mengxi, DAI Zhiheng, ZHANG Xiaoqing, et al. A calculation method of active limit support pressure for deep shield tunnels considering principal stress axis rotation[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(11): 2366-2376. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202111019.htm
[14] ZOU J F, CHEN G H, QIAN Z H. Tunnel face stability in cohesion-frictional soils considering the soil arching effect by improved failure models[J]. Computers and Geotechnics, 2019, 106: 1-17. doi: 10.1016/j.compgeo.2018.10.014
[15] IBRAHIM E, SOUBRA A H, MOLLON G, et al. Three-dimensional face stability analysis of pressurized tunnels driven in a multilayered purely frictional medium[J]. Tunnelling and Underground Space Technology, 2015, 49: 18-34. doi: 10.1016/j.tust.2015.04.001
[16] LI W, ZHANG C P, TAN Z B, et al. Effect of the seepage flow on the face stability of a shield tunnel[J]. Tunnelling and Underground Space Technology, 2021, 112: 103900. doi: 10.1016/j.tust.2021.103900
[17] MOLLON G, DIAS D, SOUBRA A H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2011, 35(12): 1363-1388. doi: 10.1002/nag.962
[18] 顾晓鲁, 郑刚, 刘畅. 地基与基础[M]. 4版. 北京: 中国建筑工业出版社, 2019. GU Xiaolu, ZHENG Gang, LIU Chang. Ground and Foundation[M]. 4th ed. Beijing: China Architecture & Building Press, 2019. (in Chinese)
[19] ZHANG C P, HAN K H, ZHANG D L. Face stability analysis of shallow circular tunnels in cohesive–frictional soils[J]. Tunnelling and Underground Space Technology, 2015, 50: 345–357. doi: 10.1016/j.tust.2015.08.007
[20] 汤旅军, 陈仁朋, 尹鑫晟, 等. 密实砂土地层盾构隧道开挖面失稳离心模型试验研究[J]. 岩土工程学报, 2013, 35(10): 1830-1838. http://www.cgejournal.com/cn/article/id/15302 TANG Lüjun, CHEN Renpeng, YIN Xinsheng, et al. Centrifugal model tests on face stability of shield tunnels in dense sand[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(10): 1830-1838. (in Chinese) http://www.cgejournal.com/cn/article/id/15302
[21] 雷华阳, 刘敏. 盾构隧道开挖面失稳破坏机理及土拱效应研究综述[J]. 太原理工大学学报, 2022, 53(1): 98-117. https://www.cnki.com.cn/Article/CJFDTOTAL-TYGY202201013.htm LEI Huayang, LIU Min. A review of recent advances in the face instability mechanism of shield tunnel and soil arching effect[J]. Journal of Taiyuan University of Technology, 2022, 53(1): 98-117. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TYGY202201013.htm
[22] LI W, ZHANG C P, ZHU W J, et al. Upper-bound solutions for the face stability of a non-circular NATM tunnel in clays with a linearly increasing undrained shear strength with depth[J]. Computers and Geotechnics, 2019, 114: 103136. doi: 10.1016/j.compgeo.2019.103136
[23] 铁路隧道设计规范: TB 10003—2016[S]. 北京: 中国铁道出版社, 2017. Code for Design of Railway Tunnel: TB 10003—2016[S]. Beijing: China Railway Publishing House, 2017. (in Chinese)
[24] 吕玺琳, 王浩然, 黄茂松. 盾构隧道开挖面稳定极限理论研究[J]. 岩土工程学报, 2011, 33(1): 57-62. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201101012.htm LÜ Xilin, WANG Haoran, HUANG Mao-song. Limit theoretical study on face stability of shield tunnels[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 57-62. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201101012.htm
-
期刊类型引用(4)
1. 叶友林，商诗健，牛奔，路志旺，徐春一. 正交下穿截污管盾构开挖面被动失稳颗粒流模拟研究. 沈阳建筑大学学报(自然科学版). 2024(01): 70-77 . 
百度学术
2. 陈一凡，沈翔，陈湘生. 海底软弱地层浅埋大直径盾构对接开挖面失稳灾变机制研究. 隧道建设(中英文). 2024(04): 712-723 . 百度学术
3. 谢强，马瑗婕，吴俊，薛孝强，涂正楠. 基坑开挖引起下穿交叉隧道变形效应分析. 地下空间与工程学报. 2024(05): 1695-1705 . 百度学术
4. 叶友林，刘晓龙，牛奔，周广宇，徐春一. 上软下硬复合地层盾构隧道开挖面稳定性分析. 沈阳工业大学学报. 2024(06): 848-854 . 百度学术
其他类型引用(6)
-
其他相关附件
计量
- 文章访问数: 436
- HTML全文浏览量: 62
- PDF下载量: 156
- 被引次数: 10
