0.   引言

滑坡作为地震作用下场地最大的次生灾害问题，一直是区域防灾减灾工作的重点难点，历次地震滑坡均给国民经济生活造成重大损失。深入揭示地震下边坡的致灾机理始终是岩土工程领域和工程地震学的科研难题。最早在1958年Clough等^[1]开展了室内小比尺模型的振动台试验，研究坝坡的动力响应特征和变形问题，自此经过60多年的长足发展，伴随着科技制造水平和测量技术的进步，开展动力条件下的物理模型试验已经成为了理解动荷载下边坡失稳机理的重要科研手段，尤其是离心模型振动台试验，以其缩尺效应和重现原型应力场的作用成为研究地震荷载下边坡稳定性问题的重要试验方法，对于在各种复杂地震条件理解边坡的响应和变形耦合机理具有重要作用^[2]。

首先表现的就是边坡加速度响应的复杂性。Madabhushi等^[3]针对陡坡开展离心机振动台试验，发现震动前后并未出现显著变形，继而通过云图的形式展现边坡内部的动力放大效应。Yu等^[4]针对干砂边坡开展系列离心动力试验，分别输入地震时程和简谐波，借助响应谱谱比的形式揭示边坡内部加速度的变化特点。Brennan等^[5]通过正弦时程重点模拟砂土边坡顶部的加速度放大效应，探究该放大效应对于坡顶结构物的影响。加速度除了上述整体上显示出的放大效应，在边坡内部不同位置的放大效果也是迥异^[6]，尤其是靠近坡面和坡体内部差异更大^[7]，如果同时考虑基底的水平和竖向输入，放大效应除了与位置有关，还与地震动频率，施加振动的方式和幅值均有密切联系^[8-9]。其次，便是复杂的变形的问题。地震下的边坡是一个响应和变形时刻耦合的复杂问题，加速度变化的同时伴随着边坡的变形，这也是耦合法^[10]改进Newmark^[11]刚性滑块法的理论依据，而振动过程累积的变形量也是地震下边坡基于性能设计的重要指标。于玉贞等^[12]开展的饱和地基上边坡振动台试验论证地基的孔压的发展与边坡的变形之间的相关性，Zhang等^[13-14]开展的泥岩边坡离心模型试验，通过塑性区分布图和试验振动前后的观测印证边坡变形累积及其与加速度之间的相关性。边坡不同位置的变形发展特征，响应过程的变形累积，以及震后变形破坏等问题在黄土边坡上也得到显著的体现^[15]。地震输入本身的复杂性加上边坡的非线性变形-响应耦合特征都说明了要进一步深入认识地震下边坡的致灾机理和失稳机制，需要开展不同条件下离心模型振动台试验。

得到共识的是，地震的发生往往是以序列地震的形式出现，在主震之后还往往伴随着震级各异的余震。近来在岩土工程领域，余震的影响作用也逐渐引起了关注，Yin等^[16]研究了汶川地震及余震影响下桩加固后的坡体的服役性能，发现该滑坡体并未在连续余震中发生失稳破坏，但观察到边坡上加速度放大效应十分明显，Wang等^[17]总结了汶川地震余震影响下绵竹地区边坡动力响应监测的结果，发现边坡的动力响应受地形和覆盖层厚度影响显著，Shi等^[18]则通过堰塞坝体常重力振动台试验，发现余震引起了坝体沉陷和开裂、加速漫顶溢流的溃决过程，但并未诱发坝体整体失稳。所以，序列地震作用下除了主震下的变形与加速度响应的耦合问题，余震的累积变形也是边坡工程设计要考量的重要因素。因此深入理解主余震序列作用下边坡的失稳机理需要进一步对主震-余震分别造成的影响进行界定和讨论，尤其是主震的地震动强度大，边坡变形-响应耦合特征更显著，而且边坡由于顺-逆坡向受力不对称性（表现的一点就是两者刻画抗震能力的屈服加速度差异显著）导致响应的复杂变化，在以往的关于加速度响应的讨论中尚未得到清楚的说明，此外还鲜有见到完整考虑主余震序列作用的边坡动力模型试验的相关成果。

鉴于此，本文通过制作室内离心模型，完成主余震序列作用下的含倾斜基岩面的边坡振动台试验，获得边坡加速度响应和变形结果。接着，分别通过响应的时程分析和谱分析讨论主震作用下边坡响应加速度的复杂特征，并借助刚性楔形滑体模型解释响应时程的截断特征以及在顺-逆坡向表现出来的放大效应的显著不一致性。然后，从累积变形的角度讨论余震效应带来的附加影响等问题。相关的研究和讨论对于后续进一步开展物理模型试验并深入探索地震序列下边坡致灾机理具有一定的借鉴和参考作用。

1.   离心模型设计与试验

1.1   模型设计

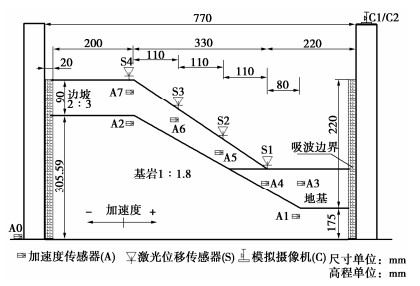
本试验在浙江大学ZJU-400(400 g·t)及配套机载振动台上进行，试验缩放比尺N=50，也就是离心加速度为50g，其中模型相似比参照规范^[19]（例如动力时间比尺1/N，速度比尺1等），采用单侧视窗的中型刚性模型箱^{[7, 9, 12]}（内部净空尺寸为长×宽×高= 770 mm×400 mm×530 mm），与剪切模型箱所不同的是刚性箱两端的纯刚性约束，会在试验过程中产生波的反射等问题，因此为了削弱这些不利的因素，本试验在箱子的两端各铺设2 cm厚的硅橡胶板^{[12, 19]}，所以实际模型箱的容许体积为长︰宽︰高=730 mm︰400 mm︰530 mm。试验采用加速度传感器和激光位移传感器，单侧的玻璃视窗配备高速照相机。本试验模型设计图如图 1所示，模型主体由边坡，基岩和地基3部分组成。单侧均质砂土边坡（潜在滑体）下覆盖一定厚度的具有倾斜接触面的混凝土基岩，地基是与前述二者相互接触的土体。其中边坡材料选用通用石英砂（D₅₀=0.16 mm，C_u=1.6），地基材料选用石英砂与10%膨润土构成的混合土作为模型材料（这里的百分比表示膨润土占总质量的比例），基岩由设定水灰比的水泥砂浆灌注凝结形成(水泥砂浆=水泥︰石英砂︰水= 0.55︰1︰0.25（外掺2%早强剂）^[9]，模型材料控制相对密度为60%，模型材料基本性质如表 1所示。

图  1  模型试验设计图

Figure  1.  Design of model tests

下载: 全尺寸图片 幻灯片

表  1  材料基本性质

Table  1.  Properties of materials

类别	黏聚力/kPa	内摩擦角/(°)	最大孔隙比	最小孔隙比	相对质量密度
石英砂	—	37.8	0.878	0.550	2.64
混合土	0.74	35.9	0.877	0.451	2.60

下载: 导出CSV 

| 显示表格

拟定模型总高度H=395 mm（代表原型19.75 m）其中边坡倾角约33.7°（竖向V︰水平H=2︰3），基岩接触面倾角约29°（竖向V︰水平H=1︰1.8）。根据相对密实度指标在浇筑完成的基岩上先分层夯实制作混合土地基，然后采用砂雨法分层浇筑边坡模型^{[8, 19]}，最后通过削坡形成模型。在模型箱外侧底部布设加速度传感器（A0）用来记录振动台的水平加速度输入，基岩布置传感器（A1，A2），其时程与A0保持一致，在地基内部布设加速度传感器（A3，A4），在边坡内部分三层布设加速度传感器（A5，A6，A7），最后在边坡表面安置竖向激光位移传感器（按照坡脚至坡顶分别编号：S1，S2，S3，S4），以上传感器均布设在模型的中轴线^[19]，加速度传感器的布置方案如表 2所示。本试验对应模型实物如图 2所示，图 2中的红色彩砂用于定性的指示边坡在震前震后的整体变形。

表  2  传感器布置

类别	高程h/mm	高程比(h/H)	传感器标记
模型箱底部	0	0	A0
基岩部分	80	0.2	A1
	300	0.76	A2
地基部分	145	0.37	A3、A4
边坡部分	215	0.55	A5
	295	0.75	A6
	365	0.92	A7

下载: 导出CSV 

| 显示表格

图  2  离心模型

Figure  2.  Centrifuge model

下载: 全尺寸图片 幻灯片

1.2   模型试验

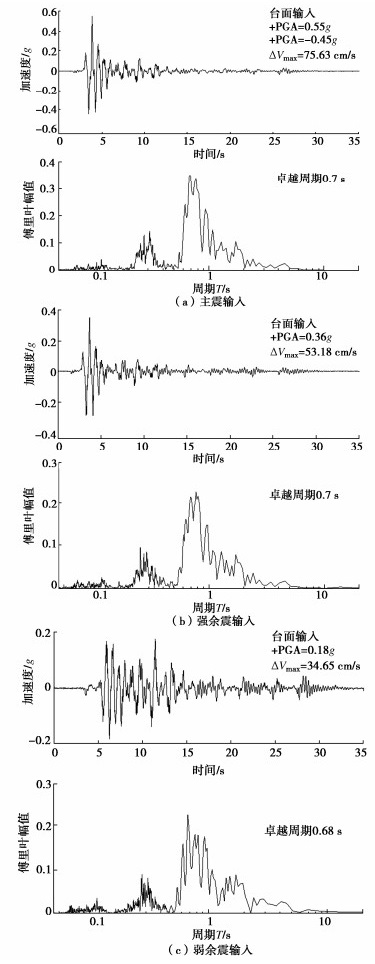
本试验的施振方案如表 3所示，以下讨论所涉及量值均换算到原型尺寸单位。全过程的水平输入包含主余震序列（主震-强余震-弱余震，见表 3）和间隔的扫频振动（阶跃波-白噪声），其中白噪声用于测试振动输入前后边坡的动力参数（如，自振频率）而低幅值阶跃波用于近似计算土层的平均剪切波速（利用波传播原理）。为了凸显试验过程中加速度响应的变化特征，使得截断现象更明显，拟采用具有显著正负峰值加速度的输入时程，因此，本次试验地震动时程筛选了来自NGA-West2数据库的Northridge地震所记录的脉冲型地震波并缩放到目标峰值加速度（PGA）。最终，振动台台面记录到的水平输入时程也就是A0的时程（包括加速度和对应的傅里叶谱）如图 3所示。特别指出，加速度时程曲线的正负标记见图 1，其中加速度传感器记录的正值表示朝着右边加速（朝顺坡向加速），负值表示朝着左边的逆坡向加速（对应惯性力朝顺坡向或向右），均有明确的物理含义。试验时，根据预定比尺要求（N=50），离心机加速稳定到预定加速度值，然后根据表 3的施振方案依次振动。

表  3  施振方案

Table  3.  Arrangement of sensors Table 3 Vibration schemes

项目	主震	强余震	弱余震
类型	脉冲型	脉冲型	无脉冲
PGA (g)	0.55	0.36	0.18
注：无脉冲型和脉冲型区别及差异性论述具体可参照近断层地震的向前方向性和滑冲效应[20]

下载: 导出CSV 

| 显示表格

图  3  台面输入

Figure  3.  Input of shaking table

下载: 全尺寸图片 幻灯片

2.   主震响应

2.1   响应时程分析

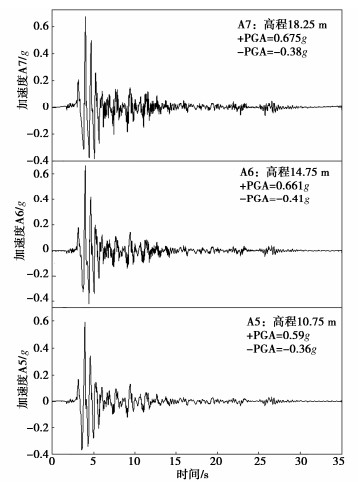
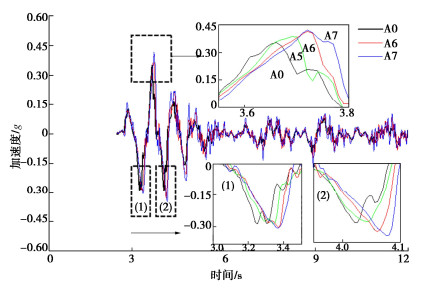
本文主要探究边坡部分的地震响应问题，由于试验传感器都是水平布设且台面是水平输入，因此记录的结果反映的是绝对水平响应加速度。图 4给出主震输入下边坡（潜在滑体）部分的加速度响应（对应加速度A5—A7），从时程曲线上可以初步感知到，随着高度的增加，加速度量值整体被放大，而且频率内容也变得更丰富。为了更进一步讨论图 4时程表现出来的放大效应，通常的方法是通过依据时程曲线峰值加速度（PGA）比值所定义的动力放大系数来表征^[13]，考虑到边坡的顺、逆坡向对地震输入的反应不同的特点，本文将动力放大系数的定义进一步划分为分别依据：正峰值（+PGA）、负峰值（-PGA）、峰值绝对值（|±PGA|）和均方根加速度（RMS）的比值，具体描述见公式（1）。

图  4  主震边坡响应

Figure  4.  Slope responses under mainshock

下载: 全尺寸图片 幻灯片

式中：${\gamma }_{正}$为依据正峰值定义的放大系数，${\gamma }_{负}$为依据负峰值定义的放大系数，${\gamma }_{绝对}$为依据时程曲线的峰值绝对值定义的放大系数而${\gamma _{{\text{RMS}}}}$是依据时程曲线计算的均方根加速度值定义的放大系数。Ai描述计算所用的传感器（本文仅针对台面输入和边坡部分的响应），i=0，5，6，7。遵照这个定义，依据图 4时程曲线所计算的各个放大系数的变化曲线见图 5。

图  5  响应放大系数

Figure  5.  Amplification coefficients of response

下载: 全尺寸图片 幻灯片

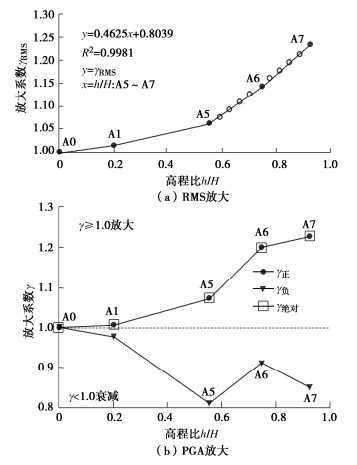
图 5（a）给出了均方根加速度（RMS）比值随着高程比（h/H）的变化情况，可以发现随着高度的增加均方根加速度不断变大，量值显示出明显的放大效应，本文将边坡部分的${\gamma _{{\text{RMS}}}}$（包含：A5—A7）三者做了线性回归（为了分析方便），结果显示边坡部分的${\gamma _{{\text{RMS}}}}$变化规律很稳定（考虑到传感器A5—A7是等间隔布设），顶部的${\gamma _{{\text{RMS}}}}$稳定在1.2~1.3，然而均方根加速度是对整体时程而言（一个积分的结果），是一个宏观的指标。更细节的问题，尤其涉及到振动过程中每时刻的边坡响应还要去追索时程及时程峰值的变化。图 5（b）中给出的依据峰值定义的情况要更复杂一些，细节也更丰富。图中依据放大系数$\gamma$划分为两个区域，$\gamma$ > 1的放大区域和$\gamma$ < 1的衰减区域。本文计算出的${\gamma }_{正}$和${\gamma }_{绝对}$相等，二者均显示随着高程的增加边坡水平响应呈现放大系数增加的放大效果（地形放大效应），在靠近边坡顶部的时候增速变缓（A6到A7的变化），最后一点跟图 5（a）的现象不同，最终顶部的量值也停在1.2~1.3（Rathje等^[21]曾指出用系数1.3近似保守考虑地形效应导致顶部加速度的放大）。通常依据时程曲线上的峰值定义的放大系数没有特别指明往往会默认选取峰值绝对值（|±PGA|），遵照这个思路，对地面水平输入进行缩放考虑顶部的放大效应，其放大系数沿着高度的分布规律，可在边坡的拟静力分析中对地震系数进行修正而用于工程计算^[8]。

然而，图 5（b）的结果表明边坡在逆坡向的加速度响应（加速度负值和-PGA指示）却不仅没有显示放大而是呈现衰减的趋势（${\gamma }_{负}$ < 1）且整体趋势也未显现出单调性变化规律，所以就放大系数来看似乎得出了与前面互相矛盾的结论。这是因为边坡的顺、逆坡向对水平输入反应不同的特点（涉及到对应的惯性力作用方向），这种同一地震动下边坡的顺、逆坡向加速度响应和放大系数显示出的显著不一致性（甚至完全相反的结果），本文称之为“响应方向性”（区别于Kramer等^[22]提出的不同方位角输入下的边坡响应方向性问题）。本文所述响应方向性是由于潜在滑体（文中边坡部分）当受到较大地震动水平时（文中PGA较大的主震作用下）在顺坡向产生相对运动（相对位移和相对加速度）所导致的。而这种沿着顺坡向的相对运动，会导致逆坡向的绝对加速度小于同方向台面输入的加速度甚至量值稳定在某个值附近，也可以说会导致逆坡向的绝对加速度表现出量值被“截断”的特征（相比于输入），于是就表现出图中${\gamma }_{负}$变小的情况。

2.2   响应方向性与截断效应的关系

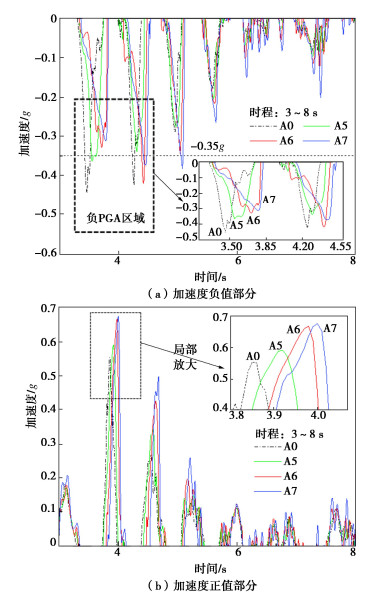
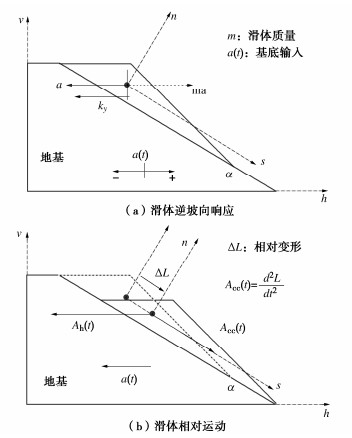
为进一步解释前述加速度“截断”问题及其与响应方向性和放大系数的关系，截取图 4边坡时程曲线和图 3的台面主震输入时程曲线的部分（时间段：3~8 s）进行对照，对比结果如图 6所示。图 6（a）给出了加速度负值部分（对应逆坡向响应），其中虚线方框部分对应的是各个高程时程曲线负PGA存在的区域，明显的发现基底输入A0的峰值最大（-PGA= -0.45g），A5到A7的峰值均呈现减小的状态（包括第一、第二峰值），对应了前述${\gamma }_{负}$ < 1的结论。而虚线框以外的区域（后续较小的峰值），连同图 6（b）正加速度部分（顺坡向响应）却立刻又呈现出随着高程的增加，加速度量值不断增加的放大效应。换句话说，逆坡向的加速度响应在某些时间段内呈现出被“截断”的现象，表现出加速度值被稳定在某个限值附近（如图中的-0.35g示意），且其绝对值小于台面输入，而这个时间段内的加速度又是负峰值出现的区域，所以相比较台面输入而言就产生了加速度衰减的情况，也就表现出响应方向性。这种逆坡向加速度时程的“截断”现象（以下文中统一称作截断效应），前文说过是由于滑体产生顺坡向的相对运动导致的，具体地说是由于滑体的滑动而对滑体的响应造成的影响（变形与响应的耦合现象），反过来也就表明这种截断效应的出现，指示该部分土体有相对滑移的产生。在这里可以通过图 7所示刚性楔形滑体模型的平面运动（模拟地震斜坡响应过程）初步解释截断效应产生的机理。

图  6  局部响应时程

Figure  6.  Time histories of partial response

下载: 全尺寸图片 幻灯片

图  7  刚性楔形滑体模型

Figure  7.  Model for rigid wedge-shaped sliding body

下载: 全尺寸图片 幻灯片

此模型边坡通过倾斜角为$\alpha$的滑移面分为两部分（也就是楔形滑体的推力角$\alpha$），滑移面以上是刚性楔形滑体，滑移面以下是地基，地基底部承受水平施加的地震荷载$a(t)$，加速度的正负定义同前文保持一致，模型内建立两套坐标系统，一个是建立于地面的笛卡尔坐标（竖向∶水平=v∶h），另一个是固定于初始楔形滑体质心位置的自然坐标（法向：切向=n∶s）。

Newmark^[11]提出用屈服加速度k_y刻画地震时滑体进入临界状态时所能承受的最大地震荷载。振动过程滑体响应加速度a朝左时（逆坡向），对应的惯性力ma就向右（顺坡向），如图 7（a）的响应分析所示。当某时刻的逆坡向水平加速度超过屈服加速度时（即：a > ${k_y}$），滑体相对于地基将沿着滑动面产生相对运动，其相对运动分析见图 7（b），根据斜面产生相对运动的瞬时动平衡关系（假设初始位置到新位置变形量为ΔL），可以得到沿着斜面的相对加速度A_cc(t)为

式中：φ为材料内摩擦角（也就是假定滑移面的土体满足莫尔-库仑强度准则）。根据加速度合成定理得到刚性滑体向左（逆坡向）的水平绝对加速度${A_{\text{h}}}(t)$为

从式（3）可以发现，${A_{\text{h}}}(t)$ < $a(t)$（逆坡向滑体响应小于同方向基底输入）这就说明了滑体水平响应加速度的截断现象，该截断限值是一个与${k_y}$有关且随着时间变化的量，且$a(t)$的幅值越大，截断效果越明显，当$a(t)$=${k_y}$，没有截断产生，处于临界状态，截断现象出现在那些响应值超过一定限值的时程范围。因此，就解释了前文所述由于滑体相对于地基的相对运动导致滑体监测的绝对加速度的截断。具体如图 6（a）所示，当A0的负PGA已经达到0.45g，而其余三者的负PGA稳定在大约0.35g附近。通过滑体响应与变形的耦合行为也可以反推，当截断效应的出现，就指示该部分土体有相对滑移产生，根据这个结论，图 1中A5到A7传感器的响应时程均指示在较大地震动水平下逆坡向的加速度监测到截断效应的产生，表明传感器深度范围内所包含的这个大区域产生了整体的相对滑移（Gazetas等^[23]根据监测资料，曾提出认为局部滑动导致坝坡同一高层处不同部位的加速度响应出现显著非对称性，表现出响应时程被截断的特点）。

为进一步说明这个结论，图 8给出了强余震作用下边坡的响应时程（时段：3~12 s，局部图给出4个传感器的数据），强余震台面输入见图 3（b），强余震与主震完全一致，而仅仅就对加速度值做了缩放（峰值缩放因子约为0.65）。但从图 8可以发现，不管顺坡还是逆坡向，各个高程的加速度响应相对于台面输入均是放大，且随着高程的增加，放大效果越明显，负值的加速度没有出现截断现象。具体以传感器A6为例按照公式（1）计算的放大系数分别为：${\gamma }_{正}$=1.162、${\gamma }_{负}$=1.154、${\gamma }_{绝对}$=1.162、${\gamma _{{\text{RMS}}}}$=1.165，保持了放大效应的一致性，并没有出现响应方向性的特征，这表明此时滑移面深度较浅，未达到传感器所在深度。而且也从旁印证了主震下表现出的相对变形对响应的影响的结论（排除了传感器倾斜等系统误差）。综上，从上述主震加速度时程的分析中发现，针对边坡而言，其时程曲线显示出的放大效应应该进一步考虑顺-逆坡向的不同，如果仅就指出PGA而不指明是哪个方向，会忽略响应方向性问题。可能存在的情况就是，当逆坡向的响应加速度被截断，但是其量值相比正加速度又占优时，那么按照峰值绝对值比值所定义的放大系数就容易得出大强度振动条件下放大系数减小甚至衰减的直观结论，没有考虑到逆坡向的响应跟滑体的变形息息相关，可能带来误判。

图  8  强余震作用下的边坡响应时程

Figure  8.  Time histories of response after a strong aftershock

下载: 全尺寸图片 幻灯片

2.3   响应谱分析

从图 4得到的初步结论是，随着高度的增加，加速度量值整体被放大，而且频率内容也变得更丰富。针对量值变化的部分在上面的响应时程分析中已经给出了较为详细的分析，顺-逆坡向的响应不同导致在由PGA定义的放大系数上表现迥异。而针对这种存在响应方向性的问题，继续对时程曲线在频域内进行分析，探究其频率内容变得更丰富的原因，尤其是揭示放大效果在各个频段的变化情况，这里通过定义傅里叶谱比的形式来体现。具体操作包括3个步骤：①准备加速度响应A5—A7连同台面输入A0的傅里叶谱（A0的傅里叶谱见图 3（a））；②对4个傅里叶谱做平滑处理（滑动平均）；③计算平滑后的谱比，谱比定义为Ai（i=5，6，7）的傅里叶谱与A0傅里叶谱的幅值之比。

如图 9所示，给出了边坡部分3个传感器相对于台面输入的傅里叶谱比。从图中可以发现随着高程的增加，大部分频率范围内的谱比值也增加，显示出放大的效果。A5位置整体上的放大效果相比A6和A7都要小，但A6与A7相比，却又在少数的若干频段内放大效果要强一点，这就产生初看图 4时的感受，整体的频率内容更丰富了。更复杂的细节从图 9中所标出的A、B和C 3个频率范围可以知道，这个3个频率区域之外，边坡各个位置的响应都得到了明显放大（大部分集中在频率低于20 Hz的相对低频范围内）。A区（对应频率范围约20~23 Hz），A6和A7仍旧是明显的放大效果，而A5相比台面输入而言却已经是衰减的状态。B区（对应频率范围约25~29 Hz），A5位置仍旧体现出衰减效果，A6，A7保持放大效应，但与A区的结果相比，此时A7的放大效果弱于A6了。C区（对应频率范围约25~29 Hz）这个区域指示边坡位置3个传感器的响应都得到了衰减，衰减程度以A5最大，A7次之，最小的是A6，这一点又恰好对应图 5（b）中衰减区3个传感器的衰减程度（${\gamma }_{负}$ (A5) < ${\gamma }_{负}$ (A7) < ${\gamma }_{负}$(A6)），而且发现3者在这个频段内虽然在谱的比值上略有差异，但是比值随着频率的变化规律却是同步的，尤其是对应频率在40~45 Hz，三者的比值变化几乎一致了。综上，从频域上对响应时程进行分析发现，就整体而言，响应的放大效应是一个与频率相关的一个量，随着高程的增加低频部分都得到了不同程度的放大，而高频部分情况就更复杂一些，衰减与放大互相掺杂变化，与高程变化的相关性就弱了。

图  9  傅里叶谱比变化曲线

Figure  9.  Variation of Fourier spectrum ratios

下载: 全尺寸图片 幻灯片

3.   余震效应

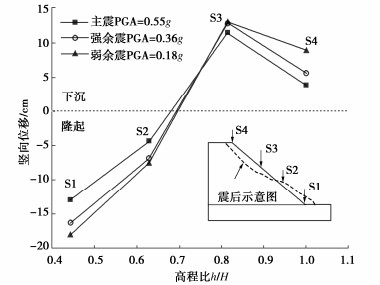
在本文中余震效应（包括强余震和弱余震）特指主震之后余震导致的边坡的变形累积状况。一方面因为余震作用下边坡响应呈现放大效应的一致性（无截断现象），但是竖向位移传感器表明余震导致变形累积，另一方面变形又是直接与地震下边坡的性能相关的参数，也是工程设计关注的指标。所以，相比主震由于地震动强度大导致的响应和变形都有较为明显的特征，本研究重点仅讨论由于后续余震的施加，所导致的变形方面的累积问题。发现试验过程中侧面实拍的断面图及彩砂均显示边坡的变形用肉眼较难分辨（例如原型S1=180 mm，模型监测到S1只有3.6 mm），所以本节用表 4和图 10的数据以及一幅震后示意图来展现地震过程中边坡的变形增量。表 4首先给出了主余震序列作用下边坡表面竖向位移分布以及余震导致的变形累积占比情况，这个占比指的是余震导致的变形增量占总变形量的比值。从表 4中可以发现，边坡上半部分(S3和S4)表现出逐步下沉的趋势，而且顶部由于余震导致的变形增量更大（占比达到56.8%），边坡的下半部分，包括坡底在内(S1和S2)不断隆起，其中S2由于余震导致的增量变形占到了总竖向位移的42.2%，另外S1和S3由主震导致的位移绝对量值是最大的（表明主震对这两个位置的影响最剧烈）。

表  4  模型边坡竖向位移

Table  4.  Vertical displacements of model slope

类别	S1/mm	S2/mm	S3/mm	S4/mm
初始	0	0	0	0
主震	-128.885	-43.23	114.95	38.57
强余震	-163.08	-67.975	128.37	56.26
弱余震	-180.31	-74.831	130.38	89.25
余震占比	28.5%	42.2%	11.8%	56.8%
注：1.表中负值代表隆起，正值代表竖向下沉。2.以上的值均是离心机加速稳定以后仅由地震荷载导致。

下载: 导出CSV 

| 显示表格

图  10  竖向位移变化曲线

Figure  10.  Variation of vertical displacements

下载: 全尺寸图片 幻灯片

进一步地，图 10给出了历次地震中，位移值沿着高度（用高程比h/H表示）的分布情况（其震后边坡表面示意图见图 10），从图中可以发现，在同一横坐标下就竖向的曲线增量而言有：S4≈S1 > S2 > S1，此外，增量上表现出S1和S2受强余震的影响明显，而S4却受弱余震的影响更大，这些现象表明竖向位移增量与地震动强度的相关性，却不一定是正相关（强度越大，变形增量越大）。需要特别指出的是，由于激光位移计测量的是震前震后模型表面的竖向位移增量值，这个量值包含有沉降，滑移以及表面的剥落或堆积等因素，是一个综合的宏观指标。综上关于竖向位移的分析，发现在本文试验边坡的表面某些部位因余震导致的总位移增量（本文称其为余震效应）可以与主震引起的变形量相当，这表明余震对边坡性能的影响也是一个比较重要的因素，除了主震外，应当关注余震效应。因此在工程设计中忽略余震冲击作用及其导致的增量累积变形问题，可能会导致结果偏于不安全。

4.   结论

本文在50g离心加速度条件下，完成主余震序列作用下含倾斜基岩面的砂土边坡离心模型振动台试验，通过对主震响应特征和余震变形累积等问题的探讨，加深对地震下边坡致灾机理的认识，进一步完善工程设计计算过程。主要得出3点结论。

（1）主震响应的时程分析表明，随着高程的增加边坡响应整体放大，但按照PGA定义的放大系数需要结合考虑边坡的顺坡、逆坡向不同所导致的响应方向性问题，否则可能导致对放大效应的误判。主震响应的谱分析表明，响应的放大效应是一个与频率有关的量，随着高程的增加低频部分得到了不同程度的放大，而高频部分情况则更复杂，衰减与放大掺杂变化。

（2）逆坡向响应时程显示出的“截断”现象指明该区域坡体有整体相对运动发生，而截断效应会导致按时程峰值计算的放大系数显现不一致的结果，这些体现变形与响应的互相作用。因此，挖掘能够深入解释响应与变形耦合现象并考虑截断效应及其在工程中的应用的分析模型是进一步研究的重点。

（3）余震效应的分析发现，边坡表面的某些部位因余震导致的总位移增量可以与主震引起的变形量相当，这表明余震对边坡性能的影响可能也是一个重要的因素，当地震发生时，常常是以地震序列的形式对场地或工程结构造成冲击，因此，在工程设计中忽略余震作用，可能会导致计算结果偏于不安全，所以仍需要对余震效应进行深入的研究。