基于黏性流体力学的液化土中桩基桩顶阻抗研究

黄娟; 胡钟伟; 余俊; 李东凯

doi:10.11779/CJGE20220322

基于黏性流体力学的液化土中桩基桩顶阻抗研究 English Version

中南大学土木工程学院, 湖南长沙 410075

基金项目:

国家自然科学基金项目 52078496

国家自然科学基金项目 51008311

详细信息

作者简介:
黄娟(1977—)，女，博士，副教授，主要从事隧道及地下工程方面的研究。E-mail: 154668562@163.com

通讯作者:
余俊, E-mail: jjyy1017@163.com

中图分类号: TU473
计量
- 文章访问数: 296
- HTML全文浏览量: 42
- PDF下载量: 66
出版历程
- 收稿日期: 2022-03-22
- 网络出版日期: 2023-05-18
- 刊出日期: 2023-04-30

Pile-top impedance of pile foundation in liquefied soil based on viscous fluid mechanics

School of Civil Engineering, Central South University, Changsha 410075, China

摘要

摘要: 将液化后的土体视为流体，考虑液化土的黏性，研究了黏性液化土体中端承桩的水平振动问题。用黏性流体运动方程模拟液化后土层的运动，用饱和多孔介质模型模拟饱和未液化土层，联系桩-流体耦合条件运用势函数法、分离变量法得到黏性流体水平振动解析解。利用上层液化土和下层饱和非液化土分界面的位移、转角和内力连续条件得到黏性液化土-饱和土分层条件下的桩顶阻抗解析表达式，将理论解与有限元解进行对比验证了解的正确性，对端承桩桩顶阻抗进行参数分析，表明在分析液化土中桩基桩顶阻抗时，需要考虑液化土的黏滞特性，以免造成刚度阻抗的高估和阻尼阻抗的低估。
- 液化土 /
- 黏性 /
- 流体 /
- 桩基 /
- 水平振动
Abstract: Regarding liquefied soil as the fluid and considering its viscosity, the horizontal vibration of the end-bearing pile in viscous liquefied soil is studied. The motion of the liquefied soil layer is simulated by using the viscous fluid motion equation, and the saturated soil layer is simulated by the saturated porous medium model. The analytical solution for the horizontal vibration of viscous fluid is obtained by separating the variables according to the pile-fluid coupling condition. Based on the continuous conditions of displacement, rotation angle and internal force of the interface between the upper liquefied soil and the lower non-liquefied saturated soil, the expression for pile-top impedance under the layered condition of viscous-liquefied-soil saturated soil is obtained. Compared with the FEM results, the correctness of the analysis is verified. A parametric analysis of the pile-top impedance shows that the viscous characteristics of the liquefied soil should be considered when analyzing the impedance of pile foundation in the liquefied soil so as to avoid the overestimation of stiffness impedance and the underestimation of damping impedance.
- liquefied soil /
- viscosity /
- fluid /
- pile foundation /
- horizontal vibration

HTML全文

0. 引言

拥有良好承载力、稳定性和较小不均匀沉降等良好特性的桩基础在中国铁路、公路、海上基础设施等重大工程项目中被广泛运用，而从近年来国内外广泛的震害调查中可以发现地震作用下的砂土液化引起的桩基破坏是导致桩基结构破坏的重要原因，地震中的砂土液化给社会经济造成了重大损失；因此对液化条件下的桩-土相互作用的研究引起了岩土工作者日益重视。从液化场地中桩基运动特性研究方法来看，目前针对液化场地桩基抗震机理研究主要集中于基于Winkler地基梁的p-y曲线研究^[1-2]、地震液化土场地桩基振动台试验^[3-5]、离心机试验^[6-7]研究以及数值模拟^[8]。根据现有的震害资料调查显示，桩周土体中含有可液化砂土层时，由动荷载作用引起的液化土较大水平位移是引起桩基破坏或失效的主要原因，因此对液化土体的流动特性的研究越来越受到关注。

NISHIMUR等^[9]将液化后土体视为流体，采用三轴扭剪试验研究液化土的流动特性。陈育民等^[10]借鉴了流体力学方法的思路，引入了剪应变率和表观黏度的概念，来分析液化后砂土的流动特性。马星宇等^[11]在室内黄土动液化试验的基础上对试样进行三轴剪切试验并利用流体力学方法对黄土液化流动性进行了研究。Usama^[12]提出光滑粒子流体力学法（SPH）和离散元法（DEM）来数值模拟强震过程中的砂土液化大变形。余俊等^[13]基于Navier-Stokes方程，将完全液化土体考虑成流体，用解析的方法研究了已液化土体中桩的水平振动问题。熊辉等^[14]考虑桩基承受竖向荷载作用时，将液化土体视为流体分析了竖向力作用下端承桩桩顶阻抗的分布。

综上，液化后的土体具有流体的特性，而黏滞系数是反映流体特征的一个重要参数，但目前针对液化土流动特性的研究往往忽略其黏滞系数的影响。Hwang等^[15]将液化土体的流动视为黏性流体流动，利用落球实验和托管试验得到液化砂土的表观黏度。陈昌昀等^[16]利用落球法测得了粉质液化土体的黏滞系数。刘涛等^[17]利用拖球法测得不同影响因素对液化土体黏滞系数的影响。本文利用解析研究的方法讨论了具有黏性流体特性的完全液化土中桩基的振动解析解，分析过程中认为桩随液化土一起振动不脱离；在求解液化土中振动桩基的桩顶阻抗时，将液化土体模拟成黏性流体，为简化计算略去流体竖向连续，考虑桩-流体的相互耦合作用，利用液化土层与未液化土层的连续关系通过解析的方法得到液化场地桩基的水平振动桩顶阻抗。

1. 计算模型及假定

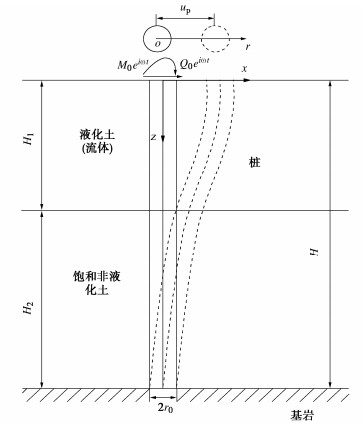
考虑地震后场地液化特征，桩基在有黏性液化土中运动时的计算简图如图 1所示。

图 1 桩基水平振动计算简图

Figure 1. Simplified calculation graph of horizontal vibration of foundation

下载: 全尺寸图片幻灯片

假定桩周上层土体为完全液化后的土体（流体），厚度为H₁；下层土为饱和非液化土，厚度为H₂^[13-14]；利用流体力学方法研究桩基的水平振动问题，假定桩基为理想圆形弹性杆，桩长H、半径r₀。M₀e^iωt、Q₀e^iωt为桩顶作用简谐激振力（ω为激振频率，t为作用时间），且桩与桩周土体在振动时均为小变形振动^[18-19]，桩-土接触面不发生滑移、脱离等现象，液化土层与饱和非液化土层接触面无相对位移。

2. 计算方程

2.1 黏性液化流体运动控制方程

根据流体力学的观点，当雷诺数较小时（孔隙介质中流体运动速度较慢），流体的黏性项作用远大于非线性项^[20]，考虑桩-土振动时流体的流速较慢，其线性解答可满足工程需要^[19]，并考虑水平振动桩基的运动对竖向运动特征影响不明显，可得柱坐标系下忽略z向黏性流体运动基本方程组为

$\frac{{\partial {u_r}}}{{\partial r}} + \frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial \theta }} + \frac{{{u_r}}}{r} = 0 \text{，}$

(1)

$\begin{array}{l} \rho \frac{{\partial {u_r}}}{{\partial t}} = - \frac{{\partial P}}{{\partial r}} + \mu \left( {\frac{{{\partial ^2}{u_r}}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {u_r}}}{{\partial r}} + {\kern 1pt} } \right.{\kern 1pt} {\kern 1pt}\\ \;\;\;\;\;\; \left. {\frac{1}{{{r^2}}}\frac{{{\partial ^2}{u_r}}}{{\partial {\theta ^2}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} + \frac{{{\partial ^2}{u_r}}}{{\partial {z^2}}} - \frac{2}{{{r^2}}}\frac{{\partial {u_\theta }}}{{\partial \theta }} - \frac{{{u_r}}}{{{r^2}}}} \right)\text{，} \end{array}$

(2)

$\begin{array}{l} \rho \frac{{\partial {u_\theta }}}{{\partial t}} = - \frac{1}{r}\frac{{\partial P}}{{\partial \theta }} + \mu \left( {\frac{{{\partial ^2}{u_\theta }}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial {u_\theta }}}{{\partial r}} + } \right.\\ \;\;\;\;\;\; \left. {\frac{1}{{{r^2}}}\frac{{{\partial ^2}{u_\theta }}}{{\partial {\theta ^2}}}{\kern 1pt} + \frac{{{\partial ^2}{u_\theta }}}{{\partial {z^2}}} + \frac{2}{{{r^2}}}\frac{{\partial {u_r}}}{{\partial \theta }} - \frac{{{u_\theta }}}{{{r^2}}}} \right)。 \end{array}$

(3)

式中：ρ为黏性液化流体的密度；r，z，θ为柱坐标系3个变量，u_r，u_θ为黏性液化流体径向、切向运动速度；P为黏性流体动压力；μ为黏滞系数。

根据计算模型及假定可得黏性液化流体满足下述边界条件：①忽略重力波对黏性流体的影响，流体表面正应力为零；②无穷远处，黏性流体振动衰减为零；③黏性液化流体底面相对位移为零。

2.2 饱和土振动方程

饱和土振动方程采用Biot动力固结方程，方程的求解过程及结果可参考文献[21]。

2.3 桩身振动方程

假定桩沿长度方向截面相等，桩长H，桩径为r₀，桩的弹性模量为E_P，桩的截面惯性矩为I_P。当 $0 \leqslant z \leqslant$ ${h_1}$ 桩的水平振动微分方程为

${E_{\text{p}}}{I_{\text{p}}}\frac{{{\partial ^4}{u_{\text{p}}}(z, t)}}{{\partial {z^4}}} + m\frac{{{\partial ^2}{u_{\text{p}}}(z, t)}}{{\partial {t^2}}} + {F_{\text{l}}} = 0 。$

(4)

式中：m为桩单位长度的质量； ${u_{\text{p}}}$ 为桩身振动； ${F_{\text{l}}}$ 为桩身所受黏性液化土流体动压力，

${F_{\text{l}}} = - \int_0^{2\pi } {{\text{(}}{\sigma _r}} {\left. {\cos \theta - {\tau _{r\theta }}\sin \theta )} \right|_{r = r}}_{_0}{r_0}{\text{d}}\theta 。$

(5)

式中： ${\sigma _r}$ ， ${\tau _{r\theta }}$ 分别为桩周所受黏性液化流体的径向、切向应力。

3. 方程求解

3.1 流体运动方程求解

对黏性液化流体引入势函数，

${u}_{r}=\frac{\partial \phi }{\partial r}+\frac{1}{r}\frac{\partial \varphi }{\partial \theta }\text{，}{u}_{\theta }=\frac{1}{r}\frac{\partial \phi }{\partial \theta }-\frac{\partial \varphi }{\partial r} 。$

(6)

式中： $\varphi$ ， $\phi$ 为液相速度势函数。

假定黏性液化土体-桩振动体系处于稳态振动状态，振动项中均含 ${{\text{e}}^{{\text{i}}\omega t}}$ 项，求解过程中均省略该项。将式（6）代入式（1）~（3）可得

${\nabla ^2}\varphi = 0\text{，}$

(7)

$\begin{array}{*{20}{c}} \rho {\text{i}}\omega \left( {\frac{{\partial \varphi }}{{\partial r}} + \frac{1}{r}\frac{{\partial \phi }}{{\partial \theta }}} \right) = - \frac{{\partial P}}{{\partial r}} + \mu \left( {\frac{1}{r}\frac{{\partial {\nabla ^2}\phi }}{{\partial \theta }} + } \right.\\ {\kern 1pt} \left. {\frac{{{\partial ^2}}}{{\partial {z^2}}}\frac{{\partial \varphi }}{{\partial r}} + \frac{1}{r}\frac{{{\partial ^2}}}{{\partial {z^2}}}\frac{{\partial \phi }}{{\partial \theta }}} \right) 。 \end{array}$

(8)

$\begin{array}{*{20}{c}} \rho {\text{i}}\omega \left( {\frac{1}{r}\frac{{\partial \varphi }}{{\partial \theta }} - \frac{{\partial \phi }}{{\partial r}}} \right) = - \frac{1}{r}\frac{{\partial P}}{{\partial \theta }} + \mu \left( { - \frac{{\partial {\nabla ^2}\phi }}{{\partial r}} - } \right.\\ \left. {\frac{{{\partial ^2}}}{{\partial {z^2}}}\frac{{\partial \phi }}{{\partial r}} + \frac{1}{r}\frac{{{\partial ^2}}}{{\partial {z^2}}}\frac{{\partial \varphi }}{{\partial \theta }}} \right)。\end{array}$

(9)

式中： ${\nabla ^2} = \frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}} + \frac{1}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {\theta ^2}}}$ 。

由式（8）、（9）可对方程解耦得

$\rho {\text{i}}\omega \phi = \mu {\nabla ^2}\phi + \mu \frac{{{\partial ^2}\phi }}{{\partial {z^2}}}\text{，}$

(10)

$\rho {\text{i}}\omega \varphi = - P + \mu \frac{{{\partial ^2}\varphi }}{{\partial {z^2}}} 。$

(11)

由式（11）可知 $\phi ，P$ 有相同的z函数形式，结合边界条件，设其为级数和形式

$\varphi = \sum\limits_{n = 1}^\infty {{\varphi ^*}(r, \theta )\cosh ({g_n}z)} \text{，}$

(12)

$P = \sum\limits_{n = 1}^\infty {{P^*}(r, \theta )\cosh ({g_n}z)} \text{，}$

(13)

$\phi = \sum\limits_{n = 1}^\infty {{\phi ^*}(r, \theta )\cosh ({g_n}z)} 。$

(14)

式中：

${g_n} = \frac{{(2n - 1){\rm{i\pi }}}}{{2{H_1}}}{\text{ (}}n = 1, 2, 3 \cdots {\text{)}} 。$

(15)

将式（12）、（13）代入式（11），式（14）代入式（10）并化简，为简便记为级数形式，可得：

$\rho {\text{i}}\omega {\varphi ^*} + {P^*} - \mu {\varphi ^*}g_n^2 = 0\text{，}$

(16)

$\rho {\text{i}}\omega {\phi ^*} - \mu {\nabla ^2}{\phi ^*} - \mu {\phi ^*}g_n^2 = 0。$

(17)

对式（17）化简：

$({\nabla ^2} - \beta _1^2){\phi ^*} = 0。$

(18)

式中：

$\beta _1^2 = \frac{{\rho {\text{i}}\omega - \mu g_n^2}}{\mu }。$

(19)

利用分离变量法解方程并结合边界条件得

$\varphi = \lambda A\frac{1}{r}\cos \theta \cosh ({g_n}z)\text{，}$

(20)

$\phi = A{K_1}({\beta _1}r)\sin \theta \cosh ({g_n}z) 。$

(21)

式中： $\lambda$ =r₀K₁( ${\beta _1}{r_0}$ )+0.5 ${\beta _1}r_0^2$ K₀( ${\beta _1}{r_0}$ )；A为任意常数；K₁(β₁r)，K₀( ${\beta _1}r$ )为贝塞尔函数；n=1，2，3，…。

由式（20），（21）可得

$P = \frac{{A\lambda }}{r}(\mu g_n^2 - \rho {\text{i}}\omega )\cos \theta \cosh ({g_n}z)。$

(22)

又由式（5）得

${F_l} = {\text{π }}A\cosh ({g_n}z) \cdot$

${\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\lambda \mu g_n^2 - \lambda \rho {\text{i}}\omega - \mu \beta _1^2{r_0}{K_1}({\beta _1}{r_0})} \right] 。$

(23)

3.2 桩顶阻抗求解

将式（23）代入式（4），并化简得

$\frac{{{{\text{d}}^4}{u_p}(z)}}{{{\text{d}}{z^4}}} - \beta _2^4{u_p}(z) = - \frac{{A{A_n}}}{{{E_{\text{p}}}{I_{\text{p}}}}}\cosh ({g_n}z) 。$

(24)

式中： ${\beta _2} = \sqrt[4]{{\frac{{m{\omega ^2}}}{{{E_{\text{p}}}{I_{\text{p}}}}}}}$ ,

${A_n} = \left\{ {{\text{π }}\left[ {\lambda \mu g_n^2 - \lambda \rho {\text{i}}\omega - \mu \beta _1^2{r_0}{K_1}({\beta _1}{r_0})} \right]} \right\}。$

设特解为

$u_{\text{p}}^\# (z) = B\cosh ({g_n}z)。$

(25)

式中：

$B = - \frac{{A{A_n}}}{{{E_{\text{p}}}{I_{\text{p}}}(g_n^4 - \beta _2^4)}} 。$

(26)

故该方程的解为

$\begin{array}{l} {u_{\text{p}}}(z) = {C_1}\sin ({\beta _2}z) + {C_2}\cos ({\beta _2}z){\kern 1pt} {\kern 1pt} + {C_3}\sinh ({\beta _2}z) + \\ \;\;\;\;\;\; \;\;\;\;\;\;{C_4}\cosh ({\beta _2}z) - \frac{{A{A_n}}}{{{E_{\text{p}}}{I_{\text{p}}}(g_n^4 - \beta _2^4)}}\cosh ({g_n}z) 。 \end{array}$

(27)

由流体与桩身不脱离：

$\frac{{\partial \varphi }}{{\partial r}}{|_{r = {r_0}}} = \frac{{\partial {u_p}}}{{\partial t}}\cos \theta 。$

(28)

将式（20），（27）代入式（28），可化简得

$\begin{array}{*{20}{c}} {{C_1}\sin ({\beta _2}z) + {C_2}\cos ({\beta _2}z) + {C_3}\sinh ({\beta _2}z) + {C_4}\cosh ({\beta _2}z)}\\ {= {A_1}\cosh ({g_n}z)\left[ {\frac{{{A_{1n}}i\omega r_0^2 - \lambda {E_{\text{p}}}{I_{\text{p}}}(g_n^4 - \beta _2^4)}}{{{E_{\text{p}}}{I_{\text{p}}}(g_n^4 - \beta _2^4)i\omega r_0^2}}} \right] 。} \end{array}$

(29)

将该式两边乘以 $\cosh ({g_m}z)$ 然后在区间 $[0, {H_1}]$ 上积分，利用余弦函数的正交性。

${\displaystyle {\int }_{0}^{{H}_{1}}\mathrm{cosh}({g}_{n}z})\mathrm{cosh}({g}_{m}z)\text{d}z=\left\{ \begin{array}{l}\frac{{H}_{1}}{2}（m=n）\\ 0\text{ }（m\ne n）\end{array} \right. 。$

(30)

可得：

${A_1} = \frac{{{C_1}{N_1} + {C_2}{N_2} + {C_3}{N_3} + {C_4}{N_4}}}{{\frac{{{H_1}}}{2}\left[ {\frac{{{A_{1n}}}}{{{E_{\text{p}}}{I_{\text{p}}}(g_n^4 - {\beta ^4})}} - \frac{\lambda }{{{\text{i}}\omega r_0^2}}} \right]}}。$

(31)

式中：N₁，N₂，N₃，N₄为积分常数。

整合常数项，令

$\vartheta = \frac{{2{\text{i}}\omega r_0^2{A_{1n}}}}{{{H_1}\left[ {{\text{i}}\omega r_0^2{A_{1n}} - \lambda {E_{\text{p}}}{I_{\text{p}}}(g_n^4 - \beta _2^4)} \right]}} 。$

(32)

可以得到方程的解为

$\begin{array}{l} {u_{\text{p}}}(z) = {C_1}\left[ {\sin ({\beta _2}z) - \sum\limits_{n = 1}^\infty {\vartheta {N_1}\cosh ({g_n}z)} } \right]{\kern 1pt} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_2}\left[ {\cos ({\beta _2}z) - \sum\limits_{n = 1}^\infty {\vartheta {N_2}\cosh ({g_n}z)} } \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_3}\left[ {\sinh ({\beta _2}z) - \sum\limits_{n = 1}^\infty {\vartheta {N_3}\cosh ({g_n}z)} } \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}{C_4}\left[ {\cosh ({\beta _2}z) - \sum\limits_{n = 1}^\infty {\vartheta {N_4}\cosh ({g_n}z)} } \right] 。 \end{array}$

(33)

由欧拉伯努利梁模型，结合材料力学中相关知识可知：

${\left[ {U{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\Phi}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{{{E_{\text{p}}}{I_{\text{p}}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{Q}{{{E_{\text{p}}}{I_{\text{p}}}}}{\kern 1pt} } \right]^{\text{T}}} = \left[ {{S_1}(z)} \right]{\left[ {{C_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_3}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_4}} \right]^{\text{T}}} 。$

(34)

${S_1}(z) = \left[ {\begin{array}{*{20}{c}} {a - e}&{b - f}&{c - g}&{d - h} \\ {{\beta _2}b - e}&{ - {\beta _2}a - f}&{{\beta _2}d - g}&{{\beta _2}c - h} \\ { - \beta _2^2a - e}&{ - \beta _2^2b - f}&{\beta _2^2c - g}&{\beta _2^2d - h} \\ { - \beta _2^3b - e}&{\beta _2^3a - f}&{\beta _2^3d - g}&{\beta _2^3c - h} \end{array}} \right] 。$

(35)

式中：a= $\sin ({\beta _2}z)$ ；b= $\cos ({\beta _2}z)$ ；c= $\sinh ({g_n}z)$ ；d= $\cosh ({g_n}z)$ ；e= $\sum\limits_{n = 1}^\infty {\vartheta {N_1}d}$ ；f= $\sum\limits_{n = 1}^\infty {\vartheta {N_2}d}$ ；g= $\sum\limits_{n = 1}^\infty {\vartheta {N_3}d}$ ；h= $\sum\limits_{n = 1}^\infty {\vartheta {N_4}d}$ 。

设桩头、液化土与饱和土交界处、桩底处桩位移，内力分别为U₀， ${{\mathit{\Phi}} _0}$ ，M₀，Q₀，U₁， ${{\mathit{\Phi}} _1}$ ，M₁，Q₁，U₂， ${{\mathit{\Phi}} _2}$ ，M₂，Q₂。则有：

$\begin{array}{*{20}{c}} {{\left[ {{U_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\Phi}} _1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{M_1}}}{{{E_{\text{p}}}{I_{\text{p}}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{Q_1}}}{{{E_{\text{p}}}{I_{\text{p}}}}}} \right]^{\text{T}}} = \left[ {{S_1}(0)} \right]{\left[ {{S_1}({H_1})} \right]^{ - 1}} \cdot}\\ {{\left[ {{U_0}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\Phi}} _0}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{M_0}}}{{{E_{\text{p}}}{I_{\text{p}}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{Q_0}}}{{{E_{\text{p}}}{I_{\text{p}}}}}} \right]^{\text{T}}} 。} \end{array}$

(36)

同理可有：

$\begin{array}{*{20}{c}} {{\left[ {{U_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\Phi}} _2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{M_2}}}{{{E_{\text{p}}}{I_{\text{p}}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{Q_2}}}{{{E_{\text{p}}}{I_{\text{p}}}}}} \right]^{\text{T}}} = \left[ {{S_2}({H_2})} \right]{\left[ {{S_2}(0)} \right]^{ - 1}} \cdot}\\ {{\left[ {{U_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\Phi}} _1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{M_1}}}{{{E_{\text{p}}}{I_{\text{p}}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{Q_1}}}{{{E_{\text{p}}}{I_{\text{p}}}}}} \right]^{\text{T}}} 。} \end{array}$

(37)

式中， $\left[{S}_{2}(z)\right]与\left[{S}_{1}(z)\right]$ 有相同的矩阵形式，可参考文献[21]，则有

${\left[ {{U_2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\Phi}} _2}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{M_2}}}{{{E_{\text{p}}}{I_{\text{p}}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{Q_2}}}{{{E_{\text{p}}}{I_{\text{p}}}}}} \right]^{\text{T}}} = \left[ {{S_n}} \right]{\left[ {{U_0}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\Phi}} _0}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{M_0}}}{{{E_{\text{p}}}{I_{\text{p}}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{Q_0}}}{{{E_{\text{p}}}{I_{\text{p}}}}}} \right]^{\text{T}}} 。$

(38)

式中：

$\left[ {{S_n}} \right] = \left[ {{S_2}({H_2})} \right]{\left[ {{S_2}(0)} \right]^{ - 1}}\left[ {{S_1}(0)} \right]{\left[ {{S_1}({H_1})} \right]^{ - 1}} 。$

(39)

（1）当桩底为固定边界

${U_2} = 0, {{\mathit{\Phi}} _2} = 0。$

(40)

于是有：

$\left[ {\frac{{{M_0}(0)}}{{{E_{\text{p}}}{I_{\text{p}}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{Q_0}(0)}}{{{E_{\text{p}}}{I_{\text{p}}}}}} \right] = {K_{\text{S}}}{\left[ {{U_0}(0){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\Phi}} _0}(0)} \right]^{\text{T}}} 。$

(41)

式中：

${K}_{\text{S}}=-{\left[\begin{array}{cc}{S}_{n}(1, 3)& {S}_{n}(1, 4)\\ {S}_{n}(2, 3)& {S}_{n}(2, 4)\end{array}\right]}^{-1}\left[\begin{array}{cc}{S}_{n}(1, 1)& {S}_{n}(1, 2)\\ {S}_{n}(2, 1)& {S}_{n}(2, 2)\end{array}\right]\text{ }\text{；}$

(42)

${S_n}(i, j)$ 为 ${S_n}$ 矩阵第i行第j列值（下同）。

（2）当桩底为自由边界

$M_2=0, \quad Q_2=0 。$

(43)

于是可以有，

$\left[ {\frac{{{M_0}(0)}}{{{E_{\text{p}}}{I_{\text{p}}}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{Q_0}(0)}}{{{E_{\text{p}}}{I_{\text{p}}}}}} \right] = {K_S}{\left[ {{U_0}(0){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\Phi}} _0}(0)} \right]^{\text{T}}} 。$

(44)

式中：

${K_{\text{S}}} = - {\left[ {\begin{array}{*{20}{c}} {{S_n}(3, 3)}&{{S_n}(3, 4)} \\ {{S_n}(4, 3)}&{{S_n}(4, 4)} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{S_n}(3, 1)}&{{S_n}(3, 2)} \\ {{S_n}(4, 1)}&{{S_n}(4, 2)} \end{array}} \right]。$

(45)

根据动力阻抗的定义，可得到单桩水平动力阻抗K_h，摇摆动力阻抗K_r以及水平-摇摆耦合动力阻抗K_hr。

$\left. \begin{array}{l} {K}_{\mathrm{h}}={K}_{S}(2, 1)\text{ }\text{，}\\ {K}_{\text{r}}={K}_{\text{S}}(1, 2)\text{ }\text{，}\\ {K}_{\text{hr}}={K}_{\text{S}}(1, 1)={K}_{\text{S}}(2, 2)\text{ }。 \end{array} \right\}$

(46)

4. 结果验证

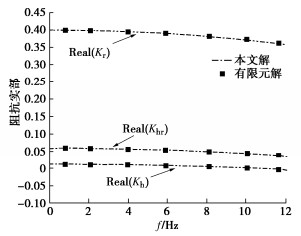
为验证本文解的正确性，利用软件ABAQUS建立液化流体-桩数值分析模型，桩-流体参数：桩长H=1.0 m，桩径r₀=1.0 m，弹性模量E_P=25.5 GPa，桩身密度 ${\rho _{\text{p}}}$ =2500 kg/m³，流体密度 $\rho$ =1000 kg/m³。为避免边界反射效应的影响，桩周流体径向距离设置为桩半径的20倍，流体外侧采用非反射边界，在有限元模型中，桩采用C3D8R单元，液化流体采用AC3D8声单元，桩-流体界面设置Embedded接触，在桩顶施加单位集中力和弯矩，输入振动频率f的区间范围为0∶12（Hz），有限元模型见图 2。

图 2 液化流体-桩数值分析模型

Figure 2. Numerical analysis model for liquefied fluid-pile

下载: 全尺寸图片幻灯片

利用有限元软件计算所得结果与本文解的对比如图 3所示，K_h为水平阻抗，K_r为摇摆阻抗，K_hr为水平-摇摆耦合阻抗，可以看出本文理论解与有限元模拟计算结果较为吻合，从而验证了本文解的正确性。

图 3 本文解与有限元解的对比

Figure 3. Comparison between calculated and FEM results

下载: 全尺寸图片幻灯片

5. 参数分析与讨论

5.1 流体黏滞系数对桩顶阻抗的影响

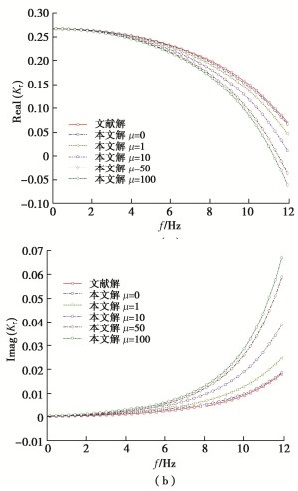
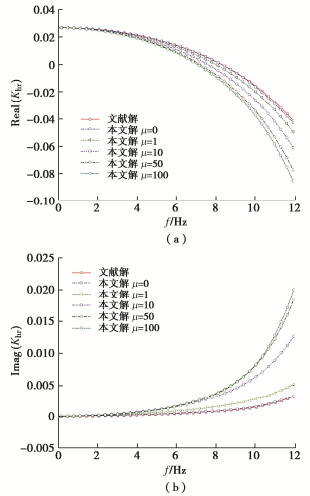
参数分析以上覆黏性流体，下部为饱和土体的地基为例，分析流体黏滞系数对分层地基中桩基础桩顶阻抗的影响，当μ=0 kPa·s时，本文解退化为无黏性液化土中桩的水平振动问题，文献[13]给出了无黏性液化流体中桩的水平振动桩顶阻抗的解析解，且文献[16, 17]给出了常见液化土体的黏滞系数，从文献可知液化砂土的黏滞系数主要集中在1~11 kPa·s，液化粉土的黏滞系数在50~100 kPa·s的范围内。

为分析黏滞系数对阻抗的影响，将本文解与文献[13]解进行计算对比（图 4），计算时参数取值如下：液化土中桩长H₁=13 m，饱和土中桩长H₂=2 m，桩径r₀=1 m，液化土黏滞系数分别取μ为0，1，10，50，100 kPa·s，桩身密度 ${\rho _{\text{p}}}$ ₌2500 kg/m³，E_P=2.55×10⁷ kPa，液化土层下饱和土层参数取值：土体孔隙率n=0.375，G=2×10⁷ kPa，饱和土骨架密度ρ_s=2700 kg/m³，饱和土的动力渗透系数 ${k'_{\text{d}}}$ =1×10^-4 m/kg·s，液化土密度ρ=2000 kg/m³。图中纵坐标Real代表实部，Imag代表虚部。

图 4 黏滞系数水平阻抗因子

Figure 4. Horizontal impedance factor of coefficent of viscosity

下载: 全尺寸图片幻灯片

从图 4~6可以看出：当μ=0 kPa·s时本文解与文献解在低频阶段基本一致，两解在高频阶段有细微差别，其在高频阶段水平阻抗、摇摆阻抗、水平-摇摆耦合阻抗计算结果最大差值分别相差7.5%，6.7%，6.4%，两解间存在的误差主要是由于本文解在求解势函数时为简化计算忽略竖向位移。从图 3可以看到激励频率较低时，复阻抗的实部随着频率增大从正到负，这是因为在参数分析时，选取的上层流体层厚较大，桩基振动特性受流体的影响较大，因此其水平阻抗的实部会随频率增大从正到负，这意味着桩基会产生与作用力相反的变形。

图 5 黏滞系数摇摆阻抗因子

Figure 5. Swing impedance factor of coefficent of viscosity

下载: 全尺寸图片幻灯片

图 6 黏滞系数耦合阻抗因子

Figure 6. Coupling impedance factor of coefficent of viscosity

下载: 全尺寸图片幻灯片

由图 4~6可得表观动力黏滞数值变化时对桩顶阻抗的影响，由图可知：在低频阶段黏性流体黏滞系数的变化对桩顶的刚度阻抗和阻尼阻抗的影响较小；随着频率的增大黏滞系数取值对阻尼阻抗的影响程度明显大于其对刚度阻抗的影响；黏滞系数增大，刚度阻抗减小，阻尼阻抗显著增大，因此在计算高频振动桩顶阻抗因子时，流体黏性的影响不可忽略。当流体的黏滞系数增加到一定数值时，黏滞系数的取值对桩顶阻抗的影响会降低，μ从50 kPa·s增加到100 kPa·s时桩顶阻抗的变化幅度已经很小了，因此砂土比粉土在液化时其桩顶阻抗受黏性特征影响更为明显。

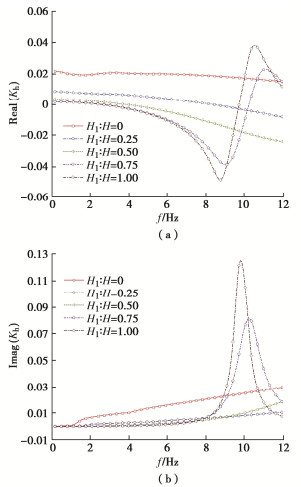
5.2 液化层厚对桩顶阻抗的影响

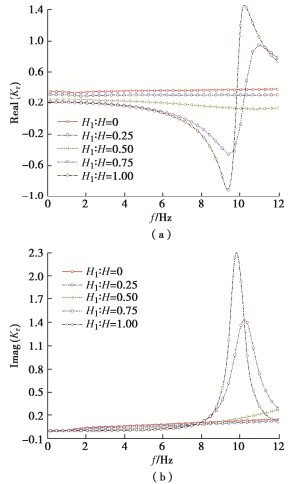
为分析液化土厚度对桩顶阻抗的影响，研究桩长一定，不同液化土层与饱和土层厚度比值时，桩顶阻抗的分布情况。分析时土层参数取值：桩长H=20 m，μ=10 kPa·s^[16-17]，H₁︰H为0，0.25，0.5，0.75，1，H₁︰H=0，H₁︰H=1分别为单层饱和土、黏性流体中嵌岩桩桩顶阻抗，其余参数同上。

由图 7~9可知：随着频率的增加，当液化层厚度增加时，桩顶刚度阻抗与阻尼阻抗均减小，并且减小的幅度逐渐增大；当液化深度大于0.5H时，阻尼阻抗在低频段基本可以认为无变化，当液化深度大于0.75H时，刚度阻抗在低频段基本可以认为无变化；在高频阶段随着液化深度的增大桩顶阻抗的共振现象变得显著，其共振频率减小，但共振幅值逐渐增大；达到共振频率时刚度阻抗幅值约为阻尼幅值的40%，且桩顶阻抗会出现负刚度的情况，故在易液化的场地进行桩基动力设计时要密切注意土体液化深度的大小。

图 7 液化深度水平阻抗因子

Figure 7. Horizontal impedance factor of liquefaction depth

下载: 全尺寸图片幻灯片

图 8 液化深度摇摆阻抗因子

Figure 8. Swing impedance factor of liquefaction depth

下载: 全尺寸图片幻灯片

图 9 液化深度耦合阻抗因子

Figure 9. Coupling impedance factor of liquefaction depth

下载: 全尺寸图片幻灯片

5.3 液化流体密度对桩顶阻抗的影响

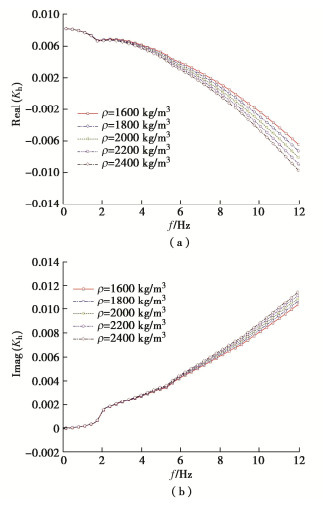
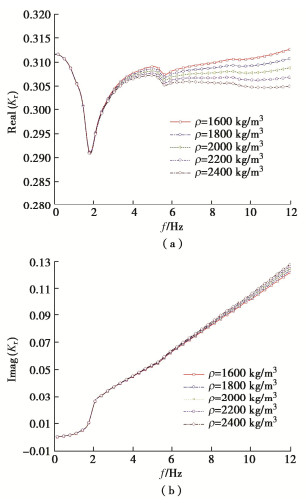
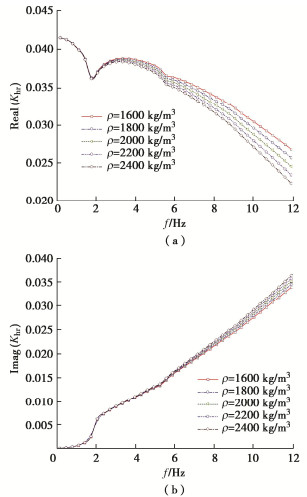
为分析液化流体密度对桩顶阻抗的影响，研究桩长一定、液化土深度一定（H₁=5 m，H₂=15 m），液化流体密度不同时（ρ为1600，1800，2000，2200，2400 kg/m³）桩顶阻抗的分布情况，分析时土层参数取值同上，μ=10 kPa·s。

图 10~12表明在低频阶段有黏性液化流体的密度对液化土中水平振动桩基的桩顶阻抗影响程度较小；频率增加，桩顶刚度阻抗随黏性流体密度增大而减小但减小的幅度随密度增大有所下降，阻尼阻抗在高频阶段随流体密度增大而增加，刚度阻抗减小的原因是黏性流体密度增大其对桩的作用力也会随频率增大。

图 10 黏性流体密度水平阻抗因子

Figure 10. Horizontal impedance factor of density of viscous fluid

下载: 全尺寸图片幻灯片

图 11 黏性流体密度摇摆阻抗因子

Figure 11. Swing impedance factor of density of viscous fluid

下载: 全尺寸图片幻灯片

图 12 黏性流体密度耦合阻抗因子

Figure 12. Coupling impedance factor of density of viscous fluid

下载: 全尺寸图片幻灯片

6. 结论

将液化后的土体视为流体并考虑其黏性，未液化按饱和土体考虑，结合黏性流体运动方程、边界条件，利用分离变量法和矩阵传递法得到黏性流体中桩顶水平振动动力阻抗解析表达式。通过与已有解对比和对端承桩桩顶阻抗的参数分析，得到4点结论。

（1）考虑液化后土体的黏性，将其视为黏性流体求解液化土中桩顶阻抗的解析解，进行有限元数值模拟可验证该解的正确性。

（2）在低频阶段液化流体黏滞系数对桩顶阻抗的影响较小，在高频阶段液化流体黏滞系数对桩顶阻抗的影响较大，高频阶段桩顶刚度阻抗随液化流体黏滞系数增加而减小；阻尼阻抗随液化流体黏滞系数增加而增大；且流体黏滞系数增大时引起的桩顶阻尼阻抗的变化幅度远大于刚度阻抗的变化。

（3）液化深度增加，桩顶阻抗减小；当液化深度大于0.5H时，阻尼阻抗在低频阶段基本可认为无变化，当液化深度大于0.75H时，刚度阻抗在低频阶段基本可认为无变化。在高频阶段液化深度增加使桩顶阻抗共振频率减小，共振幅值增大，达到共振频率时刚度阻抗幅值约为阻尼幅值的40%。

（4）低频阶段流体密度对桩顶阻抗影响较小，考虑流体对桩身的作用力，随频率增加，桩顶刚度阻抗随流体密度增加而减小，但其减小的幅度随密度的增加而降低；高频阶段阻尼阻抗随流体密度增加而增大，但其增大的幅度有限。

图 1 桩基水平振动计算简图

Figure 1. Simplified calculation graph of horizontal vibration of foundation

下载: 全尺寸图片幻灯片

图 2 液化流体-桩数值分析模型

Figure 2. Numerical analysis model for liquefied fluid-pile

下载: 全尺寸图片幻灯片

图 3 本文解与有限元解的对比

Figure 3. Comparison between calculated and FEM results

下载: 全尺寸图片幻灯片

图 4 黏滞系数水平阻抗因子

Figure 4. Horizontal impedance factor of coefficent of viscosity

下载: 全尺寸图片幻灯片

图 5 黏滞系数摇摆阻抗因子

Figure 5. Swing impedance factor of coefficent of viscosity

下载: 全尺寸图片幻灯片

图 6 黏滞系数耦合阻抗因子

Figure 6. Coupling impedance factor of coefficent of viscosity

下载: 全尺寸图片幻灯片

图 7 液化深度水平阻抗因子

Figure 7. Horizontal impedance factor of liquefaction depth

下载: 全尺寸图片幻灯片

图 8 液化深度摇摆阻抗因子

Figure 8. Swing impedance factor of liquefaction depth

下载: 全尺寸图片幻灯片

图 9 液化深度耦合阻抗因子

Figure 9. Coupling impedance factor of liquefaction depth

下载: 全尺寸图片幻灯片

图 10 黏性流体密度水平阻抗因子

Figure 10. Horizontal impedance factor of density of viscous fluid

下载: 全尺寸图片幻灯片

图 11 黏性流体密度摇摆阻抗因子

Figure 11. Swing impedance factor of density of viscous fluid

下载: 全尺寸图片幻灯片

图 12 黏性流体密度耦合阻抗因子

Figure 12. Coupling impedance factor of density of viscous fluid

下载: 全尺寸图片幻灯片

参考文献(21)

[1]	DASH S, ROUHOLAMIN M, LOMBARDI D, et al. A practical method for construction of p-y curves for liquefiable soils[J]. Soil Dynamics and Earthquake Engineering, 2017, 97: 478-481. doi: 10.1016/j.soildyn.2017.03.002
[2]	张小玲, 朱冬至, 许成顺, 等. 强度弱化条件下饱和砂土地基中桩-土相互作用p-y曲线研究[J]. 岩土力学, 2020, 41(7): 2252-2260. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202007012.htm ZHANG Xiaoling, ZHU Dongzhi, XU Chengshun, et al. Research on p-y curves of soil-pile interaction in saturated sand foundation in weakened state[J]. Rock and Soil Mechanics, 2020, 41(7): 2252-2260. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202007012.htm
[3]	EBEIDO A, ELGAMAL A, TOKIMATSU K, et al. Pile and pile-group response to liquefaction-induced lateral spreading in four large-scale shake-table experiments[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2019, 145(10): 04019080. doi: 10.1061/(ASCE)GT.1943-5606.0002142
[4]	YANG Z J, ZHANG X R, YANG R L, et al. Shake table modeling of pile foundation performance in laterally spreading frozen ground crust overlying liquefiable soils[J]. Journal of Cold Regions Engineering, 2018, 32(4): 04018012. doi: 10.1061/(ASCE)CR.1943-5495.0000171
[5]	张恒源, 钱德玲, 沈超, 等. 水平和竖向地震作用下液化场地群桩基础动力响应试验研究[J]. 岩土力学, 2020, 41(3): 905-914. ZHANG Hengyuan, QIAN Deling, SHEN Chao, et al. Experimental investigation on dynamic response of pile group foundation on liquefiable ground subjected to horizontal and vertical earthquake excitations[J]. Rock and Soil Mechanics, 2020, 41(3): 905-914. (in Chinese)
[6]	汪明武, 赵奎元, 朱其坤, 等. 可液化场地微型桩地震响应特性研究[J]. 岩土力学, 2016, 37(6): 1543-1549. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201606003.htm WANG Mingwu, ZHAO Kuiyuan, ZHU Qikun, et al. Seismic responses of a micropile in liquefiable soils[J]. Rock and Soil Mechanics, 2016, 37(6): 1543-1549. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201606003.htm
[7]	张健, 李雨润, 戎贤, 等. 液化土中斜群桩承台动力响应特性及桩身弯矩分布规律研究[J]. 地震工程与工程振动, 2021, 41(3): 235-244. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202103023.htm ZHANG Jian, LI Yurun, RONG Xian, et al. Dynamic response of pile cap and distribution law of pile bending moment for batter pile group in liquefied soil[J]. Earthquake Engineering and Engineering Dynamics, 2021, 41(3): 235-244. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC202103023.htm
[8]	WANG R, LIU X, ZHANG J M. Numerical analysis of the seismic inertial and kinematic effects on pile bending moment in liquefiable soils[J]. Acta Geotechnica, 2017, 12(4): 773-791. doi: 10.1007/s11440-016-0487-z
[9]	NISHIMURA S, TOWHATA I, HONDA T. Laboratory shear tests on viscous nature of liquefied sand[J]. Soils and Foundations, 2002, 42(4): 89-98. doi: 10.3208/sandf.42.4_89
[10]	陈育民, 刘汉龙, 周云东. 液化及液化后砂土的流动特性分析[J]. 岩土工程学报, 2006, 28(9): 1139-1143. doi: 10.3321/j.issn:1000-4548.2006.09.017 CHEN Yumin, LIU Hanlong, ZHOU Yundong. Analysis on flow characteristics of liquefied and post-liquefied sand[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1139-1143. (in Chinese) doi: 10.3321/j.issn:1000-4548.2006.09.017
[11]	马星宇, 王兰民, 王谦, 等. 饱和黄土液化流动性试验研究[J]. 岩土工程学报, 2021, 43(S1): 161-165. doi: 10.11779/CJGE2021S1029 MA Xingyu, WANG Lanmin, WANG Qian, et al. Experimental study on liquefaction fluidity of saturated loess[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(S1): 161-165. (in Chinese) doi: 10.11779/CJGE2021S1029
[12]	USAMA SHAMY E. Coupled SPH-DEM simulations of liquefaction-induced flow failure[J]. Soil Dynamics and Earthquake Engineering, 2021, 144: 106683. doi: 10.1016/j.soildyn.2021.106683
[13]	余俊, 何月, 张立, 等. 液化土中桩水平振动响应分析[J]. 岩土工程学报, 2017, 39(3): 573-580. doi: 10.11779/CJGE201703023 YU Jun, HE Yue, ZHANG Li, et al. Dynamical characteristics of piles in liquefied soil under horizontal vibration[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(3): 573-580. (in Chinese) doi: 10.11779/CJGE201703023
[14]	熊辉, 杨丰. 文克尔地基模型下液化土桩基水平振动响应分析[J]. 岩土力学, 2020, 41(1): 103-110. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202001013.htm XIONG Hui, YANG Feng. Horizontal vibration response analysis of pile foundation in liquefied soil under Winkler foundation model[J]. Rock and Soil Mechanics, 2020, 41(1): 103-110. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202001013.htm
[15]	HWANG J I, KIM C Y, CHUNG C K, et al. Viscous fluid characteristics of liquefied soils and behavior of piles subjected to flow of liquefied soils[J]. Soil Dynamics and Earthquake Engineering, 2006, 26(2-4): 313-323.
[16]	陈昌昀, 张鹏, 许国辉, 等. 落球法测定波动液化土黏滞性的试验研究[J]. 中国海洋大学学报(自然科学版), 2017, 47(6): 119-123. https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY201706015.htm CHEN Changyun, ZHANG Peng, XU Guohui, et al. The experimental study on viscosity of the wave-induced liquefaction silty soil by falling ball method[J]. Periodical of Ocean University of China, 2017, 47(6): 119-123. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-QDHY201706015.htm
[17]	刘涛, 崔逢, 张美鑫. 波浪作用下液化粉土流动特性拖球试验研究[J]. 海洋学报, 2016, 38(3): 123-130. https://www.cnki.com.cn/Article/CJFDTOTAL-SEAC201603012.htm LIU Tao, CUI Feng, ZHANG Meixin. Dragging ball test on flow characteristics of liquefied silt under wave loading[J]. Haiyang Xuebao, 2016, 38(3): 123-130. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SEAC201603012.htm
[18]	杨骁, 何光辉. 横向扩展液化土中单桩-土系统的非线性分析[J]. 岩土力学, 2012, 33(7): 2189-2195. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201207041.htm YANG Xiao, HE Guanghui. Nonlinear analysis of single pile-soil system in lateral spreading liquefied soil[J]. Rock and Soil Mechanics, 2012, 33(7): 2189-2195. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201207041.htm
[19]	黄雨, 八嶋厚, 张锋. 液化场地桩-土-结构动力相互作用的有限元分析[J]. 岩土工程学报, 2005, 27(6): 646-651. http://www.cgejournal.com/cn/article/id/11695 HUANG Yu, YASHIMA Atsushi, ZHANG Feng. Finite element analysis of pile-soil-structure dynamic interaction in liquefiable site[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(6): 646-651. (in Chinese) http://www.cgejournal.com/cn/article/id/11695
[20]	章梓雄, 董曾南. 黏性流体力学[M]. 2版. 北京: 清华大学出版社, 2011. ZHANG Zixiong, DONG Zengnan. Viscous Fluid Mechanics[M]. 2nd ed. Beijing: Tsinghua University Press, 2011. (in Chinese)
[21]	余俊, 尚守平, 李忠, 等. 饱和土中端承桩水平振动动力响应分析[J]. 岩土工程学报, 2009, 31(3): 408-415. http://www.cgejournal.com/cn/article/id/13184 YU Jun, SHANG Shouping, LI Zhong, et al. Dynamical characteristics of an end bearing pile embedded in saturated soil under horizontal vibration[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(3): 408-415. (in Chinese) http://www.cgejournal.com/cn/article/id/13184