穿断层分段柔性接头隧道纵向地震响应解析解

禹海涛; 卫一博

doi:10.11779/CJGE20220315

穿断层分段柔性接头隧道纵向地震响应解析解 English Version

禹海涛^1,,
卫一博²

1.
同济大学土木工程防灾国家重点实验室，上海 200092
2.
同济大学地下建筑与工程系，上海 200092

基金项目:

国家自然科学基金项目 41922059

国家自然科学基金项目 42177134

中央高校基本科研业务费专项资金项目

详细信息

作者简介:
禹海涛(1983—)，男，博士，教授，主要从事地下工程防灾减灾方面的研究工作。E-mail: yuhaitao@tongji.edu.cn

中图分类号: TU43
计量
- 文章访问数: 377
- HTML全文浏览量: 50
- PDF下载量: 129
出版历程
- 收稿日期: 2022-03-21
- 网络出版日期: 2023-05-18
- 刊出日期: 2023-04-30

Analytical solution for longitudinal seismic response of tunnels with segmental flexible joints crossing faults

YU Haitao^1,,
WEI Yibo²

1.
State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
2.
Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China

摘要

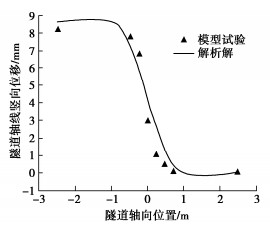
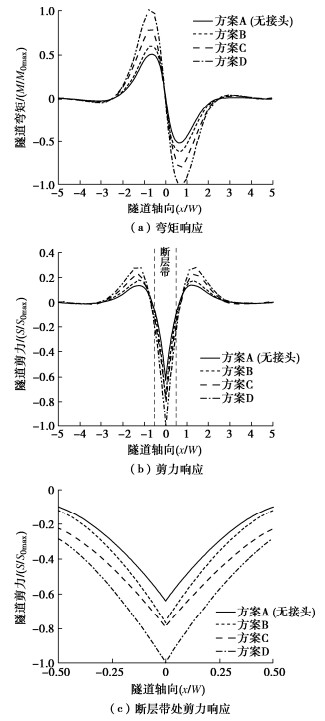
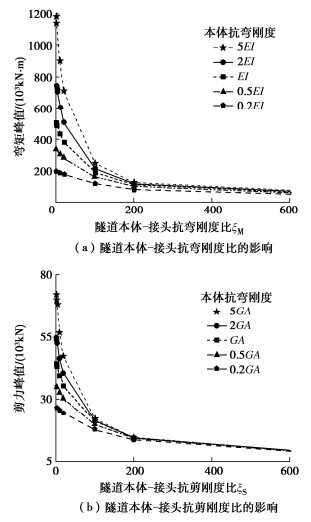
摘要: 地震发生伴随的断层错动是穿断层隧道灾变防控的重点和难点，目前比较有效的措施是通过设置柔性接头来适应断层的错动，但是对于柔性接头隧道的分段设计和参数取值缺少理论依据。以穿断层分段柔性接头隧道为研究对象，将分段隧道简化成有限长梁，隧道接头简化为剪切和弯曲弹簧元件，围岩简化为Pasternak双参数地基。为了合理考虑断层场地的不连续性，将断层带及上、下盘的非连续位移场等效为荷载施加在隧道梁上。基于建立的控制方程及边界条件，推导出分段柔性接头隧道在断层错动作用下的纵向地震响应解析解。通过与相同计算条件下的模型试验和数值计算结果对比分析，验证了解析方法的正确性。最后应用解析解对穿断层分段柔性接头隧道设计的关键参数进行敏感性分析，揭示了分段柔性接头布置方式和隧道本体-接头刚度比等因素对隧道结构内力响应的影响规律。结果表明：设置柔性接头可有效降低断层带影响区域内隧道结构纵向的内力响应，且柔性接头数量越多，隧道结构内力响应越小，若将柔性接头分别布置于断层错动面、断层与上/下盘交界面处，可以显著降低隧道结构的内力响应；而通过调整接头刚度来增大隧道本体-接头刚度比可以进一步降低隧道结构的内力响应。研究可为穿断层隧道抗震分析与分段柔性接头设计提供理论依据。
- 穿断层隧道 /
- 断层错动 /
- 分段柔性接头 /
- 地震响应 /
- 解析解
Abstract: The seismic damage induced by fault dislocation is a long-standing problem in the disaster prevention and control of tunnels crossing faults. Setting segmental flexible joints is an effective aseismic measure in the engineering practices. At present, no analytical solutions are available for the design of segmental flexible joints. An analytical solution for longitudinal seismic response of tunnels with segmental flexible joints crossing faults is presented. For the derivation, the segmental tunnel is assumed as a finite Euler-Bernoulli beam on the Pasternak two-parameter foundation, and the tunnel joints are simplified as the shear and bending spring elements. The discontinuous displacement fields in the fault zone are simplified as the external loads exerted on the beam, which considers the discontinuity of the fault site. The analytical solution for the longitudinal seismic response of tunnels with segmental flexible joints under fault dislocation is derived based on the established governing equations and boundary conditions. The proposed solution is verified by comparing its results with those from the tests and FEM model. Finally, the sensitivity analysis is carried out to investigate the influences of the setting plans for segmental flexible joints and the tunnel-joint stiffness ratio on the response of internal force of tunnel structures. The results indicate that flexible joints can effectively reduce the response of longitudinal internal force of tunnel structures in the affected area by the fault dislocation, and the response of internal force of tunnel structures is effectively reduced with the increase of flexible joints. It is concluded that the response of internal force can be significantly reduced when the flexible joints are respectively arranged on the fault dislocation surface and the interface between the faults and the hanging wall/footwall. Besides, the response of internal force of tunnels can be further reduced by increasing the tunnel-joint stiffness ratio. The research may provide a theoretical basis for the seismic analysis and the design of tunnels with flexible joints crossing faults.
- tunnel crossing fault /
- fault dislocation /
- segmental flexible joint /
- seismic response /
- analytical solution

HTML全文

0. 引言

当前中国隧道建设方兴未艾，工程中出现了不少多洞近距离并行设置的情况。隧道建设期间，相邻隧道净距较小时，将存在明显的相互影响，降低围岩稳定性。多洞并行隧道围岩稳定性及失稳破坏机理问题，亟需从理论计算分析等方面开展深入研究，以促进围岩稳定性评价及加固方案制定等工作。

对于隧道围岩稳定性课题，岩土塑性极限分析上限法可用于探究极限状态下隧道临界荷载与围岩潜在破坏模式^[1-9]。在并行隧道方面，谢骏等^[10]构建了双洞并行圆形隧道的破坏模式，获得了稳定性系数上限解；吕绍文^[11]应用平移破坏模式推导了双洞平行隧道内部支护力上限解表达式；Osman^[12]提出了双洞并行隧道连续变形破坏模式；Yamamoto等^[13]采用刚性滑块上限法和极限分析上、下限有限元法研究了双洞圆形隧道稳定性；Sahoo等^[14]应用极限分析上限有限元法分析了双洞并行隧道的稳定性；Zhang等^[15]和Yang等^[16]采用刚体平动运动单元上限法评价了多参数影响下的并行双洞椭圆和圆形隧道稳定性，获得了围岩滑移线网破坏模式。

隧道围岩稳定性评价可分为强度折减法^[17]获得安全系数和荷载增加法对应的稳定系数。上述研究多采用荷载增加法，考虑了隧道内部支护力^[10-12]、地表超载^{[13, 16]}和围岩自重^[14-15]等因素的影响。对于双洞并行隧道围岩稳定性的文献报道，还包括应用计算分析^[18]和模型试验^[19]等研究手段。

由于铁路、公路及市政交通廊道的空间限制，工程中出现了三洞并行小净距隧道^[20-23], 甚至四洞并行的情况^[24]。此时，小净距条件下相邻隧道相互影响集中体现在中夹岩区域的稳定性，净间距对围岩潜在破坏模式的影响较之并行双洞的情况更加显著，需开展定量分析研究。

本文针对多洞隧道围岩稳定性问题，考虑自重作用下并行等间距毛洞隧道的简化模型，利用刚体平动运动单元上限法^{[9, 25]}开展系统分析，探讨多洞净间距S、隧道埋深H及围岩强度等综合参数对稳定性的影响规律，并绘制稳定系数N_cr图表，以期从定量角度揭示围岩滑移线网破坏模式的演化过程，为多洞并行隧道设计、施工和加固方案的制定等问题提供数据支撑。

1. 刚体平动运动单元上限法

刚体平动运动单元上限法^{[9, 25]}（简称UB-RTME）属岩土破坏塑性极限分析上限理论范畴。采用“刚体平动三角形单元+速度间断线”的方式离散计算域，设置节点坐标与单元速度作为优化变量，通过极限状态虚功率平衡和内部耗散能最小化获取目标函数的表达式，同时满足速度间断线塑性流动约束、网格形态控制约束以及模型速度约束，建立非线性规划求解极限荷载的上限解。

非线性规划运算亦是搜索极限状态滑移线网的过程，须以多次的网格更新实现。主要包括无效单元合并与剔除、有效单元再次加密以及网格继承与修正等三类网格更新策略。计算流程如图 1。

图 1 刚体平动运动单元上限法计算流程图

Figure 1. Flow chart of upper bound method for rigid translational motion elements

下载: 全尺寸图片幻灯片

2. 多洞并行隧道围岩稳定性模型

2.1 问题描述

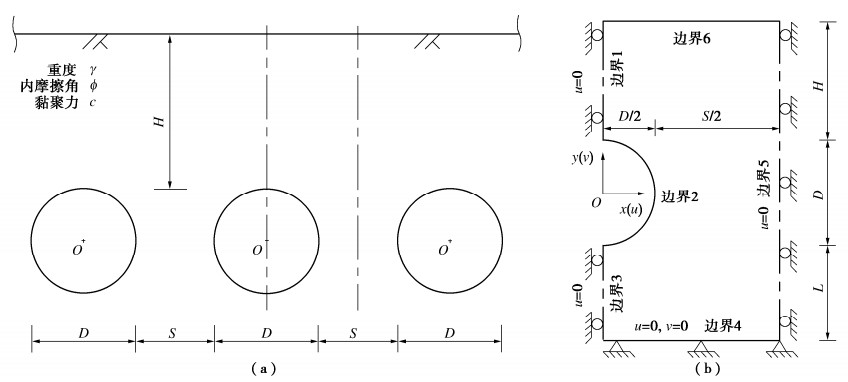
多洞并行隧道工程修建过程中，一般各单洞开挖面相互错开，属于三维空间的施工力学问题。为便于从保守角度分析围岩稳定性与破坏机理，这里作如下简化：

（1）不计施工过程，稳定性分析模型简化为平面应变问题，且多洞并行隧道按等间距设置。

（2）圆形隧道直径均为D，相邻隧道净间距均为S，地表水平且埋深均为H。

（3）围岩为均质连续的莫尔-库仑材料，强度指标为内摩擦角ϕ和黏聚力c。

（4）不考虑地下水及衬砌支护作用。

（5）按重度增加法评价围岩失稳临界状态。

如图 2，经概化的模型旨在探究围岩自重作用下的自承性能及多洞隧道潜在破坏模式的规律，以净间距S增加趋势反映中夹岩至单个隧道独立承载的演变过程，计算分析采用基于网格更新的刚体平动运动单元上限法。

图 2 多洞并行等间距隧道围岩稳定性分析模型

Figure 2. Model for stability of surrounding rock of parallel multi-line tunnels with equidistance

下载: 全尺寸图片幻灯片

2.2 运动单元上限法计算模型

如图 2（a），考虑模型对称性，对部分区域进行建模分析，建立多洞并行隧道围岩稳定性上限分析与计算模型如图 2（b）所示。图中未显示三角形网格，模型水平和竖向尺寸分别为D/2+S/2和H+D+L，其中L确定了下部范围，其值随H值变化以消除边界效应。地表（边界6）为水平自由地表，边界1，3，5均为模型对称轴，将其水平速度设为0；模型底部（边界4）水平和竖向速度均设为0。

仅考虑围岩自重荷载，按重度增加法施加体力约束为

${\displaystyle \sum _{i=1}^{{n}_{\text{e}}}{A}_{i}{v}_{i}}=-1\text{，}{A}_{i} > 0\text{ }(i=1,\cdots ,{n}_{\text{e}}) 。$

(1)

式中： ${\gamma _{{\text{cr}}}} = \sum\limits_{i = 1}^{{n_d}} {{P_{d,i}}} = c\sum\limits_{i = 1}^{{n_d}} {{{\xi ''}_i}}$ 为三角形刚体单元i的面积，其数值恒大于零， ${\gamma _{{\text{cr}}}} = \sum\limits_{i = 1}^{{n_d}} {{P_{d,i}}} = c\sum\limits_{i = 1}^{{n_d}} {{{\xi ''}_i}}$ 为单元i的竖向速度分量， ${\gamma _{{\text{cr}}}} = \sum\limits_{i = 1}^{{n_d}} {{P_{d,i}}} = c\sum\limits_{i = 1}^{{n_d}} {{{\xi ''}_i}}$ 为模型单元总数。

依极限分析上限定理，将模型所有速度间断线耗散能之和最小化，获得运动单元上限法对应的非线性规划目标函数，也就是临界重度γ_cr：

${\gamma _{{\text{cr}}}} = \sum\limits_{i = 1}^{{n_{\text{d}}}} {{P_{{\text{d}},i}}} = c\sum\limits_{i = 1}^{{n_{\text{d}}}} {{{\xi ''}_i}} 。$

(2)

为方便分析，借鉴文献[14]的定义，令稳定系数N_cr=γ_crH/c，即临界重度γ_cr和隧道埋深H乘积与黏聚力c的比值，它是内摩擦角ϕ、埋深比H/D和净距比S/D的函数，具体求解时，N_cr还可表示为

${N_{{\text{cr}}}} = {{{\gamma _{{\text{cr}}}}H} \mathord{\left/ {\vphantom {{{\gamma _{{\text{cr}}}}H} c}} \right. } c} = H\sum\limits_{i = 1}^{{n_{\text{d}}}} {{{\xi ''}_i}} 。$

(3)

式(2)，(3)中： ${P_{{\text{d}},i}}$ 为第i条速度间断线上耗散能；n_d为速度间断线总数； ${\xi _i}^{\prime \prime }$ 和 ${\xi _i}^\prime$ 为第i条速度间断线的过程变量，其表达式和约束条件为

$\Delta {x}_{i}={{x}^{\prime }}_{i}-{{x}^{″}}_{i}\text{，}\text{ }\Delta {y}_{i}={{y}^{\prime }}_{i}-{{y}^{″}}_{i}\text{ }\text{，}\text{ }$

(4a)

${{\xi }^{\prime }}_{i}=\Delta {x}_{i}{u}_{y,i}+\Delta {y}_{i}{v}_{y,i}-\Delta {x}_{i}{u}_{z,i}-\Delta {y}_{i}{v}_{z,i}\text{ }\text{，}$

(4b)

${{\xi }^{″}}_{i}=(-\Delta {y}_{i}{u}_{y,i}+\Delta {x}_{i}{v}_{y,i}+\Delta {y}_{i}{u}_{z,i}-\Delta {x}_{i}{v}_{z,i})/\mathrm{tan}\phi \text{ }\text{，}\text{ }$

(4c)

${{\xi }^{″}}_{i}+{{\xi }^{\prime }}_{i}\ge 0\text{ }\text{，}\text{ }{{\xi }^{″}}_{i}-{{\xi }^{\prime }}_{i}\ge 0\text{ }。$

(4d)

式中： $({x'_i},{\text{ }}{y'_i})$ 为第i条间断线的第一端点坐标， $({x''_i}{\text{, }}{y''_i})$ 为第二端点坐标； ${\text{ }}i = 1, \cdots ,{n_{\text{d}}}$ 。于是，以第一端点指向第二端点为正方向，顺时针和逆时针一侧的两个刚性单元对应的速度分量分别为(u_{y, i}, v_{y, i})和(u_{z, i}, v_{z, i})，。

式（4）满足了速度间断线上的相关联流动约束： $\Delta {v_i} = \left| {\Delta {u_i}} \right|{\text{tan}}\phi$ 。须知，所有间断线均施加该约束。

求解运动单元上限分析模型（见图 2（b））对应的非线性规划问题时，还需施加边界速度和几何约束：

${u}_{1,i}=0\text{ }，\text{ }{x}_{1,j}=0\text{ }，\text{ }D/2\le {y}_{1,j}\le D/2+H\text{ }$

$\text{ (}i=1,\cdots ,{n}_{1}\text{; }j=1,\cdots ,{n}_{1}\text{+1) }\text{，}\text{ }$

(5a)

${u}_{3,i}=0\text{ }，{x}_{3,j}=0\text{ }，\text{ }-D/2-L\le {y}_{3,j}\le -D/2\text{ }$

$\text{(}i=1,\cdots ,{n}_{3}\text{，}\text{ }j=1,\cdots ,{n}_{3}\text{+1) }\text{，}\text{ }$

(5b)

${u}_{4,i}=0\text{ }，\text{ }{v}_{4,i}=0\text{ }，\text{ 0}\le {x}_{4,j}\le D/2+S/2\text{ }，\text{ }{y}_{4,j}=-D/2-L$

$\text{(}i=1,\cdots ,{n}_{4}\text{ }\text{，}\text{ }j=1,\cdots ,{n}_{4}\text{+1) }\text{，}\text{ }$

(5c)

${u}_{5,i}=0\text{ }，\text{ }{x}_{5,j}\text{=}D/2+S/2\text{ }，\text{ }-D/2-L\le {y}_{5,j}\le D/2+H$

$\text{(}i=1,\cdots ,{n}_{5}\text{ }\text{，}\text{ }j=1,\cdots ,{n}_{5}\text{+1) }\text{，}$

(5d)

${\text{0}} \leqslant {x_{6,j}} \leqslant {{{D \mathord{\left/ {\vphantom {D 2}} \right. } 2} + S} \mathord{\left/ {\vphantom {{{D \mathord{\left/ {\vphantom {D 2}} \right. } 2} + S} 2}} \right. } 2},{\text{ }}{y_{6,j}} = {D \mathord{\left/ {\vphantom {D 2}} \right. } 2} + H$

$\text{(}j=1,\cdots ,{n}_{6}\text{+1) }\text{，}$

(5e)

$4({x}_{2,j}/){D}^{2}+4{({y}_{2,j}/D)}^{2}=1\text{ (}j=1,\cdots ,{n}_{2}\text{+1) }。$

(5f)

式中： ${u_{1,i}}$ 为边界1第i条边一侧单元的水平向速度， ${n_1}$ 表示边界1上施加约束的单元边总数；而 ${x_{1,j}}$ 和 ${y_{1,j}}$ 为边界1上第j个节点的坐标，式（5b）~（5f）同此命名。式（5a）~（5f）中的几何约束即限定边界上的单元节点坐标只能于相应边界上移动。如式（5f）圆方程限制隧道轮廓（边界2）上的节点只能在圆周上移动。除地表和隧道圆周轮廓上自由外，其余边界速度约束见式（5a）~（5d）。

多洞并行隧道围岩稳定性计算在既有程序基础上，设置式（1），（5）对应的速度和几何边界条件即可开展后续计算^[20]。

3. 多洞并行隧道围岩稳定系数N_cr

3.1 稳定系数N_cr变化规律

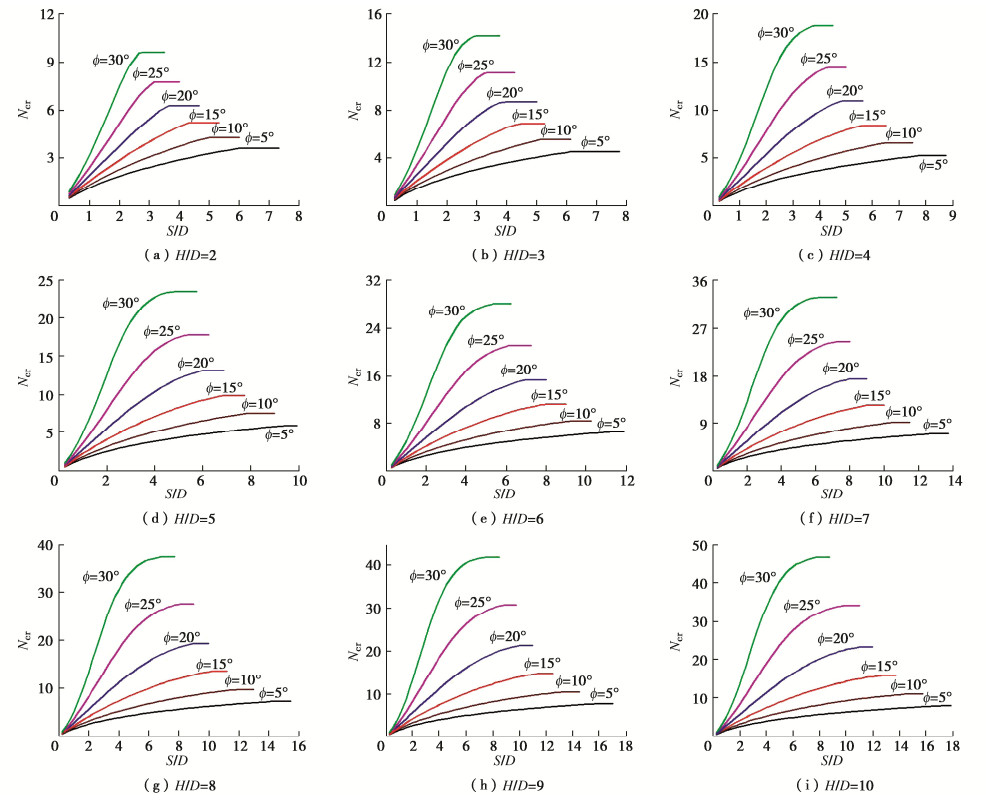
采用刚体平动运动单元上限法开展了2000余组参数条件下的多洞并行等间距隧道围岩稳定性计算，获得稳定系数N_cr与内摩擦角ϕ、埋深比H/D和净间距比S/D的关系曲线如图 3所示。选取的计算参数ϕ取值5°~30°，H/D取值2~10；S/D取值依从于H/D的变化，即不断增大S/D值依次计算直至相邻隧道的相互影响消失。此外，当接近单洞独立破坏状态时，S/D取值间隔适当减小。

图 3 不同参数条件下多洞并行等间距隧道围岩稳定系数N_cr关系曲线

Figure 3. Variation of stability number N_cr for different parameters in parallel multi-line tunnels with equidistance

下载: 全尺寸图片幻灯片

图 3（a）~3（i）分别为H/D=2~10对应的稳定系数N_cr曲线图。总体上看，随着隧道埋深比H/D的增大，相邻隧道相互影响的净间距比S/D范围变大，这与埋深增加上覆围岩荷载增大有关。净间距比S/D与稳定系数N_cr的关系可分述如下：①当S/D较小时（如S/D= 0.25），无论H/D和ϕ如何变化，N_cr值总是接近于0。这缘于中夹岩很窄，上覆岩层主要以自重荷载的形式作用于其上，从而围岩整体稳定性变差。②当S/D增大达到单洞隧道独自破坏的转化间距比S_tr/D时，N_cr增加至最大值且等于相同条件下单洞隧道围岩稳定系数 ${N_{{\text{cr(single)}}}}$ ，此时S/D继续增加，而N_cr值将不再变化。③当S/D小于S_tr/D时，N_cr值随着S/D增加而逐渐增大，且较之S/D=0.25的情况，H/D和ϕ对N_cr的影响逐渐增大。还可发现，S/D较小时N_cr值增加不明显，而S/D接近S_tr/D时，N_cr变化的差异同样很小。例如：取H/D=3、ϕ=30°，当S/D=2.875时，N_cr=14.103；而S/D=S_tr/D=4时，N_cr=14.194，相比前者仅增加了0.65%。④较之其它因素，内摩擦角ϕ增大引起N_cr迅速增大，同时随着S/D的增加，N_cr快速增至单洞条件下对应的稳定系数 ${N_{{\text{cr(Single)}}}}$ 。

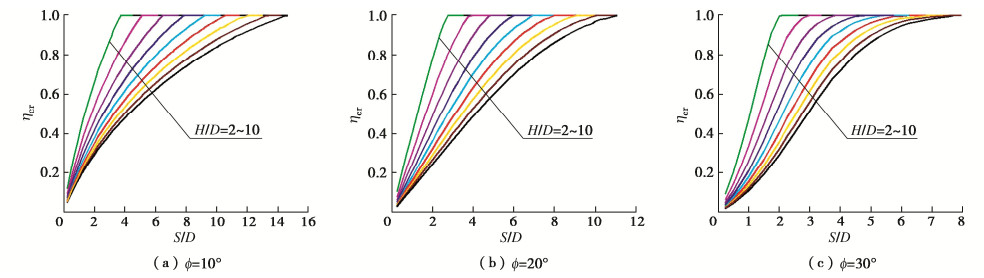
3.2 发挥系数 ${\eta _{{\text{cr}}}}$ 变化规律

定义发挥系数 ${\eta _{{\text{cr}}}}$ 为多洞稳定系数N_cr与单洞稳定系数 ${N_{{\text{cr(Single)}}}}$ 之比，即 ${\eta _{{\text{cr}}}} = {{{N_{{\text{cr}}}}} \mathord{\left/ {\vphantom {{{N_{{\text{cr}}}}} {{N_{{\text{cr(Single)}}}}}}} \right. } {{N_{{\text{cr(Single)}}}}}}$ ，于是 ${\eta _{{\text{cr}}}}$ 可反映不同净距比S/D条件下多洞与单洞稳定性之间的关联规律。绘制ϕ为10°，20°，30°对应的发挥系数 ${\eta _{{\text{cr}}}}$ 曲线如所示。可看出，当S/D比较小时， ${\eta _{{\text{cr}}}}$ 值接近0，而随着S/D的增加， ${\eta _{{\text{cr}}}}$ 值逐渐增长直至最大值1。当隧道埋深比H/D增大时， ${\eta _{{\text{cr}}}}$ 随S/D增加的趋势变缓，达到单洞破坏对应的转化间距比S_tr/D增加。对比~可知，内摩擦角ϕ较大时， ${\eta _{{\text{cr}}}}$ 值随S/D的增加更快地达到最大值1。

图 4 不同参数条件下多洞并行等间距隧道围岩稳定系数N_cr与单洞隧道

${N_{{\text{cr(Single)}}}}$ 比值η_cr变化曲线

Figure 4. Curves of ratio η_cr for stability number N_cr to single tunnel

${N_{{\text{cr(Single)}}}}$ for different parameters in parallel multi-line tunnels

下载: 全尺寸图片幻灯片

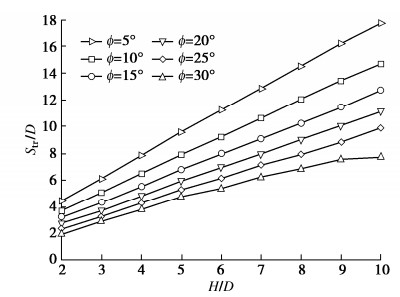
3.3 转化间距比S_tr/D变化规律

上文提到，当多洞并行等间距隧道的净间距S增大到转换间距S_tr时，从失稳破坏角度可认为相邻隧道间的相互影响消失。因此，有必要进一步探究转换间距比S_tr/D的影响因素。将转换间距比S_tr/D与埋深比H/D的关系曲线绘制见图 5。可看出，除内摩擦角ϕ=30°的情况外，S_tr/D与埋深比H/D的增长基本呈线性关系，且ϕ值越小S_tr/D增长的比率越大，这与较小内摩擦角引起围岩较大扰动范围的一般规律相符。转换间距比S_tr/D与围岩内摩擦角ϕ以及埋深比H/D均直接相关，差异在于前者负相关而后者为正相关。多洞存在相互影响时，较大埋深比H/D提供了较大的自重荷载，易诱发围岩失稳破坏。

图 5 多洞并行隧道转化间距比S_tr/D与埋深比H/D关系曲线

Figure 5. Curves for conversion spacing ratio S_tr/D and buried depth ratio H/D in parallel multi-line tunnels

下载: 全尺寸图片幻灯片

4. 多洞并行隧道围岩潜在破坏模式

4.1 典型破坏模式特征分析

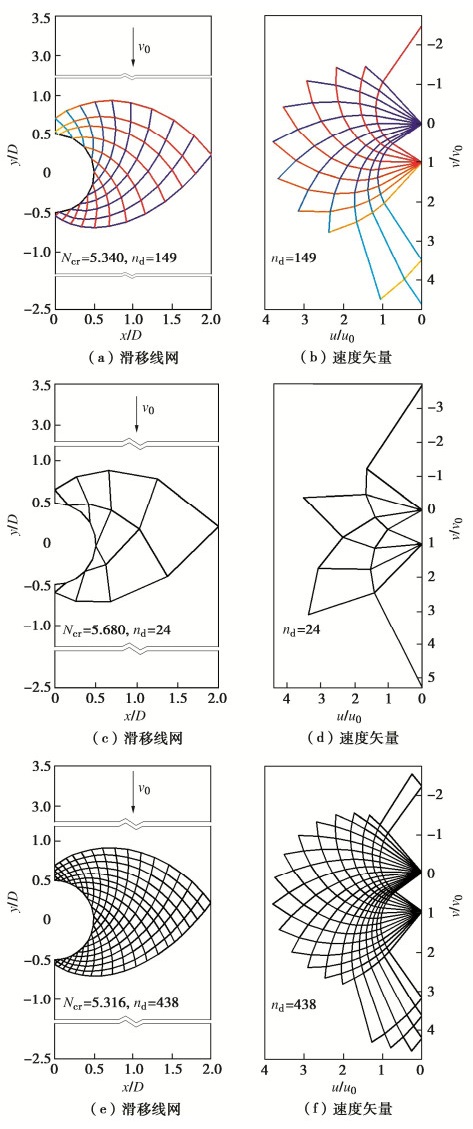
除稳定系数N_cr外，运动单元上限法对应的非线性规划运算，还可得到多洞并行隧道围岩潜在失稳破坏模式。为分析典型破坏特征及网格密度的影响规律，绘制ϕ=15°，H/D=3，S/D=3对应的滑移线网破坏模式展开讨论（图 6）。

图 6 多洞并行隧道围岩破坏模式(S/D=3, H/D=3, ϕ=15°)

Figure 6. Failure modes of surrounding rock for parallel multi-line tunnels (S/D=3, H/D=3, ϕ=15°)

下载: 全尺寸图片幻灯片

图 6（a）所示滑移线网破坏模式左右边界均为对称轴，上部和下部整体区域以简略形式显示。可看出，相邻隧道中夹岩区域的破坏表现为两簇滑移线网。从隧道周边散发，两簇滑移线于相邻隧道对称轴处交于一点。滑移线网范围内围岩破坏呈速度均不相等状态，即间断线两侧速度不连续。需说明的是，尽管模型网格划分为三角形刚体单元，后处理时筛除了无效速度间断线，因此滑移线网破坏模式更多地显示为由很多相邻三角形构成的四边形块体体系。

为揭示滑移线网速度场的规律，将破坏模式对应的速度间断线（滑移线）相对速度矢量闭合图绘制如图 6（b）。同时，定义隧道上方整体下沉区域的竖向速度为v₀，图 6（b）竖轴表示为无量纲竖向速度比v/v₀，横轴为水平速度比u/v₀；于是竖轴0到1的连线即为v₀，竖轴0到网状交叉任一点的连线为对应刚体单元的绝对速度；图 6（b）中网状速度矢量任意线段为对应速度间断线的相对速度。由图可知，隧道上方整体区域下沉速度为v₀时，滑移线网破坏区内部速度最大值超过4v₀，推测内摩擦角ϕ越大该趋势越明显，即围岩承载能力更好。

通常围岩破坏范围被速度间断线分割为多区域，其中塑性区可等效为密集的滑移线网形态。为探讨滑移网密度对稳定系数N_cr上限解的影响，将ϕ=15°，H/D=3，S/D=3时，稀疏网格对应的滑移线网破坏模式和速度矢量闭合图绘制如图 6（c），6（d），密集网格对应的绘制如图 6（e），6（f）。

对比可知，滑移线网稀疏时，速度间断线沿着两个交叉方向构成的滑移线变得棱角感突出，而速度矢量闭合图也更加稀疏曲折。然而，相同v₀条件下，滑移网破坏区内部速度矢量值更大，如最大内部速度超过5v₀，由此引起间断线总耗散能增大，这是稀疏网格（图 6（c））对应稳定系数N_cr=5.680，大于常规网格（图 6（a））对应N_cr=5.34的原因之一。依上限定理，较小的稳定系数上限解为较优解；说明网格密度增加，不仅破坏模式的刻画更为精细，同时还提高了N_cr上限解精度。

同样地，对常规网格（图 6（a））进一步加密获得滑移线网破坏模式和速度矢量图绘制如图 6（e），6（f）。可以发现，网格越密集滑移线网和速度矢量变得更加圆顺。此时，密集网格对应的稳定系数N_cr =5.316较之常规网格对应的5.34，并未带来计算精度的显著提升。然而，密集网格对应速度间断线总数n_d=438，接近常规网格n_d=149的3倍。考虑到运动单元上限分析对应的非线性规划的运算负担，速度间断线和单元数目的增加将带来运算效率的降低。因此，本文2000余组工况计算，均参考了图 6（a）对应的常规网格密度。

4.2 破坏模式演化规律

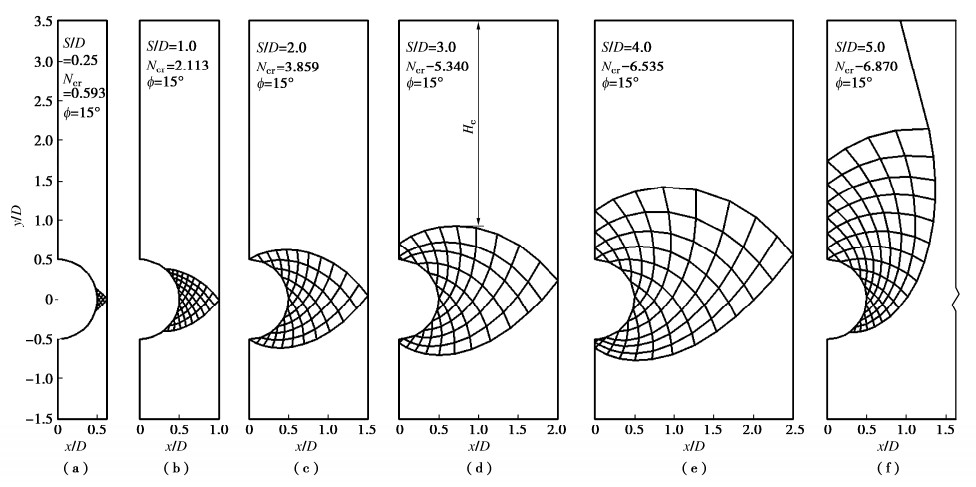
为反映相邻隧道净间距比S/D对破坏模式的影响规律，选取ϕ=15°，H/D=3条件下，不同S/D (0.25~5.0)对应的滑移网破坏模式绘制如图 7所示。为便于后续的定量分析，定义多洞并行隧道整体下沉区高度为H_c，具体见图 7（d）标示。

图 7 多洞并行隧道围岩破坏模式随净间距比S/D的演化规律(H/D=3, ϕ=15°)

Figure 7. Variation of failure mode of surrounding rock for parallel multi-line tunnels with net spacing ratio S/D(H/D=3, ϕ=15°)

下载: 全尺寸图片幻灯片

由图 7（a）知，当净间距很小（如S/D=0.25），上方围岩整体下沉引起隧道两侧岩柱产生小范围楔形破坏。当S/D逐渐增加至1.0，2.0，3.0（图 7（b）~7（d）），隧道两侧的楔形网状破坏范围逐渐扩展，大约在隧道上下中心线处开始交叉。滑移线网的扩展带来了速度间断线总数和长度的增长，引起破坏区域耗散能增加，对应于稳定系数N_cr的增大（由0.593增至5.340）。

由图 7（e）知，当S/D增加至4.0时，滑移网破坏范围进一步向外侧扩展，特别是上方于中心线处交叉范围更大，此时N_cr=6.535，与S/D=5.0单洞隧道独自破坏对应的N_cr=6.870相差不大（图 7（f））。说明由多洞相互影响破坏至单洞单独破坏的转换净间距比S_tr/D处于4.0~5.0。还可看出，单洞独自破坏时，破坏模式外侧产生了延伸到地表的贯通破坏面，且水平方向的扩展范围较小。

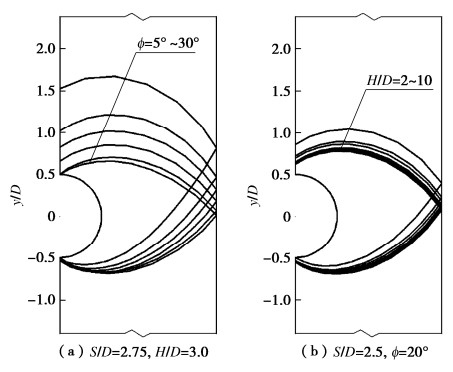
多洞并行隧道间夹岩破坏呈内部为滑移线网的楔形形状，这里将楔形体上下边线称之为主要破坏面。于是，选取典型参数绘制多洞并行隧道主要破坏面演化规律如图 8所示。

图 8 多洞并行隧道主要破坏面演化规律

Figure 8. Representative failures surface in parallel multi-line tunnels

下载: 全尺寸图片幻灯片

图 8（a）为S/D=2.75，H/D=3.0时，不同内摩擦角ϕ对应的主要破坏面。可看出ϕ由5°增大至30°，上下两条破坏面位置不断上移，上方破坏面的起点从隧道顶部上移趋势更显著，同时两条主要破坏面合围的楔形区面积也随之增长。

图 8（b）为S/D=2.5，ϕ=20°时，不同埋深比H/D对应的主要破坏面。可看出，H/D由2增大至10，上下两条破坏面位置不断下移，不过下移趋势逐渐微弱；特别对于H/D≥5的情况，相对应的主要破坏面几乎重合。说明隧道埋深增加到一定值后，上方整体下沉区以荷载形式施加于中夹岩区域，破坏形态不再演化。

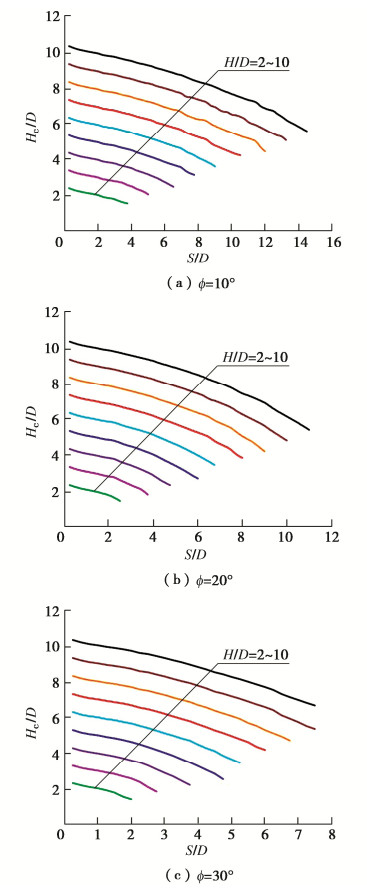
由上可知，围岩内摩擦角和隧道埋深变化将引起破坏面位置及上方整体下沉区高度H_c的改变。于是，定义无量纲参数H_c/D为整体下沉区高度比。绘制ϕ为10°，20°，30°对应的H_c/D曲线如图 9，以此分析H_c/D的变化规律。可以发现，当S/D较小时，H_c/D接近隧道埋深比H/D；随着S/D的增大，H_c/D值逐渐减小，且曲线的斜率变化也逐渐增大。对比图 9（a）~9（c）可知，内摩擦角ϕ增大，H_c/D值的变化幅度更大，相同S/D对应的下沉区高度H_c更小，这与破坏面规律分析中结果一致，即摩擦角对破坏面的影响显著，ϕ的增大会引起破坏面的上移。

图 9 多洞并行隧道围岩整体下沉区高度比H_c/D随净间距比S/D的演化规律

Figure 9. Variation of subsidence height ratio H_c/D of surrounding rock for parallel multi-line tunnels with S/D

下载: 全尺寸图片幻灯片

5. 对比分析与讨论

5.1 多洞与双洞并行隧道围岩稳定系数N_cr对比

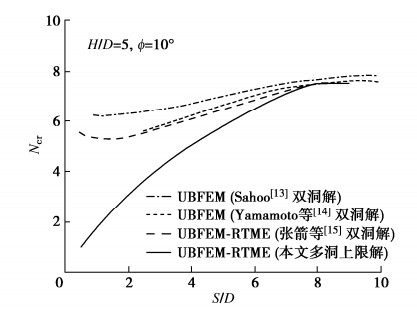
关于多洞并行隧道围岩稳定性分析的研究报道较少，这里选取双洞并行隧道已有数据展开对比分析^[13-15]。其中Sahoo和Yamamoto数据源于变形单元上限有限元分析，Zhang和本文数据来自运动单元上限分析。选取ϕ=10°、H/D=5对应的N_cr与S/D变化曲线绘制如图 10。可以看出，Yamamoto等^[13]、Sahoo等^[14]和Zhang等^[15]分别给出的双洞并行隧道稳定系数上限解N_cr随S/D变化曲线的趋势和数值吻合较好。其中以Zhang等^[15]运动单元上限解数值稍小，为严格上限理论框架下的较优解。

图 10 多洞与双洞并行隧道围岩稳定系数N_cr对比曲线

Figure 10. Comparison for N_cr of parallel multi-and twin-line tunnels

下载: 全尺寸图片幻灯片

如3.1节所述，本文多洞并行隧道围岩稳定系数N_cr上限解随S/D的增加快速增长直至达到固定值 ${N_{{\text{cr(Single)}}}}$ 。如图 10，当S/D增大至超过转化间距比S_tr/D时，多洞与双洞并行隧道围岩稳定系数N_cr值趋同，均对应于单洞隧道独自破坏而无相互影响的情况。此时，本文N_cr上限解较之已有文献结果稍小，数值吻合良好，可印证运动单元上限分析结果的可靠性。

从图 10还看出，当相邻隧道净距比S/D不断减小时，多洞与双洞并行隧道对应的稳定系数N_cr的差异稳步增大，且多洞条件对应的N_cr数值急速下降，反映出多洞围岩稳定性依赖于相邻隧道中夹岩承载性能，这缘于上方围岩难于产生成拱效应，因此稳定性较之相同条件的双洞并行隧道显著降低。

5.2 多洞与双洞并行隧道围岩潜在破坏模式对比

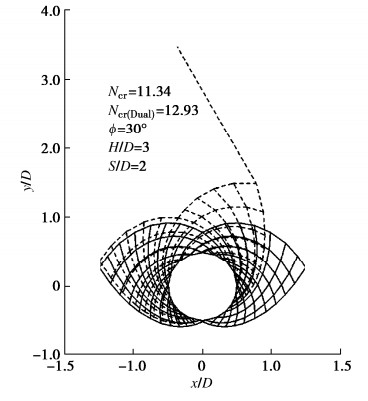
选取ϕ=30°，S/D=2.0，H/D=3.0条件下多洞并行隧道围岩破坏模式绘制如图 11，图中以实线表示滑移线网破坏模式并显示整个隧道。将相同条件下Zhang等^[15]给出的双洞并行隧道围岩滑移网破坏模式以虚线形式叠加显示。

图 11 多洞与双洞并行隧道破坏模式对比

Figure 11. Comparison between collapse mechanism of parallel multi-and twin-line tunnels

下载: 全尺寸图片幻灯片

由看出，在内侧区域（相邻隧道中夹岩区域），多洞并行隧道围岩滑移线网破坏特征与双洞并行隧道的情况较为吻合，而后者于外侧滑移线网状破坏区向上方发生显著偏移，且增加了一条斜向延伸的贯通滑动面。这体现了与多洞并行隧道围岩破坏模式最大的差异，成为解释多洞并行隧道围岩稳定系数N_cr小于双洞 ${N_{{\text{cr(Dual)}}}}$ 的主要原因，即后者外侧增加了向上破坏面并进一步减小上方围岩整体下沉范围。实质上，净间距较小时，多洞并行隧道围岩破坏机理为相邻隧道中夹岩的破坏，可以此进行双洞、三洞等并行隧道中夹岩稳定性评估。

6. 结论

采用刚体平动运动单元上限法研究了多洞并行等间距隧道围岩稳定性及潜在破坏模式，得到3点结论。

（1）多洞并行隧道净距比S/D对稳定系数N_cr和破坏模式影响显著。当S/D小于转换间距比S_tr/D时，随着S/D的减小，N_cr数值和滑移线网破坏范围逐渐减小。当S/D数值很小时，各参数影响下的N_cr均趋近于0，体现为隧道上方围岩全部发生整体下沉式失稳。当S/D大于S_tr/D时，多洞并行隧道对应的N_cr和破坏模式与相同条件下的单洞隧道吻合良好。

（2）多洞和双洞并行隧道破坏模式形态和范围差异明显，相同条件下前者围岩稳定更差。当S/D小于S_tr/D时，多洞隧道对应的N_cr小于双洞隧道 ${N_{{\text{cr(Dual)}}}}$ ，此时多洞隧道滑移线网破坏模式特征与双洞隧道的内侧区域类似，但未产生双洞隧道外侧斜向上延伸的剪切带；体现出多洞隧道破坏主要为相邻隧道间的中夹岩破坏的特点。

（3）本文多洞并行隧道围岩稳定系数和破坏模式的分析结果基于莫尔库仑屈服准则，对于其它屈服准则，如霍克布朗屈服准则的影响与差异所在，需要进一步研究。

图 1 分段柔性接头隧道示意图

Figure 1. Schematic diagram of tunnel with segmental flexible joints

下载: 全尺寸图片幻灯片

图 2 穿断层分段柔性接头隧道力学模型

Figure 2. Mechanical model for tunnels with segmental flexible joints crossing faults

下载: 全尺寸图片幻灯片

图 3 解析方法计算流程

Figure 3. Flow chart for analytical calculation

下载: 全尺寸图片幻灯片

图 4 断层位移场有限元计算模型

Figure 4. FEM model for determining field deformation of faults

下载: 全尺寸图片幻灯片

图 5 断层错动下隧道埋深处对应的自由场竖向位移

Figure 5. Free-field vertical displacements at buried depth of tunnel under fault dislocation

下载: 全尺寸图片幻灯片

图 6 柔性接头设计方案

Figure 6. Schematic diagram of setting plans for flexible joints

下载: 全尺寸图片幻灯片

图 7 不同计算方法隧道轴线偏移对比验证

Figure 7. Comparison of deviations of tunnel axis by FEM model and analytical solution

下载: 全尺寸图片幻灯片

图 8 不同计算方法隧道结构弯矩对比验证

Figure 8. Comparison of bending moments along tunnel between FEM model and proposed solution

下载: 全尺寸图片幻灯片

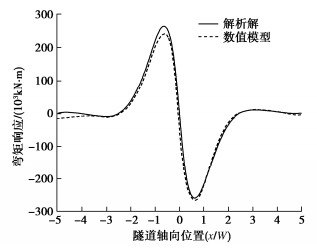
图 9 试验加载原理示意图 ^[14]

Figure 9. Schematic diagram of loading principle

下载: 全尺寸图片幻灯片

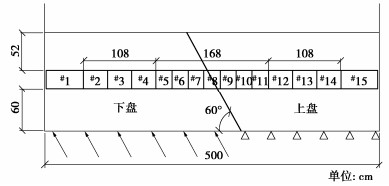
图 10 隧道模型构造细节^[14]

Figure 10. Details of tunnel plaster model

下载: 全尺寸图片幻灯片

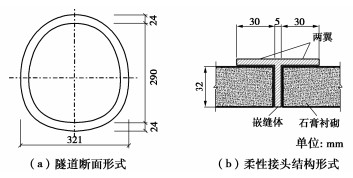
图 11 隧道模型装配^[15]

Figure 11. Installation of tunnel plaster model

下载: 全尺寸图片幻灯片

图 12 解析解计算等效模型

Figure 12. Equivalent mechanical model for analytical solution

下载: 全尺寸图片幻灯片

图 13 解析解与模型试验的隧道位移响应对比验证

Figure 13. Verification of displacement responses of tunnel between analytical solutions and model tests

下载: 全尺寸图片幻灯片

图 14 接头设计方案对隧道内力响应的影响

Figure 14. Influences of different setting plans for joints on response of internal force of tunnel

下载: 全尺寸图片幻灯片

图 15 隧道本体-接头刚度比对隧道内力响应的影响

Figure 15. Influences of tunnel-joint stiffness on response of internal force of tunnel

下载: 全尺寸图片幻灯片

表 1 算例验证计算参数

Table 1 Parameters for validation model

名称密度/
(kg·m^-3) 杨氏模量/
GPa 剪切模量/
GPa 泊松比

断层 1700 0.94 0.34 0.38

围岩 2100 1.56 0.6 0.30

衬砌 2400 30 12 0.25

下载: 导出CSV

参考文献(17)

[1]	WANG W L, WANG T T, SU J J, et al. Assessment of damage in mountain tunnels due to the Taiwan Chi-chi earthquake[J]. Tunnelling and Underground Space Technology, 2001, 16(3): 133-150. doi: 10.1016/S0886-7798(01)00047-5
[2]	YU H T, CHEN J T, BOBET A, et al. Damage observation and assessment of the Longxi tunnel during the Wenchuan earthquake[J]. Tunnelling and Underground Space Technology, 2016, 54: 102-116. doi: 10.1016/j.tust.2016.02.008
[3]	DALGIC S. Tunneling in squeezing rock, the Bolu tunnel, Anatolian motorway, Turkey[J]. Engineering Geology, 2002, 67(1/2): 73-96.
[4]	SHAHIDI A R, VAFAEIAN M. Analysis of longitudinal profile of the tunnels in the active faulted zone and designing the flexible lining (for Koohrang-Ⅲ tunnel)[J]. Tunnelling and Underground Space Technology, 2005, 20(3): 213-221. doi: 10.1016/j.tust.2004.08.003
[5]	禹海涛, 袁勇. 长大隧道地震响应分析与试验方法新进展[J]. 中国公路学报, 2018, 31(10): 19-35. doi: 10.3969/j.issn.1001-7372.2018.10.003 YU Haitao, YUAN Yong. Review on seismic response analysis and test methods for long and large tunnels[J]. China Journal of Highway and Transport, 2018, 31(10): 19-35. (in Chinese) doi: 10.3969/j.issn.1001-7372.2018.10.003
[6]	禹海涛, 李衍熹. 土-结构动力作用体系混合试验研究进展与探讨[J]. 中国公路学报, 2020, 33(12): 105-117. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202012009.htm YU Haitao, LI Yanxi. Review and discussion on recent progress of hybrid simulation for soil-structure dynamic interaction system[J]. China Journal of Highway and Transport, 2020, 33(12): 105-117. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZGGL202012009.htm
[7]	刘学增, 林亮伦. 75°倾角逆断层黏滑错动对公路隧道影响的模型试验研究[J]. 岩石力学与工程学报, 2011, 30(12): 2523-2530. LIU Xuezeng, LIN Lianglun. Research on model experiment of effect of thrust fault with 75°dip angle stick-slip dislocation on highway tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(12): 2523-2530. (in Chinese)
[8]	黄强兵, 彭建兵, 门玉明, 等. 分段柔性接头地铁隧道适应地裂缝大变形的模型试验研究[J]. 岩石力学与工程学报, 2010, 29(8): 1546-1554. HUANG Qiangbing, PENG Jianbing, MEN Yuming, et al. Model test study of sectional metro tunnel with flexible joints adapting large deformation of ground fissures[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1546-1554. (in Chinese)
[9]	MELISSIANOS V E, LIGNOS X A, BACHAS K K, et al. Experimental investigation of pipes with flexible joints under fault rupture[J]. Journal of Constructional Steel Research, 2017, 128: 633-648. doi: 10.1016/j.jcsr.2016.09.026
[10]	YAN G, SHEN Y, GAO B, et al. Damage evolution of tunnel lining with steel reinforced rubber joints under normal faulting: An experimental and numerical investigation[J]. Tunnelling and Underground Space Technology, 2020, 97: 103223. doi: 10.1016/j.tust.2019.103223
[11]	YU H T, ZHANG Z W, CHEN J T, et al. Analytical solution for longitudinal seismic response of tunnel liners with sharp stiffness transition[J]. Tunnelling and Underground Space Technology, 2018, 77: 103-114. doi: 10.1016/j.tust.2018.04.001
[12]	刘国钊, 乔亚飞, 何满潮, 等. 活动性断裂带错动下隧道纵向响应的解析解[J]. 岩土力学, 2020, 41(3): 923-932. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202003023.htm LIU Guozhao, QIAO Yafei, HE Manchao, et al. An analytical solution of longitudinal response of tunnels under dislocation of active fault[J]. Rock and Soil Mechanics, 2020, 41(3): 923-932. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202003023.htm
[13]	TANAHASHI H. Formulas for an infinitely long Bernoulli-Euler beam on the Pasternak model[J]. Soils and Foundations, 2004, 44(5): 109-118.
[14]	VESIĆ A B. Bending of beams resting on isotropic elastic solid[J]. Journal of the Engineering Mechanics Division, 1961, 87(2): 35-53.
[15]	李宏, 陈征, 王海忠, 等. 南北带南段实测地应力特征与钻孔应变观测[C]//2014年中国地球科学联合学术年会. 北京, 2014. LI Hong, CHEN Zheng, WANG Haizhong, et al. In-situ stress characteristics and borehole strain observation in the southern section of north-south belt[C]//Annual Meeting of Chinese Geoscience Union. Beijing, 2014. (in Chinese)
[16]	孙飞. 穿越活断层地铁隧道结构损伤破坏机理及抗错动性能研究[D]. 成都: 西南交通大学, 2019. SUN Fei. Study on Damage and Fracture Mechanism and Anti- Displacement Performance of Metro Tunnels Passing through Active Faults[D]. Chengdu: Southwest Jiaotong University, 2019. (in Chinese)
[17]	SHIBA Y, KAWASHIMA K, OBINATA N, et al. Evaluation procedure for seismic stress developed in shield tunnels based on seismic deformation method. [J]. Doboku Gakkai Ronbunshu, 1989(404): 385-394.

施引文献(4)

期刊类型引用(4)

1.	夏晶晶，贺姣姣. 基于直剪试验土石混合体路基的稳定性问题研究. 山西建筑. 2025(01): 125-128+172 . 百度学术
2.	杨忠平，李勇华，李诗琪，刘浩宇，高宇豪. 不同含石率土石混合体水力侵蚀分异特征及机制. 岩石力学与工程学报. 2024(01): 133-145 . 百度学术
3.	段国勇，徐广超，罗文庆，李森. 酸碱环境下泥岩土石混合体剪切特性研究. 水利水电技术(中英文). 2024(02): 148-155 . 百度学术
4.	梁越，何慧汝，许彬，张鑫强，冉裕星. 基于透明土的水力梯度对渗流侵蚀影响试验研究. 河海大学学报(自然科学版). 2024(05): 60-66 . 百度学术