0.   引言

隧道上覆土压力的预测对隧道结构的设计和施工具有重要意义。对于浅埋隧道其上方的竖向土压力可以直接采用全覆土柱法进行计算，但是随着隧道埋深的增大，地层内部产生土拱效应从而使隧道的实际松动土压力远小于全覆土重。因此，很多学者针对土拱效应下的隧道松动土压力的计算进行了研究。

Terzaghi^[1]基于Trapdoor试验建立了土拱效应下松动土压力计算的解析模型。此后其推导的公式被广泛用于隧道，地下管线以及路堤桩桩间土压力的计算。但是Terzaghi公式中对于侧向土压力系数的取值以及地层的松动范围的确定仍然有待商榷。因此很多学者对此展开研究以使得Terzaghi公式的适用性更加广阔。Handy^[2]从主应力轴旋转的角度提出拱迹线为小主应力的轨迹，并基于拱迹线为悬链线的情况推导了侧压力系数的解析公式。陈若曦等^[3]则基于主应力轴旋转提出拱迹线为大主应力拱迹线的情况来修正侧压力系数以及Terzaghi松动土压力计算公式。徐长节等^[4]基于圆弧、悬链线和抛物线3种不同形状的大主应力轨迹线，考虑隧道上方松动区内应力分布形式对松动土压力的影响，从而对Terzaghi松动土压力公式进行了修正。尽管目前针对隧道松动土压力的研究很多，但是大多数研究都是基于Terzaghi提出的破坏模式。而隧道松动区的破坏模式对松动土压力的计算至关重要。Terzaghi根据试验结果提出了等沉面概念，其认为土拱效应仅存在于等沉面之下，等沉面之上的土体作为外荷载的一部分，但是其对于等沉面高度的确定只是凭经验给出，缺乏理论依据^[5]。因此，一些学者从隧道松动区破坏形状的角度出发对松动土压力进行修正。Gong等^[6]利用椭球体理论来描述松动区的范围并推导了隧道上覆土压力计算公式，但是其计算结果较加瑞^[7]模型试验结果偏大。汪大海等^[8]则同时考虑松动区范围的变化以及在隧道开挖后主应力旋转角的分布特征来改进浅埋隧道上覆土压力的计算公式。朱孟龙等^[9]基于塔形滑移面计算模型，并考虑主应力旋转角的分布特征，推导出大主应力与水平面夹角的分布公式，以此来对松动土压力的计算公式进行修正。Shukla等^[10]和陈国舟等^[11]分别假设松动区滑动面为斜直线和曲线，从而推导了松动区竖向应力的计算公式。陈其志等^[12]从模型试验的角度对土体松动土压力及松动区位移破坏形式进行研究。

王将等^[13]基于抛物线与斜直线滑裂面假设的研究虽然在一定程度上提高了计算的精度，但这两种形状假设缺少相应的理论和试验支撑。而椭球体理论作为比较成熟的理论可以根据地质的密实程度简便地确定隧道松动区的范围。宫全美虽然提出了用椭球体理论来表征隧道上方的土体破坏范围，但是其对于隧道上方的应力分布的假设不符合实际^[4]。与此同时，椭球体理论并没有考虑地层损失对地层沉降的影响。因此，本文首先考虑地层损失对土体松动滑移范围的影响来对椭球体理论进行修正，目的是使得椭球体理论可以对不同地质和工况下隧道松动区进行更为精确简便的预测；然后通过自主设计的试验装置并结合PIV技术对修正后的椭球体理论进行对比验证；最后基于修正后的椭球体理论并考虑主应力轴旋转对隧道松动土压力公式进行修正，以期为相关的理论研究和工程实践提供借鉴和参考。

1.   隧道上方地层的破坏模式

隧道的塌方受围岩的力学特性影响较大。在软弱地层中，隧道施工过程中经常发生局部塌方，然后向上逐步扩大发展直至达到新的平衡后，塌方停止。而在地层从开始塌方至最后稳定的过程中，受影响的土体分布区域即为隧道的极限松动范围。确定了隧道的极限松动区域也就确定了隧道支护结构的界限支护压力。另一方面，从实际工程和模型试验可知，随着土体的抗剪强度的增大，隧道上方的塌方影响的范围逐渐减小。尽管普氏基于“自然拱”概念提出隧道上方会形成一个抛物线的拱。但根据弹塑性理论可知，在以自重应力场为主的地层中，隧道施工过程中其上方土体先是部分坍塌，之后慢慢趋于稳定，稳定后的形状为立椭圆^[14]。EVANS^[15]和LEE等^[16]通过模型试验也证实了隧道上方土体的极限松动区近似为椭圆形。

1.1   椭球体理论

20世纪50年代，马拉霍夫在米纳耶夫提出的放矿放出体形状为椭球体的概念之上系统论述了放矿椭球体理论。之后，中国学者在椭球体放矿理论的发展和完善中做了大量的工作，取得了很多成果，推动了椭球体理论在松散介质失稳和放出研究中的应用。

图  1  椭球体理论模型

Figure  1.  Model for ellipsoid theory

下载: 全尺寸图片 幻灯片

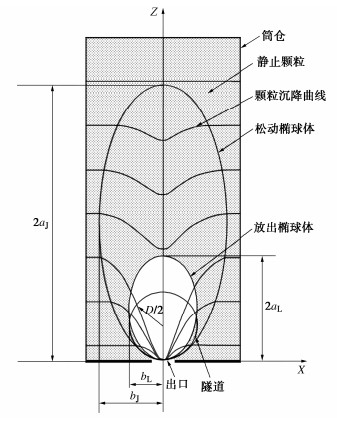
如图 1所示，椭球体理论^[17]认为，在一个储放颗粒物质的贮仓中，其底部有一个开口，当开口打开时，颗粒会向外流出。在一定时间之后，仓内颗粒物质会达到一个新的平衡。流出的颗粒物质会在仓内留下一个近似椭球体的空间，被称为放出椭球体。与之相对应会有一个松动椭球体，两个椭球体之间的颗粒物质只产生松动和位移，不会从开口处流出。松动椭球体范围之外的颗粒物质会保持其原有状态不发生位移。

由椭圆的几何关系可知，放出椭圆的第一偏心率为

式中：${a_{\text{L}}}$，${b_{\text{L}}}$分别为放出椭圆的长半轴和短半轴，在实际的工程中$e$值一般为0.90~0.98。

对于一个体积确定为${Q_{\text{L}}}$的放出椭球体，必有一个与之相对应的体积为${Q_{\text{J}}}$的松动椭球体。对于两个椭球体体积之间的关系，Janelid等^[18]提出用松动系数$\beta$来表述并假设二者偏心率相等，通过研究发现松动系数$\beta$一般为1.066~1.100，且

1.2   隧道极限松动区的确定

武军等^[17]考虑颗粒物质只受到一个方向尺寸收缩的影响，另一个方向无限长，不产生收缩影响，从而将三维问题转化为二维问题，即极限松动区和流出松动区由椭球体转化为一个椭圆区域。

因此本文取隧道在纵向方向的单位长度为研究对象，将其转化为二维问题，故式（2）转化为

式中：${S_{\text{J}}}$，${S_{\text{L}}}$分别为放出椭圆和松动椭圆的面积。

武军等^[17]假设放出椭圆的面积和隧道断面面积相等，从而来确定隧道上方的极限松动区域。但实际上地层的破坏模式和地层损失率的大小密切相关^[19]，当地层损失率增大时，地层坍塌受影响的范围也随之增大。因此在确定隧道上方地层的极限松动区时应将地层的损失率考虑进去。所以本文在武军等学者的基础之上考虑地层损失对椭圆松动区的影响，假设放出椭圆的面积和隧道断面大小以及地层损失率具有如下关系：

联合式（1），（4）得：

松动椭圆区域的面积${S_{\text{J}}}$为

式中：${a_{\text{J}}}$，${b_{\text{J}}}$为松动椭圆的长半轴和短半轴。

由于松动椭圆和放出椭圆的偏心率相同，故联立式（1）~（7）可得：

2.   试验验证及结果分析

2.1   模型试验方案

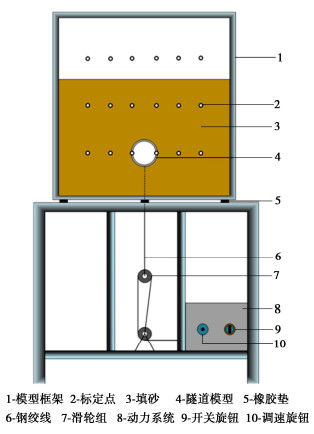
为了验证本文提出的椭球体松动区数学模型的合理性，自主设计了平面应变隧道模型试验系统，该模型试验系统由模型试验架（模型箱净空尺寸为长×宽×高=80 cm×20 cm×80 cm，隧道模型为直径为10 cm钢管）、加载系统（电机和滑轮组）和监测系统（GeoPIV软件、LED泛光灯、相机和计算机组成）三部分组成，详细的介绍可参考文献[20]。

为减小试验过程中边界效应对试验结果的影响，预先在模型箱两侧的钢板内侧粘贴光滑的丝光纸。由于丝光纸和钢化玻璃表面十分光滑，故试验过程中土体和其摩擦可忽略不计。通过细钢绞线分别连接隧道模型和电机，通过电机的牵引来使得隧道产生竖向沉降，以模拟施工和运营过程在其他因素影响下产生的地层损失，然后采用砂雨法填筑制样。最后调节电机转速为0.5 r/min使隧道以0.131 mm/s的速度缓慢沉降并采用PIV测量系统监测隧道上方地层的变形及破坏过程。

图  3  非接触式图像测量系统

Figure  3.  Non-contact image measurement system

下载: 全尺寸图片 幻灯片

2.2   试验结果分析

（1）放出椭球体试验结果分析

软土地区的地铁隧道在列车运营后容易产生沉降从而引起地层沉降等问题，如上海轨道交通一号线，人民广场站至新闸路站区间隧道，1995—1999年监测最大累计沉降值超过145 mm。因此，本文通过让隧道产生沉降使得上部土体和隧道之间产生空隙，从而使土体失去支护力向隧道区间内移动引起地层损失。地层损失率^[21]为隧道和上部土体之间产生的空隙和隧道断面的比值。隧道和上方地层产生的空隙可由隧道下沉的距离和隧道的尺寸计算得出，隧道的竖向位移可由PIV技术得出。

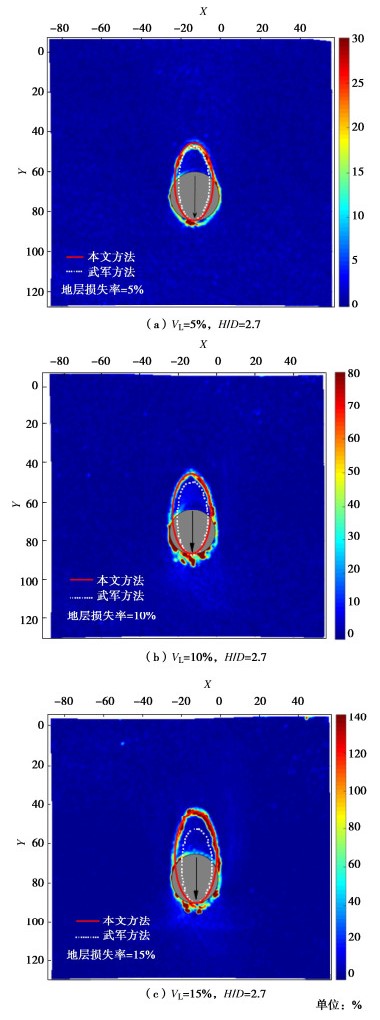
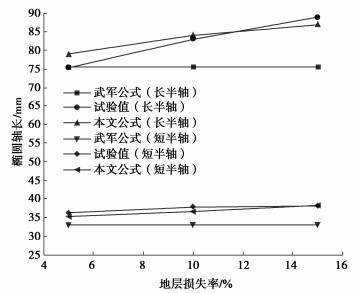
图 4为不同地层损失率下地层的沉降剪切应变图。由图可知，在填砂密实度和埋深相同的情况下，由于隧道的下沉，其上方土体逐渐失去支护，土的抗剪强度逐渐发挥直至达到其最大值而发生剪切破坏。不同地层损失情况下，隧道上方土体的破坏模式总体上相同，大致呈现出一个立椭圆的形状。随着地层体积损失率的增大，隧道上方土体的剪切应变越大，椭圆剪切松动区也逐渐增大。刘俊等^[22]基于模型试验探究不同覆跨比下隧道的破坏模式也得出类似的结果。当地层损失率为5%，10%和15%时，椭圆松动区的长半轴分别为1.57R、1.68R和1.74R（R为隧道半径）。然后将试验结果和修正后椭球体理论以及武军提出的理论进行对比可知（图 4，5），当地层损失率较小的情况下，武军公式能很好地预测土体放出椭圆的范围。但随着地层损失率的增大，本文修正公式和试验结果更加吻合，更能反映不同地层损失率下放出椭圆的实际面积。

图  4  不同损失率下地层剪切应变

Figure  4.  Shear strains of strata at different loss rates

下载: 全尺寸图片 幻灯片

图  5  地层损失和长短半轴关系图

Figure  5.  Relationship between ground loss and long and short semi-axes

下载: 全尺寸图片 幻灯片

（2）松动椭球体试验结果分析

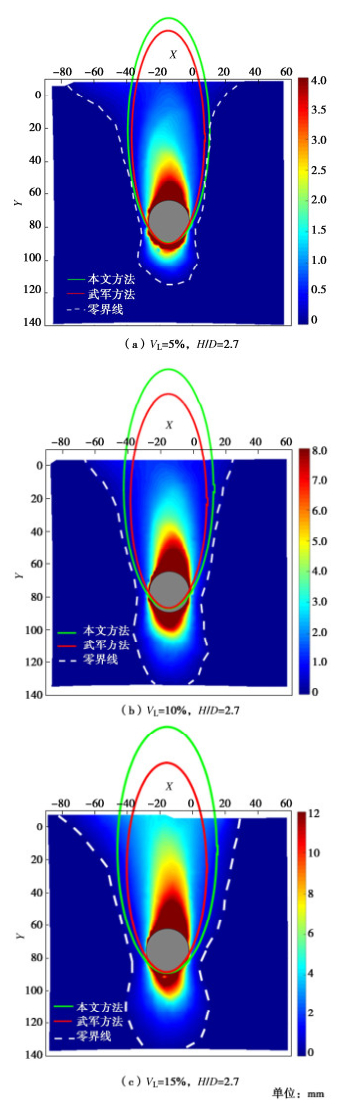
椭球体理论认为，松动椭球体和放出椭球体之间的土体部分只发生位移不会从出口流出且松动椭球体之外的土体部分保持静止。因此，接下来本文通过地层的沉降位移图来对修正后的椭球体理论中的极限松动区进行验证。本文通过使隧道分别产生4，8，12 mm的沉降来使得隧道和上部土体产生间隙以模拟不同的地层损失。图 6为不同地层损失率下土体的位移图。由图可知，由于隧道产生沉降，上部土体在重力作用下下沉，随着地层损失率的增大，地层的沉降和受扰动的范围都在逐渐增大，地层受扰动的范围近似一个立椭圆的形状。另一方面，在实际的工程中，施工水平、土质条件和隧道轴线埋深都会引起地层损失率的增大或减小^[23]。因此，在工程实践中考虑地层损失率的大小对确定土体的松动和滑移范围具有十分重要的意义。

图  6  不同损失率下地层位移

Figure  6.  Ground displacements under different loss rates

下载: 全尺寸图片 幻灯片

根据图 6的试验结果可知，武军方法在地层损失率较小情况下和试验结果吻合较好，但随着地层损失率的增大，本文修正后的椭球体理论和试验结果则更加吻合，更能反应不同地层损失情况下土体的实际松动滑移范围。与此同时，由于本文所采用的PIV技术对土体位移监测的精度可达到1.0 um，且本文通过探究松动椭球体的具体范围的最终目的是对隧道松动土压力的计算方法进行修正，所以在地层位移零界点附近的土颗粒因其位移很小故对松动土压力的影响可以忽略不计。

3.   松动土压力计算

自从Terzaghi基于trapdoor试验提出松动土压力的计算公式以来，关于隧道上方土体滑移面的研究一直是隧道工程中的热点。Chevalier等^[24]基于活动门试验提出土体的滑动面为塔形，朱孟龙等^[9]基于塔形滑动面提出了松动土压力的计算方法。SHUKLA等^[10]则提出土体的滑移面为盆形。武军则提出隧道上方土体的坍塌和滑移类似于椭球体，并基于椭球体理论对隧道松动土压力理论进行修正。本文则首先对椭球体理论进行修正，然后结合修正后的椭球体理论以及松动区土体主应力轴旋转对Terzaghi松动土压力理论进行修正。

3.1   土压力公式推导

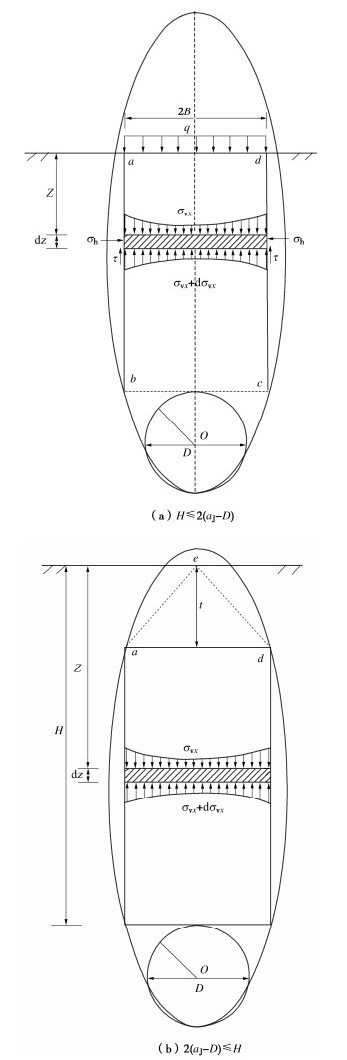
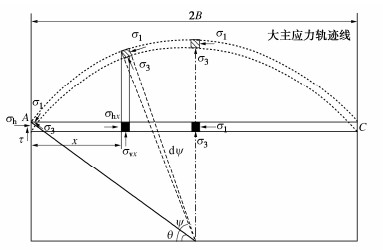
在Terzaghi所提出的松动土压力计算公式中侧压力系数取值为1，但是当土中产生土拱效应时，其土压力系数并不是一个定值，其值大小受到土体空间位置以及土拱效应的发挥程度的影响。加瑞^[7]通过模型试验得出不同位置处侧压力系数不同，随着活动门的下移侧压力系数在中轴线的位置大于1.0，然后呈正态分布规律向两侧递减。崔蓬勃等^[25]认为在隧道开挖后，拱顶位移随地层损失的发生而逐渐增大，土拱效应逐渐产生，中轴线处土单元的竖向应力和水平应力均减小，但竖向应力的减小幅度远超水平应力减小幅度，从而发生主应力旋转。因此，基于修正椭球体理论，建立如图 7所示的松动土压力分析模型。为了描述土拱效应影响下土体的应力状态，模型的基本假设：①水平微分土条上的应力状态处于同一摩尔应力圆上；②滑裂面处土体的内摩擦角$\varphi$充分发挥；③松动区内土体达到Mohr-Coulomb极限平衡状态；④土体均匀且各向同性；⑤松动区内同一深度处任意位置土体主应力大小相等^[4]，从而对于不同位置处应力可以由大小主应力以及主应力旋转角来表示。Terzaghi公式假设相同深度处竖向应力均匀分布，而由大主应力迹线圆弧拱理论可知，竖向应力自地层滑移处向隧道中轴线处逐渐递减^[4]，由此可以绘出松动滑移区土体内力分析图（图 7）。图 7（a）中，2B为椭圆松动区计算宽度，Z为隧道上覆土层厚度，q为地面分布超载，H为隧道埋深，${\sigma _{{\text{v}}x}}$和${\sigma _{{\text{h}}x}}$为极限松动滑移区内部水平微分单元任一位置x处的竖向应力和水平应力，$\psi$为该位置处大主应力方向和竖直方向的夹角，当$x \in \left[ 0 \right.,\left. B \right]$时，$\psi \in \left[ \theta \right.,\left. {{\text{π }}/2} \right]$。

图  7  改进的Terzaghi松动土压力分析模型

Figure  7.  Modified failure mechanism of Terzaghi for a tunnel

下载: 全尺寸图片 幻灯片

李瑞林等^[26]将Harrop-Williams^[27]的方法应用于大主应力拱后发现其拱迹线实际上是介于悬链线和圆弧线之间的曲线。徐长节等^[4]采用圆弧拱形、悬链线拱形和抛物线拱形的大主应力轨迹线进行计算所得应力分布之间的差异不大，并推荐相关工程中采用圆弧形大主应力轨迹线假定进行计算。因此本文基于椭球体理论假设图 8中的大主应力轨迹线为圆弧，则可以得到其半径${R_1}$和$\psi$的表达式：

图  8  松动区土体应力分析

Figure  8.  Stress analysis of soils in loosening zone

下载: 全尺寸图片 幻灯片

根据图 2中所建立的坐标系，由椭球体理论以及已知的坐标点可得滑动土体的计算宽度为

图  2  模型试验系统示意图

Figure  2.  Schematic diagram of model test system

下载: 全尺寸图片 幻灯片

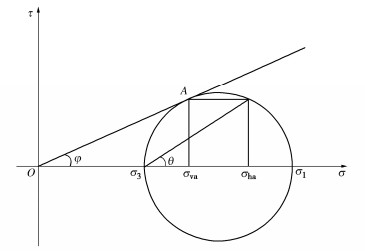
在滑裂面A点位置处的土体单元应力状态可以用图 9中的摩尔应力圆来表示。通过图 9中的几何关系可以得出：

图  9  滑裂面处土体摩尔应力圆

Figure  9.  Mohr's stress circle of soils on sliding interface

下载: 全尺寸图片 幻灯片

式（13），（14）得

式中：$K$为土拱效应发挥后土中侧向土压力系数，$\theta = {45^ \circ } - \varphi /2$；${K_{\text{a}}}$为主动土压力系数，

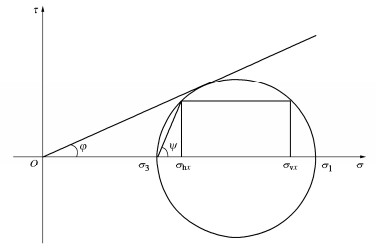
同理，通过摩尔应力圆（图 10）可得在松动区内部任一位置x处的竖向应力：

图  10  松动区内部土体应力状态

Figure  10.  Stress states of soils in loosening zone

下载: 全尺寸图片 幻灯片

如图 7所示，取一厚度为dz的水平微分单元作为研究对象，则在竖直方向上其受力平衡方程为

式中：$\gamma$为土体重度；${\bar \sigma _{\text{v}}}$为水平微分单元所受平均竖向应力，

联立式（18）~（20）并积分可得

将水平微单元任意一位置处竖向应力${\sigma _{{\text{v}}x}}$与平均竖向应力${\bar \sigma _{\text{v}}}$的比值m称为应力分布系数，用来反映隧道上方土体竖向压力在水平方向上的非线性变化特征。然后通过式（11），（17），（22）可得应力分布系数m为

假设地表超载为$q$，联立边界条件$z = 0$，${\sigma '_{\text{v}}} = q$以及式（18），（19），（23）得

假设隧道的埋深为H，地表没有外荷载，则式（24）转化为

（1）当$H \leqslant 2({a_{\text{J}}} - D)$时，即隧道的埋深小于椭圆松动区的计算高度，因此可将Z=H代入式（25）计算松动土压力。

（2）当$2({a_{\text{J}}} - D) \leqslant H \leqslant 2{a_{\text{J}}} - D$时，将超过计算高度的椭圆部分（图 7（b））折算为超载${q_0}$，然后把$Z = 2({a_{\text{J}}} - D)$，$q = {q_0}$代入式（24）计算松动土压力。${q_0}$的计算式为

（3）当$2{a_{\text{J}}} - D \leqslant H$时，即隧道的埋深超过了地层的极限松动区的范围，土体极限松动区以外的部分对隧道松动土压力不产生影响，故将$Z = 2{\text{(}}{a_{\text{J}}} - D{\text{)}}$，${q_0} = \frac{1}{2}\gamma D$代入式（24）计算松动土压力。

3.2   结果分析

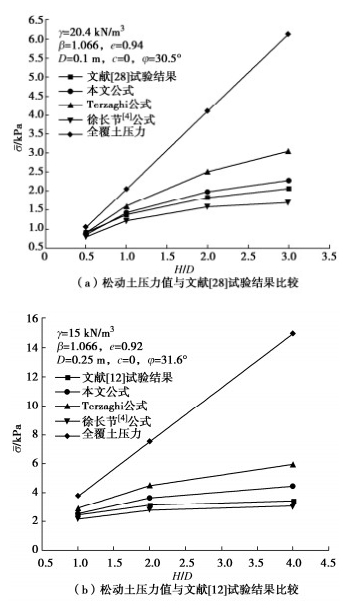
目前基于地层拱理论的隧道上覆土压力计算研究中很少考虑滑移面范围受隧道埋深的影响^[21]。椭球体理论考虑了地层受影响范围和隧道埋深的关系，故本文基于修正后的椭球体理论分析土拱效应的影响，进而对隧道松动土压力公式进行修正。为了验证修正公式的合理性，本文分别选取Shahin等^[28]和陈其志等^[12]的模型试验结果来进行对比分析。由图 11可知，随着隧道埋深的增大，土拱效应逐渐发挥，隧道上方土压力明显小于全覆土压力。另一方面，从太沙基公式、徐长节以及本文修正公式可以得出随着隧道埋深的增大，土拱效应愈来愈明显，隧道上方土压力逐渐趋向于一个定值。

图  11  平均竖向压力与H/D的关系

Figure  11.  Relationship between average vertical pressure and H/D

下载: 全尺寸图片 幻灯片

与此同时也可以看出本文修正后的公式计算结果和Shahin和陈其志两位学者的试验结果比较接近。Terzaghi松动土压力公式中侧土压力系数根据经验取值为1且没有考虑隧道上方土体破坏面和埋深的关系，导致其计算结果偏大。徐长节在Terzaghi公式的基础上对侧土压力系数进行了修正，但没有考虑隧道埋深对上方地层破坏范围的影响，导致其计算结果比试验结果小。

4.   结论

本文考虑地层损失对隧道上方土体沉降范围的影响从而对椭球体理论进行修正，然后基于椭球体理论及松动区内部土体主应力轴旋转对隧道松动土压力公式进行修正。通过对隧道极限松动区和松动土压力进行研究得出3点结论。

（1）修正后的椭球体理论综合考虑隧道的尺寸、土体的松动系数以及地层损失率对隧道上方土体沉降的影响，可以精确简便地确定隧道上方地层受影响的范围。

（2）通过自主设计的试验装置并结合PIV技术对修正后的椭球体理论进行验证得出：在土体密实度和隧道尺寸相同情况下，随着地层损失的增大，地层受影响的范围随之增大，隧道的放出椭圆区域和极限松动区也随之增大。本文修正椭球体理论和试验结果更加吻合。

（3）基于修正椭球体理论改进的隧道松动土压力计算公式，充分考虑了地层滑移变形范围以及土拱效应对隧道松动土压力的影响，其计算结果比Terzaghi公式和徐长节公式更加接近试验结果。可用于砂土地质条件下隧道、管线等结构上方的土压力计算。