粗糙岩石单裂隙非达西流动的试验和数值模拟研究

朱寅斌; 李长冬; 周佳庆; 项林语; 余海兵; 陈文强

doi:10.11779/CJGE20220307

粗糙岩石单裂隙非达西流动的试验和数值模拟研究 English Version

朱寅斌^1,,
李长冬^{1, 2, ,},
周佳庆^{1, 2},
项林语¹,
余海兵¹,
陈文强¹

1.
中国地质大学(武汉)工程学院, 湖北武汉 430074
2.
中国地质大学(武汉)湖北巴东地质灾害国家野外科学观测研究站, 湖北武汉 430074

基金项目:

国家自然科学基金项目 42090054

国家自然科学基金项目 41922055

国家自然科学基金项目 51909247

湖北省重点研发计划项目 2020BCB079

详细信息

作者简介:
朱寅斌(1997—)，男，博士研究生，主要从事岩体裂隙渗流方面的研究。E-mail: zhuyinbin2022@163.com

通讯作者:
李长冬, E-mail: lichangdong@cug.edu.cn

中图分类号: TU43
计量
- 文章访问数: 371
- HTML全文浏览量: 61
- PDF下载量: 124
出版历程
- 收稿日期: 2022-03-20
- 网络出版日期: 2023-06-07
- 刊出日期: 2023-05-31

Experimental and numerical studies on non-Darcian flow in single rough-walled rock fracture

1.
Faculty of Engineering, China University of Geosciences, Wuhan 430074, China
2.
Badong National Observation and Research Station of Geohazards, China University of Geosciences, Wuhan 430074, China

摘要

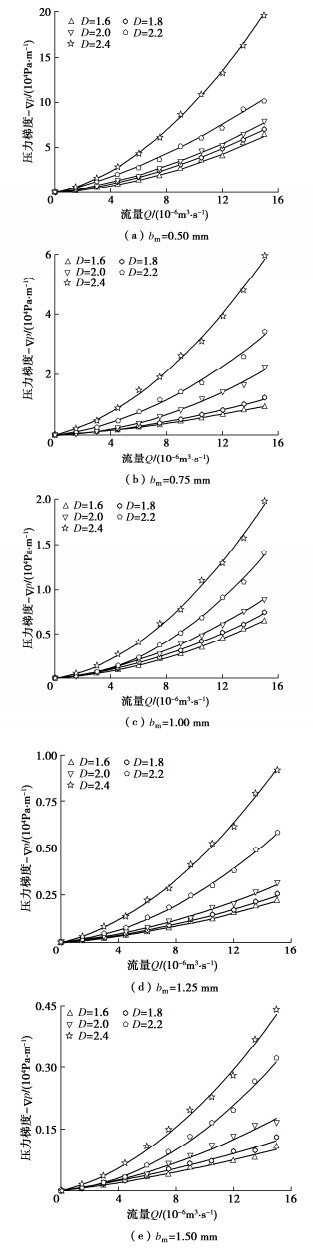
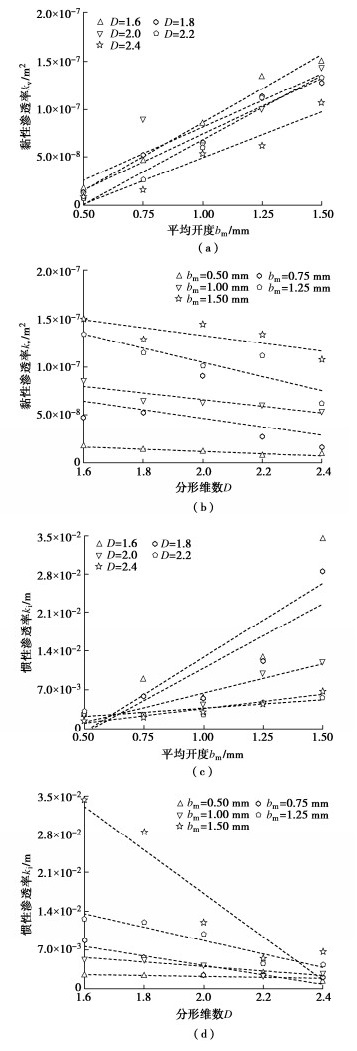
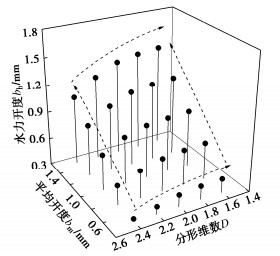
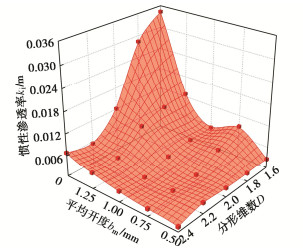
摘要: 采用3D雕刻方式制作了一批具有特定粗糙度的砂岩裂隙样品，结合自行设计的可定量调整粗糙岩石单裂隙开度的装置，实现了在试验中对岩石单裂隙试样开度和表面粗糙度的定量化控制。开展一系列不同流量下的渗流试验，研究了平均开度和表面粗糙度对粗糙岩石单裂隙非达西流动的影响。结果表明Forchheimer方程可以准确的描述裂隙中流体流量与压力梯度间的非线性关系。分形维数是表征岩石裂隙表面粗糙度的有效参数，其增大主要导致裂隙的曲折程度增大而使流动路径变得更复杂，从而促进非达西流动的发生。建立了惯性渗透率与平均开度和分形维数之间的经验定量化模型，通过直接求解Navier-Stokes方程来开展三维粗糙单裂隙渗流模拟，验证了所建立模型的准确性和所开展渗流试验的可靠性。粗糙岩石单裂隙的平均开度越小、表面粗糙度越大则所建立的经验定量化模型预测的结果就越精确。
- 粗糙岩石单裂隙 /
- 非达西流动 /
- 渗流试验 /
- 数值模拟 /
- 开度尺寸 /
- 表面粗糙度
Abstract: A series of rough-walled rock fracture specimens with specific surface roughnesses are made by using the three- dimensional carving. After that, the self-designed apparatus which can quantitatively change the aperture of single rock fracture is adopted to realize the purpose of aperture and surface roughness to be quantitatively controlled in the experiment. The seepage experiments on all rock fracture replicas at different flow rates are carried out to study the influences of the mean aperture and surface roughness on the non-Darcian flow in a single rough-walled rock fracture. The results show that the Forchheimer equation is suitable for characterizing the non-Darcian flow in rough-walled fractures. The fractal dimension is an effective parameter to reflect the surface roughness of rock fracture, and the increase of fractal dimension mainly leads to an enlargement in degree of tortuousness and results in the increased complexity of flow paths. An empirical quantification model is established to relate the inertial permeability to the mean aperture and fractal dimension. The numerical simulations by directly solving the Navier-Stokes equation are performed to investigate the non-Darcian flow in three-dimensional rough-walled fractures with different apertures and roughnesses. The inertial permeabilities of the simulated results agree well with those of the empirical quantification model and experiments, indicating that both the model and the experiments are reliable. The prediction accuracy of the empirical model increases with the decrease of the mean aperture and increase of surface roughness.
- single rough-walled rock fracture /
- non-Darcian flow /
- seepage experiment /
- numerical simulation /
- aperture size /
- surface roughness

HTML全文

0. 引言

膨胀性非饱和土是一种具有特殊结构的非饱和土，通常表现出吸水膨胀、失水收缩和浸水强度降低等特性，工程中容易使建筑物产生不均匀沉降，甚至会导致结构开裂和破坏。因此，对膨胀性非饱和土本构模型的研究具有重要工程意义，能够为预测膨胀土的变形特性从而避免工程灾害的发生提供有效手段。

1990年，Alonso等^[1]在修正剑桥模型的基础上，考虑了吸力的影响并引入了加载-湿陷屈服面（LC屈服面）和吸力增加屈服面（SI屈服面），进而提出了巴塞罗那弹塑性本构模型（BBM），能够描述非饱和土屈服应力随吸力增加而变大、湿化变形等力学特性。在此之后，Wheeler等^[2]、Sun等^[3-4]、缪林昌^[5]、赵成刚等^[6]、姚仰平等^[7-8]、Luo等^[9]也提出了多种形式的非饱和土本构模型，这些模型虽然可以描述包括湿陷变形在内的非饱和土的基本力学特性，但不能体现膨胀性非饱和土吸水膨胀的力学特性。

为更好地描述膨胀性非饱和土的力学特性，Gens等^[10]于1992年建立了膨胀性非饱和土弹塑性本构模型的理论框架模型（G-A模型）。在此基础上，Alonso等^[11]进一步建立了巴塞罗那膨胀性非饱和土弹塑性本构模型（BExM）。该模型认为膨胀土的膨胀性是由于其具有双重结构，即微观结构与宏观结构，当非饱和膨胀土湿化时，微观结构会发生膨胀，从而导致宏观结构发生塑性膨胀，最终表现出土体的整体膨胀。在此之后，许多学者在这一模型的理论基础上进行了改进和扩展，Sánchez等^[12]在G-A模型的基础上建立了考虑微观-宏观双重结构影响的广义塑性模型，并将其成功运用于有限元数值分析中；Mašín^[13]分别建立了能够描述微观结构和宏观结构的计算公式，通过引入双重结构的耦合方程建立了考虑水力耦合的非饱和膨胀土模型；卢再华等^[14]在改进的G-A模型中引入剪切屈服面（S_y），建立了非饱和原状膨胀土的弹塑性损伤本构模型；陈正汉等^[15-16]进一步针对原状膨胀性土、重塑膨胀性土和重塑膨润土等不同类型的膨胀土进行了全方位的研究，综合考虑了温度、持水特性等因素对膨胀土力学性质的影响，建立了考虑热-水-力等多场耦合特性的膨胀土模型；孙德安等^[17]考虑了饱和度对应力应变关系的影响及变形对土水特性的影响，并引入了等孔隙比线，建立了能够描述膨胀性非饱和土水力-力学耦合特性的弹塑性本构模型；曹雪山^[18]针对膨胀土干湿循环特性进一步完善模型，引入了微-宏观结构耦合参数，提出了考虑双重结构耦合的弹塑性本构模型；李舰等^[19-20]，Li等^[21]建立了适用于膨胀性非饱和土的边界面模型，并围绕其提出了有效的数值计算方法。

Yao等^[22]以修正剑桥模型为基础，提出了可以描述饱和超固结土力学特性的统一硬化（UH）本构模型，之后进一步考虑了吸力的影响，引入LC屈服面，扩展了UH模型使其可以描述非饱和土的特性^[8]。本文在非饱和土UH模型基础上，引入考虑超固结度和初始干密度影响的膨胀式，使其可以反映膨胀土湿化膨胀过程中产生的塑性变形，并进一步构建了考虑膨胀土膨胀性的非饱和土UH模型，由于本模型仅考虑了膨胀土的非饱和、胀缩性和超固结性等特性，没有考虑裂隙性^[23]，是对理想状态的膨胀土进行描述，故称理想膨胀性非饱和土UH模型。

1. 膨胀性非饱和土UH模型

1.1 吸力应力与屈服面方程

Alonso等^[1]在BBM中认为非饱和土的应变由吸力和净应力共同控制，并提出了LC屈服面和SI屈服面的概念来描述非饱和土的变形特性。Luo等 ^[9]在此基础上，根据对试验现象的分析，提出了新的吸力应力表达式，

$\begin{array}{*{20}{c}} {{p_{\text{s}}} = a\left( {1 - {e^{ - \frac{s}{a}}}} \right)} \end{array}\ \ \ \ \ \ \ 。$

(1)

式中： ${p_{\text{s}}}$ 为吸力应力，表示吸力对土体黏聚力的贡献值^[16]，可以通过恒定吸力下非饱和土的三轴试验或直剪试验测得； $a$ 为最大吸力应力，可以通过两个或两个以上不同吸力下非饱和土的三轴试验或直剪试验求得^[3]； $s$ 为吸力，是负孔隙水压力和表面张力在土骨架上的综合作用应力。区别于BBM，这里吸力应力与吸力并非正比关系，而是呈现非线性变化并存在一个最大值。

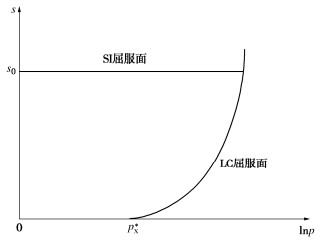
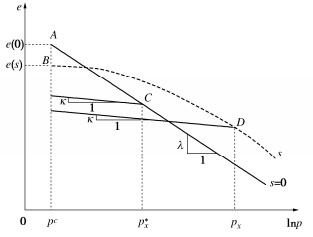
对于正常固结非饱和土，根据Sun等^[3]、Yao等^[8]和Luo等^[9]的研究，假设其等向压缩线在 $e{\text{ - ln}}(p + {p_{\text{s}}})$ 平面呈直线，如图 1所示，其等向压缩线公式可表示为

图 1 饱和土和非饱和土的等向压缩线

Figure 1. Normal compression lines for saturated and unsaturated soils

下载: 全尺寸图片幻灯片

$\begin{array}{*{20}{c}} {e = e(s) - \lambda \ln \frac{{p + {p_{\text{s}}}}}{{{p^{\text{c}}} + {p_{\text{s}}}}}} \end{array}\ \ \ \ \ \ \ 。$

(2)

式中： ${p^{\text{c}}}$ 为参考吸力应力，假设当净平均应力为 ${p^{\text{c}}}$ 时，吸力变化仅引起弹性应变， $\lambda$ 为正常固结饱和土在 $e{\text{ - ln}}p$ 平面上等向压缩线的斜率。当吸力恒定时，平均净应力变化所引起的变形可写为

$\begin{array}{*{20}{c}} {{\text{d}}e_{\text{p}}^{\text{e}} = - \kappa \frac{{{\text{d}}p}}{p}} \end{array}\ \ \ \ \ \ \ 。$

(3)

对于吸力变化引起的变形，假设历史最大吸力为 ${s_0}$ ，当吸力 $s$ 小于历史最大吸力时，吸力变化仅引起弹性变形，当吸力 $s$ 大于历史最大吸力 ${s_0}$ 时，吸力增加会引发弹塑性变形，定量表述如下：

$\begin{array}{c}de=\{\begin{array}{c}-{\kappa }_{\text{s}}\frac{\text{d}s}{s+{p}_{\text{at}}}\text{(}s\le {s}_{0}\text{)}\\ -{\lambda }_{\text{s}}\frac{\text{d}s}{s+{p}_{\text{at}}}\text{(}s＞{s}_{0}\text{)}\end{array}\end{array} \ \ \ \ \ \ \ 。$

(4)

式中： ${\lambda _{\text{s}}}$ 为吸力超过历史最大吸力 ${s_0}$ 之后非饱和土在 $e{\text{ - ln}}s$ 平面内吸力加载线的斜率， ${\kappa _{\text{s}}}$ 为非饱和土在 $e{\text{ - ln}}s$ 平面内吸力回弹线的斜率， ${p_{{\text{at}}}}$ 为标准大气压。

基于上述假设，新的LC屈服面方程可以推导为

$\begin{array}{*{20}{c}} {{{\left( {\frac{{p_{\text{x}}^*}}{{{p^{\text{c}}}}}} \right)}^{\lambda - \kappa }} = {{\left( {\frac{{{p_{\text{x}}} + {p_{\text{s}}}}}{{{p^{\text{c}}} + {p_{\text{s}}}}}} \right)}^\lambda }{{\left( {\frac{{{p_{\text{x}}}}}{{{p^{\text{c}}}}}} \right)}^{ - \kappa }}} \end{array}\ \ \ \ \ \ \ 。$

(5)

式中： ${p_{\text{x}}}$ 为不同吸力下 $p{\text{ - }}q$ 平面屈服面与 $p$ 轴的交点值， $p_{\text{x}}^{\text{*}}$ 为饱和土 $p{\text{ - }}q$ 平面屈服面与 $p$ 轴的交点值，如图 2。

图 2 LC屈服面和SI屈服面

Figure 2. Yield curves of LC and SI

下载: 全尺寸图片幻灯片

SI屈服面采用BBM中与 $p$ 轴平行的直线，如图 2，方程可写为

$\begin{array}{*{20}{c}} {s = {s_0}} \end{array}\ \ \ \ \ \ \ 。$

(6)

式中： ${s_0}$ 为历史最大吸力。

$p{\text{ - }}q$ 平面采用椭圆屈服面，

$f = {\text{ln}}\hat p + \ln \left( {1 + \frac{{{{\hat q}^2}}}{{{M^2}{{\hat p}^2}}}} \right) - \ln ({p_{\text{x}}} + {p_{\text{s}}}) = 0\ \ \ \ \ \ \ 。$

(7)

式中： $\hat p = p + {p_{\text{s}}}$ ， $\hat q = q$ 。本文提出的模型采用相关联流动法则，假设塑性势面方程与屈服面方程相同。

1.2 硬化参量

本模型屈服面的硬化参数采用 $H$ ，硬化规律可表示为

$\begin{array}{*{20}{c}} {\frac{{{\text{d}}p_{\text{x}}^*}}{{p_{\text{x}}^*}} = \frac{{1 + {e_0}}}{{\lambda - \kappa }}dH} \end{array}\ \ \ \ \ \ \ 。$

(8)

Alonso等^[11]在提出的BExM中认为膨胀土吸水膨胀与其微观结构有关，在吸力变化时土体微观结构的改变会引起宏观结构的塑性变形。对于膨胀土，湿化会使得微观结构膨胀，进而引发宏观结构的塑性膨胀。膨胀土在湿化时塑性体应变由两部分组成，一部分是净应力变化和吸力变化综合引发的塑性体应变 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ ，与非膨胀性非饱和土中的塑性体应变相同，另一部分为微观结构变化引起的宏观结构塑性体应变 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}$ 。卢再华等^[24]提出对膨胀性非饱和土湿化时的膨胀量，可采用其与土体湿化产生的弹性体变的关系来求解，参照Alonso等^[11]和卢再华等^[24]对膨胀变形的求解思路，本文假定微观结构的应变与吸力引起的弹性应变相同，将宏观结构发生的塑性体应变 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}$ 表示为微观结构体应变的函数：

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}} = {f_{\text{d}}}{\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}}} \end{array}\ \ \ \ \ \ \ 。$

(9)

式中：

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}} = \frac{{{\kappa _{\text{s}}} \cdot {\text{d}}s}}{{\left[ {(1 + {e_0})(s + {p_{{\text{at}}}})} \right]}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(10)

${f_{\text{d}}}$ 为放大系数，

$\begin{array}{*{20}{c}} {{f_{\text{d}}} = {J^{\frac{{{\rho _{\text{d}}}}}{{{\rho _{\text{w}}}}}}}{{(1 - R)}^2}} \end{array}\ \ \ \ \ \ \ 。$

(11)

式中： $J$ 为反映膨胀土膨胀能力的参数； ${\rho _{\text{d}}}$ 为土体初始干密度，根据高登辉等^[25]的研究，初始干密度对非饱和土的变形参数、强度参数和渗透参数等有重要影响，此处通过引入初始干密度来考虑其对非饱和土膨胀量的影响， ${\rho _{\text{w}}}$ 为水的密度， $R$ 为超固结系数，可通过孔隙状态参数 $\xi$ 求出，

$\begin{array}{*{20}{c}} {R = \exp \left( { - \frac{\xi }{{\lambda - \kappa }}} \right)} \end{array}\ \ \ \ \ \ \ 。$

(12)

为考虑膨胀性的影响，在屈服面中引入微观结构引起的塑性变形，即将塑性应变增量表示为两部分：

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{\text{v}}^{\text{p}} = {\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}} + {\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}} \end{array}\ \ \ \ \ \ \ 。$

(13)

屈服面采用统一硬化参量 $H$ ，并认为统一硬化参量 $H$ 只与净应力引起的塑性体应变有关，具体增量表达式为

$\begin{array}{*{20}{c}} {{\text{d}}H = \frac{{M_{\text{f}}^4 - {{\hat \eta }^4}}}{{{M^4} - {{\hat \eta }^4}}}{\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}} \end{array}\ \ \ \ \ \ \ 。$

(14)

式中： $\hat \eta$ 为应力比， $\hat \eta = \hat q/\hat p$ ； ${M_{\text{f}}}$ 为潜在强度^[26]，

$\begin{array}{*{20}{c}} {{M_{\text{f}}} = 6\left[ {\sqrt {\frac{{12(3 - M)}}{{{M^2}}}\exp \left( { - \frac{\xi }{{\lambda - \kappa }}} \right) + 1} + 1} \right]} \end{array}\ \ \ \ \ \ \ 。$

(15)

式中： $\xi$ 为孔隙状态参数，反映土体当前孔隙比下的超固结程度，

$\begin{array}{*{20}{c}} {\xi = {e_{\hat \eta }} - e} \end{array}\ \ \ \ \ \ \ 。$

(16)

式中： ${e_{\hat \eta }}$ 为当前应力状态下土体正常固结时对应的孔隙比，

${e_{\hat \eta }} = e(s) - \lambda \ln \left[ {\frac{{\hat p}}{{{p^{\text{c}}} + {p_{\text{s}}}}}\left( {1 + \frac{{{{\hat \eta }^2}}}{{{M^2}}}} \right)} \right] + \kappa \ln \left( {1 + \frac{{\hat p}}{p}\frac{{{{\hat \eta }^2}}}{{{M^2}}}} \right) \ \ \ \ \ \ \ 。$

(17)

1.3 弹性应变增量

在净应力和吸力发生变化时，土体会发生变形，其中弹性应变可以表示为弹性体应变和弹性剪应变，本模型中弹性体应变可以表示为

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{\text{v}}^{\text{e}} = {\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}} + {\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}}} \end{array}\ \ \ \ \ \ \ 。$

(18)

其包含两部分，第一部分为净应力变化引起的弹性体应变，

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}} = \frac{k}{{1 + {e_0}}}\frac{{{\text{d}}\hat p}}{p} = \frac{{{\text{d}}\hat p}}{K}} \end{array}\ \ \ \ \ \ \ 。$

(19)

式中：

$\begin{array}{*{20}{c}} {K = \frac{E}{{3{\text{(}}1 - 2v{\text{)}}}}} \end{array} \ \ \ \ \ \ \ \text{；}$

(20)

$\begin{array}{*{20}{c}} {E = \frac{{3(1 - 2v)(1 + {e_0})}}{\kappa }\hat p} \end{array}\ \ \ \ \ \ \ 。$

(21)

第二部分为吸力变化引起的弹性体应变，方程表达式见式（10）。

本模型认为吸力变化不会引起弹性剪应变，故弹性剪应变仅由净应力中的剪应力引起，可表示为

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{\text{d}}^{\text{e}} = \frac{{{\text{d}}\hat q}}{{3G}}} \end{array}\ \ \ \ \ \ \ 。$

(22)

式中：

$\begin{array}{*{20}{c}} {G = \frac{E}{{2(1 + v)}}} \end{array}\ \ \ \ \ \ \ 。$

(23)

1.4 塑性应变增量

由屈服面公式可知，净应力变化引起的应变增量可表示为

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}} = \mathit{\Lambda } \frac{{\partial f}}{{\partial \hat p}}} \end{array}\ \ \ \ \ \ \ \text{，}$

(24)

$\begin{array}{*{20}{c}} {{d} \varepsilon _{\text{d}}^{\text{p}} = \mathit{\Lambda } \frac{{\partial f}}{{\partial \hat q}}} \end{array}\ \ \ \ \ \ \ 。$

(25)

式中： $\mathit{\Lambda }$ 为塑性标量因子。

对当前屈服面函数和LC屈服面函数进行全微分，联立求解后得到

$\begin{array}{*{20}{c}} {\mathit{\Lambda } = {A_0}\frac{{\frac{{\partial f}}{{\partial \hat p}}{\text{d}}\hat p + \frac{{\partial f}}{{\partial \hat q}}{\text{d}}\hat q + {f_{\text{s}}}{\text{d}}s}}{{\frac{{\partial f}}{{\partial \hat p}}}}} \end{array}\ \ \ \ \ \ \ 。$

(26)

式中：

$\begin{array}{*{20}{c}} {{A_0} = \frac{{{c_{\text{p}}}\hat {\mathit{\Omega }} }}{{p_{\text{x}}^{\text{*}}}}\frac{{\lambda {p_{\text{x}}} - \kappa \left( {{p_{\text{x}}} + {p_{\text{s}}}} \right)}}{{\lambda - \kappa }}{{\left( {\frac{{{p_{\text{x}}}}}{{{p^{\text{c}}}}}} \right)}^{\frac{{ - \lambda }}{{\lambda - \kappa }}}}{{\left( {\frac{{{p_{\text{x}}} + {p_{\text{s}}}}}{{{p^{\text{c}}} + {p_{\text{s}}}}}} \right)}^{\frac{\lambda }{{\lambda - \kappa }}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(27)

$\begin{array}{*{20}{c}} {{f_{\text{s}}} = \frac{{ - \lambda {p_{\text{x}}} + \kappa ({p^{\text{c}}} + {p_{\text{s}}})}}{{({p^{\text{c}}} + {p_{\text{s}}})\left[ {\lambda {p_{\text{x}}} - \kappa ({p_{\text{x}}} + {p_{\text{s}}})} \right]}}{{\text{e}}^{ - \frac{s}{a}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(28)

$\begin{array}{*{20}{c}} {p_{\text{x}}^{\text{*}} = {p^{\text{c}}}{{\left( {\frac{{{p_{\text{x}}} + {p_{\text{s}}}}}{{{p^{\text{c}}} + {p_{\text{s}}}}}} \right)}^{\frac{\lambda }{{\lambda - \kappa }}}}{{\left( {\frac{{{p_{\text{x}}}}}{{{p^{\text{c}}}}}} \right)}^{\frac{{ - \kappa }}{{\lambda - \kappa }}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(29)

$\begin{array}{*{20}{c}} {{p_{\text{x}}} = p + \frac{{{{\hat q}^2}}}{{{M^2}{{\hat p}^2}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(30)

$\begin{array}{*{20}{c}} {\hat{\mathit{\Omega }} = \frac{{{M^4} - {{\hat \eta }^4}}}{{M_{\text{f}}^4 - {{\hat \eta }^4}}}} \end{array}\ \ \ \ \ \ \ 。$

(31)

综上可得：

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}} = \mathit{\Lambda } \frac{{\partial f}}{{\partial \hat p}} = {A_0}\left( {\frac{{\partial f}}{{\partial \hat p}}{\text{d}}\hat p + \frac{{\partial f}}{{\partial \hat q}}{\text{d}}\hat q + {f_{\text{s}}}{\text{d}}s} \right)} \end{array}\ \ \ \ \ \ \ \text{，}$

(32)

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{\text{d}}^{\text{p}} = \mathit{\Lambda } \frac{{\partial f}}{{\partial \hat q}} = {A_0}\frac{{\frac{{\partial f}}{{\partial \hat p}}{\text{d}}\hat p + \frac{{\partial f}}{{\partial \hat q}}{\text{d}}\hat q + {f_{\text{s}}}{\text{d}}s}}{{\frac{{\partial f}}{{\partial \hat p}}}}\frac{{\partial f}}{{\partial \hat q}}} \end{array}\ \ \ \ \ \ \ 。$

(33)

对于膨胀性非饱和土，除了上述体应变外，还有微观结构变化引起的体应变，当吸力减小时（即湿化），相应塑性体应变表达式见式（9）。

当吸力增加时，考虑LC屈服面和SI屈服面的耦合，将吸力增加引起的塑性体应变并入 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 考虑，此时 ${f_{\text{d}}} = 0$ ，即得到

$\begin{array}{*{20}{c}} {{f_{\text{d}}} = \left\{ \begin{gathered} {J^{\frac{{{\rho _{\text{d}}}}}{{{\rho _{\text{w}}}}}}}{\left( {1 - {\text{exp}}\left( { - \frac{\xi }{{\lambda - \kappa }}} \right)} \right)^2}{\text{ (d}}s < 0) \hfill \\ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\text{(d}}s \geqslant 0)\ \ \hfill \\ \end{gathered} \right.} \end{array} \ \ \ \ \ \ \ 。$

(34)

1.5 弹塑性应力应变关系

膨胀土塑性体应变由 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 和 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}$ 两部分组成，弹性体应变由 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}}$ 和 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}}$ 两部分组成，将应力应变关系表示为矩阵得到

$\begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{c}} {{\text{d}}\hat p + {B_1}{\text{d}}s} \\ {{\text{d}}\hat q + {B_2}{\text{d}}s} \end{array}} \right\} = \left( {\begin{array}{*{20}{c}} {K{A_1}}&{3KG{A_2}} \\ {3KG{A_2}}&{3G{A_3}} \end{array}} \right)\left\{ {\begin{array}{*{20}{c}} {{\text{d}}{\varepsilon _{\text{v}}}} \\ {{\text{d}}{\varepsilon _{\text{d}}}} \end{array}} \right\}} \end{array}\ \ \ \ \ \ \ 。$

(35)

式中：

$\begin{array}{*{20}{c}} {{A_1} = \frac{{12G{A_0}{{\hat \eta }^2} + \hat p({M^4} - {{\hat \eta }^4})}}{{{T_0}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(36)

$\begin{array}{*{20}{c}} {{A_2} = \frac{{ - 2{A_0}\hat \eta ({M^2} - {{\hat \eta }^2})}}{{{T_0}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(37)

$\begin{array}{*{20}{c}} {{A_3} = \frac{{{A_0}K{{({M^2} - {{\hat \eta }^2})}^2} + \hat p({M^4} - {{\hat \eta }^4})}}{{{T_0}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(38)

$\begin{array}{*{20}{c}} {{B_1} = K\frac{{12G{A_0}{{\hat \eta }^2}({T_1} - {A_0}{f_{\text{s}}}) + \hat p{T_1}({M^4} - {{\hat \eta }^4})}}{{{T_0}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(39)

${B_2} = 6G{A_0}\hat \eta \frac{{K({M^2} - {{\hat \eta }^2})({A_0}{f_{\text{s}}} - {T_1}) + \hat p{f_{\text{s}}}({M^2} + {{\hat \eta }^2})}}{{{T_0}}}\ \ \ \ \ \ \ \text{；}$

(40)

$\begin{array}{*{20}{c}} {{T_0} = {A_0}K{{({M^2} - {{\hat \eta }^2})}^2} + 12G{A_0}{{\hat \eta }^2} + \hat p({M^4} - {{\hat \eta }^4})} \end{array}\ \ \ \ \ \ \ \text{；}$

(41)

$\begin{array}{*{20}{c}} {{T_1} = {A_0}{f_{\text{s}}} + (1 + {f_{\text{d}}})\frac{{{k_{\text{s}}}}}{{(1 + {e_0})(s + {p_{{\text{at}}}})}} - \frac{{{{\text{e}}^{ - \frac{s}{a}}}}}{K}} \end{array}\ \ \ \ \ \ \ 。$

(42)

2. 模型特性分析

本节通过对几种湿化应力路径的模拟和分析，来体现本文模型在描述膨胀性非饱和土湿化过程中体积膨胀和强度降低的特性。所取模型参数： $\lambda$ =0.2， $\kappa$ =0.02， ${\lambda _{\text{s}}}$ =0.08， $\nu$ =0.3，M=1.0，N=1.96， ${\kappa _{\text{s}}}$ =0.01， ${p^{\text{c}}}$ =100 kPa，a=150 kPa， ${p_{{\text{at}}}}$ =100 kPa，初始孔隙比取0.95。

本模型中膨胀性非饱和土膨胀性的体现主要与3个参数有关，即反映土体膨胀能力的系数J、反映土体密实程度的初始干密度 ${\rho _{\text{d}}}$ 以及反映土体超固结程度的系数 $\xi$ ，其中系数J和初始干密度 ${\rho _{\text{d}}}$ 的影响可以通过膨胀系数 $C = {J^{\frac{{{\rho _{\text{d}}}}}{{{\rho _{\text{w}}}}}}}$ 综合反映，系数 $\xi$ 的影响可以通过前期固结压力体现，相同应力路径和吸力状态下，前期固结压力越大， $\xi$ 越大，即土的超固结程度越高。

2.1 等向回弹再湿化

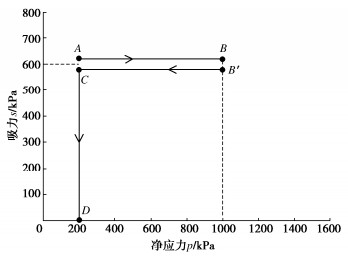
为了分析膨胀系数对膨胀量的影响，先在吸力不变的条件下将土样等向压缩后回弹，然后湿化至饱和，应力路径如中A—B( $B'$ )—C—D所示，其中A—B为等向压缩， $B'$ —C为回弹，C—D为湿化。

图 3 不同C值等向回弹湿化应力路径

Figure 3. Stress paths of isotropic unloading-wetting with different values of C

下载: 全尺寸图片幻灯片

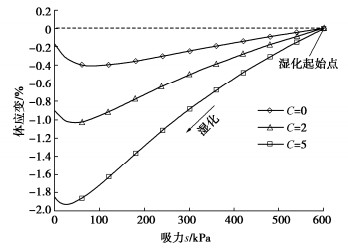
分别取膨胀系数C为0，2，5，在吸力s=600 kPa不变的条件下，将土样从初始状态（围压p=200 kPa）等向压缩至围压p=1000 kPa，然后回弹至p=200 kPa，然后再湿化至饱和（s=0 kPa），由本文所提模型预测湿化过程中土样的体应变，如图 4所示。

图 4 等向回弹湿化中不同C值下体应变

Figure 4. Variation of volumetric strain under stress path of isotropic unloading-wetting with different values of C

下载: 全尺寸图片幻灯片

可以看出，随着土体中吸力降低，土体会发生膨胀变形（负体应变代表膨胀变形），随着膨胀系数C的提高，膨胀量会随之增大；同时在吸力较低的时候土体会发生湿陷，这是因为在吸力接近0 kPa时，土样应力状态接近屈服面，吸力降低使得土体产生的塑性湿陷体应变增量 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 在数值上超过微观结构引起的塑性膨胀体应变增量 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}$ ，塑性湿陷变形在总变形中占据主导地位，土体整体表现出体积减小。

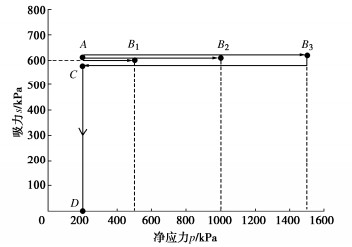
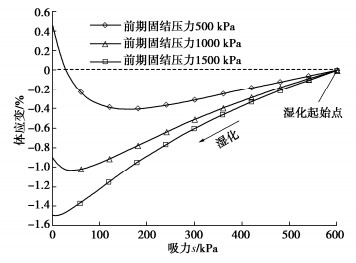
为分析等向回弹再湿化路径下不同超固结度对膨胀量的影响，取初始围压p=200 kPa，膨胀系数C=2，吸力s保持为600 kPa，将土样分别等向压缩至500，1000，1500 kPa，再回弹至200 kPa，应力路径如图 5所示A—B₁（B₂，B₃）为等向压缩过程，B₁（B₂，B₃）—C为回弹过程，C—D为湿化过程。

图 5 不同超固结度等向回弹湿化路径

Figure 5. Stress paths of isotropic unloading-wetting with different overconsolidation ratios

下载: 全尺寸图片幻灯片

3个土样湿化时的超固结程度不同，由本文所提模型预测体应变在湿化过程中的变化，如图 6所示。

图 6 等向回弹湿化不同超固结度下体应变

Figure 6. Variation of volumetric strain under stress path of isotropic unloading-wetting with different overconsolidation ratios

下载: 全尺寸图片幻灯片

可以看出，超固结程度越高，膨胀量越大，当超固结度过低时（例如前期固结压力500 kPa），甚至会发生土体整体湿陷的现象，即湿化至饱和后土体体积相比湿化前减小，体现超固结程度对膨胀性非饱和土膨胀量的重要影响。

2.2 回弹—等p剪切—湿化—加载

此路径中，吸力保持600 kPa不变，等向加载回弹后，进行等p剪切，剪切到一定程度时湿化，之后再剪切至破坏，分析剪切过程中体应变的变化。

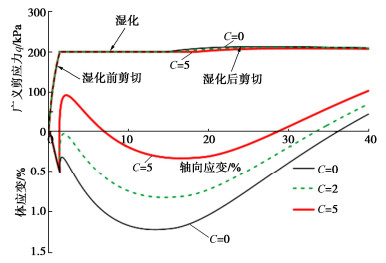
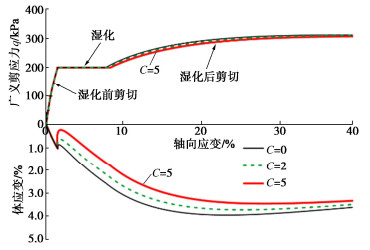
首先预测不同膨胀系数C在三轴排水剪切过程中的影响，初始围压p取200 kPa，膨胀系数C取0，2，5，等向压缩至p=1000 kPa，然后再回弹至200 kPa，之后进行等p剪切，剪切到广义剪应力q=200 kPa时进行湿化，湿化至饱和后再继续剪切，直到破坏，如图 7所示为剪切过程中体应变的变化。

图 7 等p剪切中湿化不同C值下体应变

Figure 7. Variation of volumetric strain under stress path of shearing- wetting-shearing with different values of C and constant mean effective stress

下载: 全尺寸图片幻灯片

可以看出膨胀系数C的取值不影响湿化前土体的应力应变关系，但在湿化过程中膨胀系数大的土体表现出更大的膨胀变形，甚至会使土样体积大于初始体积，这一变形导致湿化后剪切过程中土样剪缩量降低，但在不断剪切过程中，不同参数的土样体积应变趋于一致。同时通过分析湿化过程剪应力的变化，发现随着膨胀系数C值的增大，湿化后的剪切强度会降低。

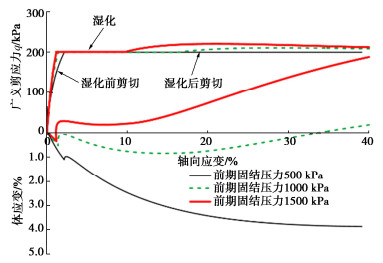
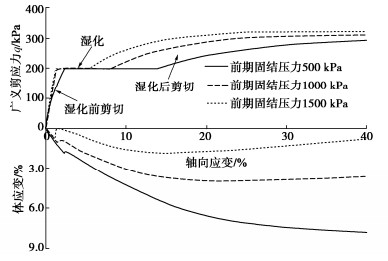
其次分析此路径下不同超固结度对膨胀特性的影响。设置初始围压为200 kPa，膨胀系数C取2，分别将土样等向压缩至500，1000，1500 kPa，然后等向回弹至200 kPa，之后等p剪切，当q=200 kPa时湿化至饱和，再剪切至破坏，分析此剪切过程中体应变与轴向应变的关系，如图 8所示。

图 8 等p剪切中湿化不同超固结度下体应变

Figure 8. Variation of volumetric strain under stress path of shearing- wetting-shearing with different overconsolidation ratios and constant mean effective stress

下载: 全尺寸图片幻灯片

可以看出不同超固结度下湿化时产生的体应变不同，当超固结度较大时，土体剪缩量会减小，使得土样提前进入剪胀阶段，同时增大剪切过程中产生的总膨胀量。

2.3 等体积湿化中的膨胀力

膨胀力是评价膨胀性非饱和土膨胀特性的基本参数，试验中可以通过三向胀缩仪测定^[27]。在土体各向同性条件下，模型中的膨胀力与 ${\text{d}}{\varepsilon _{\text{v}}} = 0$ 时的平均正应力相等。本节研究土体膨胀过程中膨胀力的变化特性。

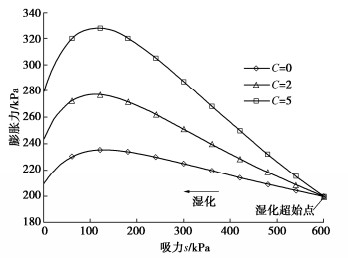
首先预测不同膨胀系数下土体膨胀力变化，初始吸力600 kPa，初始围压200 kPa，膨胀系数C分别取0，2，5，将土样等向压缩至1000 kPa，后回弹至200 kPa，改变围压维持体积不变，将土样湿化至饱和，预测湿化过程中膨胀力与吸力的关系，如图 9。

图 9 等体积湿化不同C值膨胀力变化

Figure 9. Variation of swelling pressure during wetting under constant volume with different values of C

下载: 全尺寸图片幻灯片

可以看出随着膨胀系数的提高，土体最大膨胀力也相应提高，同时在湿化至低吸力阶段时，土体膨胀力会降低，反映此阶段土体整体表现出湿陷趋势，相应的，膨胀系数C越大，低吸力阶段土体膨胀力降低越多，体现土体膨胀系数的增大会加剧产生土体塑性湿陷体应变增量 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 的趋势，使得土体整体表现出的体缩趋势更大，在本模拟中由于限制了土体变形，体缩趋势表现为膨胀力的减小。

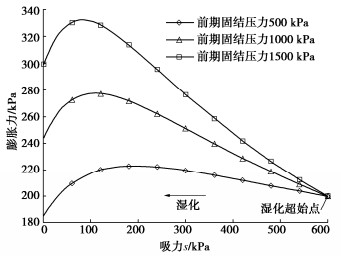
其次预测不同超固结程度下膨胀力的变化，初始吸力仍为600 kPa，膨胀系数C取2，初始围压为200 kPa，将土样分别等向压缩至500，1000，1500 kPa，然后回弹至200 kPa，保持体积不变湿化至饱和，其膨胀力与吸力的关系如图 10。

图 10 等体积湿化不同超固结度膨胀力变化

Figure 10. Variation of swelling pressure during wetting under constant volume with different overconsolidation ratios

下载: 全尺寸图片幻灯片

可见超固结度越高土体最大膨胀力越大，因土体在低吸力时有体缩趋势，当超固结度较低时，最终膨胀力甚至会低于初始围压，但相比膨胀系数C，超固结度的提高对低吸力阶段土体膨胀力降低的影响较小，不同超固结度下土体低吸力阶段膨胀力降低量相近。

2.4 回弹—三轴压缩—湿化—三轴压缩

此路径中先将土样等向压缩后回弹，之后进行三轴压缩，到达某一状态后湿化至饱和，之后再三轴压缩至破坏。首先预测不同膨胀系数对压缩过程的影响，取初始围压p=200 kPa，膨胀系数C分别取为0，2，5，初始吸力为600 kPa，先将土样等向压缩至1000 kPa，然后再回弹至200 kPa，之后进行三轴排水剪切，围压保持200 kPa，当q=200 kPa时，将土样湿化至饱和，再三轴压缩至破坏，分析此压缩过程中体应变与轴向应变的关系，如图 11。

图 11 三轴压缩中湿化不同C值下体应变

Figure 11. Variation of volumetric strain under stress path of triaxial compression-wetting-triaxial compression with different values of C

下载: 全尺寸图片幻灯片

可以看出膨胀系数并不影响湿化前过程，当土体湿化时会发生膨胀，C值越大膨胀量越大，但湿化至饱和后随着三轴压缩的不断进行，体应变会逐渐趋于一致。同时通过分析剪切过程中广义剪应力q的变化，发现随着C值的提高，湿化后土体峰值强度会降低。

其次预测分析不同超固结度的影响，初始吸力仍为600 kPa，膨胀系数C取2，初始围压为200 kPa，将土样分别等向压缩至500，1000，1500 kPa，然后再回弹至200 kPa，之后进行三轴压缩，当q=200 kPa时湿化至饱和，再三轴压缩至破坏，分析压缩过程中体应变与轴向应变之间的关系，如图 12。

图 12 三轴压缩中湿化不同超固结度体应变

Figure 12. Variation of volumetric strain under stress path of triaxial compression-wetting-triaxial compression with different overconsolidation ratios

下载: 全尺寸图片幻灯片

可以看出，超固结度越高，湿化过程中土体膨胀量越大，湿化至饱和后土体三轴剪切阶段体应变的变化趋势与一般非饱和土基本一致。

3. 模型的试验验证

为验证模型的合理性，分别对Zhan等^[28]和Alonso等^[29]的湿化膨胀试验数据进行预测。

3.1 模型的试验验证Ⅰ

Zhan等^[28]对中国湖北枣阳某边坡的膨胀黏土进行了室内试验，土体干密度为1.52~1.60 g/cm³，经测定，土样中砂砾含量3%、粉土颗粒含量58%，黏土颗粒含量39%，液限为50.5%，塑性指数为31，Zhan等^[28]利用非饱和土三轴试验仪对土样进行了多组试验研究，本节取其不同围压下的湿化路径作为验证试验数据。

本文建立的膨胀性非饱和模型需要10个参数，其中力学模型参数 $\lambda ，\kappa ，M，\nu ，N$ 与修正剑桥模型相同，参数 $\lambda ，\kappa ，N$ 可通过饱和土等向压缩回弹试验求得，参数 $M$ 可通过饱和土三轴压缩试验求得，参数 ${\lambda }_{s}，{\kappa }_{s}，{p}^{c}$ 与巴塞罗那模型相同，参数 ${\lambda }_{s}，{\kappa }_{s}$ 可由等围压的干化和湿化试验得到，参数 ${p^{\text{c}}}$ 可通过不同吸力下等向压缩回弹再湿化试验得到，参数 $a$ 可通过不同吸力下的三轴压缩试验得到，反映土体膨胀能力的参数J可根据土体不同围压下的湿化试验求得，根据文献[，]得到参数： $\lambda$ =0.1， $\kappa$ =0.01， ${\lambda _{\text{s}}}$ =0.1， $\nu$ =0.3，M=1.0，N=1.18， ${\kappa _{\text{s}}}$ =0.01， ${p^{\text{c}}}$ =125 kPa，a=150 kPa，J=1.55。大气压 ${p_{{\text{at}}}}$ 取为100 kPa。

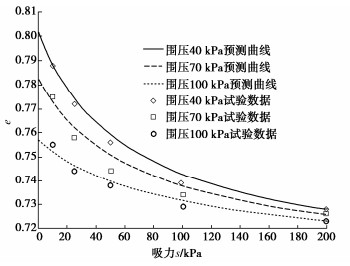
此试验取了3组土样，经过吸力平衡，控制土样吸力保持在200 kPa，然后维持吸力不变，分别在40, 70, 100 kPa围压下进行等向固结，在固结完成后，进行湿化试验。湿化过程中保持各自围压不变，吸力从200 kPa降至0 kPa，湿化前土体干密度取1.56 g/cm³，不同围压下湿化过程的试验结果与预测结果对比如图 13所示。

图 13 Zhan等^[28]试验预测对比

Figure 13. Comparison between predicted values and experimental results by Zhan et al. ^[28]

下载: 全尺寸图片幻灯片

可以看出3组土样在试验过程中都发生体积膨胀，但围压不同体积膨胀的幅度不同，围压较大的土样膨胀量较小，预测曲线与试验数据符合较好，可以反映出土体湿化过程中体积膨胀的过程，并体现不同围压下体积膨胀量的不同。

3.2 模型的试验验证Ⅱ

Alonso等^[29]利用Boom膨胀黏土进行了室内试验，其液限为55.9%，塑性指数为29.2，土体的高岭土、伊利石和蒙脱石的含量分别为20%，30%, 10%。试验土样初始干密度为1.40 g/cm³，Alonso等^[29]利用土样进行了不同等向围压下的干湿循环试验，本次验证选取其试验中第一次湿化的试验数据进行验证。

同上一节参数确定方法，本次试验根据文献[，]及参数拟合确定参数： $\lambda$ =0.15， $\kappa$ =0.014， ${\lambda _{\text{s}}}$ =0.1， $\nu$ =0.3，M=1.0，N=1.6， ${\kappa _{\text{s}}}$ =0.008， ${p^{\text{c}}}$ =45 kPa，a=120 kPa，J=1.65。

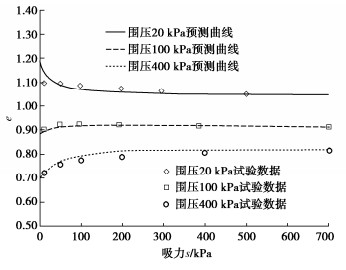
Chen^[30]将土样分为3组，控制吸力分别为500，500，700 kPa，保持吸力不变，分别在等向压力20，100，400 kPa下等向固结，固结完成后保持围压不变，进行湿化试验，将土样吸力从500 kPa或700 kPa降低到0 kPa，预测土样的体积变化，试验结果与预测结果如图 14。

图 14 Alonso等^[29]试验预测对比

Figure 14. Comparison between predicted values and experimental results by Alonso et al. ^[29]

下载: 全尺寸图片幻灯片

可以看出，由于围压不同，土体在湿化过程中体积变化也有区别，低围压下土体湿化会发生体积膨胀，但当围压增大到足够大时，土体在湿化过程中会发生体积收缩，且随着围压的进一步提高体积收缩也会加剧，这是因为随着围压的提高，土体超固结程度降低，湿化过程中更容易发生屈服，产生更大的湿陷塑性体应变 $\varepsilon _{{\text{vp}}}^{\text{p}}$ ，引发更大的湿陷变形，当围压足够大时这种湿陷变形会占主导地位，使得土体整体表现出体积的收缩，预测曲线可以反映出膨胀土的这一特性，且与试验结果符合较好。

4. 结论

本文提出了考虑膨胀土超固结度和初始干密度的膨胀式，将其融入非饱和土UH模型得到可以考虑理想膨胀性非饱和土的UH模型，该模型具有以下3个特点。

（1）通过引入与土体超固结度和初始干密度有直接关系的膨胀式，可以考虑不同的超固结度和初始干密度对膨胀土应力应变关系的影响，同时可以反映湿化过程中土体超固结度的变化。

（2）以UH模型为基础，并采用硬化参量H，可以体现膨胀土在超固结状态下不同于正常固结状态的应力软化特性和剪胀特性。

（3）本模型在一般非饱和土模型基础上引入的新参数较少，可以通过基础土力学试验获取，模型应用简便。经过模型特性分析与试验结果的验证可以显示出其预测膨胀土应力应变关系的合理性。

另一方面，本模型未考虑水量变化等水力作用对膨胀性非饱和土应力应变关系的影响，需在之后的研究中进一步完善。

图 1 试验装置示意图

Figure 1. Illustration of hydraulic test apparatus

下载: 全尺寸图片幻灯片

图 2 一阶导数均方根Z₂与分形维数D的关系图

Figure 2. Relationship between fractal dimension D and root-mean square of first derivative of profile Z₂

下载: 全尺寸图片幻灯片

图 3 具有不同表面粗糙度的砂岩裂隙试样

Figure 3. Fractured sandstone specimens with different roughnesses

下载: 全尺寸图片幻灯片

图 4 流量Q与压力梯度-▽p关系图

Figure 4. Relationship between flow rate Q and pressure gradient -▽p

下载: 全尺寸图片幻灯片

图 5 黏性渗透率k_v和惯性渗透率k_i与平均开度b_m和分形维数D的关系图

Figure 5. Dependency of viscous (k_v) and inertial (k_i) permeabilities on mean aperture b_m and fractal dimension D

下载: 全尺寸图片幻灯片

图 6 水力开度b_h与平均开度b_m和分形维数D的关系

Figure 6. Variation of hydraulic aperture b_h with mean aperture b_m and fractal dimension D

下载: 全尺寸图片幻灯片

图 7 惯性渗透率k_i与平均开度b_m和分形维数D的关系

Figure 7. Variation of inertial permeability k_i with mean aperture b_m and fractal dimension D

下载: 全尺寸图片幻灯片

图 8 三维裂隙模型边界条件

Figure 8. Boundary conditions for three-dimensional fracture model

下载: 全尺寸图片幻灯片

图 9 网格数量敏感性分析

Figure 9. Sensitivity analysis of mesh of numerical solutions

下载: 全尺寸图片幻灯片

图 10 惯性渗透率k_i作为平均开度b_m和分形维数D的函数

Figure 10. Inertial permeability k_i as a function of mean aperture b_m and fractal dimension D

下载: 全尺寸图片幻灯片

参考文献(24)

[1]	CHEN Y D, SELVADURAI A P S, ZHAO Z H. Modeling of flow characteristics in 3D rough rock fracture with geometry changes under confining stresses[J]. Computers and Geotechnics, 2021, 130: 103910. doi: 10.1016/j.compgeo.2020.103910
[2]	SNOW D T. A Parallel Plate Model of Fractured Permeable Media[D]. Berkeley: University of California of Berkeley, 1965.
[3]	LOMIZE G M. Flow in Fractured Rock[M]. Moscow: Gosemergoizdat, 1951.
[4]	LOUIS C. Rock hydraulics[M]// Rock Mechanics. Vienna: Springer Vienna, 1972.
[5]	速宝玉, 詹美礼, 赵坚. 仿天然岩体裂隙渗流的实验研究[J]. 岩土工程学报, 1995, 17(5): 19-24. doi: 10.3321/j.issn:1000-4548.1995.05.004 SU Baoyu, ZHAN Meili, ZHAO Jian. Study on fracture seepage in the imitative nature roke[J]. Chinese Journal of Geotechnical Engineering, 1995, 17(5): 19-24. (in Chinese) doi: 10.3321/j.issn:1000-4548.1995.05.004
[6]	XIONG X B, LI B, JIANG Y J, et al. Experimental and numerical study of the geometrical and hydraulic characteristics of a single rock fracture during shear[J]. International Journal of Rock Mechanics and Mining Sciences, 2011, 48(8): 1292-1302. doi: 10.1016/j.ijrmms.2011.09.009
[7]	LIU R C, JING H W, HE L X, et al. An experimental study of the effect of fillings on hydraulic properties of single fractures[J]. Environmental Earth Sciences, 2017, 76(20): 684. doi: 10.1007/s12665-017-7024-8
[8]	ZHANG Z Y, NEMCIK J. Fluid flow regimes and nonlinear flow characteristics in deformable rock fractures[J]. Journal of Hydrology, 2013, 477(16): 139-151. http://www.sciencedirect.com/science/article/pii/S0022169412010037
[9]	CHEN Y F, ZHOU J Q, Hu S H, et al. Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures[J]. Journal of Hydrology, 2015, 529: 993-1006. doi: 10.1016/j.jhydrol.2015.09.021
[10]	SHAO J L, ZHANG Q, SUN W B, et al. Numerical simulation on non-darcy flow in a single rock fracture domain inverted by digital images[J]. Geofluids, 2020, 2020: 1-13. http://www.xueshufan.com/publication/3037631765
[11]	BAGHBANAN A, JING L R. Hydraulic properties of fractured rock masses with correlated fracture length and aperture[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(5): 704-719. doi: 10.1016/j.ijrmms.2006.11.001
[12]	ZHAO Z H, LI B, JIANG Y J. Effects of fracture surface roughness on macroscopic fluid flow and solute transport in fracture networks[J]. Rock Mechanics and Rock Engineering, 2014, 47(6): 2279-2286. doi: 10.1007/s00603-013-0497-1
[13]	ZHANG X, SANDERSON D J. Effects of stress on the two-dimensional permeability tensor of natural fracture networks[J]. Geophysical Journal International, 1996, 125(3): 912-924. doi: 10.1111/j.1365-246X.1996.tb06034.x
[14]	速宝玉, 詹美礼, 张祝添. 充填裂隙渗流特性实验研究[J]. 岩土力学, 1994, 15(4): 46-52. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX404.005.htm SU Baoyu, ZHAN Meili, ZHANG Zhutian. Experimental research of seepage characteristic for filled fracture[J]. Rock and Soil Mechanics, 1994, 15(4): 46-52. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX404.005.htm
[15]	王志良, 申林方, 徐则民, 等. 岩体裂隙面粗糙度对其渗流特性的影响研究[J]. 岩土工程学报, 2016, 38(7): 1262-1268. doi: 10.11779/CJGE201607013 WANG Zhiliang, SHEN Linfang, XU Zemin, et al. Influence of roughness of rock fracture on seepage characteristics[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1262-1268. (in Chinese) doi: 10.11779/CJGE201607013
[16]	NI X D, NIU Y L, WANG Y, et al. Non-darcy flow experiments of water seepage through rough-walled rock fractures[J]. Geofluids, 2018, 2018: 1-12. http://doc.paperpass.com/foreign/rgArti2018282828152.html
[17]	RONG G, TAN J, ZHAN H B, et al. Quantitative evaluation of fracture geometry influence on nonlinear flow in a single rock fracture[J]. Journal of Hydrology, 2020, 589: 125162. doi: 10.1016/j.jhydrol.2020.125162
[18]	YIN P J, ZHAO C, Ma J J, et al. Experimental study of non-linear fluid flow though rough fracture based on fractal theory and 3D printing technique[J]. International Journal of Rock Mechanics and Mining Sciences, 2020, 129: 104293. http://www.sciencedirect.com/science/article/pii/S1365160919310032
[19]	周新, 盛建龙, 叶祖洋, 等. 岩体粗糙裂隙几何特征对其Forchheimer型渗流特性的影响[J]. 岩土工程学报, 2021, 43(11): 2075-2083. doi: 10.11779/CJGE202111014 ZHOU Xin, SHENG Jianlong, YE Zuyang, et al. Effects of geometrical feature on Forchheimer- flow behavior through rough-walled rock fractures[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(11): 2075-2083. (in Chinese) doi: 10.11779/CJGE202111014
[20]	ZHOU J Q, CHEN Y F, WANG L C, et al. Universal relationship between viscous and inertial permeability of geologic porous media[J]. Geophysical Research Letters, 2019, 46(3): 1441-1448. doi: 10.1029/2018GL081413
[21]	DETWILER R L. Experimental observations of deformation caused by mineral dissolution in variable-aperture fractures[J]. Journal of Geophysical Research: Solid Earth, 2008, 113(B8). http://www.onacademic.com/detail/journal_1000035647835010_76bb.html
[22]	OGILVIE S R, ISAKOV E, GLOVER P W J. Fluid flow through rough fractures in rocks. Ⅱ: A new matching model for rough rock fractures[J]. Earth and Planetary Science Letters, 2006, 241(3-4): 454-465. http://www.onacademic.com/detail/journal_1000035381379510_8e06.html
[23]	MYERS N O. Characterization of surface roughness[J]. Wear, 1962, 5(3): 182-189. http://www.sciencedirect.com/science/article/pii/0043164862900029
[24]	ZHOU J Q, WANG L C, LI C D, et al. Effect of fluid slippage on eddy growth and non-Darcian flow in rock fractures[J]. Journal of Hydrology, 2020, 581: 124440.

施引文献(3)

期刊类型引用(2)

1.	王涛，凡红，王康任，周国庆，王亮亮. 高温冻土双屈服面统一本构模型及其验证. 岩土工程学报. 2025(01): 135-143 . 本站查看
2.	柳伟，徐长节，杜昊东，朱怀龙，王长虹. 基于修正统一硬化模型的超固结非饱和红黏土边坡稳定分析. 岩土力学. 2024(04): 1233-1241 . 百度学术