Improved Knothe surface dynamic subsidence prediction model and its parameter analysis
-
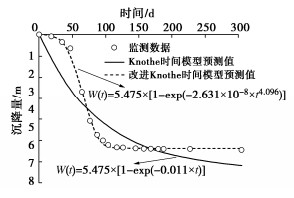
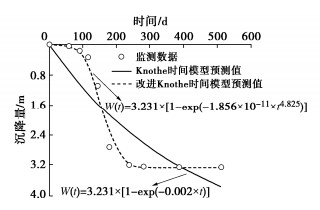
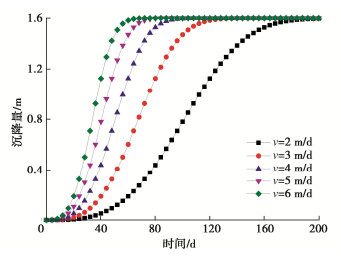
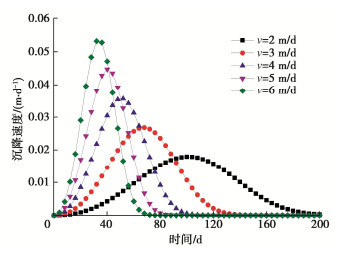
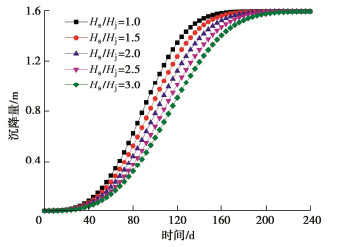
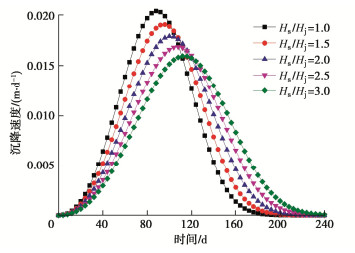
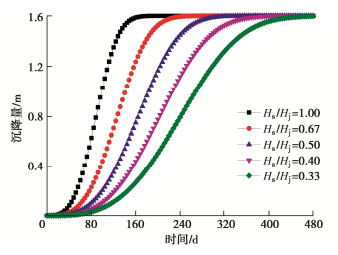
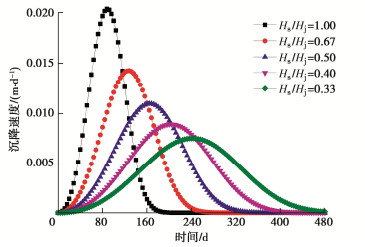
摘要: 针对传统Knothe时间模型描述地表动态沉降过程中的不足，在Knothe时间模型基础上考虑了上覆地层非线性力学特征，建立改进Knothe时间模型，理论分析表明改进后时间模型符合地表单点沉降、沉降速度和沉降加速度变化规律；结合现场实测数据和双介质法，给出改进Knothe时间模型参数计算表达式。采用兴隆庄煤矿4326工作面、三道沟煤矿35101工作面和阳泉二矿8403综采工作面开采地表沉降监测数据，对传统Knothe时间模型和改进Knothe时间模型精度进行对比分析。结果表明：改进时间模型能够更真实地反映地表随开采时间的动态变化过程，预测值和实测值的平均相对标准偏差仅为3.22%，远低于Knothe时间模型的15.72%，验证了改进时间模型的精确性和可靠性；地表动态沉降过程受煤层回采速度v、松散层厚度Hs、基岩层厚度Hj、松散层充分采动角φs和基岩充分采动角φj影响，且影响敏感度依次为：Hj，v，Hs，φj，φs。研究可为煤层开采地表动态沉陷预测提供一定的借鉴和参考。
-
关键词:
- 地表沉降 /
- Knothe时间模型 /
- 动态预测 /
- 沉降速度 /
- 敏感性
Abstract: In view of the shortcomings of the traditional Knothe time model in describing the process of surface dynamic subsidence, based on the Knothe time model, considering the nonlinear mechanical characteristics of the overlying strata, an improved Knothe time model is established. The theoretical analysis shows that the improved time model conforms to the variation laws of surface single point subsidence, subsidence velocity and subsidence acceleration. Based on the field measured data and the two-medium method, the expression for parameters of the improved Knothe time model is given. Based on the surface subsidence monitoring data of 4326 working face of Xinglongzhuang Coal Mine, 35101 working face of Sandaogou Coal Mine and 8403 fully mechanized working face of Yangquan No. 2 Coal Mine, the accuracies of the traditional Knothe time model and the improved Knothe time model are compared and analyzed. The results show that the improved time model can more truly reflect the dynamic change process of the surface with the mining time. The average relative standard deviation between the predicted and measured values is only 3.22%, which is far lower than 15.72% of the Knothe time model, which verifies the accuracy and reliability of the improved time model. The process of surface dynamic subsidence is affected by the mining speed v of coal seam, the thickness Hs of loose layer, the thickness Hj of bedrock layer and the full mining angle of loose layer φi and the full mining angle of bedrock φj, and the impact sensitivity is in the order of Hj, v, Hs, φj and φi. The results may provide some reference for the prediction of surface subsidence in coal seam mining.-
Keywords:
- surface subsidence /
- Knothe time model /
- dynamic prediction /
- subsidence velocity /
- susceptibility
-
0. 引言
在松软饱和地层、城市密集区域、穿越河海段等隧道工程建设中，传统的人工钻爆工法将面临严峻的挑战与巨大的风险，盾构技术的引进为此提供解决方案。随着机械设备与施工技术的不断发展，盾构工法已逐渐推广应用于城市给排水、水资源配置、发电引水、农业灌溉等水利建设工程，国内外已有大量成功案例，见表 1。
表 1 国内外部分单层衬砌盾构输水隧洞工程Table 1. Some single-layer lining shield water conveyance tunnel projects at home and abroad区别于交通隧道，水工隧洞工作条件更为复杂，结构承担管片衬砌的外部水土荷载和内部水压力，使得接缝张开、管片受力等呈现不同的结构承载与变形特点[7-8]。目前，国内外针对地铁、公路等无内压管片衬砌结构的研究已取得丰富的成果[9-11]，而专门针对有内压管片衬砌结构的研究相对薄弱。章青等[12]基于不连续介质变形体的界面应力元理论建立了能模拟管片接头不连续变形的盾构输水隧洞计算模型；赵大洲等[13]依托南水北调西线工程，借助数值仿真手段探讨了围岩变形及内、外水压力对管片衬砌受力变形的影响；佘成学等[14]结合青松电站引水隧洞针对管片衬砌在高内水压力作用下的力学响应展开了数值计算；闫治国等[1]结合青草沙水源地原水工程，针对管片接头开展原型试验；周龙等[15]针对蓄排水盾构隧洞开展了足尺荷载试验及数值分析，揭示了管片衬砌在内压下的变形规律及错缝拼装效应；Zhang等[2]、刘威等[16]分别基于上海苏州河段深层排水调蓄管道系统工程开展室内足尺模型试验及数值计算，研究了隧洞对于内压、埋深、封顶块位置及螺栓预紧力等因素的敏感性。
综上，现有研究主要通过室内模型试验和数值模拟，探讨衬砌结构的承载与变形机理。但受条件制约，室内试验在结构尺寸、内水压力模拟、外部水土荷载施加等方面需要进行简化与等效，难以真实表征管片环在内水压力作用下的力学响应，一定程度上影响了理论分析和数值计算的可靠性。为了弥补上述研究的局限性，本文依托珠江三角洲水资源配置工程，提出一种基于“高压囊体-反力支架-伺服泵机”装置的内压模拟方式，并采用“光纤传感技术”与“振弦式仪器”相结合的测量系统，对华南地区盾构输水隧洞单层衬砌结构开展原位试验研究，揭示了该结构在真实地层条件下承受内压的受力变形规律。在此基础上，采用三维有限元模型对不同围岩条件下单层管片衬砌结构的内压承载变形特性开展进一步的分析，为长距离输水工程衬砌结构选型设计提供参考与借鉴。
1. 输水盾构隧洞结构试验
1.1 试验概况
珠江三角洲水资源配置工程是广东省有史以来线路最长、内压最高的跨流域调水工程，最大设计内压达1.5 MPa。输水隧洞将穿越多种地层，沿线涉及泵站、水库、调压塔等水工建筑物，使得各标段隧洞设计内压差异较大。综合考虑工程安全性与经济性，衬砌结构的选型与设计面临诸多难题，需开展原位试验为工程实践提供有效参考。本试验共设置4组盾构区间，每组长度为15 m，衬砌型式分别采用单层管片、钢筋混凝土内衬、分离式及叠合式钢管内衬结构。区间隧洞埋深为19.5~20.0 m，处于全风化花岗片麻岩层，地下水位深度为6.6~13.8 m。本文重点针对区间1的单层管片衬砌结构展开讨论，该区间由10环C55预制钢筋混凝土管片错缝拼接而成，隧洞上覆土层分布及衬砌结构型式见图 1。管片内外侧均设置HRB400环向受力筋(12φ18)，内、外侧钢筋保护层厚度分别为30，40 mm；每环管片由6个分块组成，包括3个标准块(B1~B3)、2个邻接块(L1、L2)和1个封顶块(F)；管片间采用A4-70级M24弯螺栓连接，每道纵缝布置2根环向螺栓；每道环缝等间距布置10根纵向螺栓。
![]()
图 1 试验区间的地质条件及衬砌结构型式Figure 1. Geological conditions and lining structure of in-situ tests1.2 加载方案
为确保洞内试验安全和加载效率，本试验专门设计了一套“高压囊体-反力支架-伺服泵机”系统模拟内水压力，如图 2所示，即，在衬砌结构内部设置圆筒形反力支架，将16个高压囊体均布于反力支架与预制管片之间，操作液压伺服系统，通过泵机对高压囊体同步注水。囊体不断膨胀并将压力传递于管片内表面，以实现内水压力的模拟。
鉴于试验区间后续将应用于实际工程，需保证结构安全和正常使用，本次试验将最大内压设置为0.30 MPa，以0.02 MPa为梯度逐级加载。
1.3 测量系统
区别于室内模型试验，现场原位试验的操作环境更加复杂，监测难度更大。本试验采用振弦类与光纤类传感器对结构的受力与变形规律进行了监测，以确保测量系统在复杂的地下环境中仍保持较高的精度和效率，监测内容主要包括螺栓应力、纵缝张开量、钢筋应力、混凝土应变等，仪器参数及布置如图 3所示。在原位试验区间内，围岩以全风化花岗片麻岩为主，地层条件相对均匀，未出现断层、破碎带等不利地层，故本文重点考虑衬砌横断面的承载变形特征。
2. 三维地层-结构模型
受限于洞内试验和现场监测的复杂性，原位试验仅针对单一地质条件下的衬砌结构开展较小内压加载测试，难以针对该衬砌结构开展系统研究，因此，本文基于数值仿真技术进一步探讨单层管片衬砌结构在不同内水压力、围岩类型等条件下承载变形机理。
2.1 有限元网格与边界条件
根据区间1的结构型式及地层状况建立有限元模型，如图 4所示。其中，左右及下边界各取5倍隧洞外径，上边界与原位试验区间埋深相同(取20 m)。考虑管片环间的错缝拼装效应(错缝角度为180°)及管片间的连接螺栓，岩土体及管片均采用实体单元，连接螺栓以杆单元形式嵌入管片单元，共计119380个单元和172977个节点。围岩左右边界约束x向位移，前后边界约束y向位移，底部边界约束z向位移。为消除首尾环的边界效应，本次计算取第5环管片作为参考。
2.2 本构关系与接触关系
土体材料采用Drucker-Prager塑性模型，管片采用损伤塑性本构模型，螺栓采用双折线塑性强化模型，塑性加强段弹性模量为弹性段的1/100，主要参数详见表 2。“管片-管片”、“管片-围岩”之间设置面-面接触，即，切向上服从库仑摩擦定律，当切向应力达到临界值后允许发生滑移，摩擦系数取0.5[7]；法向上定义为硬接触，允许接触面之间发生分离。
表 2 主要材料物理力学参数Table 2. Mechanical parameters of materials材料 密度/(g·cm-3) 弹性模量/MPa 泊松比 内摩擦角/(°) 黏聚力/kPa 屈服强度/MPa 极限强度/MPa 抗压强度标准值/MPa 抗拉强度标准值/MPa 人工填土 2.03 40 0.48 12 8 — — — — 砂质黏性土 1.98 120 0.45 19 10 — — — — 全风化花岗片麻岩 1.97 200 0.38 20 50 — — — — A4-70级螺栓 7.85 210000 0.30 — — 450 700 — — HRB400钢筋 7.85 210000 0.30 — — 400 540 — — C55混凝土 2.50 35500 0.20 — — — — 35.5 2.74 2.3 加载方式
通过引入土层饱和状态下的容重，以反映外水作用，其中，外部水位与现场相同。为准确模拟管片衬砌周边围岩的应力分布，在施加管片衬砌之前，对围岩进行地应力平衡获得围岩初始应力；在管片内表面沿高度方向施加不均匀分布的内水压力，增量设为0.05 MPa/步。
3. 不同内压下结构响应
图 5~8为试验监测与数值计算结果，其中，拉应力、拉应变和径向扩张取“+”；压应力、压应变和径向收缩取“-”。结构达到正常使用极限状态时的限值列如表 3。
表 3 结构正常使用极限状态限值[17]Table 3. Values of structural response in normal service limit state结构响应 正常使用极限状态 收敛变形/mm 12 钢筋应力/MPa 400 接缝张开量/mm 2 螺栓应力/MPa 450 3.1 收敛变形
从试验结果(图 5)不难发现，当衬砌无内压时，管片在外部水土压力作用下，呈现竖向收敛、横向扩张的“横椭圆”变形规律。随着内压增加，整体逐渐呈现向外膨胀趋势，且“横椭圆”变形特征更为明显，相关模型试验亦呈现类似变形规律[15-16]。当内压为0.30 MPa时，左、右拱腰的拉应变增量分别为303.0×10-6和384.0×10-6，但考虑到洞内试验测量环境的复杂性，仅依据混凝土环向应变增量无法准确判断局部混凝土是否开裂，有待结合其他监测指标进行综合判断。数值计算结果反映出与试验相似的变形规律，但前者环向应变分布相对监测结果更加均匀。
3.2 钢筋应力
如图 6所示，数值计算与试验监测结果具有良好的可比性，随着内压增加，钢筋应力均呈现拉应力增加或压应力减少趋势。当内压为0.30 MPa时，管片钢筋应力皆处于较小水平，局部未出现突变；由此可见，管片内表面混凝土尚未出现开裂现象。
3.3 接缝张开量
由试验和数值结果(图 7)可见，接缝张开量随内压的增加而增大。在试验中，隧洞仰拱处L1-B1接缝变化规律最显著，而其余接缝张开量变化平缓，且量值较小。当内压超过0.20 MPa时，张开量逐步进入快速增长阶段；当内压为0.30 MPa时，L1-B1接缝张开量为2.0 mm，已达到规范限值[17]。对应于前述管片“横椭圆”变形模式，管片衬砌仰拱和拱顶处的接缝张开量大于其余位置。相比于试验，数值计算结果偏小，当内压为0.30 MPa时，最大接缝张开量仅为0.5 mm，且为外侧张开量。值得注意的是，受限于现场测量条件，测缝计只能布设于管片内表面，在内压加载过程中，接缝将产生一定的错台变形，使得测缝计无法准确获取管片外表面的接缝变形情况，影响监测结果。
对于输水隧洞而言，接缝张开或错台等变形必然导致洞内壁糙率增大，从而造成一定水头损失，甚至引发内水外渗。因此，对于采用管片衬砌的水工隧洞，须加强隧洞防渗措施。根据相关工程经验[1, 3, 18]，建议采用预埋铸铁件的手孔接头、设置双排连接螺栓、双层止水等措施约束接缝变形，以增强防渗效果。
3.4 螺栓应力
螺栓应力与接缝张开量变化趋势基本相对应，见图 8。在原位试验中，L1-B1螺栓应力增长显著，当内压为0.30 MPa时，达到230.5 MPa的拉应力，但螺栓尚未屈服，而其余螺栓应力变化不明显，应力水平偏小。相比于试验，在数值仿真中，所有的螺栓应力均呈现拉应力平稳增大的趋势。数值结果真实表征螺栓整体应力情况，但原位试验通过在螺栓外侧埋置光纤，仅能反映局部应力分布，当管片出现正负弯矩时，螺栓(特别是弯螺栓)内外侧应力差异大，测量结果存在较大误差。
4. 围岩对管片衬砌承载变形特性的影响
考虑到引调水工程沿线地质条件复杂多变，洞身所处的围岩差异较大，而原位试验未能针对多种地层进行深入研究。本文选取III、IV和V类围岩，针对不同围岩条件下，单层管片衬砌结构的力学和变形响应开展数值仿真研究。根据相关规范[17, 19-20]，结合现场工程地质勘测资料，选取上述三类围岩最不利工况作为本次数值计算参数，如表 4所示。“+”和“-”定义同第3节。
表 4 各类围岩物理力学参数Table 4. Mechanical parameters of various surrounding rocks围岩类别 密度/(g·cm-3) 弹性模量/MPa 泊松比 内摩擦角/(°) 黏聚力/kPa III 2.10 3000 0.28 35 200 IV 1.97 200 0.38 20 50 V 1.70 70 0.42 15 10 4.1 收敛变形
图 9(a)，(b)分别为3种围岩等级下管片衬砌结构的横向扩张量和竖向收敛量随内压发展曲线。在内压与外部水土压力的作用下，3种围岩下的管片衬砌均呈现拱顶及仰拱向内收敛、左右拱腰向外扩张的“横椭圆”变形；内压越大，“横椭圆”变形特征越明显。当内压达0.40 MPa时，V类围岩下的管片衬砌的横向扩张量已达13.1 mm，超过规范限制的2‰隧道外径[17]，竖向收敛量已达10.2 mm，为规范限值的85.0%。如图 9(c)所示，在相同内压下，V类围岩下管片衬砌“横椭圆”变形趋势相比III类、IV类围岩更加明显。当内压为0.60 MPa时，处于IV类围岩下的管片衬砌最大径向变形为横向扩展(5.5 mm)，为规范限值的45.8%；处于III类围岩下的管片衬砌竖向收敛量与横向扩张量的最大值均为0.6 mm，为规范限值的5.0%。
可见，随着围岩力学性能的提高，围岩对衬砌结构的约束变形作用增强，管片衬砌的“横椭圆”变形特征减弱。从管片收敛变形来看，衬砌在V类围岩下承受的内压不宜超过0.35 MPa，综合相应的外部水土压力状况，衬砌可承担的内外压差不宜超过0.15 MPa。
4.2 螺栓应力和接缝张开量
由图 10，11可见，随围岩力学性能的提高，螺栓应力和接缝张开量逐渐减小。在内压作用下，管片螺栓应力与接缝张开量呈现相似的变化规律，其中，前者相对接后者更易达到结构正常使用极限状态。本次数值模拟中，V类与IV类围岩下的螺栓应力随内压增长较快，分别于0.40，0.50 MPa超过屈服强度，对应最大接缝张开量分别为1.4，1.3 mm，尚未达到规范限值；III类围岩下的螺栓应力随内压缓慢增长，当内压为0.60 MPa时，最大螺栓应力为168.1 MPa，最大接缝张开量为0.2 mm，仍具有较大安全储备。因而，从螺栓应力和接缝张开量来看，管片衬砌在V类和IV类围岩下承受的内压不宜超过0.35，0.45 MPa，综合相应的外部水土压力状况，衬砌可承担的内外压差极限分别为0.15，0.25 MPa。
5. 结论
本文针对单层管片衬砌结构开展了原位试验与数值仿真研究，揭示了结构在内水压力作用下的变形规律，并探讨了结构在20 m埋深，3种围岩条件下结构的承载变形特性，得到以下3点结论。
(1) 在内压作用下，管片衬砌结构呈现“横椭圆”变形且向外膨胀趋势，接缝张开量和螺栓应力随内压增加而增大。对于V类围岩，宜综合衬砌收敛变形和螺栓应力判断结构是否达到正常使用极限状态，而对于IV类围岩，螺栓应力为结构达到正常使用极限状态的控制因素。
(2) 随着围岩力学性能的提高，结构在内压作用下结构响应减小，围岩分担内压的效果增强。综合结构承载变形特性及工程经济性的考虑，管片衬砌适用于穿越IV或V类围岩且内外压差较小的水工隧洞。其中，IV类围岩中的内外压差不宜超过0.25 MPa，V类围岩的内外压差不宜超过0.15 MPa；若需承载更高内水压力，建议采用钢筋混凝土或钢管内衬的复合衬砌结构。对于穿越III类及以上类别围岩的水工隧洞，当内外压差达0.40 MPa时，管片衬砌仍具有较大安全储备。
(3) 单层管片衬砌输水隧洞需加强接缝变形控制，接缝张开或错台等变形将增大洞内壁糙率，造成水头损失，同时，容易引发内水外渗，尤其对于砂质软土地层，更应加强防渗措施，以防出现流砂、管涌等破坏现象。建议采用预埋铸铁手孔接头、设置双排连接螺栓、双层止水等措施约束接缝变形，从而达到较好的防渗效果。
-
![]()
图 1 改进模型地表沉降、沉降速度及沉降加速度曲线
Figure 1. Curves of surface subsidence, subsidence velocity and subsidence acceleration by improved model
![]()
图 3 拟合结果与兴隆庄煤矿实测结果对比
Figure 3. Comparison between fitting results and measured results of Xinglongzhuang Coal Mine
![]()
图 4 拟合结果与三道沟煤矿实测结果对比
Figure 4. Comparison between fitting results and measured results of Sandaogou Coal Mine
![]()
图 5 拟合结果与阳泉二矿实测结果对比
Figure 5. Comparison between fitting results and measured results of Yangquan No. 2 Coal Mine
![]()
图 7 回采速度对地表沉降速度的影响
Figure 7. Influences of mining speed on velocity of surface subsidence
![]()
图 8 松散层厚度对地表沉降的影响
Figure 8. Influences of thickness of loose layer on surface subsidence
![]()
图 9 松散层厚度对地表沉降速度的影响
Figure 9. Influences of thickness of loose layer on velocity of surface subsidence
![]()
图 10 基岩层厚度对地表沉降的影响
Figure 10. Influences of thickness of bedrock layer on surface subsidence
![]()
图 11 基岩层厚度对地表沉降速度的影响
Figure 11. Influences of thickness of bedrock layer on velocity of surface subsidence
![]()
图 12 松散层充分采动角对地表沉降的影响
Figure 12. Influences of full mining angle of loose layer on surface subsidence
![]()
图 13 松散层充分采动角对地表沉降速度的影响
Figure 13. Influences of full mining angle of loose layer on velocity of surface subsidence
![]()
图 14 基岩充分采动角对地表沉降的影响
Figure 14. Influences of full mining angle of bedrock layer on surface subsidence
![]()
图 15 基岩充分采动角对地表沉降速度的影响
Figure 15. Influences of full mining angle of bedrock layer on velocity of surface subsidence
表 1 改进模型沉降、沉降速度和沉降加速度变化
Table 1 Change of subsidence, subsidence velocity and subsidence acceleration of improved model
参数 时间 t1 (t1，t2) t2 (t2，t3) t3 W(t) 0 增大 增大 增大 W0 V(t) 0 加速 最大 减速 0 a(t) 0 > 0 0 < 0 0 
下载: 导出CSV
表 2 3个矿区工作面开采参数
Table 2 Mining parameters of working faces in three mining areas
序号 工作面 平均采深/m 松散层厚度/m 基岩层厚度/m 最大沉降量/m 开采速度/(m·d-1) 煤层厚度/m 1 兴隆庄矿4326 517 198 319 5.475 3.80 8.6 2 三道沟煤矿35101 135 70 65 1.673 3.50 2.0 3 阳泉二矿8403 300 10 290 3.231 3.20 6.5
下载: 导出CSV
表 3 预测结果精度分析
Table 3 Accuracy analysis of predicted results
煤矿名称 改进Knothe时间模型 Knothe时间模型 标准差/m 相对标准偏差/% 标准差/m 相对标准偏差/% 兴隆庄煤矿 0.105 1.92 0.836 15.26 三道沟煤矿 0.065 3.88 0.323 19.32 阳泉二矿 0.126 3.86 0.708 12.57 平均值 0.098 3.22 0.622 15.72
下载: 导出CSV
表 4 主要因素对地表动态沉降影响的敏感性
Table 4 Sensitivity of main factors to influence of surface dynamic subsidence
影响
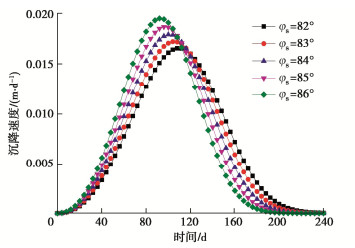
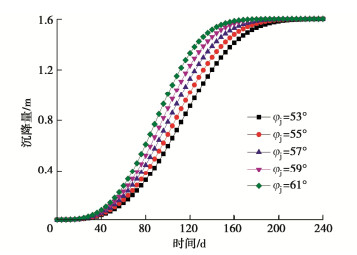
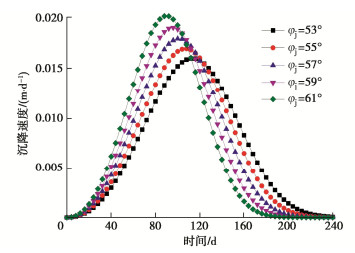
因素变化范围 与达到最大沉降的时间关系 影响幅度/% 与达到最大沉降速度的时间关系 影响幅度/% 与最大沉降速度关系 影响幅度/% v 2~6 m/d 负相关 65.96 负相关 68.00 正相关 194.44 Hs 200~600 m 正相关 29.27 正相关 27.27 负相关 20.00 Hj 200~600 m 正相关 173.17 正相关 177.27 负相关 65.00 φs 82~86° 负相关 15.69 负相关 14.81 正相关 15.15 φj 53~61° 负相关 22.64 负相关 21.43 负相关 25.00
下载: 导出CSV
-
[1] HU Q F, CUI X M, WANG G, et al. Key technology of predicting dynamic surface subsidence based on knothe time function[J]. Journal of Software, 2011, 6(7): 1273–1280.
[2] 高超, 徐乃忠, 孙万明, 等. 基于Bertalanffy时间函数的地表动态沉陷预测模型[J]. 煤炭学报, 2020, 45(8): 2740-2748. GAO Chao, XU Naizhong, SUN Wanming, et al. Dynamic surface subsidence prediction model based on Bertalanffy time function[J]. Journal of China Coal Society, 2020, 45(8): 2740-2748. (in Chinese)
[3] HEJMANOWSKI R, MALINOWSKA A. Evaluation of reliability of subsidence prediction based on spatial statistical analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(2): 432–438. doi: 10.1016/j.ijrmms.2008.07.012
[4] JAROSZ A, KARMIS M, SROKA A. Subsidence development with time—experiences from longwall operations in the Appalachian Coalfield[J]. International Journal of Mining and Geological Engineering, 1990, 8(3): 261-273. doi: 10.1007/BF01554045
[5] 孙闯, 徐乃忠, 刘义新, 等. 基于双因素时间函数的松散地层条件下地表点动态沉降预计[J]. 岩土力学, 2017, 38(3): 821-826, 865. SUN Chuang, XU Naizhong, LIU Yixin, et al. Prediction of dynamic subsidence of ground point under loose stratum based on two-factor time function[J]. Rock and Soil Mechanics, 2017, 38(3): 821-826, 865. (in Chinese)
[6] 王军保, 刘新荣, 刘小军. 开采沉陷动态预测模型[J]. 煤炭学报, 2015, 40(3): 516-521. WANG Junbao, LIU Xinrong, LIU Xiaojun. Dynamic prediction model for mining subsidence[J]. Journal of China Coal Society, 2015, 40(3): 516-521. (in Chinese)
[7] 唐君, 王金安, 王磊. 薄冲积层下开采地表动态移动规律与特征[J]. 岩土力学, 2014, 35(10): 2958-2968. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201410029.htm TANG Jun, WANG Jinan, WANG Lei. Dynamic laws and characteristics of surface movement induced by mining under thin alluvium[J]. Rock and Soil Mechanics, 2014, 35(10): 2958-2968. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201410029.htm
[8] 刘玉成, 庄艳华. 地下采矿引起的地表下沉的动态过程模型[J]. 岩土力学, 2009, 30(11): 3406-3410, 3416. doi: 10.3969/j.issn.1000-7598.2009.11.031 LIU Yucheng, ZHUANG Yanhua. Model for dynamic process of ground surface subsidence due to underground mining[J]. Rock and Soil Mechanics, 2009, 30(11): 3406-3410, 3416. (in Chinese) doi: 10.3969/j.issn.1000-7598.2009.11.031
[9] 张凯, 胡海峰, 廉旭刚, 等. 地表动态沉陷预测正态时间函数模型优化研究[J]. 煤炭科学技术, 2019, 47(9): 235-240. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201909030.htm ZHANG Kai, HU Haifeng, LIAN Xugang, et al. Optimization of surface dynamic subsidence prediction normal time function model[J]. Coal Science and Technology, 2019, 47(9): 235-240. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201909030.htm
[10] 李德海. 覆岩岩性对地表移动过程时间影响参数的影响[J]. 岩石力学与工程学报, 2004, 23(22): 3780-3784. LI Dehai. Influence of cover rock characteristics on time influencing parameters in process of surface movement[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(22): 3780-3784. (in Chinese)
[11] 常占强, 王金庄. 关于地表点下沉时间函数的研究: 改进的克诺特时间函数[J]. 岩石力学与工程学报, 2003, 22(9): 1496-1499. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200309018.htm CHANG Zhanqiang, WANG Jinzhuang. Study on time function of surface subsidence—the improved knothe time function[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(9): 1496-1499. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200309018.htm
[12] 张兵, 崔希民, 赵玉玲, 等. 优化分段Knothe时间函数求参方法[J]. 煤炭学报, 2018, 43(12): 3379-3386. ZHANG Bing, CUI Ximin, ZHAO Yuling, et al. Parameter calculation method for optimized segmented Knothe time function[J]. Journal of China Coal Society, 2018, 43(12): 3379-3386. (in Chinese)
[13] 朱广轶, 沈红霞, 王立国. 地表动态移动变形预测函数研究[J]. 岩石力学与工程学报, 2011, 30(9): 1889-1895. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201109020.htm ZHU Guangyi, SHEN Hongxia, WANG Liguo. Study of dynamic prediction function of surface movement and deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1889-1895. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201109020.htm
[14] CHENG H, ZHANG L L, GUO L H, et al. A new dynamic prediction model for underground mining subsidence based on inverse function of unstable creep[J]. Advances in Civil Engineering, 2021, 2021: 1-9.
[15] ZHU X J, GUO G L, ZHA J F, et al. Surface dynamic subsidence prediction model of solid backfill mining[J]. Environmental Earth Sciences, 2016, 75(12): 1007.
[16] ZHANG L L, CHENG H, YAO Z S, et al. Application of the improved knothe time function model in the prediction of ground mining subsidence: a case study from Heze city, Shandong Province, China[J]. Applied Sciences, 2020, 10(9): 3147.
[17] 崔希民, 缪协兴, 赵英利, 等. 论地表移动过程的时间函数[J]. 煤炭学报, 1999, 24(5): 453-456. https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB199905001.htm CUI Ximin, MIAO Xiexing, ZHAO Yingli, et al. Discussion on the time function of time dependent surface movement[J]. Journal of China Coal Society, 1999, 24(5): 453-456. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTXB199905001.htm
[18] 王正帅, 邓喀中. 采动区地表动态沉降预测的Richards模型[J]. 岩土力学, 2011, 32(6): 1664-1668. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201106015.htm WANG Zhengshuai, DENG Kazhong. Richards model of surface dynamic subsidence prediction in mining area[J]. Rock and Soil Mechanics, 2011, 32(6): 1664-1668. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201106015.htm
[19] 张兵, 崔希民, 胡青峰. 开采沉陷动态预计的正态分布时间函数模型研究[J]. 煤炭科学技术, 2016, 44(4): 140-145, 174. ZHANG Bing, CUI Ximin, HU Qingfeng. Study on normal distributed time function model to dynamically predict mining subsidence[J]. Coal Science and Technology, 2016, 44(4): 140-145, 174. (in Chinese)
[20] 席国军, 洪兴, 邵红旗. 改进Logistic函数模型在地表下沉预计中的应用[J]. 煤炭科学技术, 2013, 41(8): 114-117, 128. https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201308032.htm XI Guojun, HONG Xing, SHAO Hongqi. Application of improved logistic function model to prediction of surface subsidence[J]. Coal Science and Technology, 2013, 41(8): 114-117, 128. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-MTKJ201308032.htm
-
期刊类型引用(2)
1. 吴彦燊，徐博远，刘璐，薄昭，吴琪. 砂-粉混合料不排水剪切相变强度特性试验研究. 人民长江. 2025(01): 187-192 . 
百度学术
2. 王钰轲，蒋睿，郭成超，王复明. 考虑相变状态及温度效应的冻结砂土非关联弹塑性本构模型. 岩石力学与工程学报. 2025(04): 1026-1039 . 百度学术
其他类型引用(0)
-
其他相关附件
计量
- 文章访问数: 292
- HTML全文浏览量: 68
- PDF下载量: 78
- 被引次数: 2
