Stability analysis of surrounding rock of mountain tunnels based on deformation prediction and parameter inversion
-
摘要: 隧道围岩变形与岩体力学参数之间存在复杂的非线性关系，是围岩状态改变最直观的表现，也是围岩稳定性综合判别的重要指标。提出一种基于变形时序预测和力学参数反演的山岭隧道围岩稳定性分析方法。首先引入Tent混沌扰动和自适应警戒调整机制，构建基于自适应混沌麻雀搜索算法优化极限学习机（ACSSA-ELM）的变形时序预测模型和力学参数反演模型，进一步采用三次样条插值和变分模态分解（VMD）对已开挖断面围岩实测变形预处理，利用变形时序预测模型采取窗口滚动单步预测的方式对已开挖断面围岩最终变形值进行预测，并用于力学参数反演模型中获取开挖段围岩的“修正”力学参数，基于数值模型正算结果和开挖段已测变形值预测开挖段围岩变形和变形速率，进而分析其稳定性。依托重庆市花阳隧道进行了方法的验证与应用，并对隧道ZK40+820断面围岩的稳定性进行了合理可靠的预测分析。最后对方法的使用条件和反演参数的准确性进行了讨论。Abstract: There is a complex nonlinear relationship between the deformation of the surrounding rock of tunnels and the mechanical parameters of rock mass, which is the most intuitive expression for change of state of the surrounding rock, and is also an important index for the comprehensive discrimination of its stability. A stability analysis method for the surrounding rock of tunnels based on the deformation prediction and the mechanical parameter inversion is proposed. Firstly, by introducing the tent chaotic disturbance and the adaptive vigilance adjustment mechanism, the deformation time series prediction model and the mechanical parameter inversion model based on the adaptive chaos sparrow algorithm optimized extreme learning machine (ACSSA-ELM) are established. Further, the cubic spline interpolation and the variational modal decomposition (VMD) are used to preprocess the measured deformation values of the surrounding rock of the excavated section, and the deformation time series prediction model is used to predict the final deformation values of the surrounding rock of the excavated section using the dynamic window rolling single-step prediction, which is used to obtain the real mechanical parameters of the surrounding rock of the excavation section in the mechanical parameter inversion model. Based on the forward calculation results of the numerical model and the measured deformation values of the excavation section, the deformation and deformation rate of the surrounding rock in the excavation section are predicted, and then its stability is analyzed. Taking the Huayang tunnel of Chongqing as an example, the proposed method is verified and applied, and the stability of the surrounding rock of ZK40+820 section of the tunnel is reliably predicted and analyzed. Finally, the application conditions of the method and the accuracy of the inversion parameters are discussed.
-
0. 引言
山岭隧道多穿越复杂地质环境，隧道开挖导致围岩的初始应力状态发生急剧改变，从而对围岩的稳定性产生较大影响，支护措施采取不当极易引发隧道失稳、塌方等工程灾害[1-3]。隧道围岩的变形规律和变形值是反映围岩稳定性最直观有效的指标[4]，利用已有的变形监测资料对隧道现阶段和未来一定时期内围岩的稳定性进行分析具有重要的工程指导意义。
根据围岩力学参数采用数值方法获取围岩的变形规律，进而分析隧道围岩稳定状态是工程中常用的手段[5]，如何快速、准确地获取围岩力学参数成为了岩土工程领域的重难点问题。围岩的力学参数和变形之间存在复杂的非线性关系，近年来，基于变形值的力学参数反分析方法具有计算速度快、成本低等优势，成为了解决上述问题的一种有效手段。尤其是随着计算机技术的发展，不少学者将诸如粒子群算法、灰狼算法、BP神经网络和支持向量机等机器学习方法应用到力学参数反演中[6-11]，取得了丰硕成果。利用已有变形监测数据反演围岩力学参数，进而对隧道围岩未来一定时期内的变形和稳定状态进行预测具有较高的可行性。参数反演的本质是构建围岩变形和力学参数组合的一一对应的非线性关系，准确可靠的变形值是确保反演参数合理有效的基础。然而，施工中难以在短时间内获取围岩最终变形值，采用变形过程中的监测值进行参数反演显然是不准确的。变形预测方法可以利用前期足够数量的已测变形数据对围岩的最终变形值进行较好的预测，进而将预测的最终变形值用于力学参数反演。常用的变形预测方法有回归分析[12]、灰色模型等[13-14]。同样的，机器学习领域的粒子群算法和人工神经网络等[15-18]也在变形预测方面得到了较为广泛的应用。基于机器学习的围岩力学参数反演方法和变形预测方法虽然有了一定的应用，但仍存在一些不足：①机器学习模型的计算精度受参数选择影响较大，稳定性不佳，泛化能力弱。②参数寻优算法存在“早熟”收敛现象，容易陷入局部最优解。③变形预测模型对监测数据的连续性和时效性要求较高，数据的适应性不强。④力学参数反演正算数值模型过于简化，不能很好地模拟真实施工工况。
鉴于此，本文引入寻优能力更强的自适应混沌麻雀搜索算法，建立基于自适应混沌麻雀搜索算法优化极限学习机（ACSSA-ELM）的时序预测模型和参数反演模型，将时序预测方法与参数反演理论有机结合，提出一种基于变形预测和参数反演的隧道围岩稳定性分析方法，以重庆市花阳隧道ZK40+800-820段为例对本文方法进行了说明和验证。该方法可以对开挖段围岩当前和未来一定时期内稳定性进行合理分析和预测，是一种较好的尝试。
1. 算法原理及监测数据预处理
1.1 自适应混沌麻雀搜索算法
麻雀搜索算法是一种新型群智能优化算法，算法具有较好的稳定性、收敛速度和局部搜索能力[19]，可以很好地解决复杂优化问题。
假设麻雀种群个体数量为n，每个麻雀个体作为d维解空间中的一个解，则麻雀种群可以表示为
$$ X=\left[\begin{array}{cccc} x_{1, 1} & x_{1, 2} & \cdots & x_{1, d} \\ x_{2, 1} & x_{2, 2} & \cdots & x_{2, d} \\ \vdots & \vdots & \vdots & \vdots \\ x_{n, 1} & x_{n, 2} & \cdots & x_{n, d} \end{array}\right] 。 $$ (1) 式中：d为解空间的维度；xn, d为种群中第n只麻雀在第d维的位置。
种群的适应度F(X)可以表示为
$$ F\left( X \right) = \left[ \begin{array}{l} f\left( {\left[ {{x_{1, 1}}{\text{ }}{x_{1, 2}}{\text{ }} \cdots {\text{ }}{x_{1, d}}} \right]} \right)\\ f\left( {\left[ {{x_{2, 1}}{\text{ }}{x_{2, 2}}{\text{ }} \cdots {\text{ }}{x_{2, d}}} \right]} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \quad{\text{ }} \vdots \quad{\text{ }} \vdots \quad{\text{ }} \vdots \\ f\left( {\left[ {{x_{n, 1}}{\text{ }}{x_{n, 2}}{\text{ }} \cdots {\text{ }}{x_{n, d}}} \right]} \right)。 \end{array} \right] $$ (2) 式中，f(x)为种群个体的适应度值。
在迭代过程中，个体的位置会不断地发生改变，发现者位置更新如下：
$$ X_{i, j}^{T+1}= \begin{cases}X_{i, j}^T \cdot \exp \left(-\frac{i}{\alpha \cdot \text { iter }_{\max }}\right) & \left(R_2<S T\right) \\ X_{i, j}^T+Q \cdot Z & \left(R_2 \geqslant S T\right)\end{cases} 。 $$ (3) 式中：$ X_{i, j}^T $为第T代种群中第i只麻雀的第j维位置；α为(0, 1]中的均匀随机数；Q为一个服从标准正态分布的随机数；itermax为种群的最大迭代次数；R2∈[0, 1]为预警值；ST∈[0.5, 1]表示警戒阈值；Z为元素为1的1×d阶矩阵。
跟随者位置更新如下：
$$ X_{i, j}^{T+1}= \begin{cases}Q \cdot \exp \left(\frac{X_{\mathrm{w}}-X_{i, j}^T}{i^2}\right) & (i>n / 2) \\ X_{\mathrm{P}}^{T+1}+\frac{1}{d} \sum\limits_{j=1}^d\left(K \cdot\left|X_{P, j}^T-X_{i, j}^T\right|\right) & (i \leqslant n / 2)\end{cases} 。 $$ (4) 式中：Xp为当前种群中发现者的最优位置；Xw为全局最差位置；K为[-1, 1]均匀随机数。
警戒者位置更新如下：
$$ X_{i, j}^{T+1}=\left\{\begin{array}{ll} X_{\mathrm{b}}^T+\varsigma \cdot\left|X_{i, j}^T-X_{\mathrm{b}, j}^T\right| & \left(f_i \neq f_{\mathrm{g}}\right) \\ X_{i, j}^T+K \cdot\left(\frac{\left|X_{i, j}^T-X_{\mathrm{w}}^T\right|}{\left|f_i-f_{\mathrm{w}}\right|+\varepsilon}\right) & \left(f_i=f_{\mathrm{g}}\right) \end{array}\right. 。 $$ (5) 式中：Xb为全局最优位置；$ \varsigma $为符合标准正态分布的随机数；ε为防止分母为零的最小的常数，fi为当前麻雀个体适应度值，fg，fw为当前全局最优和最差的适应度值。
麻雀搜索算法虽然具有较强的局部搜索能力和较快的收敛速度，但其全局搜索能力较弱，易陷入局部最优。Tent映射具有较好的遍历均匀性和随机性[20]，有利于算法跳出局部最优解从而大幅增强算法的全局寻优能力。因此，本文在麻雀算法的基础上引入改进的Tent混沌扰动以提高算法的全局寻优能力。
改进Tent映射通过增加随机变量克服了落入小周期和不稳定周期点的缺陷，其表达式为
$$ y_{j+1}=\left\{\begin{array}{ll} 2 y_j+\operatorname{rand}(0, 1) \cdot \frac{1}{N} & (0 \leqslant y \leqslant 0.5) \\ 2\left(1-y_j\right)+\operatorname{rand}(0, 1) \cdot \frac{1}{N} & (0.5<y \leqslant 1) \end{array} 。\right. $$ (6) 式中：yj为混沌序列中的第j个值；N为混沌序列粒子的总数。以发现者位置更新为例说明改进Tent混沌扰动的具体实施方式。
假设第i个发现者位置为${X_i} = ({x_{i, 1}}, {x_{i, 2}}, \cdots , {x_{i, d}})$，适应度值为fi。设置混沌搜索计数器初始值m=0和最大值为M，根据式（6）采用改进Tent映射产生一个混沌序列$ {y}_{m}=(y{}_{m，}{}_{1}, {y}_{m，}{}_{2}, \cdots , {y}_{m，}{}_{d}) $，利用混沌序列ym对发现者当前位置进行扰动，并计算扰动后位置的适应度fm：
$$ \left.\begin{array}{l} X_i^m=X_i+\lambda \cdot \rho \cdot r \cdot y_m, \\ \rho=1-\frac{T-1}{\operatorname{iter}_{\max }}, \\ r=\frac{u_{\mathrm{b}}-l_{\mathrm{b}}}{10} 。 \end{array}\right\} $$ (7) 式中：$X_i^m$为第m次混沌搜索时发现者的位置；$\lambda $为搜索方向因子，取值为1或-1；$\rho $为衰减因子，可以在迭代初期给予个体较大的扰动，以扩大个体的搜索范围，随着迭代次数的增加，扰动逐渐减小，有利于精确搜索；r为混沌搜索半径，${u_{\text{b}}}$，${l_{\text{b}}}$分别为边界的上下限。
若fm＞fi，则fi =fm，并用扰动后的位置代替原位置，执行下一次混沌扰动；否则，直接执行下一次扰动，依次迭代，直至达到最大扰动次数M。
警戒者的数量较多有利于算法进行全局搜索，较少则利于加快收敛并在小范围内进行局部搜索。提出自适应警戒机制，在算法的前期赋予种群较高的警戒者比例，增强种群的全局搜索能力，随着种群迭代次数的增加逐渐降低警戒者比例，加快算法收敛速度。
$$ P=\left\{\begin{array}{ll} P_0 \cdot\left(1-\frac{T}{\text { iter }_{\max }}\right) & \left(P>P_{\min }\right) \\ P_{\min } & \left(P \leqslant P_{\min }\right) \end{array}\right. \text { 。 } $$ (8) 式中：P为警戒者比例；P0为警戒者比例初始值，本文取30%；Pmin为警戒者比例最小值，本文取10%。
1.2 极限学习机
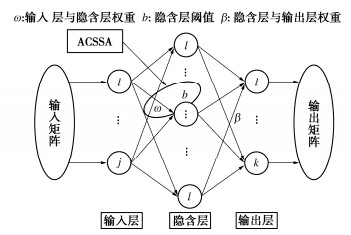
极限学习机（ELM）是一种单隐含层前馈神经网络，能够很好地解决小样本数据的回归问题[21]，其原理及应用已十分成熟，本文不再详细赘述。本文采用自适应混沌麻雀搜索算法（ACSSA）对极限学习机的初始权值和阈值进行优化，以提高其计算精度和稳定性，具有j个输入层神经元，l个隐含层神经元和k个输出层神经元的自适应混沌麻雀算法优化极限学习机的网络结构如图 1所示。
1.3 监测数据预处理
变形数据的连续性是保证时序预测精度的前提。工程中往往依据围岩的变形速率，选择不同的监测频率进行变形监测，实测变形值往往是不连续的，难以满足时序预测的要求。3次样条插值具有逼近程度高、光滑稳定和计算简单等优势，本文采用3次样条插值法对实测变形数据进行插值等距化处理。
变分模态分解（VMD）是一种非递归变分模式的分解方法，可以实现信号频域内各个分量的自适应分割，从而有效避免经验模态分解（EMD）存在的模态混叠问题，且可以人为设置模态数，在诸多领域受到了广泛应用[22]。本文采用变分模态分解将时序变形数据分解为低频趋势项变形$ d(t) $和高频随机项变形$\delta (t)$，进而分别对其进行时间序列预测，
$$ S(t) = d(t) + \delta (t)。 $$ (9) 式中：S(t)为实测总变形；d(t)为趋势项变形；δ(t)为随机项变形。
2. 模型的建立
2.1 ACSSA-ELM变形时序预测模型
监测数据的数量和时效性是保证时序预测精度的前提。在保证模型充分学习的基础上，需要不断对样本进行更新以达到最佳的预测效果。提出一种窗口滚动单步预测方法，通过合理选择滑动窗口的大小W，使用新的预测数据不断更新学习样本，实现单步滚动预测。将ACSSA-ELM算法与窗口滚动单步预测原理结合，构建ACSSA-ELM变形时序预测模型。窗口滚动单步预测原理如图 2所示。
2.2 ACSSA-ELM力学参数反演模型
采用ACSSA-ELM算法构建围岩力学参数反演模型。以监测点的实测变形值作为模型的输入值，待反演的围岩力学参数作为模型输出值，通过对大量有代表性的样本进行学习，最终建立围岩变形与力学参数间的非线性映射关系。采用正交和均匀实验设计分别构造反演模型的学习样本和测试样本[23]。具体为建立接近施工实际的数值计算模型，将正交设计和均匀设计的各参数组合代入数值模型中并进行计算，同时对各监测点的变形值进行记录，将参数组合与对应的变形值进行整理统计，构造模型学习样本和测试样本。
2.3 模型性能评价
为进一步验证变形时序预测模型和力学参数反演模型的性能，采用均方根误差RMSE、平均相对误差ARE和对称平均绝对百分比误差SMAPE对模型的计算精度进行客观评价。
$$ \left.\begin{array}{l} \mathrm{RMSE}=\sqrt{\frac{1}{q} \sum\limits_{i=1}^q\left(\hat{Y}_i-Y_i\right)^2} , \\ \mathrm{ARE}=\frac{1}{q} \sum\limits_{i=1}^q \frac{\left|\hat{Y}_i-Y_i\right|}{Y_i}, \\ \mathrm{SMAPE}=\frac{100 \%}{q} \sum\limits_{i=1}^q \frac{\left|\hat{Y}_i-Y_i\right|}{\left(\left|\hat{Y}_i\right|+\left|Y_i\right|\right) / 2} 。 \end{array}\right\} $$ (10) 式中：q为测试样本的数量；$ {\hat Y_i} $，$ {Y_i} $分别为模型预测值和测试样本真实值。
2.4 围岩稳定性分析流程
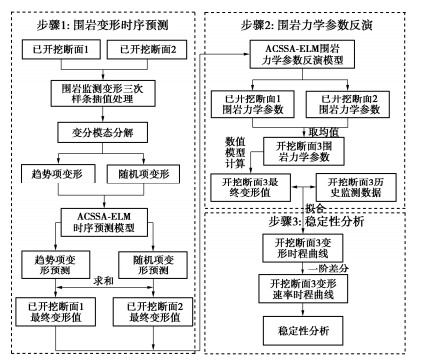
提出一种基于变形预测和力学参数反演的山岭隧道围岩稳定性分析方法，方法的基本流程如图 3所示。
步骤1：围岩变形时序预测。对临近已开挖断面的变形监测值进行三次样条插值等距化，采用变分模态分解将等距化后的数据分解为趋势项变形和随机项变形，采用ACSSA-ELM时序预测模型分别进行预测，求和后得到已开挖断面围岩预测最终变形值。
步骤2：围岩力学参数反演。将已开挖断面围岩最终预测变形值代入到ACSSA-ELM力学参数反演模型中，反演出已开挖断面围岩力学参数，多断面取平均值作为开挖断面围岩力学参数，将开挖断面围岩力学参数代入数值模型中计算该断面围岩最终变形值。
步骤3：稳定性分析。对开挖断面已测变形数据和数值模型计算最终变形值进行曲线拟合，并进行一阶差分处理，获取开挖断面围岩变形时程曲线和变形速率时程曲线，对开挖断面围岩的稳定性进行分析。
3. 工程实例
3.1 工程概况
花阳隧道位于重庆市渝北区木耳镇广佛村，隧道总长430 m，平均埋深约50 m，属于浅埋短隧道。以花阳隧道ZK40+800—820段为研究对象，该区段下伏基岩为侏罗系中上统沙溪庙砂岩和泥岩不等厚度互层，隧址区整体呈单斜构造，岩层产状为120°∠22°，岩体内裂隙稍发育，可大致分为8个优势组。裂隙面较平直，张开约0.5~2 mm，延伸约3~5 m。区域内未见不良地质现象，地质较稳定。
3.2 模型检验
隧道ZK40+800—820段采用三台阶开挖法施工，由监控量测资料可知：ZK40+800—805段已开挖完成，且已监测至开挖后(60±2) d；ZK40+810段已完成开挖，拱顶和上台阶已监测60 d，中台阶已监测50 d，下台阶已监测40 d；ZK40+815段已完成开挖，拱顶和上台阶已监测50 d，中台阶已监测45 d，下台阶已监测40 d；ZK40+820段正在开挖，拱顶和上台阶已监测25 d，中台阶已监测15 d，下台阶正在施工未布设监测点。以ZK40+800断面为例，对本文模型的性能进行检验。
（1）时序预测模型的性能检验
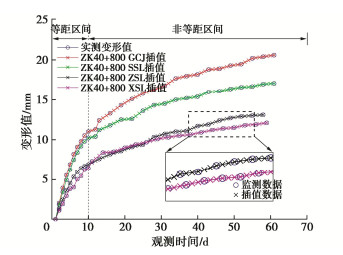
采用三次样条插值法对ZK40+800断面围岩拱顶沉降（GCJ）、上台阶收敛（SSL）、中台阶收敛（ZSL）和下台阶收敛（XSL）实测变形值进行等距化处理，获取连续变形数据如图 4所示。
![]()
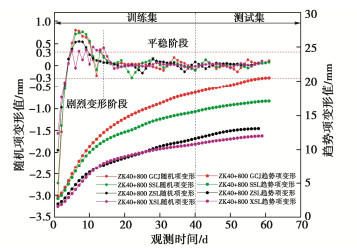
图 4 插值处理后ZK40+800断面实测变形值Figure 4. Measured values of ZK40 + 800 section after interpolation采用变分模态分解将插值后的数据提取趋势项和随机项变形。为保证预测精度，模型训练集与测试集的比例一般取7︰3，最低不小于2︰1[16]。结合工程实际，取前40 d的变形值为训练集，后20 d为测试集，对时序预测模型的预测精度进行检验。ZK40+800断面趋势项和随机项变形提取如图 5所示。观察可知，该断面随机项变形在前13 d处于剧烈变形阶段，13 d以后进入平稳波动阶段，且波动峰值不超过±0.3 mm，其预测结果对该断面围岩最终变形值影响较小，因此，模型检验中将趋势项变形最终预测值作为该段围岩最终变形值，不再对随机项变形进行预测。
![]()
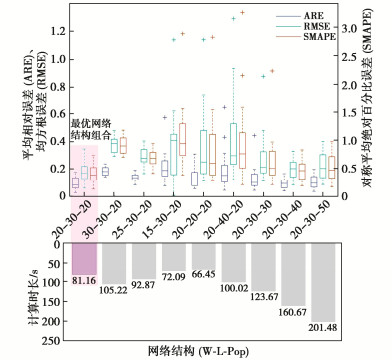
图 5 ZK40+800断面变形值的变分模态分解Figure 5. Variational modal decomposition of ZK40 + 800 section设置麻雀种群发现者比例为70%，跟随者比例30%，警戒者比例P0=30%，Pmin=10%，警戒阈值ST=0.6，种群最大迭代次数itermax=100，混沌搜索计数器最大值M=40，边界上限ub=1，下限lb=-1，激活函数为“sig”函数，时序预测窗口长度W、隐含层神经元个数L和麻雀种群大小Pop由试算选取。以ZK40+800断面GCJ趋势项变形数据为试算样本，分别选取9种网络结构进行10次试算。如图 6所示，当预测窗口长度W=20，隐含层神经元个数L=30，麻雀种群大小Pop=20时，变形时序预测模型的预测精度最高，计算用时最短。因此，选取网络结构为“20—30—20”。需要说明的是，网络结构不是一层不变的，具体结构要根据数据类型灵活选择。
![]()
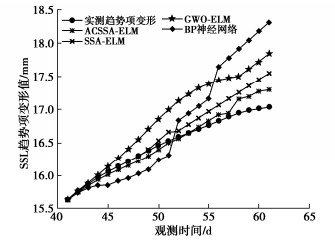
图 6 时序预测模型最佳网络结构选取Figure 6. Selection of best network structure of time series prediction model采用ACSSA-ELM时序预测模型对ZK40+800断面上台阶趋势项变形进行时序预测，并与SSA-ELM、GWO-ELM和BP神经网络模型（无窗口多步预测）对比。计算结果表明，ACSSA-ELM模型的预测结果最优，SSA-ELM和GWO-ELM模型次之，但预测精度可满足一般施工需要，BP神经网络由于缺少样本更新机制，模型不能对新的变形规律进行准确把握和学习，预测效果最差。部分预测结果如图 7和表 1所示。
![]()
图 7 4种模型上台阶收敛变形预测结果对比Figure 7. Comparison of predicted results of upper step convergence deformation by four models表 1 ZK40+800断面4种模型趋势项变形预测结果对比Table 1. Comparison of predicted results of trend-term deformation by four models for ZK40 + 800 section指标 监测点 ACSSA-ELM SSA-ELM GWO-ELM BP 监测点 ACSSA-ELM SSA-ELM GWO-ELM BP RMSE GCJ 0.11 0.46 0.33 1.15 SSL 0.11 0.21 0.46 0.59 ARE 0.09 0.39 0.27 0.91 0.08 0.14 0.39 0.45 SMAPE 0.46 1.97 1.34 4.36 0.49 0.84 2.26 2.60 RMSE ZSL 0.25 0.28 0.35 0.61 XSL 0.15 0.52 0.34 0.33 ARE 0.19 0.24 0.28 0.48 0.13 0.42 0.25 0.22 SMAPE 1.50 1.92 2.17 3.66 1.14 3.52 2.07 1.81 （2）参数反演模型的样本构造
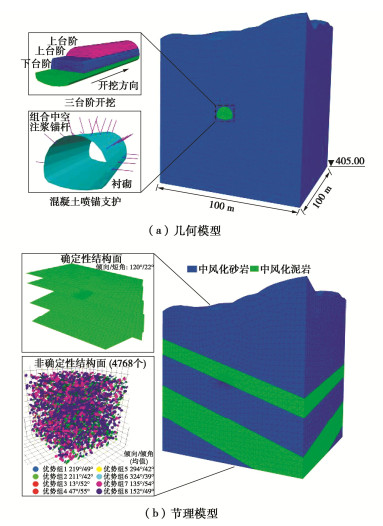
采用“RHINO-GRIDDLE-3DEC”联合建模建立隧道开挖数值模型，模型垂直和平行于隧道轴线方向的尺寸为100 m×100 m，竖向从海拔405 m到基岩表面。为模型添加确定岩层结构面，并采用DFN随机离散裂隙模拟岩体内非确定性结构面，其密度由地质结构素描图计算获取。为提高模型计算效率，编写小尺寸结构面过滤函数，对尺寸小于3 m的微型结构面进行过滤，剩余4768条主要结构面。
岩体本构采用摩尔库伦模型，节理本构采用区域接触弹塑性模型。模型四周设置法向约束，底部为三向约束，顶部为自由面，初始地应力只考虑自重应力影响，围岩初始应力$ {\sigma _z} $=-1.22 MPa，$ {\sigma _x} $=$ {\sigma _y} $=-0.61 MPa（受压为负）。隧道开挖后，初期支护采用喷锚支护。建立隧道开挖数值计算模型如图 8所示。
结合工程实际，该区域为中风化泥岩和砂岩不等厚度互层，围岩平均重度$ \gamma $=22.03 kN/m3，内摩擦角为φ=31°，两参数变化范围较小，本文仅对弹性模量E，黏聚力C和泊松比μ3个力学参数进行反演。根据地质勘查资料，在相应的取值范围内对弹性模量、黏聚力和泊松比进行5水平划分，并选用L25(53)正交表设计训练集试验方案，选用U5(53)均匀设计表设计测试集实验方案，依次代入数值模型中进行计算，最终得到模型训练集和测试集见表 2，3。
表 2 围岩力学参数反演模型训练样本集Table 2. Training sample sets of mechanical parameter inversion model for surrounding rock样本编号 E/GPa c/MPa μ GCJ/mm SSL/mm ZSL/mm XSL/mm 1 1.5000 0.3000 0.2500 34.5285 24.1551 19.3244 14.7527 2 1.8750 0.3000 0.2500 28.0792 19.3012 14.3012 11.3671 3 2.2500 0.3000 0.2500 23.8682 15.1129 11.4967 9.8530 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 25 3.0000 1.2000 0.3500 15.6302 12.9397 9.6325 8.2561 表 3 围岩力学参数反演模型测试样本集Table 3. Test sample sets of mechanical parameter inversion model for surrounding rock样本编号 E/GPa c/MPa μ GCJ/mm SSL/mm ZSL/mm XSL/mm 1 1.5000 0.4500 0.2625 33.3623 25.1538 19.5234 15.8074 2 1.8750 0.6500 0.2875 26.5388 20.1030 15.2248 13.2724 3 2.2500 0.8500 0.3125 21.8077 16.8328 14.2017 12.3318 4 2.6250 1.0500 0.3375 18.2687 13.9744 11.6823 10.1458 5 3.0000 1.2500 0.3625 15.3268 13.3857 9.6086 8.8342 （3）力学参数反演模型的性能检验
同理，保持ACSSA-ELM算法其他参数不变，改变隐含层神经元数L，种群大小Pop和最大迭代次数itermax进行试算。结果表明，L=20，Pop=40，itermax=100时，待反演参数的反演值与目标值相对误差最小。
选取ACSSA-ELM围岩力学参数反演模型网络结构为“20—40—100”，将测试集样本代入模型，计算结果见表 4。采用SSA-ELM、GWO-ELM和BP神经网络模型计算并与本模型比对，SSA-ELM模型各参数平均相对误差为0.236%，1.990%，0.558%，GWO-ELM模型各参数平均相对误差为0.200%，2.074%，0.514%，BP神经网络模型各参数平均相对误差为0.514%，2.487%，0.693%。比较可知，相比于其他3种模型，ACSSA-ELM围岩力学参数反演模型的反演精度最高，模型具有较好的应用价值。
表 4 ACSSA-ELM围岩力学参数反演模型计算结果Table 4. Results of ACSSA-ELM mechanical parameter inversion model for surrounding rock编号 E/GPa c/MPa μ 目标值 反演值 相对误差% 目标值 反演值 相对误差% 目标值 反演值 相对误差% 1 1.5000 1.4956 0.293 0.4500 0.4508 0.178 0.2625 0.2668 1.638 2 1.8750 1.8792 0.224 0.6500 0.6301 3.060 0.2875 0.2867 0.278 3 2.2500 2.2472 0.124 0.8500 0.8526 0.306 0.3125 0.3114 0.325 4 2.6250 2.6300 0.042 1.0500 1.0864 3.467 0.3375 0.3374 0.089 5 3.0000 3.0022 0.190 1.2500 1.2848 2.784 0.3625 0.3594 0.030 平均相对误差% 0.175 1.959 0.472 3.3 稳定性分析
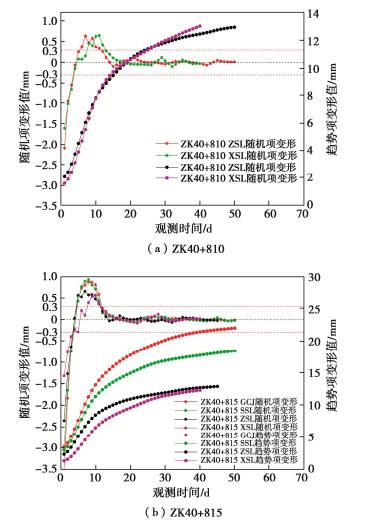
采用本方法对花阳隧道ZK40+820断面围岩的稳定性进行分析。隧道ZK40+810和815断面已完成开挖，且ZK40+810断面拱顶和上台阶收敛已完成60日监测。因此，对ZK40+810断面中、下台阶已测变形和ZK40+815断面拱顶沉降、上、中和下台阶已测变形进行三次样条插值处理后，采用变分模态分解提取趋势项变形和随机项变形，分解结果如图 9所示。
![]()
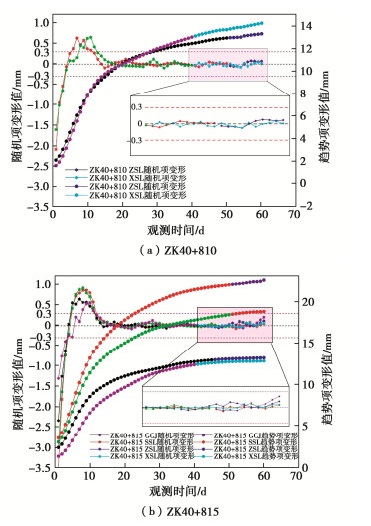
图 9 ZK40+810和ZK40+815断面已测变形分解Figure 9. Decomposition of measured deformation at ZK40 + 810 and ZK40 + 815 sections保持ACSSA-ELM变形时序预测模型参数不变，采用本模型对ZK40+810断面中、下台阶收敛变形和ZK40+815断面拱顶沉降、上、中和下台阶收敛变形进行时序预测，以第60天变形预测值作为该断面各监测点最终变形值。ZK40+810断面第60天中台阶趋势项变形和随机项变形预测值分别为13.3196，0.0698 mm，下台阶趋势项变形和随机项变形预测值分别为14.2587，0.0080 mm，结合监测资料可得ZK40+810断面拱顶沉降、上、中和下台阶预测最终变形值为21.4931，17.4328，13.3894，14.2667 mm。同理，ZK40+815断面拱顶沉降、上、中和下台阶收敛最终变形值为22.8006，18.8797，13.3304，12.8789 mm。ZK40+810和ZK40+815断面时序预测结果如图 10所示。
![]()
图 10 ZK40+810和ZK40+815断面变形时序预测Figure 10. Deformation time series prediction of ZK40 + 810 and ZK40 + 815 sections保持参数反演模型网络结构不变，以ZK40+810和815断面围岩最终变形值为输入矩阵，反演得ZK40+810断面围岩弹性模量E=2.2383 GPa，黏聚力c=1.0326 MPa，泊松比μ=0.3314，ZK40+815断面围岩弹性模量E=2.1654 GPa，黏聚力c=0.8004 MPa，泊松比μ=0.3056。两断面围岩力学参数取均值作为ZK40+820开挖断面力学参数，ZK40+820开挖段围岩力学参数为E=2.2019 GPa，黏聚力c=0.9165 MPa，泊松比μ=0.3185。将ZK40+820开挖段围岩力学参数代入到隧道开挖数值计算模型中，经计算提取ZK40+820段围岩拱顶沉降变形GCJ=22.0751 mm，上台阶收敛变形SSL=17.6669 mm，中台阶收敛变形ZSL=14.6456 mm，下台阶收敛变形XSL=12.7484 mm。
ZK40+820断面正在施工，上台阶和中台阶已开挖完成，下台阶正在开挖未布设监测点。限于监测日期较短，且已有监测数据多处于变形急剧增长阶段，此时采用时序预测方法对围岩变形进行预测将会出现较大误差。原因在于，时序预测是建立在对监测数据变化规律充分学习基础上进行的，利用变形急剧增长阶段的有限的数据无法对后期的变形规律和变形值做出合理判断和预测，导致预测最终变形值不收敛，且预测误差存在“累积放大”效应，前期较小的预测误差可能导致最终预测结果与实际变形严重不符。
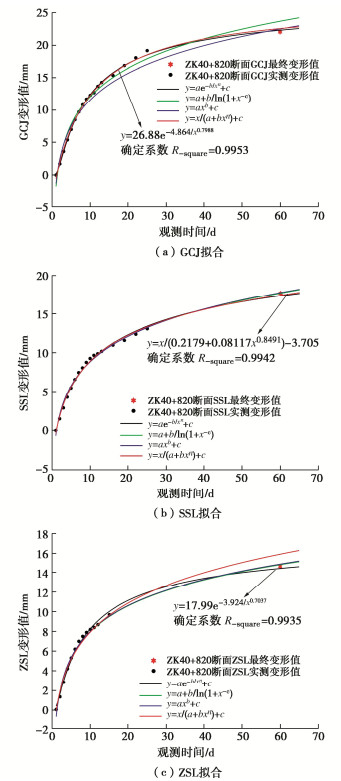
鉴于此，本文借助MATLAB拟合工具箱，对ZK40+820断面已测变形数据和数值模型计算的最终变形值进行非线性函数拟合，进而对该开挖断面围岩的稳定性进行分析。经试算，ZK40+820断面拱顶沉降和中台阶收敛变形采用指数函数拟合效果最佳，上台阶收敛变形采用双曲函数拟合效果最佳，拟合曲线确定系数均接近1，具有较高的可信度，可对隧道围岩变形的全过程进行较好的模拟。拟合结果见表 5和图 11。
表 5 ZK40+820断面变形最佳拟合曲线Table 5. Best fitting curves of deformation of ZK40 + 820 section监测点位 曲线方程 SSE R-square Adjusted R-square RMSE GCJ $ y=26.88 \mathrm{e}^{-4.864 / x^{0.7988}} $ 1.068 0.9983 0.9981 0.2668 SSL $ y = x/(0.2179 + 0.08117{x^{0.8491}}) - 3.705 $ 1.568 0.9952 0.9942 0.3347 ZSL $ y = 17.99{\mathrm{e}^{ - 3.924/{x^{0.7037}}}} $ 0.9977 0.9945 0.9935 0.3012 ![]()
图 11 ZK40+820断面变形值曲线拟合Figure 11. Fitting curves of deformation value of ZK40 + 820 section（1）基于最大变形值的稳定性分析
根据《公路隧道施工技术规范：JTG/T 3660—2020》[24]，隧道设计的预留变形量U0为允许变形极限值，实测变形量U不应大于变形极限值。由花阳隧道施工设计资料可知，ZK40+800—820段设计预留变形量为120 mm，ZK40+820断面变形理论值UGCJ=22.0751 mm < 40 mm，USSL=17.6669 mm < 40 mm，UZSL=14.6456 mm < 40 mm，隧道最大变形最终稳定在变形极限值以内，且各监测点最大变形值均小于U0/3，施工过程中可采取Ⅲ级管理，正常开展施工作业。
（2）基于变形速率的稳定性分析
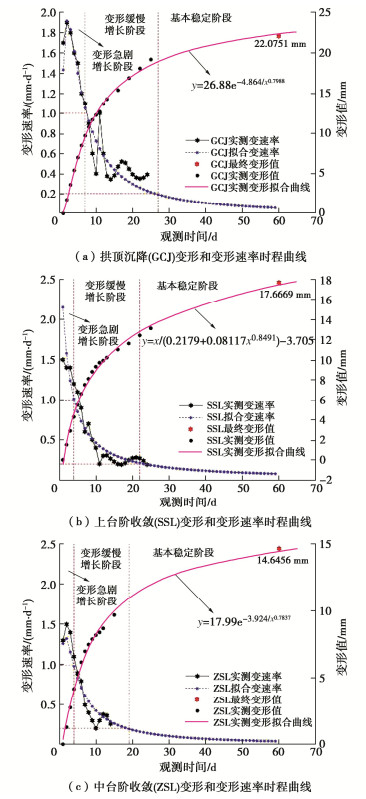
对已测变形数据和拟合变形数据进行3次样条插值，提取插值后的连续变形数据分别进行一阶差分处理得到实测变形速率和拟合变形速率，围岩变形和变形速率时程曲线如图 12所示。根据《公路隧道施工技术规范：JTG/T 3660—2020》第18.6.3节围岩稳定性的综合判别有关规定，变形时程曲线可依据变形速率划分为以下3个阶段：变形急剧增长阶段（变形速率大于1.0 m m/d）；变形缓慢增长阶段（变形速率1~0.2 mm/d）；基本稳定阶段（变形速率小于0.2 mm/d）。
![]()
图 12 ZK40+820断面围岩变形和变形速率时程曲线Figure 12. Time-history curves of deformation and deformation rate of surrounding rock of ZK40 + 820 section如图 12所示，ZK40+820断面拱顶沉降、上台阶和中台阶收敛变形在开挖后约1周内随着围岩的应力重分布表现为变形急剧增长状态。后续2~3周内围岩应力重分布逐渐完成，各测点变形速率逐渐下降，围岩整体表现为变形缓慢增长。随着开挖和初期支护施作完毕，该断面拱顶沉降、上台阶和中台阶收敛变形预计在该测点的监测开始日起第27天、第22天和第19天进入基本稳定阶段，且变形速率在较长一段时间内稳定在0~0.2 mm/d的范围内，直至围岩变形最终稳定。
观察可知，本文方法可以对各监测点变形趋势进行较好模拟，实测变形速率与拟合变形速率对应区间的变化规律基本一致。此外，拟合变形速率曲线的后期变形规律与国内外类似工程基本一致[25]，也符合《公路隧道施工技术规范：JTG/T 3660—2020》中正常变形速率时程曲线的相关规定，变形速率拟合曲线同样可以对各监测点的变形速率进行较好地预测。
4. 讨论
4.1 方法的适用条件
变形和变形速率时程曲线是分析围岩稳定状态的有效手段，两种曲线往往依据现场实测数据直接绘制。然而，实际施工有着严密的施工组织计划和进度安排，这就要求在较短的时间内通过有限数量的监测数据获取开挖断面的围岩变形情况和稳定状态，对开挖断面当前和未来一定时期内的稳定性进行超前判断，进而指导后续施工，实现施工风险最小化。因此，对有限的监测数据进行变形拟合分析或采取时序预测的方法进行变形预测是十分必要的。
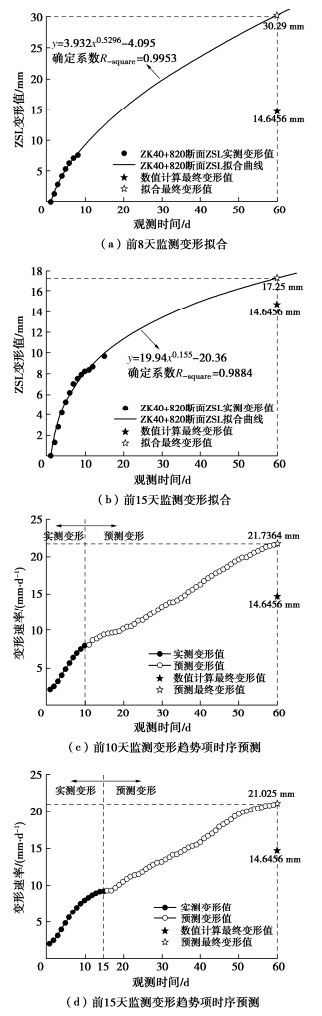
拟合分析和时序预测均要求监测变形数据满足一定的数量要求，数量过少容易产生过拟合，拟合值或预测值难以反应真实的变形规律。以ZK40+820断面为例，利用前8 d和前15 d监测变形值分别进行非线性拟合，ACSSA-ELM变形时序预测模型参数同前文，窗口长度W分别取8，10，利用前10 d和前15 d插值后的趋势项变形数据进行时序预测，拟合和预测结果如图 13所示。
![]()
图 13 少量监测数据的变形拟合和时序预测Figure 13. Deformation fitting and time series prediction of a small amount of monitoring data观察可知，当数据量较少时，两种方法对后期变形进行预测时仍旧保持前期数据的变化趋势，导致变形不能及时收敛，预测结果误差较大。当监测数据满足数量要求时，该断面往往已经完成开挖，此时进行稳定性分析意义不大。
因此，当开挖断面已测变形数据较少，不能完整地反映围岩变形规律时，采用本文方法可以对当前开挖断面的围岩稳定性状态进行较好的预测。且本文方法是基于对临近空间内若干已开挖断面和开挖断面历史监测数据充分学习和挖掘的基础上进行的，预测结果具有更强的合理性和可信性。
4.2 反演参数的准确性
以花阳隧道ZK40+775，780，790，800断面围岩实测变形值作为本文力学参数反演模型的输入值，分别对上述断面围岩的弹性模量E、黏聚力c和泊松比μ进行反演，并与实测值对比，验证反演参数与实测力学参数的吻合度。
提取4个断面围岩拱顶沉降、上、中和下台阶收敛第60日实测变形监测值见表 6，代入本文参数反演模型，各断面围岩力学参数反演结果见表 7。
表 6 已开挖断面实测变形值Table 6. Measured deformation values of excavated section监测断面 GCJ/mm SSL/mm ZSL/mm XSL/mm ZK40+775 20.270 15.274 13.578 11.022 ZK40+780 21.077 11.679 8.897 7.114 ZK40+790 19.263 12.572 10.733 8.993 ZK40+800 20.672 17.117 13.135 12.104 表 7 力学参数反演值Table 7. Inverse values of mechanical parameters监测断面 E/GPa c/MPa μ ZK40+775 2.5974 0.5571 0.2786 ZK40+780 2.6545 0.5780 0.2476 ZK40+790 2.6554 0.7751 0.3028 ZK40+800 2.3744 1.0083 0.3284 工程地质勘查报告实测值 2.8000 0.6200 0.3600 比较可知，4个断面围岩力学参数反演结果与工程地质勘察报告提供本区域围岩力学参数建议取值存在一定的误差，其中黏聚力c反演值与实测值误差最大，达到了38.5%。其原因是由实测力学参数存在误差、数值模型存在局限性和简化、参数反演模型样本有限、部分反演参数敏感性不强以及变形量测存在误差等多种因素造成。
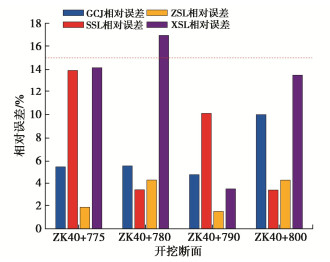
将各断面力学参数反演值代入到数值模型中进行正算，提取拱顶沉降、上、中和下台阶收敛变形值，并将正算变形值与实测变形值进行对比，对比结果如图 14所示。
4个断面离散元正算变形值与工程实测变形值较为吻合，最大误差为16.97%，最小误差为1.52%，且多数监测点的变形值与实测值误差在15%以内。因此，反演力学参数可作为实测力学参数的“修正”代入数值模型进行计算，其计算变形值与实测变形值较为接近。
5. 结论
（1）引入Tent混沌扰动和自适应警戒机制优化麻雀搜索算法，并用以搜寻极限学习机的最佳权值和阈值，提出了计算精度高、稳定性好和泛化能力强的ACSSA-ELM算法，为变形时序预测模型和围岩力学参数反演模型的构建提供了算法保证。
（2）将ACSSA-ELM算法和窗口滚动单步预测原理结合，构建ACSSA-ELM变形时序预测模型；基于ACSSA-ELM算法构建围岩力学参数反演模型，借助3DEC计算并构造参数反演模型的训练样本和测试样本；分别对ACSSA-ELM时序预测和参数反演模型的性能进行检验并与SSA-ELM、GWO-ELM和BP神经网络模型对比，结果表明本文模型具有更高的精度和稳定性。
（3）应用本文方法对花阳隧道ZK40+820断面的变形值和变形速率进行了合理预测，并从最大位移值和变形速率两方面分别讨论了该断面围岩的稳定性：ZK40+820断面围岩在施工全过程中较稳定，可按Ⅲ级管理正常开展施工作业；拱顶沉降、上、中台阶收敛变形预计在各测点监测开始日起第27天、第22天和第19天进入基本稳定阶段，变形速率在较长一段时间稳定在0~0.2 mm/d的范围内，可为实际施工提供参考。
（4）当开挖断面已测变形数据较少时，采用本文方法可较好地预测该断面围岩的稳定状态。反演参数与实测力学参数存在一定的误差，但可作为实测参数的“修正”代入数值模型进行变形正算。
-
![]()
图 4 插值处理后ZK40+800断面实测变形值
Figure 4. Measured values of ZK40 + 800 section after interpolation
![]()
图 5 ZK40+800断面变形值的变分模态分解
Figure 5. Variational modal decomposition of ZK40 + 800 section
![]()
图 6 时序预测模型最佳网络结构选取
Figure 6. Selection of best network structure of time series prediction model
![]()
图 7 4种模型上台阶收敛变形预测结果对比
Figure 7. Comparison of predicted results of upper step convergence deformation by four models
![]()
图 9 ZK40+810和ZK40+815断面已测变形分解
Figure 9. Decomposition of measured deformation at ZK40 + 810 and ZK40 + 815 sections
![]()
图 10 ZK40+810和ZK40+815断面变形时序预测
Figure 10. Deformation time series prediction of ZK40 + 810 and ZK40 + 815 sections
![]()
图 11 ZK40+820断面变形值曲线拟合
Figure 11. Fitting curves of deformation value of ZK40 + 820 section
![]()
图 12 ZK40+820断面围岩变形和变形速率时程曲线
Figure 12. Time-history curves of deformation and deformation rate of surrounding rock of ZK40 + 820 section
![]()
图 13 少量监测数据的变形拟合和时序预测
Figure 13. Deformation fitting and time series prediction of a small amount of monitoring data
表 1 ZK40+800断面4种模型趋势项变形预测结果对比
Table 1 Comparison of predicted results of trend-term deformation by four models for ZK40 + 800 section
指标 监测点 ACSSA-ELM SSA-ELM GWO-ELM BP 监测点 ACSSA-ELM SSA-ELM GWO-ELM BP RMSE GCJ 0.11 0.46 0.33 1.15 SSL 0.11 0.21 0.46 0.59 ARE 0.09 0.39 0.27 0.91 0.08 0.14 0.39 0.45 SMAPE 0.46 1.97 1.34 4.36 0.49 0.84 2.26 2.60 RMSE ZSL 0.25 0.28 0.35 0.61 XSL 0.15 0.52 0.34 0.33 ARE 0.19 0.24 0.28 0.48 0.13 0.42 0.25 0.22 SMAPE 1.50 1.92 2.17 3.66 1.14 3.52 2.07 1.81 
下载: 导出CSV
表 2 围岩力学参数反演模型训练样本集
Table 2 Training sample sets of mechanical parameter inversion model for surrounding rock
样本编号 E/GPa c/MPa μ GCJ/mm SSL/mm ZSL/mm XSL/mm 1 1.5000 0.3000 0.2500 34.5285 24.1551 19.3244 14.7527 2 1.8750 0.3000 0.2500 28.0792 19.3012 14.3012 11.3671 3 2.2500 0.3000 0.2500 23.8682 15.1129 11.4967 9.8530 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 25 3.0000 1.2000 0.3500 15.6302 12.9397 9.6325 8.2561
下载: 导出CSV
表 3 围岩力学参数反演模型测试样本集
Table 3 Test sample sets of mechanical parameter inversion model for surrounding rock
样本编号 E/GPa c/MPa μ GCJ/mm SSL/mm ZSL/mm XSL/mm 1 1.5000 0.4500 0.2625 33.3623 25.1538 19.5234 15.8074 2 1.8750 0.6500 0.2875 26.5388 20.1030 15.2248 13.2724 3 2.2500 0.8500 0.3125 21.8077 16.8328 14.2017 12.3318 4 2.6250 1.0500 0.3375 18.2687 13.9744 11.6823 10.1458 5 3.0000 1.2500 0.3625 15.3268 13.3857 9.6086 8.8342
下载: 导出CSV
表 4 ACSSA-ELM围岩力学参数反演模型计算结果
Table 4 Results of ACSSA-ELM mechanical parameter inversion model for surrounding rock
编号 E/GPa c/MPa μ 目标值 反演值 相对误差% 目标值 反演值 相对误差% 目标值 反演值 相对误差% 1 1.5000 1.4956 0.293 0.4500 0.4508 0.178 0.2625 0.2668 1.638 2 1.8750 1.8792 0.224 0.6500 0.6301 3.060 0.2875 0.2867 0.278 3 2.2500 2.2472 0.124 0.8500 0.8526 0.306 0.3125 0.3114 0.325 4 2.6250 2.6300 0.042 1.0500 1.0864 3.467 0.3375 0.3374 0.089 5 3.0000 3.0022 0.190 1.2500 1.2848 2.784 0.3625 0.3594 0.030 平均相对误差% 0.175 1.959 0.472
下载: 导出CSV
表 5 ZK40+820断面变形最佳拟合曲线
Table 5 Best fitting curves of deformation of ZK40 + 820 section
监测点位 曲线方程 SSE R-square Adjusted R-square RMSE GCJ y=26.88e−4.864/x0.7988 1.068 0.9983 0.9981 0.2668 SSL y=x/(0.2179+0.08117x0.8491)−3.705 1.568 0.9952 0.9942 0.3347 ZSL y=17.99e−3.924/x0.7037 0.9977 0.9945 0.9935 0.3012
下载: 导出CSV
表 6 已开挖断面实测变形值
Table 6 Measured deformation values of excavated section
监测断面 GCJ/mm SSL/mm ZSL/mm XSL/mm ZK40+775 20.270 15.274 13.578 11.022 ZK40+780 21.077 11.679 8.897 7.114 ZK40+790 19.263 12.572 10.733 8.993 ZK40+800 20.672 17.117 13.135 12.104
下载: 导出CSV
表 7 力学参数反演值
Table 7 Inverse values of mechanical parameters
监测断面 E/GPa c/MPa μ ZK40+775 2.5974 0.5571 0.2786 ZK40+780 2.6545 0.5780 0.2476 ZK40+790 2.6554 0.7751 0.3028 ZK40+800 2.3744 1.0083 0.3284 工程地质勘查报告实测值 2.8000 0.6200 0.3600
下载: 导出CSV
-
[1] 孙振宇, 张顶立, 侯艳娟, 等. 基于现场实测数据统计的隧道围岩全过程变形规律及稳定性判据确定[J]. 岩土工程学报, 2021, 43(7): 1261-1270, 1376. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18670.shtml SUN Zhenyu, ZHANG Dingli, HOU Yanjuan, et al. Whole-process deformation laws and determination of stability criterion of surrounding rock of tunnels based on statistics of field measured data[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(7): 1261-1270, 1376. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18670.shtml
[2] 王述红, 董福瑞, 朱宝强, 等. 山岭隧道围岩参数智能反演及稳定性分析[J]. 应用基础与工程科学学报, 2021, 29(5): 1171-1185. WANG Shuhong, DONG Furu, ZHU Baoqiang, et al. Intelligent inversion and stability analysis of surrounding rock of mountain tunnel[J]. Journal of Basic Science and Engineering, 2021, 29(5): 1171-1185. (in Chinese)
[3] 田明杰, 牟智恒, 仇文革. 基于BP神经网络的隧道稳定性分析研究[J]. 土木工程学报, 2017, 50(增刊2): 260-266. doi: 10.15951/j.tmgcxb.2017.s2.041 TIAN Mingjie, MOU Zhiheng, QIU Wenge. Research of the model comprehensive judgement for tunnel stability based on BP neural network[J]. China Civil Engineering Journal, 2017, 50(S2): 260-266. (in Chinese) doi: 10.15951/j.tmgcxb.2017.s2.041
[4] 吴秋军, 王明年, 刘大刚. 基于现场位移监测数据统计分析的隧道围岩稳定性研究[J]. 岩土力学, 2012, 33(增刊2): 359-364. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2012S2057.htm WU Qiujun, WANG Mingnian, LIU Dagang. Research on stability of tunnel surrounding rocks based on statistical analysis of on-site displacement monitoring data[J]. Rock and Soil Mechanics, 2012, 33(S2): 359-364. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2012S2057.htm
[5] 孙潇昊, 缪林昌, 林海山. 不同埋深盾构隧道开挖面稳定问题数值模拟[J]. 东南大学学报(自然科学版), 2017, 47(1): 164-169. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201701028.htm SUN Xiaohao, MIAO Linchang, LIN Haishan. Numerical simulation research on excavation face stability of different depths of shield tunnel[J]. Journal of Southeast University (Natural Science Edition), 2017, 47(1): 164-169. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201701028.htm
[6] 阮永芬, 高春钦, 刘克文, 等. 基于粒子群算法优化小波支持向量机的岩土力学参数反演[J]. 岩土力学, 2019, 40(9): 3662-3669. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201909042.htm RUAN Yongfen, GAO Chunqin, LIU Kewen, et al. Inversion of rock and soil mechanics parameters based on particle swarm optimization wavelet support vector machine[J]. Rock and Soil Mechanics, 2019, 40(9): 3662-3669. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201909042.htm
[7] 阮永芬, 余东晓, 吴龙, 等. DE-GWO算法优化SVM反演软土力学参数[J]. 岩土工程学报, 2021, 43(增刊1): 166-170. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18739.shtml RUAN Yongfen, YU Dongxiao, WU Long, et al. DE-GWO algorithm to optimize SVM inversion mechanical parameters of soft soil[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(S1): 166-170. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18739.shtml
[8] GAO W, CHEN D L, DAI S, et al. Back analysis for mechanical parameters of surrounding rock for underground roadways based on new neural network[J]. Engineering With Computers, 2018, 34(1): 25-36.
[9] 王开禾, 罗先启, 沈辉, 等. 围岩力学参数反演的GSA-BP神经网络模型及应用[J]. 岩土力学, 2016, 37(增刊1): 631-638. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S1083.htm WANG Kaihe, LUO Xianqi, SHEN Hui, et al. GSA-BP neural network model for back analysis of surrounding rock mechanical parameters and its application[J]. Rock and Soil Mechanics, 2016, 37(S1): 631-638. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S1083.htm
[10] BERTUZZI R. Back-analysing rock mass modulus from monitoring data of two tunnels in Sydney, Australia[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2017, 9(5): 877-891.
[11] JIANG A N, LI P. Back-analysis of mechanics parameters of tunnel based on particle swarm optimization and numerical simulation[J]. Key Engineering Materials, 2011(474/475/476): 1373-1376.
[12] 刘开云, 方昱, 刘保国, 等. 隧道围岩变形预测的进化高斯过程回归模型[J]. 铁道学报, 2011, 33(12): 101-106. LIU Kaiyun, FANG Yu, LIU Baoguo, et al. Intelligent deformation prediction model of tunnel surrounding rock based on genetic-Gaussian process regression coupling algorithm[J]. Journal of the China Railway Society, 2011, 33(12): 101-106. (in Chinese)
[13] 李茂达, 樊磊, 李磊, 等. 隧道与地下工程围岩变形的灰色优化与预测[J]. 土木建筑与环境工程, 2013, 35(增刊2): 143-145. https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN2013S2037.htm LI Maoda, FAN Lei, LI Lei, et al. Tunnels and underground engineering optimization and gray rock deformation prediction[J]. Journal of Civil, Architectural & Environmental Engineering, 2013, 35(S2): 143-145. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JIAN2013S2037.htm
[14] 靖洪文, 吴俊浩, 马波, 等. 基于模糊灰色系统的深部巷道围岩变形预测模型及应用[J]. 煤炭学报, 2012, 37(7): 1099-1104. JING Hongwen, WU Junhao, MA Bo, et al. Prediction model and its application of deep mine tunnel surrounding rock deformation based on fuzzy-gray system[J]. Journal of China Coal Society, 2012, 37(7): 1099-1104. (in Chinese)
[15] ZHANG L, SHI B, ZHU H H, et al. PSO-SVM-based deep displacement prediction of Majiagou landslide considering the deformation hysteresis effect[J]. Landslides, 2021, 18(1): 179-193.
[16] 朱宝强, 王述红, 张泽, 等. 基于时间序列与DEGWO-SVR模型的隧道变形预测方法[J]. 浙江大学学报(工学版), 2021, 55(12): 2275-2285. https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC202112007.htm ZHU Baoqiang, WANG Shuhong, ZHANG Ze, et al. Prediction method of tunnel deformation based on time series and DEGWO-SVR model[J]. Journal of Zhejiang University (Engineering Science), 2021, 55(12): 2275-2285. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZDZC202112007.htm
[17] YANG B B, YIN K L, LACASSE S, et al. Time series analysis and long short-term memory neural network to predict landslide displacement[J]. Landslides, 2019, 16(4): 677-694.
[18] XU S L, NIU R Q. Displacement prediction of Baijiabao landslide based on empirical mode decomposition and long short-term memory neural network in Three Gorges area, China[J]. Computers and Geosciences, 2018, 111(1): 87-96. doi: 10.1016/j.cageo.2017.10.013
[19] XUE J K, SHEN B. A novel swarm intelligence optimization approach: sparrow search algorithm[J]. Systems Science & Control Engineering, 2020, 8(1): 22-34.
[20] 滕志军, 吕金玲, 郭力文, 等. 一种基于Tent映射的混合灰狼优化的改进算法[J]. 哈尔滨工业大学学报, 2018, 50(11): 40-49. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX201811007.htm TENG Zhijun, LV Ji-ling, GUO Liwen, et al. An improved hybrid grey wolf optimization algorithm based on Tent mapping[J]. Journal of Harbin Institute of Technology, 2018, 50(11): 40-49. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX201811007.htm
[21] 王培珍, 刘曼, 王高, 等. 基于改进极限学习机的焦煤惰质组分类方法[J]. 煤炭学报, 2020, 45(9): 3262-3268. WANG Peizhen, LIU Man, WANG Gao, et al. Classification approach for inertinite of coking coal based on an improved extreme learning machine[J]. Journal of China Coal Society, 2020, 45(9): 3262-3268. (in Chinese)
[22] 罗亦泳, 黄城, 张静影. 基于变分模态分解的变形监测数据去噪方法[J]. 武汉大学学报(信息科学版), 2020, 45(5): 784-790. LUO Yiyong, HUANG Cheng, ZHANG Jingying. Denoising method of deformation monitoring data based on variational mode decomposition[J]. Geomatics and Information Science of Wuhan University, 2020, 45(5): 784-790. (in Chinese)
[23] 张霄. 基于改进极限学习机的隧道围岩位移反分析[D]. 成都: 西南交通大学, 2017. ZHANG Xiao. Displacement Back Analysis of Tunnel Surrounding Rock Based on Improved Limit Learning Machine[D]. Chengdu: Southwest Jiaotong University, 2017. (in Chinese)
[24] 公路隧道施工技术规范: JTG/T 3660—2020[S]. 北京: 人民交通出版社, 2020. Technical Specifications for Construction of Highway Tunnel: JTG/T 3660—2020[S]. Beijing: China Communications Press, 2020. (in Chinese)
[25] 王述红, 朱宝强. 山岭隧道洞口段地表沉降时序预测研究[J]. 岩土工程学报, 2021, 43(5): 813-821. http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18612.shtml WANG Shuhong, ZHU Baoqiang. Time series prediction for ground settlement in portal section of mountain tunnels[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(5): 813-821. (in Chinese) http://manu31.magtech.com.cn/Jwk_ytgcxb/CN/abstract/abstract18612.shtml
-
期刊类型引用(11)
1. 王伊立，丁景花，马力骏. 基于SSA-ENN神经网络的软岩隧道围岩变形预测模型. 广州建筑. 2025(01): 19-22 . 
百度学术
2. 张林清. 基于指数平滑法的隧道围岩变形预测研究. 施工技术(中英文). 2025(04): 54-59+94 . 百度学术
3. 刘俭. 山岭隧道围岩稳定性分析及管棚支护优化研究. 施工技术(中英文). 2025(04): 67-73 . 百度学术
4. 肖时辉，王峰，何柏延，徐国元，黄伟真，李伟鹏. 基于LHS-WOA-ELM的隧道围岩参数反演分析. 矿业研究与开发. 2025(03): 91-100 . 百度学术
5. 周杜，杨遵俭，刘运雄，贺亚青，罗泽毅. 引水隧洞不良地质段超前地质预报技术及应用. 山东交通科技. 2024(04): 108-112 . 百度学术
6. 李成辉. CNN-LSTM组合模型在隧道衬砌变形预测中的应用. 国防交通工程与技术. 2024(06): 35-40 . 百度学术
7. 范明辉，杨普新，李薇，任文渊，马驰骋. 高性能混凝土的早期抗压强度预测和极值寻优. 硅酸盐通报. 2024(12): 4339-4349 . 百度学术
8. 王浩宇，李鹏飞，聂鼎. 水工隧洞衬砌混凝土多尺度开裂机理及防裂技术研究进展. 重庆交通大学学报(自然科学版). 2024(12): 27-40 . 百度学术
9. 易铭，李军，王浩，傅鹤林，易海东. 来米坡连拱隧道洞身围岩扰动与变形控制研究. 交通科学与工程. 2024(06): 25-33 . 百度学术
10. 杨春山，杨雪强，王雅甜，林永贵. 建筑敏感区隧道破除抗滑桩进洞转换体系设计与施工方案优选. 现代隧道技术. 2023(06): 220-227 . 百度学术
11. 曾淑珍. 输水隧洞开挖过程中围岩受力变形分析. 水利科技与经济. 2023(12): 60-63 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 340
- HTML全文浏览量: 56
- PDF下载量: 101
- 被引次数: 15
