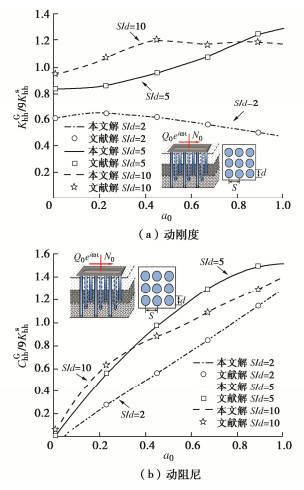
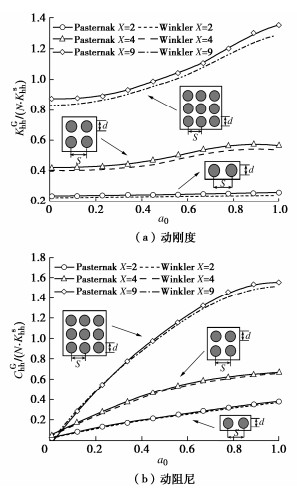
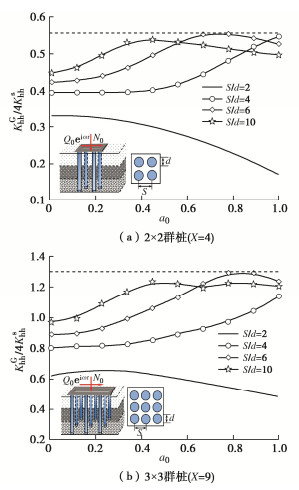
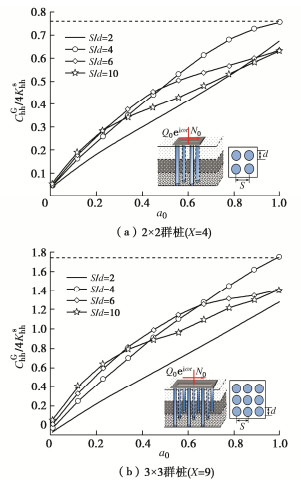
Analytical solutions for horizontal dynamic response for pile groups based on Pasternak model
-
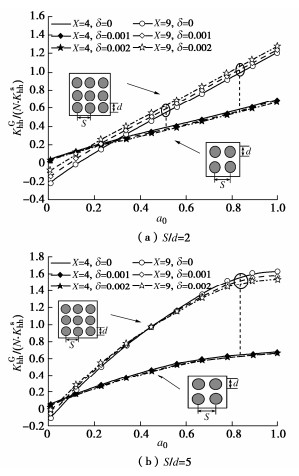
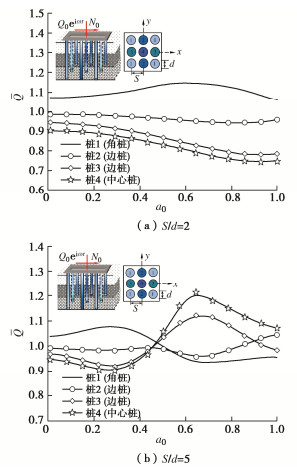
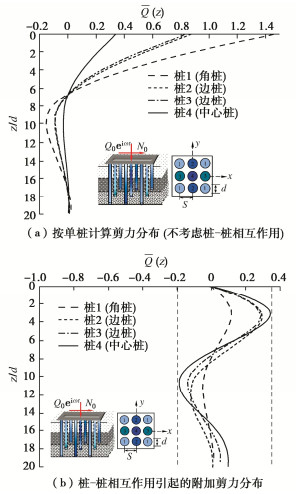
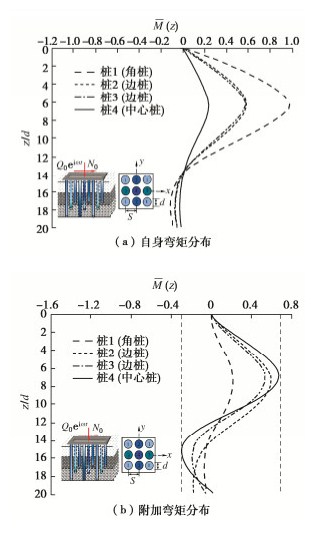
摘要: 基于Pasternak地基和Euler梁振动理论,提出了一种能考虑轴向荷载影响的单桩水平振动简化分析力学模型,建立了层状地基中桩-土耦合作用下单桩水平振动控制方程;采用微分变换的方法对方程解耦,进一步结合桩-土边界连续条件求出单桩水平位移、转角及内力解析解答。然后,考虑主动桩Ⅰ振动引起被动桩Ⅱ的动态位移,建立被动桩Ⅱ的水平振动控制方程,求解得到被动桩Ⅱ的响应解析解答,依据动力相互作用因子定义进一步求得桩-桩水平动力相互作用因子。最后,利用叠加原理求得群桩水平动力阻抗,并与已有相关解析解进行退化对比验证其合理性。在此基础上,通过参数化分析探讨了地基剪切系数、布桩类型、桩距径比、轴向特征参数对群桩水平阻抗以及桩顶反力分布、桩身内力分布的影响规律,可为实际工程群桩桩基设计提供理论指导和参考作用。
-
关键词:
- 群桩 /
- 动力阻抗 /
- 水平振动 /
- 桩-桩动力相互作用 /
- Pasternak地基
Abstract: A simplified model for a single pile is established based on the Pasternak foundation and Euler beam models considering the axial second-order effects of pile shaft. The corresponding analytical solutions are derived by utilizing the differential transformation methods and the double-shear theory as well as the pile-soil continuity conditions. Then, considering the dynamic displacement of receiver pile Ⅱ caused by the vibration of source pile Ⅰ, the control equation for horizontal vibration of receiver pile Ⅱ is established, and the analytical solutions for the response of receiver pile Ⅱ are obtained. According to the definition of dynamic interaction factor, the pile-pile horizontal dynamic interaction factor is further obtained. Finally, the superposition principle is used to solve the horizontal dynamic impedance of pile groups, and its rationality is verified by comparing with the existing analytical solutions. On this basis, the influences of soil shear coefficient, pile type, pile to diameter ratio and axial feature parameters on the horizontal impedance of pile groups are discussed through the parametric analysis, and the distribution of the reaction force at the top of the pile and the distribution of the internal force of the pile body are discussed. It may provide theoretical guidance and reference for the design of pile groups in practical engineering. -
0. 引言
土壤液化是国际上具有普遍意义的典型震害现象,是土木工程防灾减灾中的复杂难题之一。真实场地的液化响应规律及特征,仍是当今液化研究中没有解决好的突出问题之一,尚需深入研究[1]。
试验是液化研究中不可或缺的手段。然而,迄今尚没有一种试验,能够完全复现真实场地的液化响应过程及行为特征。室内液化试验,具有大量且突出的优点。可是,无论动三轴等土单元试验,还是振动台或动力离心机等模型试验,目前都不能同时、全面地对可液化土所处的现场条件和影响因素进行模拟,与真实液化场地存在差距。作为室内试验的一种补充,直接开展现场液化试验或现场液化监测,逐渐成为当今土壤液化研究的必需手段[2]。采用室内和现场液化试验两种不同的研究手段,通过不断地“相互对比、验证、补充”,可以进一步完善、修正当前的液化分析方法。
相比室内液化试验方面的丰富成果,人工激振下现场液化试验的研究成果尚少,目前国际上总体处于探索阶段[2]。中国虽有现场液化试验方面的研究成果并取得一些开创性的进展[3-7],但是总体仍处于起步阶段,亟待进一步发展。
值得注意的是,目前国内外已有的人工激振下现场液化试验,无论是基于原状土还是重塑土,可液化土的上覆压力基本不超过20 kPa,绝大多数在10 kPa以内,大致对应1~2 m的土层埋深。根据对1962—2010年中国大陆地区地震液化实例的统计,液化土层的埋深集中在0~6 m,约占总数的80%,其中2~4 m最为集中。而其地下水位埋深集中在0~3 m,约占总数的90%,其中1~2 m最为集中[8]。以此粗略推算,真实地震中液化土层所对应的上覆压力范围应集中在0~120 kPa,最为集中的均值约50 kPa左右。众所周知,上覆压力(或埋深)是控制土壤液化响应的主要因素之一。显然,当今开展的现场液化试验中可液化土的上覆压力较低,与真实液化场地存在较大差距。而且,由于试验操作的扰动,有效围压50 kPa以下的室内土单元试验成果相对很少。这也导致了已有现场液化试验成果难以和室内液化试验,尤其是动三轴等土单元试验,在相近的动、静应力水平下进行对比分析。可以说,过低的上覆压力,使得目前通过现场液化试验研究土壤液化问题的价值大打折扣。
现有的振动台或动力离心机液化试验中,模型土的上覆压力和真实液化场地也会存在差距,往往通过堆载重物的方式来改善[9-10]。动力离心机试验,当应力水平无法满足时,在ng重力环境下,采用比土的密度大几倍的材料(如钢材)作为堆载重物,通过较小的堆载高度就会达到理想效果。然而,在振动台或现场试验等1g重力环境下,当所需上覆压力较大时,通过堆载重物的方式并不理想,甚至不可行。毕竟,试验中堆载重物的高度不可能无限制增加,而且实际加压效果、可操作性等都会遇到问题。若采用传统的“千斤顶+反力架”的方式,似乎非常容易实现对模型土施加上覆压力,且能完全满足液化试验需求的压力上限值。然而,对于液化试验而言,这种传统的加压方式并不可行。因为液化发生前,土体一定会率先出现沉降变形,微小的沉降都会导致通过千斤顶施加的荷载无法传递,造成上覆压力“瞬间消失”。因此,需专门发展试验技术,才能开展考虑上覆压力影响的现场液化试验。
鉴于此,笔者在已有现场液化试验研究基础上[6-7],围绕能够开展“多工况、可重复、易操作、低成本”试验的基本设想,专门研制施加上覆压力的设备,发展考虑上覆压力影响的现场液化试验技术,设计完成2次不同上覆压力(25,50 kPa)的饱和砂、干砂对比试验,分析其动力响应规律及特征,并与已有认识对比,验证试验技术的可靠性。本文研究成果,可为当今人工激振下现场液化试验的发展提供技术借鉴,也为在1g重力环境下,以更接近真实场地的模拟条件开展土壤液化问题研究,提供一种简单实用、可操作性强的试验新方法。
1. 试验孔压比的概念
为评价考虑上覆压力影响的现场液化试验是否成功实施,本文首先提出试验孔压比的概念,并阐述其必要性和合理依据。
由于现场液化试验是在1g重力环境下进行,上覆压力必须通过特定技术手段施加给试验土体。在动荷载开始前,预先施加给土体的上覆压力能够较容易地保持平稳和恒定状态。但是,在动荷载作用下,人为施加的上覆压力会发生很大变化,尤其是采用机械设备以“接触力传递”方式施加的上覆压力。理论上,液化的土体会软化和变形,通过机械设备一直维持初始施加的上覆压力的平稳,几乎不可能,因为液化的土体无法提供良好的反力支撑。但是,在液化发展阶段,尤其是超静孔压急剧上升时,如果预先施加的上覆压力下降(损失)过快、过大,则必然会对现场液化试验结果产生较大影响,甚至失去考虑和控制上覆压力的意义。因此,在现场液化试验中,施加给土体的上覆压力应保持大致的稳定。只有预先施加的上覆压力损失有限,以此得到的现场液化试验结果才有价值。而且,需要对现场液化试验中上覆压力的损失程度,进行定量评价和判断。
一方面,根据已有试验结果和液化认识,当孔压比达到0.4~0.6左右,是液化变形及对地震动产生影响等动力响应特征的阈值[6, 11-12]。另一方面,从液化机理上,当土壤液化的条件均能充分满足时,超静残余孔压的发展是不可能大于其上覆压力的。也就是说,如果设备预先施加的上覆压力下降(损失)过快、过大,超静孔压一定不会发展过高。
因此,在土壤液化的条件均能满足的情况下,只要现场液化试验中的超静孔压与预先施加的初始上覆压力的最大比值能够达到0.4~0.6及以上,就可获取该上覆压力作用下土壤液化的主要响应特征。本文将该最大比值,定义为试验孔压比,以区别通常描述液化特征的孔压比。因此,试验孔压比,可初步判断预先施加的上覆压力是否大致稳定,从而评价可考虑上覆压力影响的现场液化试验是否成功实施(有价值)。
当然,当土体抗液化强度较高或动荷载较小时,液化发展程度本身有限,就不会发生较大的土体软化或变形,预先施加的上覆压力自然也会保持较平稳状态。此时,则无需采用试验孔压比进行评价。
2. 试验设计
2.1 试验材料
本文现场液化试验,所用的砂土全部采用福建标准砂。通过室内土工试验实测,其物理指标如表 1所示,其颗粒级配曲线如图 1所示。
表 1 试验砂物理指标Table 1. Physical indexes of sands used in tests最大干密度ρdmax/(g·cm-3) 最小干密度ρdmin/(g·cm-3) 有效粒径d10/mm 特征粒径d30/mm 控制粒径d60/mm 不均匀系数Cu 1.953 1.538 0.309 0.475 0.889 2.877 2.2 试验设备
本文现场液化试验所用的动力加载设备,与笔者以往开展的现场液化试验相同[6-7]。该设备是自主研发,主要有由激振装置、刚体基础、变频控制器、电动机等组成,能在试验场地中激励产生水平向的等幅正弦波地震动。加速度传感器型号为LC0113M,量程±2g,灵敏度2500 mv/g左右。孔压传感器型号为HC-25,量程0~50 kPa,灵敏度0.2%FS;土压力传感器型号HC-16,量程0~150 kPa,灵敏度0.2%FS。位移传感器型号为HCW-20,量程0~15 cm,灵敏度0.1%FS。动态数据采集设备,采用日本东京测器研究所生产的TMR多功能记录仪,最高数据采样率可达100 kHz。部分试验设备及传感器如图 2所示。由图可知,所用的加速度、孔压、土压力传感器体积小,能够满足土体“点测量”的基本要求。
施加上覆压力的设备,是本文现场液化试验能否成功实施的关键硬件。笔者自主研发了适用于现场液化试验的施加上覆压力的设备。该设备主要由钢筋混凝土反力架、液压千斤顶、加载钢板及持压装置组成,其示意图及现场实景如图 3所示。该设备,是在传统的“反力架+千斤顶”模式的基础上,增加了自主研发的持压装置,解决了因土体沉降导致上覆压力“瞬间消失”的问题。持压装置的工作原理,是通过合理刚度的弹簧的回弹来补偿沉降,从而实现“伺服”控制。通过该设备,现场液化试验所需的上覆压力,不但可以被定量施加,而且能够在液化发展阶段保持大致稳定的状态。该设备是无源工作,操作简单,尤其适合野外试验环境。
2.3 试验方案
本文试验的主要目的,是在已有重塑土现场液化试验基础上,围绕“多工况、可重复、易操作、低成本”的基本设想,发展考虑上覆压力影响的现场液化试验技术并验证其可靠性。考虑到本文试验的探索性,并为后续针对性地开展具体液化问题的研究奠定认识基础,本次试验方案设计遵循以下基本原则:①设置同工况的干砂试验,作为对比参照;②仅把上覆压力作为试验变量,其他影响液化因素暂不考虑。如前文所述,考虑当前上覆压力基本现状,优先设计上覆压力分别为25,50 kPa的两次工况的现场液化试验。
基于上述设想,在试验场地直接开挖2个相同尺寸的试坑,然后在坑内分别制备干砂、饱和砂。人工激励产生的水平向震动,通过刚体基础周围的土层传递,以“地震动”的形式直接对试坑内的砂土施加动荷载,因此不存在振动台试验的动力边界效应问题。由于试坑尺寸的大小不会对试验技术可行性产生实质影响,经综合考虑,试坑的尺寸确定为40 cm×40 cm×50 cm。试坑和刚体基础的空间相对位置关系如图 4所示。
本文设计试坑内砂土的初始相对密实度Dr为40%。砂土的制备技术及操作方法,与笔者之前进行的现场液化试验相同[6-7]。饱和砂,仍采用水沉法制备,其内部的传感器布置方案如图 5所示。干砂内部,除不放置孔压传感器外,其他布置均与饱和砂相同。考虑到试验的探索性,砂土内部的传感器均采用“备份”原则布置。即在砂土中心和左边的不同深度测点,逐一对应,布置相同类型的传感器。在干砂试坑一侧的地表,与砂土表面中心对应(均距离基础边缘70 cm),单独埋设1个加速度传感器,其实测加速度作为试验的输入地震动。位移传感器固定于反力架上端,通过加载钢板来测量砂土的地表沉降。
为表述方便,本文上覆压力为25 kPa工况的试验命名为Test-L试验,上覆压力为50 kPa工况的试验命名为Test-H试验。实际中,施加至设计上覆压力后,砂土均有一定程度的沉降。根据沉降值估算,在Test-L试验中,干砂的密实度变为49%,饱和砂密实度变为46%。在Test-H试验中,干砂的密实度为54%,饱和砂变为50%。砂土密实度的变化程度,均在可接受的范围。动荷载频率,与笔者之前的现场液化试验相同,仍为15 Hz。输入地震动的加速度幅值为0.11g左右,数据采样频率为100 Hz。两个工况现场试验分别加载。
3. 试验结果分析与讨论
3.1 试验结果概述
根据笔者观察,加载期间,无论Test-L试验,还是Test-H试验,饱和砂土均出现明显的喷砂冒水现象。图 6为Test-H试验后的饱和砂土表面实景,可以看出大量的砂堆积在加载钢板的一角,是加载期间喷出。相比笔者以前的现场液化试验,本文试验中饱和砂土的喷水高度、喷砂量均有大幅增加。这应该是,较大的上覆压力,导致砂土液化时超静孔压明显升高的结果。试验宏观现象初步表明,两次现场液化试验均取得了成功。加载期间,除去Test-L试验干砂中的土压力时程数据因电源线意外故障导致采集失败外,其他测点均成功采集到了数据。
3.2 输入加速度
图 7分别给出了两个工况现场试验中试坑外侧的地表加速度时程。经对比,试坑内砂土底部的加速度与其一致,限于篇幅不再给出,并将该数据视为试验的地震动输入加速度。可以看出,两次试验的输入加速度的幅值几乎一致,均在0.11g~0.12g左右。
3.3 超静孔压响应
超静孔压是液化发展程度最直接的反映和标志。由于试坑内饱和砂土中的孔压传感器距离真实地表仅15 cm,如前文所述,倘若没有额外施加的上覆压力,超静的残余孔压是不可能超过1.5 kPa的(即大致15 cm高度饱和砂的有效自重)。图 8给出了两次现场液化试验饱和砂中心测点的超静孔压时程。结合图 7的地表加速度时程可知,在地震动开始的最初3 s内(约45个荷载循环),超静孔压迅速发展并达到最大值,之后孔压开始逐渐消散,这与以往的现场液化试验孔压响应规律和认识一致[6-7]。所不同的是,超静孔压到达最大值后,便表现为消散趋势且速率较快,这应该与实际排水路径过短(此处仅15 cm)有关。从图 8中可以看出,Test-L试验中超静孔压的最大值约为17 kPa,与其初始上覆压力23 kPa的比值,即试验孔压比,为0.75。Test-H试验中超静孔压的最大值约为25 kPa,与初始上覆压力50 kPa的比值为0.5。超静孔压的响应表明,现场液化试验中,设备施加给饱和砂的上覆压力能够保持大致稳定。这也说明两次现场液化试验均是成功的,可以结合土压力、地表沉降等响应做进一步分析。
另外,从理论角度,上覆压力是影响液化响应的重要因素。相比Test-L试验,在相同的加速度幅值(0.11g左右)和相对密度(50%左右)下,Test-H试验中的试验孔压比相对较小,应该还与饱和砂本身的上覆压力过大(50 kPa)有较大关系。后文,结合上覆压力的响应,这点也被证实。为后续分析需要,图 9分别给出两次现场液化试验中饱和砂中心和左边测点的超静孔压时程。为图示清晰,仅保留残余孔压。由图 9可知,同一工况试验中,两测点的孔压时程几乎完全一致。
3.4 土压(上覆压力)与孔压响应
砂土中的上覆压力通过土压传感器实测得到。上覆压力,是本文试验非常关心的问题,直接关系试验技术的可行性,进行重点分析。
图 10给出了两次现场试验的砂土中心和左边测点的土压力时程,也即上覆压力时程。低上覆压力工况Test-L试验中,因未能成功采集到加载期间的干砂的土压力时程数据,故无法给出。根据试验记录,加载前,Test-L试验干砂中心和左边测点实测上覆压力分别为23,20 kPa。从图 10可以看出,饱和砂中心和左边测点的上覆压力为25,21 kPa,两者基本一致。在高上覆压力工况Test-H试验中,干砂中心和左边测点的上覆压力分别为60,40 kPa,对应的饱和砂上覆压力约为61,42 kPa,中心和左边测点的上覆压力值差别较大。
砂土的上覆压力,是由液压千斤顶通过加载钢板中心位置施加给砂土。笔者分析认为,中心和边侧压力值差别较大,主要原因应是加载板的刚度不够大导致了应力集中。只是荷载较小的情况下,加载板的刚度影响尚不明显。从理论角度,施加的上覆压力越大时,加载板的受力就越接近于点荷载模式。根据弹性力学的Boussinesq解答,砂土中应力分布的规律就应该是中间大,两侧小。定性上,实测结果与理论解答相符。由于土压力、孔压传感器体积很小,能够实现“点”测量,上覆压力和孔压均可实测得到,因此考虑上覆压力对液化响应的影响时,可以做到精确分析。基于简化考虑,本文施加上覆压力时,将中心和左边测点的上覆压力平均值视为最终的上覆压力。实际中,Test-L试验干砂、饱和砂的最终上覆压力分别为22,23 kPa,Test-H试验干砂、饱和砂的最终上覆压力分别为50,51 kPa,达到试验设计预期。
为更好地分析上覆压力响应,略去实测数值的动态波动,并同时给出孔压比时程,如图 11所示,并将孔压急剧上升阶段前后的5~6 s时程详细给出。图 11给出的孔压比是每一时刻的残余孔压与对应的平均上覆压力的比值,这与通常液化分析中的孔压比的概念完全一致。
从图 11可以看出,地震动开始时(两次试验的时程上分别为20.5,13.0 s处),上覆压力均有短暂的小幅度增加,推测仍与加载钢板刚度不够大引起的弹性回弹有关。在动荷载作用下,干砂只会发生沉降,不存在土体软化问题。从其上覆压力响应可以看出,在整个加载过程中,Test-H试验中干砂的平均上覆压力缓慢下降,最终从50 kPa下降至40 kPa左右,而且中心和左边测点处的上覆压力下降趋势和程度基本一致。根据试验记录,Test-L试验中干砂的平均上覆压力,最终从22 kPa下降至14 kPa左右。干砂的上覆压力响应表明,施加上覆压力设备的工作性能是较为理想的。相比之下,饱和砂的上覆压力,随着超静孔压的急剧上升和土体软化,在短时间内出现了较为明显的下降,尤其是饱和砂的中心测点处。对于液化试验,重点关注孔压急剧上升阶段。当超静孔压发展到最大值时,Test-L试验中的平均上覆压力从23 kPa跌至18 kPa左右,孔压比最大值约为0.85;Test-H试验中的平均上覆压力从51 kPa跌至35 kPa左右,孔压比最大值约为0.68。由于Test-L和Test-H工况试验中,仅存在上覆压力上的差别,即使考虑加载期间上覆压力的下降,从图 11中可知,当孔压比发展到最大时,Test-H试验中的上覆压力最低值也大于Test-L试验中的初始上覆压力。因此,这充分说明,Test-H试验中孔压发展程度较低(即孔压比相对较小),是上覆压力较高导致。也就是说,Test-H试验中的试验孔压比虽然为0.5,若在更大幅值的加速度作用下,还会增大的。这也表明,其他条件相同时,上覆压力越大,饱和砂的抗液化强度越高,这与目前对液化的理论认识和实际震害调查结果一致。
由图 11还可以看出,同一工况试验中,饱和砂中心和左边测点的上覆压力响应不同,在初始压力值、下降程度两方面均有差异。尤其是,在孔压上升阶段,中心测点处上覆压力的下降程度明显大于左边测点,这应该与边侧的饱和砂受到非液化土的约束有关。为进一步分析上覆压力对液化响应的影响,将两测点处的孔压比分别计算,即为该测点处每一时刻的残余孔压与对应的上覆压力的比值,如图 12所示。为了图示清晰,仅给出孔压急剧上升阶段前后的5 s时程。由图 12可知,Test-L试验饱和砂中心和左边测点的最大孔压比分别为1和0.7,Test-H试验饱和砂中心和左边测点的最大孔压比分别为0.75和0.6。Test-L试验中,砂土中心测点处的孔压比为1,这说明此处的砂土已经完全液化。
值得注意的是,Test-L和Test-H工况试验中,两者上覆压力的差别本身并不大,仅有25 kPa,但是在地震动加速度幅值0.11g下,饱和砂的液化程度(孔压比)却有较大差异。而且,对于同一工况试验而言,饱和砂中心和两侧的液化发展程度也不一样。从图 12中也可看到,Test-L和Test-H试验中,中心和左边测点的孔压比时程曲线均存在交叉现象。由此可知,液化发展初期(边侧上覆压力较小),边侧的孔压比是大于中心处的,随着发展(边侧上覆压力变大),边侧的孔压比是小于中心处的。这说明,在此工况条件下,上覆压力对液化的影响较为明显。尤其值得注意的是,Test-L工况试验中,中心和左侧处的上覆压力差值仅有4 kPa(相当于40 cm厚的饱和土层),但是时程曲线上仍表现出交叉现象,定性上的响应规律与Test-H工况是一致的。这更表明,在上覆压力水平较低(至少50 kPa以下)时,上覆压力这一因素对液化响应的影响是敏感的。
上覆压力50 kPa,大致对应真实场地中埋深2.5~5 m土层的埋藏条件。可以说,真实地震中,普遍且大量存在着上覆压力为50 kPa及以下的液化场地。但是,目前液化研究中,上覆压力(有效围压)50 kPa以下的液化试验成果相对很少,很多问题尚缺乏清晰认识。而且,当前一些实用的液化分析方法,考虑埋深影响的修正,也多是以上覆压力(有效围压)100 kPa作为基准参照。因此,低上覆压力水平(0~50 kPa)下的液化响应问题,应需重视并进行深入探究。
3.5 地表沉降与孔压响应
本文现场液化试验的反力架是稳定可靠的固定端,因此能够方便、准确地获取整个加载期间的砂土地表沉降时程。
图 13给出了两次现场试验的砂土地表沉降位移和孔压比时程,并将孔压急剧上升阶段前后的5~6 s时程详细给出。从图 13中可以看出,无论Test-L试验还是Test-H试验中,孔压迅速发展阶段,饱和砂发生的地表沉降了约为3.5~4.5 mm,将该沉降值换算成体应变约为1%(砂土高度300 mm)。孔压刚开始发展(触发)时的沉降太小,实测的位移难以准确甄别,但是可以确定当地表沉降在0.3~0.5 mm时,即体应变约为0.1%时,孔压比发展到约0.1左右。由此可知,当体应变在0.1%以下时,孔压就已经开始发展。当体应变在0.1%~1%时,孔压快速地大幅度发展。本文得到的孔压与应变关系的定量结果,与笔者之前的现场液化结果基本一致[6],也与目前国际上普遍认同的Dobry等人有关应变与孔压关系的定量认识基本一致[13]。需说明的是,Dobry等试验结果的剪应变,是根据土样轴向应变,通过=(1+)的理论关系换算得到,其泊松比取为0.5。由于前面的系数仅为1.5,因此剪应变和侧限条件下体应变的量级不会发生变化。因此,定量认识上两者是一致的。这表明,本文试验中获取的地表沉降响应是可靠的,能够反映液化的主要变形特征,并可做进一步分析。
从图 13中还可以发现,地震动开始阶段,同等工况下的干砂、饱和砂的沉降量和沉降速率几乎完全一致。但是,当饱和砂的孔压比发展到0.6左右时,两者的沉降响应开始出现明显差异。此后一段时间,饱和砂的沉降量和沉降速率要明显小于同等工况下的干砂,这可能与饱和砂的超静孔隙水无法及时排出有较大关系,而干砂内的气体却能随时排出,从而表现出这种沉降差异现象。随着孔压的逐渐消散,饱和砂的沉降量和沉降速率明显增大,并最终大于干砂。由此可知,饱和砂液化后的沉降主要发生在孔压消散阶段。这一沉降规律,与他人的动力离心机液化试验一致,也与真实地震现场观察到的现象一致[14-15]。这也说明,本文现场液化试验,能够较理想地再现真实液化场地的地表沉降响应特征。
通过对宏观试验现象以及超静孔压、土压力(上覆压力)、地表沉降等响应的分析,并与已有的液化认识对比,本文设计完成的两个不同上覆压力工况的现场液化试验,均可得到液化的主要响应特征和规律,并能够以此获取新认识。这说明,本文提出的考虑上覆压力影响的现场液化试验技术,总体上是可行和可靠的,能够为在1g重力环境下,以更接近真实场地的模拟条件开展液化相关问题研究,提供一种可能的新手段。
4. 结论
本文在已有现场液化试验工作基础上,围绕“多工况、可重复、易操作、低成本”的基本设想,提出了一套考虑上覆压力影响的现场液化试验技术,设计完成了2次不同上覆压力(25,50 kPa)的饱和砂、干砂对比现场试验,分析了其动力响应规律及特征,并与已有认识对比,验证了试验技术的可靠性。主要得到以下3点结论。
(1)新提出的试验孔压比这一概念,可作为评价考虑上覆压力影响的现场液化试验是否成功的基本指标。两个工况的现场试验表明,新提出的考虑上覆压力影响的现场液化试验技术可行,能够得到土壤液化的主要响应特征。这为1g重力环境下,以更接近真实场地的模拟条件开展液化相关问题研究,提供了一种可能的新手段。
(2)在低上覆压力水平(0~50 kPa)下,大致对应真实场地0~5 m的埋深,上覆压力是影响土壤液化响应的敏感因素。实际地震中,普遍且大量存在上覆压力50 kPa及以下条件的液化场地,而目前与该静应力水平一致的液化研究成果并不丰富,相关认识也不清晰。低上覆压力水平(0~50 kPa)下的土壤液化响应问题,应需重视并进行深入探究。
(3)当饱和砂的体应变在0.1%以下时,孔压已经开始发展;当饱和砂体应变在0.1%~1%时,孔压迅速且大幅度发展。当孔压比发展到0.6左右时,同等工况下的干砂、饱和砂的地表沉降响应出现差异。并且,液化砂土的沉降主要发生在孔压消散阶段。
-
-
[1] KUO K A, HUNT H E M. Dynamic models of piled foundations[J]. Applied Mechanics Reviews, 2013, 65(3): 031003. doi: 10.1115/1.4024675
[2] ALLANI M, HOLEYMAN A. Numerical evaluation of effects of nonlinear lateral pile vibrations on nonlinear axial response of pile shaft[J]. Soils and Foundations, 2013, 53(3): 395-407. doi: 10.1016/j.sandf.2013.04.002
[3] 艾智勇, 李志雄. 冲刷作用下层状横观各向同性土中群桩水平振动响应[J]. 岩土工程学报, 2016, 38(4): 613-618. doi: 10.11779/CJGE201604004 AI Zhiyong, LI Zhixiong. Horizontal vibration of a pile group in transversely isotropic layered soils under scour conditions[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(4): 613-618. (in Chinese) doi: 10.11779/CJGE201604004
[4] POULOS H G. Analysis of the settlement of pile groups[J]. Géotechnique, 1968, 18(4): 449-471. doi: 10.1680/geot.1968.18.4.449
[5] LUAN L B, ZHENG C J, KOURETZIS G, et al. Development of a three-dimensional soil model for the dynamic analysis of end-bearing pile groups subjected to vertical loads[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2019, 43(9): 1784-1793. doi: 10.1002/nag.2932
[6] LUAN L, ZHENG C, KOURETZIS G, et al. Dynamic analysis of pile groups subjected to horizontal loads considering coupled pile-to-pile interaction[J]. Computers and Geotechnics, 2020, 117: 103276. doi: 10.1016/j.compgeo.2019.103276
[7] KAYNIA A M, KAUSEl E. Dynamic Stiffness and Seismic Response of Pile Groups[R]. Cambridge: Massachusetts Institute of Technology, 1982.
[8] MYLONAKIS G, GAZETAS G. Lateral vibration and internal forces of grouped piles in layered soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1999, 125(1): 16-25. doi: 10.1061/(ASCE)1090-0241(1999)125:1(16)
[9] 蒯行成, 沈蒲生. 层状介质中群桩水平动力阻抗的简化计算方法[J]. 振动工程学报, 1998, 11(3): 258-264. doi: 10.16385/j.cnki.issn.1004-4523.1998.03.002 KUAI Xingcheng, SHEN Pusheng. Simplified method for calculating horizontal dynamic impedances of pile groups in layered media[J]. Journal of Vibration Engineering, 1998, 11(3): 258-264. (in Chinese) doi: 10.16385/j.cnki.issn.1004-4523.1998.03.002
[10] 吴志明, 黄茂松, 吕丽芳. 桩-桩水平振动动力相互作用研究[J]. 岩土力学, 2007, 28(9): 1848-1855. doi: 10.3969/j.issn.1000-7598.2007.09.015 WU Zhiming, HUANG Maosong, LÜ Lifang. Research on pile-pile dynamic interaction of lateral vibration[J]. Rock and Soil Mechanics, 2007, 28(9): 1848-1855. (in Chinese) doi: 10.3969/j.issn.1000-7598.2007.09.015
[11] 黄茂松, 吴志明, 任青. 层状地基中群桩的水平振动特性[J]. 岩土工程学报, 2007, 29(1): 32-38. doi: 10.3321/j.issn:1000-4548.2007.01.005 HUANG Maosong, WU Zhiming, REN Qing. Lateral vibration of pile groups in layered soil[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(1): 32-38. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.01.005
[12] 高广运, 赵元一, 高盟, 等. 分层土中群桩水平动力阻抗的改进计算[J]. 岩土力学, 2010, 31(2): 509-515. doi: 10.3969/j.issn.1000-7598.2010.02.029 GAO Guangyun, ZHAO Yuanyi, GAO Meng, et al. Improved calculation for lateral dynamic impedance of pile groups in layered soil[J]. Rock and Soil Mechanics, 2010, 31(2): 509-515. (in Chinese) doi: 10.3969/j.issn.1000-7598.2010.02.029
[13] 黄茂松, 钟锐. 海上风机部分埋入群桩水平-摇摆振动与结构共振分析[J]. 岩土工程学报, 2014, 36(2): 286-294. doi: 10.11779/CJGE201402003 HUANG Maosong, ZHONG Rui. Coupled horizontal-rocking vibration of partially embedded pile groups and its effect on resonance of offshore wind turbine structures[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 286-294. (in Chinese) doi: 10.11779/CJGE201402003
[14] PASTERNAK P L. Fundamentals of a New Method of Analyzing Structures on an Elastic Foundation by Means of Two Foundation Constants[M]. Moscow: Gosudarstvennoe Izdatelstro Liberaturi Po Stroitelstvui Arkhitekture, 1954.
[15] YOKOYAMA T. Vibrations of Timoshenko beam-columns on two-parameter elastic foundations[J]. Earthquake Engineering & Structural Dynamics, 1991, 20(4): 355-370.
[16] FILIPICH C P, ROSALES M B. A further study about the behaviour of foundation piles and beams in a Winkler-Pasternak soil[J]. International Journal of Mechanical Sciences, 2002, 44(1): 21-36. doi: 10.1016/S0020-7403(01)00087-X
[17] ZHOU D, LO S H, AU F T K, et al. Three dimensional free vibration of thick circular plates on Pasternak foundation[J]. Journal of Sound and Vibration, 2006, 292 (3): 726-741.
[18] HIZAL C, CATAL H H. Rotary inertia and higher modes effect on the dynamic response of Timoshenko beams on two-parameter elastic foundation[J]. Teknik Dergi, 2019, 30(4): 9289-9308. doi: 10.18400/tekderg.408772
[19] 张治国, 徐晨, 宫剑飞. 考虑桩侧土体三维效应和地基剪切变形的隧道开挖对邻近桩基影响分析[J]. 岩土工程学报, 2016, 38(5): 846-856. doi: 10.11779/CJGE201605010 ZHANG Zhiguo, XU Chen, GONG Jianfei. Influence of tunneling on deflection of adjacent piles considering shearing deformation of foundation and 3D effects of lateral soils beside piles[J] Chinese Journal of Geotechnical Engineering, 2016, 38(5): 846-856. (in Chinese) doi: 10.11779/CJGE201605010
[20] WANG J, ZHOU D, LIU W. Horizontal impedance of pile groups considering shear behavior of multilayered soils[J]. Soils and Foundations, 2014, 54(5): 927-937. doi: 10.1016/j.sandf.2014.09.001
[21] WANG J, LO S H, ZHOU D. Effect of a forced harmonic vibration pile to its adjacent pile in layered elastic soil with double-shear model[J]. Soil Dynamics and Earthquake Engineering, 2014, 67: 54-65. doi: 10.1016/j.soildyn.2014.09.001
[22] VEGA-POSADA C A, GALLANT A P, AREIZA-HURTADO M. Simple approach for analysis of beam-column elements on homogeneous and non-homogeneous elastic soil[J]. Engineering Structures, 2020, 221: 111110. doi: 10.1016/j.engstruct.2020.111110
[23] HALABE U B. Lateral free vibration of a single pile with or without an axial load[J]. Journal of Sound and Vibration, 1996, 195(3): 531-544. doi: 10.1006/jsvi.1996.0443
[24] 熊辉, 尚守平. 轴、横向力作用下土-群桩动力效应简化分析[J]. 岩土力学, 2006, 27(12): 2163-2168. doi: 10.3969/j.issn.1000-7598.2006.12.015 XIONG Hui, SHANG Shouping. Simplified analysis of pile-group-soil effect under axial and horizontal interactive excitation[J]. Rock and Soil Mechanics, 2006, 27(12): 2163-2168. (in Chinese) doi: 10.3969/j.issn.1000-7598.2006.12.015
[25] 任青, 黄茂松, 韩东晓. 考虑轴力的部分埋入群桩基础水平振动特性[J]. 岩石力学与工程学报, 2011, 30(9): 1932-1944. REN Qing, HUANG Maosong, HAN Dongxiao. Lateral vibration properties of partially embedded pile groups foundation considering axial forces[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1932-1944. (in Chinese)
[26] 熊辉, 江雅丰, 禹荣霞. 层状地基中基于Laplace变换的桩基横向振动阻抗计算[J]. 岩土力学, 2018, 39(5): 1901-1907. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201805044.htm XIONG Hui, JIANG Yafeng, YU Rongxia. Lateral vibration impedance of piles embedded in layered soil based on Laplace transform[J]. Rock and Soil Mechanics, 2018, 39(5): 1901-1907. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201805044.htm
[27] JIANG J G, ZHOU X H, ZHANG J S. Dynamic interaction factor considering axial load[J]. Geotechnical and Geological Engineering, 2007, 25(4): 423-429.
-
期刊类型引用(1)
1. 梁越,李越,许彬,杨牛虎,张斌,潘剑,尹朝恒. 考虑围压影响的间断级配散粒土潜蚀规律试验研究. 河海大学学报(自然科学版). 2025(01): 80-86 .  百度学术
百度学术
其他类型引用(1)



 下载:
下载: