考虑钙质砂颗粒破碎的分数阶边界面本构模型

汪成贵; 束善治; 肖杨; 路德春; 刘汉龙

doi:10.11779/CJGE20220229

考虑钙质砂颗粒破碎的分数阶边界面本构模型 English Version

汪成贵^1,,
束善治²,
肖杨^{1, 3, 4, ,},
路德春⁵,
刘汉龙^{1, 3, 4}

1.
重庆大学土木工程学院, 重庆 400045
2.
Kiewit, 10055 Trainstation Circle, Lone Tree, CO 80124
3.
重庆大学山地城镇建设与新技术教育部重点实验室, 重庆 400045
4.
库区环境地质灾害防治国家地方联合工程研究中心, 重庆 400045
5.
北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124

基金项目:

国家自然科学基金项目 51922024

国家自然科学基金项目 52078085

详细信息

作者简介:
汪成贵(1993—)，男，博士研究生，主要从事粗粒土颗粒破碎、本构关系及数值计算方面研究。E-mail: cgwangic@163.com

通讯作者:
肖杨, E-mail: hhuxyanson@163.com

中图分类号: TU43
计量
- 文章访问数: 332
- HTML全文浏览量: 50
- PDF下载量: 99
出版历程
- 收稿日期: 2022-03-03
- 网络出版日期: 2023-06-07
- 刊出日期: 2023-05-31

Fractional-order bounding surface model considering breakage of calcareous sand

WANG Chenggui^1,,
SHU Shanzhi²,
XIAO Yang^{1, 3, 4, ,},
LU Dechun⁵,
LIU Hanlong^{1, 3, 4}

1.
School of Civil Engineering, Chongqing University, Chongqing 400045, China
2.
Kiewit, 10055 Trainstation Circle, Lone Tree, CO 80124, USA
3.
Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing University, Chongqing 400045, China
4.
National Joint Engineering Research Center of Geohazards Prevention in the Reservoir Areas, Chongqing 400045, China
5.
Key Lab of Urban Security and Disaster Engineering, Ministry of Education, Beijing University of Technology, Beijing 100124, China

摘要

摘要: 钙质砂作为海洋工程中广泛应用的建筑材料，颗粒破碎会导致其强度和剪胀性降低，压缩性增加，影响构筑物的安全和稳定。通过引入破碎应力建立考虑颗粒破碎的临界状态线来描述破碎对临界状态线位置和形状的影响；并基于分数阶微分和状态相关理论建立了统一的状态相关分数阶塑性流动法则；在边界面塑性理论和临界状态理论框架下建立了考虑钙质砂颗粒破碎和状态相关特性的分数阶塑性边界面本构模型。模型能够模拟不同初始密实度和围压条件下钙质砂三轴排水试验结果和颗粒破碎影响下的状态相关行为，并验证了模型的适用性。
- 钙质砂 /
- 颗粒破碎 /
- 状态相关 /
- 分数阶 /
- 本构模型
Abstract: The calcareous sand is widely used as the construction materials in marine engineering. Particle breakage will reduce the strength and dilatancy, and increase the compressibility, which affects the security and stability of the constructions. In this study, the influences of breakage on the position and shape of the critical state line are described by introducing the crushing stress. A unified state-dependent fractional plastic flow rule is established based on fractional differential and state-dependent theory. A fractional-order plasticity boundary surface constitutive model considering the particle breakage and state-dependent behavior of the calcareous sand is established under the framework of the boundary surface plasticity and the critical state theory. The model can simulate the drained triaxial test results of the calcareous sand under different initial densities and confining pressures and reflect the state-dependent behavior under the influences of the particle breakage, which verifies the applicability of the proposed model.
- calcareous sand /
- particle breakage /
- state-dependent behavior /
- fractional-order /
- constitutive model

HTML全文

0. 引言

软黏土地层盾构隧道不均匀沉降问题普遍^[1-2]，部分工程出现列车降速运行、停运加固等问题，严重影响列车运营安全及隧道结构服役寿命。下方地层注浆是盾构隧道过大沉降治理的常用技术手段。然而，注浆扰动地层产生超孔压，注浆结束后超孔压消散引起地基固结和隧道沉降，导致最终抬升量小于注浆过程中的抬升量峰值。例如，为调控上海地铁2号线某区间过大沉降，在隧道下方采取分阶段微扰动注浆，各注浆阶段结束后隧道均发生明显沉降，最终抬升量相比抬升量峰值减少53%^[3]。

目前，工程案例的注浆参数选取主要依赖经验，缺乏定量预测方法。例如，上海地铁2号线盾构隧道下卧地层注浆最大抬升量为10 mm，隧道抬升量与总注浆体积的比值大约为1︰40 mm/L^[4]。盾构隧道注浆抬升过程本质上是注浆使隧道下卧地层隆起，产生竖向抬升力，进而导致隧道抬升。根据地层-隧道相互作用的两阶段分析方法^[5-6]，该过程隧道抬升量与地层隆起变形和基床系数相关。同时，软黏土地层注浆引起的超孔隙水压力分布与土体结构性密切相关。例如，刘维正等^[7]利用考虑软黏土结构性损伤的柱孔扩张模型开展分析，结果表明：土体结构性越强，柱形孔孔壁处的超孔压越大且沿径向衰减越快。因此，考虑到不同地区软黏土在基床系数和结构性相关参数（如灵敏度和屈服应力比）等影响注浆抬升效率方面存在较大差别，各地区经验很难适用其他地区。除此之外，目前鲜有下方注浆引起的隧道抬升-沉降计算方法。付艳斌等^[8]假定隧道侧下方注浆体为圆柱体，将圆形隧道通过面积等效为正方形，建立了盾构隧道注浆抬升量计算模型，但并未考虑注浆后地基固结沉降引起的隧道再沉降。因此，有必要提出软黏土地层注浆引起的上覆盾构隧道抬升量与沉降量计算方法，探明影响盾构隧道抬升效率的主要因素，为软黏土地层盾构隧道的注浆抬升提供参数支撑。

针对软黏土地层盾构隧道注浆抬升问题，综合运用源汇法、圆柱孔扩张理论和隧道-地层相互作用理论，提出了盾构隧道底部注浆抬升量-沉降量两阶段计算方法，并应用于实际案例。通过参数分析，探讨了注浆参数、地层参数与隧道参数对盾构隧道注浆抬升效率的影响规律。研究成果可以为软黏土地层盾构隧道注浆抬升预测与控制技术提供支撑。

1. 计算方法

软黏土地层盾构隧道底部注浆竖向位移发展呈现两个阶段（）：①注浆过程隧道抬升。软黏土渗透系数低，注浆挤压地层引起的周围地层变形可以认为满足不排水条件。②注浆后隧道沉降。注浆过程会导致周围土体产生超孔压，注浆后超孔压消散引起隧道下卧地基固结沉降，进而导致隧道沉降。因此，本文将盾构隧道底部注浆最终抬升量 $\Delta \delta$ 分为两个部分进行计算，即先根据注浆引起的体积膨胀计算注浆过程隧道抬升量 $\Delta {\delta _1}$ ，再根据注浆引起的地层超孔压计算注浆后的隧道沉降量 $\Delta {\delta _2}$ 。隧道最终量为 $\Delta \delta$ = $\Delta {\delta _1}$ − $\Delta {\delta _2}$ ，抬升效率η为 $\Delta \delta$ / $\Delta {\delta _1}$ 。

图 1 盾构隧道底部注浆抬升-沉降演化过程示意图

Figure 1. Schematic of evolution process of grouting-induced uplift and settlement of overlying shield tunnel

下载: 全尺寸图片幻灯片

1.1 注浆过程盾构隧道抬升量 $\Delta {\delta _1}$ 计算方法

针对注浆抬升过程较短的工况，注浆过程地层响应满足不排水条件，利用源汇法^[9]计算注浆作用下隧道底部自由场地层的纵向变形，其中注浆体简化为若干个等直径球体膨胀的线性叠加（图 2）。需注意的是，本方法不适用于隧道注浆抬升过程较长的情况。然后，基于文克尔地基上的隧道铁木辛柯梁模型^[1]，建立注浆过程隧道底部附加应力及抬升量的计算公式，通过有限差分法求解。本方法主要计算流程如图 3所示。

图 2 注浆过程隧道抬升量计算模型

Figure 2. Theoretical model for calculating tunnel uplift during underlying grouting

下载: 全尺寸图片幻灯片

图 3 注浆过程盾构隧道抬升量计算流程

Figure 3. Calculation process of uplift of shield tunnel during underlying grouting

下载: 全尺寸图片幻灯片

（1）基本假定

a）土体为半无限空间中各向同性的线弹性体，注浆过程土体响应满足不排水条件。

b）注浆方式为囊袋注浆对应的理想压密注浆，注浆体为圆柱体，浆液不会在土体中发生劈裂，不考虑浆液凝固引起的体积变化，每个注浆体由若干半径相等的子球体叠加而成（图 2）。

c）盾构隧道简化为文克尔地基模型上的一维均质铁木辛柯梁模型，隧道纵向附加应力和变形计算均针对隧道底部。

d）隧道纵向附加应力计算采用的地层变形为注浆引起的隧道拱底位置地层隆起量，附加应力沿纵向分布呈现非均匀性。

（2）自由场土体位移

Segaseta^[9]利用镜像原理，提出了半无限空间中由于地层损失引起任意一点土体位移的计算公式，称为源汇法。该方法被广泛应用于不排水条件下基坑围护墙后地层变形计算^[10]。同时，Segaseta^[9]还提出引入负的地层损失可以计算非渗透材料的膨胀，如本文的低渗透地层注浆问题，可以将隧底注浆简化为若干球体膨胀，进而得到隧底土体隆起变形：

$\begin{gathered} {S_z} = \frac{{{a^3}}}{3}\frac{{z - {z_0}}}{{{r_1}^3}} - \frac{{{a^3}}}{3}\frac{{z{\text{ + }}{z_0}}}{{{r_1}^3}}{\text{ + }}\mathop {\lim }\limits_{b \to \infty } \mathop {\lim }\limits_{c \to \infty } \int_{{y_0} - b}^{{y_0} + b} {\int_{{x_0} - c}^{{x_0} + c} {\frac{{{a^3}}}{\mathtt{π} } \cdot } } \hfill \\ \left\{ {\frac{{{z_0}(u - {x_0})(x - u)}}{{{{[{{(u - {x_0})}^2} + {{(t - {y_0})}^2} + {z_0}^2]}^{\frac{5}{2}}}}}\left[ {\frac{z}{{{R^3}}} + \frac{{1 - 2\mu }}{{R(R + z)}}} \right]{\text{ + }}} \right. \hfill \\ \left. {\frac{{{z_0}(t - {y_0})(y - t)}}{{{{[{{(u - {x_0})}^2} + {{(t - {y_0})}^2} + {z_0}^2]}^{\frac{5}{2}}}}}\left[ {\frac{z}{{{R^3}}} + \frac{{1 - 2\mu }}{{R(R + z)}}} \right]} \right\}dudt \text{，} \end{gathered}$

(1)

$\left.\begin{array}{l} r_1=\left[\left(x-x_0\right)^2+\left(y-y_0\right)^2+\left(z-z_0\right)^2\right]^{1 / 2}, \\ r_2=\left[\left(x-x_0\right)^2+\left(y-y_0\right)^2+\left(z+z_0\right)^2\right]^{1 / 2} ，\\ R=\left[(x-u)^2+(y-t)^2+z^2\right]^{1 / 2} 。 \end{array}\right\}$

(2)

式中：a为膨胀半径（m）；μ为土体泊松比；（x₀，y₀，z₀），（x，y，z）分别为膨胀点、计算点坐标；r₁，r₂，R为计算点与源点、像点、地面切应力积分点的距离（m）；S_z(x)为隧底土体隆起量（m）。

（3）隧道附加应力及隧道抬升

为简化计算，假定隧道上覆及下卧地层均被简化为文克尔地基模型。此外，考虑到隧道纵向长度远大于直径且纵向变形由弯曲变形和剪切变形共同组成，本文将盾构隧道简化为铁木辛柯梁模型^[11]。

注浆压力作用下受挤压土体会产生作用于隧道底部、竖直向上的抬升力，该附加应力q(x)为

$q(x) = {k_1}D{S_z}(x) 。$

(3)

式中：D为隧道外径（m）；k₁为下卧地层基床系数（kN/m³）。

已知q(x)后，隧道竖向变形w(x)的微分方程为

$(EI)'\frac{{{\text{d}^4}w(x)}}{{\text{d}{x^4}}} - \frac{{{k_2}D(EI)'}}{{({\text{κGA}})'}}\frac{{{\text{d}^2}w(x)}}{{\text{d}{x^2}}} + {k_2}Dw(x) \\ = q(x) - \frac{{(EI)'}}{{({\text{κGA}})'}}\frac{{{\text{d}^2}q(x)}}{{\text{d}{x^2}}}。$

(4)

式中：k₂为隧道上覆地层基床系数（kN/m³）； $(EI)'$ 为隧道纵向等效抗弯刚度（kN·m²）； $({\text{κGA}})'$ 为隧道等效剪切刚度（kN）。本文采用有限差分法求解。

（4）参数确定

本计算方法所需参数分为隧道参数、土体参数和注浆参数3类。其中，隧道参数包括埋深C、直径D、纵向等效抗弯刚度 $(EI)'$ 以及等效剪切刚度 $({\text{κGA}})'$ 。土体参数包括泊松比μ、基床系数k。注浆参数包括单孔注浆体积V₀、注浆体数量N、注浆体高度h、注浆子层数n_z、注浆体半径a、隧道底-注浆体竖向间距d。主要参数物理意义详见图 2。

a）隧道参数

隧道纵向等效抗弯刚度 $(EI)'$ 及纵向等效剪切刚度 $({\text{κGA}})'$ 是影响隧道变形及内力分布的重要参数，不同隧道的刚度取值可以采用经验法^[12]。

b）土体参数

地基基床系数k计算方法为^[13]

$k = \frac{{3.08}}{{{\eta _\text{p}}D}}\frac{{{E_\text{s}}}}{{1 - {\mu ^2}}}\sqrt[{^8}]{{\frac{{{E_\text{s}}{D^4}}}{{(EI)'}}}} \text{，}$

(5)

$\eta_{\mathrm{p}}=\left\{\begin{array}{ll} 2.18 & (C / D \leqslant 0.5) \\ 1+\frac{1}{1.7 D / h} & (C / D \geqslant 0.5) \end{array},\right.$

(6)

${E_\text{s}} = 350{c_\text{u}}。$

(7)

式中：η_p为地基基床系数深度修正系数；D为隧道外径（m）；C为隧道埋深（m）；μ为土体泊松比；E_s为土体弹性模量（kPa），软黏土可由式（7）^[14]估算；c_u为土体不排水抗剪强度（kPa）。

c）注浆参数

实际施工中，通常将注浆管通过隧道衬砌预留孔插至隧底土体，将每个注浆孔分成若干子层，然后自下而上分层注浆。本文假设每个注浆体为以各子层点为球心的若干球体的叠加（图 2），因而注浆总体积V计算公式为

$V = N{V_0} = N{n_\text{z}}\left( {\frac{4}{3}\mathtt{π} {a^3}} \right) 。$

(8)

式中：N为注浆体数量；V₀为单孔注浆体积；n_z为注浆子层数；a为注浆体半径（m）。

1.2 注浆后的隧道沉降量 $\Delta {\delta _2}$ 计算方法

基于注浆后超孔压消散引起土体固结并导致隧道沉降的基本原理，本节提出了注浆后隧道沉降量的计算方法：利用考虑结构性的柱孔扩张理论^[7]计算塑性区范围的超孔压分布（图 4），通过Mindlin解^[15]以及分层总和法得到隧道下卧土体固结沉降量，再基于文克尔地基上的铁木辛柯梁模型，利用有限差分法求解隧道沉降量。整体计算流程如图 5所示。

图 4 注浆后隧道沉降量理论模型

Figure 4. Theoretical model for tunnel settlement after grouting

下载: 全尺寸图片幻灯片

图 5 注浆后隧道沉降量计算流程

Figure 5. Calculation process of tunnel settlement after grouting

下载: 全尺寸图片幻灯片

（1）基本假定

为简化计算，本计算方法做如下假定：

a）土体固结过程中弹性模量不变，仅考虑塑性区范围内的土体固结沉降。

b）注浆体为规则的圆柱体，内部产生各向同性的注浆压力。注浆体上下边界的超孔压均布且分别等于边界1和边界2在注浆体边缘处（r=0）的塑性区超孔压大小。超孔压消散后将完全转化为隧道下卧地层竖向附加应力。

c）不考虑注浆体凝固引起的体积变形对注浆后上覆盾构隧道沉降的影响。

d）上覆盾构隧道简化为文克尔地基模型上的一维均质铁木辛柯梁模型，隧道纵向附加应力、变形计算均针对隧道底部。

e）隧道纵向附加应力计算采用的地层变形为注浆引起的隧道拱底位置地层沉降量，附加应力沿纵向分布呈现非均匀性。

（2）塑性区土体超孔压分布

刘维正等^[7]针对软黏土的施工扰动及结构性，基于剑桥模型的屈服准则，推导了考虑土结构性损伤的软黏土柱孔扩张弹塑性解，并提出了塑性区的超孔压为

$\begin{array}{l} \Delta u(r) = {\sigma _ \text{r}} - \left[ {\frac{{{q_\text{u}}}}{{\sqrt 3 }} + {{p'}_0}{{\left( {\frac{{ \text{YSR}}}{2}} \right)}^\varLambda }} \right]\left[ {1 - \left( {1 - \frac{1}{{{S_\text{t}}}}} \right)\frac{{\ln \frac{r}{{{r_\text{p}}}}}}{{\ln \frac{{{r_\text{p}}}}{a}}}} \right] \hfill \\ = {\sigma _0} + \frac{{{q_\text{u}}}}{{\sqrt 3 }} - \frac{{2{q_\text{u}}}}{{\sqrt 3 }}\left[ {\ln \frac{r}{{{r_\text{p}}}} + \frac{{1 - \frac{1}{{{S_\text{t}}}}}}{{2\ln \frac{{{r_\text{p}}}}{a}}}{{\left( {\ln \frac{r}{{{r_\text{p}}}}} \right)}^2}} \right] - \hfill \\ \left[ {\frac{{{q_\text{u}}}}{{\sqrt 3 }} + {{p'}_0}{{\left( {\frac{{ \text{YSR}}}{2}} \right)}^\varLambda }} \right]\left[ {1 - \left( {1 - \frac{1}{{{S_\text{t}}}}} \right)\frac{{\ln \frac{r}{{{r_\text{p}}}}}}{{\ln \frac{{{r_\text{p}}}}{a}}}} \right] \text{，} \end{array}$

(9)

${q_\text{u}} = M{p'_0}{\left( {\frac{{ \text{YSR}}}{2}} \right)^\varLambda }\text{，}$

(10)

${r_\text{p}} = a\sqrt {\frac{{\sqrt 3 G}}{{{q_\text{p}}}}} \text{，}$

(11)

${q_\text{p}} = M{p'_0}\sqrt { \text{YSR} - 1} \text{，}$

(12)

$\varLambda = 1 - \frac{\kappa }{\lambda }\text{，}$

(13)

$\text{YSR} = \frac{{{{p'}_{\text{y}}}}}{{{{p'}_0}}}。$

(14)

式中：Δu为超孔压（kPa）；σ₀为初始内应力（kPa）；q_u为极限偏应力（kPa）；q_p为弹塑性交界处应力（kPa）； ${p'_0}$ 为初始有效平均应力（kPa）， ${p'_0}$ =s₀；p_y'为等向固结屈服应力（kPa）；a为注浆体半径（m）；r_p为塑性区半径（m）；S_t为土体灵敏度；M为破坏应力比；G为剪切模量（kPa）；YSR为屈服应力比；Λ为塑性体积比；λ为e-lnp'坐标中正常固结线的斜率；κ为e-lnp'坐标中回弹线的斜率。

（3）隧道底部土体固结沉降

本计算方法将发生固结沉降的土层分为3个部分，包括压缩层1、压缩层2及压缩层3（图 4）。其中，压缩层1为与注浆体同高度的塑性区土体，压缩层2为注浆体顶部与隧道间的土体，压缩层3为注浆体底部以下的土体。注浆后隧道下卧土体的固结沉降量由压缩层1~压缩层3的变形直接叠加得到。

（4）地层超孔压及附加应力计算方法验证

为验证土体超孔压和地层附加应力计算方法的合理性，本文对比了福州淤泥夹砂地层囊袋注浆室内试验^[16]获得的超孔压与计算值。

a）超孔压水平分布规律

本节计算了式（9）在室内试验条件下的理论值，并与室内试验孔压计测得的超孔压结果对比（图 6）。可以发现：下囊袋注浆时，B断面的试验结果与理论计算曲线趋势相同且数值较为接近，证明了式（9）的适用性。在桶壁处两者数据存在差距，主要是模型桶边界效应影响所致。

图 6 B断面超孔压分布曲线

Figure 6. Distribution of excess pore water pressure at Section B

下载: 全尺寸图片幻灯片

b）竖向应力增量云图

针对上述注浆引起的地层竖向应力增量计算假设，本文结合式（9），（16）计算了室内注浆试验条件下地层竖向应力增量并与试验结果进行对比（图 7（a），（b））。提取模型桶对称轴处（d=0）的竖向应力增量值并绘制其沿深度的变化曲线（图 7（c）），可以发现：室内试验与本文方法计算结果趋势相同、数值接近，但两者仍存在一定差异，主要是受模型桶顶板边界效应的影响。

图 7 竖向应力增量计算结果与试验结果对比

Figure 7. Comparison between measured and calculated additional vertical stresses

下载: 全尺寸图片幻灯片

（5）隧道附加应力及沉降

与注浆过程隧道抬升量计算方法一致，注浆后隧道沉降计算中仍将隧道-地层相互作用简化为文克尔地基上的隧道铁木辛柯梁模型。

（6）参数确定

本计算方法涉及隧道参数、土体参数以及注浆参数3类参数。

a）土体参数

土体参数包括剪切模量G₀、有效内摩擦角φ'、临界状态比M、对数硬化模量λ、各向等压膨胀指数k、塑性比体积Λ、等向固结屈服应力 ${p'_{\text{y}}}$ 、等向固结屈服应力比YSR、灵敏度S_t。

其中，剪切模量G₀为^[17]

$\frac{{{G_0}}}{{{p_\text{a}}}} = Sf(e){\left( {\frac{{p'}}{{{p_\text{a}}}}} \right)^n} = S{(1 + {e_0})^{ - 2.4}}{\left( {\frac{{p'}}{{{p_{\text{a}}}}}} \right)^n} 。$

(15)

式中：p_a为参考应力（kPa），取100 kPa；p'为平均有效应力（kPa）， $p'$ =（ ${s'_{\text{v}}}$ + 2 ${s'_{\text{h}}}$ ）/3；n，S为经验参数，对于软黏土，n取0.5，S取24000~30000；e₀为初始孔隙比。

有效内摩擦角φ'和临界状态比M可分别为^[18]

$\varphi ' = 30.4{e_0}^{ - 0.65} \text{，}$

(16)

$M = \frac{{6\sin \varphi '}}{{3 - \sin \varphi '}}。$

(17)

等向固结屈服应力 ${p'_{\text{y}}}$ 可以基于一维固结试验得到的屈服应力p_y并结合剑桥模型的屈服函数计算：

$f \equiv {q^2} + {M^2}p'(p' - {p'_{\text{y}}}) = 0。$

(18)

三轴应力状态下：

$\begin{array}{l}{q}^{\prime }={{\sigma }^{\prime }}_{1}-{{\sigma }^{\prime }}_{3}=(1-{k}_{0}){{\sigma }^{\prime }}_{\text{v}}\text{ }\text{，}\\ {p}^{\prime }=\frac{{{\sigma }^{\prime }}_{1}\text{+2}{{\sigma }^{\prime }}_{3}}{3}=\frac{(1+2{k}_{0}){{\sigma }^{\prime }}_{\text{v}}}{3}。\end{array}\}$

(19)

进而可以得到等向固结屈服应力 ${p'_{\text{y}}}$ ：

${p'_{\text{y}}} = \frac{{(1 + 2{K_0}){p_\text{y}}}}{3} + \frac{{3(1 - {K_0}){p_\text{y}}}}{{{M^2}(1 + 2{K_0})}}。$

(20)

式中：K₀为土体静止侧压力系数；p_y为一维固结试验得到的屈服应力（kPa）；M为临界状态比。

等向固结屈服应力比YSR为等向固结屈服应力 ${p'_{\text{y}}}$ 与初始固结应力p₀之比。

b）隧道参数

隧道参数包括埋深C、直径D、纵向等效抗弯刚度 $({\text{EI}})'$ 以及纵向等效剪切刚度 $({\text{κGA}})'$ 。

c）注浆参数

注浆参数包括初始孔径a₀、注浆体半径a、注浆体高度h、注浆体-隧道竖向间距d。其中，初始孔径a₀为注浆管实际外径，注浆体-隧道竖向间距d为注浆体顶部与隧道底部的距离。

2. 案例应用

本文将上述计算方法应用于宁波地铁2号线某区间盾构隧道注浆抬升工程^[4]。

2.1 工程概况

（1）工程地质条件

宁波市位于中国东部沿海，地貌为第四纪淤积平原，广布深厚淤泥质黏土层。宁波地铁2号线某区间盾构隧道埋深约10~11 m，隧道上部为①₁杂填土、①₂黏土层，隧道主要位于④₁淤泥质黏土中，底部土层为⑤₂粉质黏土，地下水位位于地表以下1 m处，地质剖面如图 8所示。

图 8 宁波地铁2号线地质剖面及注浆方案（166环~174环）

Figure 8. Geological profile and grouting scheme of Ningbo Metro Line 2 (Ring 166 to Ring 174)

下载: 全尺寸图片幻灯片

（2）盾构隧道

盾构隧道采用预制钢筋混凝土管片错缝拼装，外径6.2 m，厚度0.35 m，环宽1.2 m。如图 9所示，隧道环向均布16个预留注浆孔H1~H16，注浆孔直径60 mm。隧道贯通数月后测量发现该区间出现较大差异沉降，最大沉降达214 mm，出现在169环。

图 9 盾构隧道抬升量实测值与计算值对比

Figure 9. Comparison between measured and calculated uplifts of shield tunnel

下载: 全尺寸图片幻灯片

（3）隧道抬升方案

该工程借鉴上海地铁2号线经验，采用微扰动注浆技术抬升隧道，注浆材料为水泥、水玻璃双液浆。

根据隧道沉降情况确定综合治理范围为R166~R175，由管片预留注浆孔H8和H10两个孔竖直注浆（图 8）。根据治理后隧道最小曲率半径目标值及工程经验确定基本注浆参数为：每环设计注浆总量为1900 L，每孔设计注浆量为950 L，将每个注浆孔分成10个子层，每个子层注浆量为95 L，注浆深度范围为隧道底部以下0~2 m。

（4）计算参数

根据隧道结构特征和场地地层条件，本文获得了隧道、土体及注浆计算参数（表 1）。

表 1 宁波地铁2号线盾构隧道注浆抬升工程参数

Table 1. Parameters of grouting uplift project for shield tunnel of Ningbo Metro Line 2

参数名称		参数取值
隧道参数	C/m	10
	D/m	6.2
	(EI)'/(kN·m²)	1.91×10⁸
	(κGA)'/kN	4.14×10⁶
土体参数（淤泥质黏土）	v	0.4
	E_s/MPa	2.83
	S_t	2.22
	k/(kN·m^-3)	4273
	G/MPa	40
	κ	0.01
	λ	0.2
	Μ	1.5
注浆参数	V/L	13300
	V₀/L	950
	N/个	14
	n_z/个	10
	r/m	0.283
	h/m	2
	注浆方式	连续双孔

下载: 导出CSV

| 显示表格

2.2 结果对比

通过对比本文计算值与实测结果（图 9），可以发现本文计算方法得到的最终隧道抬升曲线与实测曲线的趋势基本吻合，数值也较为接近，一定程度上说明了计算方法的有效性。另外，根据本文计算结果，可以得到隧道抬升效率η约51%，与同为淤泥质黏土地层的上海2号线隧道抬升案例^[19]的抬升效率十分吻合。此外，实测结果在治理区段略小于计算值且曲线更平缓，可能是由于实际工程中对盾构隧道内部进行了钢支撑加固，导致该区段纵向刚度变大，隧道更不容易变形且结构差异变形更小。

3. 影响因素分析

本节分别讨论土体屈服应力比、注浆体积以及隧道埋深对隧道最终抬升量及抬升效率的影响规律。

3.1 屈服应力比

图 10（a），（b）分别为地层不同屈服应力比YSR下的隧道最终抬升量δ及抬升效率η纵向分布曲线。可以发现：随着屈服应力比增大，注浆后隧道的最终抬升量及抬升效率减小。根据式（9），这主要是注浆产生的超孔隙水压力大小与土体屈服应力比呈正相关，导致注浆后隧道出现更大沉降，降低隧道抬升效率。另外，随着屈服应力比增大，隧道抬升效率沿纵向分布更加不均匀。

图 10 土体屈服应力比对隧道最终抬升量及抬升效率的影响

Figure 10. Effects of yield stress ratio on final uplift amount and uplifting efficiency of tunnel

下载: 全尺寸图片幻灯片

3.2 注浆体积

图 11（a），（b）分别为不同注浆体积V₀下隧道最终抬升量δ及抬升效率η纵向分布曲线。可以发现：随注浆体积增加，隧道最终抬升量不断增大，隧道抬升效率也不断提高且变化率越来越小。需注意的是，当注浆体积过大时，所需的注浆压力相应增大，可能造成地层劈裂。因此，工程中应综合考虑注浆压力和地层劈裂等影响，确定合理的注浆体积。

图 11 注浆体积对隧道最终抬升量及抬升效率的影响

Figure 11. Effects of grouting volume on final uplift amount and uplifting efficiency of tunnel

下载: 全尺寸图片幻灯片

3.3 隧道埋深比

图 12（a），（b）分别为不同隧道埋深比C/D下的隧道最终抬升量δ及抬升效率η纵向分布曲线。可以发现：随着隧道埋深比增大，注浆范围内的隧道最终抬升量减小，而抬升效率基本不变。因此，结合前述注浆体积对隧道最终抬升量的参数分析结果，若需保证不同埋深比隧道产生相同的抬升量，注浆体积应该随隧道埋深比增大而增大。

图 12 隧道埋深比对隧道最终抬升量及抬升效率的影响

Figure 12. Effects of cover-to-diameter ratio of tunnel on final uplift amount and uplifting efficiency

下载: 全尺寸图片幻灯片

4. 结论

围绕软黏土地层盾构隧道注浆抬升问题，提出了考虑土体结构性的盾构隧道底部注浆抬升量-沉降量两阶段计算方法，得到2点结论。

（1）本文计算方法应用于宁波地铁2号线隧道过大沉降区段注浆抬升工程，计算得到的最终抬升量纵向曲线与实测曲线趋势基本吻合。实测结果在抬升区段略小于计算值且曲线更加平缓，主要是因为抬升前隧道内部钢支撑加固提高了其结构刚度。

（2）隧道最终抬升量及抬升效率与基床系数、注浆体积正相关，与地层结构性负相关。同时，随隧道埋深比增大，注浆治理区域内的隧道最终抬升量减小，抬升效率基本不变。

图 1 颗粒破碎临界状态线示意图

Figure 1. Schematic diagram of critical state line of breakage

下载: 全尺寸图片幻灯片

图 2 屈服面、边界面与硬化规律示意图

Figure 2. Schematic diagram of yield surface, bounding surface and hardening law

下载: 全尺寸图片幻灯片

图 3 压缩平面颗粒破碎临界状态线的演化

Figure 3. Evolution of BCSL in compression plane

下载: 全尺寸图片幻灯片

图 4 破碎应力与颗粒破碎指数拟合关系

Figure 4. Relationship between breakage stress and index

下载: 全尺寸图片幻灯片

$q$ - $p'$ 平面临界状态线^[34]

CSLs in $q$ - $p'$ plane^[34]

下载: 全尺寸图片幻灯片

图 6 模型参数影响分析

Figure 6. Analysis of model parameters on simulations

下载: 全尺寸图片幻灯片

模型模拟结果和试验结果^[33] ( ${D_r}$ =30%)对比

Comparison between simulations and test data^[33]with ${D_r}$ =30%

下载: 全尺寸图片幻灯片

模型模拟结果和试验结果^[33] ( ${D_r}$ =60%)对比

Comparison between simulations and test data^[33]with ${D_r}$ =60%

下载: 全尺寸图片幻灯片

模型模拟结果和试验结果^[33] ( ${D_r}$ =90%)对比

Comparison between simulations and test data^[33]with ${D_r}$ =90%

下载: 全尺寸图片幻灯片

表 1 模型参数

Table 1 Model parameters

弹性参数	颗粒破碎临界状态参数	边界面形状参数	硬化参数
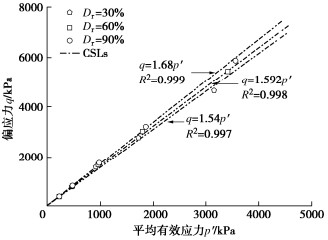
$\kappa = 0.005$ $\nu = 0.3$	$\mathit{\Pi} = 2.4$ ^，2.332^，2.285^** $\lambda = 0.19$ ${M_\mathrm{c}} = 1.54$ ^, 1.592^，1.68^** $\mathbb{Z}$ =671 $\vartheta$ =5.88	$\beta = 0.58$	$\rho = 0.1$ ${h_0} = 1.2$
注：上标“^，^，^**”分别代表相对密实度30%，60%，90%的取值。

下载: 导出CSV

参考文献(37)

[1]	张家铭, 汪稔, 石祥锋, 等. 侧限条件下钙质砂压缩和破碎特性试验研究[J]. 岩石力学与工程学报, 2005, 24(18): 3327-3331. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200518021.htm ZHANG Jiaming, WANG Ren, SHI Xiangfeng, et al. Compression and crushing behavior of calcareous sand under confined compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(18): 3327-3331. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200518021.htm
[2]	蔡正银, 侯贺营, 张晋勋, 等. 密度与应力水平对珊瑚砂颗粒破碎影响试验研究[J]. 水利学报, 2019, 50(2): 184-192. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201902004.htm CAI Zhengyin, HOU Heying, ZHANG Jinxun, et al. Experimental study on the influence of density and stress level on particle breakage of coral sand[J]. Journal of Hydraulic Engineering, 2019, 50(2): 184-192. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201902004.htm
[3]	吴杨, 崔杰, 李能, 等. 岛礁吹填珊瑚砂力学行为与颗粒破碎特性试验研究[J]. 岩土力学, 2020, 41(10): 3181-3191. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202010002.htm WU Yang, CUI Jie, LI Neng, et al. Experimental study on the mechanical behavior and particle breakage characteristics of hydraulic filled coral sand on a coral reef island in the South China Sea[J]. Rock and Soil Mechanics, 2020, 41(10): 3181-3191. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202010002.htm
[4]	SHARMA S S, ISMAIL M A. Monotonic and cyclic behavior of two calcareous soils of different origins[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(12): 1581-1591. doi: 10.1061/(ASCE)1090-0241(2006)132:12(1581)
[5]	HASSANLOURAD M, SALEHZADEH H, SHAHNAZARI H. Dilation and particle breakage effects on the shear strength of calcareous sands based on energy aspects[J]. International Journal of Civil Engineering, 2008, 6: 108-119. http://www.iust.ac.ir/ijce/article-1-199-en.pdf
[6]	GHAFGHAZI M, SHUTTLE D A, DEJONG J T. Particle breakage and the critical state of sand[J]. Soils and Foundations, 2014, 54(3): 451-461. doi: 10.1016/j.sandf.2014.04.016
[7]	COOP M R. The mechanics of uncemented carbonate sands[J]. Géotechnique, 1990, 40(4): 607-626. doi: 10.1680/geot.1990.40.4.607
[8]	BANDINI V, COOP MR. The influence of particle breakage on the location of the critical state line of sands[J]. Soils and Foundations, 2011, 51(4): 591-600. doi: 10.3208/sandf.51.591
[9]	YU F W. Particle breakage and the critical state of sands[J]. Géotechnique, 2017, 67(8): 713-719. doi: 10.1680/jgeot.15.P.250
[10]	王刚, 杨俊杰, 王兆南. 钙质砂临界状态随颗粒破碎演化规律分析[J]. 岩土工程学报, 2021, 43(8): 1511-1517. doi: 10.11779/CJGE202108016 WANG Gang, YANG Junjie, WANG Zhaonan. Evolution of critical state of calcareous sand during particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(8): 1511-1517. (in Chinese) doi: 10.11779/CJGE202108016
[11]	孙吉主, 罗新文. 考虑剪胀性与状态相关的钙质砂双屈服面模型研究[J]. 岩石力学与工程学报, 2006, 25(10): 2145-2149. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200610029.htm SUN Jizhu, LUO Xinwen. Study on a two-yield surface model with consideration of state-dependent dilatancy for calcareous sand[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(10): 2145-2149. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200610029.htm
[12]	蔡正银, 侯贺营, 张晋勋, 等. 考虑颗粒破碎影响的珊瑚砂临界状态与本构模型研究[J]. 岩土工程学报, 2019, 41(6): 989-995. doi: 10.11779/CJGE201906001 CAI Zhengyin, HOU Heying, ZHANG Jinxun, et al. Critical state and constitutive model for coral sand considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(6): 989-995. (in Chinese) doi: 10.11779/CJGE201906001
[13]	曾凯锋, 刘华北. 考虑颗粒破碎的钙质砂修正邓肯-张E-B模型[J]. 工程地质学报, 2020, 28(1): 94-102. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202001011.htm ZENG Kaifeng, LIU Huabei. A modified Duncan-Chang E-B model with particle breakage for calcareous sand[J]. Journal of Engineering Geology, 2020, 28(1): 94-102. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ202001011.htm
[14]	王兆南, 王刚, 叶沁果, 等. 考虑颗粒破碎的钙质砂边界面循环本构模型[J]. 岩土工程学报, 2021, 43(5): 886-892. doi: 10.11779/CJGE202105012 WANG Zhaonan, WANG Gang, YE Qinguo, et al. Cyclic bounding surface model for carbonate sand incorporating particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(5): 886-892. (in Chinese) doi: 10.11779/CJGE202105012
[15]	SUMELKA W. A note on non-associated Drucker-Prager plastic flow in terms of fractional calculus[J]. Journal of Teoretical and Applied Mechanics, 2014, 52(2): 571-574. http://www.istic.ac.cn/suoguan/detailed.htm?dbname=xw_qk&wid=0220140600537161
[16]	孙逸飞, 高玉峰, 鞠雯. 分数阶塑性力学及其砂土本构模型[J]. 岩土工程学报, 2018, 40(8): 1535-1541. doi: 10.11779/CJGE201808021 SUN Yifei, GAO Yufeng, JU Wen. Fractional plasticity and its application in constitutive model for sands[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(8): 1535-1541. (in Chinese) doi: 10.11779/CJGE201808021
[17]	LIANG J Y, LU D C. Reply to discussion on "fractional elastoplastic constitutive model for soils based on a novel 3D fractional plastic flow rule" [J]. Computers and Geotechnics, 2020, 119: 103282.
[18]	梁靖宇, 杜修力, 路德春, 等. 特征应力空间中土的分数阶临界状态模型[J]. 岩土工程学报, 2019, 41(3): 581-587. doi: 10.11779/CJGE201903022 LIANG Jingyu, DU Xiuli, LU Dechun, et al. Fractional-order critical state model for soils in characteristic stress space[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(3): 581-587. (in Chinese) doi: 10.11779/CJGE201903022
[19]	RUSSELL A R, KHALILI N. A bounding surface plasticity model for sands exhibiting particle crushing[J]. Canadian Geotechnical Journal, 2004, 41(6): 1179-1192. http://www.onacademic.com/detail/journal_1000035993372810_ffff.html
[20]	DAOUADJI A, HICHER P Y, RAHMA A. An elastoplastic model for granular materials taking into account grain breakage[J]. European Journal of Mechanics - A, 2001, 20(1): 113-137. http://www.xueshufan.com/publication/2074028549
[21]	WOOD D M, MAEDA K. Changing grading of soil: effect on critical states[J]. Acta Geotechnica, 2008, 3(1): 3-14. doi: 10.1007%2Fs11440-007-0041-0.pdf
[22]	XIAO Y, LIU H L. Elastoplastic constitutive model for rockfill materials considering particle breakage[J]. International Journal of Geomechanics, 2017, 17(1): 04016041. http://www.nstl.gov.cn/paper_detail.html?id=a469ef02be8c4fe536db7be068b73db5
[23]	XIAO Y, SUN Z C, STUEDLEIN A W, et al. Bounding surface plasticity model for stress-strain and grain-crushing behaviors of rockfill materials[J]. Geoscience Frontiers, 2020, 11(2): 495-510
[24]	XIAO Y, WANG C G, ZHANG Z C, et al. Constitutive modeling for two sands under high pressure[J]. International Journal of Geomechanics, 2021, 21(5): 04021042. http://www.nstl.gov.cn/paper_detail.html?id=106bd04196747daef04c5a38cbce4b43
[25]	TONG C X, ZHAI M Y, LI H C, et al. Particle breakage of granular soils: changing critical state line and constitutive modelling[J]. Acta Geotechnica, 2022, 17(3): 755-768. doi: 10.1007/s11440-021-01231-8
[26]	孙增春, 汪成贵, 刘汉龙, 等. 粗粒土边界面塑性模型及其积分算法[J]. 岩土力学, 2020, 41(12): 3957-3967. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202012015.htm SUN Zengchun, WANG Chenggui, LIU Hanlong, et al. Bounding surface plasticity model for granular soil and its integration algorithm[J]. Rock and Soil Mechanics, 2020, 41(12): 3957-3967. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202012015.htm
[27]	XIAO Y, SUN Y F, HANIF K F. A particle-breakage critical state model for rockfill material[J]. Science China Technological Sciences, 2015, 58(7): 1125-1136. http://www.researchgate.net/profile/Yifei_Sun8/publication/277904256_A_particle-breakage_critical_state_model_for_rockfill_material/links/59be7e27aca272aff2dedaa7/A-particle-breakage-critical-state-model-for-rockfill-material.pdf
[28]	XIAO Y, LIU H L, CHEN Y M, et al. Bounding surface model for rockfill materials dependent on density and pressure under triaxial stress conditions[J]. Journal of Engineering Mechanics, 2014, 140(4): 04014002. http://www.nstl.gov.cn/paper_detail.html?id=814b8a6fe8d6b9dc46b7a370be0f3c4c
[29]	YIN Z Y, HICHER P Y, DANO C, et al. Modeling mechanical behavior of very coarse granular materials[J]. Journal of Engineering Mechanics, 2017, 143(1): C4016006.
[30]	BARDET J P. Bounding surface plasticity model for sands[J]. Journal of Engineering Mechanics, 1986, 112(11): 1198-1217. doi: 10.1061/%28ASCE%290733-9399%281986%29112%3A11%281198%29
[31]	LIANG J Y, LU D C, ZHOU X, et al. Non-orthogonal elastoplastic constitutive model with the critical state for clay[J]. Computers and Geotechnics, 2019, 116: 103200. http://www.sciencedirect.com/science/article/pii/S0266352X19302642
[32]	BEEN K, JEFFERIES M G. A state parameter for sands[J]. Géotechnique, 1985, 35(2): 99-112. http://www.nrcresearchpress.com/servlet/linkout?suffix=rg4/ref4&dbid=16&doi=10.1139%2FT08-085&key=10.1680%2Fgeot.1985.35.2.99
[33]	SUN Y F, SONG S X, XIAO Y, et al. Development and application of state-dependent fractional plasticity in modeling the non-associated behavior of granular aggregates[J]. Acta Mechanica Solida Sinica, 2017, 30(5): 507-519.
[34]	WU Y, LI N, WANG X, et al. Experimental investigation on mechanical behavior and particle crushing of calcareous sand retrieved from South China Sea[J]. Engineering Geology, 2021, 280: 105932. http://www.sciencedirect.com/science/article/pii/S0013795220318299
[35]	LIU M C, GAO Y F. Constitutive modeling of coarse-grained materials incorporating the effect of particle breakage on critical state behavior in a framework of generalized plasticity[J]. International Journal of Geomechanics, 2017, 17(5): 04016113. http://www.onacademic.com/detail/journal_1000039646245110_f5f4.html
[36]	刘恩龙, 陈生水, 李国英, 等. 堆石料的临界状态与考虑颗粒破碎的本构模型[J]. 岩土力学, 2011, 32(增刊2): 148-154. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S2024.htm LIU Enlong, CHEN Shengshui, LI Guoying, et al. Critical state of rockfill materials and a constitutive model considering grain crushing[J]. Rock and Soil Mechanics, 2011, 32(S2): 148-154. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S2024.htm
[37]	LIU R M, HOU H Y, CHEN Y Y, et al. Elastoplastic constitutive model of coral sand considering particle breakage based on unified hardening parameter[J]. Marine Georesources & Geotechnology, 2022, 40(6): 655-667. http://www.researchgate.net/publication/351604694_Elastoplastic_constitutive_model_of_coral_sand_considering_particle_breakage_based_on_unified_hardening_parameter