双层非饱和土地基一维固结半解析解

李林忠; 秦爱芳; 江良华

doi:10.11779/CJGE202202013

双层非饱和土地基一维固结半解析解 English Version

上海大学力学与工程科学学院, 上海 200444

基金项目:

国家自然科学基金项目 42072292

详细信息

作者简介:
李林忠(1992—)，男，博士研究生，主要从事土体固结方面的研究工作。E-mail: heartbeatsllz@163.com

通讯作者:
秦爱芳，E-mail: qinaifang@shu.edu.cn

中图分类号: TU433
计量
- 文章访问数: 215
- HTML全文浏览量: 44
- PDF下载量: 168
出版历程
- 收稿日期: 2021-01-26
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-01-31

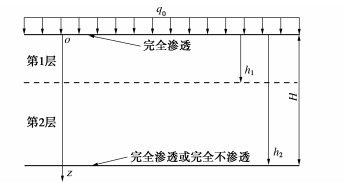
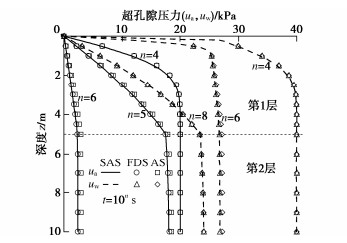
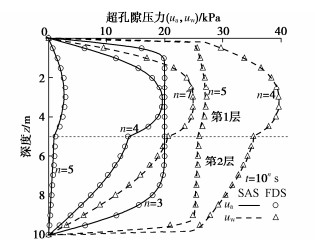
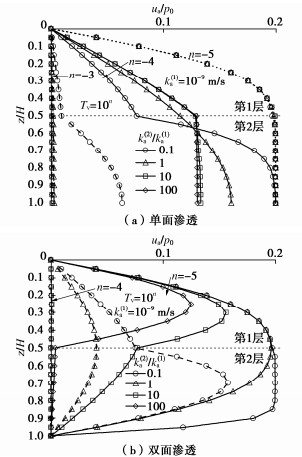
Semi-analytical solution to one-dimensional consolidation of double-layered unsaturated ground

School of Mechanics and Engineering Science, Shanghai University, Shanghai 200444, China

摘要

摘要: 基于Fredlund和Hasan的非饱和土一维固结理论，将非饱和地基假定为双层，引入层间渗流连续条件，得到双层非饱和土地基一维固结控制方程。采用Laplace变换将偏微分方程组转化为常微分方程组，求解得到双层非饱和土地基在单面、双面渗透边界条件下超孔隙压力和沉降在Laplace域内的解；并利用Crump数值方法实现Laplace逆变换，最终得到时间域内双层非饱和土地基一维固结的半解析解。通过与已有文献和有限差分解的结果比较，验证了所得半解析解的有效性。基于得到的解答，结合算例考察了不同层间渗透系数比下，双层非饱和土地基中超孔隙压力的分布规律；并通过参数分析讨论了土层厚度比和层间渗透系数比对双层非饱和土地基沉降的影响。
- 非饱和土 /
- 双层地基 /
- 一维固结 /
- Laplace变换 /
- 半解析解
Abstract: Combining the one-dimensional (1D) consolidation theory of unsaturated soils proposed by Fredlund and Hasan and the interfacial continuity conditions during the consolidation, the 1D consolidation model for a double-layered unsaturated ground is obtained in this study. The Laplace transformation is adopted to convert the partial differential equations into the ordinary ones, and the solutions to the excess pore pressures and settlements in the Laplace domain can be acquired. The semi-analytical solution to 1D consolidation of the double-layered unsaturated ground in the time domain is calculated after taking the inverse Laplace transformation by numerical Crump method. A comparison with the finite difference solution and the available analytical solution illustrates that the proposed solution is effective. Based on the proposed semi-analytical solution, the distribution of the excess pore pressures with ratio of various permeability coefficients in the two-layered unsaturated ground is studied, and the parametric studies are made to investigate the influences of the thickness ratio of the soil layer and the ratio of permeability coefficients on the settlement of the double-layered unsaturated ground.
- unsaturated soil /
- double-layered ground /
- 1D consolidation /
- Laplace transformation /
- semi-analytical solution

HTML全文

0. 引言

由于沉积条件、应力历史、风化程度、埋藏条件以及其它地质作用的差异,岩土工程中土性参数具有显著的空间变异性,而由于所经历的地质、化学和环境作用的差异,土性参数整体又呈现沿埋深变化的波动性和趋势性。上述岩土参数的空间变异性对岩土工程尤其是边坡稳定可靠性的影响已广为学术界和工程界关注^[1]。对于绝大多数边坡稳定性研究,平稳随机场常用来表征土性参数的空间变异性^[2]。然而大量现场试验和相关试验数据表明,土性参数如黏聚力、内摩擦角、土壤重度以及不排水抗剪强度等的统计特征参数沿土体埋深呈现明显的非均匀分布特征。如王长虹等^[3]统计表明,天津地铁^#5、^#6线环湖西路站—宾馆西路站四线隧道交叠区间断面黏聚力和内摩擦角均值随埋深非连续性变化,具有间断性。Jaksa等^[4]和Cafaro等^[5]分别调查了澳大利亚南部某港市典型地层和意大利塔兰托地区典型地层,显示剖面黏土层的锥尖阻力 $q_{c}$ 沿埋深具有明显的分层特性。林军等^[6]和Chenari等^[7]调查发现江苏海相黏土 $q_{c}$ 和乌尔米耶湖场地黏土 $q_{c}$ 沿深度方向同样呈现明显的分层趋势。由此可见,忽略土性参数均值和标准差随埋深非连续性变化的趋势而建立的平稳随机场用来表征土性参数的空间变异性是不合理的。

土性参数的统计特征参数沿埋深方向的非均匀分布特征对岩土结构可靠度有重要影响,有学者对此进行了有益探索。Griffiths等^[8]在考虑不排水抗剪强度均值和标准差沿埋深线性增加的前提下,采用随机有限元法分析了边坡可靠度问题；祁小辉等^[9]探讨了不排水抗剪强度统计特征参数的非均匀分布特征对条形地基极限承载力影响；Wu等^[10]采用非平稳随机场模拟了不排水抗剪强度的空间变异性对深基坑开挖稳定可靠度的影响；蒋水华等^[11]提出了不排水抗剪强度的非平稳随机场模型,讨论了不排水抗剪强度的统计特征参数的非均匀分布特征对边坡可靠度的影响规律。以上学者的研究均采用趋势分量和随机波动分量来表征土性参数的非平稳性,考虑了趋势分量的不确定性或随机波动分量的不确定性,从而建立的非平稳随机场。该方法不足之处在于只适于同类土或相似土构成的边坡,对于不同类别土壤构成的边坡,会导致对土性参数变异性的不准确估计。

为此,本文提出了多涨落尺度（fluctuation scale,为免与物理中的波动混淆,在此称为涨落尺度）^[12]的土性参数分层非平稳随机场模型。该模型主要针对多种类型土壤组成的边坡土性参数的统计特征参数的非连续的非平稳特性。与现有平稳随机场模型和其他非平稳随机场模型的比较显示,所建模型可合理描述土性参数的分层特性。通过一实际工程边坡算例验证了所建模型的有效性,并研究了黏聚力和内摩擦角的统计特征参数的非连续非平稳特征对临界滑移面形状、位置以及边坡稳定可靠度的影响。

1. 统计参数连续变化的非平稳随机场

若参数的均值与方差不随土体空间位置而变化,其协方差函数只与空间两点的相对位置有关,而与绝对位置无关,则认为土性参数随机场是平稳或均匀的（homogeneous random field,记作HRF）,由参数均值、方差、相关函数或相关长度即可构建一个平稳随机场^[13]。若土性参数的协方差函数与空间两点的绝对位置有关,则为非平稳或非均匀随机场（non- homogeneous random field,即NHRF）。根据参数统计特性随深度的变化情况,目前已有的土性参数随机场主要包括均值和标准差沿深度不变的平稳随机场；均值随深度线性增加而标准差不变的非平稳随机场以及均值与标准差均随深度线性增加的非平稳随机场^[14]。

边坡工程研究采用较多的是参数平稳随机场模型,然而大量原位测试与试验数据统计分析表明,土性参数的统计特征参数存在非平稳性,特别体现在沿深度方向的趋势性与随机波动性,如图1所示。

图 1 土性参数的统计特征参数沿埋深的变异性

Figure 1. Variability of statistical characteristic parameters of soil parameters with depth

下载: 全尺寸图片幻灯片

土性参数 $ζ (z)$ 沿深度的变化可以表示为

$ζ (z) = t (z) + ω (z)$ ,

(1)

式中, $z$ 为土体埋深, $t (z)$ 为趋势分量函数,如土性参数沿埋深 $z$ 的均值函数, $ω (z)$ 为随机波动分量函数,通常为均值 $μ_{ω} = 0$ ,标准差为 $σ_{ω}$ 的正态平稳随机场。

土的不排水抗剪强度 $s_{u}$ 可以看作是地表处的不排水抗剪强度 $s_{u 0}$ 随埋深线性增加^[15],即

$s_{u} (z) = s_{u 0} + b {σ^{'}}_{v} = s_{u 0} + b γ z$ ,

(2)

式中, $s_{u 0}$ 对应特定场地的地表抗剪强度,为常数, $b$ 为不排水抗剪强度随埋深增加的速率, ${σ^{'}}_{v}$ 为垂直有效应力, ${σ^{'}}_{v} = γ z$ , $γ$ 为土体重度,为常数。

为模拟不排水抗剪强度的非平稳特征,Griffiths等^[8]采用去趋势分析方法将 $s_{u 0}$ 模拟为均值为 $μ_{s_{u0}}$ 和标准差为 $σ_{s_{u0}}$ 的对数正态平稳随机场,得到如下 $s_{u}$ 的非平稳随机场：

$s_{u} (z) = s_{u 0} (z) + \frac{s_{u0} (z)}{μ_{s_{u 0}}} \cdot b γ z$ 。

(3)

则 $s_{u}$ 的均值和标准差分别为

$\begin{array}{l} μ_{s_{u}} (z) = μ_{s_{u 0}} + b γ z, \\ σ_{s_{u}} (z) = \frac{μ_{s_{u 0}} + b γ z}{μ_{s_{u 0}}} \cdot σ_{s_{u 0}} 。 \end{array}}$

(4)

式中, $s_{u}$ 的均值和标准差均为埋深的单调增加函数。

祁小辉等^[9]将参数 $b$ 模拟为均值为 $μ_{b}$ 和标准差为 $σ_{b}$ 的对数正态平稳随机场,得到 $s_{u}$ 的非平稳随机场模型：

$s_{u} (z) = s_{u 0} + γ z b (z)$ ,

(5)

则 $s_{u}$ 的均值和标准差分别为

$\begin{array}{l} μ_{s_{u}} (z) = s_{u 0} + γ z μ_{b}, \\ σ_{s_{u}} (z) = γ z σ_{b} 。 \end{array}}$

(6)

该模型中, $s_{u}$ 的均值和标准差也随深度单调增加。

蒋水华等^[11]在上述研究的基础上分别考虑了不排水抗剪强度的趋势分量和随机波动分量的不确定性,将 $s_{u 0}$ 和 $b$ 分别模拟为对数正态随机变量ln ( $μ_{s_{u 0}}$ , $σ_{s_{u 0}}$ )和ln( $μ_{b}$ , $σ_{b}$ ),并引入零均值平稳正态随机分量 $ω (x, z)$ 表示水平向x和竖向z的其他随机涨落,从而得到 $s_{u}$ 的二维非平稳随机场：

$s_{u} (x, z) = s_{u 0} + b γ z \exp [ω (x, z)]$ ,

(7)

则 $s_{u}$ 的均值和标准差分别为

$\begin{array}{l} μ_{s_{u}} (z) = μ_{s_{u 0}} + γ z μ_{b}, \\ σ_{s_{u}} (z) = \sqrt{σ_{s_{u 0}}^{2} + γ^{2} z^{2} {(μ_{b}^{2} + σ_{b}^{2}) [\exp (σ_{ω}^{2}) - 1] + σ_{b}^{2}}} 。 \end{array}}$

(8)

图2给出了分别采用Griffiths模型、祁小辉模型和蒋水华模型得到的不排水抗剪强度的若干典型实现。与Griffiths模型及祁小辉模型相比,蒋水华模型由于在趋势项基础上进一步叠加了随机涨落分量,其不排水抗剪强度沿埋深表现出更为显著的非平稳性,个别样本沿深度方向表现出剧烈变化。但总体而言,以上3种模型所描述的土性参数均值和标准差均随深度连续变化,其中均值随深度线性增大。这与由同类土壤构成的单一土层的特性是相符的^[14-17]。

图 2

$s_{u}$ 随机场沿土体埋深方向的典型实现

Figure 2. Typical realizations of random field of undrained shear strength with depth

下载: 全尺寸图片幻灯片

然而,对于规模较大的边坡工程,通常沿深度方向由不同类别的土壤构成,表现出显著的分层特性。由王长虹等^[3]对天津地铁^#5、^#6线环湖西路站—宾馆西路站四线隧道交叠区间、深度为36 m的断面黏聚力和内摩擦角参数所作调查统计结果表明,其黏聚力均值 $μ_{c}$ 与内摩擦角均值 $μ_{φ}$ 随深度方向呈非连续的阶梯状变化。土性参数的统计特征参数的这一非连续性变化,如抗剪强度参数均值、方差沿埋深的突然降低或增强,会导致临界滑移面的改变,对边坡稳定可靠性、地基承载力可靠性等会造成较大影响。可见,对于尺度较大的由不同类别土壤构成的土体,上述均值连续线性变化的非平稳随机场模型不再适用,而需建立更为合理的非平稳随机场模型。

针对土性参数的复杂空间变异性,Wei等^[18-19]提出了不精确随机模拟法,认为统计特征参数也具有不确定性,称其为模型不确定性^[20],并将统计特征参数也视为随机变量。这类模型较为复杂,其随机场离散难度与计算量都大大增加。Phoon等^[21]则假设局部场地与较大范围（如全球范围的同类或相似土壤）的土性参数空间变异性相近,基于贝叶斯机器学习提出了利用较大空间区域的参数预测并补足局部场地参数缺失值的方法。该方法是由大空间范围的数据而非通过建立特定场地的参数非平稳随机场模型来模拟局部场地数据,其预测或补充参数的合理性依赖于给定边坡或土层与其他已知区域空间变异性的相似性,对于由多种土壤构成的边坡其适用性与合理性还有待验证。

2. 统计参数非连续变化的分层非平稳随机场

对于深度较大的土体,沿深度方向可能由多种类别土壤构成,具有明显的分层特性,土性参数均值与方差等随土体深度呈非连续变化。而对于尺度较小的土体,虽然可近似视为由单一类别土壤构成,但若存在局部薄弱层,也会造成土性参数均值和方差的非连续变化,以下针对土体的这一分层特性,提出土性参数的分层非平稳随机场模型。

2.1 分层非平稳随机场模型

在此主要考虑土性参数沿深度方向的变异性。设土性参数 $ζ$ 的非平稳随机场模型为

$ζ (z) = μ_{ζ} (z) + b (z) \cdot z \cdot \exp [ω (z)]$ ,

(9)

式中, $ζ （ z)$ 可为黏聚力、内摩擦角、重度、渗透率等土性参数, $μ_{ζ} (z)$ 为土性参数的均值函数, $ω (z)$ 为零均值、标准差为 $σ_{ω} (z)$ 的土性参数非平稳随机场,表示参数方差随深度的变异性, $b (z)$ 为随机涨落分量。

针对前述土体的分层特性,可设在由同类土构成的同一土层内,土性参数为均值和方差随深度线性增加的非平稳随机场,即在同一层土体内, $b (z)$ 为均值为 $μ_{b_{I}}$ 、标准差为 $σ_{b_{I}}$ 的平稳随机场,对不同土层其均值与标准差不同,则有

$\begin{array}{l} μ_{ζ_{I}} (z) = μ_{ζ_{I 0}} + μ_{b_{I}} \cdot z, \\ σ_{ζ_{I}} (z) = z \cdot \sqrt{(μ_{b_{I}}^{2} + σ_{b_{I}}^{2}) [\exp (σ_{ω_{I}}^{2}) - 1] + σ_{b_{I}}^{2}} 。 \end{array}}$

(10)

式中,下标I对应第I个土层, $μ_{ζ_{I 0}}$ 为第I个土层土性参数的参考均值。 $l_{I - 1} \leq z < l_{I}$ , $Δ l_{I} = | l_{I} - l_{I - 1} |$ （ $I = 1 \sim N$ ）为第I层的土层厚度,可由经验或各层土的相关函数决定。

进一步地,可将上述分层非平稳随机场简化为均值与随机涨落函数沿土层跳跃变化的随机方波过程,即同一土层的土性参数为平稳随机场,其均值和方差不随深度变化, $b (z)$ 为零均值、标准差为 $σ_{b_{I}}$ 的平稳随机场,则式（10）可简化为

$ζ (z) = μ_{ζ} (z) + b (z) \times z$ 。

(11)

土性参数沿深度方向的均值和方差均为分段取值的常数：

${\begin{cases} μ_{ζ} (z) = μ_{ζ_{I 0}}, \\ σ_{ζ} (z) = σ_{ζ_{I}} = σ_{b_{I}} 。 \end{cases}$

(12)

如此建立的分层非平稳随机场模型如图3所示。

图 3 土性参数的统计特征参数随埋深的变化

Figure 3. Variation of statistical characteristic parameters of soil parameters with depth

下载: 全尺寸图片幻灯片

2.2 分层非平稳随机场的离散

根据式（11）,（12）可建立分层非平稳随机场沿深度方向的协方差矩阵。根据Bergado等^[22]和Li等^[23]的研究,边坡稳定可靠性对自相关函数的形式不敏感,而对相关长度敏感,故采用形式较为简单的指数衰减型相关函数,并根据式（10）对其进行修正,得到同一土层中任意两点i,j的协方差 $B_{i j}$ 为

$B_{i j} = σ (z_{i}) \cdot σ (z_{j}) \cdot \exp (- \frac{2 | z_{i} - z_{j} |}{θ})$ ,

(13)

式中, $| z_{i} - z_{j} |$ 是i,j两点之间的距离, $σ (z_{i})$ 和 $σ (z_{j})$ 分别是其标准差, $θ$ 是该点所在土层的相关长度。由N层土壤构成的土体分层非平稳协方差矩阵为

$B = [\begin{array}{l} \begin{matrix} B_{11} & B_{12} & \dots & \begin{matrix} B_{1 I} & \begin{matrix} \dots & B_{1 N} \end{matrix} \end{matrix} \end{matrix} \\ \begin{matrix} B_{22} & \dots & \begin{matrix} B_{2 I} & \begin{matrix} \dots & B_{2 N} \end{matrix} \end{matrix} \end{matrix} \\ \begin{matrix} ⋱ & \begin{matrix} \begin{matrix} ⋮ \end{matrix} \end{matrix} \end{matrix} \\ \begin{matrix} B_{I I} & \begin{matrix} B_{I J} & \begin{matrix} \dots & B_{I N} \end{matrix} \end{matrix} \end{matrix} \\ \begin{matrix} 对称 & \begin{matrix} ⋱ & \begin{matrix} ⋮ \end{matrix} \end{matrix} \end{matrix} \\ \begin{matrix} \begin{matrix} \begin{matrix} B_{N N} \end{matrix} \end{matrix} \end{matrix} \end{array}] (I, J = 1 \sim N)$ 。

(14)

协方差矩阵 $B$ 为正定矩阵,不同层之间协方差为零,即 $B_{I J} = 0 (I \neq J)$ 。对其进行Cholesky分解,有

$B = L \times L_{}^{T}$ ,

(15)

式中, $L$ 为下三角矩阵, $L_{I J} =$ 0（I<J）。当 $I = J$ 时,记作 $B_{I J} = B_{I}$ , $L_{I J} = L_{I}$ 。

将式（15）代入式（11）,可得土性参数的分层非平稳随机场模型为

$ζ_{I} (z) = L_{I} \times ε + μ_{ζ_{I}} (z) + b_{I} (z) \times z$ ,

(16)

式中, $ε$ 为向量, $ε = {〈 ε_{1}, ε_{2}, \dots, ε_{k}, \dots, ε_{n} 〉}^{T}$ , $ε_{k}$ 为服从标准正态分布的随机变量。

上述土性参数分层非平稳随机场模拟方法的步骤如下：

（1）根据边坡剖面图,沿深度方向将边坡分为N层,通过连续回归分析确定各层土性参数的统计特征,包括均值、方差、分布类型、自相关函数或相关长度等。

（2）依照方差结构,建立第I个土层的非平稳协方差矩阵 $B_{I}$ ,见式（13）,（14）。

（3）利用Cholesky分解技术,对非平稳协方差矩阵进行分解,见式（15）,得到下三角矩阵 $L_{I}$ 。

（4）利用常用的平稳随机场模拟方法得到 $b_{I}$ 。

（5）引入向量 $ε$ ,从而得到第I层随机场模型 $ζ_{I} (z) = L_{I} \times ε + μ_{ζ_{I}} (z) + b_{I} (z) \times z$ ,见式（16）。

（6）重复步骤（2）～（5）,得到分层非平稳随机场 $ζ (z) = L \times ε + μ_{ζ} (z) + b (z) \times z$ 。

本文采用K-L方法^[24]对平稳随机场进行离散。具体应用时,分层厚度可根据检测数据结合工程经验确定,或根据检测数据的相关性分析确定。如由土性参数沿深度方向的方差函数 $γ (T)$ 或相关函数 $ρ (τ)$ ^[25],可得到土性参数涨落尺度 $θ$ ：

$\begin{matrix} θ = \lim_{T \to \infty} T γ (T) \\ = 2 \lim_{T \to \infty} \int_{0}^{T} (1 - \frac{τ}{T}) ρ (τ) d τ = 2 \int_{0}^{\infty} ρ (τ) d τ 。 \end{matrix}$

(17)

其中,当两点之间距离大于涨落尺度时,可认为参数不相关,属于不同土层。据此,可近似确定同类土的土层厚度。工程上,通常也近似取相关函数值衰减到 $e^{- 1}$ 时的值,作为涨落尺度的近似。

考察分层厚度与该所在位置处的相关长度之间的相对误差是否满足收敛准则,若不满足,则改变分层厚度,直至满足为止。

$\lim_{I} \frac{| θ_{I} - Δ l_{I} |}{Δ l_{I}} \leq ε$ ,

(18)

式中, $θ_{I}$ 为某深度处土性参数的相关长度。

图4为某湿陷性黄土高填方边坡剖面,坡高64 m,坡度为1∶2.5,边坡土体的分类情况列于图4。表1列出了各类土对应的土性参数平均值。根据表1中的数据,参照场地等级规范,该边坡上部土体可视为同一土层,分别建立两种分层模型,其一是忽略较薄的软弱层,将边坡划分为两层,上层为填筑土,厚度64 m,下层为粉质黏土,厚度40 m；其二是考虑软弱夹层,将边坡划分为三层,上层为填筑土,厚度64 m,中层为黄土状粉土,厚度3 m,下层为粉质黏土,厚度37 m,边坡分层模型如图5所示。该简化模型忽略了土层倾角的变化,并将相似土层视为同类土。前者简化可能会造成对临界滑移面预测的误差,而后者的差异可通过引入同类土的空间变异性予以考虑。

图 4 土体剖面

Figure 4. Profile of soil slope

下载: 全尺寸图片幻灯片

表 1 边坡的基本土性参数

Table 1. Key soil parameters of soil slope

土类	c/kPa	φ/(°)	γ/(kN·m^-3)	E/MPa
填筑体	40	20	19.0	6.0
3-1	18	22	14.7	1.8
3-2	26	23	19.2	7.3
4	28	22	19.7	7.8
5	29	20	20.5	8.2
6	31	22	20.9	8.5
7-1	80	23	—	25.0

下载: 导出CSV

| 显示表格

图 5 简化土坡剖面

Figure 5. Simplified profile of soil slope

下载: 全尺寸图片幻灯片

采用K-L方法^[24]进行随机场离散。表2列出了针对图4边坡采用不同随机场模型的土性参数随机场模型的相关统计特征参数,其中,黏聚力、内摩擦角以及土体重度的相关参数取自Phoon等^[17]。

表 2 土性参数随机场模型相关参数

Table 2. Soil parameters of random field model

随机场模型	土性参数	μ	COV	l_h/m	l_v/m
平稳模型	γ/(kN·m^-3)	18.4	0.18	40	6
	c/kPa	35	0.24	40	4
	φ/(°)	21	0.22	40	4
蒋水华非平稳模型	γ/(kN·m^-3)	18.4	—	—	—
	c/kPa	35	0.24	40	4
	φ/(°)	21	0.22	40	4
两层非平稳模型	γ₁/(kN·m^-3)	18.1	0.16	40	6
	c₁/kPa	40	0.30	40	10
	φ₁/(°)	20	0.30	40	10
	γ₂/(kN·m^-3)	19	0.21	40	6
	c₂/kPa	27	0.22	40	4
	φ₂/(°)	22	0.19	40	4
三层非平稳模型	γ₁/(kN·m^-3)	18.1	0.16	40	6
	c₁/kPa	40	0.30	40	10
	φ₁/(°)	20	0.30	40	10
	γ₂/(kN·m^-3)	14.7	0.14	40	6
	c₂/kPa	18	0.30	40	4
	φ₂/(°)	22	0.21	40	4
	γ₃/(kN·m^-3)	19	0.21	40	6
	c₃/kPa	27	0.22	40	4
	φ₃/(°)	22	0.19	40	4

下载: 导出CSV

| 显示表格

采用本文所提出的分层非平稳随机场,建立了抗剪强度参数黏聚力和内摩擦角随机场,其典型实现如图6所示。考虑到蒋水华模型^[11]同时考虑了均值和方差函数随深度的变化,选取该模型作为对比,图6还给出了平稳随机场模型下黏聚力 $c$ 和内摩擦角 $φ$ 的实现值。

图 6 不排水抗剪强度参数

$c$ ,

$φ$ 值沿埋深的典型实现

Figure 6. Typical simulated samples of undrained shear strength parameters with depth

下载: 全尺寸图片幻灯片

从图6可以看出,根据本文所建立分层非平稳随机场模型,所得黏聚力与内摩擦角均值沿土体埋深非连续变化,呈现明显的非平稳特征,与实际边坡剖面土性参数的分布特点一致。采用蒋水华模型所得黏聚力和内摩擦角的均值则随深度线性连续增大,其随机场实现值在均值两侧较均匀随机波动,能够较好描述土性参数的非平稳特征,但不能有效描述其分层特性。而采用平稳随机场模型得到的黏聚力和内摩擦角的均值随埋深不变,其随机场实现值在均值两侧波动,不能体现土性参数的非平稳分布特征。由此可见,对于由不同类别土壤构成的土质边坡,由于土性参数的统计特征参数具有显著非连续变化的非平稳特征,分层非平稳随机场对此可以有效描述,而均值连续线性变化的非平稳随机场模型对此阶跃式非连续变化特性的描述欠完备。

3. 边坡稳定可靠性分析与讨论

根据表2的土性参数统计值,针对图5所示简化边坡模型,分别建立平稳随机场模型、连续非平稳随机场模型^[11]以及本文提出的分层非平稳随机场模型,并利用有限元极限分析方法（finite element limit analysis,简记为FELA）,进行边坡稳定可靠度计算。

3.1 边坡稳定可靠性分析方法

FELA基于塑性极限分析理论,结合广义变分原理与混合有限元方法,通过建立静力许可应力场和运动许可速度场,用线性规划算法,从而求解破坏荷载（或极限承载力）下限与上限的一种数值分析方法^[26-28]。FELA能快速得到问题的严格上下限以及可能的临界滑移面^[13]。

假设土为理想弹塑性材料,比例加载,土质边坡稳定性问题的广义变分原理可写为

$\begin{matrix} \min_{\dot{u}} \max_{σ, α} α + \int_{V} σ^{T} \nabla \dot{u} d v - \int_{V} f^{T} \dot{u} d v - \int_{S} (α t_{ext} + t_{s})^{T} \dot{u} d s \\ s .t . F (σ) \leq 0 \end{matrix}$ 。

(19)

式中 $α$ 为荷载因子； $σ$ 为边坡内任一点应力状态； $f$ 为边坡内体积力矢量,通常为重力矢量； $\dot{u}$ 为边坡速度矢； $t_{ext}$ 为边坡外荷载矢量,对于边坡失稳问题,通常只考虑重力作用,该项为零； $t_{s}$ 为孔隙压力, $F (σ)$ 为理想弹塑性材料屈服函数,可采用多面体近似将其转化为线性约束：

$f_{i} σ - k_{i} \leq 0 (i = 1 ~ n)$ ,

(20)

式中, $f_{i}, k_{i}$ 为对应的分段线性化屈服函数。

将上述有限元极限分析理论,结合强度折减法,对边坡进行稳定性分析,边坡安全系数为

$F_{s} = \frac{土体抗剪强度}{极限平衡状态剪应力} = \frac{\tan φ}{\tan φ_{cr}} = \frac{c}{c_{cr}}$ 。

(21)

由于土性参数的空间变异性,导致边坡安全系数不再为常数,而是随机变量。采用Monte Carlo法结合FELA法进行边坡稳定可靠性分析^[29]。边坡失效概率 $P_{f}$ 为

$P_{f} = P [g (X) \leq 0] = P [F_{s} - 1 \leq 0] = \int_{F_{s} \leq 1} f (F_{s}) d F_{s}$ ,

(22)

式中, $f (F_{s})$ 为边坡安全系数的概率密度函数, $X =$ ${x_{1}, x_{2}, \dots, x_{n}}^{T}$ 为参数随机场。

3.2 边坡安全系数分布特点

采用Monte Carlo法模拟2000次,各参数随机场模型所得的边坡安全系数分布如图7所示。

图 7 各模型的边坡稳定安全系数分布规律

Figure 7. Distribution of safety factor of soil slope

下载: 全尺寸图片幻灯片

经检验,各模型边坡安全系数分布均服从对数正态分布。采用平稳随机场模型时,如图7（a）,（b）所示,安全系数上下限均值分别为1.747,1.700,为各种模型中最大者；其次为连续非平稳随机场模型结果,如图7（c）,（d）所示,安全系数上下限均值分别是1.518,1.501,均小于平稳随机场分析值；采用两层非平稳随机场,如图7（e）,（f）所示,安全系数上下限均值分别为1.274,1.247；3层非平稳随机场模型（图7（g）,（h））,安全系数上下限均值分别为1.187,1.159。3层非平稳模型由于明确考虑了软弱层的影响,安全系数的上下限均值是各种模型中最小者。上述4种模型中,参数线性连续变化非平稳随机场模型的安全系数分布图较其他模型尖窄,由图8所示各模型典型临界滑移面可知,这可能是由于该随机场模型给出的滑移模式较为集中所致。上述安全系数的差异表明,平稳随机场模型由于忽略了参数的非平稳特性,会高估边坡失稳风险。

图 8 抗剪强度参数云图和边坡临界滑移面

Figure 8. Nephogram of shear strength parameters and critical slip surface of soil slope

下载: 全尺寸图片幻灯片

3.3 各模型滑坡模式比较

进一步对比采用不同参数随机场模型所得到的边坡临界滑移面的形状和位置差异。图8选取了4种随机场模型的典型边坡临界滑移面及其相应的抗剪强度参数c,φ样本云图。平稳随机场模型,由于忽略统计特征参数的空间变异性,可以得到位于坡面或坡脚的浅层或深层滑移模式,其中,与安全系数均值区域对应的典型滑移模式主要为滑移面下凹、剪出口位于坡底的深层滑坡,如图8（a）所示；采用蒋水华等提出的线性连续非平稳随机场模型,该模型虽然可以生成抗剪强度参数急剧变化的个别样本（图2（c））,但由于黏聚力与内摩擦角的均值函数总体沿埋深线性连续增大,因此,所得到的边坡失效模式主要为沿坡面的浅层失稳模式,滑坡剪出口位于上部坡面,未穿过薄弱层,如图8（b）所示；两层非平稳随机场,滑移面处于相对较弱的下层土中,其滑坡剪出口位于坡脚,滑移面形状与平稳随机场模型类似,如图8（c）所示；三层非平稳随机场的边坡失效模式为处于软弱夹层中,滑坡剪出口位于坡脚,滑移面形状也与平稳随机场模型类似,如图8（d）所示,这与实际工程经验较为吻合。而平稳随机场模型以及线性连续非平稳随机场模型,所给出的位于边坡顶部的浅层滑移模式均与实际不符。综上,对于由多种类别土壤构成的具有分层特性的边坡,土性参数统计特征参数沿深度的非连续变化对边坡失效模式以及边坡安全系数均有显著影响,参数随机场模型应合理,并有效考虑这一非连续非平稳特性。

4. 结论

本文针对由多种类别土壤构成的具有分层特性的边坡,提出并建立了土性参数分层非平稳随机场模型,采用有限元极限分析方法,进行了边坡稳定可靠性分析,通过不同随机场模型下边坡稳定可靠性计算结果的对比分析,研究了黏聚力和内摩擦角的非均匀涨落特征对边坡稳定可靠度的影响。主要结论如下：

（1）对于具有明显分层特征的土质边坡,与平稳随机场模型以及均值线性连续变化的非平稳随机场模型相比,本文提出的分层非平稳随机场模型能有效考虑土性参数的统计特征参数随埋深非连续变化,为合理表征分层边坡土性参数的非平稳特性提供了一条有效途径。

（2）土性参数的空间变异性导致边坡存在多种失效模式,不同的抗剪强度参数随机场模型会导致对边坡临界滑移面的形状和位置的估计的显著差异。平稳随机场模型,由于忽略统计特征参数的空间变异性,所得到典型滑移模式主要为滑移面下凹、剪出口位于坡底的深层滑坡；采用线性连续非平稳随机场模型,由于黏聚力与内摩擦角的均值函数沿埋深线性连续增大,所得到的边坡失效模式均为沿坡面的浅层失稳模式,滑坡剪出口位于上部坡面,未穿过薄弱层。本文提出的分层非平稳随机场模型,明确考虑了软弱层,给出的边坡临界滑移面处于相对较弱的土层或软弱夹层中,与工程经验较为吻合。

（3）对于由多种类别土壤构成的分层边坡工程,忽略土性参数均值与方差沿空间的变异性的平稳随机场模型,会高估边坡稳定性；与均值线性连续变化的非平稳随机场模型相比,考虑土性参数的统计特征参数沿深度非连续变化的分层非平稳随机场模型的计算结果更为合理。

图 1 双层非饱和土一维固结模型

Figure 1. 1D consolidation model for double-layered unsaturated soils

下载: 全尺寸图片幻灯片

图 2 单面渗透边界下超孔隙压力等时线比较

Figure 2. Isochrone comparisons of excess pore pressures for single drainage

下载: 全尺寸图片幻灯片

图 3 双面渗透边界下超孔隙压力等时线比较

Figure 3. Isochrone comparisons of excess pore pressures for double drainage

下载: 全尺寸图片幻灯片

图 4 超孔隙气压分布曲线

Figure 4. Curves for distribution of excess pore-air pressure with depth

下载: 全尺寸图片幻灯片

图 5 超孔隙水压分布曲线

Figure 5. Curves for distribution of excess pore-water pressure with depth

下载: 全尺寸图片幻灯片

图 6 不同h₁/H的沉降–时间曲线

Figure 6. Curves of settlement vs. time for different values of h₁/H

下载: 全尺寸图片幻灯片

不同 $k_{\text{a}}^{(2)}/k_{\text{a}}^{(1)}$ 的沉降–时间曲线

Curves of settlement vs. time for different values of $k_{\text{a}}^{(2)}/k_{\text{a}}^{(1)}$

下载: 全尺寸图片幻灯片

不同 $k_{\text{w}}^{(2)}/k_{\text{w}}^{(1)}$ 的沉降–时间曲线

Curves of settlement vs. time for different values of $k_{\text{w}}^{(2)}/k_{\text{w}}^{(1)}$

下载: 全尺寸图片幻灯片

参考文献(30)

[1]	TERZAGHI K. Theoretical Soil Mechanics[M]. New York: John Wiley and Sons, 1943.
[2]	FREDLUND D G, HASAN J U. One-dimensional consolidation theory: unsaturated soils[J]. Canadian Geotechnical Journal, 1979, 16(3): 521–531. doi: 10.1139/t79-058
[3]	谢康和. 双层地基一维固结理论与应用[J]. 岩土工程学报, 1994, 16(5): 24–35. doi: 10.3321/j.issn:1000-4548.1994.05.004 XIE Kang-he. Theory of one dimensional consolidation of double-layered ground and its applications[J]. Chinese Journal of Geotechnical Engineering, 1994, 16(5): 24–35. (in Chinese) doi: 10.3321/j.issn:1000-4548.1994.05.004
[4]	BIOT M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155–164. doi: 10.1063/1.1712886
[5]	BARDEN L. Consolidation of compacted and unsaturated clays[J]. Géotechnique, 1965, 15(3): 267–286. doi: 10.1680/geot.1965.15.3.267
[6]	杨代泉, 沈珠江. 非饱和土一维固结简化计算[J]. 岩土工程学报, 1991, 13(5): 70–78. doi: 10.3321/j.issn:1000-4548.1991.05.008 YANG Dai-quan, SHEN Zhu-jiang. Simplified computation of one-dimensional consolidation of unsaturated soils[J]. Chinese Journal of Geotechnical Engineering, 1991, 13(5): 70–78. (in Chinese) doi: 10.3321/j.issn:1000-4548.1991.05.008
[7]	陈正汉, 谢定义, 刘祖典. 非饱和土固结的混合物理论(Ⅰ)[J]. 应用数学和力学, 1993, 14(2): 127–137. https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX199302004.htm CHEN Zheng-han, XIE Ding-yi, LIU Zu-dian. Consolidation theory of unsaturated soil based on the theory of mixture(Ⅰ)[J]. Applied Mathematics and Mechanics, 1993, 14(2): 127–137. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX199302004.htm
[8]	陈正汉. 非饱和土固结的混合物理论(Ⅱ)[J]. 应用数学和力学, 1993, 14(8): 687–698. https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX199302004.htm CHEN Zheng-han. Consolidation theory of unsaturated soil based on the theory of mixture(Ⅱ)[J]. Applied Mathematics and Mechanics, 1993, 14(8): 687–698. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YYSX199302004.htm
[9]	殷宗泽, 凌华. 非饱和土一维固结简化计算[J]. 岩土工程学报, 2007, 29(5): 633–637. doi: 10.3321/j.issn:1000-4548.2007.05.001 YIN Zong-ze, LING Hua. Simplified computation of 1D consolidation for partially saturated soil[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(5): 633–637. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.05.001
[10]	陈正汉. 非饱和土与特殊土力学的基本理论研究[J]. 岩土工程学报, 2014, 36(2): 201–272. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201402002.htm CHEN Zheng-han. On basic theories of unsaturated soils and special soils[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 201–272. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201402002.htm
[11]	陈正汉, 黄海, 卢再华. 非饱和土的非线性固结模型与弹塑性固结模型及其应用[J]. 应用数学和力学, 2001, 22(1): 93–103 doi: 10.3321/j.issn:1000-0887.2001.01.011 CHEN Zheng-han, HUANG Hai, LU Zai-hua. Non-linear and elasto-plasticity consolidation models of unsaturated soil and applications. Applied Mathematics and Mechanics, 2001, 22(1): 93–103. (in Chinese) doi: 10.3321/j.issn:1000-0887.2001.01.011
[12]	YAO Z H, CHEN Z H, FANG X W, et al. Elastoplastic damage seepage–consolidation coupled model of unsaturated undisturbed loess and its application[J]. Acta Geotechnica, 2020, 15(6): 1637–1653. doi: 10.1007/s11440-019-00873-z
[13]	QIN A F, CHEN G J, TAN Y W, et al. Analytical solution to one-dimensional consolidation in unsaturated soils[J]. Applied Mathematics and Mechanics (English Edition), 2008, 29(10): 1329–1340. doi: 10.1007/s10483-008-1008-x
[14]	QIN A F, SUN D A, TAN Y W. Analytical solution to one-dimensional consolidation in unsaturated soils under loading varying exponentially with time[J]. Computers and Geotechnics, 2010, 37(1/2): 233–238.
[15]	秦爱芳, 张九龙. 考虑渗透系数变化的非饱和土固结性状分析[J]. 岩土力学, 2015, 36(6): 1521–1528, 1536. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201506001.htm QIN Ai-fang, ZHANG Jiu-long. Analysis of consolidation of unsaturated soil with variable permeability coefficient[J]. Rock and Soil Mechanics, 2015, 36(6): 1521–1528, 1536. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201506001.htm
[16]	SHAN Z D, LING D S, DING H J. Exact solutions for one-dimensional consolidation of single-layer unsaturated soil[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2012, 36(6): 708–722. doi: 10.1002/nag.1026
[17]	ZHOU W H, ZHAO L S, LI X B. A simple analytical solution to one-dimensional consolidation for unsaturated soils[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(8): 794–810. doi: 10.1002/nag.2231
[18]	HO L, FATAHI B, KHABBAZ H. Analytical solution to one-dimensional consolidation in unsaturated soil deposit incorporating time-dependent diurnal temperature variation[J]. International Journal of Geomechanics, 2018, 18(5): 04018029. doi: 10.1061/(ASCE)GM.1943-5622.0001153
[19]	WANG L, SUN D A, LI L Z, et al. Semi-analytical solutions to one-dimensional consolidation for unsaturated soils with symmetric semi-permeable drainage boundary[J]. Computers and Geotechnics, 2017, 89: 71–80. doi: 10.1016/j.compgeo.2017.04.005
[20]	李红坡, 陈征, 冯健雪, 等. 双层地基水平排水砂垫层位置优化研究[J]. 岩土力学, 2020, 41(2): 437–444. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202002013.htm LI Hong-po, CHEN Zheng, FENG Jian-xue, et al. Study on position optimization of horizontal drainage sand blanket of double-layer foundation[J]. Rock and Soil Mechanics, 2020, 41(2): 437–444. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202002013.htm
[21]	叶梓, 艾智勇. 变荷载下层状非饱和土地基全耦合固结特性研究[J]. 岩土力学, 2021, 42(1): 135–142. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202101015.htm YE Zi, AI Zhi-yong. Fully-coupled consolidation characteristics of layered unsaturated soils subjected to varying loadings[J]. Rock and Soil Mechanics, 2021, 42(1): 135–142. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202101015.htm
[22]	SHAN Z D, LING D S, DING H J. Analytical solution for the 1D consolidation of unsaturated multi-layered soil[J]. Computers and Geotechnics, 2014, 57: 17–23. doi: 10.1016/j.compgeo.2013.11.009
[23]	ZHOU W H, ZHAO L S. Consolidation of a two-layer system for unsaturated soil with the differential quadrature method[C]// Geo-Congress. Atlanta, 2014: 3994–4003.
[24]	MORADI M, KESHAVARZ A, FAZELI A. One dimensional consolidation of multi-layered unsaturated soil under partially permeable boundary conditions and time-dependent loading[J]. Computers and Geotechnics, 2019, 107: 45–54. doi: 10.1016/j.compgeo.2018.11.020
[25]	LI P C, WANG K Y, LU D T. Analytical solution of plane-strain poroelasticity due to surface loading within a finite rectangular domain[J]. International Journal of Geomechanics, 2017, 17(4): 04016089.
[26]	汪磊, 孙德安, 解益, 等. 任意荷载下分数阶导数黏弹性饱和土体一维固结[J]. 岩土工程学报, 2017, 39(10): 1823–1831. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201710014.htm WANG Lei, SUN De-an, XIE Yi, et al. One-dimensional consolidation of fractional derivative viscoelastic saturated soils under arbitrary loading[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(10): 1823–1831. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201710014.htm
[27]	WANG L, XU Y F, XIA X H, et al. A series of semianalytical solutions of one-dimensional consolidation in unsaturated soils[J]. International Journal of Geomechanics, 2020, 20(6): 06020005.
[28]	周祥运, 孙德安, 林宇亮. 基于散热的高放废物处置库废物罐间距研究[J]. 岩土工程学报, 2020, 42(11): 2069–2077. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202011016.htm ZHOU Xiang-yun, SUN De-an, LIN Yu-liang. Canister spacing in a high level radioactive nuclear waste repository based on heat conduction[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(11): 2069–2077. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202011016.htm
[29]	FREDLUND D G, RAHARDJO H. Soil Mechanics for Unsaturated Soils[M]. Hoboken: John Wiley & Sons, Inc, 1993.
[30]	CRUMP K S. Numerical inversion of Laplace transforms using a Fourier series approximation[J]. Journal of the ACM, 1976, 23(1): 89–96.

施引文献(8)

期刊类型引用(4)

1.	王体强，王永志，梁小丛，王德咏，陈卓识. 超重力模型试验干–饱和砂动剪切模量阻尼比特性研究. 岩石力学与工程学报. 2023(06): 1546-1559 . 百度学术
2.	陈平山，梁小丛，王体强，王德咏，王永志，樊旭，陈卓识，袁晓铭. 珊瑚礁砂与标准砂场地液化特征动力离心试验研究. 岩石力学与工程学报. 2023(09): 2283-2294 . 百度学术
3.	黄晓实，黄俊清，颜业敢，汪玉冰. 基于动土压力影响的坝基动剪切模量反演研究. 岩土力学. 2023(10): 2889-2898 . 百度学术
4.	王永志，王体强，袁晓铭，张雪东，陈卓识. 动力离心试验反演分析砂土模量阻尼比特征与可靠性. 岩石力学与工程学报. 2022(08): 1717-1727 . 百度学术