考虑热效应的污染物在土中扩散、渗透和固结耦合模型

田改垒; 张志红

doi:10.11779/CJGE202202009

考虑热效应的污染物在土中扩散、渗透和固结耦合模型 English Version

田改垒,
张志红^,

北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124

基金项目:

国家自然科学基金面上项目 51678012

详细信息

作者简介:
田改垒(1990—)，女，博士，主要从事环境岩土工程研究。E-mail: bjuttian@163.com

通讯作者:
张志红，E-mail: zhangzh2002@bjut.edu.cn

中图分类号: TU431
计量
- 文章访问数: 285
- HTML全文浏览量: 54
- PDF下载量: 224
出版历程
- 收稿日期: 2020-12-24
- 网络出版日期: 2022-09-22
- 刊出日期: 2022-01-31

Coupled model for contaminant diffusion, osmosis and consolidation in soil considering thermal effects

TIAN Gai-lei,
ZHANG Zhi-hong^,

The Key Laboratory of Urban Security and Disaster Engineering, Ministry of Education, Beijing University of Technology, Beijing 100124, China

摘要

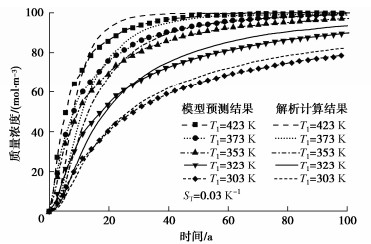
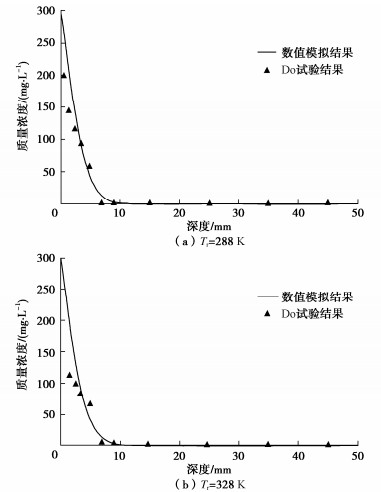
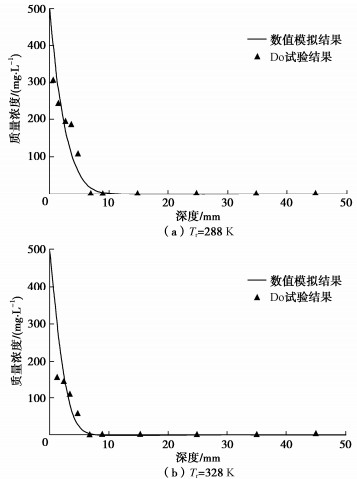
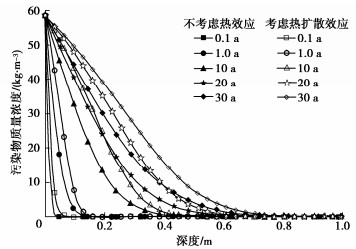
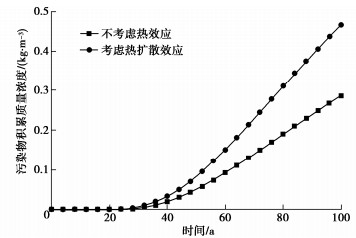
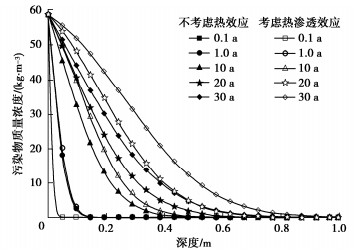
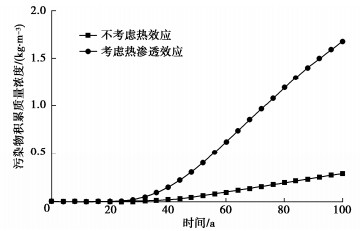
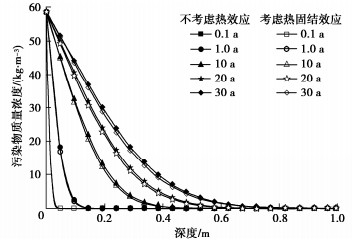
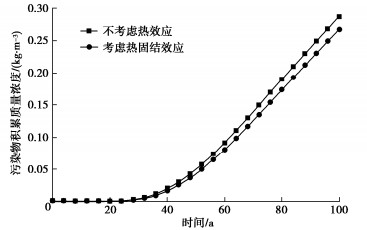
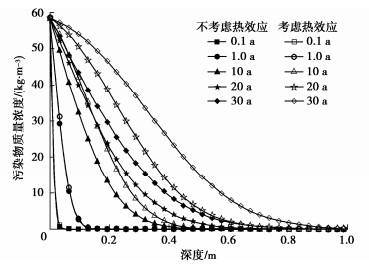
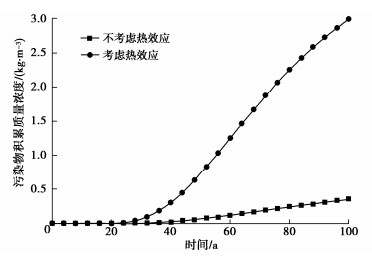
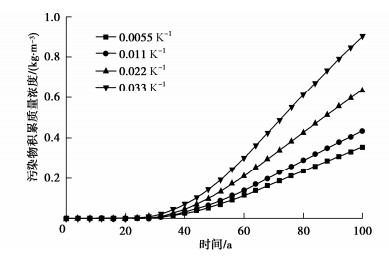
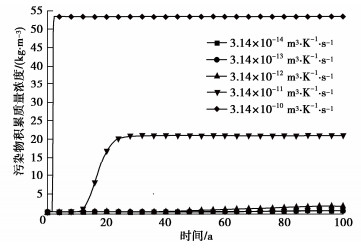
摘要: 为探究温度对污染物运移进程的影响，建立了考虑热效应的污染物在土中扩散、渗透和固结耦合模型，该模型不仅能够体现污染物运移过程中土体物理特性及输运性质的动态变化，同时实现了扩散、渗透和固结机制的耦合。在验证模型有效性的基础上，分析了热扩散、热渗透、热固结及其综合效应对污染物运移规律的影响。结果表明：热扩散、热渗透能够显著加快污染物运移，且随着索雷特系数和热渗透系数的增大，热扩散和热渗透效应对污染物运移的促进作用增强。而热固结效应则能够减缓污染物运移，但随着土体热膨胀系数的增加，垫层底部污染物积累质量浓度变化不大。当温差为40 K时，与不考虑热效应工况相比，考虑热扩散、热渗透和热固结综合效应影响下的污染物击穿时间缩短54 a。
- 热扩散 /
- 热渗透 /
- 热固结 /
- 污染物运移
Abstract: To explore the influences of temperature on pollutant transport, a coupled model for contaminant diffusion in soils, osmosis and consolidation considering the thermal effects is proposed to reflect the dynamic changes of physical properties of soils and transport properties in the process of pollutant transport and realize the coupling of diffusion, osmosis and consolidation. On the basis of verifying the validity of the model, the effects of thermal diffusion, thermo-osmosis, thermal consolidation and their combined effect on pollutant transport are analyzed. The simulated results show that the thermal diffusion and thermo-osmosis can accelerate contaminant transport, and with the increase of Soret coefficient and thermal permeability, the thermal diffusion and thermo-osmosis effects enhance. However, the thermal consolidation can slow down the pollutant transport rate, but with the increase of expansion coefficient of soils, the accumulation concentration of pollutant at the bottom of clay layer has little change. When the temperature difference is 40 K, the breakthrough time with considering the combined effects of thermal diffusion, thermo-osmosis and thermal consolidation can be shortened by 53.97 years compared with the results without considering the thermal effects.
- thermal diffusion /
- thermo-osmosis /
- thermal consolidation /
- contaminant transport

HTML全文

0. 引言

管棚超前预支护技术能在一定范围内较大幅度提高天然土体强度、刚度，有效减小地表沉降、拱顶沉降，确保隧道掘进支护安全，且因具有施工简便、经济、支护距离长和安全效益高的特点而成为经常采用的超前预支护方法。

目前国内外学者关于管棚预支护技术的作用机理和加固效果开展了大量研究。Hisatake等^[1]、Juneja等^[2]通过离心机模型试验，考虑了开挖效果的影响，研究了管棚支护的作用效果。郭璇等^[3]采用设计正交模型试验的方法，研究了管棚预支护的作用效果以及管棚对土压力分布的影响。周顺华等^[4]在原位观测和室内模型离心模型试验的基础上，提出了管棚作用的棚架原理。董新平^[5]则基于棚架体系建立了管棚的空间分析模型，研究了管棚支护作用的主要特征。Chungsik等^[6]、Ali等^[7]通过建立三维数值模型研究了管棚的受力和变形特征以及预支护效果。在理论分析方面，由于基于弹性地基梁理论的管棚分析模型具有简单实用的特点，故而具有很高的进一步研究完善的价值。李忠凯^[8]通过建立基于Winkler地基模型的管棚分析模型，推导出一个开挖循环过程中管棚内力和变形的计算表达式。郑俊杰等^[9]考虑了开挖对基床系数的影响，提出了变基床系数下管棚的地基梁模型。丁祖德等^[10]则对弹性地基梁模型中基床系数的取值展开详细研究。王炳智等^[11]通过改进弹性地基约束形式，采用Pasternak弹性地基理论建立管棚的分析模型并进行了求解。王道远等^[12]通过对比两个地基模型的计算结果与现场试验值的比较，得到基于Pasternak弹性地基理论的管棚模型更具合理性，并通过讨论地层反力系数以及管棚直径对管棚作用效果的影响，得出通过调整注浆改善地层反力系数或直径的方法来控制管棚变形效果甚微的结论。武松等^[13]根据弹性理论的刚度等效法，将管棚的一维弹性地基梁模型拓展至二维弹性地基各向异性板模型，并采用有限元法对模型进行了求解。

综上所述，针对基于弹性地基梁理论的管棚分析模型的研究已较为成熟，但在模型的建立过程中，对荷载的分布范围和管棚约束形式的认识上还存在矛盾，并且通过对模型的求解，并没有得到关于管棚设计和施工参数对管棚支护效果影响的一般性结论。预支护区段开挖支护完成后管棚全长范围内力和变形的最终分布并不明确。本文结合管棚超前预支护技术在实际运用过程中的问题以及国内外学者对管棚预支护技术研究的基础上，考虑掌子面失稳段对管棚约束的弱化以及隧道开挖支护动态施工过程，通过建立基于Pasternak弹性地基梁理论的管棚分析模型，采用理论推导的方法研究管棚预支护技术的支护效果以及受力特点，并系统地研究各设计施工参数对管棚力学响应的影响，从而为管棚的设计施工提供参考和借鉴。

1. 管棚分析模型的建立

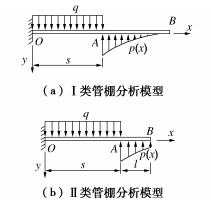
根据管棚作用下隧道开挖过程的施工经验以及管棚既有设计方法，可采用Euler-Bernoulli梁来对管棚的受力和变形进行分析计算。根据管棚的受力特点，可将管棚沿纵向分为初期支护段、开挖段和未开挖段3部分来进行分析（见图 1）。位于洞口的导向墙由于具有独立的基础和仅承受管棚作用的特点，可认为导向墙对管棚的约束形式为固定端约束，且无初始位移。在隧道开挖过程中，开挖段在围岩压力的作用下将力传递给导向墙或初期支护以及掌子面前方围岩，管棚发生变形。将该开挖段支护后，管棚则以该变形状态固结在初期支护中，初期支护前端对管棚的约束可认为具有初始位移和初始转角的固定端约束，而此处管棚的变形值即为下个循环开挖分析时管棚起固定端处的初始变形值。在掌子面前方，可认为由于隧道的开挖，掌子面在地应力作用下发生失稳，则该段围岩将无法承受管棚变形引起的附加应力，则可认为掌子面失稳段与开挖段具有相同的性质。失稳段前方围岩承受因管棚变形而产生的附加力，该段管棚受围岩的弹性地基约束。

图 1 管棚预支护段施工示意图

Figure 1. Construction diagram of pre-support section of pipe roof

下载: 全尺寸图片幻灯片

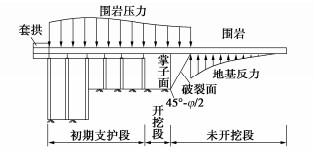
在单个循环进尺的分析中，以初期支护前端作为分析模型的起点，为具有初始竖向位移 ${\omega _{\text{0}}}$ 和初始转角 ${\theta _{\text{0}}}$ 的固定端。管棚承受开挖段及掌子面失稳段上方的围岩压力。根据莫尔–库仑强度准则，可假设掌子面沿开挖方向失稳的破裂面与铅垂线的夹角为45° $- \varphi {\text{/2}}$ ，若单个循环开挖进尺长度为 $a$ ，则围岩压力作用范围为 $s = a + H\tan ({45^ \circ } - \varphi /2)$ ，其中 $H$ 为上台阶高度。由于一个循环开挖进尺长度较短，可认为作用于管棚上的围岩压力值在该分析段保持不变。而围岩压力在纵向方向上的连续变化可离散为每个开挖区段上的常围岩压力。破裂面前方围岩以弹性地基约束形式作用于管棚，从而建立单个循环进尺的管棚分析模型（见图 2）。在管棚超前支护作用下隧道的循环开挖，其力学行为等价于单个循环进尺的管棚分析模型的不断移动，通过迭代计算可得到管棚全长范围最终的内力和变形分布。

图 2 单个循环进尺的管棚分析模型

Figure 2. Analysis model for pipe roof with single cycle footage

下载: 全尺寸图片幻灯片

通过对管棚受力过程的分析，针对管棚的分析模型提出以下假设：①导向墙或初期支护对管棚的约束假设为固定端约束；②导向墙处管棚无初始挠度和转角；③假设掌子面前方失稳段围岩对管棚不具有约束作用；④掌子面前方岩体对管棚的约束反力采用Pasternak弹性地基理论来确定。

围岩对管棚的弹性地基约束根据管棚长度可分为两种类型。类型Ⅰ，埋入围岩中的管棚长度足够长，该条件下可认为管棚B端的边界条件为：当 $x \to \infty$ 时， $\omega (x) = 0$ ， $\theta (x) = 0$ ，分析图示如图 2（a）所示。类型Ⅱ，以类型Ⅰ为基本分析模型，随着在管棚预支护范围内开挖的不断推进，在对预支护段的最后一个循环进尺进行分析时，B端将发生变形。此时B端的边界条件为：当 $x = s + l$ 时， $M(x) = 0$ ， $Q(x) = 0$ ，其中 $l$ 为搭接长度，分析如图 2（b）所示。

管棚作为松散破碎地层中开挖隧道所采用的预支护技术，其预支护地层往往是破碎的散体介质，因此在进行管棚结构的分析计算时，采用松散围岩压力计算方法确定作用于管棚结构上的荷载比较符合实际情况。本模型浅埋隧道围岩压力的计算采用全土柱理论，深埋隧道围岩压力的计算采用普氏理论，则围岩压力可表示为统一的表达式：

。

${q^ * } = \gamma \cdot h。$

(1)

式中 $\gamma$ 为围岩重度（kN/m³）； $h$ 为上覆松动围岩的高度（m），浅埋隧道为取隧道埋深，深埋隧道取压力拱高度。

Pasternak弹性地基模型是在Winkler弹性地基模型的基础上假定弹簧之间存在剪切作用，引入地基剪切模量 ${G_{\text{p}}}$ ，则弹性地基作用于梁上的约束反力为

。

$p(x) = k{b^ * }\omega (x) - {G_{\text{p}}}{b^ * }\frac{{{{\text{d}}^2}\omega (x)}}{{{\text{d}}{x^2}}}。$

(2)

式中 $k$ 为地基基床系数（kN/m³）； $\omega (x)$ 为 $x$ 点处梁的挠度（m）； ${G_{\text{p}}}$ 为地基剪切模量（kN/m）； ${b^ * }$ 为地基剪切层的等效宽度（m），满足 ${b^ * } = b[1 + \sqrt {{G_{\text{p}}}{\text{/}}k} /b]$ ， $b$ 为管棚钢管的管径。Pasternak弹性地基模型相比Winkler地基模型通过引入地基剪切模量，弥补了Winkler模型地基不连续的缺陷，因此更符合实际情况，并且相比弹性半空间模型，Pasternak模型大大降低了计算复杂度。

2. 管棚分析模型的求解

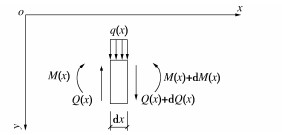
分析Euler-Bernoulli梁在受外荷载作用发生变形时，在梁上任选微段作为分析单元，其中，剪力、弯矩及荷载的正方向均如图 3所示。

图 3 梁单元分析图示

Figure 3. Diagram of beam element analysis

下载: 全尺寸图片幻灯片

根据平衡条件可得

，

$\frac{{{\text{d}}Q(x)}}{{{\text{d}}x}} = - q(x)\text{，}$

(3)

。

$\frac{{{\text{d}}M(x)}}{{{\text{d}}x}} = Q(x)。$

(4)

再根据梁的挠曲线近似微分方程：

。

$EI\frac{{{\text{d}}{\omega ^2}(x)}}{{{\text{d}}{x^2}}} = - M(x)。$

(5)

将式（4），（5）代入式（3），即可得到分布荷载作用下，梁的变形控制微分方程为

。

$EI\frac{{{{\text{d}}^4}\omega (x)}}{{{\text{d}}{x^4}}} = q(x)。$

(6)

单个循环进尺的管棚分析模型如图 2所示，根据荷载和约束的分布形式，可分段建立管棚的控制微分方程并求解，得到OA段控制微分方程：

，

$EI\frac{{{{\text{d}}^4}\omega (x)}}{{{\text{d}}{x^4}}} = q\text{，}$

(7)

式中， $q = j{q^ * }$ ， $j$ 为管棚环向间距（m），即作用于单根梁上围岩压力的宽度。其通解为

。

${\omega _{\text{1}}}(x) = \frac{q}{{24EI}}{x^4} + {B_1}{x^3} + {B_2}{x^2} + {B_3}x + {B_4}。$

(8)

根据式（5）~（7）表示的梁的弯矩、剪力和荷载与梁挠度之间的微分关系，将挠度表达式进行求导运算，即可得到管棚转角、弯矩和剪力的分段表达式。其中OA段转角、弯矩和剪力的解析表达式分别为

，

${\theta _1}{\text{(}}x{\text{)}} = \frac{q}{{6EI}}{x^3} + 3{B_1}{x^2} + 2{B_2}x + {B_3}\text{，}$

(9)

${M_{\text{1}}}(x) = - EI\left( {\frac{q}{{2EI}}{x^2} + 6{B_1}x + 2{B_2}} \right) \text{，}$

(10)

${Q_1}(x) = - EI\left( {\frac{q}{{EI}}x + 6{B_1}} \right)。$

(11)

根据AB段的荷载分布形式，建立控制微分方程：

$EI\frac{{{{\text{d}}^4}\omega (x)}}{{{\text{d}}{x^4}}} - {G_{\text{p}}}{b^ * }\frac{{{{\text{d}}^2}\omega (x)}}{{{\text{d}}{x^2}}} + k{b^ * }\omega (x) = 0\text{，}$

(12)

令 ${\lambda ^{\text{4}}}{\text{ = }}\frac{{k{b^ * }}}{{4EI}}$ ， $\alpha = \sqrt {1 + \frac{{{G_{\text{p}}}{\lambda ^2}}}{k}}$ ， $\beta = \sqrt {1 - \frac{{{G_{\text{p}}}{\lambda ^2}}}{k}}$ ，求得其通解为

${\omega _2}(x) = {{\text{e}}^{ - \alpha \lambda x}}({B_5}\cos \beta \lambda x + {B_6}\sin \beta \lambda x) + \\ \;\;\;\;\;{{\text{e}}^{\alpha \lambda x}}({B_7}\cos \beta \lambda x + {B_8}\sin \beta \lambda x)。$

(13)

同理求得AB段转角、弯矩和剪力的解析表达式分别为

${\theta _2}(x) = - {B_5}{{\text{e}}^{ - \alpha \lambda x}}(\beta \lambda \sin \beta \lambda x + \alpha \lambda \cos \beta \lambda x) + \\ \;\;\;\;\;\;\;\;\;{B_6}{{\text{e}}^{ - \alpha \lambda x}}(\beta \lambda \cos \beta \lambda x - \alpha \lambda \sin \beta \lambda x) + \\ \;\;\;\;\;\;\;\;\;{B_7}{{\text{e}}^{\alpha \lambda x}}(\alpha \lambda \cos \beta \lambda x - \beta \lambda \sin \beta \lambda x) + \\ \;\;\;\;\;\;\;\;\; {B_8}{{\text{e}}^{\alpha \lambda x}}(\beta \lambda \cos \beta \lambda x + \alpha \lambda \sin \beta \lambda x)\text{，}$

(14)

${M_2}(x) = - EI\{ {B_5}{{\text{e}}^{ - \alpha \lambda x}}[{\text{(}}{\alpha ^2} - {\beta ^2}{\text{)}}{\lambda ^2}\cos \beta \lambda x + 2\alpha \beta {\lambda ^2}\sin \beta \lambda x] + \\ \;\;\; {B_6}{{\text{e}}^{ - \alpha \lambda x}}[({\alpha ^2} - {\beta ^2}){\lambda ^2}\sin \beta \lambda x - 2\alpha \beta {\lambda ^2}\cos \beta \lambda x] + \\ \;\;\; {B_7}{{\text{e}}^{\alpha \lambda x}}[({\alpha ^2} - {\beta ^2}){\lambda ^2}\cos \beta \lambda x - 2\alpha \beta {\lambda ^2}\sin \beta \lambda x] + \\ \;\;\; {B_8}{{\text{e}}^{\alpha \lambda x}}[({\alpha ^2} - {\beta ^2}){\lambda ^2}\sin \beta \lambda x + 2\alpha \beta {\lambda ^2}\cos \beta \lambda x]\} \text{，}$

(15)

${Q_2}(x) = - EI\{ {B_5}{{\text{e}}^{ - \alpha \lambda x}}[(3\alpha {\beta ^2} - {\alpha ^3}){\lambda ^3}\cos \beta \lambda x + ({\beta ^3} - 3{\alpha ^2}\beta ){\lambda ^3} \cdot \\ \sin \beta \lambda x] + {B_6}{{\text{e}}^{ - \alpha \lambda x}}[(3\alpha {\beta ^2} - {\alpha ^3}){\lambda ^3}\sin \beta \lambda x - ({\beta ^3} - 3{\alpha ^2}\beta ){\lambda ^3} \cdot \\ \cos \beta \lambda x] + {B_7}{{\text{e}}^{\alpha \lambda x}}[({\alpha ^3} - 3\alpha {\beta ^2}){\lambda ^3}\cos \beta \lambda x + ({\beta ^3} - 3{\alpha ^2}\beta ){\lambda ^3} \cdot \\ \sin \beta \lambda x] + {B_8}{{\text{e}}^{\alpha \lambda x}}[({\alpha ^3} - 3\alpha {\beta ^2}){\lambda ^3}\sin \beta \lambda x + (3{\alpha ^2}\beta - {\beta ^3}){\lambda ^3} \cdot \\ \;\;\;\;\;\; \cos \beta \lambda x]\} \text{，}$

(16)

式中， ${B_1}$ ， ${B_2}$ ， ${B_3}$ ， ${B_4}$ ， ${B_5}$ ， ${B_6}$ ， ${B_7}$ ， ${B_8}$ 均为待求积分常数。

2.1 Ⅰ类管棚分析模型的求解

类型Ⅰ的模型示意图如图 2（a）所示，对于AB段梁，由于B端满足 ${\omega _2}(x)\left| {_{x \to \infty } = 0} \right.$ ， ${\theta _2}(x)\left| {_{x \to \infty } = 0} \right.$ 的边界条件，则代入式（13）可求得 ${B_7}{\text{ = }}{B_{\text{8}}}{\text{ = 0}}$ 。由边界条件 ${\omega _1}(x)\left| {_{x = 0} = {\omega _0}} \right.$ ， ${\theta _{\text{1}}}(x)\left| {_{x = 0} = {\theta _0}} \right.$ ， ${\omega _1}(x)\left| {_{x = s} = {\omega _2}(x)} \right.\left| {_{x = s}} \right.$ ， ${\theta _1}(x)\left| {_{x = s} = {\theta _2}(x)} \right.\left| {_{x = s}} \right.$ ， ${M_1}(x)\left| {_{x = s} = {M_2}(x)} \right.\left| {_{x = s}} \right.$ ， ${Q_1}(x)\left| {_{x = s}} \right. =$ ${Q_2}(x)\left| {_{x = s}} \right.$ ，得方程组：

$\left[ {\begin{array}{*{20}{c}} {\text{0}}&{\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {{s^3}}&{{s^2}}&s&1&{{\varphi _{35}}}&{{\varphi _{36}}} \\ {3{s^2}}&{2s}&1&0&{{\varphi _{45}}}&{{\varphi _{46}}} \\ {6s}&2&0&0&{{\varphi _{55}}}&{{\varphi _{56}}} \\ 6&0&0&0&{{\varphi _{65}}}&{{\varphi _{57}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{B_1}} \\ {{B_2}} \\ {{B_3}} \\ {{B_4}} \\ {{B_5}} \\ {{B_6}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\omega _0}} \\ {{\theta _0}} \\ {{\psi _3}} \\ {{\psi _4}} \\ {{\psi _5}} \\ {{\psi _6}} \end{array}} \right]\text{，}$

(17)

式中， ${\varphi _{35}} = - {{\text{e}}^{ - \alpha \lambda s}}\cos \beta \lambda s$ ， ${\varphi _{3{\text{6}}}} = - {{\text{e}}^{ - \alpha \lambda s}}\sin \beta \lambda s$ ， ${\varphi _{{\text{4}}5}} =$ ${\text{e}}^{-\alpha \lambda s}(\beta \lambda \mathrm{sin}\beta \lambda s+\alpha \lambda \mathrm{cos}\beta \lambda s)，{\phi }_{\text{46}}=-{\text{e}}^{-\alpha \lambda s}(\beta \lambda \mathrm{cos}\beta \lambda s-$ $\alpha \lambda \mathrm{sin}\beta \lambda s)，{\phi }_{\text{5}5}=-{\text{e}}^{-\alpha \lambda s}[2\alpha \beta {\lambda }^{2}\mathrm{sin}\beta \lambda s+({\alpha }^{2}-{\beta }^{2}){\lambda }^{2}\cdot$ $\mathrm{cos}\beta \lambda s]，{\phi }_{\text{56}}=-{\text{e}}^{-\alpha \lambda s}[-2\alpha \beta {\lambda }^{2}\mathrm{cos}\beta \lambda s+({\alpha }^{2}-{\beta }^{2}){\lambda }^{2}\cdot$ $\mathrm{sin}\beta \lambda s]，{\phi }_{\text{6}5}=-{\text{e}}^{-\alpha \lambda s}[({\beta }^{3}-3{\alpha }^{2}\beta ){\lambda }^{3}\mathrm{sin}\beta \lambda s-({\alpha }^{3}-3\alpha {\beta }^{2})\cdot$ ${\lambda }^{3}\mathrm{cos}\beta \lambda s]，{\phi }_{\text{66}}={\text{e}}^{-\alpha \lambda s}[({\beta }^{3}-3{\alpha }^{2}\beta ){\lambda }^{3}\mathrm{cos}\beta \lambda s+({\alpha }^{3}-$ $3\alpha {\beta ^2}){\lambda ^3}\sin \beta \lambda s]$ ， ${\psi _3} = - q{s^4}/(24EI)$ ， ${\psi }_{\text{4}}=-q{s}^{\text{3}}/(\text{6}EI)，$ ${\psi _{\text{5}}} = - q{s^{\text{2}}}/(2EI)$ ， ${\psi _{\text{6}}} = - qs/(EI)$ 。

通过式（17）即可求得积分常数 ${B_1}$ ， ${B_2}$ ， ${B_3}$ ， ${B_4}$ ， ${B_5}$ ， ${B_6}$ ，将其回代到挠度、转角、弯矩和剪力表达式中，即可求得满足类型Ⅰ分析模型边界条件下管棚的变形和受力分布。

2.2 Ⅱ类管棚分析模型的求解

类型Ⅱ的模型示意图如所示，由边界条件 ${\omega _1}(x)\left| {_{x = 0} = {\omega _0}} \right.$ ， ${\theta _{\text{1}}}(x)\left| {_{x = 0} = {\theta _0}} \right.$ ， ${\omega _1}(x)\left| {_{x = s} = {\omega _2}(x)} \right.\left| {_{x = s}} \right.$ ， ${\theta _1}(x)\left| {_{x = s} = {\theta _2}(x)} \right.\left| {_{x = s}} \right.$ ， ${M_1}(x)\left| {_{x = s} = {M_2}(x)} \right.\left| {_{x = s}} \right.$ ， ${Q_1}(x)\left| {_{x = s} = } \right.$ ${Q_2}(x)\left| {_{x = s}} \right.$ ， ${M_{\text{2}}}(x)\left| {_{x = s + l} = } \right.0$ ， ${Q_2}(x)\left| {_{x = s + l}} \right. = 0$ ，得方程组：

$\left[ {\begin{array}{*{20}{c}} {\text{0}}&{\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {\text{0}}&{\text{0}}&{\text{1}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}}&{\text{0}} \\ {{s^3}}&{{s^2}}&s&1&{{\varphi _{35}}}&{{\varphi _{36}}}&{{\varphi _{37}}}&{{\varphi _{38}}} \\ {3{s^2}}&{2s}&1&0&{{\varphi _{45}}}&{{\varphi _{46}}}&{{\varphi _{47}}}&{{\varphi _{48}}} \\ {6s}&2&0&0&{{\varphi _{55}}}&{{\varphi _{56}}}&{{\varphi _{57}}}&{{\varphi _{58}}} \\ 6&0&0&0&{{\varphi _{65}}}&{{\varphi _{66}}}&{{\varphi _{67}}}&{{\varphi _{68}}} \\ 0&0&0&0&{{\varphi _{75}}}&{{\varphi _{76}}}&{{\varphi _{77}}}&{{\varphi _{78}}} \\ 0&0&0&0&{{\varphi _{85}}}&{{\varphi _{86}}}&{{\varphi _{87}}}&{{\varphi _{88}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{B_1}} \\ {{B_2}} \\ {{B_3}} \\ {{B_4}} \\ {{B_5}} \\ {{B_6}} \\ {{B_7}} \\ {{B_8}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\omega _0}} \\ {{\theta _0}} \\ {{\psi _3}} \\ {{\psi _4}} \\ {{\psi _5}} \\ {{\psi _6}} \\ 0 \\ 0 \end{array}} \right]\text{，}$

(18)

式中， ${\varphi _{35}} = - {{\text{e}}^{ - \alpha \lambda s}}\cos \beta \lambda s$ ， ${\phi }_{3\text{6}}=-{\text{e}}^{-\alpha \lambda s}\mathrm{sin}\beta \lambda s，{\phi }_{37}=$ $-{\mathrm{e}}^{\alpha \lambda s}\mathrm{cos}\beta \lambda s，$ ${\phi }_{3\text{8}}=-{e}^{\alpha \lambda s}\mathrm{sin}\beta \lambda s，{\phi }_{\text{4}5}={\text{e}}^{-\alpha \lambda s}(\beta \lambda \mathrm{sin}\beta \cdot$ $\lambda s + \alpha \lambda \cos \beta \lambda s)$ ， ${\varphi _{{\text{46}}}} = - {{\text{e}}^{ - \alpha \lambda s}}(\beta \lambda \cos \beta \lambda s - \alpha \lambda \sin \beta \lambda s)$ ， ${\varphi _{{\text{47}}}} = - {{\text{e}}^{\alpha \lambda s}}(\alpha \lambda \cos \beta \lambda s - \beta \lambda \sin \beta \lambda s)$ ， ${\varphi _{{\text{48}}}} = - {{\text{e}}^{\alpha \lambda s}} \cdot (\beta \lambda$ $\mathrm{cos}\beta \lambda s\text{+}\alpha \lambda \mathrm{sin}\beta \lambda s)，{\phi }_{\text{5}5}=-{\text{e}}^{-\alpha \lambda s}[2\alpha \beta {\lambda }^{2}\mathrm{sin}\beta \lambda s+({\alpha }^{2}-$ ${\beta }^{2}){\lambda }^{2}\mathrm{cos}\beta \lambda s]，{\phi }_{\text{56}}=-{\text{e}}^{-\alpha \lambda s}[-2\alpha \beta {\lambda }^{2}\mathrm{cos}\beta \lambda s+({\alpha }^{2}-{\beta }^{2})$ ${\lambda ^2}\sin \beta \lambda s]$ ， ${\varphi _{{\text{57}}}} = - {{\text{e}}^{\alpha \lambda s}}[ - 2\alpha \beta {\lambda ^2}\sin \beta \lambda s + ({\alpha ^2} - {\beta ^2}){\lambda ^2}$ $\mathrm{cos}\beta \lambda s]，$ ${\varphi _{{\text{58}}}} = - {{\text{e}}^{\alpha \lambda s}}[2\alpha \beta {\lambda ^2}\cos \beta \lambda s + ({\alpha ^2} - {\beta ^2}){\lambda ^2} \cdot \sin \beta$ $\lambda s]，{\phi }_{\text{6}5}=-{\text{e}}^{-\alpha \lambda s}[({\beta }^{3}-3{\alpha }^{2}\beta ){\lambda }^{3}\mathrm{sin}\beta \lambda s-({\alpha }^{3}-3\alpha {\beta }^{2})\cdot {\lambda }^{3}$ $\mathrm{cos}\beta \lambda s]，{\phi }_{\text{66}}={\text{e}}^{-\alpha \lambda s}[({\beta }^{3}-3{\alpha }^{2}\beta ){\lambda }^{3}\mathrm{cos}\beta \lambda s+({\alpha }^{3}-3\alpha {\beta }^{2})\cdot {\lambda }^{3}$ $\mathrm{sin}\beta \lambda s]，{\phi }_{\text{67}}=-{\text{e}}^{\alpha \lambda s}[({\alpha }^{3}-3\alpha {\beta }^{2}){\lambda }^{3}\mathrm{cos}\beta \lambda s\text{+}({\beta }^{3}-3{\alpha }^{2}\beta )\cdot$ ${\lambda }^{3}\mathrm{sin}\beta \lambda s]，{\phi }_{\text{68}}=-{\text{e}}^{\alpha \lambda s}[({\alpha }^{3}-3\alpha {\beta }^{2}){\lambda }^{3}\mathrm{sin}\beta \lambda s-({\beta }^{3}-3{\alpha }^{2}\beta )\cdot$ ${\lambda ^3}\cos \beta \lambda s]$ ， ${\varphi _{{\text{7}}5}} = {{\text{e}}^{ - \alpha \lambda (s + l)}}[2\alpha \beta {\lambda ^2}\sin \beta \lambda (s + l) + ({\alpha ^2} -$ ${\beta ^2})$ ${\lambda ^2}\cos \beta \lambda (s + l)]$ ， ${\varphi _{{\text{76}}}} = {{\text{e}}^{ - \alpha \lambda (s + l)}}[ - 2\alpha \beta {\lambda ^2}\cos \beta \lambda (s +$ $l)+({\alpha }^{2}-{\beta }^{2}){\lambda }^{2}\mathrm{sin}\beta \lambda (s+l)]，{\phi }_{\text{77}}={\text{e}}^{\alpha \lambda (s+l)}[-2\alpha \beta {\lambda }^{2}\cdot$ $\sin \beta \lambda (s + l) + ({\alpha ^2} - {\beta ^2}){\lambda ^2}\cos \beta \lambda (s + l)]$ ， ${\varphi _{{\text{78}}}} = {{\text{e}}^{\alpha \lambda (s + l)}} \cdot$ $[2\alpha \beta {\lambda }^{2}\mathrm{cos}\beta \lambda (s+l)+({\alpha }^{2}-{\beta }^{2}){\lambda }^{2}\mathrm{sin}\beta \lambda (s+l)]，{\phi }_{\text{8}5}={\text{e}}^{-\alpha \lambda (s+l)}\cdot$ $[({\beta ^3} - 3{\alpha ^2}\beta ){\lambda ^3}\sin \beta \lambda (s + l) - ({\alpha ^3} - 3\alpha {\beta ^2}) \cdot {\lambda ^3}\cos \beta \lambda (s +$ $l)]，{\phi }_{\text{86}}={\text{e}}^{-\alpha \lambda (s+l)}[(3{\alpha }^{2}\beta -{\beta }^{3}){\lambda }^{3}\mathrm{cos}\beta \lambda (s+l)-({\alpha }^{3}-3\alpha {\beta }^{2})\cdot$ ${\lambda }^{3}\mathrm{sin}\beta \lambda (s+l)]，{\phi }_{\text{87}}={\text{e}}^{\alpha \lambda (s+l)}[({\beta }^{3}-3{\alpha }^{2}\beta )\cdot {\lambda }^{3}\mathrm{sin}\beta \lambda (s+$ $l)+({\alpha }^{3}-3\alpha {\beta }^{2}){\lambda }^{3}\mathrm{cos}\beta \lambda (s+l)]，{\phi }_{\text{88}}={\text{e}}^{\alpha \lambda (s+l)}\cdot [(3{\alpha }^{2}\beta -$ ${\beta }^{3}){\lambda }^{3}\mathrm{cos}\beta \lambda (s+l)+({\alpha }^{3}-3\alpha {\beta }^{2}){\lambda }^{3}\mathrm{sin}\beta \lambda (s+l)]，{\psi }_{3}=$ $- q{s^4}/(24EI)$ ， ${\psi _{\text{4}}} = - q{s^{\text{3}}}/({\text{6}}EI)$ ， ${\psi _{\text{5}}} = - q{s^{\text{2}}}/(2EI)$ ， ${\psi _{\text{6}}} =$ $- qs{\text{/}}(EI)$ 。

同理，通过式（18）即可求得积分常数 ${B_1}$ ， ${B_2}$ ， ${B_3}$ ， ${B_4}$ ， ${B_5}$ ， ${B_6}$ ， ${B_7}$ ， ${B_8}$ ，将其回代到挠度、转角、弯矩和剪力表达式中，即可求得满足类型Ⅱ分析模型边界条件下管棚的变形和受力分布。

3. 案例计算

南宁至崇左铁路引入机场隧道起讫里程DK25+615—DK28+935，全长3320 m。其中DK25+940—DK27+234段长度1294 m为暗挖区间，埋深3.4~15.2 m，施工工法为CRD法（350 m）和三台阶临时仰拱（944 m）；该隧道暗挖区间存在浅埋、开挖下穿既有道路、临近既有构（建）筑物。隧址内岩层上部为杂填土，下部为粉质黏土、泥质砂岩夹砂质泥岩、砾岩，弱风化至全风化，岩溶发育，层面起伏变化大。本隧道进口明暗分界处拱部设置一环35 m长Φ108 mm×6 mm管棚加强支护，管棚环向间距40 cm，具体参数见表 1。

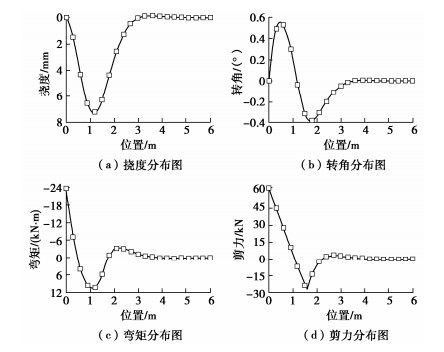
表 1 设计参数取值

Table 1. Values of design parameters

基床系数/(kN·m^-3)	地基剪切模量/(kN·m^-1)	隧道埋深/m	内摩擦角/(°)	围岩重度/(kN·m^-3)	等效惯性矩/m⁴	等效弹性模量/kPa	开挖高度/m	管棚间距/m	进尺深度/m
30000	2800	6	45.6	24	6.68×10^-6	7.89×10⁷	2.4	0.4	0.6

下载: 导出CSV

| 显示表格

本文以隧道进口明暗分界处拱顶单根钢管为研究对象，则该钢管的挠曲变形与隧道因开挖引起的拱顶沉降值相同。对管棚分析模型中的参数分别确定取值，并利用MATLAB编程进行应用分析。第一个循环进尺下管棚挠度、转角、弯矩和剪力在开挖方向上的分布曲线如图 4所示。

图 4 管棚的变形及内力分布

Figure 4. Distribution of deformation and internal force of pipe roof

下载: 全尺寸图片幻灯片

图 4表明，管棚挠度在OA段逐渐增大，且在A点处达到最大值7.2 mm。AB段挠度逐渐减小，当计算深度为4 m时，该循环开挖对该处管棚的变形无影响。随计算深度的加深，弯矩呈震荡形式趋近于零，其中最大值位于固定端处为-23.5 kN·m。剪力的分布同样随计算深度的增大而收敛于零，最大值同样位于固定端处，大小为62.6 kN。当计算深度达到4 m时，管棚的弯矩和剪力将趋近于零，由此可得一个循环开挖区段对管棚的影响范围长度为4 m。

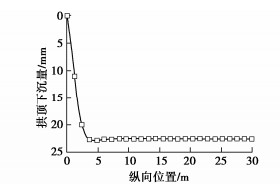
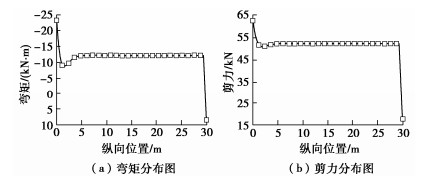
通过以上单个开挖区段的分析，得到管棚在该分析区段的变形和受力特征。该区段前0.6 m的变形与受力将随初期支护的完成而与初期支护固结在一起，0.6 m处的变形值将成为下一个分析区段的位移初值。通过迭代计算，可得到管棚预支护范围内30 m全部开挖支护完成后隧道拱顶下沉分布如图 5所示，管棚全长范围内内力的分布情况如图 6所示。

图 5 管棚预支护范围内拱顶下沉纵向分布

Figure 5. Longitudinal distribution of vault settlement within scope of pre-support of pipe roof

下载: 全尺寸图片幻灯片

图 6 管棚全长范围的内力分布

Figure 6. Distribution of internal force in whole length of pipe roof

下载: 全尺寸图片幻灯片

图 5表明，管棚的挠曲变形随掌子面的不断推进而逐渐增大。当拱顶沉降达到22.8 mm时，随掌子面的进一步推进，拱顶沉降将基本保持不变。

王道远等^[12]通过现场试验得出，管棚的变形整体呈凹形分布，在开挖初期，管棚的变形速率较快。而图中管棚变形分布特征符合这一规律，且管棚变形的数量级基本一致，从而证明了该分析模型的合理性和实用性。

图 6表明，管棚的弯矩和剪力的最不利截面均发生在导向墙的约束处，其中弯矩最大值为23.5 kN·m，剪力最大值为62.6 kN。管棚全长范围内弯矩基本保持在12 kN·m，剪力基本保持在52 kN。

综上所述，利用该分析模型可以系统地对管棚的支护效果和受力特征进行预测。通过对算例的数值计算，得到管棚预结构的受力和变形分布特征，从而体现了管棚预支护体系的主要特征。

4. 参数分析

本节在前述理论研究的基础上，通过调整管棚的环向间距、管径、开挖进尺长度以及搭接长度的设计参数，研究各设计参数对管棚受力和变形的影响形式和程度，从而指导管棚的设计和施工。

4.1 环向间距对管棚受力和变形的影响分析

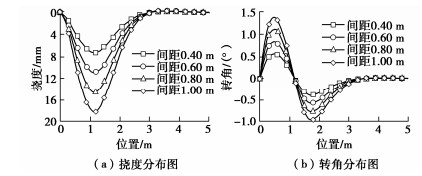
取其他参数不变，当管棚环向间距j为0.40，0.60，0.80，1.00 m时，分别计算并绘出管棚的变形分布曲线（见图 7）和内力分布曲线（见图 8），研究环向间距对管棚变形和受力的影响。

图 7 环向间距对管棚变形的影响

Figure 7. Influences of circumferential spacing on deformation of pipe roof

下载: 全尺寸图片幻灯片

图 8 环向间距对管棚受力的影响

Figure 8. Influence of circumferential spacing on stress of pipe roof

下载: 全尺寸图片幻灯片

表明，管棚环向间距的变化不改变其变形分布形式，最大挠度 ${\omega _{\max }}{\text{(mm)}}$ 和最大转角 ${\theta _{\max }}$ (°)发生的位置不变，其中最大挠度和最大转角均与环向间距之间满足线性增长关系，关系式分别为

$\left. \begin{array}{l}{\omega }_{\mathrm{max}}=18.159j\text{ }\text{，}\\ {\theta }_{\mathrm{max}}=1.3\text{8}63j\text{ }。\end{array} \right\}$

(19)

表明，管棚环向间距同样不改变管棚的内力分布形式，最不利截面不随环向间距的变化而变化，管棚的最大弯矩 ${M_{\max }}{\text{(kN}} \cdot {\text{m)}}$ 和最大剪力 ${Q_{\max }}{\text{(kN)}}$ 均与环向间距之间满足线性增长关系，关系式分别为

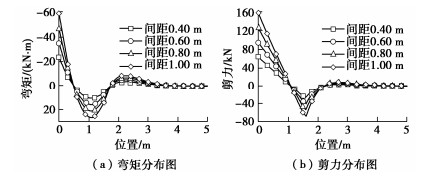
$\left. \begin{array}{l}{M}_{\mathrm{max}}=58.657j\text{ }\text{，}\\ {Q}_{\mathrm{max}}=156.61j\text{ }。\end{array} \right\}$

(20)

4.2 管径对管棚受力和变形的影响分析

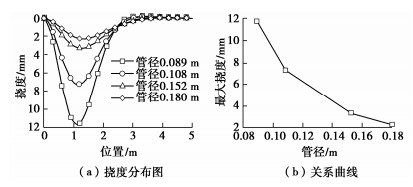
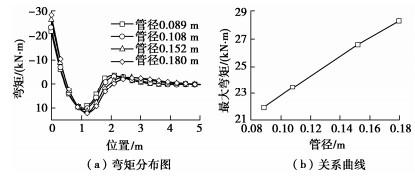
取其他参数不变，当管径 $b$ 分别为0.089，0.108，0.152，0.180 m时，分别计算并绘制出管棚的挠度分布曲线（见图 9）和弯矩分布曲线（见图 10），研究管径对管棚变形和受力的影响。当管棚的管径发生变化时，管棚的等效截面惯性矩和等效弹性模量均发生变化，根据刚度等效法^[14]求得不同管径下的等效截面惯性矩和等效弹性模量见表 2。

图 9 管径对管棚挠度的影响

Figure 9. Influence of pipe diameter on deflection of pipe roof

下载: 全尺寸图片幻灯片

图 10 管径对管棚弯矩的影响

Figure 10. Influences of pipe diameter on bending moment of pipe roof

下载: 全尺寸图片幻灯片

表 2 不同管径的截面计算参数

Table 2. Cross section calculation parameters of different pipe diameters

管径/m	等效惯性矩/(10^-6 m⁴)	等效弹性模量/(10⁷ kPa)
0.089	3.08	9.24
0.108	6.68	7.89
0.152	26.00	5.89
0.180	51.50	5.07

下载: 导出CSV

| 显示表格

从可以看出，管径越粗，管棚的挠曲变形越平缓，随着管径的增大，最大挠度 ${\omega _{\max }}$ 逐渐减小，并且随着管径的不断增大对管棚挠曲变形的影响将越来越小。最大挠度 ${\omega _{\max }}$ 与管径b(m)之间满足

${\omega _{\max }} = 0.0397{b^{ - 2.346}}。$

(21)

从可以看出，随着管径的增大，弯矩的危险截面位置不变，管棚所受的最大弯矩 ${M_{\max }}$ （kN·m）也随着增大。最大弯矩与管径之间满足

${M_{\max }} = - 115.67{b^2} + 100.87b + 13.917。$

(22)

4.3 开挖进尺长度对管棚受力和变形的影响分析

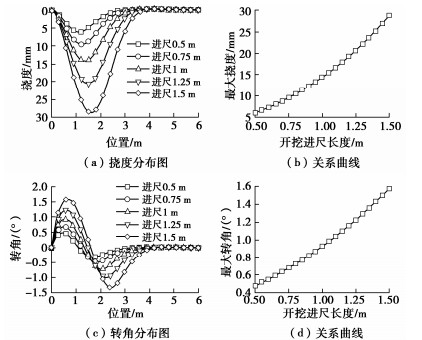
取其他参数不变，当开挖进尺长度 $a$ 分别为0.5，0.75，1，1.25，1.5 m时，分别绘制出管棚变形分布曲线（图 11）和内力分布曲线（图 12），研究开挖进尺长度对管棚变形和受力的影响。

图 11 开挖进尺长度对管棚变形的影响

Figure 11. Influences of excavation footage length on deformation of pipe roof

下载: 全尺寸图片幻灯片

图 12 开挖进尺长度对管棚受力的影响

Figure 12. Influences of excavation footage length on stress of pipe roof

下载: 全尺寸图片幻灯片

表明，随着开挖进尺长度的增大，管棚最大变形位置不断前移，且最大值不断增大。通过开挖进尺长度与最大变形关系曲线图可得到，开挖进尺长度与最大挠度 ${\omega _{\max }}$ 和最大转角 ${\theta _{\max }}$ 之间呈非线性增长关系，进尺越长，变形增长速度越快，关系式分别为

$\left. \begin{array}{l}{\omega }_{\mathrm{max}}=9.6241{a}^{2}+1.9131a+2.6503\text{ }\text{，}\\ {\theta }_{\mathrm{max}}=0.2622{a}^{2}+0.487a+0.1679\text{ }。\end{array} \right\}$

(23)

说明开挖进尺长度是控制管棚变形的关键施工技术指标。

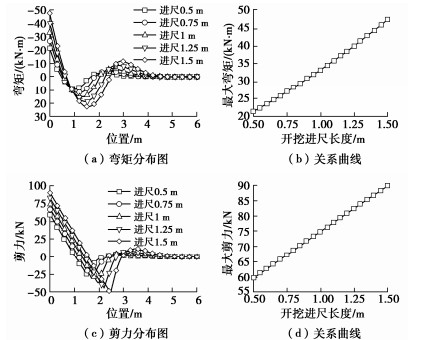
表明，开挖进尺长度的增大同样会使管棚的内力分布前移，但最不利截面总位于固定端处。最大弯矩 ${M_{\max }}$ 与开挖进尺长度之间满足非线性关系式：

${M_{\max }} = 4.5114{a^2} + 17.093a + 11.583\text{，}$

(24)

式中，开挖进尺长度 $a$ （m）， ${M_{\max }}$ 最大弯矩（kN·m）。而最大剪力 ${Q_{\max }}$ （kN）与开挖进尺长度之间满足线性关系式：

${Q_{\max }} = 30.841x + 44.13。$

(25)

4.4 搭接长度对管棚受力和变形的影响分析

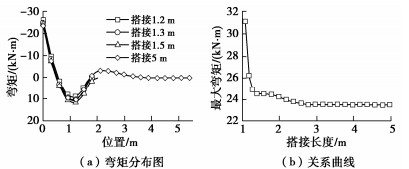
由类型Ⅱ分析模型可计算管棚搭接长度对管棚作用效果的影响，搭接长度 $D = H\tan ({45^ \circ } - \varphi /$ $2) + l$ ，分别取搭接长度为1.1，1.3，1.5，5 m，分别绘制出管棚挠度分布曲线以及搭接长度与最大挠度关系曲线（图 13）和弯矩分布曲线以及搭接长度与最大弯矩关系曲线（图 14），研究搭接长度对管棚变形和受力的影响。

图 13 搭接长度对管棚挠度的影响

Figure 13. Influences of lap length on deflection of pipe roof

下载: 全尺寸图片幻灯片

图 14 搭接长度对管棚弯矩的影响

Figure 14. Influences of lap length on bending moment of pipe roof

下载: 全尺寸图片幻灯片

图 13表明，随着搭接长度的增大，管棚发生最大挠度的位置和挠度分布形式基本不变。当搭接长度大于2.5 m时，最大挠度将趋近于7.3 mm而保持不变。

图 14表明，随着搭接长度的增大，管棚的最不利截面位置和弯矩的分布形式基本不变。当搭接长度大于2.5 m时，最大弯矩将趋近于23.5 kN·m而保持不变。综上所述，在该工程条件下，当管棚搭接长度大于2.5 m时，搭接长度的变化将对管棚的变形和受力基本没有影响。

5. 结论

（1）通过建立和求解基于Pasternak弹性地基理论的单个循环进尺下管棚分析模型可得管棚的受力和变形的分布特征。考虑隧道开挖支护动态施工过程，通过迭代计算可有效预测管棚预支护段开挖支护完成后管棚整体的受力和变形分布，且其理论值与已有文献实测结果具有相同的分布特征，从而证明了模型的合理性。

（2）管棚环向间距的变化不改变管棚内力和变形的分布形式，且最不利截面位置保持不变，管棚的受力和变形与环向间距之间呈线性增长关系，随环向间距的增大而增大。

（3）选用的管径越粗，管棚的挠曲变形越平缓，挠曲变形越小，并且随着管径的不断增大，管径对管棚挠曲变形的影响将越来越小。随着管径的增大，弯矩的危险截面位置不变，管棚的最大弯矩与管径之间呈非线性增长关系。

（4）随着开挖进尺长度的增大，管棚最大变形位置不断前移，最大变形值与开挖进尺长度之间呈非线性增长关系，开挖进尺越长，变形增长速度越快。说明开挖进尺长度是控制管棚变形的关键施工技术指标。开挖进尺长度越大，最大弯矩和最大剪力越大。

（5）管棚的最大内力及变形随搭接长度的增长而迅速趋于收敛。在本文案例工况下，当管棚搭接长度大于2.5 m时，搭接长度的变化将对管棚的变形和受力基本没有影响。

图 1 不同温差条件下溶质质量浓度积累对比结果

Figure 1. Comparison of solute concentration accumulation under different temperature differences

下载: 全尺寸图片幻灯片

图 2 不同索雷特系数条件下溶质质量浓度积累对比结果

Figure 2. Comparison of solute concentration accumulation under different Soret coefficients

下载: 全尺寸图片幻灯片

图 3 Neumann边界条件下溶质质量浓度分布对比结果

Figure 3. Comparison of solute concentration distribution under Neumann boundary conditions

下载: 全尺寸图片幻灯片

图 4 Dirichle边界条件下溶质质量浓度分布对比结果

Figure 4. Comparison of solute concentration distribution under Dirichle boundary conditions

下载: 全尺寸图片幻灯片

图 5 Cd²⁺质量质量浓度随深度变化曲线

Figure 5. Distribution of Cd²⁺ concentrations with depth

下载: 全尺寸图片幻灯片

图 6 Zn²⁺质量浓度随深度变化曲线

Figure 6. Distribution of Zn²⁺ concentrations with depth

下载: 全尺寸图片幻灯片

图 7 热扩散效应对污染物质量浓度随深度变化影响

Figure 7. Influences of thermal diffusion on variation of contaminant concentration with depth

下载: 全尺寸图片幻灯片

图 8 热扩散效应对污染物积累质量浓度随时间变化规律影响

Figure 8. Influences of thermal diffusion on variation of contaminant accumulation concentration with time

下载: 全尺寸图片幻灯片

图 9 热渗透效应对污染物质量浓度随深度变化影响

Figure 9. Influences of thermo-osmosis on variation of contaminant concentration with depth

下载: 全尺寸图片幻灯片

图 10 热渗透效应对污染物积累质量浓度随时间变化影响

Figure 10. Influences of thermo-osmosis on variation of contaminant accumulation concentration with time

下载: 全尺寸图片幻灯片

图 11 热固结效应对污染物质量浓度随深度变化影响

Figure 11. Influences of thermal consolidation on variation of contaminant concentration with depth

下载: 全尺寸图片幻灯片

图 12 热固结效应对污染物积累质量浓度随时间变化影响

Figure 12. Influences of thermal consolidation on variation of contaminant accumulation concentration with time

下载: 全尺寸图片幻灯片

图 13 热效应对污染物质量浓度随深度变化影响

Figure 13. Influences of thermal effect on variation of contaminant concentration with depth

下载: 全尺寸图片幻灯片

图 14 热效应对污染物积累质量浓度随时间变化影响

Figure 14. Influences of thermal effect on contaminant accumulation concentration with time

下载: 全尺寸图片幻灯片

图 15 索雷特系数变化对污染物积累质量浓度影响

Figure 15. Influences of variation of Soret coefficient on contaminant accumulation concentration

下载: 全尺寸图片幻灯片

图 16 热渗透系数变化对污染物积累质量浓度影响

Figure 16. Influences of variation of coefficient of thermo-osmosis on contaminant accumulation concentration

下载: 全尺寸图片幻灯片

图 17 土体热膨胀系数变化对污染物积累质量浓度影响

Figure 17. Influences of variation of coefficient of thermal expansion of soil on contaminant accumulation concentration

下载: 全尺寸图片幻灯片

表 1 模型参数

Table 1 Model parameters

初始孔隙率n₀	扩散系数 D₀	索雷特系数S_T	分配系数 R_d
0.5	2.8×10^-10 m²/s	0.03K^-1	1
注：参数取值与文献[6]相同。

下载: 导出CSV

表 2 模型参数

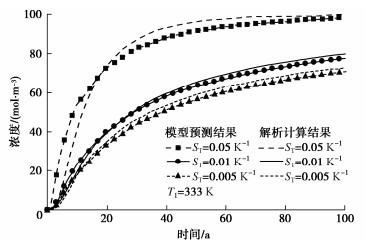
Table 2 Model parameters

初始孔隙率n₀	扩散系数 D₀	索雷特系数S_T	分配系数 R_d
0.5	1×10^-10 m²·s^-1	0.01K^-1	1
注：参数取值与文献[30]相同。

下载: 导出CSV

表 3 模型参数

Table 3 Model parameters

扩散系数 D₀/(10^-11 m²·s^-1)	初始孔隙率n₀	摩尔质量/(kg·m^-3)
扩散系数 D₀/(10^-11 m²·s^-1)	初始孔隙率n₀	Zn²⁺	Cd²⁺
1.15，4.05	0.43	0.065	0.112
注：参数取值与文献[31]相同。

下载: 导出CSV

表 4 模型参数

Table 4 Model parameters

参数	取值
自由水体分子扩散系数D₀	5×10^-10 m²·s^-1
初始渗透系数k₀	1×10^-10 m·s^-1
泊松比 $\nu$	0.3
弹性模量E	1.49×10^-10 Pa^-1
化学渗透效率系数ω	0.005
初始孔隙率n₀	0.5
吸附系数k_d	0.814×10^-3 m³
荷载引起的体变系数m_v	5×10^-7 m·s²·kg^-1
质量浓度引起的体变系数m_c	0.105×10^-7 m^-1·s²·kg^-1
索雷特系数S_T	0.033 K^-1
热渗透系数k_T	3.14×10^-12 m·K·s^-1
土体热膨胀系数 $\alpha$	2×10^-4 K^-1
流体压缩系数 $\beta _{\text{T}}^{}$	4.5×10^-10 Pa^-1
流体热膨胀系数 $\beta _{\text{f}}^{\text{T}}$	3.5×10^-4 K^-1
固体土颗粒比热容C_ps	732 J·kg^-1·K^-1
孔隙流体比热容C_pf	4186 J·kg^-1·K^-1
土体固有热传导系数 $\lambda _{\text{T}}^{}$	1.69 W·m^-1·K^-1
水力梯度i	3

下载: 导出CSV

参考文献(34)

[1]	陈云敏, 谢海建, 张春华. 污染物击穿防污屏障与地下水土污染防控研究进展[J]. 水利水电科技进展, 2016, 36(1): 1–10. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD201601002.htm CHEN Yun-min, XIE Hai-jian, ZHANG Chun-hua. Review on penetration of barriers by contaminants and technologies for groundwater and soil contamination control[J]. Advances in Science and Technology of Water Resources, 2016, 36(1): 1–10. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD201601002.htm
[2]	RAMREDDY C, MURTHY P V S N, CHAMKHA A J, et al. Soret effect on mixed convection flow in a nanofluid under convective boundary condition[J]. International Journal of Heat and Mass Transfer, 2013, 64: 384–392. doi: 10.1016/j.ijheatmasstransfer.2013.04.032
[3]	张春华. 填埋场复合衬垫污染物热扩散运移规律及其优化设计方法[D]. 杭州: 浙江大学, 2018. ZHANG Chun-hua. Mechanisms for Contaminant Transport in Landfill Composite Liners under Thermal Effect and its Optimization Design Method[D]. Hangzhou: Zhejiang University, 2018. (in Chinese)
[4]	ROSANNE R, PASZKUTA M, TEVISSEN E, et al. Thermodiffusion in compact clays[J]. Journal of Colloid and Interface Science, 2003, 267(1): 194–203. doi: 10.1016/S0021-9797(03)00670-2
[5]	ROSANNE M, PASZKUTA M, ADLER P M. Thermodiffusional transport of electrolytes in compact clays[J]. Journal of Colloid and Interface Science, 2006, 299(2): 797–805. doi: 10.1016/j.jcis.2006.03.002
[6]	XIE H J, ZHANG C H, SEDIGHI M, et al. An analytical model for diffusion of chemicals under thermal effects in semi-infinite porous media[J]. Computers and Geotechnics, 2015, 69: 329–337. doi: 10.1016/j.compgeo.2015.06.012
[7]	吴珣, 施建勇, 何俊. 非等温条件下有机污染物在黏土衬垫中的扩散分析[J]. 水文地质工程地质, 2014, 41(3): 120–124. https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201403024.htm WU Xun, SHI Jian-yong, HE Jun. An analysis of organic contaminant diffusion through clay liner under the condition of transient temperature[J]. Hydrogeology & Engineering Geology, 2014, 41(3): 120–124. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SWDG201403024.htm
[8]	何俊, 颜兴, 胡晓瑾, 等. 考虑热扩散的黏土衬垫中污染物运移简化计算[J]. 工程地质学报, 2018, 26(2): 400–406. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201802015.htm HE Jun, YAN Xing, HU Xiao-jin, et al. Simplified calculation method for contaminant transport in compacted clay liner considering thermal diffusion[J]. Journal of Engineering Geology, 2018, 26(2): 400–406. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ201802015.htm
[9]	ROSHAN H, ANDERSEN M S, ACWORTH R I. Effect of solid-fluid thermal expansion on thermo-osmotic tests: an experimental and analytical study[J]. Journal of Petroleum Science and Engineering, 2015, 126: 222–230. doi: 10.1016/j.petrol.2014.12.005
[10]	GONÇALVÈS J, TRÉMOSA J. Estimating thermo-osmotic coefficients in clay-rocks: I. Theoretical insights[J]. Journal of Colloid and Interface Science, 2010, 342(1): 166–174. doi: 10.1016/j.jcis.2009.09.056
[11]	GONCALVES J, JI Y C, MATRAY J M, et al. Analytical expressions for thermo-osmotic permeability of clays[J]. Geophysical Research Letters 2018, 45(2): 691–698. doi: 10.1002/2017GL075904
[12]	YANG Y, GUERLEBECK K, SCHANZ T. Thermo-osmosis effect in saturated porous medium[J]. Transport in Porous Media, 2014, 104(2): 253–271. doi: 10.1007/s11242-014-0332-5
[13]	ZAGORŠČAK R, SEDIGHI M, THOMAS H R. Effects of thermo-osmosis on hydraulic behavior of saturated clays[J]. International Journal of Geomechanics, 2017, 17(3): 04016068. doi: 10.1061/(ASCE)GM.1943-5622.0000742
[14]	ZAGORSCAK R, Thomas H R. Thermo-osmosis in saturated shale[C]// ACME-UK: Conference on Computational Mechanics. ACM, 2016.
[15]	PAASWELL R E. Temperature effects on clay soil consolidation[J]. Journal of the Soil Mechanics and Foundations Division, 1967, 93(3): 9–22. doi: 10.1061/JSFEAQ.0000982
[16]	JOSHAGHANI M, GHASEMI-FARE O. A study on thermal consolidation of fine grained soils using modified consolidometer[C]// Eighth International Conference on Case Histories in Geotechnical Engineering. March 24–27, 2019, Philadelphia, Pennsylvania. Reston, VA, USA: American Society of Civil Engineers, 2019: 148–156.
[17]	HABIBAGAHI K. Temperature effect and the concept of effective void ratio[J]. Indian Geotechnical Journal, 1977, 7(1): 14–34.
[18]	MITCHELL J K, KAO T C. Measurement of soil thermal resistivity[J]. Journal of the Geotechnical Engineering Division, 1978, 104(10): 1307–1320. doi: 10.1061/AJGEB6.0000706
[19]	白冰. 岩土颗粒介质非等温—维热固结特性研究[J]. 工程力学, 2005, 22(5): 186–191. doi: 10.3969/j.issn.1000-4750.2005.05.034 BAI Bing. One- dimensional thermal consolidation characteristics of geotechnical media under non-isothermal condition[J]. Engineering Mechanics, 2005, 22(5): 186–191. (in Chinese) doi: 10.3969/j.issn.1000-4750.2005.05.034
[20]	DELAGE P, SULTAN N, CUI Y J. On the thermal consolidation of Boom clay[J]. Canadian Geotechnical Journal, 2000, 37(2): 343–354. doi: 10.1139/t99-105
[21]	SANAVIA L, BONIFETTO G, LALOUI L. Thermo-elasto- plastic consolidation analysis with water phase change[C]// Fifth Biot Conference on Poromechanics. 2013, Vienna, Austria. Reston, VA, USA: American Society of Civil Engineers, 2013.
[22]	钮家军, 凌道盛, 王秀凯, 等. 饱和单层土体一维热固结精确解[J]. 岩土工程学报, 2019, 41(9): 1715–1723. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909018.htm NIU Jia-jun, LING Dao-sheng, WANG Xiu-kai, et al. Exact solutions for one-dimensional thermal consolidation of single-layer saturated soil[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1715–1723. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909018.htm
[23]	孙德安, 薛垚, 汪磊. 变荷载作用下考虑半透水边界热传导性的一维饱和土热固结特性研究[J]. 岩土力学, 2020(5): 1465–1473. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202005002.htm (SUN De-an, XUE Yao, WANG Lei. Analysis of one-dimensional thermal consolidation of saturated soil considering heat conduction of semi-permeable drainage boundary under varying loading[J]. Rock and Soil Mechanics, 2020(5): 1465–1473. (in Chinese https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202005002.htm
[24]	PETERS G P, SMITH D W. The influence of advective transport on coupled chemical and mechanical consolidation of clays[J]. Mechanics of Materials, 2004, 36(5/6): 467–486.
[25]	FRANÇOIS B, LALOUI L, LAURENT C. Thermo-hydro- mechanical simulation of ATLAS in situ large scale test in Boom Clay[J]. Computers and Geotechnics, 2009, 36(4): 626–640. doi: 10.1016/j.compgeo.2008.09.004
[26]	HART R D, ST JOHN C M. Formulation of a fully-coupled thermal—mechanical—fluid flow model for non-linear geologic systems[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1986, 23(3): 213–224.
[27]	THOMAS H R, HE Y. A coupled heat-moisture transfer theory for deformable unsaturated soil and its algorithmic implementation[J]. International Journal for Numerical Methods in Engineering, 1997, 40(18): 3421–3441. doi: 10.1002/(SICI)1097-0207(19970930)40:18<3421::AID-NME220>3.0.CO;2-C
[28]	MALUSIS M A, KANG J B, SHACKELFORD C D. Restricted salt diffusion in a geosynthetic clay liner[J]. Environmental Geotechnics, 2015, 2(2): 68–77. doi: 10.1680/envgeo.13.00080
[29]	张志红, 韩林, 田改垒. 饱和土体热–水–力–化全耦合一维溶质运移模型[J]. 东南大学学报(自然科学版), 2019, 49(6): 1178–1186. https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201906022.htm ZHANG Zhi-hong, HAN Lin, TIAN Gai-lei. One-dimensional transport model for solute with thermo-hydro-mechanical-chemical soupling in saturated soil[J]. Journal of Southeast University (Natural Science Edition), 2019, 49(6): 1178–1186. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DNDX201906022.htm
[30]	YAN H X, SEDIGHI M, XIE H J. Thermally induced diffusion of chemicals under steady-state heat transfer in saturated porous media[J]. International Journal of Heat and Mass Transfer, 2020, 153: 119664. doi: 10.1016/j.ijheatmasstransfer.2020.119664
[31]	DO N Y, LEE S R. Temperature effect on migration of Zn and Cd through natural clay[J]. Environmental Monitoring and Assessment, 2006, 118(1/2/3): 267–291.
[32]	吴瑞潜. 饱和土一维热固结解析理论研究[D]. 杭州: 浙江大学, 2008. WU Rui-qian. Analytical Study on One-Dimensional Thermal Consolidation Theory of Saturated Soil[D]. Hangzhou: Zhejiang University, 2008. (in Chinese)
[33]	HONG P Y, PEREIRA J M, TANG A M, et al. On some advanced thermo-mechanical models for saturated clays[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2013, 37(17): 2952–2971. doi: 10.1002/nag.2170
[34]	张文杰, 陈云敏, 詹良通. 垃圾填埋场渗滤液穿过垂直防渗帷幕的渗漏分析[J]. 环境科学学报, 2008, 28(5): 925–929. doi: 10.3321/j.issn:0253-2468.2008.05.018 ZHANG Wen-jie, CHEN Yun-min, ZHAN Liang-tong. Transport of leachate through vertical curtain grouting in landfills[J]. Acta Scientiae Circumstantiae, 2008, 28(5): 925–929. (in Chinese) doi: 10.3321/j.issn:0253-2468.2008.05.018

施引文献(20)

期刊类型引用(8)

1.	邹增富，唐世禄，廖云朋，代荣，谢昌志. 直墙拱型引水隧洞洞口段管棚预加固技术分析. 四川建筑. 2024(02): 132-134+138 . 百度学术
2.	张小波，荣耀，张雕，孙洋. 考虑初支滞后性的软弱地层隧道进洞段管棚注浆加固效果研究. 公路. 2024(08): 425-433 . 百度学术
3.	王晓东. 基于最大开挖进尺的管棚设计参数研究. 铁道建筑技术. 2023(03): 40-43 . 百度学术
4.	张小波，张雕，姚池，杨建华，蒋水华，荣耀. 考虑微拱效应的隧道洞口段管棚合理间距确定方法及参数分析. 岩土力学. 2023(06): 1625-1635 . 百度学术
5.	姬云鹏，房灵国，唐昊天，张兴丽，王祥金，白云天，李健，赵红华. 隧道开挖全过程管棚支护受力研究. 现代隧道技术. 2023(03): 123-138 . 百度学术
6.	石钰锋，张涛，曹成威，阳军生，陈祥胜. 基于双参数地基的隧道预支护拱棚壳体力学模型. 工程科学与技术. 2023(04): 142-152 . 百度学术
7.	李奎双，王峥，尹学鑫，程星源. 浅埋软弱地层中超大跨度地铁隧道管棚支护效果研究. 四川建筑. 2023(04): 133-137 . 百度学术
8.	施英，罗春. 隧道管棚超前支护作用机理及其影响因素研究. 人民长江. 2022(11): 130-135 . 百度学术