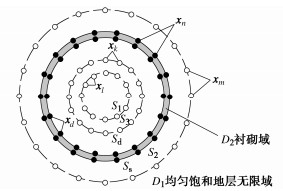
Influence mechanism of permeability coefficient in homogeneously saturated strata on responses of deep tunnels under incidence of SV waves
-
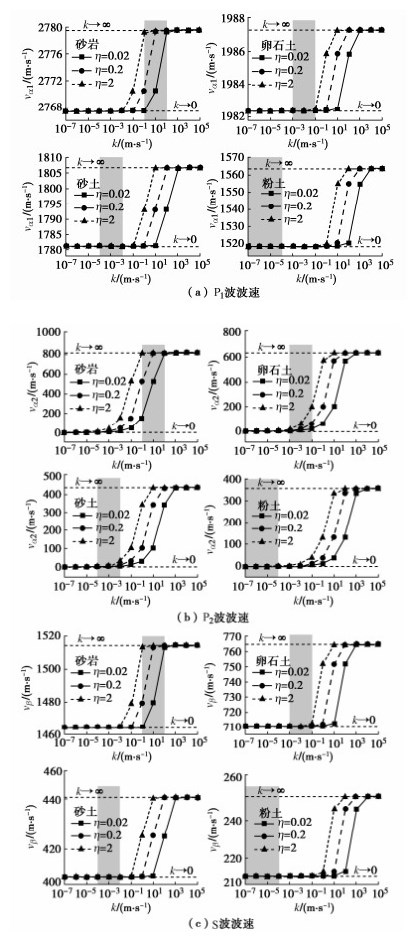
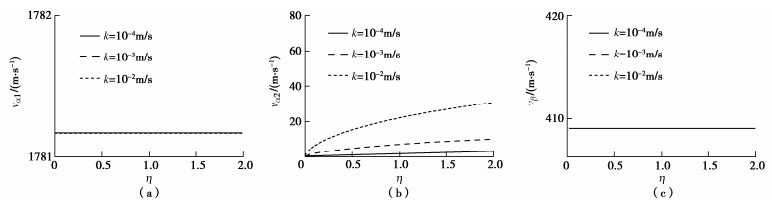
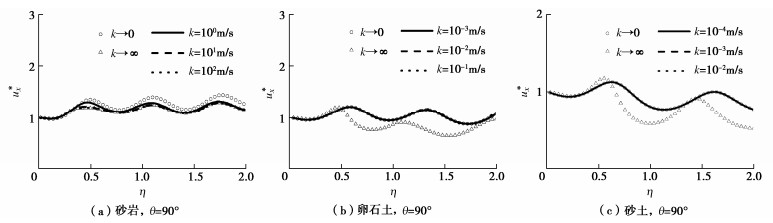
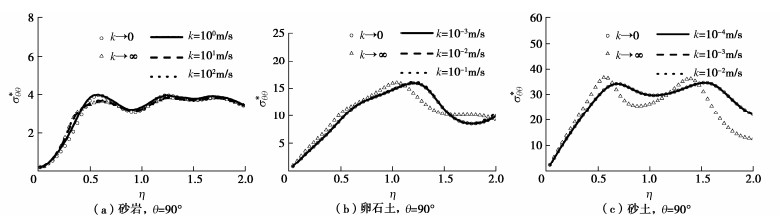
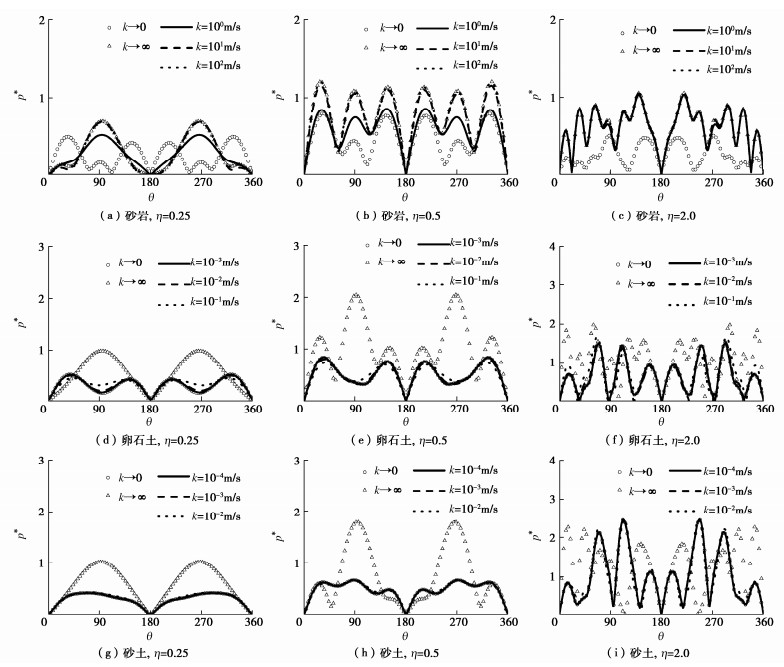
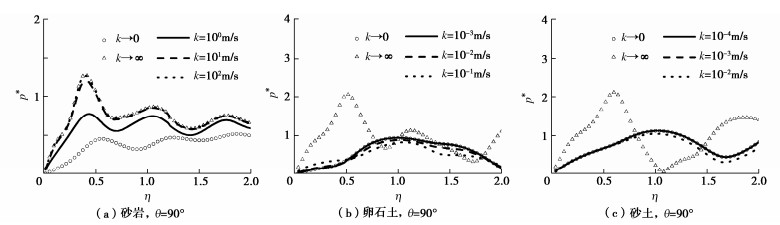
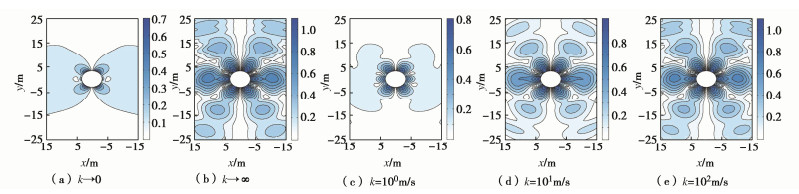
摘要: 对于饱和场地中地下结构的抗震分析问题，地层渗透系数决定了孔隙水与土骨架耦合作用的强弱，是研究饱和地层–结构动力相互作用的关键参数之一。然而，目前研究通常基于渗透系数为零或无穷大的假定，忽略了实际地层的渗透特性且对其影响机制尚不清晰。针对不同类型均匀饱和地层对应的渗透系数分布范围，基于Biot两相介质理论，首先建立了饱和地层不同渗透系数情况下的u-w格式模型，推导渗透系数分别为有限值、零和无穷大3种情况下P1，P2，S波的波速解析表达式，分析了地层渗透系数变化对自由场波速的影响规律；进而，建立了不同类型饱和地层与深埋隧道动力作用分析模型，并与典型算例精确解对比验证了本模型的有效性；在此基础上，分别研究了砂岩、卵石土、砂土、粉土4种类型饱和地层渗透系数变化及两种极端值情况下隧道结构及周围地层孔隙水压力的响应机制。结果表明：对于不同类型饱和地层，3种体波在地层中的传播速度均随渗透系数k增加呈上升趋势，当k < 10-4 m/s时，波速为最小值且与k→0极端情况一致，当k > 102 m/s时，波速为最大值且与k→∞极端情况一致；对于饱和砂岩，随着渗透系数增加，隧道及地层孔压响应幅值逐渐增大且趋向于k→∞假设情况，而对于卵石土和砂土，随着渗透系数减小，隧道结构及地层孔压响应幅值逐渐增大且趋向于k→0假设情况。研究还发现，对于渗透系数在10-4~102 m/s范围内的饱和地层，隧道结构与地层响应结果相比渗透系数为两种极端值情况下的结果均相差较大，即此时计算模型不宜采用渗透系数为零或无穷大的假定。因此，实际工程抗震设计应重视饱和地层渗透系数对隧道结构及周围地层的影响。Abstract: For the seismic analysis of underground structures in saturated sites, the coupling effects of pore water and soil skeleton are determined by the permeability coefficient of strata, which is one of the key parameters in the interaction analysis between saturated strata and structures. However, the current researches are usually based on the assumption that the permeability coefficient is zero or infinite, ignoring the permeability of the actual formation, and its influence mechanism is still unclear. Based on the Biot poroelasticity theory, firstly the u-w format model is established for homogeneously saturated strata with different permeability coefficients. According to the distribution ranges of the permeability coefficients corresponding to different types of saturated strata, the analytical expressions for wave velocity of P1, P2 and S waves are derived when the permeability coefficient is finite, zero and infinite respectively, and the influences of variation of the permeability coefficient on the free-field wave velocity is analyzed. In addition, a dynamic analysis model is established for different types of saturated strata and deep tunnels, and the proposed model is verified by providing comparisons with the known solutions of typical examples. Furthermore, the response mechanisms of the tunnel structures and surrounding pore water pressures in four typical saturated strata, including sandstone, pebble soil, sandy soil and silt soil, are investigated under the scenarios of variable permeability coefficients and two extreme values (i.e., zero and infinite). The results show that the propagation velocities of three kinds of waves (P1, P2 and S waves) in different strata all increase with the permeability coefficient k. When k is less than 10-4 m/s, the wave velocity reaches the minimum and is consistent with that of the extreme value k=0. When k is greater than 102 m/s, the wave velocity reaches the maximum and is consistent with that of the extreme value k=∞. More specifically, for the saturated sandstone, the amplitudes of tunnel response and pore water pressure of strata gradually increase with the permeability coefficient and tend to the extreme case with the assumption of k=∞. While for the pebble soil and the sandy soil, the amplitudes of tunnel response and pore water pressure of strata gradually increase with the decrease of the permeability coefficient and tend to the extreme case with the assumption of k=0. What's more, for the saturated strata with permeability coefficient in the range of 10-4 m/s~102 m/s, the dynamic responses of tunnel structures and strata are quite different from those with permeability coefficient of two extreme values, which indicates the assumption that the permeability coefficient is zero or infinite cannot be used in the computational model for this situation. Therefore, the permeability coefficient of saturated strata has a significant influence on the dynamic responses of the tunnel structures and surrounding strata, and should be considered in the seismic design of practical projects.
-
0. 引言
堆积体在中国的分布十分广泛，对工程的建设及人民生命财产安全具有重要的影响[1]。随着中国“十四五”期间清洁能源战略基地的实施，工程建设不可避免地会遇到越来越多的堆积体，对坝址坝型选择、枢纽布置、库岸稳定及移民安置带来重大影响。堆积体为非均质各向异性介质，其稳定性除受堆积体基覆界面、边界条件影响外，还与其斜坡结构等有关。堆积体的稳定性研究逐渐成为高山峡谷地区修建水电工程必须面对的主要工程地质问题之一[2]。
堆积体的稳定分析计算方面，国内外众多学者进行了一系列的研究工作，主要为边坡稳定计算方法及原理的研究。目前，研究边坡稳定的传统方法主要有极限平衡法、概率分析法、极限分析法、基于数值计算的稳定性评价方法、物理模拟法、非线性方法等[3]。随着研究的深入，研究方法和技术日臻完善，一些新方法、新技术逐渐被应用于堆积体的稳定分析当中。徐文杰[4]通过工程地质力学分析等手段研究了大型土石混合体滑坡空间效应与稳定性；张玉等[5]运用三维极限平衡方法和大变形拉格朗日有限差分法，定性、定量对堆积体稳定性进行了评价；吴火珍等[6]运用非饱和土力学方法对滑坡体在降雨条件下的动态稳定性特征进行了分析；王自高等[7]通过试验对大型堆积体岩土力学特性进行了研究；朱继良等[8]对堆积体稳定性采用三维数值方法模拟分析进行了模拟分析。
虽然堆积体的地质特性及稳定计算方法日益完善与成熟，对堆积体进行稳定分析的工程也较多，降雨、蓄水、地震等影响边坡稳定的致灾因素也有不少研究[9-11]，但对水库区堆积体蓄水过程中的稳定性分析、灾害分析、致灾过程及防治措施的研究较少，因此，对堆积体在不同蓄水位情况下，系统性分析其稳定性的变化规律、失稳机制及风险是十分必要的。
鉴于RM堆积体的规模大，距坝址近，失稳后对工程影响较大，本文应用刚体极限平衡法、虚功率法、有限元差分法、有限元强度折减法计算分析其典型单一剖面的稳定性变化规律，采用三维数值模拟和刚体极限衡法系统性的分析堆积体整体区域失稳变化规律。研究堆积体失稳过程，灾变模式，失稳后的涌浪产生过程及传播规律，并以此为依据制定不同的工程治理措施，分析其治理效果，最终选用预防为主的措施有效抵挡堆积体滑坡产生的涌浪灾害。通过一系列的研究分析，得出堆积体的灾变规律、风险评价，并针对性提出相应的治理措施，对后续类似工程的治理具有重要的借鉴意义。
1. RS工程地质条件
RS堆积体位于LC左岸，距RM水电站坝址约5.4 km。堆积体顺河向长约1.4 km，垂直河向宽约700 m，自然坡度32°~37°，靠河床局部岸坡稍陡，自然坡度40°左右，厚10~100 m，规模巨大，方量约4700万m3，属崩坡积型堆积体。正常蓄水位2895 m以下，方量2700万m3，占总方量的57%。
堆积体的内部物质组成主要分为3类：①上部为有一定胶结的含细粒土砾，砾石粒径一般3~6 cm，含量50%~60%，其间为砂质土充填，较为密实。②中部为较松散的碎砾石层，碎石粒径一般5~20 cm，局部有少量20~50 cm的块石，结构松散。③下部为碎块石土、夹有少量砂卵砾石，碎石含量40%左右，粒径6~20 cm；块石含量20%左右，粒径20~40 cm；卵石总体含量10%左右，粒径1~10 cm。
结合堆积体表面地形坡度、现场碎砾石天然休止角、28组现场大剪试验、40组现场密度试验、21组室内颗分试验、21组室内直剪试验、平硐反演分析、数值模拟法试验研究成果，最终物理力学参数选取如表 1所示。
表 1 RS堆积体稳定计算岩土体物理力学参数取值表Table 1. Physical and mechanical parameters of rock and soil for stability calculation of RS accumulation土层编号 物质组成 重度/(kN·m-3) 水上天然抗剪强度 水下饱和抗剪强度 天然 饱和 黏聚力/kPa 内摩擦角/(°) 黏聚力/kPa 内摩擦角/(°) ①上部 较松散的碎砾石层 22.0 23.0 10 34.5 5 30.5 ②中部 有一定胶结的含细粒土砾 21.0 22.5 50 33.0 25 29.5 ③下部 碎石土夹少量砂卵砾石 21.5 22.5 20 35.5 10 31.5 2. 灾变分析
2.1 滑动模式计算分析
根据堆积体的物质组成，堆积体可能的滑动破坏模式有3种：①以基覆界面为主滑面，堆积体向下向外滑移；②土体内部产生圆弧形滑塌；③下部产生圆弧形滑塌，上部沿胶结较差的碎砾石层弱面产生滑移。RS堆积体典型计算模型及破坏模式如图 1所示。
根据库区RS堆积体地质地形情况，选取堆积体上游至下游R1~R10共计10个剖面，对可能的3种滑动模式进行计算分析。由图 2可知，随着水位的上升，堆积体沿基覆界面滑动时，边坡安全系数从1.272降低到1.003，沿内部圆弧面滑动时，边坡安全系数从1.257降至0.959，沿弱面滑动时，边坡安全系数从1.218降至1.002。计算结果表明，堆积体滑动最可能滑动模式为沿土体内部圆弧滑动，其主要原因为内部圆弧滑动时，自动搜索最不利滑动面，滑移路径相对较优，使得土体自身抗滑力较小，而沿基覆界面及弱面滑动为指定滑动面，滑移路径较长，增加了土体自身的抗滑力，进而使得边坡安全系数相对较高。
![]()
图 2 蓄水过程–安全系数关系曲线Figure 2. Relationship between impoundment process and safety factor2.2 典型剖面稳定分析
针对堆积体典型剖面R2，采用极限平衡法、虚功率法、有限元差分法及有限元强度拆减法进行对比计算分析，分析其天然水位2654.0 m、施工低水位2744.8 m、死水位2815.0 m、施工高水位2863.8 m和正常蓄水位2895.0 m时的边坡稳定性及其变化规律。
计算结果如图 3所示，不同计算方法其安全系数具有一定差异。随着库区水位的上升，刚体极限平衡法安全系数介于1.161~1.003，虚功率法安全系数介于1.138~0.909，有限元差分法安全系数介于1.080~0.901，有限元强度拆减法安全系数介于1.060~0.860。相比而言，刚体极限平衡法计算出的安全系数较大，有限元强度拆减法计算出的安全系数偏小，虚功率法和有限元水库区大型堆积体灾变分析及对策研究差分法计算出的安全系数居中。但基本规律一致，即天然状态低水位时，边坡安全系数均大于1.05，处于稳定状态，随着蓄水位不断提高，边坡稳定安全系数呈降低趋势，正常蓄水位2895.0 m时，边坡安全系数均小于1.0，处于失稳状态或临界失稳状态。
![]()
图 3 蓄水过程–安全系数关系曲线(R2剖面)Figure 3. Relationship between impoundment process and safety factor for section R22.3 整体稳定灾变分析
为研究堆积体整体失稳灾变规律，采用刚体极限平衡法对R1~R10共计10个剖面进行稳定计算分析，计算结果如图 4所示，R1、R3、R7剖面在施工高水位2863.8 m时率先出现失稳，其余各剖面在蓄水至正常蓄水位时，处于临界稳定状态，其安全系数在1.0左右，不满足规范设计要求。
![]()
图 4 蓄水过程–安全系数关系曲线(R1~R10剖面)Figure 4. Relationship between impoundment process and safety factor for sections of R1 to R10图 5，6表明，在蓄水过程中R1、R7区域首先出现小区域失稳，滑坡量为360万m3，接着R3剖面出现小区域失稳，滑坡量为190万m3。最终在蓄水至2895.0 m水位时，其它区域在首滑区和次滑区的拖拽作用下将会出现整体失稳。整体分析结果表明，随着蓄水位不断提高，堆积体边坡安全系数逐渐降低，堆积体边坡由稳定状态渐逐变化为局部失稳状态，到最终整体失稳，其灾变过程由稳定—局部失稳—整体失稳缓慢变化。
![]()
图 6 堆积体边坡蓄水失稳过程Figure 6. Process of impoundment and instability of accumulation slope为进一步研究RS堆积体的失稳灾变规律和潜在破坏特征，通过三维数值计算进行对比分析。三维计算FLAC3D建模通过三维地质模型直接转换的方式，网格尺寸则根据计算要求确定，在重点区域采用小尺寸网格，而非重点部位如基岩则采用稀疏网格。RS堆积体三维地质模型如图 7所示。在地形、物质分层等地质因素影响作用下，RS堆积体变形与稳定性质存在分区特征，边坡最不利部位分布于堆积体上游侧。意味着从三维空间的角度，RS堆积体并非出现整体性失稳破坏，而是河流出现拐弯段为界，其上游侧A区安全性较低、应先于下游侧B区失稳(图 8)。从现场地质情况看，下游侧基岩底板为反坡缓倾节理面，堆积体层厚较薄一些，也有利于维持相对较好的稳定性。安全性相对较差的上游侧A区稳定特征也存在一定的分区特征，其中上部崩坡积物的稳定性略低于下部冰水堆积物。
![]()
图 8 堆积体强度与变形关系曲线Figure 8. Relationship between strength and deformation of accumulation2.4 涌浪传播规律
根据RS堆积体及周边地形的地质资料，以南北11000 m，东西9500 m为参考区域，建立三维模型，如图 9所示。同时为定量描述涌浪的传播和规模，选取了3个坝体周围测点以及12个库区测点，观测这些位置处的水面高程变化，监测点布置如图 10所示。
![]()
图 9 涌浪分析计算所用三维地质模型Figure 9. Three-dimensional geological model for surge analysis and calculationRS堆积体稳定计算结果表明，蓄水后处于不稳定状态。选取安全系数较小的3种滑动情况进行计算分析：滑况1(整体滑动)，滑况2(底层滑动)，滑况3(上层滑动)。滑坡涌浪分析按最不利工况考虑，假定其失稳模式为刚体失稳，失稳时水库在正常蓄水位附近运行。滑坡体最高滑速采用Heller法、ASCE法、Scheidegger法、Vacondio法进行计算[12]，计算结果如表 2所示，4种方法估计的滑速值均在10~30 m/s，这符合多年滑坡涌浪研究成果以及实际涌浪事件的反演，但具体数值有一定的差异。
表 2 RS堆积体3种滑况最高滑速计算成果Table 2. Calculated results of maximum sliding velocity of RS accumulation under three sliding conditions滑况 滑动模式 最小安全系数K 滑坡体高度H/m 方量/(104 m3) 最高滑速值/(m·s-1) 滑况1 整体滑动 1.22 67.75 2865.9 18~27 滑况2 底层滑动 1.01 58.32 1397.3 23 滑况3 上层滑动 1.22 136.83 1977.4 25~35 采用光滑粒子动力学法，建立滑坡涌浪的水土耦合动力学模型，对筛选的3个典型滑坡体入水的首浪进行数值计算，分析首浪特征参数及爬升高度。
涌浪传播的计算以首浪高度及范围作为初始条件，以上下游可传播涌浪时间过程作为边界校准条件，在库区范围内求解浅水方程得到涌浪的传播过程，同时在坝体附近采用浅水方程和加密的网格求解涌浪的爬升过程。可传播涌浪浪高计算结果汇总见表 3，库区RS下游监测点及坝体周围监测的水位过程线如图 11，12所示。
表 3 RS堆积体滑坡可传播涌浪浪高计算成果Table 3. The calculation results of surge height can be spread by RS accumulation landslide滑况 滑速/(m·s-1) 首浪高度/m 可传播浪计算代表值/m 坝前浪高/m 坝顶波浪爬高高程/m 滑况1 18 26.8 7.17 5.42 2906.44 27 29.8 滑况2 23 27.9 5.25 — — 敏感性分析1 5 13.4 3.66 2.77 2900.69 敏感性分析2 10 21.5 5.73 4.43 2904.25 ![]()
图 11 库区RS下游监测点的水位过程线Figure 11. Hydrograph of water level of RS downstream monitoring point![]()
图 12 坝体周围监测点的水位过程线Figure 12. Hydrograph of water level of monitoring points around dam在正常蓄水位2895 m时，RS堆积体在库区监测点7和8之间的位置失稳滑入水中，失稳产生首浪高度29.8 m，在库区内形成7.17 m左右的可传播浪，首浪发生后约170 s传到坝前，传播至坝前的波高约5.42 m，随后向坝体传播，在坝体1∶2.1的坝面上爬升并产生爬坡效应，坝顶附近增加至11.44 m的最大浪高，在坝顶爬升的最大浪高高程为2906.44 m。
3. 防治对策研究
3.1 治理措施
(1) 治理方案
库区RS堆积体在空间上分布较广，为便于工程设计，将该堆积体从上游到下游按提供的剖面R1~R10进行分区治理设计。首先针对每个分区分别进行治理方案设计，然后可根据各分区治理方案的成果差异情况考虑采用统一治理方案或分区治理方案。通过对排水措施、削坡减载、抗滑桩、预应力锚索抗滑桩和格构锚固等治理措施进行方案比选，最终选取削坡减载方式一(全削)、削坡减载方式二(半削)、减重反压方案进行治理方案设计。
(2) 治理效果评价
RS堆积体采用全削方案(方案一)和减重反压方案(方案三)治理后稳定性效果最好，堆积体各剖面在所有工况和滑动模式下稳定性基本满足设计要求；而采用半削方案(方案二)治理后堆积体沿基覆界面整体滑动稳定性基本能够满足设计要求，但在沿内部圆弧滑动和弱面滑动模式下，堆积体稳定尚无法达到设计要求，甚至仍可能发生失稳。
采用全削和半削方案的施工难度较小，但设计开挖渣料运距约18 km，所产生的大量土方堆渣问题对环境有一定影响；减重反压方案施工难度相对复杂，可将开挖料就地反压回填至库区河道的措施，保证土方挖填方量基本平衡，有效解决堆渣问题，一定程度上改变了堆积体所在的天然河床形态，对天然河道流态等会产生较大影响，但在可接受范围内。
综合治理效果、环境保护、施工难度等因素考虑，减重反压方案对边坡稳定性提高明显。但RS堆积体治理的措施费用较高，高达10.5亿元，且施工难度较大。
3.2 避让措施
RS堆积体地质灾害危害性大，处理难度高，通过工程治理措施加以解决不太现实，根据堆积体的变形特征及致灾特点，从坝址、坝型及枢纽布置选择方面研究分析采取工程避让措施的可行性。
坝址方面，RS以上河段，该河段河谷较陡，存在水能资源不能合理利用，交通条件极差和施工布置十分困难等不利因素，不适宜选作坝址河段；绒曲沟口下游河段地形地质条件差且社会影响因素大，不适宜选作坝址；RS以上河段与下游梯级脱水段较长，水头利用率较小，交通运输条件差，相应经济指标较差，也不宜作为本梯级坝址的河段；RS至绒曲沟沟口河段，该河段河谷相对较窄，地形较为完整，基岩大部分裸露，岩质坚硬，覆盖层浅薄，地质条件相对较好，是较为理想的坝址河段，推荐坝址位于RS堆积体下游5.4 km。
坝型方面，从工程规模、筑坝技术难度和坝址河谷形态、地形地质条件等分析，心墙堆石坝、面板堆石坝、混凝土拱坝及混凝土重力坝四种坝型对RM坝址均有其适应性，但各有利弊。从工程条件、建坝技术、工程投资等综合分析，坝址处心墙坝优于其它坝型。从不同水位比较的成果分析，均是心墙堆石坝更适应于工程的地形地质条件和当前的技术经济条件，推荐心墙堆石坝为选定坝型。
枢纽布置方面，坝址处呈“S”形河谷，坝址河段弯曲河谷有利于当地材料坝枢纽布置，左右岸均具备布置引水发电建筑物条件，可充分利用河弯地形将岸边过水建筑物截弯取直布置于右岸。经左右岸引水、泄洪建筑物布置多方案比选后，推荐砾石土心墙堆石坝+洞式溢洪道+泄洪洞+放空洞+引水发电系统。
综上所述，RM库区RS堆积体从坝址、坝型及枢纽布置上均不具备避让条件。
3.3 预防措施
(1) 预防方案
RS堆积体工程治理难度大，采取工程治理措施可行性较小；枢纽建筑物选址、选型设计过程中经论证比选之后，认为均不具备避让条件。故考虑从工程主体本身出发，研究其采取预防措施的可行性。
RS堆积体距离坝址7 km。RS堆积体滑坡涌浪在2895 m蓄水位时，产生首浪29.8 m，可传播浪7.17 m的条件下，传播至坝前的浪高约5.42 m，到坝顶最大浪高高程2906.44 m，超过原坝顶设计高程2902 m，一旦发生滑坡，将会威胁到坝体的安全。
预防方案结合涌浪传波浪高及大坝结构体型进行设计，考虑大坝加高5 m，坝顶高程加高至2907 m。坝体上、下游坝体轮廓相应外扩，坝坡同原方案设计，上游坝坡坡比1∶2.1，下游坝坡坡比1∶2.0。加高之后的大坝结构顶部高程2907 m，高于堆积体滑坡涌浪最大高程2906.44 m，可防止堆积体滑坡产生涌浪翻坝。
(2) 预防方案评价
坝顶高程加高至2907 m之后，高于坝顶最大浪高高程2906.44 m，可抵挡RS堆积体滑坡涌浪产生的灾害风险；经坝坡稳定、渗流、静力应力应变计算研究，结果表明坝顶高程加高之后，大坝结构设计满足有关规范要求；虽然坝顶高程增加之后，工程投资相应增加9578万元，但相比RS堆积体的工程治理措施费10.5亿元，工程投资较为节省。因此，RS堆积体采取预防为主的治理措施是合理可行的。
4. 结论
(1) RS堆积体计算过程中，采用刚体极限平衡法、虚功率法、有限元差分法、有限元强度折减法对RS堆积体典型剖面进行对比计算分析，计算结果表明，不同计算方法其安全系数有一定差异，但基本规律一致。即随着库区水位的不断升高，边坡稳定安全系数呈降低趋势。
(2) 堆积体整体范围内，从上游至下游选取10个典剖面，对其整体稳定性进行系统性计算分析，并采用三维数值方法并行对比计算，研究堆积体的整体失稳机制及灾变模式，计算分析结果表明，堆积体变形及灾变过程为一渐变过程，随着蓄水位的提高，边坡稳定状态由稳定—变形—局部失稳—较大规模失稳—大规模失稳，逐渐演变为灾变过程。
(3) 开展了RS堆积体风险分析，确定堆积体滑坡产生的致灾范围，及致灾事件发生的可能性，计算结果表明RS堆积体现状处于稳定状态，蓄水后可能发生局部滑动，滑坡将导致涌浪，并向坝前传播。
(4) RS堆积体规模巨大，采取工程治理措施，工程投资高，施工难度大。坝址、坝型及枢纽布置选择方面研究分析表明，不具备避让条件。结合堆积体稳定分析、涌浪影响、风险分析及大坝防浪结构设计等综合分析，RS堆积体采取坝顶高程加高的预防处理方式，抵挡滑坡涌浪产生的次生灾害。
(5) 为进一步验证理论和数值计算出的堆积体失稳规律，后期计划开展大比尺物理模型试验对堆积体失发机理及滑坡涌浪传播过程进行试验研究，进一步研究其灾变失稳模式并制定相应的监测预警方式和应急措施。
-
![]()
图 4 不同入射频率下4类饱和地层P1，P2和S波波速与渗透系数的关系
Figure 4. Relationship between P1, P2 and S wave velocities and permeability coefficients of four types of saturated soils under incidence of SV waves with different frequencies
![]()
图 5 砂土P1，P2和S波速与入射频率的关系曲线
Figure 5. Velocity responses of P1, P2 and S waves of sands under incidence of SV waves with different frequencies
![]()
图 6 不同渗透系数下衬砌周向水平位移幅值曲线
Figure 6. Amplitude curves of circumferential horizontal displacement of linings under different permeability coefficients
![]()
图 7 不同渗透系数下衬砌水平位移幅值谱
Figure 7. Amplitude spectra of horizontal displacement of linings under different permeability coefficients
![]()
图 8 不同渗透系数下衬砌周向动应力集中因子幅值曲线
Figure 8. Amplitude curves of circumferential dynamic stress concentration factor of linings under different permeability coefficients
![]()
图 9 不同渗透系数下衬砌动应力集中因子幅值谱
Figure 9. Amplitude spectra of dynamic stress concentration factor of linings under different permeability coefficients
![]()
图 10 不同渗透系数下土–衬砌交界面孔隙水压力幅值曲线
Figure 10. Amplitude curves of pore water pressure at soil-lining interface under different permeability coefficients
![]()
图 11 不同渗透系数下土–衬砌交界面孔隙水压力幅值谱
Figure 11. Amplitude spectra of pore pressure at soil-lining interface under different permeability coefficients
![]()
图 12 不同渗透系数砂岩的孔隙水压力分布图
Figure 12. Distribution of pore water pressure of sandstone under different permeability coefficients
![]()
图 13 不同渗透系数卵石土的孔隙水压力分布图
Figure 13. Distribution of pore water pressure of pebble soil under different permeability coefficients
![]()
图 14 不同渗透系数砂土的孔隙水压力分布图
Figure 14. Distribution of pore water pressure of sand under different permeability coefficients
表 1 不同类型饱和土渗透系数分布范围
Table 1 Permeability coefficients of saturated soils
饱和地层类型 静力作用下渗透系数范围k/(m·s-1) 地震作用下渗透系数范围k/(m·s-1) 岩石、堆石料等 101~10-1 1.9×102~1.9×100 级配好卵石土、砾石等 10-2~10-4 1.9×10-1~1.9×10-3 级配较好砂土等 10-3~10-5 1.9×10-2~1.9×10-4 粉土、黏质、砂细砂等 10-5~10-8 1.9×10-4~1.9×10-7 淤泥质黏土等 10-8~10-11 1.9×10-7~1.9×10-10 
下载: 导出CSV
表 2 4类饱和地层参数及渗透系数范围
Table 2 Four types of parameters of saturated soils and range of permeability coefficient
饱和地层 剪切模量/MPa 泊松比 土颗粒体积模量/MPa 液体体积模量/MPa 土骨架平均体积模量/MPa 固体密度/(kg·m-3) 液体密度/(kg·m-3) 孔隙率 渗透系数[11] /(m·s-1) 砂岩[13] 3700 0.20 36000 2000 6166.7 2650 1000 0.300 1~102 卵石土[14] 854.7 0.17 45000 2000 1010.1 2150 1000 0.400 10-2~1 砂土[14] 277.8 0.26 30000 2000 486.1 2100 1000 0.400 10-4~10-2 粉土[14] 64.15 0.30 20000 2000 139.0 1970 1000 0.594 10-7~10-4
下载: 导出CSV
-
[1] 黄雨, 叶为民, 唐益群, 等. 上海深厚饱和覆盖土层的动力耦合地震反应分析[J]. 岩土力学, 2002, 23(4): 411–416. doi: 10.3969/j.issn.1000-7598.2002.04.004 HUANG Yu, YE Wei-min, TANG Yi-qun, et al. Coupled seismic response analysis of deep saturated soil covering layers in Shanghai[J]. Rock and Soil Mechanics, 2002, 23(4): 411–416. (in Chinese) doi: 10.3969/j.issn.1000-7598.2002.04.004
[2] WANG Z H, ZHAO C G, DONG L. An approximate spring-dashpot artificial boundary for transient wave analysis of fluid-saturated porous media[J]. Computers and Geotechnics, 2009, 36(1/2): 199–210.
[3] 谷音, 庄舒曼, 卓卫东, 等. 考虑饱和土的地铁车站结构非线性地震反应研究[J]. 岩土力学, 2015, 36(11): 3243–3251. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201511028.htm GU Yin, ZHUANG Shu-man, ZHUO Wei-dong, et al. Analysis of nonlinear seismic response of subway station considering saturated soil[J]. Rock and Soil Mechanics, 2015, 36(11): 3243–3251. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201511028.htm
[4] 李亮, 吴利华, 王相宝, 等. 基于流固耦合动力模型的饱和土体-隧道体系地震反应研究[J]. 地震工程学报, 2016, 38(6): 862–868. https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201606003.htm LI Liang, WU Li-hua, WANG Xiang-bao, et al. Seismic response of saturated soil-tunnel system based on fluid-solid coupling dynamic model[J]. China Earthquake Engineering Journal, 2016, 38(6): 862–868. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-ZBDZ201606003.htm
[5] LI P, SONG E X. A viscous-spring transmitting boundary for cylindrical wave propagation in saturated poroelastic media[J]. Soil Dynamics and Earthquake Engineering, 2014, 65: 269–283. doi: 10.1016/j.soildyn.2014.06.022
[6] LIU Z X, JU X, WU C Q, et al. Scattering of plane P1 waves and dynamic stress concentration by a lined tunnel in a fluid-saturated poroelastic half-space[J]. Tunnelling and Underground Space Technology, 2017, 67: 71–84. doi: 10.1016/j.tust.2017.04.017
[7] FETTER C W. Applied Hydrogeology[M]. Long Grove: Waveland Press, 1994.
[8] 刘中宪, 琚鑫, 梁建文. 饱和半空间中隧道衬砌对平面SV波的散射IBIEM求解[J]. 岩土工程学报, 2015, 37(9): 1599–1612. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509008.htm LIU Zhong-xian, JU Xin, LIANG Jian-wen. IBIEM solution to scattering of plane SV waves by tunnel lining in saturated poroelastic half-space[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(9): 1599–1612. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201509008.htm
[9] HAN B, ZDRAVKOVIC L, KONTOE S. Numerical and analytical investigation of compressional wave propagation in saturated soils[J]. Computers and Geotechnics, 2016, 75: 93–102. doi: 10.1016/j.compgeo.2016.01.019
[10] BIOT M A. Mechanics of deformation and acoustic propagation in porous media[J]. Journal of Applied Physics, 1962, 33(4): 1482–1498. doi: 10.1063/1.1728759
[11] WONG H L. Diffraction of P, SV, and Rayleigh waves by surface topography[M]. California: University of California, 1979.
[12] 钟启凯. 地下圆形组合衬砌洞室在地震波下的动力反应分析[D]. 长沙: 湖南大学, 2009. ZHONG Qi-kai. Dynamic Response Aanalysis of Underground Cylindrical Composite- Lining Cavern Subjected to Seismic Waves[D]. Changsha: Hunan University, 2009. (in Chinese)
[13] LIN C H, LEE V W, TRIFUNAC M D. The reflection of plane waves in a poroelastic half-space saturated with inviscid fluid[J]. Soil Dynamics and Earthquake Engineering, 2005, 25(3): 205–223. doi: 10.1016/j.soildyn.2004.10.009
[14] 宋佳. 饱和土场地波动数值模拟方法及其工程应用[D]. 北京: 北京工业大学, 2017. SONG Jia. Wave Numerical Method of Saturated Site Soil and its Engineering Application[D]. Beijing: Beijing University of Technology, 2017. (in Chinese)
[15] HASHASH Y M A, HOOK J J, SCHMIDT B, et al. Seismic design and analysis of underground structures[J]. Tunnelling and Underground Space Technology, 2001, 16(4): 247–293. doi: 10.1016/S0886-7798(01)00051-7
[16] 李瑞山, 袁晓铭, 吴晓阳. 抗震规范等效剪切波速简化算法适用性研究[J]. 地震工程与工程振动, 2018, 38(3): 30–36. https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201803004.htm LI Rui-shan, YUAN Xiao-ming, WU Xiao-yang. Study on the applicability of simplified equivalent shear wave velocity calculation method in seismic design code[J]. Earthquake Engineering and Engineering Dynamics, 2018, 38(3): 30–36. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DGGC201803004.htm
-
期刊类型引用(8)
1. 范永丰，罗锦，徐衍，郭庆彪，万战胜. 采空区残余沉降对深挖边坡稳定性的影响. 工业建筑. 2024(04): 166-172 . 
百度学术
2. 胡大儒，吴述或，罗超鹏，邓辉，李鹏飞，王照英. 澜沧江某巨型堆积体蓄水失稳诱发涌浪预测. 地质科技通报. 2024(06): 78-88 . 百度学术
3. 陈世壮，徐卫亚，石安池，闫龙，许晓逸，汪华晨，王环玲. 高坝大库滑坡涌浪灾害链研究综述. 水利水电科技进展. 2023(03): 83-93 . 百度学术
4. ZHANG Xin，TU Guo-xiang，LUO Qi-feng，TANG Hao，ZHANG Yu-lin，LI An-run. Failure mechanism of a large-scale composite deposits caused by the water level increases. Journal of Mountain Science. 2023(05): 1369-1384 . 必应学术
5. 魏东旭，万利，刘传利，郑国胜. 卢家湾大桥堆积体滑坡稳定性分析及处治措施研究. 岩土工程技术. 2023(03): 291-296 . 百度学术
6. 张珍珍，李岩. 涌浪作用下库岸边坡的影响因素分析. 江西建材. 2023(05): 113-115 . 百度学术
7. 罗博，刘宇昊，涂国祥，张鑫，张燕媚，李安润. 水库蓄水诱发大型岸坡堆积体失稳破坏机理研究：以澜沧江RS库区堆积体为例. 水利水电技术(中英文). 2023(08): 156-166 . 百度学术
8. 苏珅，陈丽丽. 点荷载试验下的大型水库近场区构造稳定性数值模拟. 水利技术监督. 2022(11): 178-182 . 百度学术
其他类型引用(2)
计量
- 文章访问数: 281
- HTML全文浏览量: 21
- PDF下载量: 265
- 被引次数: 10
