折线型复合式滑坡渐进破坏稳定性状态的力学判别

杜毅; 晏鄂川; 蔡静森; 高旭; 柳万里

doi:10.11779/CJGE20220184

折线型复合式滑坡渐进破坏稳定性状态的力学判别 English Version

中国地质大学(武汉)工程学院，湖北武汉 430074

基金项目:

国家自然科学基金项目 41972289

国家自然科学基金项目 41807264

详细信息

作者简介:
杜毅（1993—），男，博士研究生，从事滑坡变形破坏机制与防治方面的研究工作。E-mail：duyi2171@qq.com

中图分类号: TU43
计量
- 文章访问数: 350
- HTML全文浏览量: 53
- PDF下载量: 125
出版历程
- 收稿日期: 2022-02-21
- 网络出版日期: 2023-02-08
- 刊出日期: 2023-05-31

Mechanical discrimination of stability state of progressive failure of broken-line complex landslides

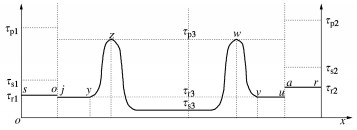
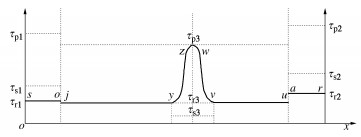
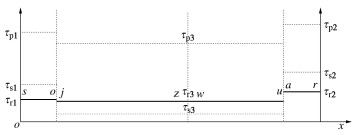
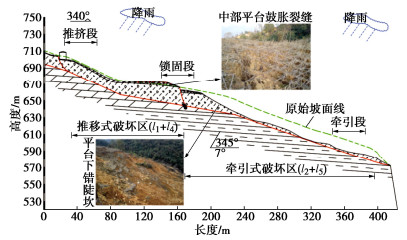
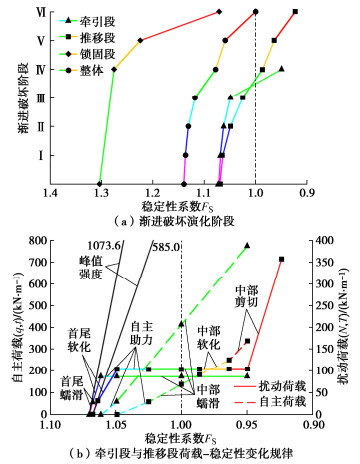
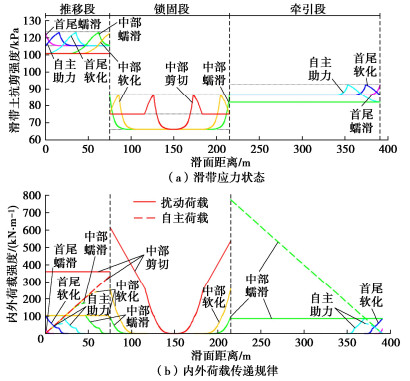
Faculty of Engineering, China University of Geosciences, Wuhan 430074, China

摘要

摘要: 折线型复合式滑坡各区段岩土体性质及应力状态的差异加剧了稳定性判别的难度，以该类滑坡为对象，研究其渐进破坏稳定性状态演化的力学判别。结合滑带土应变软化特性构建滑坡力学模型，将其渐进破坏过程划分为8个演化阶段，并依据静力平衡条件及传递系数法建立与之对应的稳定性计算方程，以示滑坡渐进发展中由首尾向中部区段间的荷载传递机制，揭示滑坡局部和整体所受荷载、应力分布与稳定性状态间的量化差异及演变规律。研究结果表明：演化初期滑坡稳定性降幅较小，当渐进破坏发展至中部锁固段时，滑坡稳定性开始大幅衰减。处于滑坡自主助力阶段之前于首尾两端布设的防治工程将是节能高效的，若处于该阶段内则需结合扰动荷载传递位置及自主荷载积累的大小来判定防治部位，错过该治理关键阶段应考虑以锁固段的稳定为主。
- 折线型复合式滑坡 /
- 应变软化 /
- 渐进破坏 /
- 荷载传递 /
- 稳定性状态
Abstract: The difference in properties and stress states of soils in each section of a broken-line complex landslide exacerbates the difficulty of judging its stability. Taking this kind of landslide as the object, the mechanical discrimination of evolution of stability state of progressive failure is studied. Considering the strain-softening characteristics of soils in sliding zone, the mechanical model for the landslide is established, and its progressive failure process is divided into eight evolutionary stages. According to the static equilibrium principle and the transfer coefficient method, the relevant equation for calculating stability of each stage of the landslide is established. The load transfer mechanism between the front and rear to the middle section in the progressive development of the landslide is shown, and the quantitative difference and evolution law of the loads, stress distribution and stability states between the part and the whole of the landslide are revealed. The results show that the stability of the landslide decreases slightly at the initial stage of evolution, and when the progressive failure develops to the middle locking section, the it begins to decline greatly. The control projects laid at the front and rear before the self-imposed load stage of the landslide are energy-saving and efficient. If it is at this stage, the control position should be determined by combining the position of the equivalent load transfer and the accumulation of the self-imposed loads, and the stability of locking section should be considered when missing the key stage of control.
- broken-line complex landslide /
- strain softening /
- progressive failure /
- load transfer /
- stability state

HTML全文

0. 引言

膨胀性非饱和土是一种具有特殊结构的非饱和土，通常表现出吸水膨胀、失水收缩和浸水强度降低等特性，工程中容易使建筑物产生不均匀沉降，甚至会导致结构开裂和破坏。因此，对膨胀性非饱和土本构模型的研究具有重要工程意义，能够为预测膨胀土的变形特性从而避免工程灾害的发生提供有效手段。

1990年，Alonso等^[1]在修正剑桥模型的基础上，考虑了吸力的影响并引入了加载-湿陷屈服面（LC屈服面）和吸力增加屈服面（SI屈服面），进而提出了巴塞罗那弹塑性本构模型（BBM），能够描述非饱和土屈服应力随吸力增加而变大、湿化变形等力学特性。在此之后，Wheeler等^[2]、Sun等^[3-4]、缪林昌^[5]、赵成刚等^[6]、姚仰平等^[7-8]、Luo等^[9]也提出了多种形式的非饱和土本构模型，这些模型虽然可以描述包括湿陷变形在内的非饱和土的基本力学特性，但不能体现膨胀性非饱和土吸水膨胀的力学特性。

为更好地描述膨胀性非饱和土的力学特性，Gens等^[10]于1992年建立了膨胀性非饱和土弹塑性本构模型的理论框架模型（G-A模型）。在此基础上，Alonso等^[11]进一步建立了巴塞罗那膨胀性非饱和土弹塑性本构模型（BExM）。该模型认为膨胀土的膨胀性是由于其具有双重结构，即微观结构与宏观结构，当非饱和膨胀土湿化时，微观结构会发生膨胀，从而导致宏观结构发生塑性膨胀，最终表现出土体的整体膨胀。在此之后，许多学者在这一模型的理论基础上进行了改进和扩展，Sánchez等^[12]在G-A模型的基础上建立了考虑微观-宏观双重结构影响的广义塑性模型，并将其成功运用于有限元数值分析中；Mašín^[13]分别建立了能够描述微观结构和宏观结构的计算公式，通过引入双重结构的耦合方程建立了考虑水力耦合的非饱和膨胀土模型；卢再华等^[14]在改进的G-A模型中引入剪切屈服面（S_y），建立了非饱和原状膨胀土的弹塑性损伤本构模型；陈正汉等^[15-16]进一步针对原状膨胀性土、重塑膨胀性土和重塑膨润土等不同类型的膨胀土进行了全方位的研究，综合考虑了温度、持水特性等因素对膨胀土力学性质的影响，建立了考虑热-水-力等多场耦合特性的膨胀土模型；孙德安等^[17]考虑了饱和度对应力应变关系的影响及变形对土水特性的影响，并引入了等孔隙比线，建立了能够描述膨胀性非饱和土水力-力学耦合特性的弹塑性本构模型；曹雪山^[18]针对膨胀土干湿循环特性进一步完善模型，引入了微-宏观结构耦合参数，提出了考虑双重结构耦合的弹塑性本构模型；李舰等^[19-20]，Li等^[21]建立了适用于膨胀性非饱和土的边界面模型，并围绕其提出了有效的数值计算方法。

Yao等^[22]以修正剑桥模型为基础，提出了可以描述饱和超固结土力学特性的统一硬化（UH）本构模型，之后进一步考虑了吸力的影响，引入LC屈服面，扩展了UH模型使其可以描述非饱和土的特性^[8]。本文在非饱和土UH模型基础上，引入考虑超固结度和初始干密度影响的膨胀式，使其可以反映膨胀土湿化膨胀过程中产生的塑性变形，并进一步构建了考虑膨胀土膨胀性的非饱和土UH模型，由于本模型仅考虑了膨胀土的非饱和、胀缩性和超固结性等特性，没有考虑裂隙性^[23]，是对理想状态的膨胀土进行描述，故称理想膨胀性非饱和土UH模型。

1. 膨胀性非饱和土UH模型

1.1 吸力应力与屈服面方程

Alonso等^[1]在BBM中认为非饱和土的应变由吸力和净应力共同控制，并提出了LC屈服面和SI屈服面的概念来描述非饱和土的变形特性。Luo等 ^[9]在此基础上，根据对试验现象的分析，提出了新的吸力应力表达式，

$\begin{array}{*{20}{c}} {{p_{\text{s}}} = a\left( {1 - {e^{ - \frac{s}{a}}}} \right)} \end{array}\ \ \ \ \ \ \ 。$

(1)

式中： ${p_{\text{s}}}$ 为吸力应力，表示吸力对土体黏聚力的贡献值^[16]，可以通过恒定吸力下非饱和土的三轴试验或直剪试验测得； $a$ 为最大吸力应力，可以通过两个或两个以上不同吸力下非饱和土的三轴试验或直剪试验求得^[3]； $s$ 为吸力，是负孔隙水压力和表面张力在土骨架上的综合作用应力。区别于BBM，这里吸力应力与吸力并非正比关系，而是呈现非线性变化并存在一个最大值。

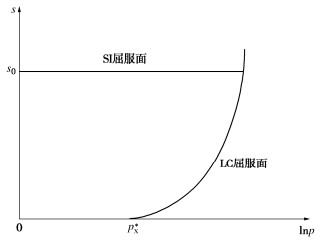
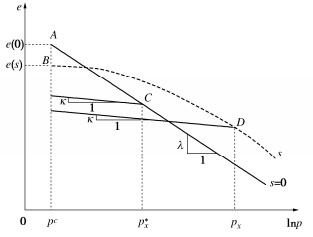
对于正常固结非饱和土，根据Sun等^[3]、Yao等^[8]和Luo等^[9]的研究，假设其等向压缩线在 $e{\text{ - ln}}(p + {p_{\text{s}}})$ 平面呈直线，如图 1所示，其等向压缩线公式可表示为

图 1 饱和土和非饱和土的等向压缩线

Figure 1. Normal compression lines for saturated and unsaturated soils

下载: 全尺寸图片幻灯片

$\begin{array}{*{20}{c}} {e = e(s) - \lambda \ln \frac{{p + {p_{\text{s}}}}}{{{p^{\text{c}}} + {p_{\text{s}}}}}} \end{array}\ \ \ \ \ \ \ 。$

(2)

式中： ${p^{\text{c}}}$ 为参考吸力应力，假设当净平均应力为 ${p^{\text{c}}}$ 时，吸力变化仅引起弹性应变， $\lambda$ 为正常固结饱和土在 $e{\text{ - ln}}p$ 平面上等向压缩线的斜率。当吸力恒定时，平均净应力变化所引起的变形可写为

$\begin{array}{*{20}{c}} {{\text{d}}e_{\text{p}}^{\text{e}} = - \kappa \frac{{{\text{d}}p}}{p}} \end{array}\ \ \ \ \ \ \ 。$

(3)

对于吸力变化引起的变形，假设历史最大吸力为 ${s_0}$ ，当吸力 $s$ 小于历史最大吸力时，吸力变化仅引起弹性变形，当吸力 $s$ 大于历史最大吸力 ${s_0}$ 时，吸力增加会引发弹塑性变形，定量表述如下：

$\begin{array}{c}de=\{\begin{array}{c}-{\kappa }_{\text{s}}\frac{\text{d}s}{s+{p}_{\text{at}}}\text{(}s\le {s}_{0}\text{)}\\ -{\lambda }_{\text{s}}\frac{\text{d}s}{s+{p}_{\text{at}}}\text{(}s＞{s}_{0}\text{)}\end{array}\end{array} \ \ \ \ \ \ \ 。$

(4)

式中： ${\lambda _{\text{s}}}$ 为吸力超过历史最大吸力 ${s_0}$ 之后非饱和土在 $e{\text{ - ln}}s$ 平面内吸力加载线的斜率， ${\kappa _{\text{s}}}$ 为非饱和土在 $e{\text{ - ln}}s$ 平面内吸力回弹线的斜率， ${p_{{\text{at}}}}$ 为标准大气压。

基于上述假设，新的LC屈服面方程可以推导为

$\begin{array}{*{20}{c}} {{{\left( {\frac{{p_{\text{x}}^*}}{{{p^{\text{c}}}}}} \right)}^{\lambda - \kappa }} = {{\left( {\frac{{{p_{\text{x}}} + {p_{\text{s}}}}}{{{p^{\text{c}}} + {p_{\text{s}}}}}} \right)}^\lambda }{{\left( {\frac{{{p_{\text{x}}}}}{{{p^{\text{c}}}}}} \right)}^{ - \kappa }}} \end{array}\ \ \ \ \ \ \ 。$

(5)

式中： ${p_{\text{x}}}$ 为不同吸力下 $p{\text{ - }}q$ 平面屈服面与 $p$ 轴的交点值， $p_{\text{x}}^{\text{*}}$ 为饱和土 $p{\text{ - }}q$ 平面屈服面与 $p$ 轴的交点值，如图 2。

图 2 LC屈服面和SI屈服面

Figure 2. Yield curves of LC and SI

下载: 全尺寸图片幻灯片

SI屈服面采用BBM中与 $p$ 轴平行的直线，如图 2，方程可写为

$\begin{array}{*{20}{c}} {s = {s_0}} \end{array}\ \ \ \ \ \ \ 。$

(6)

式中： ${s_0}$ 为历史最大吸力。

$p{\text{ - }}q$ 平面采用椭圆屈服面，

$f = {\text{ln}}\hat p + \ln \left( {1 + \frac{{{{\hat q}^2}}}{{{M^2}{{\hat p}^2}}}} \right) - \ln ({p_{\text{x}}} + {p_{\text{s}}}) = 0\ \ \ \ \ \ \ 。$

(7)

式中： $\hat p = p + {p_{\text{s}}}$ ， $\hat q = q$ 。本文提出的模型采用相关联流动法则，假设塑性势面方程与屈服面方程相同。

1.2 硬化参量

本模型屈服面的硬化参数采用 $H$ ，硬化规律可表示为

$\begin{array}{*{20}{c}} {\frac{{{\text{d}}p_{\text{x}}^*}}{{p_{\text{x}}^*}} = \frac{{1 + {e_0}}}{{\lambda - \kappa }}dH} \end{array}\ \ \ \ \ \ \ 。$

(8)

Alonso等^[11]在提出的BExM中认为膨胀土吸水膨胀与其微观结构有关，在吸力变化时土体微观结构的改变会引起宏观结构的塑性变形。对于膨胀土，湿化会使得微观结构膨胀，进而引发宏观结构的塑性膨胀。膨胀土在湿化时塑性体应变由两部分组成，一部分是净应力变化和吸力变化综合引发的塑性体应变 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ ，与非膨胀性非饱和土中的塑性体应变相同，另一部分为微观结构变化引起的宏观结构塑性体应变 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}$ 。卢再华等^[24]提出对膨胀性非饱和土湿化时的膨胀量，可采用其与土体湿化产生的弹性体变的关系来求解，参照Alonso等^[11]和卢再华等^[24]对膨胀变形的求解思路，本文假定微观结构的应变与吸力引起的弹性应变相同，将宏观结构发生的塑性体应变 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}$ 表示为微观结构体应变的函数：

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}} = {f_{\text{d}}}{\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}}} \end{array}\ \ \ \ \ \ \ 。$

(9)

式中：

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}} = \frac{{{\kappa _{\text{s}}} \cdot {\text{d}}s}}{{\left[ {(1 + {e_0})(s + {p_{{\text{at}}}})} \right]}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(10)

${f_{\text{d}}}$ 为放大系数，

$\begin{array}{*{20}{c}} {{f_{\text{d}}} = {J^{\frac{{{\rho _{\text{d}}}}}{{{\rho _{\text{w}}}}}}}{{(1 - R)}^2}} \end{array}\ \ \ \ \ \ \ 。$

(11)

式中： $J$ 为反映膨胀土膨胀能力的参数； ${\rho _{\text{d}}}$ 为土体初始干密度，根据高登辉等^[25]的研究，初始干密度对非饱和土的变形参数、强度参数和渗透参数等有重要影响，此处通过引入初始干密度来考虑其对非饱和土膨胀量的影响， ${\rho _{\text{w}}}$ 为水的密度， $R$ 为超固结系数，可通过孔隙状态参数 $\xi$ 求出，

$\begin{array}{*{20}{c}} {R = \exp \left( { - \frac{\xi }{{\lambda - \kappa }}} \right)} \end{array}\ \ \ \ \ \ \ 。$

(12)

为考虑膨胀性的影响，在屈服面中引入微观结构引起的塑性变形，即将塑性应变增量表示为两部分：

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{\text{v}}^{\text{p}} = {\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}} + {\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}} \end{array}\ \ \ \ \ \ \ 。$

(13)

屈服面采用统一硬化参量 $H$ ，并认为统一硬化参量 $H$ 只与净应力引起的塑性体应变有关，具体增量表达式为

$\begin{array}{*{20}{c}} {{\text{d}}H = \frac{{M_{\text{f}}^4 - {{\hat \eta }^4}}}{{{M^4} - {{\hat \eta }^4}}}{\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}} \end{array}\ \ \ \ \ \ \ 。$

(14)

式中： $\hat \eta$ 为应力比， $\hat \eta = \hat q/\hat p$ ； ${M_{\text{f}}}$ 为潜在强度^[26]，

$\begin{array}{*{20}{c}} {{M_{\text{f}}} = 6\left[ {\sqrt {\frac{{12(3 - M)}}{{{M^2}}}\exp \left( { - \frac{\xi }{{\lambda - \kappa }}} \right) + 1} + 1} \right]} \end{array}\ \ \ \ \ \ \ 。$

(15)

式中： $\xi$ 为孔隙状态参数，反映土体当前孔隙比下的超固结程度，

$\begin{array}{*{20}{c}} {\xi = {e_{\hat \eta }} - e} \end{array}\ \ \ \ \ \ \ 。$

(16)

式中： ${e_{\hat \eta }}$ 为当前应力状态下土体正常固结时对应的孔隙比，

${e_{\hat \eta }} = e(s) - \lambda \ln \left[ {\frac{{\hat p}}{{{p^{\text{c}}} + {p_{\text{s}}}}}\left( {1 + \frac{{{{\hat \eta }^2}}}{{{M^2}}}} \right)} \right] + \kappa \ln \left( {1 + \frac{{\hat p}}{p}\frac{{{{\hat \eta }^2}}}{{{M^2}}}} \right) \ \ \ \ \ \ \ 。$

(17)

1.3 弹性应变增量

在净应力和吸力发生变化时，土体会发生变形，其中弹性应变可以表示为弹性体应变和弹性剪应变，本模型中弹性体应变可以表示为

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{\text{v}}^{\text{e}} = {\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}} + {\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}}} \end{array}\ \ \ \ \ \ \ 。$

(18)

其包含两部分，第一部分为净应力变化引起的弹性体应变，

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}} = \frac{k}{{1 + {e_0}}}\frac{{{\text{d}}\hat p}}{p} = \frac{{{\text{d}}\hat p}}{K}} \end{array}\ \ \ \ \ \ \ 。$

(19)

式中：

$\begin{array}{*{20}{c}} {K = \frac{E}{{3{\text{(}}1 - 2v{\text{)}}}}} \end{array} \ \ \ \ \ \ \ \text{；}$

(20)

$\begin{array}{*{20}{c}} {E = \frac{{3(1 - 2v)(1 + {e_0})}}{\kappa }\hat p} \end{array}\ \ \ \ \ \ \ 。$

(21)

第二部分为吸力变化引起的弹性体应变，方程表达式见式（10）。

本模型认为吸力变化不会引起弹性剪应变，故弹性剪应变仅由净应力中的剪应力引起，可表示为

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{\text{d}}^{\text{e}} = \frac{{{\text{d}}\hat q}}{{3G}}} \end{array}\ \ \ \ \ \ \ 。$

(22)

式中：

$\begin{array}{*{20}{c}} {G = \frac{E}{{2(1 + v)}}} \end{array}\ \ \ \ \ \ \ 。$

(23)

1.4 塑性应变增量

由屈服面公式可知，净应力变化引起的应变增量可表示为

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}} = \mathit{\Lambda } \frac{{\partial f}}{{\partial \hat p}}} \end{array}\ \ \ \ \ \ \ \text{，}$

(24)

$\begin{array}{*{20}{c}} {{d} \varepsilon _{\text{d}}^{\text{p}} = \mathit{\Lambda } \frac{{\partial f}}{{\partial \hat q}}} \end{array}\ \ \ \ \ \ \ 。$

(25)

式中： $\mathit{\Lambda }$ 为塑性标量因子。

对当前屈服面函数和LC屈服面函数进行全微分，联立求解后得到

$\begin{array}{*{20}{c}} {\mathit{\Lambda } = {A_0}\frac{{\frac{{\partial f}}{{\partial \hat p}}{\text{d}}\hat p + \frac{{\partial f}}{{\partial \hat q}}{\text{d}}\hat q + {f_{\text{s}}}{\text{d}}s}}{{\frac{{\partial f}}{{\partial \hat p}}}}} \end{array}\ \ \ \ \ \ \ 。$

(26)

式中：

$\begin{array}{*{20}{c}} {{A_0} = \frac{{{c_{\text{p}}}\hat {\mathit{\Omega }} }}{{p_{\text{x}}^{\text{*}}}}\frac{{\lambda {p_{\text{x}}} - \kappa \left( {{p_{\text{x}}} + {p_{\text{s}}}} \right)}}{{\lambda - \kappa }}{{\left( {\frac{{{p_{\text{x}}}}}{{{p^{\text{c}}}}}} \right)}^{\frac{{ - \lambda }}{{\lambda - \kappa }}}}{{\left( {\frac{{{p_{\text{x}}} + {p_{\text{s}}}}}{{{p^{\text{c}}} + {p_{\text{s}}}}}} \right)}^{\frac{\lambda }{{\lambda - \kappa }}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(27)

$\begin{array}{*{20}{c}} {{f_{\text{s}}} = \frac{{ - \lambda {p_{\text{x}}} + \kappa ({p^{\text{c}}} + {p_{\text{s}}})}}{{({p^{\text{c}}} + {p_{\text{s}}})\left[ {\lambda {p_{\text{x}}} - \kappa ({p_{\text{x}}} + {p_{\text{s}}})} \right]}}{{\text{e}}^{ - \frac{s}{a}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(28)

$\begin{array}{*{20}{c}} {p_{\text{x}}^{\text{*}} = {p^{\text{c}}}{{\left( {\frac{{{p_{\text{x}}} + {p_{\text{s}}}}}{{{p^{\text{c}}} + {p_{\text{s}}}}}} \right)}^{\frac{\lambda }{{\lambda - \kappa }}}}{{\left( {\frac{{{p_{\text{x}}}}}{{{p^{\text{c}}}}}} \right)}^{\frac{{ - \kappa }}{{\lambda - \kappa }}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(29)

$\begin{array}{*{20}{c}} {{p_{\text{x}}} = p + \frac{{{{\hat q}^2}}}{{{M^2}{{\hat p}^2}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(30)

$\begin{array}{*{20}{c}} {\hat{\mathit{\Omega }} = \frac{{{M^4} - {{\hat \eta }^4}}}{{M_{\text{f}}^4 - {{\hat \eta }^4}}}} \end{array}\ \ \ \ \ \ \ 。$

(31)

综上可得：

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}} = \mathit{\Lambda } \frac{{\partial f}}{{\partial \hat p}} = {A_0}\left( {\frac{{\partial f}}{{\partial \hat p}}{\text{d}}\hat p + \frac{{\partial f}}{{\partial \hat q}}{\text{d}}\hat q + {f_{\text{s}}}{\text{d}}s} \right)} \end{array}\ \ \ \ \ \ \ \text{，}$

(32)

$\begin{array}{*{20}{c}} {{\text{d}}\varepsilon _{\text{d}}^{\text{p}} = \mathit{\Lambda } \frac{{\partial f}}{{\partial \hat q}} = {A_0}\frac{{\frac{{\partial f}}{{\partial \hat p}}{\text{d}}\hat p + \frac{{\partial f}}{{\partial \hat q}}{\text{d}}\hat q + {f_{\text{s}}}{\text{d}}s}}{{\frac{{\partial f}}{{\partial \hat p}}}}\frac{{\partial f}}{{\partial \hat q}}} \end{array}\ \ \ \ \ \ \ 。$

(33)

对于膨胀性非饱和土，除了上述体应变外，还有微观结构变化引起的体应变，当吸力减小时（即湿化），相应塑性体应变表达式见式（9）。

当吸力增加时，考虑LC屈服面和SI屈服面的耦合，将吸力增加引起的塑性体应变并入 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 考虑，此时 ${f_{\text{d}}} = 0$ ，即得到

$\begin{array}{*{20}{c}} {{f_{\text{d}}} = \left\{ \begin{gathered} {J^{\frac{{{\rho _{\text{d}}}}}{{{\rho _{\text{w}}}}}}}{\left( {1 - {\text{exp}}\left( { - \frac{\xi }{{\lambda - \kappa }}} \right)} \right)^2}{\text{ (d}}s < 0) \hfill \\ 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\text{(d}}s \geqslant 0)\ \ \hfill \\ \end{gathered} \right.} \end{array} \ \ \ \ \ \ \ 。$

(34)

1.5 弹塑性应力应变关系

膨胀土塑性体应变由 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 和 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}$ 两部分组成，弹性体应变由 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{e}}$ 和 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{e}}$ 两部分组成，将应力应变关系表示为矩阵得到

$\begin{array}{*{20}{c}} {\left\{ {\begin{array}{*{20}{c}} {{\text{d}}\hat p + {B_1}{\text{d}}s} \\ {{\text{d}}\hat q + {B_2}{\text{d}}s} \end{array}} \right\} = \left( {\begin{array}{*{20}{c}} {K{A_1}}&{3KG{A_2}} \\ {3KG{A_2}}&{3G{A_3}} \end{array}} \right)\left\{ {\begin{array}{*{20}{c}} {{\text{d}}{\varepsilon _{\text{v}}}} \\ {{\text{d}}{\varepsilon _{\text{d}}}} \end{array}} \right\}} \end{array}\ \ \ \ \ \ \ 。$

(35)

式中：

$\begin{array}{*{20}{c}} {{A_1} = \frac{{12G{A_0}{{\hat \eta }^2} + \hat p({M^4} - {{\hat \eta }^4})}}{{{T_0}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(36)

$\begin{array}{*{20}{c}} {{A_2} = \frac{{ - 2{A_0}\hat \eta ({M^2} - {{\hat \eta }^2})}}{{{T_0}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(37)

$\begin{array}{*{20}{c}} {{A_3} = \frac{{{A_0}K{{({M^2} - {{\hat \eta }^2})}^2} + \hat p({M^4} - {{\hat \eta }^4})}}{{{T_0}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(38)

$\begin{array}{*{20}{c}} {{B_1} = K\frac{{12G{A_0}{{\hat \eta }^2}({T_1} - {A_0}{f_{\text{s}}}) + \hat p{T_1}({M^4} - {{\hat \eta }^4})}}{{{T_0}}}} \end{array}\ \ \ \ \ \ \ \text{；}$

(39)

${B_2} = 6G{A_0}\hat \eta \frac{{K({M^2} - {{\hat \eta }^2})({A_0}{f_{\text{s}}} - {T_1}) + \hat p{f_{\text{s}}}({M^2} + {{\hat \eta }^2})}}{{{T_0}}}\ \ \ \ \ \ \ \text{；}$

(40)

$\begin{array}{*{20}{c}} {{T_0} = {A_0}K{{({M^2} - {{\hat \eta }^2})}^2} + 12G{A_0}{{\hat \eta }^2} + \hat p({M^4} - {{\hat \eta }^4})} \end{array}\ \ \ \ \ \ \ \text{；}$

(41)

$\begin{array}{*{20}{c}} {{T_1} = {A_0}{f_{\text{s}}} + (1 + {f_{\text{d}}})\frac{{{k_{\text{s}}}}}{{(1 + {e_0})(s + {p_{{\text{at}}}})}} - \frac{{{{\text{e}}^{ - \frac{s}{a}}}}}{K}} \end{array}\ \ \ \ \ \ \ 。$

(42)

2. 模型特性分析

本节通过对几种湿化应力路径的模拟和分析，来体现本文模型在描述膨胀性非饱和土湿化过程中体积膨胀和强度降低的特性。所取模型参数： $\lambda$ =0.2， $\kappa$ =0.02， ${\lambda _{\text{s}}}$ =0.08， $\nu$ =0.3，M=1.0，N=1.96， ${\kappa _{\text{s}}}$ =0.01， ${p^{\text{c}}}$ =100 kPa，a=150 kPa， ${p_{{\text{at}}}}$ =100 kPa，初始孔隙比取0.95。

本模型中膨胀性非饱和土膨胀性的体现主要与3个参数有关，即反映土体膨胀能力的系数J、反映土体密实程度的初始干密度 ${\rho _{\text{d}}}$ 以及反映土体超固结程度的系数 $\xi$ ，其中系数J和初始干密度 ${\rho _{\text{d}}}$ 的影响可以通过膨胀系数 $C = {J^{\frac{{{\rho _{\text{d}}}}}{{{\rho _{\text{w}}}}}}}$ 综合反映，系数 $\xi$ 的影响可以通过前期固结压力体现，相同应力路径和吸力状态下，前期固结压力越大， $\xi$ 越大，即土的超固结程度越高。

2.1 等向回弹再湿化

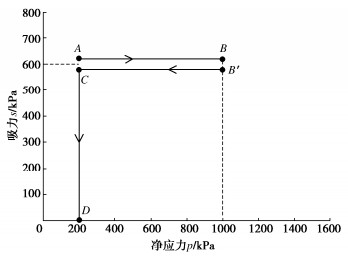
为了分析膨胀系数对膨胀量的影响，先在吸力不变的条件下将土样等向压缩后回弹，然后湿化至饱和，应力路径如中A—B( $B'$ )—C—D所示，其中A—B为等向压缩， $B'$ —C为回弹，C—D为湿化。

图 3 不同C值等向回弹湿化应力路径

Figure 3. Stress paths of isotropic unloading-wetting with different values of C

下载: 全尺寸图片幻灯片

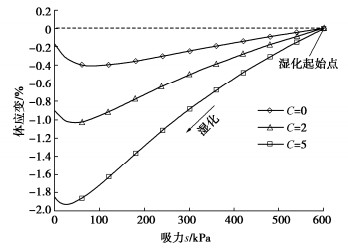
分别取膨胀系数C为0，2，5，在吸力s=600 kPa不变的条件下，将土样从初始状态（围压p=200 kPa）等向压缩至围压p=1000 kPa，然后回弹至p=200 kPa，然后再湿化至饱和（s=0 kPa），由本文所提模型预测湿化过程中土样的体应变，如图 4所示。

图 4 等向回弹湿化中不同C值下体应变

Figure 4. Variation of volumetric strain under stress path of isotropic unloading-wetting with different values of C

下载: 全尺寸图片幻灯片

可以看出，随着土体中吸力降低，土体会发生膨胀变形（负体应变代表膨胀变形），随着膨胀系数C的提高，膨胀量会随之增大；同时在吸力较低的时候土体会发生湿陷，这是因为在吸力接近0 kPa时，土样应力状态接近屈服面，吸力降低使得土体产生的塑性湿陷体应变增量 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 在数值上超过微观结构引起的塑性膨胀体应变增量 ${\text{d}}\varepsilon _{{\text{vs}}}^{\text{p}}$ ，塑性湿陷变形在总变形中占据主导地位，土体整体表现出体积减小。

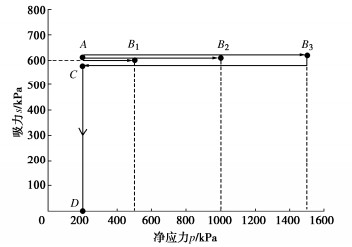
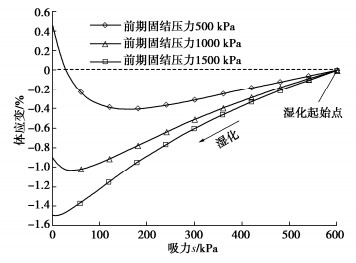
为分析等向回弹再湿化路径下不同超固结度对膨胀量的影响，取初始围压p=200 kPa，膨胀系数C=2，吸力s保持为600 kPa，将土样分别等向压缩至500，1000，1500 kPa，再回弹至200 kPa，应力路径如图 5所示A—B₁（B₂，B₃）为等向压缩过程，B₁（B₂，B₃）—C为回弹过程，C—D为湿化过程。

图 5 不同超固结度等向回弹湿化路径

Figure 5. Stress paths of isotropic unloading-wetting with different overconsolidation ratios

下载: 全尺寸图片幻灯片

3个土样湿化时的超固结程度不同，由本文所提模型预测体应变在湿化过程中的变化，如图 6所示。

图 6 等向回弹湿化不同超固结度下体应变

Figure 6. Variation of volumetric strain under stress path of isotropic unloading-wetting with different overconsolidation ratios

下载: 全尺寸图片幻灯片

可以看出，超固结程度越高，膨胀量越大，当超固结度过低时（例如前期固结压力500 kPa），甚至会发生土体整体湿陷的现象，即湿化至饱和后土体体积相比湿化前减小，体现超固结程度对膨胀性非饱和土膨胀量的重要影响。

2.2 回弹—等p剪切—湿化—加载

此路径中，吸力保持600 kPa不变，等向加载回弹后，进行等p剪切，剪切到一定程度时湿化，之后再剪切至破坏，分析剪切过程中体应变的变化。

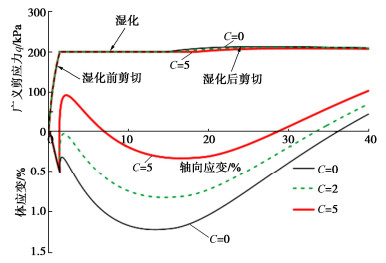
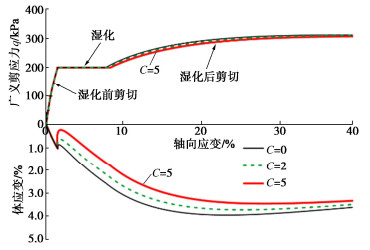
首先预测不同膨胀系数C在三轴排水剪切过程中的影响，初始围压p取200 kPa，膨胀系数C取0，2，5，等向压缩至p=1000 kPa，然后再回弹至200 kPa，之后进行等p剪切，剪切到广义剪应力q=200 kPa时进行湿化，湿化至饱和后再继续剪切，直到破坏，如图 7所示为剪切过程中体应变的变化。

图 7 等p剪切中湿化不同C值下体应变

Figure 7. Variation of volumetric strain under stress path of shearing- wetting-shearing with different values of C and constant mean effective stress

下载: 全尺寸图片幻灯片

可以看出膨胀系数C的取值不影响湿化前土体的应力应变关系，但在湿化过程中膨胀系数大的土体表现出更大的膨胀变形，甚至会使土样体积大于初始体积，这一变形导致湿化后剪切过程中土样剪缩量降低，但在不断剪切过程中，不同参数的土样体积应变趋于一致。同时通过分析湿化过程剪应力的变化，发现随着膨胀系数C值的增大，湿化后的剪切强度会降低。

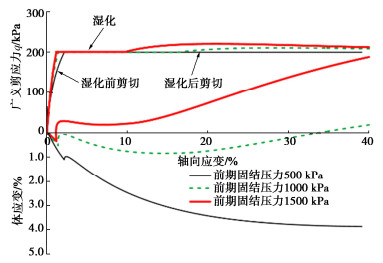
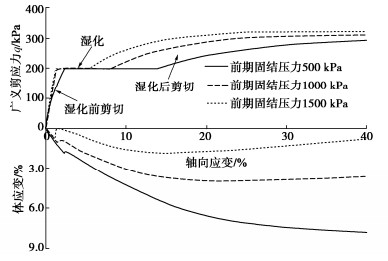
其次分析此路径下不同超固结度对膨胀特性的影响。设置初始围压为200 kPa，膨胀系数C取2，分别将土样等向压缩至500，1000，1500 kPa，然后等向回弹至200 kPa，之后等p剪切，当q=200 kPa时湿化至饱和，再剪切至破坏，分析此剪切过程中体应变与轴向应变的关系，如图 8所示。

图 8 等p剪切中湿化不同超固结度下体应变

Figure 8. Variation of volumetric strain under stress path of shearing- wetting-shearing with different overconsolidation ratios and constant mean effective stress

下载: 全尺寸图片幻灯片

可以看出不同超固结度下湿化时产生的体应变不同，当超固结度较大时，土体剪缩量会减小，使得土样提前进入剪胀阶段，同时增大剪切过程中产生的总膨胀量。

2.3 等体积湿化中的膨胀力

膨胀力是评价膨胀性非饱和土膨胀特性的基本参数，试验中可以通过三向胀缩仪测定^[27]。在土体各向同性条件下，模型中的膨胀力与 ${\text{d}}{\varepsilon _{\text{v}}} = 0$ 时的平均正应力相等。本节研究土体膨胀过程中膨胀力的变化特性。

首先预测不同膨胀系数下土体膨胀力变化，初始吸力600 kPa，初始围压200 kPa，膨胀系数C分别取0，2，5，将土样等向压缩至1000 kPa，后回弹至200 kPa，改变围压维持体积不变，将土样湿化至饱和，预测湿化过程中膨胀力与吸力的关系，如图 9。

图 9 等体积湿化不同C值膨胀力变化

Figure 9. Variation of swelling pressure during wetting under constant volume with different values of C

下载: 全尺寸图片幻灯片

可以看出随着膨胀系数的提高，土体最大膨胀力也相应提高，同时在湿化至低吸力阶段时，土体膨胀力会降低，反映此阶段土体整体表现出湿陷趋势，相应的，膨胀系数C越大，低吸力阶段土体膨胀力降低越多，体现土体膨胀系数的增大会加剧产生土体塑性湿陷体应变增量 ${\text{d}}\varepsilon _{{\text{vp}}}^{\text{p}}$ 的趋势，使得土体整体表现出的体缩趋势更大，在本模拟中由于限制了土体变形，体缩趋势表现为膨胀力的减小。

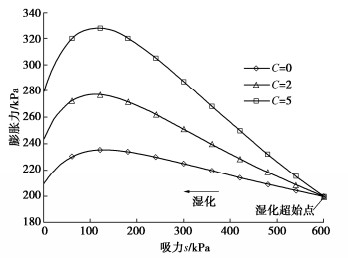
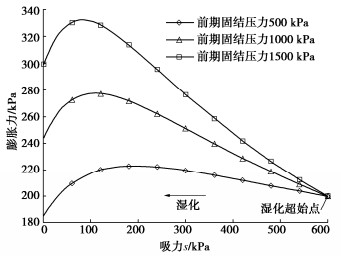
其次预测不同超固结程度下膨胀力的变化，初始吸力仍为600 kPa，膨胀系数C取2，初始围压为200 kPa，将土样分别等向压缩至500，1000，1500 kPa，然后回弹至200 kPa，保持体积不变湿化至饱和，其膨胀力与吸力的关系如图 10。

图 10 等体积湿化不同超固结度膨胀力变化

Figure 10. Variation of swelling pressure during wetting under constant volume with different overconsolidation ratios

下载: 全尺寸图片幻灯片

可见超固结度越高土体最大膨胀力越大，因土体在低吸力时有体缩趋势，当超固结度较低时，最终膨胀力甚至会低于初始围压，但相比膨胀系数C，超固结度的提高对低吸力阶段土体膨胀力降低的影响较小，不同超固结度下土体低吸力阶段膨胀力降低量相近。

2.4 回弹—三轴压缩—湿化—三轴压缩

此路径中先将土样等向压缩后回弹，之后进行三轴压缩，到达某一状态后湿化至饱和，之后再三轴压缩至破坏。首先预测不同膨胀系数对压缩过程的影响，取初始围压p=200 kPa，膨胀系数C分别取为0，2，5，初始吸力为600 kPa，先将土样等向压缩至1000 kPa，然后再回弹至200 kPa，之后进行三轴排水剪切，围压保持200 kPa，当q=200 kPa时，将土样湿化至饱和，再三轴压缩至破坏，分析此压缩过程中体应变与轴向应变的关系，如图 11。

图 11 三轴压缩中湿化不同C值下体应变

Figure 11. Variation of volumetric strain under stress path of triaxial compression-wetting-triaxial compression with different values of C

下载: 全尺寸图片幻灯片

可以看出膨胀系数并不影响湿化前过程，当土体湿化时会发生膨胀，C值越大膨胀量越大，但湿化至饱和后随着三轴压缩的不断进行，体应变会逐渐趋于一致。同时通过分析剪切过程中广义剪应力q的变化，发现随着C值的提高，湿化后土体峰值强度会降低。

其次预测分析不同超固结度的影响，初始吸力仍为600 kPa，膨胀系数C取2，初始围压为200 kPa，将土样分别等向压缩至500，1000，1500 kPa，然后再回弹至200 kPa，之后进行三轴压缩，当q=200 kPa时湿化至饱和，再三轴压缩至破坏，分析压缩过程中体应变与轴向应变之间的关系，如图 12。

图 12 三轴压缩中湿化不同超固结度体应变

Figure 12. Variation of volumetric strain under stress path of triaxial compression-wetting-triaxial compression with different overconsolidation ratios

下载: 全尺寸图片幻灯片

可以看出，超固结度越高，湿化过程中土体膨胀量越大，湿化至饱和后土体三轴剪切阶段体应变的变化趋势与一般非饱和土基本一致。

3. 模型的试验验证

为验证模型的合理性，分别对Zhan等^[28]和Alonso等^[29]的湿化膨胀试验数据进行预测。

3.1 模型的试验验证Ⅰ

Zhan等^[28]对中国湖北枣阳某边坡的膨胀黏土进行了室内试验，土体干密度为1.52~1.60 g/cm³，经测定，土样中砂砾含量3%、粉土颗粒含量58%，黏土颗粒含量39%，液限为50.5%，塑性指数为31，Zhan等^[28]利用非饱和土三轴试验仪对土样进行了多组试验研究，本节取其不同围压下的湿化路径作为验证试验数据。

本文建立的膨胀性非饱和模型需要10个参数，其中力学模型参数 $\lambda ，\kappa ，M，\nu ，N$ 与修正剑桥模型相同，参数 $\lambda ，\kappa ，N$ 可通过饱和土等向压缩回弹试验求得，参数 $M$ 可通过饱和土三轴压缩试验求得，参数 ${\lambda }_{s}，{\kappa }_{s}，{p}^{c}$ 与巴塞罗那模型相同，参数 ${\lambda }_{s}，{\kappa }_{s}$ 可由等围压的干化和湿化试验得到，参数 ${p^{\text{c}}}$ 可通过不同吸力下等向压缩回弹再湿化试验得到，参数 $a$ 可通过不同吸力下的三轴压缩试验得到，反映土体膨胀能力的参数J可根据土体不同围压下的湿化试验求得，根据文献[，]得到参数： $\lambda$ =0.1， $\kappa$ =0.01， ${\lambda _{\text{s}}}$ =0.1， $\nu$ =0.3，M=1.0，N=1.18， ${\kappa _{\text{s}}}$ =0.01， ${p^{\text{c}}}$ =125 kPa，a=150 kPa，J=1.55。大气压 ${p_{{\text{at}}}}$ 取为100 kPa。

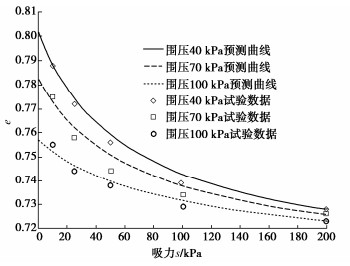
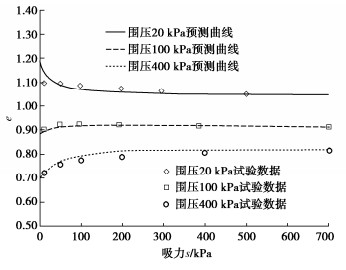
此试验取了3组土样，经过吸力平衡，控制土样吸力保持在200 kPa，然后维持吸力不变，分别在40, 70, 100 kPa围压下进行等向固结，在固结完成后，进行湿化试验。湿化过程中保持各自围压不变，吸力从200 kPa降至0 kPa，湿化前土体干密度取1.56 g/cm³，不同围压下湿化过程的试验结果与预测结果对比如图 13所示。

图 13 Zhan等^[28]试验预测对比

Figure 13. Comparison between predicted values and experimental results by Zhan et al. ^[28]

下载: 全尺寸图片幻灯片

可以看出3组土样在试验过程中都发生体积膨胀，但围压不同体积膨胀的幅度不同，围压较大的土样膨胀量较小，预测曲线与试验数据符合较好，可以反映出土体湿化过程中体积膨胀的过程，并体现不同围压下体积膨胀量的不同。

3.2 模型的试验验证Ⅱ

Alonso等^[29]利用Boom膨胀黏土进行了室内试验，其液限为55.9%，塑性指数为29.2，土体的高岭土、伊利石和蒙脱石的含量分别为20%，30%, 10%。试验土样初始干密度为1.40 g/cm³，Alonso等^[29]利用土样进行了不同等向围压下的干湿循环试验，本次验证选取其试验中第一次湿化的试验数据进行验证。

同上一节参数确定方法，本次试验根据文献[，]及参数拟合确定参数： $\lambda$ =0.15， $\kappa$ =0.014， ${\lambda _{\text{s}}}$ =0.1， $\nu$ =0.3，M=1.0，N=1.6， ${\kappa _{\text{s}}}$ =0.008， ${p^{\text{c}}}$ =45 kPa，a=120 kPa，J=1.65。

Chen^[30]将土样分为3组，控制吸力分别为500，500，700 kPa，保持吸力不变，分别在等向压力20，100，400 kPa下等向固结，固结完成后保持围压不变，进行湿化试验，将土样吸力从500 kPa或700 kPa降低到0 kPa，预测土样的体积变化，试验结果与预测结果如图 14。

图 14 Alonso等^[29]试验预测对比

Figure 14. Comparison between predicted values and experimental results by Alonso et al. ^[29]

下载: 全尺寸图片幻灯片

可以看出，由于围压不同，土体在湿化过程中体积变化也有区别，低围压下土体湿化会发生体积膨胀，但当围压增大到足够大时，土体在湿化过程中会发生体积收缩，且随着围压的进一步提高体积收缩也会加剧，这是因为随着围压的提高，土体超固结程度降低，湿化过程中更容易发生屈服，产生更大的湿陷塑性体应变 $\varepsilon _{{\text{vp}}}^{\text{p}}$ ，引发更大的湿陷变形，当围压足够大时这种湿陷变形会占主导地位，使得土体整体表现出体积的收缩，预测曲线可以反映出膨胀土的这一特性，且与试验结果符合较好。

4. 结论

本文提出了考虑膨胀土超固结度和初始干密度的膨胀式，将其融入非饱和土UH模型得到可以考虑理想膨胀性非饱和土的UH模型，该模型具有以下3个特点。

（1）通过引入与土体超固结度和初始干密度有直接关系的膨胀式，可以考虑不同的超固结度和初始干密度对膨胀土应力应变关系的影响，同时可以反映湿化过程中土体超固结度的变化。

（2）以UH模型为基础，并采用硬化参量H，可以体现膨胀土在超固结状态下不同于正常固结状态的应力软化特性和剪胀特性。

（3）本模型在一般非饱和土模型基础上引入的新参数较少，可以通过基础土力学试验获取，模型应用简便。经过模型特性分析与试验结果的验证可以显示出其预测膨胀土应力应变关系的合理性。

另一方面，本模型未考虑水量变化等水力作用对膨胀性非饱和土应力应变关系的影响，需在之后的研究中进一步完善。

图 1 折线型土体本构关系

Figure 1. Constitutive relation of broken-line soils

下载: 全尺寸图片幻灯片

图 2 滑坡地质力学模型

Figure 2. Geomechanical model for landslide

下载: 全尺寸图片幻灯片

图 3 首尾蠕滑阶段地质力学状态

Figure 3. Geomechanical states at front and rear creep stages

下载: 全尺寸图片幻灯片

图 4 首尾软化阶段应力状态

Figure 4. Stress states at front and rear softening stages

下载: 全尺寸图片幻灯片

图 5 自主助力阶段应力状态

Figure 5. Stress states at self-imposed load stage

下载: 全尺寸图片幻灯片

图 6 中部蠕滑阶段地质力学状态

Figure 6. Geomechanical states at middle part creep stage

下载: 全尺寸图片幻灯片

图 7 中部软化阶段应力状态

Figure 7. Stress states at middle part softening stage

下载: 全尺寸图片幻灯片

图 8 中部剪切阶段应力状态

Figure 8. Stress states at middle part shear stage

下载: 全尺寸图片幻灯片

图 9 相向剪切阶段应力状态

Figure 9. Stress states at shear advance stage

下载: 全尺寸图片幻灯片

图 10 整体贯通阶段应力状态

Figure 10. Stress states at integral penetration stage

下载: 全尺寸图片幻灯片

图 11 龙家台H1滑坡地质剖面

Figure 11. Geological profile of Longjiatai H1 landslide

下载: 全尺寸图片幻灯片

图 12 H1滑坡渐进破坏稳定性状态

Figure 12. Stability states of progressive failure of H1 landslide

下载: 全尺寸图片幻灯片

图 13 H1滑坡渐进演化力学过程

Figure 13. Mechanical process of progressive evolution of H1 landslide

下载: 全尺寸图片幻灯片

表 1 滑坡物理力学参数

Table 1 Physical and mechanical parameters of landslide

滑坡区段	l/m	l₄/m	l₅/m	h/m	a/(°)	r/(g·cm^-³)	E/MPa	t_s/kPa	t_p/kPa	t_r/kPa	δ_p/m	δ_o/m	δ_r/m
推移段	75	—	—	15.0	25	1.82	4.5	115.4	123.2	110.9	0.005	0.027	0.04
锁固段	140	80	60	20.0	10	1.91	4.0	66.3	86.4	75.1	0.006	—	0.04
牵引段	176	—	—	14.5	18	1.93	4.5	86.5	92.6	82.1	0.005	0.027	0.04

下载: 导出CSV

参考文献(18)

[1]	刘爱华, 王思敬. 平面坡体渐进破坏模型及其应用[J]. 工程地质学报, 1994, 2(1): 1-8. https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ401.000.htm LIU Aihua, WANG Sijing. Progressive failure model for slope with plane sliding sorface and its application[J]. Journal of Engineering Geology, 1994, 2(1): 1-8. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-GCDZ401.000.htm
[2]	刘虎虎, 缪海波, 陈志伟, 等. 三峡库区侏罗系顺层滑坡滑带土的剪切蠕变特性[J]. 岩土工程学报, 2019, 41(8): 1573-1580. doi: 10.11779/CJGE201908024 LIU Huhu, MIAO Haibo, CHEN Zhiwei, et al. Shear creep behaviors of sliding-zone soil of bedding landslide in Jurassic stratum in Three Gorges Reservoir area[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(8): 1573-1580. (in Chinese) doi: 10.11779/CJGE201908024
[3]	SKEMPTON A W. Long-term stability of clay slopes[J]. Géotechnique, 1964, 14(2): 77-102. doi: 10.1680/geot.1964.14.2.77
[4]	黄晓虎, 易武, 龚超, 等. 开挖致使古滑坡复活变形机理研究[J]. 岩土工程学报, 2020, 42(7): 1276-1285. doi: 10.11779/CJGE202007011 HUANG Xiaohu, YI Wu, GONG Chao, et al. Reactivation and deformation mechanism of ancient landslides by excavation[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(7): 1276-1285. (in Chinese) doi: 10.11779/CJGE202007011
[5]	吴益平, 卢里尔, 薛阳. 基于临界状态的边坡渐进破坏力学模型分析及应用[J]. 地质科技通报, 2020, 39(5): 1-7. https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202005001.htm WU Yiping, LU Lier, XUE Yang. Application of landslide progressive failure mechanical model based on the critical stress state[J]. Bulletin of Geological Science and Technology, 2020, 39(5): 1-7. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZKQ202005001.htm
[6]	卢应发, 黄学斌, 刘德富. 边坡力的分布特征和稳定性分析[J]. 岩土工程学报, 2017, 39(7): 1321-1329. doi: 10.11779/CJGE201707019 LU Yingfa, HUANG Xuebin, LIU Defu. Distribution characteristics of force and stability analysis of slope[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(7): 1321-1329. (in Chinese) doi: 10.11779/CJGE201707019
[7]	TANG H, ZOU Z, XIONG C, et al. An evolution model of large consequent bedding rockslides, with particular reference to the Jiweishan rockslide in Southwest China[J]. Engineering Geology, 2015, 186: 17-27. http://www.researchgate.net/profile/Huiming_Tang2/publication/265910074_An_evolution_model_of_large_consequent_bedding_rockslides_with_particular_reference_to_the_Jiweishan_rockslide_in_Southwest_China/links/54fdaceb0cf20700c5ec0a7e.pdf
[8]	张龙飞, 吴益平, 苗发盛, 等. 推移式缓倾浅层滑坡渐进破坏力学模型与稳定性分析[J]. 岩土力学, 2019, 40(12): 4767-4776. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912025.htm ZHANG Longfei, WU Yiping, MIAO Fasheng, et al. Mechanical model and stability analysis of progressive failure for thrust-type gently inclined shallow landslide[J]. Rock and Soil Mechanics, 2019, 40(12): 4767-4776. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201912025.htm
[9]	孙立娟, 崔凯, 王溢轩. 库水复活型滑坡牵引滑动机理模型试验研究[J]. 哈尔滨工业大学学报, 2021, 53(11): 162-170. https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX202111020.htm SUN Lijuan, CUI Kai, WANG Yixuan. Model test study on retrogressive and sliding mechanism of reservoir-reactivated landslide[J]. Journal of Harbin Institute of Technology, 2021, 53(11): 162-170. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-HEBX202111020.htm
[10]	谭福林. 基于不同演化模式的滑坡—抗滑桩体系动态稳定性评价方法研究[D]. 武汉: 中国地质大学, 2018. TAN Fulin. Evaluation Method for Dynamic Stability of Landslide Stabilizing Pile System with Different Evolution Modes[D]. Wuhan: China University of Geosciences, 2018. (in Chinese)
[11]	WANG J J, XIAO L L, ZHANG J, et al. Deformation characteristics and failure mechanisms of a rainfall-induced complex landslide in Wanzhou County, Three Gorges Reservoir, China[J]. Landslides, 2020, 17(2): 419-431. doi: 10.1007/s10346-019-01317-1
[12]	杜毅, 晏鄂川, 蔡静森, 等. 直线型复合式滑坡渐进破坏力学模型及稳定性研究[J]. 岩石力学与工程学报, 2021, 40(3): 490-502. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202103004.htm DU Yi, YAN Echuan, CAI Jingsen, et al. A mechanical model of progressive failure of linear complex landslides[J]. Chinese Journal of Rock Mechanics and Engineering, 2021, 40(3): 490-502. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX202103004.htm
[13]	LOCAT A, JOSTAD H P, LEROUEIL S. Numerical modeling of progressive failure and its implications for spreads in sensitive clays[J]. Canadian Geotechnical Journal, 2013, 50(9): 961-978. http://d.wanfangdata.com.cn/periodical/033614bbc0bb0ee70d2ffbdb5cae0127
[14]	范志强, 唐辉明, 谭钦文, 等. 滑带土环剪试验及其对水库滑坡临滑强度的启示[J]. 岩土工程学报, 2019, 41(9): 1698-1706. doi: 10.11779/CJGE201909014 FAN Zhiqiang, TANG Huiming, TAN Qinwen, et al. Ring shear tests on slip soils and their enlightenment to critical strength of reservoir landslides[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1698-1706. (in Chinese) doi: 10.11779/CJGE201909014
[15]	陈达. 刘涧滑坡变形破坏机理及运动过程研究[D]. 西安: 西安科技大学, 2018. CHEN Da. Study on Deformation and Failure Mechanism and Motion Process of Liujian Landslide[D]. Xi'an: Xi'an University of Science and Technology, 2018. (in Chinese)
[16]	GILBERT R B, LONG J H, MOSES B E. Analytical model of progressive slope failure in waste containment systems[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1996, 20(1): 35-56. doi: 10.1002/(SICI)1096-9853(199601)20%3A1<35%3A%3AAID-NAG806>3.0.CO%3B2-B
[17]	QIN S Q, JIAO J J, WANG S J, et al. A nonlinear catastrophe model of instability of planar-slip slope and chaotic dynamical mechanisms of its evolutionary process[J]. International Journal of Solids and Structures, 2001, 38(44/45): 8093–8109. http://hydro.geo.ua.edu/jiao/research/FullPaper/Qin3.pdf
[18]	TERZAGHI K. Stability of slopes of natural clay[J]. Proceedings of the 1st International Conference of Soil Mechanics and Foundations, 1936: 161-165. http://www.researchgate.net/publication/285438622_Stability_of_slopes_of_natural_clay

施引文献(3)

期刊类型引用(2)

1.	王涛，凡红，王康任，周国庆，王亮亮. 高温冻土双屈服面统一本构模型及其验证. 岩土工程学报. 2025(01): 135-143 . 本站查看
2.	柳伟，徐长节，杜昊东，朱怀龙，王长虹. 基于修正统一硬化模型的超固结非饱和红黏土边坡稳定分析. 岩土力学. 2024(04): 1233-1241 . 百度学术