0.   引言

聚苯乙烯（EPS）颗粒轻质混合土（以下简称EPS轻质土）是一种轻质土工合成材料，由原料土、EPS颗粒、胶结材料和水按一定比例混合而成，具有高强质比、绿色环保、施工方便等优点。将EPS轻质土与纤维结合提高土体韧性^[1]、减轻膨胀土病害^[2]则进一步拓展其应用范围。

早期对EPS轻质土力学特性的研究多采用一维压缩、三轴剪切等方法。近年来针对EPS轻质土的蠕变特性^[3-4]、循环加载响应^[5-8]和侧向土压力系数^[9]等问题也有一定程度研究。基于已有试验结果，侯天顺等^[10]采用Ducan-Chang双曲线模型与Prevost软化模型拟合了EPS轻质土的三轴剪切结果；肖杨等^[11]基于椭圆-抛物双屈服面发展了EPS轻质土的本构模型。

EPS轻质土宏观力学特性取决于其独特的微细观结构。朱伟等^[12]、姬凤玲等^[13]将疏浚淤泥EPS轻质土的宏观力学响应与微观结构观察相关联，定性分析了试样的渐进性3阶段特征，即线弹性变形阶段（细观裂纹产生）、弹塑性阶段（细观裂纹稳定扩展）、软化阶段（细观裂纹整体贯通）。王庶懋等^[14]采用CT扫描结果探讨了砂土、EPS颗粒、水泥混合轻质土在不同水泥含量下的微观结构，强调了该轻质土局部孔隙比分布差异较大的细观结构特征。EPS轻质土的微细观结构对其力学特性的影响非常显著，主要有3方面的试验证据：①原料土为砂土^{[7, 14-16]}或细粒土^{[10, 12, 17-18]}时EPS轻质土的力学特性有明显差异，EPS颗粒与砂砾石颗粒之间的相对大小关系对侧向土压力系数及内部荷载传递机理有明显影响^[9]；②马时冬^[19]试验发现，EPS颗粒形态对EPS轻质土的力学影响一般规律为球状优于碎粒状、优于片状；③对基于等体积比^[15]或等质量比^[20-21]掺入不同尺寸（范围）EPS颗粒的轻质土的剪切试验表明，EPS颗粒粒径越小，EPS轻质土的抗剪强度和初始切线（或割线）模量越大。

因此，从EPS轻质土本身的特有的微细观结构特征出发研究其力学特性具有重要理论意义。兰鑫等^[22]尝试采用离散元法模拟EPS轻质土的力学特性。OMINE等^[23]、顾欢达等^[16]基于EPS颗粒和胶结土各自的本构模型，采用体积加权方法推导了EPS轻质土的本构模型，但其中关于EPS颗粒和胶结土应变能增量一致、EPS颗粒和胶结土各应力分量同比例分担等关键假设均需进一步论证。EPS轻质土的固相是由较刚较强的水泥土和较软较弱的EPS颗粒复合而成，有其独特的微细观结构，且这种结构对其宏观力学特性的影响已广泛为试验结果证实，但对这种影响的机理认识还不充分。故而有必要从微细观角度研究EPS轻质土宏观力学特性的微细观机制。为此，本研究基于EPS轻质土三轴剪切试验结果，借助精细化数值模拟手段，研究剪切变形过程中试样的宏细观变形机理。首先介绍水泥土、EPS材料以及两者界面的本构模型与参数，随后介绍EPS轻质土的精细化数值模型构建，最后分析讨论EPS轻质土内部应力、应变的非均匀分布特征，揭示宏观变形模式的细观机理。

1.   水泥土的本构模型与参数

1.1   水泥土的典型力学特性

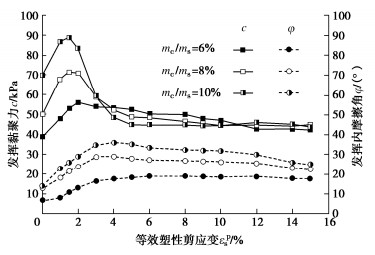
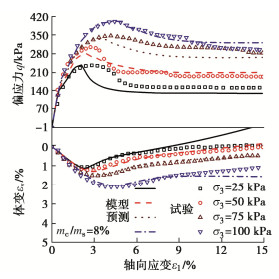
本研究中EPS轻质土的原料土为南京地区淤泥质粉质黏土，其含水率为48.1%，饱和密度为1.68 g/cm³，土粒相对质量密度为2.74，液限为39.2%，塑限为22.6%。胶结材料为P•C32.5R复合硅酸盐水泥，拌合采用纯净水。水泥土试样为实心圆柱样，直径为39.1 mm，高为80 mm，水泥掺入比m_c/m_s（水泥掺入质量m_c与原料干土质量m_s之比）取6%，8%，10%。以8%水泥掺入比为例，不同围压σ₃（取25，50，75，100 kPa）下的水泥土三轴剪切力学特性如图 1所示。其力学特性有以下规律：①应力-应变曲线形态为软化型、体变为剪胀型，围压增大减缓剪胀和软化特性；②水泥掺入增加提高试样强度，软化与剪胀愈加明显。本研究采用适合岩土材料的Mohr-Coulomb模型描述水泥土的力学特性，以下从弹性模型、屈服函数与应变硬化/软化规律和塑性流动准则3方面介绍该模型。

图  1  水泥土的三轴剪切力学特性（m_c/m_s = 8%）

Figure  1.  Mechanical behaviors of cemented soils under triaxial loading (m_c/m_s = 8%)

下载: 全尺寸图片 幻灯片

1.2   弹性模型

采用各向同性弹性模型描述水泥土的弹性变形特性。由图 1可知，围压对水泥土的初始弹性参数影响较小；为简化模型，不考虑围压对弹性参数的影响。通过三轴剪切试验曲线初始段可推得水泥土弹性参数: 水泥掺入比6%，8%，10%对应的弹性模量分别为15，30，39 MPa，泊松比均取0.25。

1.3   屈服函数与应变硬化/软化规律

采用Mohr-Coulomb屈服函数描述水泥土的剪切屈服特性，屈服函数为

式中：${\sigma _1}$，${\sigma _3}$分别为大、小主应力（应力、应变均以压为正，下同）；${N_\varphi } = (1{{\text{ + }}}\sin \varphi )/(1 - \sin \varphi )$，φ为发挥内摩擦角；c为发挥黏聚力。φ，c的变化规律即为应变硬化/软化规律，一般表达为等效塑性剪应变的函数以反映屈服面随塑性变形的扩大或缩小。本研究中等效塑性剪应变定义为

式中：$\delta e_{ij}^p$为塑性应变偏张量增量。

在特定等效塑性剪应变$\varepsilon _{{\text{s}}}^{{\text{p}}}$下，不同围压的各水泥土试样在p-q空间中的应力状态点可拟合为一条直线，其截距和斜率分别用μ，M表示，其中球应力p = σ_ii/3，偏应力$q = \sqrt {3{J_2}}$，J₂为应力偏张量第二不变量。某等效塑性剪应变下的φ，c分别由换算得：

发挥强度指标随等效塑性剪应变$\varepsilon _{{\text{s}}}^{{\text{p}}}$的变化规律如图 2所示。可以看到，随$\varepsilon _{{\text{s}}}^{{\text{p}}}$增加，发挥内摩擦角从约10°的初始值开始逐渐增长，在$\varepsilon _{{\text{s}}}^{{\text{p}}}$超过4%后略有降低并趋近于某一稳定值；发挥黏聚力初期随$\varepsilon _{{\text{s}}}^{{\text{p}}}$增加而增大，在$\varepsilon _{{\text{s}}}^{{\text{p}}}$约2%时达到峰值，随后快速衰减并在$\varepsilon _{{\text{s}}}^{{\text{p}}}$超过4%后转为缓慢衰减，逐渐趋近于某一稳定值。在$\varepsilon _{{\text{s}}}^{{\text{p}}}$趋近零时，水泥土的发挥强度不为零，对应初始屈服状态。

图  2  水泥土发挥强度指标随等效塑性剪应变的变化

Figure  2.  Variation of mobilized strength indices with equivalent plastic shear strain for cemented soils

下载: 全尺寸图片 幻灯片

为使水泥土不至产生不合理的拉应力，增加拉伸屈服面：

式中：$\sigma _{{{\text{C - soil}}}}^{{\text{t}}}$为水泥土抗拉强度。

直接测定$\sigma _{{{\text{C - soil}}}}^{{\text{t}}}$较为困难，一般可取$\sigma _{{{\text{C - soil}}}}^{{\text{t}}} =$ ${{\alpha c} \mathord{\left/ {\vphantom {{\alpha c} {\tan \varphi }}} \right. } {\tan \varphi }}$，$\alpha$为小于1的常数。考虑到水泥土拉伸的弹脆性响应特点，在拉伸方向不考虑硬化/软化过程，一旦应力状态达到拉伸屈服，材料将永久失去抗拉能力（即令$\sigma _{{{\text{C - soil}}}}^{{\text{t}}} = 0$）。

1.4   塑性流动准则

在拉伸方向简单采用关联流动法则。在剪切方向，采用非关联流动准则描述水泥土的剪切塑性流动规律。剪切塑性势面为

式中：${N_\psi } = (1{{\text{ + }}}\sin \psi )/(1 - \sin \psi )$，ψ为发挥剪胀角。

根据水泥土三轴剪切体变曲线整理得到剪胀角ψ随等效塑性剪应变$\varepsilon _{{\text{s}}}^{{\text{p}}}$、应力比$\eta$和平均应力p的变化关系可拟合为

式中：a₁，a₂，a₃，a₄，a₅均为拟合参数，如表 1所示。

表  1  不同水泥掺入比下水泥土发挥剪胀角公式的拟合参数

Table  1.  Fitting parameters for mobilized dilation angle of cemented soils under different cement contents

水泥掺入 比/%	a1	a2	a3	a4	a5
6	398	7.0	0.40	-0.020	-56
8	177	3.2	0.72	-0.030	-53
10	70.0	1.3	0.75	-0.008	-57

下载: 导出CSV 

| 显示表格

1.5   模型能力检验

利用FLAC3D软件提供的应变软化型Mohr- Coulomb模型框架，自编FISH函数植入上述总结的规律，采用一个立方体单元模拟的三轴剪切加载结果与试验对比如图 1所示，可见上述模型能很好反映水泥土的典型力学特性。当剪胀角 < -10°（此时等效塑性剪应变小于2%，$\eta {{\text{/}}}{\eta _{{{\text{cr}}}}} \leqslant 0.8$），剪胀角拟合误差较大；相应在图 1中剪切初期，由于试样体积应变中弹性分量占比较大，塑性部分占比较小，剪胀角拟合误差导致的塑性体变误差表现不明显。可以认为剪胀角 > -10°是拟合的剪胀方程适用的范围。

2.   EPS材料的本构模型与参数

2.1   EPS材料的典型力学特性

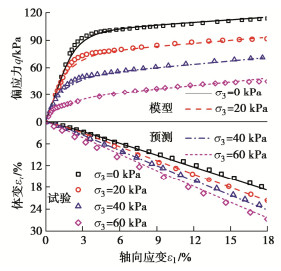
总结文献试验资料^[24-30]，EPS材料在三轴剪切下的典型力学特性如图 3所示，表现出以下特点：①初始弹性段斜率受围压影响很小，初始屈服点（线性段终点）受围压影响，围压越大初始屈服应力越低；②剪切屈服后，剪应力随轴向应变增大而继续增长，增长斜率逐渐降低并最终稳定在某一定值，该稳定斜率受围压影响较小；③在常见试验围压范围内（100 kPa以内），抗剪强度随围压增大而减小（与土体等摩擦性材料显著不同），内摩擦角为负；④围压越大，塑性体变越大，塑性体变与轴向应变的比值在加载过程中基本不变；⑤真三轴加载获得的π平面上屈服面为圆形^[29]；⑥力学特性明显受EPS材料密度影响。值得注意的是，上述试验现象是基于EPS颗粒黏聚形成的EPS块体试验得到的。当前尚无文献报道EPS材料本身的力学特性（因其以颗粒形态存在，难以进行力学试验）。故本研究采用EPS块体力学特性近似反映EPS材料的力学特性。

图  3  EPS材料的典型三轴剪切力学响应（ρ=20 kg/m³）^[30]

Figure  3.  Typical mechanical behaviors of EPS materials under triaxial shear loading

下载: 全尺寸图片 幻灯片

由于EPS材料在π平面上屈服面为圆形，适合选用Drucker-Prager模型描述其塑性力学特性，并有必要引入应变硬化规律。以下从弹性模型、屈服函数与应变硬化规律和塑性流动准则3方面介绍该模型。

2.2   弹性模型

采用各向同性弹性模型描述EPS材料的弹性变形特性。EDO^[31]给出的EPS材料泊松比$\nu$与密度的经验关系为

式中：$\rho$为密度，单位取kg/m³。

HORVATH^[32]总结的EPS材料弹性模量与密度的经验关系为

式中：E为弹性模量，单位取MPa；$\rho$为密度，单位取kg/m³。

2.3   屈服函数与应变硬化规律

采用Drucker-Prager屈服函数描述EPS材料的剪切屈服特性，屈服函数为

式中：${q_\varphi }$，${k_\varphi }$为与发挥强度参数φ，c有关变量。

为规避内摩擦角为负导致的数值计算问题，此处令内摩擦角φ为0，并根据球应力p调整等效黏聚力$\bar c$来反映“围压增大剪切强度减小”的特性，此时有${q_\varphi }$=0、${k_\varphi }{{\text{ = }}}{{2\bar c} \mathord{\left/ {\vphantom {{2\bar c} {\sqrt 3 }}} \right. } {\sqrt 3 }}$。对常规三轴剪切路径，等效发挥黏聚力$\bar c = ({\sigma _1} - {\sigma _3})/2$，初始屈服时的等效黏聚力${\bar c_{{\text{0}}}}$取为应力-应变曲线上开始偏离初始直线段的点，${\bar c_{{\text{0}}}}$与初始屈服时的球应力p近似成线性关系，当密度为30 kg/m³时有${\bar c_{{\text{0}}}}(p) = {{\text{71}}}{{\text{.4}}} - {{\text{0}}}{{\text{.266}}}p$（p的单位为kPa）。

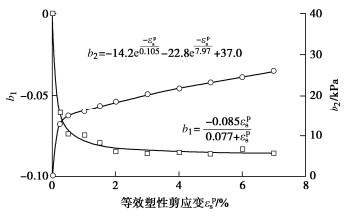
剪切应变硬化过程可表示为$\bar c - {\bar c_0}(p)$随等效塑性剪应变$\varepsilon _{{\text{s}}}^{{\text{p}}}$的变化过程。不同等效塑性剪应变水平下$\bar c - {\bar c_0}(p)$随球应力p近似线性变化，其线性拟合的斜率b₁和截距b₂都随等效塑性剪应变而变化，如图 4所示。则EPS块体的应变硬化规律可表达为

图  4  EPS材料的剪切硬化拟合参数b₁，b₂的变化（ρ=30 kg/m³，数据源自文献[27]）

Figure  4.  Variation of b₁ and b₂ in shear hardening law of EPS materials (ρ=30kg/m³, data adapted from Reference [27])

下载: 全尺寸图片 幻灯片

图 4以密度30 kg/m³的EPS材料为例（其他密度EPS材料也服从相同规律，此处不再赘述），基于试验数据拟合得${b_1}(\varepsilon _{{\text{s}}}^{{\text{p}}})$，${b_2}(\varepsilon _{{\text{s}}}^{{\text{p}}})$，${\bar c_0}(p)$的具体表达式，EPS材料的压剪应变硬化规律表达为等效发挥黏聚力的变化规律：

EPS材料抗拉强度远大于其抗压屈服强度，为描述其受拉变形特性，考虑拉伸屈服面：

式中：$\sigma _{{{\text{EPS}}}}^{{\text{t}}}$为EPS材料单向拉伸强度。

根据KANG等^[33]、HORVATH^[34]的研究，EPS块体抗拉强度与密度近似成线性关系：

式中：$\sigma _{{{\text{EPS}}}}^{{\text{t}}}$单位取kPa，$\rho$单位取kg/m³。

KANG等^[33]的试验结果表明，EPS材料拉伸破坏表现出弹脆性特点，故在拉伸方向不考虑硬化/软化过程，一旦应力状态达到拉伸屈服，材料将永久失去抗拉能力（即令$\sigma _{{{\text{EPS}}}}^{{\text{t}}} = 0$）。

2.4   塑性流动准则

在拉伸方向简单采用关联流动法则。在剪切方向，采用非关联流动准则描述EPS材料的剪切塑性流动规律。剪切塑性势面为

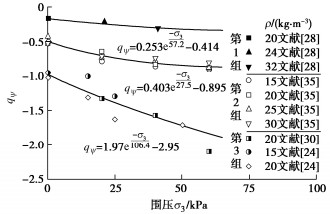
式中：${q_\psi }$为塑性体变参数，在三轴剪切中${q_\psi } = - {\varepsilon _{{\text{v}}}}/$ $({\varepsilon _{{\text{1}}}} - {\varepsilon _{{\text{3}}}})$。根据CHUN等^[35]和ATMATZIDIS等^[24]的试验数据，${q_\psi }$在塑性变形阶段几乎保持定值；EPS材料的密度对${q_\psi }$影响较小，而围压对${q_\psi }$影响较大。在图 5中，忽略EPS材料密度对${q_\psi }$的影响，拟合得${q_\psi }$随小主应力（围压）的变化关系为

图  5  剪切塑性势参数${q_\psi }$随围压的变化

Figure  5.  Variation of parameter ${q_\psi }$ in shear plastic potential function with confining pressure

下载: 全尺寸图片 幻灯片

式中：c₁，c₂，c₃为拟合参数，${\sigma _3}$单位取kPa。因所用EPS块体来源不同，图 5中各组数据可按照式（15）拟合出三组参数。模拟表明，图 5中3组拟合公式对EPS轻质土的体变影响很小（由于轻质土的体变主要受水泥土控制）。本文后续模拟采用基于ATMATZIDIS等^[24]、WONG等^[30]两个团队的试验数据拟合的参数c₁ = 1.97，c₂= -106.4，c₃ = -2.95。

2.5   模型能力检验

利用FLAC3D软件提供的Drucker-Prager模型框架，自编FISH函数植入上述总结的规律，采用一个立方体单元模拟的三轴剪切加载结果与试验对比如图 3（a）所示，可见上述模型能很好反映EPS材料的典型力学特性。

3.   EPS-水泥土界面的本构模型与参数

采用Mohr-Coulomb模型描述界面的抗剪强度：

式中：${\tau _{{\text{f}}}}$为发挥抗剪强度，${\sigma _{{\text{n}}}}$为法向应力，c，φ分别为界面的发挥摩擦角和发挥黏聚力。

为探究c，φ的变化规律，开展了EPS块体-水泥土界面直剪试验。试验中，水泥土与EPS块体均为为圆饼形，直径61.8 mm，EPS密度为30 kg/m³，水泥土配比同1.1节。当剪切位移小于0.8 mm时，剪应力与剪切位移呈线性关系，界面处于弹性状态；当剪切位移超过0.8 mm后，剪应力-剪切位移曲线呈现非线性特征。简化起见，超过0.8 mm的剪切位移都认为是塑性剪切位移。基于不同法向应力下的界面剪切试验，界面硬化/软化规律可拟合为

式中：S^p为塑性剪切位移（mm）。发挥黏聚力用与水泥掺入比有关的参数c^*归一化，水泥掺量分别为6%，8%，10%时c^*为18.38，25.52，27.52 kPa。

EPS材料与水泥土界面有一定抗拉强度，但难以直接测量，一般可取界面抗拉强度为$\beta c/\tan \varphi$，β为小于1的常数。由于EPS材料较软，剪切过程中法向位移不明显，故不考虑界面剪胀或剪缩，即取剪胀角为0。接触面的法向刚度k_n和剪切刚度k_s按照数值模拟经验，一般取接触面周围“最硬”单元等效刚度的10倍。

4.   EPS轻质土的精细化数值模拟

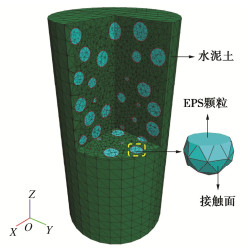
EPS轻质土的数值模型由EPS颗粒、水泥土及二者接触界面3部分构成。数值模型几何尺寸为室内三轴试验试样尺寸一半（试算表明取一半尺寸不影响整体力学特性和宏细观变形特征，且节省大量计算时间），EPS颗粒材料密度30 kg/m³、堆积密度15.9 kg/m³、颗粒直径3.2 mm（与试验相同）。首先根据EPS含量计算颗粒数量，在圆柱形试样空间中随机生成球体代表EPS颗粒，各球体不重叠且尽可能分散。试样空间中排除EPS后的部分代表水泥土。采用FLAC3D软件模拟，以EPS颗粒含量为25%（EPS颗粒掺入体积V_E与原料干土体积V_S之比）的轻质土为例，网格剖分如图 6所示。实体采用四面体剖分，界面采用三角面片划分。

图  6  EPS轻质土的三轴剪切数值模型

Figure  6.  Numerical model for EPS-mixed soils under triaxial shear loading

下载: 全尺寸图片 幻灯片

轻质土中的水泥掺入比、EPS材料密度、接触面力学特性对轻质土力学特性的影响均通过前述本构模型参数反映，水泥土、接触面抗拉强度参数α =β = 0.3，EPS颗粒含量通过几何模型反映。为模拟三轴剪切，在圆柱形试样的侧面施加恒定面力（围压），对上下端面施加恒定速度模拟加载，端部仅约束中心点的水平向位移，相当于端部无侧向约束的理想情形。

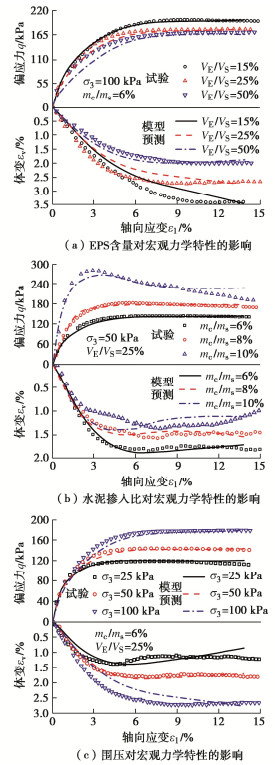
图 7为不同工况下，EPS轻质土的数值模拟与室内试验的应力-应变和体变曲线对比。如图 7（a）所示，在相同的水泥含量及围压条件下，数值模拟与室内试验得到的EPS含量对试样力学特性的影响规律相同：随EPS含量提高，试样的偏应力水平降低，减缩体变减小。如图 7（b），7（c）所示，数值模拟能很好反映水泥含量、围压对EPS轻质土三轴剪切力学响应的影响规律。

图  7  各因素对EPS轻质土力学特性的影响

Figure  7.  Effects of various factors on mechanical behavior of EPS-mixed soils

下载: 全尺寸图片 幻灯片

图 8对比了EPS轻质土试样的典型变形与破坏模式，数值模拟基本能再现试验观察到的整体剪切带、局部鼓胀和整体均匀3种变形模式。整体而言，数值模拟得到的偏应力较为准确，体变误差稍大但在可接受范围，能再现EPS轻质土试样变形模式。

图  8  EPS轻质土模拟与试验剪切变形

Figure  8.  Simulated and tested deformations of EPS-mixed soils

下载: 全尺寸图片 幻灯片

5.   EPS轻质土的宏细观变形机理

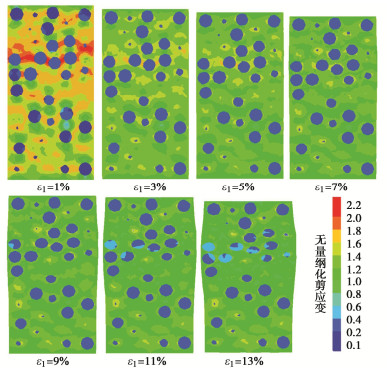
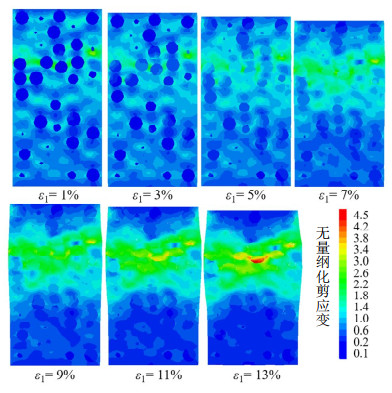
利用图 9，10所示试样内部的剪应力、剪应变分布揭示EPS轻质土宏细观变形特征与机理，图中剪应力、剪应变分别用各轴向应变下试样整体的剪应力、剪应变无量纲化。

图  9  EPS轻质土内部的剪应力分布(m_c/m_s=6%, V_E/V_S=25%, σ₃=50 kPa)

Figure  9.  Distribution of deviator stress in EPS-mixed soils (m_c/m_s= 6%, V_E/V_S=25%, σ₃=50 kPa)

下载: 全尺寸图片 幻灯片

图  10  EPS轻质土内部的剪应变分布(m_c/m_s=6%, V_E/V_S=25%, σ₃=50 kPa)

Figure  10.  Distribution of deviator strain in EPS-mixed soils (m_c/m_s= 6%, V_E/V_S=25%, σ₃=50 kPa)

下载: 全尺寸图片 幻灯片

对图 9所示的剪应力分布，在加载初期（ε₁ < 1%），试样内剪应力分布极不均匀，这是由于EPS颗粒较“软”导致其应力分担比例小，在EPS颗粒周围形成空间拱形传力路径，EPS颗粒之间的水泥土区域为拱脚位置，剪应力相对集中；拱脚重叠区域整体呈水平带状分布；试样上部因EPS颗粒在局部间距较小，“拱脚”应力集中更为明显，因而试样上部剪应力明显高于中下部。随着加载进行（ε₁为3%~7%），水泥土发生应变软化使得其剪应力有所降低，而EPS颗粒发生应变硬化使得其剪应力有所提高，二者共同作用降低了试样内应力分布不均匀程度。当轴向应变超过7%后，试样上部由于应力集中程度高导致应变局部化发生，该区域剪应变较其他区域发展更充分，水泥土应变软化和EPS颗粒应变硬化导致应力不均匀程度有所降低；而其他区域因无剪应变的进一步发展而仍保持较高的应力不均匀性；上部区域的应力集中使得试样整体发生局部（上部）鼓胀变形。

相对应地，对图 10所示的剪应变分布，在加载初期（ε₁ < 1%）剪应变也表现出明显的不均匀分布特征，EPS颗粒与周围水泥土之间有明显的变形不协调性，试样上部EPS颗粒间距较小处的水泥土剪应变比其他位置更大。随着加载进行，水泥土胶结作用尚失（软化），软化区开始贯通，逐渐形成薄弱区，EPS颗粒与水泥土之间的应变不协调程度有所减缓，但试样整体的剪应变集中于上部的应变局部化区域。

6.   结论

（1）分别在Mohr-Coulomb模型和Drucker-Prager模型框架下，基于水泥土和EPS材料力学特性试验结果，总结了两种材料的本构模型方程与经验公式；基于水泥土和EPS材料界面剪切试验，提炼了界面剪切硬化/软化本构模型。

（2）对EPS轻质土单元试验进行了精细化数值建模，很好预测了EPS轻质土宏观力学特性，再现了EPS含量、水泥土掺入比和围压对宏观力学的影响规律和整体剪切、局部鼓胀、整体均匀3种变形模式。

（3）EPS轻质土的宏观变形模式由EPS颗粒与水泥土两种材料的力学特性差异和EPS颗粒非均匀排列共同决定，材料力学特性差异引起应力、应变分布的非均匀性，EPS颗粒排列非均匀性将强化应力、应变非均匀程度，进而引起试样宏观变形的非均匀性。