Disaster analysis and countermeasures of large accumulation in reservoir areas
-
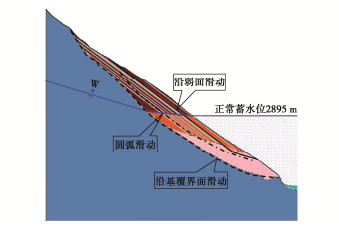
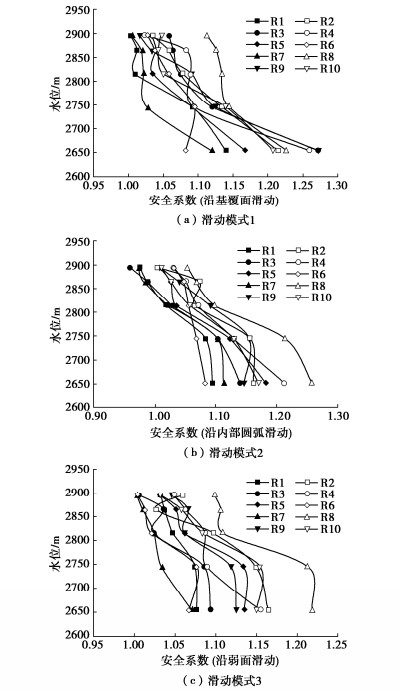
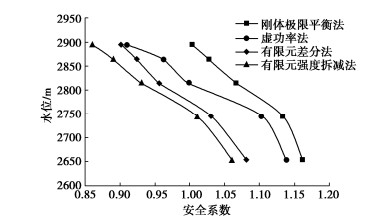
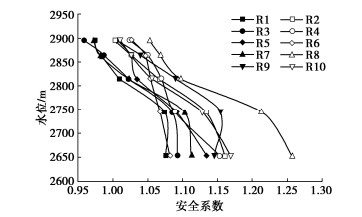
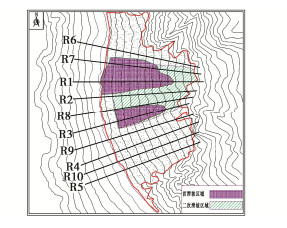
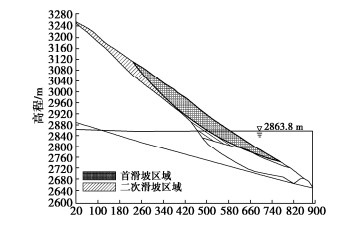
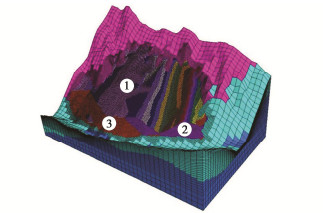
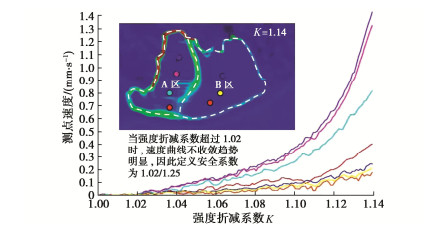
摘要: RM水电站RS堆积体方量高达4700万m3，其规模巨大，距坝址较近，在水库蓄水过程中，受水动力作用影响，边坡的物理力学参数指标降低，有可能发生失稳破坏进而危害工程安全。分别采用刚体极限平衡法、虚功率法、有限差分法、有限元强度折减法以及三维数值模拟针对RS堆积体稳定性及灾变过程进行分析，结果表明，在天然状态下，边坡基本处于稳定状态，随着蓄水过程水位抬高，边稳失稳的可能性很大。边坡稳定状态由稳定—变形—局部失稳—较大规模失稳—大规模失稳，逐渐演变为灾变过程。模拟揭示堆积体在失稳条件下的涌浪产生过程及传播规律，对其进行风险分析。研究堆积体的治理原则和治理措施，提出预防为主的治理措施，研究成果可为类似工程问题提供有意义的参考。Abstract: The volume of RS accumulation of RM hydropower station is as large as 47 million m3, which is huge and close to the dam site. In the process of reservoir impoundment, the physical and mechanical parameters of the slope are reduced due to the hydrodynamic effect, which may cause instability and damage to the safety of the project. In this study, the rigid body limit equilibrium method, virtual power method, finite difference method, finite element strength reduction method and three-dimensional numerical simulation are used to analyze the stability and catastrophe process of RS accumulation body. The results show that the slope is basically stable in the natural state, and the possibility of edge stability and instability is great with the rise of water level in the process of water storage. The state of slope stability changes from the process of stability- deformation→local instability large→scale instability→largest→scale instability to the catastrophic process. The simulation reveals the generating process and propagation law of surge under instability, and its risk is analyzed. The research results can provide a meaningful reference for similar engineering problems.
-
0. 引言
基于性能的抗震设计代表了未来结构抗震研究发展的主要方向[1]，作为基于性能抗震设计的重要组成模块，概率地震需求分析（PSDA，probabilistic seismic demand analysis）[2]主要求解基于特定地震动强度指标（IM，intensity measure）的结构或构件的地震响应（D）超越某一特定值（d）的概率（Pd），如式（1）所示：
Pd=P[D⩾d|IM]。 (1) 地震动强度指标的选择直接影响不确定性因素在结构概率地震需求分析中的传播。因此，学者们关于如何确定最优IM指标的问题开展了一系列的研究[3-13]。Padgeet等[5]建议在典型多跨度钢结构桥梁的概率地震需求分析中采用峰值加速度PGA或加速度反应谱强度Sa作为IM。Guo等[6]对斜拉桥结构在不同场地下的地震强度指标进行了分析，研究认为峰值速度PGV最适宜作为IM进行地震风险评估分析。Khosravikia等[7]在原有效性、实用性的评价标准基础上，提出了一种改进的IM检验标准，并基于改进后的标准对不同IM行了研究，结果表明与速度相关的IM如PGV）更适合于桥梁结构的概率地震需求分析。Pejovic等[8]推荐在高层钢筋混凝土框架结构的概率地震需求分析中采用包含频谱特性或速度相关的IM。周颖等[9]建议采用考虑三阶振型的加速度反应谱作为IM建立高层结构的地震易损性曲线。Du等[10]在单自由度建筑结构的地震动强度指标研究中指出，选择加速度反应谱作为IM进行概率地震需求分析效果最佳。Huang[11]研究了不同埋深下隧道地震需求的最优地震强度指标，结果表明：PGA适用于浅埋隧道，而PGV则适用于深埋隧道。张成明等[12]提出以持续最大加速度为圆形隧道损伤评价的地震强度指标。赵密等[13]对地下结构最优地震动强度指标随埋深的变化规律进行了研究，结果表明，随着埋深的增加，结构的最优地震动强度指标也会发生显著改变。目前，有关适用于浅埋地下框架结构的地震动强度指标在地震易损性分析中的选取尚未形成共识。而现有研究表明[14]，不同类型结构地震需求的地震动强度指标最优选择存有显著差异。
综上所述，至今未有城市地铁车站地下结构概率地震需求分析的最优地震动强度指标研究的公开报道。本文以浅埋（定义埋深为0~7 m）[15]地铁车站地下框架结构为研究对象，通过数值分析，评估了15种地震动强度指标在地铁车站地下框架结构PSDA中的适用性。
1. 地震强度指标评价标准
根据Cornell等[16]的研究，结构在多条地震动激励下的响应数据样本服从对数正态分布，也即，描述结构地震响应的工程需求参数（EDP：engineering demand parameter）均值与地震动强度指标之间存有以下线性关系：
lnSD=b⋅lnIM+lna， (2) 式中，SD为结构地震响应EDP的估计均值，a，b为线性回归系数。
因此，可采用高斯分布函数进一步对式（1）的概率地震需求模型函数表达为
P（D>d|IM）=1−ϕ(lnd−lnSDβD|IM)， (3) 式中，ϕ为标准正态累计分布函数，βD|IM为结构地震响应的对数标准差。
结构概率地震需求模型的建立首要任务是确定合适的地震动强度指标。本文基于效率性、实用性、有益性及充分性对地下结构地震需求的最优IM进行分析[5]，相关的评价标准见图 1。基于EDP-IM数据样本的自然对数标准差βD|IM来检验候选IM的效率性；采用式（2）中回归系数b来衡量IM的实用性；本文在判断IM是否具备充分性时，首先提取EDP的残差ε|IM，然后对残差与其它地震动信息参数所组成的样本进行独立性检验。
概率地震需求分析中地震动参数的优选不仅与地震动记录本身信息相关，也与所选结构的EDP有关。在基于性能的结构抗震设计中，所选的EDP一般应与结构的震后破坏状态紧密相关，该EDP也被定义为损伤指标（DM，damage measures）。基于大开地铁车站的地震破坏机理与相关地下结构抗震分析研究表明[17-19]，峰值层间位移角与结构的破坏状态密切相关。杜修力等[20]、Du等[21]以层间位移角（IDR：inter-story drift ratio）量化地下框架结构的抗震性能指标。因此，本文选用层间位移角作为结构损伤指标进行地铁车站地下结构概率地震需求分析。本文选取15种常见地震动强度参数作为备选指标，所选的IMs可区分为4个类型：结构频谱特性相关，加速度相关，速度相关，位移相关，见表 1，IMs的具体含义见文献[4]。
表 1 不同地震动强度指标的表达式Table 1. Equations for various ground motion intensity measures类别 名称 表达式 加速度相关 PGA max|a(t)| 均方加速度arms arms=√1t2−t1∫t2t1a2(t)dt 加速度平方积分asq asq=∫tf0a2(t)dt Arias强度Ia π 2g∫tf0a2(t)dt 特征强度Ic (arms)3/2⋅√ttot 速度相关 PGV max|v(t)| 均方根速度vrms vrms=√1t2−t1∫t2t1v2(t)dt 速度平方积分vsq vsq=∫tf0v2(t)dt Fajfar强度IF IF=PGVt0.25d 位移相关 PGD max|d(t)| 均方根位移drms drms=√1t2−t1∫t2t1d2(t)dt 位移平方积分dsq dsq=∫tf0d2(t)dt 周期谱相关 加速度反应谱Sa(Tn) Sa(T = 0.2,ξ=0.05) 速度反应谱Sv(Tn) Sv(T = 0.2,ξ=0.05) 位移反应谱Sd(Tn) Sd(T = 0.2,ξ=0.05) 由于缺乏历史震害数据，通常基于数值分析获取概率地震需求模型中所需的地震响应数据样本，其中，以增量动力分析（IDA，incremental dynamic analysis）[22-26]方法的应用最为广泛，其核心思想是输入幅值逐步增大的地震动记录对结构进行非线性动力时程分析，以获得结构从弹性至弹塑性整个过程的地震响应状态。
2. 计算模型
2.1 地铁车站工程参数
3种典型地铁车站地下框架结构横断面如图 2所示。断面A为两层两跨车站，顶板埋深2 m，结构主体混凝土等级为C40，中柱混凝土等级为C50，其主钢筋型号为HRB335；断面B为两层三跨车站，顶板埋深3 m，结构主体混凝土等级为C40，中柱混凝土等级为C50，其主钢筋型号为HRB335；断面C为三层三跨车站，顶板埋深2.5 m，结构主体与中柱混凝土等级均为C50，其主钢筋型号为HRB335。断面A、断面B以及断面C所在场地土的基本物理力学性质见表 2，动剪模量衰减比-应变G/Gmax-γ与阻尼比-应变λ-γ曲线如图 3所示。
表 2 土层物理力学参数Table 2. Physical and mechanical parameters of soils编号 岩土性质 厚度/m 密度/(kg·m-3) 剪切波速/(m·s-1) 泊松比 断面类型 断面
A断面
B断面
C断面
A断面
B断面
C断面
A断面
B断面
C断面
A断面
B断面
C断面
A断面
B断面
C1 填土 填土 填土 2 2.5 2.0 1700 1700 1800 147 169 168 0.35 0.29 0.35 2 粉土 粉土 粉土 6 2.0 4.2 2020 2020 2030 190 213 212 0.35 0.31 0.35 3 黏土 黏土 黏土 7 7.0 5.6 2000 1930 1950 193 231 224 0.36 0.29 0.35 4 砂土 粉土 粉土 2 4.0 2.2 2050 2020 2060 274 246 242 0.33 0.31 0.35 5 黏土 黏土 细砂 10 1.5 2.5 2020 1960 2020 300 253 267 0.36 0.29 0.32 6 砂土 粉土 粉土 3 2.0 1.6 2050 2080 2060 328 289 243 0.33 0.31 0.35 7 黏土 砂土 黏土 2 8.0 1.5 1990 2020 2030 331 352 250 0.36 0.26 0.36 8 砂土 砂土 黏土 6 14.0 5.8 2050 2020 1980 368 396 273 0.33 0.26 0.36 9 粉土 基岩 粉土 7 — 136.0 2000 2500 2060 382 — 273 0.35 — 0.35 10 基岩 黏土 — — 2.6 2500 — 1980 — — 291 — — 0.36 2.2 有限元模型
以断面A为例，基于ABAQUS/Standard软件平台建立二维有限元数值分析模型，如图 4所示。模型长度取车站横断面宽度5倍或以上，模型深度取至基岩面。土体模型的网格划分原则上保证单元尺寸小于地震波长的1/10[27]，全局尺寸取0.5 m，结构附近土体单元网格尺寸为0.25 m，结构与钢筋的单元网格尺寸均为0.25 m。分别选用实体单元模拟土体、梁单元模拟混凝土结构、桁架单元模拟钢筋，钢筋通过关键字*Rebar与结构进行绑定。为考虑土-结构相互作用，结构与土体接触面的径向采用硬接触，切向采用摩擦接触，其摩擦系数取0.4[28-30]。模型底部，固定两侧采用已广泛应用于地下结构数值分析的捆绑边界[17, 31-32]，即对同一高度的侧边节点进行运动耦合约束，但保持其在水平与垂直方向上的自由度，以模拟土体在地震动荷载作用下的剪切运动。本文采用振动法进行地震动记录的输入，模型荷载主要分位两步：第一步，为重力荷载，第二步为动力荷载，值得注意的是，所有模型均进行了地应力平衡，详细方法见文献[20]。
地下结构所受的地震作用具有循环往复的特性。因此，本文选择混凝土塑性损伤本构模型[18, 33]考虑混凝土结构的动力学行为。该模型引入标量损伤参数来模拟材料的各向同性损伤，损伤系数直接与材料的退化刚度相关。选用理想弹塑性本构[34]模拟钢筋；采用基于Davidenkov骨架曲线的non-Masing滞回本构模型描述岩土的动力非线性和滞回特性[35, 36]。
参考报告FEMA-P695[37]，本文选取22条远场地震动记录（44条加速度时程曲线）作为本文非线性动力时程分析的输入荷载。如图 5所示，对输入地震动记录进行调幅，基于IDA方法，获取不同强度的该地震动记录作用下的地下结构非线性响应数据，步骤如下：
（1）选取拟输入的地震动记录i（i =1），基于PGA调幅至aj=1 = 0.05g，进行土-地下结构体系非线性动力时程分析，获取峰值层间位移角。
（2）若峰值层间位移角大于地下结构的倒塌极限，返回（1），对下一条拟输入的地震动记录（i = i+1）重复（1）的过程；当i =44时，即计算完成。若峰值层间位移角小于地下结构的倒塌极限，进入（3）。
（3）令j = j+1，基于PGA调幅至aj+1，例如，aj+1=0.1g，再次进行土-地下结构体系非线性动力时程分析，并获取结构峰值层间位移角，返回（2）。
3. 结果分析与讨论
3.1 效率性分析结果
表 3统计了车站断面A、断面B和断面C基于不同IM指标下IDR的标准差。可以看出，标准差值分布在0.3~1.0，多数在0.5左右，其中，基于PGA指标的标准差值最小，断面A为0.351，断面B为0.339，断面C为0.352。由此说明以PGA作为IM指标进行结构概率地震需求分析的效率性最好。基于加速度平方积分指标的标准差值仅仅大于基于PGA指标的标准差值。这表明以加速度平方积分作为IM指标进行概率地震需求分析的效率性，虽然差于PGA指标，但明显优于其它IM指标。然而，基于PGD、均方根位移、位移平方积分和位移反应谱等指标计算的标准差值较大，均超过了0.7，也即上述4种IM指标的效率性不太理想。此外，基于与加速度相关的IM指标计算的标准差要普遍小于其它3种类型的IM指标（表 1），且基于与位移相关的IM指标计算的标准差值最大。上述结果表明：采用加速度相关的IM指标，一般都可以保证较好的效率性，且以基于PGA指标的效率性最好。进一步观察表 4可以发现，断面A、断面B以及断面C的效率性评价结果无明显区别，这说明地铁车站断面类型对IM的效率性评价结果的影响甚微。
表 3 基于效率性、实用性以及有益性的分析结果Table 3. Analysis results based on efficiency, practicality and proficiencyIM 断面A 断面B 断面C 标准差 系数b 系数ζ 标准差 系数b 系数ζ 标准差 系数b 系数ζ PGA 0.351 1.063 0.330 0.339 1.027 0.330 0.352 1.089 0.323 PGV 0.405 1.007 0.402 0.416 0.953 0.437 0.428 1.038 0.412 PGD 0.721 0.637 1.132 0.714 0.598 1.194 0.764 0.695 1.099 arms 0.507 0.899 0.564 0.473 0.875 0.541 0.533 0.945 0.564 asq 0.391 0.513 0.762 0.370 0.494 0.749 0.396 0.530 0.747 Ia 0.426 0.494 0.862 0.379 0.486 0.780 0.433 0.510 0.849 Ic 0.559 0.560 0.998 0.503 0.559 0.900 0.574 0.588 0.976 vrms 0.616 0.768 0.802 0.610 0.723 0.844 0.661 0.812 0.814 vsq 0.543 0.436 1.245 0.544 0.410 1.327 0.567 0.458 1.238 IF 0.449 0.960 0.468 0.430 0.928 0.463 0.477 0.978 0.488 drms 0.856 0.400 2.140 0.835 0.379 2.203 0.924 0.444 2.081 dsq 0.780 0.271 2.878 0.764 0.256 2.984 0.826 0.299 2.763 Sa(Tn) 0.536 0.894 0.600 0.507 0.878 0.577 0.546 0.953 0.573 Sv(Tn) 0.408 1.009 0.404 0.416 0.968 0.430 0.423 1.047 0.404 Sd(Tn) 0.714 0.648 1.102 0.707 0.608 1.163 0.756 0.706 1.071 表 4 基于残差-震级与残差-震源距回归分析所得到的P-valuesTable 4. P-values obtained from regression analysis based on residual-magnitude and residual-distanceIM P-value (震级) P-value (震源距) 断面A 断面B 断面C 断面A 断面B 断面C PGA 0.874 0.813 0.578 0.618 0.740 0.541 PGV 0.084 0.181 0.182 0.137 0.180 0.179 PGD 0.098 0.155 0.128 0.021 0.032 0.021 arms 0.310 0.291 0.161 0.124 0.165 0.079 asq 0.591 0.561 0.353 0.428 0.533 0.344 Ia 0.616 0.588 0.387 0.749 0.832 0.661 Ic 0.566 0.525 0.326 0.332 0.389 0.239 vrms 0.250 0.334 0.344 0.227 0.240 0.249 vsq 0.260 0.350 0.368 0.184 0.201 0.205 IF 0.083 0.161 0.181 0.128 0.163 0.168 drms 0.127 0.179 0.154 0.024 0.033 0.023 dsq 0.134 0.188 0.166 0.028 0.037 0.027 Sa(Tn) 0.696 0.664 0.503 0.419 0.485 0.339 Sv(Tn) 0.147 0.255 0.274 0.442 0.452 0.515 Sd(Tn) 0.096 0.153 0.126 0.021 0.033 0.022 3.2 实用性分析结果
表 3列出了基于不同IM指标与IDR回归分析所得的系数b值，主要分布在0.2~1.1。由表 3可知，断面A、断面B与断面C基于PGA指标所得到的b值分别为1.063，1.027，1.089，在所有IMs中最大。由此可知，在概率地震需求分析中，以PGA作为IM指标的实用性评估结果最佳。基于PGV、速度反应谱及Fajfar强度等指标计算的b值与基于PGA指标的计算结果非常接近。因此，上述3种IM指标的实用性不太理想。
由表 3可知，基于Arias强度、均方根位移以及位移平方积分等指标计算的b值均小于0.5，由此说明，上述3种IM指标的实用性相对较差。在所有类型的IM指标中，基于位移相关的IM指标计算的b值相对较小，说明该类型IM指标的实用性较差。基于断面A、断面B与断面C的IM指标的实用性评估的结果基本一致，这说以上IM指标的实用性分析结论在任何类型断面地铁车站均适用。
3.3 有益性评价结果
表 3列出了基于不同IM指标所得到的有益性系数计算结果，可以看出，有益性系数分布在0.3~1.2之间。其中，基于PGA指标的有益性评价结果最为理想，如断面A、断面B与断面C基于PGA指标计算的有益性系数分别为0.33，0.33，0.323。基于速度反应谱、PGV以及Fajfar强度等指标计算的有益性系均小于0.5，以上3种IM指标的有益性评估结果仅仅差于PGA指标。在15中IM指标中，基于PGD、速度平方积分、位移均方根、位移平方积分以及位移反应谱等指标的有益性结果相对较差，其有益性系数均大于1。进一步对比基于不同地铁车站断面类型的有益性分析结果可以发现，其有益性系数基本一致。由此说明，地铁车站地下框架结构断面类型对IM指标有益性的评价结果的影响甚微。
3.4 充分性分析结果
表 4列出了基于不同IM指标计算的P-value值。由表 4可知，所有IM指标基于残差-震级回归分析所得到的P-value值均大于5%，由此说明，15种IM指标与震级均不存在相关性，即所有IM指标相对于震级的充分性评价均成立。然而，在基于残差-震源距的回归分析中，以PGD、均方根位移、位移平方积分与位移反应谱等指标计算所得到的P-value值均小于5%，以上IM指标不满足充分性检验。
综上所述，在地铁车站地下框架结构概率地震需求分析中，基于效率性、实用性以及有益性等标准的分析结果表明：以PGA、速度反应谱、PGV作为IM指标较为理想，其中又以PGA指标最佳。分析认为，地下结构的破坏与结构变形相关，但由于受周围土层的约束，结构的变形基本由一维场地的动力响应决定，而自由场响应在某种程度上与所输入的PGA密切相关，因此，本文的研究结论在一定程度上与当前地下结构地震响应规律的认识相呼应。而PGD、速度平方积分、均方根位移、位移平方积分以及位移反应谱作等指标不适合应用于地下结构的概率地震需求分析。
基于充分性标准的分析结果表明：除PGD、均方根位移、位移平方积分与位移反应谱等指标，其它11种IM指标均满足充分性检验。此外，不同断面类型的地铁车站之间的IM指标分析结果并无显著差异，由此说明IM指标的选择与地下结构断面类型无关。分析认为，本文的断面类型虽有不同，但均属于浅埋地下框架结构，这决定了本文分析对象的地震响应规律与破坏机理是基本一致的。在此前提下，由于地下结构受周围土层约束，其峰值层间位移随输入地震动强度的变化规律，基本与自由场响应随输入地震动强度的变化规律一致。由此推断，基于效率性、实用性、有益性及充分性4个标准对层间位移角-PGA的评价结果，与自由场响应-PGA的评价结果相一致，因此，浅埋地下框架结构断面类型的改变并不会改变地震动强度指标的评价结果。
4. 结论
本文从基于性能的抗震设计理念出发，开展了浅埋地铁车站地下框架结构最优IM指标的研究。选取了3种不同断面类型的地铁车站，基于ABAQUS/ Standard软件平台建立了土-结构相互作用有限元分析模型。数值模型中考虑了土体在循环荷载作用下的非线性动力特性以及钢筋混凝土结构在单轴拉压下的塑性损伤力学特性。参考所出台的FEMA-P695报告，选取了22条远场地震动记录，并通过IDA方法获取了地下结构在不同地震动强度激励下的地震响应。以峰值层间位移角作为结构的损伤指标，并基于效率性、实用性、有益性以及充分性4个标准对15种IM指标进行评估，得到以下5点结论。
（1）基于效率性的分析结果表明，加速度相关的IM指标一般具有较好的效率性。其中，PGA指标的效率性最好，其次为加速度平方积分指标，而基于PGD、均方根位移、位移平方积分与位移反应谱等指标的效率性相对较差。
（2）基于实用性的分析结果表明，以PGA、PGV与速度反应谱等指标的实用性相对较好，而基于Arias强度、均方根位移与位移平方积分等指标的实用性最差。此外，基于位移相关的IM指标的实用性表现相对较差。
（3）基于有益性的分析结果表明，PGA指标最适合应用于地下结构在概率地震需求分析，其次为加速度反应谱与PGV等指标。基于PGD、速度平方积分、均方根位移、位移平方积分与位移反应谱强度等指标的有益性相对较差。
（4）基于充分性的检验结果表明，15种候选IM指标均满足震级的充分性检验。然而，基于PGD、均方根位移、位移平方积分与位移反应谱强度等指标不满足基于震源距的充分性检验，因此，以上4种IM指标不适合应用于地下结构的概率地震需求分析。
（5）通过对比3种不同断面类型地铁车站的分析结果可以发现，IM指标的最优选择与地下结构的断面类型无关。
综上所述，本文建议选取PGA作为IM指标进行浅埋地铁车站地下框架结构的概率地震需求分析，速度反应谱强度指标与PGV指标可作为备选。其成果可为浅埋地下框架结构地震危险性分析或基于性能的抗震设计提供科学研究基础。然而，本文所研究的对象仅考虑了浅埋地铁车站工程，且所输入荷载的均选自远场地震动记录。因此，有关深埋或其它特性地震动记录输入下地下结构地震动强度指标的选择有待进一步研究。
-
![]()
图 2 蓄水过程–安全系数关系曲线
Figure 2. Relationship between impoundment process and safety factor
![]()
图 3 蓄水过程–安全系数关系曲线(R2剖面)
Figure 3. Relationship between impoundment process and safety factor for section R2
![]()
图 4 蓄水过程–安全系数关系曲线(R1~R10剖面)
Figure 4. Relationship between impoundment process and safety factor for sections of R1 to R10
![]()
图 6 堆积体边坡蓄水失稳过程
Figure 6. Process of impoundment and instability of accumulation slope
![]()
图 8 堆积体强度与变形关系曲线
Figure 8. Relationship between strength and deformation of accumulation
![]()
图 9 涌浪分析计算所用三维地质模型
Figure 9. Three-dimensional geological model for surge analysis and calculation
![]()
图 11 库区RS下游监测点的水位过程线
Figure 11. Hydrograph of water level of RS downstream monitoring point
![]()
图 12 坝体周围监测点的水位过程线
Figure 12. Hydrograph of water level of monitoring points around dam
表 1 RS堆积体稳定计算岩土体物理力学参数取值表
Table 1 Physical and mechanical parameters of rock and soil for stability calculation of RS accumulation
土层编号 物质组成 重度/(kN·m-3) 水上天然抗剪强度 水下饱和抗剪强度 天然 饱和 黏聚力/kPa 内摩擦角/(°) 黏聚力/kPa 内摩擦角/(°) ①上部 较松散的碎砾石层 22.0 23.0 10 34.5 5 30.5 ②中部 有一定胶结的含细粒土砾 21.0 22.5 50 33.0 25 29.5 ③下部 碎石土夹少量砂卵砾石 21.5 22.5 20 35.5 10 31.5 
下载: 导出CSV
表 2 RS堆积体3种滑况最高滑速计算成果
Table 2 Calculated results of maximum sliding velocity of RS accumulation under three sliding conditions
滑况 滑动模式 最小安全系数K 滑坡体高度H/m 方量/(104 m3) 最高滑速值/(m·s-1) 滑况1 整体滑动 1.22 67.75 2865.9 18~27 滑况2 底层滑动 1.01 58.32 1397.3 23 滑况3 上层滑动 1.22 136.83 1977.4 25~35
下载: 导出CSV
表 3 RS堆积体滑坡可传播涌浪浪高计算成果
Table 3 The calculation results of surge height can be spread by RS accumulation landslide
滑况 滑速/(m·s-1) 首浪高度/m 可传播浪计算代表值/m 坝前浪高/m 坝顶波浪爬高高程/m 滑况1 18 26.8 7.17 5.42 2906.44 27 29.8 滑况2 23 27.9 5.25 — — 敏感性分析1 5 13.4 3.66 2.77 2900.69 敏感性分析2 10 21.5 5.73 4.43 2904.25
下载: 导出CSV
-
[1] 王自高. 西南地区深切河谷大型堆积体工程地质研究[D]. 成都: 成都理工大学, 2015. WANG Zi-gao, Engineering Geological Study on Large Quaternary Deposits in the Deeply Valley Southwestern China[D]. Chengdu: Chengdu University of Technology, 2015. (in Chinese)
[2] 王自高, 胡瑞林, 张瑞, 等. 大型堆积体岩土力学特性研究[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3836–3843. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2107.htm WANG Zi-gao, HU Rui-lin, ZHANG Rui, et al. Study of geotechnical mechanical characteristics of a large soil-rock mixture in a hydropower project[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3836–3843. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2107.htm
[3] 陈祖煜. 岩质边坡稳定分析: 原理·方法·程序[M]. 北京: 中国水利水电出版社, 2005. CHEN Zu-yu. Rock Slope Stability Analysis: Theory Methods and Programs[M]. Beijing: China WaterPower Press, 2005. (in Chinese)
[4] 徐文杰. 大型土石混合体滑坡空间效应与稳定性研究[J]. 岩土力学, 2009, 30(增刊2): 328–333. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2009S2071.htm XU Wen-jie. Study of spatial effect and stability of large scale soil-rock mixture landslide[J]. Rock and Soil Mechanics, 2009, 30(S2): 328–333. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2009S2071.htm
[5] 张玉, 徐卫亚, 石崇, 等. 大型滑坡堆积体稳定性的三维数值分析[J]. 岩土力学, 2011, 32(11): 3487–3496. doi: 10.3969/j.issn.1000-7598.2011.11.047 ZHANG Yu, XU Wei-ya, SHI Chong, et al. Three-dimensional numerical analysis of stability of large-scale landslide accumulation body[J]. Rock and Soil Mechanics, 2011, 32(11): 3487–3496. (in Chinese) doi: 10.3969/j.issn.1000-7598.2011.11.047
[6] 吴火珍, 冯美果, 焦玉勇, 等. 降雨条件下堆积层滑坡体滑动机制分析[J]. 岩土力学, 2010, 31(增刊1): 324–329. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2010S1053.htm WU Huo-zhen, FENG Mei-guo, JIAO Yu-yong, et al. Analysis of sliding mechanism of accumulation horizon landslide under rainfall condition[J]. Rock and Soil Mechanics, 2010, 31(S1): 324–329. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2010S1053.htm
[7] 王自高, 胡瑞林, 张瑞, 等. 大型堆积体岩土力学特性研究[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3836–3843. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2107.htm WANG Zi-gao, HU Rui-lin, ZHANG Rui, et al. Study of geotechnical mechanical characteristics of a large soil-rock mixture in a hydropower project[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S2): 3836–3843. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2013S2107.htm
[8] 朱继良, 黄润秋. 某水电站坝前堆积体稳定性的三维数值模拟分析[J]. 岩土力学, 2005, 26(8): 1318–1322. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200508027.htm ZHU Ji-liang, HUANG Run-qiu. Study on stability of talus slope in front of a dam in a huge hydroelectric station by using 3D numerical simulation[J]. Rock and Soil Mechanics, 2005, 26(8): 1318–1322. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX200508027.htm
[9] 徐卫亚, 周伟杰, 闫龙. 降雨型堆积体滑坡渗流稳定性研究进展[J]. 水利水电科技进展, 2020, 40(4): 87–94. https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD202004015.htm XU Wei-ya, ZHOU Wei-jie, YAN Long. Research progress on seepage stability of rainfall-induced accumulation landslide[J]. Advances in Science and Technology of Water Resources, 2020, 40(4): 87–94. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLSD202004015.htm
[10] 杨继红, 王俊梅, 董金玉, 等. 水库蓄水过程中堆积体边坡瞬态稳定性分析[J]. 岩土力学, 2011, 32(增刊1): 464–470. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S1084.htm YANG Ji-hong, WANG Jun-mei, DONG Jin-yu, et al. Analysis of transient stability of deposits slope in process of reservoir impounding[J]. Rock and Soil Mechanics, 2011, 32(S1): 464–470. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2011S1084.htm
[11] 孙志亮, 孔令伟, 郭爱国, 等. 地震作用下堆积体边坡的坡面变形与失稳机制[J]. 岩土力学, 2015, 36(12): 3465–3472, 3481. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201512017.htm SUN Zhi-liang, KONG Ling-wei, GUO Ai-guo, et al. Surface deformations and failure mechanisms of deposit slope under seismic excitation[J]. Rock and Soil Mechanics, 2015, 36(12): 3465–3472, 3481. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201512017.htm
[12] 中国电建集团贵阳勘测设计研究院有限公司. 库区滑坡涌浪特征及传播评估[R]. 贵阳: 中国电建集团贵阳勘测设计研究院有限公司, 2017. Power China Guiyang Engineering Co. LTD. Characteristics and Propagation Assessment of Landslide Surge in Reservoir Area[R]. Guiyang: Power China Guiyang Engineering Co. LTD, 2017. (in Chinese)
-
期刊类型引用(7)
1. 蒋家卫，李文彪，赵雅芝，陈国兴，杜修力. 场地均质性对浅埋地铁车站地下结构地震易损性的影响. 振动与冲击. 2024(06): 151-156+178 . 
百度学术
2. 韩俊艳，李玉凤，钟紫蓝，缪惠全，杜修力. 不同场地条件下埋地腐蚀钢管地震易损性评价. 岩土工程学报. 2024(04): 774-783 . 本站查看
3. 林峻岑，孙纬宇，李国玉，严松宏，佟浩. 基于矢量IMs的浅埋偏压黄土隧道地震易损性. 东南大学学报(自然科学版). 2024(02): 432-440 . 百度学术
4. 蒋家卫，黄文婷，赵凯，陈国兴，杜修力. 典型浅埋矩形框架地铁车站地下结构地震易损性分析. 工程力学. 2024(09): 9-17 . 百度学术
5. 郭志辉. 复杂高层建筑结构抗震设计方法研究. 砖瓦. 2023(03): 95-97 . 百度学术
6. 谭灿星，周瑾. 两层三跨岛式地铁车站的地震响应研究. 广东土木与建筑. 2023(04): 73-77 . 百度学术
7. 谢宏飞，蔡海兵. 地铁地下车站抗震研究主要方法与现状. 建井技术. 2023(06): 85-90 . 百度学术
其他类型引用(8)
计量
- 文章访问数: 240
- HTML全文浏览量: 20
- PDF下载量: 188
- 被引次数: 15
