拱坝坝肩多块体滑动的三维极限平衡分析方法

孙平; 张强; 陈祖煜; 王玉杰

doi:10.11779/CJGE202201014

拱坝坝肩多块体滑动的三维极限平衡分析方法 English Version

中国水利水电科学研究院岩土工程研究所, 北京 100044

基金项目:

国家重点研发计划项目 2017YFC1501100

详细信息

作者简介:
孙平(1976—)，男，博士，正高级工程师，主要从事大坝与高边坡稳定、变形方面的研究工作。E-mail: sunping@iwhr.com

通讯作者:
张强, E-mail: zhangq@iwhr.com

中图分类号: TU43
计量
- 文章访问数: 232
- HTML全文浏览量: 24
- PDF下载量: 178
出版历程
- 收稿日期: 2021-02-18
- 网络出版日期: 2022-09-22
- 刊出日期: 2021-12-31

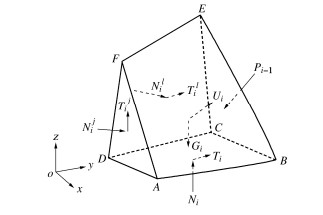
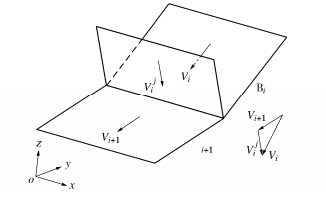
Three-dimensional rigid limit equilibrium analysis method for multi-block sliding in arch dam abutment

Institute of Geotechnical Engineering, China Institute of Water Resource and Hydropower Research, Beijing 100044, China

摘要

摘要: 多块体滑动是拱坝坝肩一种常见且重要的失稳模式，目前已建立的各种稳定分析方法，普遍存在一定的缺陷或局限性，如必须引入大量假定才能使问题变为静定可解，或仅讨论了各块体的滑动模式为沿底滑面与侧滑面交线的双面滑动的情况等，不适合拱坝坝肩多块体滑动问题的求解。提出了一种理论基础严格、计算步骤相对简单的三维稳定分析方法，即针对滑体中各块体的滑动模式分别为双面滑动与单面滑动两种情况，通过建立各块体在3个方向的静力平衡方程与相邻块体之间的位移协调方程，使安全系数的求解归结于一个含若干个自由度的极小值问题，结合全局最优化方法可获得较好的收敛性。将该方法应用于典型三维楔体与小湾拱坝坝肩的稳定分析，验证了其合理性与实用性。该方法是二维Sarma法在三维多块体领域的扩展，在理论上获得塑性力学上限定理的支持。同时，该方法还给出了三维多块体串联滑动问题的闭合解求解方法，可为各种三维边坡稳定分析程序的合理性验证提供考核算例。
- 拱坝 /
- 坝肩稳定 /
- 多块体滑动 /
- 三维极限平衡法 /
- 位移协调
Abstract: Multi-block sliding is a common and important failure mode in arch dam abutment. The current stability analysis methods established generally have certain deficiencies: a lot of assumptions must be introduced to make the problem static, or some methods only discuss that the sliding mode of the individual block is double-face sliding along the bottom and lateral slip surface. These methods are not suitable for solving the multi-block sliding problems of arch dam abutment. A new 3D limit equilibrium method with a strict theoretical basis and simple calculation steps is proposed. More specifically, considering that the sliding mode of each block is double-face sliding and single-face sliding, the method involves converting the multi-block stability analysis to a non-linear minimum problem containing several degrees of freedom by creating the equations for static equilibrium along x, y and z directions of each block and the equation for displacement compatibility of two adjacent blocks, thus good convergence can be obtained by combining with the global optimization methods. The method proposed is applied to a 3D wedge problem and the abutment stability of Xiaowan arch dam, so the validity and practicability are verified. The method is actually an extension of 2D Sarma method in 3D multi-block field, and is theoretically supported by the upper bound theorem of plasticity. Meanwhile, it gives the closed solution method for multi-block series sliding problems, and can provide an example for the rationality verification of various 3D slope stability programs.
- arch dam /
- abutment stability /
- multi-block sliding /
- 3D rigid limit equilibrium method /
- displacement compatibility

HTML全文

0. 引言

盐渍土具有溶陷、冻胀及腐蚀等特殊工程性质，盐渍土地区修建道路在工程上常采用换填土层处理。黑龙江省处于季冻区，路基土受到交通动荷载、冬季低温及冻融循环综合作用，路基土的力学性能和动力特性因此发生改变，主要体现在土体动剪切模量和阻尼比的变化^[1]。目前对于盐渍土的研究主要包括温度变化下水盐迁移运动研究^[2-3]，通过室内试验结果，分析水盐运动主要影响因素，建立温度梯度下盐渍土水–热–盐多场耦合模型，揭示水盐运动规律；土体冻胀和溶陷特性研究，将湿陷和溶陷加以区分，提出峰值溶陷系数以描述不同含盐量对压缩、湿陷和溶陷的影响。考虑冻胀和盐胀综合作用，分析冻胀影响因素^[4-6]；盐渍土改性剂种类和掺量以及改良盐渍土的静力性质研究，采用不同改性剂对盐渍土进行改良，并对改良盐渍土抗剪强度及破坏强度进行测定，根据试验结果，建立考虑多重因素的改良盐渍土破坏强度及抗剪强度预测模型^[7-8]。以上研究多针对未处理盐渍土，或主要考虑改良盐渍土静力性质。若通过石灰改良含盐量较低的盐渍土，使其满足路基力学性能的要求，可以降低成本并节约土壤资源。综上，目前对于季冻区低温及冻融循环作用下的石灰改良盐渍土动力特性研究偏少但其影响不容忽视。

本文以黑龙江省哈肇公路沿线盐渍土为研究对象，经石灰改良后进行循环三轴试验，研究其在不同动荷载频率、围压、温度以及冻融循环作用下的动剪切模量及阻尼比变化规律。并基于Hardin双曲线模型进行曲线拟合，分析石灰改良盐渍土动力参数在不同因素下的响应规律，为工程设计提供动力参数，并为进一步研究不同改性剂种类及不同盐分种类的改良盐渍土动力特性提供理论基础。

1. 试验材料与试验方案

1.1 试验材料

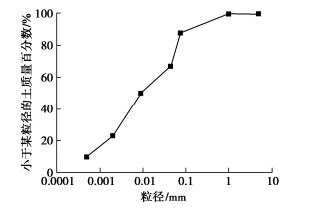
试验土样取自黑龙江省哈肇公路沿线，依据《公路土工试验规程：JTG E40-2007》，测得土样基本物理参数：天然含水率为6.85%，液限为21.2%，塑限为14.2%，最大干密度为1.79 g/cm³，最佳含水率为16%。土样的颗粒级配曲线如图 1所示，由试验结果可知该土样属于低液限黏土，土样中各离子种类及含量如表 1所示。由试验结果可知此土样总含盐量为0.5047%，其中CO₃^2-离子含量最高达0.2205%，夹杂有含量0.1086%的HCO₃^-离子和0.1134%的Cl^-离子，由此判定此土样为含有少量Cl^-的碳酸盐渍土且含盐量较低。

图 1 试验用土颗粒级配曲线

Figure 1. Grain-size distribution curves of test specimens

下载: 全尺寸图片幻灯片

表 1 盐渍土离子含量测定值

Table 1. Measured values of ion content of saline soil (%)

阳离子					阴离子
K⁺	Na⁺	Ca²⁺	Mg²⁺	总量	CO₃^2-	HCO₃^-	SO₄^2-	Cl^-	总量
0.21	0.2173	0.0244	0.0357	0.4870	0.2205	0.1086	0.0622	0.1134	0.5047

下载: 导出CSV

| 显示表格

1.2 试样制备

依据《公路路基设计规范：JTG D30—2015》选择压实度为96%，并查阅相关文献及结合工程实际，确定石灰掺量为6%^[9]。

试样制备采用击实法，烘干土样经0.25 mm土工标准筛筛分，并与蒸馏水充分混合后装入塑料袋中后闷料24 h。按照石灰掺量称取一定质量的石灰均匀拌入盐渍土中，称取所需质量的土样，分3层制成直径39.1 mm，高80 mm的圆柱试样，将其密封后进行恒温恒湿养护28 d。

1.3 试验仪器

试验采用英国GDS公司的动态三轴试验系统（GDSTAS），仪器可以施加最大荷载为10 kN，荷载频率范围为1~5 Hz，最大围压为200 MPa，温度调节范围为-20℃~20℃。冻融循环过程采用DP.CDR-2型快速冻融试验设备。

1.4 试验条件和方案

试验主要控制条件为温度和冻融循环次数。根据相关文献及该地区路基冬季低温温度范围^[10-11]，低温试验温度设置为20℃，0℃，-2℃，-4℃，-6℃，-8℃，-10℃，-16℃共8个温度变化梯度，养护后的试样在设定温度下冻结24 h后，进行温度控制的循环加载试验。冻融循环次数为0，1，3，5，7，9次，冻融循环试验的冻结温度为-16℃，融化温度为20℃。

研究动荷载频率及围压对动力特性影响时采用未冻融试样，试验温度为20℃。荷载参数^[12-14]参考公路交通荷载设置频率为1，3，5 Hz，围压为50，100，150 kPa。试验方案见表 2。

表 2 试验方案

Table 2. Test plan

试验编号	试验温度 /℃	频率/Hz	有效围压 /kPa	冻融循环次数
S1	20	1	100	0
S2~S3	20	3，5	100	0
S4~S6	20	1	50，100，150	0
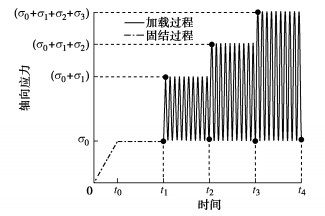
S7~S13	0，-2，-4，-6， -8，-10，-16	1	100	0
S14~S18	20	1	100	1，3，5，7，9

下载: 导出CSV

| 显示表格

养护完成的试样进行试验前，需在动三轴仪器上进行CO₂排气，水头差饱和、多级反压饱和，当B值大于0.95时结束饱和。试样等压固结后，施加分级正弦波荷载，固结过程及动荷载加载过程见图 2。进行低温加载试验时，养护后的试样经饱和后需按照设定温度冻结24 h，并预先将试验仪器温度控制在设定温度后再进行试验。终止加载条件为轴向变形达到5%或破坏。

图 2 正弦形式轴向动荷载示意图

Figure 2. Schematic diagram of sinusoidal axial dynamic load

下载: 全尺寸图片幻灯片

2. 试验结果与分析

2.1 不同频率下动力参数的变化

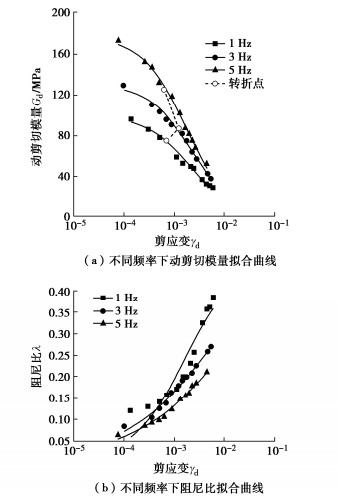
未冻融，围压100 kPa，温度20℃，不同频率石灰改良盐渍土动剪切模量变化如图 3（a）所示。3种频率下，随着剪应变的增大，动剪切模量呈衰减趋势，曲线形式为上凸形。剪应变较小时，动剪切模量衰减速度较慢。剪应变较大时，动剪切模量衰减速度加快。在动剪切模量–剪应变曲线变化过程中存在转折点，Lin等^[15]认为转折点动剪切模量可以评价不同因素对于动剪切模量的影响。动荷载频率由1 Hz增加到5 Hz，转折点动剪切模量增加168%。

图 3 不同频率下动剪切模量及阻尼比拟合曲线

Figure 3. Fitting curves of dynamic shear modulus and damping ratio at different frequencies

下载: 全尺寸图片幻灯片

不同频率下阻尼比变化情况如图 3（b）所示，3种频率下，随着剪应变的增大，阻尼比逐渐增加，较低剪应变水平时阻尼比增长缓慢，较高剪应变水平时阻尼比迅速增长，频率增大引起阻尼比降低。以剪应变最小时对应的阻尼比为最小阻尼比，当动荷载频率由1 Hz增长到5 Hz，最小阻尼比下降0.06。

对不同频率下的动剪切模量–剪应变，阻尼比–剪应变曲线按照Hardin等^[16-17]的双曲线模型进行拟合，拟合公式为

${\tau _{\text{d}}} = \frac{{{\gamma _{\text{d}}}}}{{{a} + b{\gamma _{\rm{d}}}}} \text{，}$

(1)

${{G} _{\text{d}}}{\text{ = }}\frac{{{\tau _{\text{d}}}}}{{{\gamma _{\rm{d}}}}}{\text{ = }}\frac{1}{{{a} + b{\gamma _{\rm{d}}}}} \text{，}$

(2)

$\lambda = {\lambda _{\rm{max}}}{\left( {1 - \frac{{G} }{{{{G} _{\rm{max}}}}}} \right)^{n} } = {\lambda _{\rm{max}}}{\left( {1 - \frac{1}{{1 + \frac{{{\gamma _{\text{d}}}}}{c}}}} \right)^n} 。$

(3)

式中 ${\tau _{\text{d}}}$ 为动应力； ${\lambda _{\rm{max}}}$ 为最大阻尼比；a，b，c，n为拟合参数，拟合参数如表 3所示，拟合曲线如图 3所示。

表 3 不同频率及围压下动剪切模量及阻尼比的拟合参数

Table 3. Fitting parameters of dynamic shear modulus and damping ratio under different frequencies and confining pressures

频率/Hz	动剪切模量G_d			阻尼比 $\lambda$
频率/Hz	a	b	R²	${\lambda _{\max }}$	c	n	R²
1	0.0101	4.7873	0.9865	0.46	0.0025	0.6845	0.9183
3	0.0076	3.4389	0.9886	0.39	0.0096	0.3665	0.9893
5	0.0056	3.3365	0.9887	0.36	0.0169	0.3469	0.9950

围压/kPa	动剪切模量G_d			阻尼比λ
围压/kPa	a	b	R²	λ_max	c	n	R²
50	0.0145	4.7686	0.9942	0.55	0.0036	0.4693	0.9940
100	0.0101	4.7873	0.9865	0.46	0.0025	0.6845	0.9183
150	0.0080	3.4256	0.9941	0.43	0.1306	0.2455	0.9802

下载: 导出CSV

| 显示表格

当式（2）中 ${\gamma _{\text{d}}}$ →0时

${{G} _{{\text{dmax}}}} = \frac{1}{{a} } \text{；}$

(4)

当式（2）中 ${\gamma _{\text{d}}}$ →+∞时，得到

${\tau _{{\text{dult}}}} = \frac{1}{{b} } 。$

(5)

式中，G_dmax为最大动剪切模量， ${\tau _{{\text{dult}}}}$ 为最终动应力幅值。由式（3）可以得到 ${\lambda _{\rm{max}}}$ ，由式（4）可以得出不同温度下的G_dmax。不同频率下G_dmax及 ${\lambda _{\rm{max}}}$ 如表 4所示。

表 4 不同频率及围压下最大动剪切模量及阻尼比

Table 4. Maximum dynamic shear modulus and damping ratios under different frequencies and confining pressures

参数	频率/Hz			围压/kPa
参数	1	3	5	50	100	150
G_dmax/MPa	98.81	130.89	177.31	69.11	98.81	125.31
λ_max	0.46	0.39	0.36	0.55	0.46	0.42

下载: 导出CSV

| 显示表格

曲线变化的原因与试样中土粒重新排列有关，较低剪应变水平时，石灰与土体形成稳定结构使得土体变形较小，动剪切模量和阻尼比变化缓慢。较高剪应变水平时，石灰与土体形成的稳定结构逐渐破坏，土粒重新排列，黏滞性水膜在荷载作用下发生流动，产生较大变形，动剪切模量和阻尼比迅速变化。对于不同频率而言，频率增大使得加载速率提高，相同加载周次中塑性变形积累速度变慢，达到同样塑性变形所需动应力增加。同时，试样中黏滞性水膜流动和重新排列效应减弱，土粒重组时间减少，塑性变形相应减弱，塑性变形耗能降低，表现出动剪切模量增加，阻尼比降低的特性。

2.2 不同围压下动力参数的变化

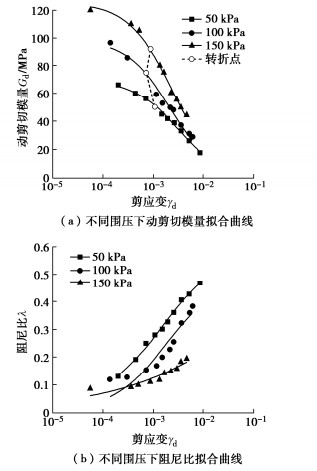
未冻融，20℃，1Hz加载的石灰改良盐渍土动剪切模量在不同围压下的变化情况如图 4（a）所示，不同围压曲线变化趋势与频率相同，围压增加，转折点动剪切模量增加，阻尼比下降。转折点动剪切模量增加84%，最小阻尼比降低0.05。围压增加，试样中土颗粒发生位移，孔隙得到填充，土体结构性得到增强，强度得到提升。不同围压下拟合曲线如图 4所示，拟合参数如表 3所示，不同围压下G_dmax及 ${\lambda _{\rm{max}}}$ 如表 4所示。

图 4 不同围压下动剪切模量及阻尼比拟合曲线

Figure 4. Fitting curves of dynamic shear modulus and damping ratio under different confining pressures

下载: 全尺寸图片幻灯片

由不同频率及围压下石灰改良盐渍土动剪切模量和阻尼比的拟合参数 ${\lambda _{\rm{max}}}$ ，得到最大阻尼比，并通过式（4）计算不同频率及围压下石灰改良盐渍土最大动剪切模量，如表 4所示。

2.3 温度对动力参数影响及温度修正系数

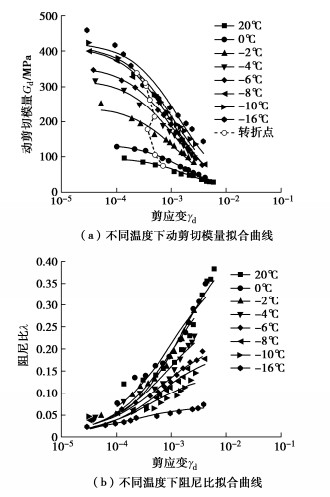
不同温度下的动剪切模量–剪应变，阻尼比–剪应变曲线同样按照式（1）~（3）进行拟合，拟合参数如表 5所示，拟合曲线见图 5。

表 5 不同温度下动剪切模量及阻尼比的拟合参数

Table 5. Fitting parameters of dynamic shear modulus and damping ratio under different temperatures

温度/℃	动剪切模量G_d			阻尼比 $\lambda$
温度/℃	a	b	R²	${\lambda _{\max }}$	c	n	R²
20	0.0101	4.7873	0.9865	0.4546	0.0025	0.6845	0.9183
0	0.0073	4.1682	0.9965	0.3928	0.0018	0.5971	0.9384
-2	0.0041	3.2572	0.9728	0.3718	0.0016	0.6851	0.9707
-4	0.0031	2.7513	0.9908	0.2818	0.0015	0.6153	0.9330
-6	0.0028	2.5054	0.9989	0.2170	0.0013	0.5750	0.9742
-8	0.0024	2.5351	0.9966	0.1915	0.0010	0.6831	0.9409
-10	0.0024	2.1925	0.9811	0.1441	0.0008	0.5857	0.9024
-16	0.0024	1.7242	0.9247	0.0700	0.0006	0.4172	0.9567

下载: 导出CSV

| 显示表格

图 5 不同温度下动剪切模量及阻尼比拟合曲线

Figure 5. Fitting curves of dynamic shear modulus and damping ratio under different temperatures

下载: 全尺寸图片幻灯片

由不同温度下石灰改良盐渍土动剪切模量和阻尼比的拟合参数 ${\lambda _{\rm{max}}}$ 得到最大阻尼比，并通过式（4）计算不同温度下石灰改良盐渍土最大动剪切模量，如表 6所示。

表 6 不同温度下最大动剪切模量及阻尼比

Table 6. Maximum dynamic shear modulus and damping ratios under different temperatures

温度/℃	G_dmax/MPa	${\lambda _{\rm{max}}}$
20	98.81	0.46
0	137.17	0.39
-2	242.13	0.37
-4	320.51	0.28
-6	357.14	0.22
-8	413.22	0.19
-10	414.94	0.14
-16	423.73	0.07

下载: 导出CSV

| 显示表格

随着温度的降低，动剪切模量增加，阻尼比降低。温度由20℃降低至-16℃，转折点动剪切模量增加263 MPa（75→338 MPa），阻尼比减小0.10。随着温度降低，土中水分不断结冰，土体结构更加致密使黏结力增大。抗动荷载能力及抗变形能力增加，动剪切模量增大，达到相同动应力幅值所需能量降低，阻尼比减小。

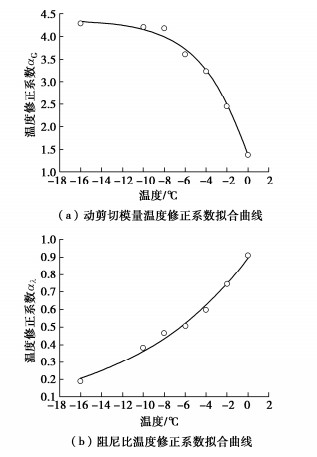
根据不同温度下动力参数试验结果，提出温度修正系数：

${G'_{\rm{dmax}}} = {\alpha _{\rm{G}}}{{G} _{\rm{dmax}}} \text{，}$

(6)

${\lambda '_{\rm{dmax}}} = {\alpha _\lambda }{\lambda _{\rm{max}}} 。$

(7)

式中， ${\alpha _{\rm{G}}}$ 为动剪切模量的温度修正系数， ${\alpha _\lambda }$ 为阻尼比的温度修正系数。基于孙锐等^[18]对于负温下的黏土动力参数预测公式，对 ${\alpha _G}$ 和 ${\alpha _\lambda }$ 进行拟合分析：

${\alpha _G} = {\alpha _1}\left( {\frac{{{{A} _1} - {{A} _2}}}{{1 + {{\text{e}}^{(T - {T_{\text{0}}})/{r_1}}}}} + {{A} _2}} \right) + {\alpha _2}({{y} _0} + {{A} _0}{e^{{{ - {T} } \mathord{\left/ {\vphantom {{ - {T} } {{{r} _2}}}} \right. } {{{r} _2}}}}}) \text{，}$

(8)

${\alpha _\lambda } = {y_0} + {A'_0}{{\text{e}}^{{T \mathord{\left/ {\vphantom {T {{{r'}_2}}}} \right. } {{{r'}_2}}}}} 。$

(9)

拟合参数如表 7所示，拟合曲线如图 6所示。得到温度修正系数表达式为

$\begin{array}{c} {\alpha _G} = 0.53\left( {\frac{{2.76 + 0.29}}{{1 + {{\text{e}}^{{{\left( {T + 0.76} \right)} \mathord{\left/ {\vphantom {{\left( {T + 0.76} \right)} {2.26}}} \right. } {2.26}}}}}} - 0.29} \right) + \\ 0.66(4.48-3.12{\text{e}}^{-T/-4.32})\text{ }\text{，} \end{array}$

(10)

${\alpha _\lambda } = - 0.019 + 0.91{{\text{e}}^{{T \mathord{\left/ {\vphantom {T {11.42}}} \right. } {11.42}}}} 。$

(11)

表 7 温度修正系数的拟合参数

Table 7. Fitting parameters of temperature correction coefficient

A₁	A₂	T₀	r₁	A₀	y₀	r₂
2.76	-0.29	-0.76	2.26	-4.32	4.48	-3.12

${\alpha _1}$	${\alpha _2}$	R²	${y'_0}$	${A'_0}$	${r'_2}$	R²
0.53	0.66	0.991	-0.019	0.91	11.42	0.990

下载: 导出CSV

| 显示表格

图 6 动剪切模量和阻尼比温度修正系数拟合曲线

Figure 6. Fitting curves of temperature correction coefficient for dynamic shear modulus and damping ratio

下载: 全尺寸图片幻灯片

由图 6可知，温度修正系数转折点位于-6℃附近，T < -6℃时，温度修正系数下降缓慢；T > -6℃时，温度修正系数迅速下降。

2.4 冻融循环作用对动力参数影响及冻融修正系数

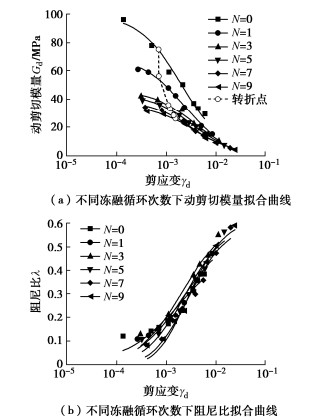
在不同冻融循环次数下，动剪切模量–剪应变、阻尼比–剪应变曲线按式（1）~（3）拟合，a₂，b₂，c₂，n₂为拟合参数，拟合参数如表 8所示，拟合曲线如图 7所示。

表 8 不同冻融循环次数动剪切模量及阻尼比的拟合参数

Table 8. Fitting parameters of dynamic shear modulus and damping ratio under different freeze-thaw cycles

冻融循环次数	动剪切模量G_d			阻尼比λ
冻融循环次数	a₂	b₂	R²	${\lambda _{\rm{max}}}$	c₂	n₂	R²
0	0.0102	4.7873	0.9865	0.4649	0.0025	0.6972	0.8884
1	0.0145	6.1150	0.9960	0.5675	0.0040	0.7006	0.9551
3	0.0214	6.1155	0.9984	0.6641	0.0049	0.6692	0.9631
5	0.0227	6.9325	0.9951	0.6827	0.0061	0.7094	0.9558
7	0.0262	7.8786	0.9953	0.7022	0.0075	0.7610	0.9514
9	0.0283	7.6030	0.9983	0.7124	0.0085	1.0048	0.9741

下载: 导出CSV

| 显示表格

图 7 不同冻融循环次数下动剪切模量及阻尼比拟合曲线

Figure 7. Fitting curves of dynamic shear modulus and damping ratio under different freeze-thaw cycles

下载: 全尺寸图片幻灯片

由不同冻融循环次数下石灰改良盐渍土动剪切模量和阻尼比的拟合参数 ${\lambda _{\rm{max}}}$ ，得到最大阻尼比，并通过式（4）计算不同冻融循环次数下石灰改良盐渍土最大动剪切模量，如表 9所示。

表 9 不同冻融循环次数下最大动剪切模量及阻尼比

Table 9. Maximum dynamic shear modulus and damping ratios under different freeze-thaw cycles

冻融循环次数	G_dmax/MPa	${\lambda _{\rm{max}}}$

0	98.81	0.47
1	70.08	0.57
3	46.53	0.66
5	43.80	0.68
7	39.26	0.70
9	35.65	0.71

下载: 导出CSV

| 显示表格

由图 7（a）可知，动剪切模量在冻融循环作用后显著下降，尤其是第3次冻融后，动剪切模量下降40 MPa（75→35 MPa），降幅约为47%。当冻融循环次数超过3次后，动剪切模量衰减趋于稳定。第9次冻融循环作用后，较高剪应变水平时，试件的动剪切模量衰减至较低数值，强度几乎损失殆尽。随着冻融循环作用次数的增加，阻尼比不断增大，3次冻融循环作用后，阻尼比变化不明显。

土体冻结伴随着盐胀作用，土体中孔隙增加。融化后土体中的孔隙仍然存在，石灰胶结土体的稳定结构受到一定程度的破坏，导致土体结构较冻融前更加松散。在动荷载作用下土体塑性变形增加，动剪切模量大幅降低。达到同样动应力幅值需要的能量增加使得阻尼比提升。随着冻融循环作用次数的增加，特别是冻融循环次数超过3次后，试样土体结构中孔隙大幅增加，石灰胶结土体的稳定结构遭到破坏。同时试样土体内的楔形力不断增长，内部的应力累计超过土体自身黏结力导致土体结构破坏，但由于没有来自外界的水分补充，这种破坏效应逐渐停止，动剪切模量降低到较低状态后趋于稳定。

根据不同冻融循环次数下动力参数试验结果，提出冻融修正系数：

${G'_{\rm{dmax}}} = {\beta _G}{{G} _{\rm{dmax}}} \text{，}$

(12)

${\lambda '_{\max }} = {\beta _\lambda }{\lambda _{\max }} \text{，}$

(13)

式中， ${\beta _{\rm{G}}}$ 为动模量的冻融修正系数， ${\beta _\lambda }$ 为阻尼比的冻融修正系数。

根据严晗等^[19]、张向东等^[20]提出的冻融修正系数公式，对本试验的冻融修正系数进行拟合分析，拟合公式为

${\beta _G} = {{a} _3}{{b} _3}{{\text{e}}^{\frac{{ - N}}{{{c_3}}}}} \text{，}$

(14)

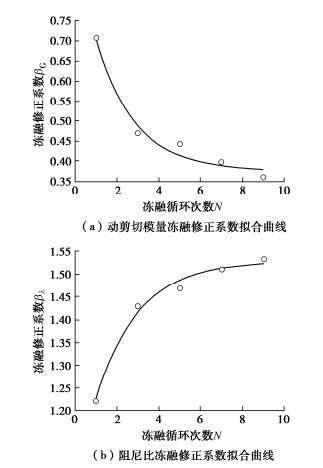
${\beta _\lambda } = {{a} _4} - {{b} _4}{e^{{c_4}N}} 。$

(15)

拟合参数如表 10所示，拟合曲线如图 8所示。

表 10 冻融循环修正系数的拟合参数

Table 10. Fitting parameters of freeze-thaw cycle correction coefficient

${a_3}$	${b_3}$	${c_3}$	${R^2}$
0.56	1.87	0.38	0.991

${a_4}$	${b_4}$	${c_4}$	${R^2}$
1.53	-0.50	0.65	0.980

下载: 导出CSV

| 显示表格

图 8 动剪切模量和阻尼比冻融修正系数拟合曲线

Figure 8. Fitting curves of freeze-thaw correction coefficient for dynamic shear modulus and damping ratio

下载: 全尺寸图片幻灯片

得到冻融修正系数：

${\beta _G} = 0.56 - 1.87{{\text{e}}^{\frac{{ - N}}{{0.38}}}} \text{，}$

(16)

${\beta _\lambda } = 1.53 - 0.50{{\text{e}}^{0.65N}} 。$

(17)

由图 8可知，冻融转折点为第3次冻融循环，第3次冻融循环之前，曲线变化急促，当冻融循环次数大于3时，冻融修正系数曲线趋于平缓。这也同样印证冻融循环作用使得土体内水分冻结，融化后对土体产生不可逆破坏，土体动剪切模量大幅下降。由于缺少外界水分的补充，在冻融循环3次之后，动剪切模量修正系数的衰减趋于停止。

3. 结论

针对季冻区低温冻融环境下，采用GDS冻土动三轴试验系统，对不同试验温度、不同冻融循环次数下的石灰改良盐渍土的动力参数进行研究，并提出两种修正系数，根据建立的动力参数的预测模型，为工程设计中提供所需的动力参数，同时对长期冻融循环劣化作用后石灰改良盐渍土路基稳定性分析提供参考。

（1）随剪应变的增加石灰改良盐渍土的动剪切模量不断衰减，存在动剪切模量转折点，经过转折点后动剪切模量衰减速度加快；阻尼比随剪应变的增加而增加。动荷载频率及围压增加，石灰改良盐渍土的动剪切模量增加，阻尼比降低。

（2）温度降低，石灰改良盐渍土动剪切模量转折点不断提高，阻尼比下降。提出温度修正系数，对不同温度下动剪切模量和阻尼比进行修正，并对温度修正系数进行曲线拟合，基于此提出温度修正系数公式，该系数在-6℃存在转折点，转折点后低温影响逐渐减弱。

（3）冻融1次后，动剪切模量转折点大幅降低，冻融3次后，动剪切模量转折点进一步降低并趋于稳定，随着冻融循环次数增加阻尼比小幅上升。提出冻融修正系数，对不同冻融循环次数下动剪切模量和阻尼比进行修正，并对冻融修正系数进行曲线拟合，拟合曲线在3次冻融循环处存在转折点，冻融循环的劣化作用存在极限，转折点后影响变小直至忽略不计。提出冻融循环修正系数，基于未冻融动力参数对不同冻融次数下动力参数进行预测。

图 1 拱坝坝肩多块体滑动模式示意图

Figure 1. Sketch map of multi-block sliding mode in abutment of arch dam

下载: 全尺寸图片幻灯片

图 2 作用在块体上的力

Figure 2. Forces applied on one block of sliding mass

下载: 全尺寸图片幻灯片

图 3 多块体滑动模式的速度场

Figure 3. Velocity fields of multi-block sliding mode

下载: 全尺寸图片幻灯片

图 4 三维楔体滑动算例示意图

Figure 4. Sketch map of 3D wedge example

下载: 全尺寸图片幻灯片

图 5 分界面J₃的摩擦角φ_j与楔体安全系数F_s的关系曲线

Figure 5. Relationship between friction angle of interface J₃ and F_s of wedge

下载: 全尺寸图片幻灯片

图 6 分界面J₃的摩擦角取值不同时，各块体滑动方向的计算结果

Figure 6. Results of sliding direction of each block under different friction angles of interface J₃

下载: 全尺寸图片幻灯片

图 7 小湾拱坝坝址区地形拟合图

Figure 7. Topographic map of dam site of Xiaowan arch dam

下载: 全尺寸图片幻灯片

图 8 左右坝肩台阶状滑面示意图

Figure 8. Sketch map of stepped slip surface of left and right abutments

下载: 全尺寸图片幻灯片

图 9 左右坝肩潜在滑体的空间形状

Figure 9. Schematic view of potential sliding mass of left and right abutments

下载: 全尺寸图片幻灯片

图 10 左右坝肩台阶状滑面的空间形状

Figure 10. Schematic view of stepped slip surface of left and right abutments

下载: 全尺寸图片幻灯片

图 11 台阶高度h不同取值时滑体中各块体的滑动方向示意图

Figure 11. Schematic map of sliding direction of each block in sliding mass under different step heights h

下载: 全尺寸图片幻灯片

表 1 多块体滑动问题中的未知量与已知条件数目统计结果

Table 1 Statistical results of number of unknowns and equations in multi-block sliding problem

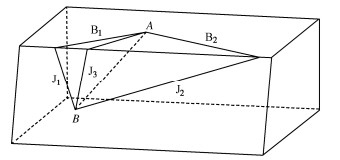
滑动模式	未知量	数目	已知方程	数目
单滑面滑动模式	底滑面的法向力	n	各块体沿x轴的静力平衡	n
	分界面的法向力	n-1	各块体沿y轴的静力平衡	n
	底滑面的单位速度矢量	n	各块体沿z轴的静力平衡	n
	分界面的单位速度矢量	n-1	相邻块体之间满足位移协调条件	n-1
	安全系数F	1	—	—
	合计	4n-1	合计	4n-1
双滑面滑动模式	底滑面的法向力	n	各块体沿x轴的静力平衡	n
	侧滑面的法向力	n	各块体沿y轴的静力平衡	n
	分界面的法向力	n-1	各块体沿z轴的静力平衡	n
	分界面的单位速度矢量	n-1	相邻块体之间满足位移协调条件	n-1
	安全系数F	1	—	—
	合计	4n-1	合计	4n-1

下载: 导出CSV

表 2 三维楔体算例的几何参数与强度参数表

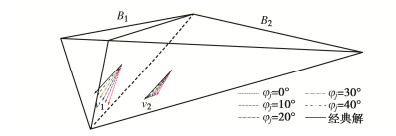
Table 2 Geometric and strength parameters of 3D wedge example

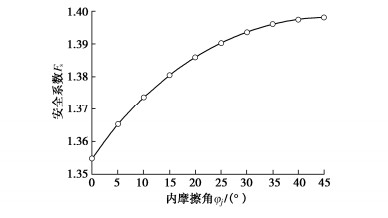
面类型	倾角/(°)	倾向/(°)	内摩擦角φ/(°)	黏聚力c /kPa
左滑面J₁	60	105	20	30
右滑面J₂	25	195	30	20
坡顶面	0	180	—	—
坡面	70	160	—	—
注：楔体高度H=100 m，岩体重度 $\gamma$ =26 kN/m³。

下载: 导出CSV

表 3 坝址区发育的顺河向结构面产状分布

Table 3 Occurrence distribution of joints along river developed in dam site

结构面类型	高程/m	左岸	右岸
陡倾角结构面	950.0~1245	N5°E/NW∠90°	N5°W/NE∠90°
中缓倾角结构面	1050~1240	N5°E/NW∠40°	N5°W/NE∠40°
	975~1050	N5°E/NW∠26°	N5°W/NE∠26°
	950.5~975	N5°E/NW∠7°	N5°W/NE∠7°

下载: 导出CSV

表 4 岩桥与结构面的抗剪强度参数及连通率计算参数

Table 4 Strength parameters of rock bridge, joints and persistence ratio adopted in stability analysis

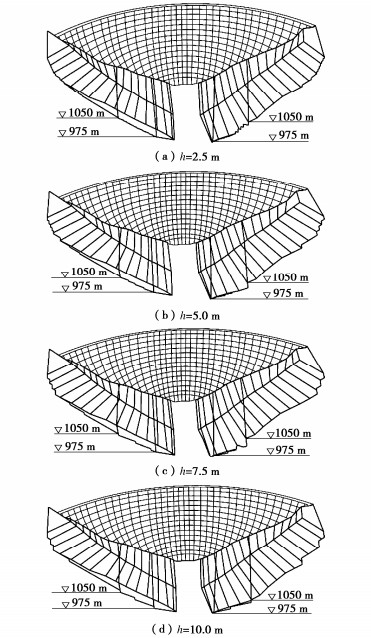
材料分区	强度参数	岩桥	SN向陡倾角结构面	顺坡向中缓倾角结构面
Ⅰ+Ⅱ类	f′	1.5	0.63	0.7
	c/MPa	2	0.08	0.1
	连通率k	—	0.5	0.3
Ⅲ类	f′	1.1	0.51	0.55
	c/MPa	0.8	0.06	0.07
	连通率k	—	0.7	0.6
Ⅳ_a类	f′	1	0.47	0.5
	c/MPa	0.6	0.05	0.05
	连通率k	—	0.7	0.7

下载: 导出CSV

表 5 左右坝肩各滑体的抗滑稳定分析成果

Table 5 F_s of sliding mass of left and right abutments

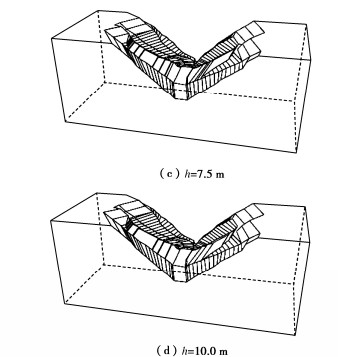
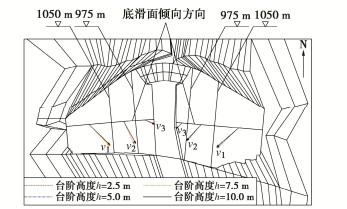
位置	台阶高度h/m
位置	2.5	5.0	7.5	10.0
左坝肩	4.07	4.05	3.97	3.96
右坝肩	3.89	3.84	3.80	3.77

下载: 导出CSV

参考文献(25)

[1]	李瓒, 陈兴华, 郑建波, 等. 混凝土拱坝设计[M]. 中国电力出版社, 2000. LI Zan, CHEN Xin-hua, ZHENG Jian-bo, et al. Concrete Arch Dam Design[M]. Beijing: China Electric Power Press, 2000. (in Chinese)
[2]	Federal Energy Regulatory Commission. Engineering Guidelines for the Evaluation of Hydropower Projects, Chapter 11: Arch Dams[S]. Division of Dam Safety and Inspections Washington, DC 20426. 1999.
[3]	朱伯芳, 高季章, 陈祖煜, 等. 拱坝设计与研究[M]. 中国水利水电出版社, 2002. ZHU Bo-fang, GAO Ji-zhang, CHEN Zu-yu, et al. Design and research for concrete arch dams[M]. China WaterPower Press, 2002. (in Chinese)
[4]	潘家铮. 建筑物的抗滑稳定和滑坡分析[M]. 北京: 水利出版社, 1980. PAN Jia-zheng. Stability Analysis of Building Structures and Landslides[M]. Beijing: China Water Conservancy Press, 1980. (in Chinese)
[5]	WANG R K. Key technologies in the design and construction of 300 m ultra-high arch dams[J]. Engineering, 2016, 2(3): 350–359. doi: 10.1016/J.ENG.2016.03.012
[6]	KOTTENSTETTE J T. Block theory techniques used in arch dam foundation stability analysis[J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(3/4): 573–578.
[7]	GOODMAN R E, POWELL C. Investigations of blocks in foundations and abutments of concrete dams[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(2): 105–116. doi: 10.1061/(ASCE)1090-0241(2003)129:2(105)
[8]	MIRZABOZORG H, VARMAZYARI M, HOSEINI M, et al. A comparative study of rock wedge stability of an arch dam abutment subjected to static and seismic loading[J]. Soil Mechanics and Foundation Engineering, 2015, 52(5): 292–300. doi: 10.1007/s11204-015-9344-6
[9]	宋战平, 李宁, 陈飞熊. 高拱坝坝肩裂隙岩体的三维非线性抗震稳定性分析[J]. 岩土工程学报, 2004, 26(3): 361–366. doi: 10.3321/j.issn:1000-4548.2004.03.013 SONG Zhan-ping, LI Ning, CHEN Fei-xiong. Three dimensional nonlinear seismic stability analysis of abutment jointed rock mass of high arch dam[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(3): 361–366. (in Chinese) doi: 10.3321/j.issn:1000-4548.2004.03.013
[10]	YU X, ZHOU Y F, PENG S Z. Stability analyses of dam abutments by 3D elasto-plastic finite-element method: a case study of Houhe gravity-arch dam in China[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(3): 415–430. doi: 10.1016/j.ijrmms.2005.01.001
[11]	刘喜康, 张建海, 赵文光. 基于动力有限元分析的任意滑块稳定分析方法[J]. 岩土工程学报, 2013, 35(增刊2): 363–368. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2063.htm LIU Xi-kang, ZHANG Jian-hai, ZHAO Wen-guang. Stability analysis method for arbitrary slip block based on dynamic finite element method[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 363–368. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2063.htm
[12]	郭明伟, 葛修润, 李春光, 等. 边坡和坝基抗滑稳定分析的三维矢量和法及其工程应用[J]. 岩石力学与工程学报, 2010, 29(1): 8–20. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201001001.htm GUO Ming-wei, GE Xiu-run, LI Chun-guang, et al. Three-dimensional vector sum method employed in slope and dam foundation stability analyses and its applications to practical engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(1): 8–20. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201001001.htm
[13]	徐卫亚, 狄圣杰, 郑文棠, 等. 白鹤滩水电站上坝线左拱座楔形体安全性能分析[J]. 岩石力学与工程学报, 2011, 30(5): 910–916. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201105007.htm XU Wei-ya, DI Sheng-jie, ZHENG Wen-tang, et al. Safety performance analysis of rock wedges under left skewback of upstream dam line in Baihetan hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(5): 910–916. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201105007.htm
[14]	肖珍珍, 王登银, 陈建叶, 等. 碾压混凝土高拱坝坝肩稳定及坝体开裂静动力分析[J]. 岩土力学, 2015, 36(12): 3541–3547, 3575. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201512026.htm XIAO Zhen-zhen, WANG Deng-yin, CHEN Jian-ye, et al. Static and dynamic analyses of abutment stability and dam cracking of a roller-compacted concrete high-arch dam[J]. Rock and Soil Mechanics, 2015, 36(12): 3541–3547, 3575. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201512026.htm
[15]	张泷, 刘耀儒, 杨强, 等. 杨房沟拱坝整体稳定性的三维非线性有限元分析与地质力学模型试验研究[J]. 岩土工程学报, 2013, 35(增刊1): 239–246. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S1040.htm ZHANG Long, LIU Yao-ru, YANG Qiang, et al. Global stability of Yangfanggou Arch Dam by 3D nonlinear FEM analysis and geomechanical model tests[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S1): 239–246. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S1040.htm
[16]	杨宝全, 张林, 陈媛, 等. 锦屏一级高拱坝坝基结构面弱化效应研究及坝肩稳定性分析[J]. 水利学报, 2016, 47(7): 907–915. https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201607010.htm YANG Bao-quan, ZHANG Lin, CHEN Yuan, et al. Study on weakening effect of structural plane and stability analysis of Jinping I high arch dam[J]. Journal of Hydraulic Engineering, 2016, 47(7): 907–915. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SLXB201607010.htm
[17]	混凝土拱坝设计规范: DL/T 5346—2006[S]. 2006. Design Specification for Concrete Arch Dams: DL/T 5346—2006[S]. 2006. (in Chinese)
[18]	混凝土拱坝设计规范: SL 282—2018[S]. 2018. Design Specification for Concrete Arch Dams: SL 282—2018[S]. 2018. (in Chinese)
[19]	任青文. 拱坝坝肩稳定分析中非线性方程组的线性化解法[J]. 河海大学学报, 1991, 19(3): 120–124. doi: 10.3321/j.issn:1000-1980.1991.03.018 REN Qing-wen. Linearized solution to the nonlinear equations in stability analysis for arch dam abutment[J]. Journal of Hohai University, 1991, 19(3): 120–124. (in Chinese) doi: 10.3321/j.issn:1000-1980.1991.03.018
[20]	陈祖煜, 汪小刚, 杨健, 等. 岩质边坡稳定分析-原理·方法·程序[M]. 北京: 中国水利水电出版社, 2005. CHEN Zu-yu, WANG Xiao-gang, YANG Jian, et al. Rock Slope Stability Analysis-Theory, Method and Programs[M]. Beijing: China WaterPower Press, 2005. (in Chinese)
[21]	陈祖煜, 弥宏亮, 汪小刚. 边坡稳定三维分析的极限平衡方法[J]. 岩土工程学报, 2001, 23(5): 525–529. doi: 10.3321/j.issn:1000-4548.2001.05.001 CHEN Zu-yu, MI Hong-liang, WANG Xiao-gang. A three- dimensional limit equilibrium method for slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(5): 525–529. (in Chinese) doi: 10.3321/j.issn:1000-4548.2001.05.001
[22]	李同录, 王艳霞, 邓宏科. 一种改进的三维边坡稳定性分析方法[J]. 岩土工程学报, 2003, 25(5): 611–614. doi: 10.3321/j.issn:1000-4548.2003.05.020 LI Tong-lu, WANG Yan-xia, DENG Hong-ke. An improved method for three-dimensional slope stability analysis[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(5): 611–614. (in Chinese) doi: 10.3321/j.issn:1000-4548.2003.05.020
[23]	卢坤林, 朱大勇, 甘文宁, 等. 一种边坡稳定性分析的三维极限平衡法及应用[J]. 岩土工程学报, 2013, 35(12): 2276–2282. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201312023.htm LU Kun-lin, ZHU Da-yong, GAN Wen-ning, et al. 3D limit equilibrium method for slope stability analysis and its application[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(12): 2276–2282. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201312023.htm
[24]	HOEK E, BRAY J D. Rock Slope Engineering[M]. Boca Raton: CRC Press, 1981.
[25]	中国水电西北勘测设计研究院. 特高拱坝枢纽分析与重点问题研究[M]. 北京: 中国电力出版社, 2004. Northwest Investigation Design and Research Institute. Analysis and studies on project and major technical issues of Super-High Arch dams[M]. Beijing: China Electric Power Press, 2004. (in Chinese)

施引文献(10)

期刊类型引用(8)

1.	王炜，窦锦钟，袁青云，韩磊，孙旻. 抽水蓄能电站绿色施工技术. 施工技术(中英文). 2024(18): 129-133+153 . 百度学术
2.	张昕阳，申玉生，常铭宇，王浩鱇，潘笑海，王岩岩. 基于GA-BP神经网络的隧道围岩相似材料配合比设计. 现代隧道技术. 2024(06): 82-91 . 百度学术
3.	廖光明. 胶凝砂砾石坝抗滑稳定可靠度分析方法研究. 湖南水利水电. 2023(02): 22-25 . 百度学术
4.	丁泽霖，王肖楠，张宏洋，王婧，包闯. 复杂地基重力坝与胶凝砂砾石坝变形破坏对比分析. 工程科学与技术. 2023(04): 197-206 . 百度学术
5.	杨锐婷，万露. 折线形胶凝砂砾石坝三维静力有限元分析. 吉林水利. 2023(07): 14-20 . 百度学术
6.	丁泽霖，徐良杰，王肖楠. 基于多元优化的百米级胶凝砂砾石坝设计方法. 水力发电学报. 2023(12): 119-131 . 百度学术
7.	杨玉坚，刘艳华，陈雪冬. 胶凝砂砾石坝导流设计方法研究. 水利建设与管理. 2023(S1): 35-39 . 百度学术
8.	刘欢. 基于AutoBANK的流固耦合场沙田水库坝体渗流变形特征研究. 水利科学与寒区工程. 2022(08): 26-30 . 百度学术