软土地区基坑工程变形控制方法及工程应用

郑刚

doi:10.11779/CJGE202201001

软土地区基坑工程变形控制方法及工程应用 English Version

郑刚^{1, 2, 3,}

1.
天津大学建筑工程学院, 天津 300072
2.
滨海土木工程结构与安全教育部重点实验室(天津大学), 天津 300072
3.
天津大学水利工程仿真与安全国家重点试验室, 天津 300072

基金项目:

国家自然科学基金重点项目 41630641

详细信息

作者简介:
郑刚(1967—)，男，博士，教授，博士生导师，主要从事城市岩土工程的教学与科研工作。E-mail: zhenggang1967@163.com

中图分类号: TU470
计量
- 文章访问数: 1144
- HTML全文浏览量: 123
- PDF下载量: 864
出版历程
- 收稿日期: 2021-11-30
- 网络出版日期: 2022-09-22
- 刊出日期: 2021-12-31

Method and application of deformation control of excavations in soft ground

ZHENG Gang^{1, 2, 3,}

1.
School of Civil Engineering, Tianjin University, Tianjin 300072, China
2.
Key Laboratory of Coast Civil Structure Safety, Ministry of Education(Tianjin University)
3.
State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China

摘要

摘要: 基坑变形控制是软土地区基坑工程的核心内容，不仅与自身工程安全密切相关，更涉及到对周边环境的影响。随着城市地上、地下各类建（构）筑物越来越密集，基坑工程施工产生的变形对环境影响的控制愈加成为基坑工程的焦点问题。首先，从基坑施工全过程控制的视角，分析了基坑施工全过程各阶段的变形特征、机理以及对环境的影响。进而，将基坑变形及其对环境影响的控制划分为“基于基坑支护体系的变形控制”和“基于邻近基坑保护对象的变形控制”两类方法。针对基于邻近基坑保护对象的变形控制，提出了不是基于对基坑支护体系，而是直接着眼于保护对象的变形主动控制理论，通过对关键区域土体的应力和变形的控制，实现对保护对象的测控一体化靶向控制。此外，提出了基坑无支撑支护理论并发展了一系列软弱土地区基坑绿色无支撑支护技术，实现了在较大的深度条件下也可进行坑无支撑支护设计。通过“基坑施工全过程控制”“基坑变形主动控制理论”“基坑无支撑支护控制体系”的变形控制理论及工程应用，努力推动基坑工程变形控制向“高效、智能、绿色、低碳”方向发展。
- 基坑工程 /
- 变形控制 /
- 全过程 /
- 无支撑支护 /
- 主动控制
Abstract: The main task of excavations in soft ground is the deformation control, which is closely rated to their safety and environmental impact. With the increase of the buildings and structures in the urban areas, the construction-induced deformation has become the focus of the excavations. The characteristics, mechanism and environmental impact of the deformation caused by each excavation phase are analyzed in a view of the whole-process control. Furthermore, the control methods for the deformation and environmental impact of the excavations are classified into two types, i.e., the control based on the retaining system of the excavations and that based on the protected objects adjacent to them. For the latter type, the active control theory is proposed focusing on the deformation of the protected objects instead of the retaining system. This active targeting technology integrated with the measurement and control for the protected objects is realized by controlling the stress and deformation of the key zone. Finally, the strut-free retaining theory is proposed and a series of strut-free retaining technologies are developed for the excavations in soft ground. The design of strut-free retaining for the excavations with relatively large depth can be realized using these technologies. The theories and applications of the whole-process control, the active control and the strut-free retaining system promote the deformation control of the excavations towards the efficient, intelligent, green and low-carbon aim.
- excavation /
- deformation control /
- whole process /
- strut-free retaining /
- active control

HTML全文

0. 引言

浅基础地基承载力计算是土力学中的一个基本课题，几乎所有土力学教科书中均对有关理论和方法有专章予以介绍。业内不少人士得到的印象是，地基承载力的理论及计算方法已经难以再行改进，而实际并非如此。

目前，针对非偏心竖向荷载下条形基础广泛采用的地基承载力计算公式有3项：cN_c，qN_q和0.5 $\gamma$ BN_γ，分别对应于黏聚力c、埋深相应的基础周围超载q以及地基土重度 $\gamma$ 或基础宽度对承载力的贡献，N_c，N_q及N_γ是仅与土的摩擦角φ有关的承载力系数^[1-3]，对其他基础形状、倾斜荷载等情况，再对上述每一项乘以相应的修正系数^[2]。在不计地基土重度的情况下，前两个承载力系数N_c，N_q分别由Prandtl和Reissner给出，且在理论上是精确的^[1-3]，而当考虑地基土重度的影响时问题便复杂得多。

太沙基于1943年最早考虑地基土重度进行条形基础下地基承载力的计算^[1]，他认为此时基底与土之间存在的摩擦及黏着作用将在基底下方产生一个三角形弹性核，进而通过分析给出地基承载力的3项，其中的3个承载力系数仍然只是内摩擦角的函数，但前2个系数参考Prandtl和Reissner所给相应土压力的解给出了计算式，第3个系数N_γ只能给出数值解，所以太沙基解一般是以图表形式给出。因问题复杂，太沙基解的一个重要近似处理是，在求解第3项时采用了与前两项不同的破坏滑移面，这就决定了这解答是有误差的，且有些情况下误差可达30%（见本文第3节）。

因此，在太沙基之后很多研究者对地基承载力的计算进行研究，给出各不相同的承载力系数N_γ。较著名的解有Meyerhof给出的N_γ为(N_q-1)tan(1.4φ)^[3]；Vesic^[4]在Caquot和Kerisel工作基础上给出的2(N_q+ 1)tanφ；Hansen^[5]则给出1.8(N_q-1)tanφ，后又将系数由1.8改为1.5，而Verruijt则认为这系数取2.0在总体上更精确些^[6]。对前两个承载力系数多数研究者采用Prandtl和Reissner针对无刚性核情况下提出的解。由这些解相互之间的显著差异可见，地基承载力的计算还很值得研究。所以，直至目前仍有不少研究者讨论地基承载力第3项的承载力系数计算，Diaz-Segura^[7]曾比较了60篇文献给出的各不相同但均与上述类似的承载力系数N_γ，发现差异明显。

由上述分析可见，目前地基承载力不能准确计算的根本原因，是对极限荷载计算这一塑性力学问题采用了叠加计算，亦即对于地基承载力计算式中本非相互独立的三部分按相互独立进行计算。近年来一些研究者注意到这一点，采用不同的思路研究系数N_γ的计算，考虑多个参数对N_γ的影响。文献[8]较早进行了这方面的研究，文献[9]则在综述前人研究的基础上，采用数值滑移线法进行计算拟合给出N_γ的近似计算式。

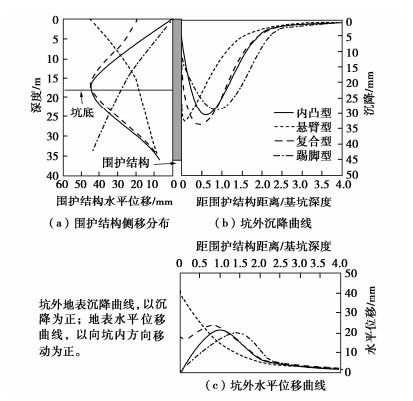
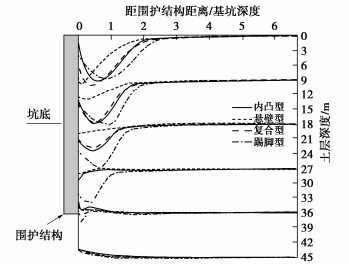
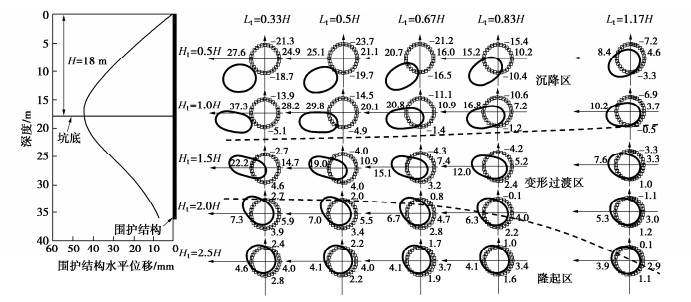
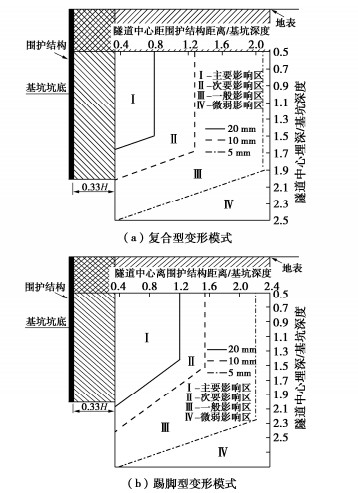
本文摒弃叠加思路，统一考虑地基及基础的有关参数，力求给出综合考虑各参数影响的高精度计算公式。为此，首先深入分析地基承载力的内在机理，揭示了与埋深相应的超载q可以等效转换为黏聚力来考虑其对地基承载力的贡献，而地基土的重度可等效转换为随深度线性增大的黏聚力，进而利用本课题组此前针对饱和黏性土地基承载力的计算，考虑其不固结不排水强度随深度线性增大的情况所提出的计算方法^[10-11]。针对承受非偏心竖向荷载的条形基础下地基发生整体剪切破坏时的承载力问题，构建了一个将经典公式的三项统一为一个整体的计算公式，克服了以往计算公式的理论缺陷，显著改进了地基承载力的计算精度。

对于地基土相对较软或基础埋深相对较大情况下地基的局部剪切破坏，对于其他形状的基础、倾斜荷载等情况，也建议了利用本文公式进行计算的方法。

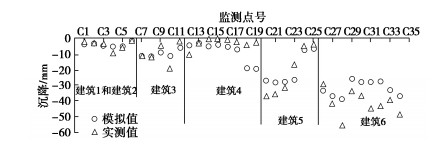
本文除给出地基承载力计算的较为完善的公式之外，重要的是深入阐释了地基承载的机理，提出一种全新的计算思路，这对有关研究同样有重要参考价值。

1. 地基土重度与地基承载力的内在联系

本节深入分析地基承载力的机理，揭示埋深相应超载q与地基土重度作用的实质。

首先，考察埋深相应的基础周围超载q的作用与黏聚力c的联系。实际上，由于Prandtl与Reissner给出的解是精确的，q与c的关系自然应含于他们所给计算式之中。由Reissner所给地基承载力系数N_q与Prandtl地基承载力系数N_c的关系有

$q{N_q} = q({N_c}\tan \varphi + 1) = q\tan \varphi {N_c} + q 。$

(1)

考察式（1）不难得出以下认识：q对承载力的贡献首先是使地基承载力提高一倍q值，进而在φ > 0的情况下又使地基承载力提高qtan φ N_c。这意味着qtanφ在承载力的计算中可以与同值的黏聚力等效，而超载q使地基承载力即便在φ=0时也会提高一倍q值。其力学机理按笔者的理解是，基础周围的地面超载与基底压力中等于q的部分共同构成满布于地基顶面的均布荷载，这均布荷载显然不会使地基破坏，而在φ > 0时，又进一步按黏聚力等同于qtanφ提高地基承载力。由于Prandtl和Reissner给出的承载力系数N_c和N_q在理论上是精确的，又按太沙基所给N_c和N_q的关系，同样可以得出式（1），所以上述推理的结论是肯定的，同时也回答了为什么N_q的下限为1。

在理解了q的上述本质作用之后，进一步深入分析则不难理解土体重度 $\gamma$ 的作用与黏聚力的等效作用。从基底往下任一深度z，其下土层所受到的满布压力在超载q之外又增加 $\gamma z$ ，按上段的论证可理解这相当于等效黏聚力增大 $\gamma z\tan \varphi$ ，这样 $\gamma \tan \varphi$ 则等同于黏聚力随深度的增大率。这一理解在地基承载力计算中的合理性和正确性，将由下面给出的计算对比进一步予以证实。

为验证土体重度 $\gamma$ 与黏聚力随深度增大率的等效性，这里采用基于极限分析上、下限定理的有限元极限分析这一精细数值方法^[12-13]进行如下两种计算对比：一计算中照常输入地基土强度指标c、φ及重度 $\gamma$ 进行地基承载力计算，而在另一计算中将土体重度 $\gamma$ 设为0，同时取地基土的黏聚力为c+ $\gamma z\tan \varphi$ ，亦即黏聚力从基底往下随深度的增长率为 $\gamma \tan \varphi$ 。所完成的大量计算表明，两套输入参数下的有限元极限分析结果完全相同。计算中分别按基底光滑和粗糙进行计算，也就是假定基底与其下土体间可以相对滑动和不可相互滑动来进行计算。为节省篇幅，表 1仅列出基底粗糙情况下部分计算给出的破坏滑移面深度及地基承载力值，可见两种参数下的计算结果几乎没有差异，这就又从数值计算方面证实了两者的精确等价。

表 1 基底粗糙时土体重度γ与黏聚力随深度增大率的等效性验证

Table 1. Verification of equivalence between γ and the rate of cohesion increase with depth under rough footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	滑移面深度/m		地基承载力/kPa
算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	原模型	重度等效模型	原模型	重度等效模型
1	5	10	20	3	0	1.91	1.94	77.4	77.3
2	5	10	20	6	0	3.32	3.32	87.2	87.2
3	10	10	10	6	20	4.22	4.22	167.7	167.8
4	20	5	20	6	0	3.77	3.77	309.0	309.0
5	30	0	20	6	20	5.82	5.82	1509.2	1509.5
6	40	0	20	6	0	7.76	7.76	5107.1	5104.9

下载: 导出CSV

| 显示表格

2. 地基承载力计算的统一公式

2.1 总体思路

这里首先考虑非偏心竖向荷载下条形基础的地基承载力问题。由第1节的分析可知，与基础埋深对应的基础周边超载q的作用，除首先将地基承载力提高1倍q外，在土的内摩擦角大于零时另有与 $q\tan \varphi$ 等值的黏聚力作用，而地基土重度 $\gamma$ 的作用则等价于黏聚力随深度的增长率 $\gamma \tan \varphi$ 。这样，借鉴此前针对饱和黏性土地基在不排水强度随深度线性增大情况下承载力计算方法的思路，此时的地基承载力同样可取一半滑移面深度处的黏聚力乘以与黏聚力对应的承载力系数N_c，并考虑滑移面形状变化引入一修正系数进行计算，亦即可给出如下形式的计算公式：

${p_{\text{u}}} = {\text{(}}c{\text{ + }}q\tan \varphi {\text{ + }}0.5\beta \gamma \tan \varphi {Z_{\max }}){N_c}{\text{ + }}q \text{，}$

(2)

式中，Z_max为滑移面最大深度， $\beta$ 为考虑滑移面形状变化对地基承载力系数影响的修正系数。这样式（2）右端的前一项近似是滑移面平均深度处的等效黏聚力与Prandtl地基承载力系数N_c的乘积，后一项为单独列出的基础周围超载q对地基承载力的最低贡献。

式（2）是统一考虑基础宽度B、地基土强度指标c与φ、基础埋深对应的基础周围超载q以及地基土重度γ作用的地基承载力计算公式。它没有叠加计算的理论缺陷，如能较好确定其滑移面的最大深度Z_max及滑移面形状修正系数β，则可得到计算精度显著改善的计算结果。随后的计算对比可以证实这理论的正确。

2.2 表征等效黏聚力深度增长率的无量纲参数

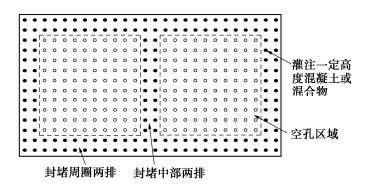
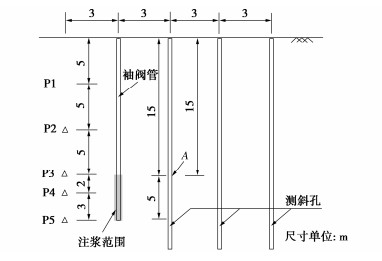
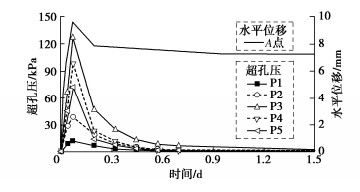
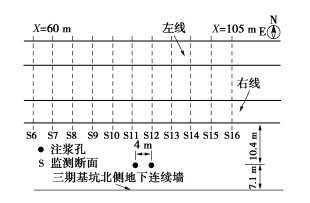
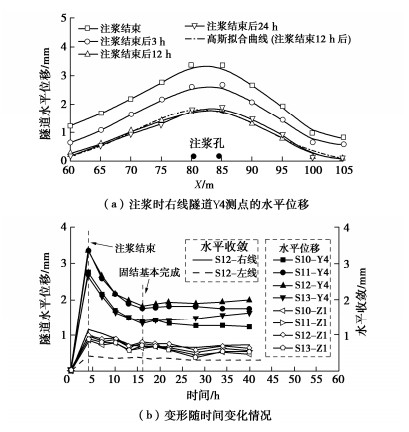
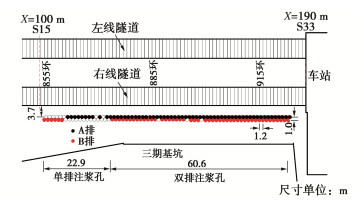
显然，按式（2）计算地基承载力的关键之一是确定地基破坏时的滑移面深度Z_max。据力学基本原理，对于诸如地基承载力之类的极限荷载问题，极限荷载的大小及相应的滑移面深度等与材料的刚度参数无关，而只与材料的强度及地基基础的几何参数等有关。将这里所考虑的地基在强度特性本质方面与Prandtl- Reissner地基比较可见，这里地基的不同点仅仅是“黏聚力”随深度线性增大，因为地基土重度的作用可等效视为黏聚力的深度增长率。而对于Prandtl和Reissner所考虑的地基，由其所给滑移线形状不难得到滑移面最大深度的计算式。所以这里确定滑移面深度的思路是在Prandtl-Reissner滑移面深度的基础上考虑黏聚力随深度增大予以修正。而黏聚力随深度增大这一特性应可以也应该采用一个无量纲的相对增长率来表征，也就是应采用等效黏聚力在一定深度上的增加值与其稳定值的比来表征。根据所有这些深度理论思考，建议取下式定义的无量纲参数：

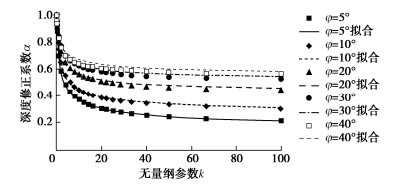
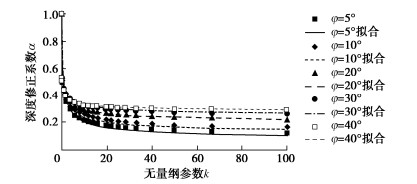
$k{\text{ = }}\frac{{B\gamma \tan \varphi }}{{c + q\tan \varphi }} 。$

(3)

式（3）中，分子是从基底往下一倍基础宽度的深度处等效黏聚力的增加值，而分母是等效黏聚力的稳定值。对此无量纲参数的正确性，由上述的严格论证可以理解是肯定的。但这里仍进一步通过大量有限元极限分析计算对其予以检验。计算结果表明，对任意可能的给定φ值，可以在可能的取值范围内任意变化B，c，q和 $\gamma$ ，但只要按式（3）计算的k值相同，实际滑移面深度与Prandtl-Reissner滑移面深度的比值是恒定的。将这一比值记为深度修正系数 $\alpha$ ，表 2，3分别列出基底粗糙和光滑时不同参数时的计算情况。

表 2 基底粗糙时无量纲参数k确定滑移面深度的检验

Table 2. Validation of dimensionless parameter k to determine depth of slip plane for rough footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	深度/m	深度修正系数α
1	10	10	20	3	0.0	1.06	1.95	0.73
2	10	0	20	3	56.7	1.06	1.95	0.73
3	10	10	10	6	0.0	1.06	3.91	0.73
4	10	10	20	6	56.7	1.06	3.91	0.73
5	20	20	10	6	0.0	1.09	5.51	0.79
6	20	0	10	6	54.9	1.09	5.51	0.79
7	20	10	20	6	0.0	4.37	4.36	0.63
8	20	0	20	6	27.5	4.37	4.36	0.63
9	20	5	20	6	0.0	8.74	3.77	0.54
10	20	10	20	12	0.0	8.74	7.54	0.54
11	30	5	10	6	0.0	6.93	5.95	0.63
12	30	5	20	6	8.7	6.93	5.95	0.63
13	30	0	20	6	0.0	无穷	4.66	0.49
14	30	0	20	12	0.0	无穷	9.33	0.49

下载: 导出CSV

| 显示表格

表 3 基底光滑时无量纲参数k确定滑移面深度的检验

Table 3. Validation of dimensionless parameter k to determine depth of slip plane for smooth footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	深度/m	深度修正系数α
1	10	10	20	3	0.0	1.06	1.15	0.43
2	10	0	20	3	56.7	1.06	1.15	0.43
3	10	10	10	6	0.0	1.06	2.31	0.43
4	10	10	20	6	56.7	1.06	2.31	0.43
5	20	20	10	6	0.0	1.09	3.04	0.44
6	20	0	10	6	54.9	1.09	3.04	0.44
7	20	10	20	6	0.0	4.37	2.30	0.33
8	20	0	20	6	27.5	4.37	2.30	0.33
9	20	5	20	6	0.0	8.74	2.13	0.31
10	20	10	20	12	0.0	8.74	4.27	0.31
11	30	5	10	6	0.0	6.93	3.18	0.33
12	30	5	20	6	8.7	6.93	3.18	0.33
13	30	0	20	6	0.0	无穷	2.36	0.25
14	30	0	20	12	0.0	无穷	4.72	0.25

下载: 导出CSV

| 显示表格

如无机理分析，仅看计算数值的变化趋势，就很可能会给出一个式（3）的分子中没有 $\tan \varphi$ 也无实际物理意义的无量纲参数，将增加后续拟合高精度计算式的难度。

2.3 滑移面深度及形状修正系数的确定

为由式（2）计算地基承载力，需首先确定地基失稳破坏时的滑移面深度Z_max与考虑滑移面形状变化使承载力系数变化的修正系数β。

首先看滑移面深度。当不考虑地基土重度时，对于地基典型的整体剪切破坏形式，由Prandtl-Reissner滑移面形状得出其滑移面最大深度为

${Z_{{\text{PR}}}}{\text{ = }}{{\text{e}}^{\left( {\frac{{\text{π }}}{4} + \frac{\varphi }{2}} \right)\tan \varphi }}\sin \left( {\frac{{\text{π }}}{4} + \frac{\varphi }{2}} \right)B \text{，}$

(4)

滑移面最大深度是基础宽度B的倍数，而这倍数只与内摩擦角φ有关。当地基土的重度对地基承载力有贡献时（亦即φ > 0时），与Prandtl-Reissner地基的唯一本质差别是等效“黏聚力”随深度增长，而反映这增长的无量纲参数是式（3）定义的k，所以此时的滑移面最大深度应为

${Z_{\max }}{\text{ = }}\alpha (\varphi , k){Z_{{\text{PR}}}} \text{，}$

(5)

亦即由Prandtl滑移面深度乘以修正系数α给出实际滑移面的最大深度Z_max，修正系数α是无量纲参数k和内摩擦角φ的函数。

修正系数α可通过拟合精细数值计算的结果来确定。本文拟合给出修正系数 $\alpha$ 的计算式为

$\alpha (\varphi , k) = 1 - {{\text{e}}^{ - M{k^{ - 0.5}} - N}} \text{，}$

(6)

其中，基底粗糙的情况下：

$M{\text{ = }}1.0 \text{，}\ \ N{\text{ = }}0.8\sin 2\varphi \text{；}$

(7)

而在基底光滑的情况下：

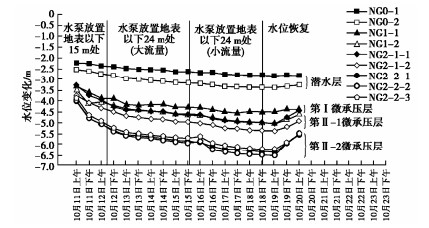
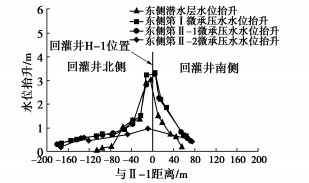
$M = 0.6 - 0.4\tan \varphi \text{，}\ \ N{\text{ = }}0.33\sin 2\varphi 。$

(8)

图 1，2分别为基底粗糙和光滑情况下，对不同φ值，相应修正系数α随无量纲参数k变化的情况，其中实线为按式（6）拟合的结果，离散点为精细数值计算的结果，可见拟合情况良好。同时由图 1，2可见，滑移面最大深度随φ和k的增大而减小，但减小的速率递减。此外，基底粗糙时的滑移面深度较大。

图 1 基底粗糙时滑移面深度修正系数的拟合

Figure 1. Fitting of slip surface depth correction coefficient for rough footings

下载: 全尺寸图片幻灯片

图 2 基底光滑时滑移面深度修正系数的拟合

Figure 2. Fitting of slip surface depth correction coefficient for smooth footings

下载: 全尺寸图片幻灯片

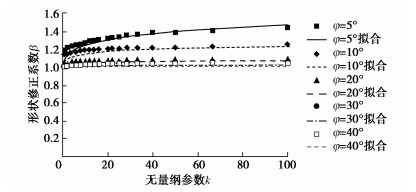
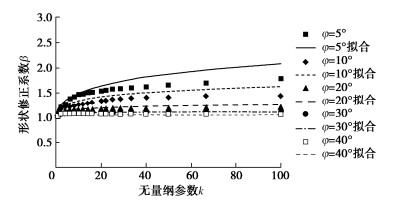
现在看滑移面形状修正系数 $\beta$ 。这系数实际是考虑滑移面形状与Prandtl滑移面不同时，承载力系数N_c的改变，只用于与地基土重度 $\gamma$ 有关的部分。计算表明，对常见情况这系数 $\beta$ 可取1.0，也就是不需修正。但是，当k值很大，也就是与土重度 $\gamma$ 对应的等效黏聚力随深度相对增长率很大，且内摩擦角很小的情况下，滑移面深度很小，其形状极为扁平，此时的承载力系数N_c要显著增大，也就是β需取较大值。

修正系数的取值可通过拟合精细数值计算的地基承载力结果来确定。本文结合以上类似的定性规律分析，通过大量计算拟合给出修正系数β的计算式。对于基底粗糙的情况，

$\beta {\text{ = 1 + }}\frac{1}{{\sqrt 2 {N_c}({k^{ - 0.5}} + 1.5\tan \varphi )}} \text{，}$

(9)

而当基底光滑时，

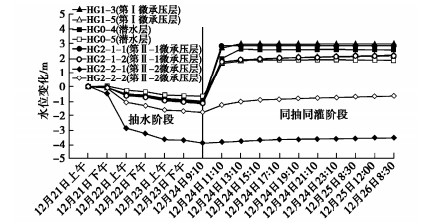
$\beta = {\text{1 + }}\frac{1}{{\sqrt 2 (0.6 - 0.4\tan \varphi ){N_c}({k^{ - 0.5}} + 0.9\tan \varphi )}} 。$

(10)

图 3，4分别为基底粗糙和光滑情况下，对不同φ值，相应修正系数β随无量纲参数k变化的情况，其中实线为按式（9）或式（10）拟合的结果，离散点为精细数值计算的结果。由图可见，拟合情况总体良好，但当摩擦角小且基底光滑时的拟合误差稍大。不过，此时地基土重度对整个地基承载力的贡献所占比例较小，故所计算地基承载力的误差会远小于 $\beta$ 的误差。

图 3 基底粗糙时滑移面形状修正系数的拟合

Figure 3. Fitting of slip surface shape correction coefficient for rough footings

下载: 全尺寸图片幻灯片

图 4 基底光滑时滑移面形状修正系数的拟合

Figure 4. Fitting of slip surface shape correction coefficient for smooth footings

下载: 全尺寸图片幻灯片

2.4 其他复杂情况下的承载力计算

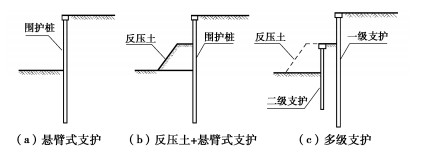
至此，针对承受非偏心竖向荷载条形基础下地基的整体剪切破坏，本文提出了统一考虑各有关因素的地基承载力计算公式。但实际工程中有多种复杂情况，这里简要说明其他情况下利用本文公式的计算方法。当地基土相对较软或埋深相对较大情况下，地基可能发生局部剪切破坏而非前述的整体剪切破坏，此时建议仍按太沙基的做法，采用折减的强度指标进行计算，亦即将土的强度指标折减后再如上进行计算。

对于其他形状的基础、荷载倾斜、地面倾斜等情况，建议仍采用Hansen等给出的修正系数^{[2, 5]}。此时需明确，本文的计算公式仍可如经典公式一样写成3项，即式（2）可改写为

${p_{\text{u}}} = c{N_c}{\text{ + (}}{N_c}\tan \varphi + 1)q{\text{ + }}0.5\beta \gamma \tan \varphi {Z_{\max }}{N_c} 。$

(11)

式（11）右端3项与经典公式的3项逐一对应，只是改进了第3项的计算。当计算诸如矩形基础的地基极限承载力时，可先按宽度等于矩形宽度的条形基础如上计算式（11）右端的3项，再分别乘以Hansen所给基础形状系数s_c，s_q和s_γ。可以理解，这样计算的精度不会较原公式有任何降低。限于篇幅，这里不再展示相应的算例。

此外，对式（11）的最后一项还可以整理为经典公式中第3项的样式，从而可以清楚而肯定地认识到N_γ到底与哪些参数或参数的组合式有关。

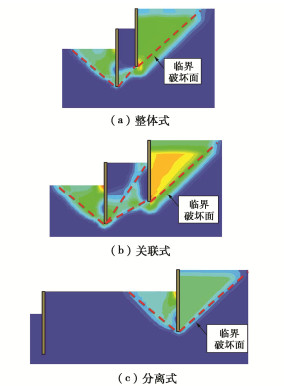
2.5 计算方法的检验

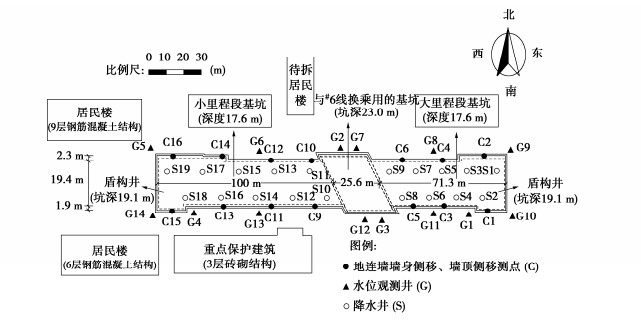
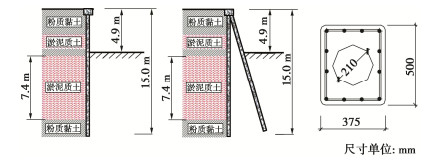
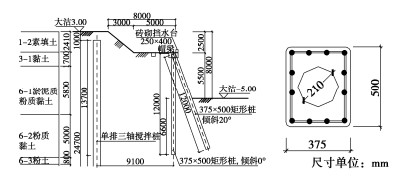
为检验上述整个计算方法的正确性及计算精度，针对承受非偏心竖向荷载的条形基础取多种不同的基础宽度B、土体强度指标c、φ及重度 $\gamma$ ，以及基础埋深对应的超载q，分别按上述计算公式和有限元极限分析方法计算相应滑移面深度Z_max及地基极限承载力p_u，结果表明所提出的计算方法的计算精度很高，相对误差一般不大于5%。表 4，5分别给出基底粗糙和基底光滑情况下的部分计算对比。对比两表计算结果还可以看出，基底粗糙时的地基承载力明显大于基底光滑时的值，特别是在内摩擦角和土体重度大的情况下。

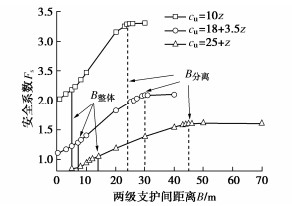
表 4 基底粗糙时计算方法的检验

Table 4. Verification of calculation method for rough footings

算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	极限分析			公式计算		承载力相对误差/%
算例编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	Z_max/m	Α	p_u/kPa	α	p_u/kPa	承载力相对误差/%
1	5	20	10	3	0	0.13	2.24	0.94	136.8	0.94	136.4	-0.3
2	5	5	20	3	0	1.05	1.58	0.66	43.6	0.67	42.4	-2.8
3	5	0	20	3	0	无穷	0.40	0.17	3.4	0.13	3.2	-5.3
4	10	10	20	3	0	1.06	1.86	0.69	116.8	0.71	113.5	-2.9
5	10	0	20	6	40	3.00	3.11	0.58	153.4	0.57	148.6	-3.1
6	10	0	20	6	0	无穷	1.50	0.28	26.0	0.24	24.9	-4.2
7	20	20	10	6	0	1.09	5.40	0.77	458.3	0.77	446.3	-2.6
8	20	5	20	6	0	8.74	3.89	0.56	308.9	0.57	301.7	-2.3
9	20	0	20	6	0	无穷	2.81	0.40	169.9	0.40	164.5	-3.2
10	30	20	20	6	0	3.46	6.40	0.67	1823.2	0.71	1793.8	-1.6
11	30	5	20	6	0	13.86	5.42	0.57	1195.4	0.62	1194.2	-0.1
12	30	0	20	6	0	无穷	4.66	0.49	884.6	0.50	849.7	-3.9
13	40	20	20	6	0	5.03	8.80	0.62	7737.9	0.71	7850.8	1.5
14	40	0	20	6	0	无穷	7.55	0.54	5113.0	0.55	4889.8	-4.4

下载: 导出CSV

| 显示表格

表 5 基底光滑时计算方法的检验

Table 5. Verification of calculation method for smooth footings

模型编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	极限分析			公式计算		承载力相对误差/%
模型编号	φ/(°)	c/kPa	γ/(kN·m^-3)	B/m	q/kPa	无量纲参数k	Z_max/m	α	P_u/kPa	α	P_u/kPa	承载力相对误差/%
1	5	20	10	3	0	0.13	1.42	0.60	133.4	0.80	135.6	1.7
2	5	5	20	3	0	1.05	1.03	0.43	38.7	0.46	39.7	2.6
3	5	0	20	3	0	无穷	0.28	0.12	2.6	0.06	2.6	0.5
4	10	10	20	3	0	1.06	1.15	0.43	101.9	0.47	104.4	2.5
5	10	0	20	6	40	3.00	1.80	0.34	130.8	0.34	131.7	0.7
6	10	0	20	6	0	无穷	0.84	0.16	16.9	0.11	16.9	0.1
7	20	20	10	6	0	1.09	3.04	0.44	384.2	0.48	393.7	2.5
8	20	5	20	6	0	8.74	2.21	0.32	207.8	0.31	207.7	-0.1
9	20	0	20	6	0	无穷	1.49	0.21	94.6	0.19	95.0	0.4
10	30	20	20	6	0	3.46	3.58	0.38	1269.0	0.38	1276.1	0.6
11	30	5	20	6	0	13.86	2.98	0.31	716.1	0.32	722.2	0.8
12	30	0	20	6	0	无穷	2.36	0.25	457.9	0.25	461.8	0.8
13	40	20	20	6	0	5.03	4.80	0.34	4835.7	0.36	4785.6	-1.0
14	40	0	20	6	0	无穷	3.84	0.27	2571.0	0.28	2586.4	0.6

下载: 导出CSV

| 显示表格

3. 与现有主流计算公式的对比

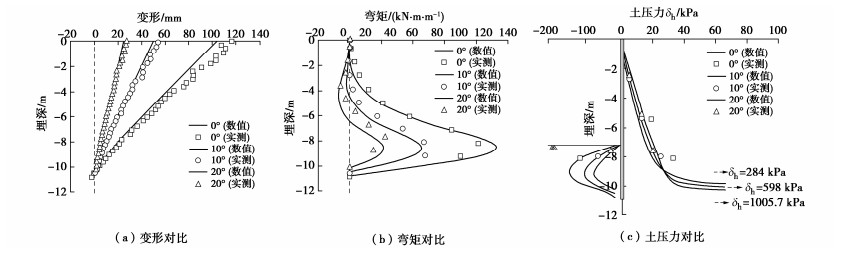
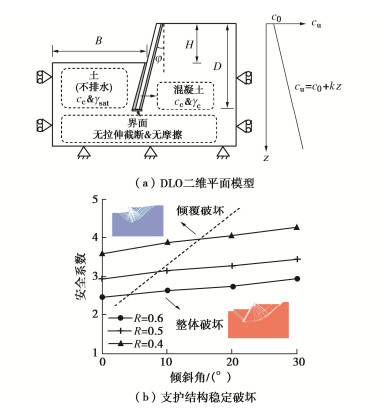
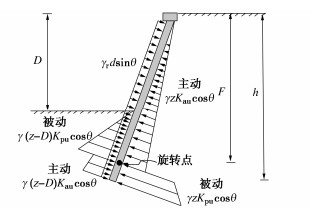
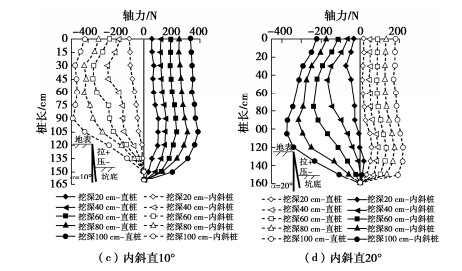
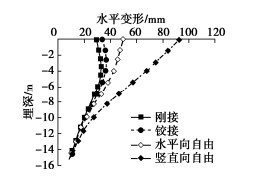
3.1 与太沙基解的比较

本节将本文公式与太沙基解进行比较。太沙基解是假定基底粗糙给出地基承载力的3个系数，其中前两个系数 ${N_c}$ 与 ${N_q}$ 较Prandtl-Reissner给出的要大。因其第3个承载力系数 ${N_\gamma }$ 仅能给出数值解，故其承载力系数在多数土力学教科书中是以曲线形式给出，但文献[14]列表给出了太沙基承载力系数值，这里在按太沙基公式计算时采用文献[14]给出的系数值。

表 6列出不同土体强度参数取值时太沙基公式、本文式（2）与有限元极限分析计算结果的对比。这里取基础宽度B=6 m，周边超载q=0，地基土重度γ=20 kN/m³。按太沙基的假定，认为基底粗糙，故这里的有限元极限分析和本文计算公式均按基底粗糙来考虑。由表 6可见，太沙基公式误差最高可达30%。且在φ=0时，太沙基公式仍是不准确的，这说明太沙基公式中的系数N_c存在误差。实际上φ=0时即使假定基底粗糙，还是Prandtl-Reissner解精确。

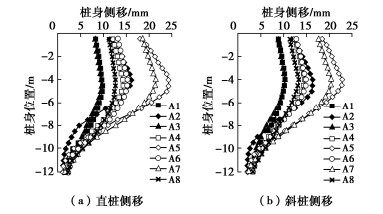
表 6 与太沙基公式的比较

Table 6. Comparisons with Terzaghi formula

算例编号	φ/(°)	c/kPa	极限分析承载力/kPa	太沙基公式/kPa	太沙基公式相对误差/%	本文公式/kPa	本文公式相对误差/%
1	0	5	25.7	28.5	10.9	25.7	0.0
2	5	5	51.7	66.5	28.7	49.7	-3.9
3	10	5	92.3	120.0	30.0	88.4	-4.2
4	20	5	308.9	388.5	25.8	301.7	-2.3
5	30	5	1195.5	1368.0	14.4	1194.2	-0.1
6	40	5	5968.4	6502.5	8.9	6074.9	1.8
7	44	5	12705.0	16359.5	28.7	13033.0	2.6
8	0	50	257.1	285.0	10.9	257.1	0.0
9	5	50	351.7	395.0	12.3	349.9	-0.5
10	10	50	492.6	552.0	12.1	486.3	-1.3
11	20	50	1074.6	1185.0	10.3	1049.7	-2.3
12	30	50	2880.0	3042.0	5.6	2825.9	-1.9
13	40	50	10609.0	10809.0	1.9	10700.1	0.9
14	44	50	20430.0	23195.0	13.5	20938.2	2.5

下载: 导出CSV

| 显示表格

3.2 与Hansen解的比较

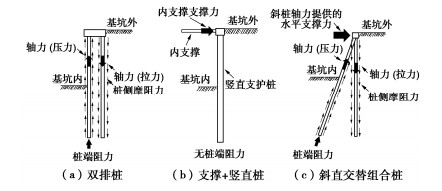
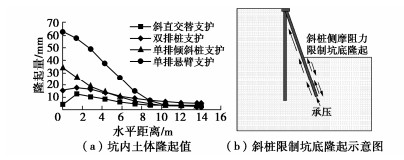
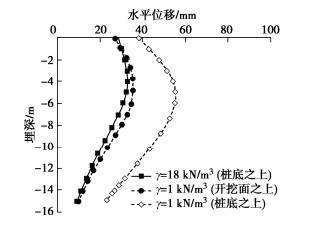
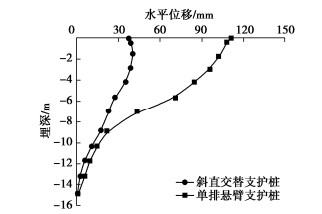
Hansen解是为改进太沙基解的计算精度而提出的，其前两个地基承载力系数与Prandtl-Reissner的相同，而第3个系数 ${N_\gamma }$ 的计算式为

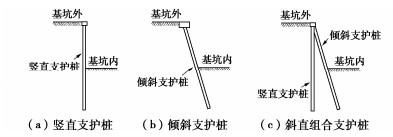
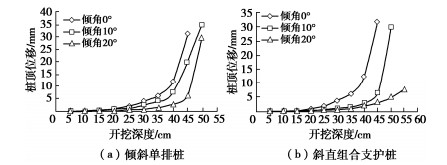
${N_\gamma } = 1.8({N_q} - 1)\tan \varphi 。$

(12)

式（12）中的系数1.8是Hansen最初建议的^[5]，后来改为1.5^[2]，而Verruijt认为这系数理论上取2.0更准确些^[6]。

这里同样取基础宽度B=6 m，基础周边超载q=0，地基土重度 $\gamma$ =20 kN/m³。有限元极限分析和本文计算公式均按基底粗糙进行计算。表 5列出与Hansen公式计算结果的比较，其中对Hansen所给式（12）中的系数分别取3种不同的值。可见系数取1.5时承载力普遍偏小，相对误差绝对值接近30%，而取2.0时确实总体误差绝对值减小，但φ较大且c较小时出现正的误差，亦即结果偏大。

表 7 与Hansen公式的比较

Table 7. Comparisons with Hansen formula

算例编号	φ/(°)	c/kPa	极限分析承载力/kPa	系数1.5		系数1.8		系数2.0		本文公式/kPa	本文公式相对误差/%
算例编号	φ/(°)	c/kPa	极限分析承载力/kPa	Hansen解/kPa	相对误差/%	Hansen解/kPa	相对误差/%	Hansen解/kPa	相对误差/%	本文公式/kPa	本文公式相对误差/%
1	0	5	25.7	25.7	0.0	25.7	0.0	25.7	0.0	25.7	0.0
2	5	5	51.7	36.9	-28.6	37.8	-26.9	38.4	-25.7	49.7	-3.9
3	10	5	92.3	65.1	-29.5	69.7	-24.4	72.9	-21.1	88.4	-4.2
4	20	5	308.9	251.0	-18.7	286.4	-7.3	310.0	0.4	301.7	-2.3
5	30	5	1195.5	1054.9	-11.8	1235.7	3.4	1356.3	13.4	1194.2	-0.1
6	40	5	5968.4	5149.0	-13.7	6103.5	2.3	6739.8	12.9	6074.9	1.8
7	0	50	257.1	257.1	0.0	257.1	0.0	257.1	0	257.1	0.0
8	5	50	351.7	328.9	-6.5	329.8	-6.2	330.4	-6.1	349.9	-0.5
9	10	50	492.6	440.6	-10.6	445.3	-9.6	448.4	-9.0	486.3	-1.3
10	20	50	1074.6	918.6	-14.5	954.0	-11.2	977.6	-9.0	1049.7	-2.3
11	30	50	2880.0	2411.2	-16.3	2592.0	-10.0	2712.6	-5.8	2825.9	-1.9
12	40	50	10609.0	8538.1	-19.5	9492.6	-10.5	10128.9	-4.5	10700.1	0.9

下载: 导出CSV

| 显示表格

尽管Hansen解在计算N_γ时，其计算式中的系数用1.5普遍偏保守，但笔者的观点是，在可能条件还是尽量准确计算，之后再考虑参数的可能误差及工程之重要性来决定安全系数的大小。否则，决策是盲目的，对复杂工程未必安全。

此外，如将Hansen解与基底光滑情况下的有限元极限分析结果比较，即使取其中的系数为1.5，Hansen解也多给出偏大的结果，且正误差最大超过50%，限于篇幅这里不再列出详细结果。

4. 结论

本文针对目前一般地基承载力计算中存在的问题，在深入分析地基承载力机理的基础上，提出一种新的改进计算方法。

（1）现有计算公式在理论上存在的突出问题是对极限荷载问题采用了叠加计算的思路，故难以达到较好的计算精度。太沙基解的误差可达30%，Hansen解的误差稍小，但最大也接近30%。

（2）本文深入分析了地基承载的机理，揭示了基础埋深对应的基础周围超载和地基土自重在地基承载力的计算中可分别等价为黏聚力和黏聚力随深度增长率，从而可采用统一的方法予以考虑。

（3）采用理论分析确定公式形式、数值计算拟合确定修正系数的方法，针对非偏心竖向荷载下的条形基础给出了综合考虑地基土强度、基础埋深和地基土重度的无量纲参数以及相应的地基承载力统一计算式，分别考虑了基底粗糙和光滑两种情况，与精细数值计算结果的对比表明所提出无量纲参数及地基承载力计算公式的合理性、正确性及高精度。

（4）与目前已有太沙基解、Hansen解的计算对比，表明本文所提方法的计算精度显著提高。

（5）对于其他形状的基础、倾斜荷载等情况，利用本文公式计算时仍可采用已有的修正系数。

致谢: 感谢土力学和岩土工程界各位同行的信任，让笔者有幸成为今年黄文熙讲座的主讲人。笔者自1989年师从于顾晓鲁教授，开始了基坑工程领域的学习，建立了对岩土工程浓厚的兴趣，并持续至今，积累了一些粗浅的认识和工程经验。感谢团队刁钰副教授、程雪松副教授、周海祚副教授、张天奇副研究员、雷华阳教授、刘畅副教授，以及笔者的学生杜一鸣博士、李志伟博士、曾超峰副教授、魏少伟博士、刘景锦博士等对本文提供的巨大帮助！感谢笔者的博士生苏奕铭、黄建友、栗晴瀚、何晓佩、焦陈磊、甘伟等，他们对本文也提供了很多具体帮助。感谢深圳市工勘岩土集团有限公司雷斌先生为本文提供了三级支护工程图片。

图 1 基坑支护结构及周边地层变形

Figure 1. Deformations of excavation retaining structures and soils

下载: 全尺寸图片幻灯片

图 2 地下连续墙成槽引起土体水平位移

Figure 2. Horizontal displacements of soils due to trenching

下载: 全尺寸图片幻灯片

图 3 某工程中群孔效应引发的周边建筑物沉降

Figure 3. Settlements of adjacent buildings induced by group borehole effects

下载: 全尺寸图片幻灯片

图 4 单孔和群孔成孔效应离心机试验

Figure 4. Centrifuge tests on single and group borehole effects

下载: 全尺寸图片幻灯片

图 5 单孔和群孔成孔引起地表沉降

Figure 5. Ground surface settlements induced by single and group borehole

下载: 全尺寸图片幻灯片

图 6 多孔合并前后地表曲线对比

Figure 6. Comparison of ground surface settlements with and without simplification of group borehole

下载: 全尺寸图片幻灯片

图 7 群孔效应多孔合并模拟简化方法示意

Figure 7. Simplified simulation of group borehole effects

下载: 全尺寸图片幻灯片

图 8 多孔合并示意图

Figure 8. Simplified simulation of group borehole effects

下载: 全尺寸图片幻灯片

图 9 监测点沉降模拟值和实测值对比

Figure 9. Comparison of measured and predicted settlements

下载: 全尺寸图片幻灯片

图 10 部分空孔回填控制群孔效应影响

Figure 10. Filling of partial boreholes to control group borehole effects

下载: 全尺寸图片幻灯片

图 11 基坑平面图

Figure 11. Plan of excavations

下载: 全尺寸图片幻灯片

图 12 基坑预降水引起地下连续墙变形

Figure 12. Wall deflections induced by pre-dewatering of excavations

下载: 全尺寸图片幻灯片

图 13 基坑预降水引起地下连续墙变形和建筑物沉降

Figure 13. Wall deflections induced by pre-dewatering of excavations

下载: 全尺寸图片幻灯片

图 14 某大面积基坑降水井及监测点平面布置

Figure 14. Plan of dewatering wells and field monitoring paints

下载: 全尺寸图片幻灯片

图 15 某大面积基坑预降水过程中围护结构变形情况

Figure 15. Wall deflections induced by pre-dewatering of excavations

下载: 全尺寸图片幻灯片

图 16 考虑预降水4个效应的变形计算模型

Figure 16. Deformation prediction model considering 4 effects of pre-excavation dewatering

下载: 全尺寸图片幻灯片

图 17 承压层抽水引发土体变形发展规律

Figure 17. Prediction model for deformation considering 4 effects of pre-dewatering of excavations

下载: 全尺寸图片幻灯片

图 18 基坑水平支撑平面和支护桩侧移变形监测点

Figure 18. Plan of structs and monitoring points of lateral displacements of retaining piles

下载: 全尺寸图片幻灯片

图 19 某基坑工程围护结构变形实测

Figure 19. Measured lateral deformations of retaining wall

下载: 全尺寸图片幻灯片

图 20 不同变形模式下坑外地表土体位移对比

Figure 20. Comparison of ground surface deformations under different lateral deformation modes of retaining wall

下载: 全尺寸图片幻灯片

图 21 围护结构不同变形模式下坑外深层土体沉降对比

Figure 21. Comparison of ground deformations behind retaining wall under different lateral deformation models of retaining wall

下载: 全尺寸图片幻灯片

图 22 某地铁车站基坑周边建筑情况

Figure 22. Plan view of surround buildings of metro station

下载: 全尺寸图片幻灯片

图 23 建筑物的三维沉降分布图

Figure 23. 3D settlement distribution of building

下载: 全尺寸图片幻灯片

图 24 纵墙墙体拉应变最大值变化曲线

Figure 24. Variation of maximum tensile strain of longitudinal wall

下载: 全尺寸图片幻灯片

图 25 纵墙墙体拉应变最大值随角度变化曲线

Figure 25. Relationship between maximum tensile strain of longitudinal wall and arbitrary angle

下载: 全尺寸图片幻灯片

图 26 围护结构为内凸型模式时坑外不同位置处隧道变形

Figure 26. Deformations of tunnels at different locations caused by convex deformation of retaining structures

下载: 全尺寸图片幻灯片

图 27 围护结构不同变形模式下隧道变形影响区

Figure 27. Influenced zones determined by different profiles of deflection of retaining structures

下载: 全尺寸图片幻灯片

图 28 某实际工程隧道渗漏引发的沉降和错台

Figure 28. Settlements and dislocation of tunnel segments induced by leakage of water and soils

下载: 全尺寸图片幻灯片

图 29 隧道底部多点渗漏模拟试验

Figure 29. Model tests with multiple leakage points

下载: 全尺寸图片幻灯片

图 30 隧道底部两点渗漏模拟试验

Figure 30. Simulation test for two leakage points under tunnel

下载: 全尺寸图片幻灯片

图 31 隧道底部不同距离两点渗漏模拟试验

Figure 31. Results of two-leakage-point tests with different spacings

下载: 全尺寸图片幻灯片

图 32 不同砂土–黏土界面位置时隧道底部渗漏试验

Figure 32. Large-scale model tests considering position of sand-clay interface relative to tunnel

下载: 全尺寸图片幻灯片

图 33 漏水漏砂侵蚀大型模型试验结果

Figure 33. Erosion of sand due to inflow of sand and water

下载: 全尺寸图片幻灯片

图 34 悬臂式排桩桩顶位移比较

Figure 34. Comparison of displacements at cantilever pile top

下载: 全尺寸图片幻灯片

图 35 基坑与地铁平面图

Figure 35. Plan view of excavations and metro lines

下载: 全尺寸图片幻灯片

图 36 多种保护措施下左线隧道水平位移对比

Figure 36. Comparison of tunnel displacements with different types of protection measures

下载: 全尺寸图片幻灯片

图 37 基坑与地铁的平面图

Figure 37. Plan view of excavations and metro lines

下载: 全尺寸图片幻灯片

图 38 三期基坑分仓施工平面图

Figure 38. Plan of zoned excavation of 3rd stage excavation

下载: 全尺寸图片幻灯片

图 39 一期、二期基坑开挖时地铁结构Y4测点的水平位移

Figure 39. Horizontal displacements of metro structures at Y4 during 1st and 2nd stages of excavation

下载: 全尺寸图片幻灯片

图 40 主动控制的关键区域土体

Figure 40. Key soil zone to control deformation of structures to be protected

下载: 全尺寸图片幻灯片

图 41 袖阀管注浆对土体水平变形影响的试验布置图

Figure 41. Field tests on effect of TAM grouting on lateral displacement of soils

下载: 全尺寸图片幻灯片

图 42 注浆量及注浆距离对土体侧向变形的影响

Figure 42. Effects of grouting volume and distance on lateral displacement of soils

下载: 全尺寸图片幻灯片

图 43 超孔压及A点土体位移随时间发展曲线

Figure 43. Development of excess pore water pressure and horizontal displacement at point A with time

下载: 全尺寸图片幻灯片

图 44 袖阀管注浆对隧道位移控制现场试验

Figure 44. Field tests on effects of TAM grouting on control of deformation of tunnels

下载: 全尺寸图片幻灯片

图 45 隧道水平位移、水平收敛及随时间的变化规律

Figure 45. Development of horizontal displacement and convergence of tunnels with time due to TAM grouting

下载: 全尺寸图片幻灯片

图 46 注浆项目布置平面图及注浆孔

Figure 46. Plan view of grouting program and grouting holes

下载: 全尺寸图片幻灯片

图 47 注浆引起的隧道水平位移增量和水平收敛增量

Figure 47. Increments and convergence increments of horizontal displacement of tunnels caused by TAM grouting

下载: 全尺寸图片幻灯片

图 48 第一次注浆前后地铁隧道结构的水平位移

Figure 48. Horizontal displacements of metro structures before and after 1^st TAM grouting

下载: 全尺寸图片幻灯片

图 49 工况4中4次注浆前后隧道的水平位移

Figure 49. Horizontal displacements of tunnel before and after 4 times of TAM grouting for case 4

下载: 全尺寸图片幻灯片

图 50 试验剖面布置图

Figure 50. Profile of field tests

下载: 全尺寸图片幻灯片

图 51 珠海成层土中袖阀管注浆引起土体水平位移

Figure 51. Horizontal displacements due to TAM grouting in stratified soils in Zhuhai

下载: 全尺寸图片幻灯片

图 52 试膨胀后的囊体

Figure 52. Expanded capsule after grouting

下载: 全尺寸图片幻灯片

图 53 珠海成层土中囊体扩张引起土体水平位移

Figure 53. Horizontal displacements due to capsule grouting in stratified soils in Zhuhai

下载: 全尺寸图片幻灯片

图 54 天津成层土中囊体扩张引起土体水平位移

Figure 54. Horizontal displacements due to capsule grouting in stratified soils in Tianjin

下载: 全尺寸图片幻灯片

图 55 囊体扩张对桩侧向变形控制现场试验

Figure 55. Field tests on lateral deformation of piles due to capsule expansion

下载: 全尺寸图片幻灯片

图 56 隧道与基坑关系及试验平、剖面布置图

Figure 56. Plan and profile of field test tunnel and excavation

下载: 全尺寸图片幻灯片

图 57 试验隧道水平位移控制量

Figure 57. Increments of horizontal displacement of tunnel

下载: 全尺寸图片幻灯片

图 58 囊体膨胀主动控制前后隧道Z1测点水平位移

Figure 58. Increments of lateral displacement of tunnel at Z1

下载: 全尺寸图片幻灯片

图 59 承压含水层回灌控沉

Figure 59. Settlement control by recharge of artesian aquifer

下载: 全尺寸图片幻灯片

图 60 基坑外各含水层典型观测井水位变化曲线

Figure 60. Variation of water level in aquifers during and after dewatering

下载: 全尺寸图片幻灯片

图 61 第Ⅰ微承压含水层回灌时各含水层水位变化曲线

Figure 61. Variation of water level in aquifer due to recharge of artesian aquifer Ⅰ

下载: 全尺寸图片幻灯片

图 62 基坑内开始抽水后对第Ⅰ微承压含水层回灌时各含水层水位变化曲线

Figure 62. Variation of water-level in aquifer due to recharge of artesian aquifer Ⅰ after commencement of dewatering inside diaphragm

下载: 全尺寸图片幻灯片

图 63 反压土支护

Figure 63. Retaining walls with earth berm

下载: 全尺寸图片幻灯片

图 64 考虑反压土作用的悬臂支护分析模型

Figure 64. Analysis model for cantilever retaining piles considering effects of earth berm

下载: 全尺寸图片幻灯片

图 65 双排桩平面杆系有限元模型

Figure 65. FEM model for double-row retaining piles

下载: 全尺寸图片幻灯片

图 66 多级支护形式

Figure 66. Types of multi-level retaining excavations

下载: 全尺寸图片幻灯片

图 67 二级支护和三级支护实例

Figure 67. Case histories of multi-level retaining excavations

下载: 全尺寸图片幻灯片

图 68 多级支护3种破坏模式

Figure 68. Failure modes of multi-level retaining excavations

下载: 全尺寸图片幻灯片

图 69 多级支护3种破坏模式与多级支护宽度关系

Figure 69. Failure modes of multi-level retaining excavations with respect to width

下载: 全尺寸图片幻灯片

图 70 倾斜桩支护

Figure 70. Inclined retaining piles

下载: 全尺寸图片幻灯片

图 71 砂土中竖直桩、倾斜桩、斜直组合支护桩模型试验

Figure 71. Model tests on inclined retaining piles in sand

下载: 全尺寸图片幻灯片

图 72 不同支护结构直桩桩身变形

Figure 72. Wall deformation of vertical wall for different retaining structures

下载: 全尺寸图片幻灯片

图 73 倾斜桩无支撑支护结构形式

Figure 73. Strut-free inclined retaining structures

下载: 全尺寸图片幻灯片

图 74 内撑式和无支撑支护结构变形对比

Figure 74. Comparison of deformations of strut-free inclined retaining piles and braced vertical retaining piles

下载: 全尺寸图片幻灯片

图 75 倾斜桩无支撑支护结构形式

Figure 75. Comparison of bending moments of strut-free inclined retaining piles and braced vertical retaining piles

下载: 全尺寸图片幻灯片

图 76 离心机试验实测与数值计算结果

Figure 76. Comparison of centrifuge tests and numerical analyses

下载: 全尺寸图片幻灯片

图 77 倾斜桩稳定破坏模式与倾斜角的关系

Figure 77. Variation of failure mode of inclined retaining piles with respect to angle of inclination

下载: 全尺寸图片幻灯片

图 78 桩身重度的影响

Figure 78. Effects of self-weight on ultimate depth of excavations

下载: 全尺寸图片幻灯片

图 79 抗倾覆稳定性计算模型

Figure 79. Analysis model for stability against overturning

下载: 全尺寸图片幻灯片

图 80 离心机验证

Figure 80. Validation of centrifuge tests

下载: 全尺寸图片幻灯片

图 81 7种试验工况极限挖深对比

Figure 81. Ultimate depths of excavations with different types of retaining structures

下载: 全尺寸图片幻灯片

图 82 不同支护结构变形图

Figure 82. Deformations of different types of retaining structures

下载: 全尺寸图片幻灯片

图 83 不同支护结构弯矩图

Figure 83. Bending moments of different types of retaining structures

下载: 全尺寸图片幻灯片

图 84 不同支护结构桩身轴力分布

Figure 84. Comparison of axial force

下载: 全尺寸图片幻灯片

图 85 不同支护方式受力机理图

Figure 85. The mechanism of different retaining structures

下载: 全尺寸图片幻灯片

图 86 不同支护形式的坑内土体隆起

Figure 86. Uplifts of soils in excavations with different strut forms

下载: 全尺寸图片幻灯片

图 87 不同约束条件下变形图

Figure 87. Wall deflection under different constraint conditions

下载: 全尺寸图片幻灯片

图 88 不同桩间土重对变形影响

Figure 88. Wall deflections under different soil weights

下载: 全尺寸图片幻灯片

图 89 斜直组合桩

Figure 89. Inclined-vertical retaining wall

下载: 全尺寸图片幻灯片

图 90 桩身水平位移实测数据

Figure 90. Measured horizontal wall deflections

下载: 全尺寸图片幻灯片

图 91 基坑支护剖面

Figure 91. Profile of retaining structures

下载: 全尺寸图片幻灯片

图 92 桩身水平位移曲线

Figure 92. Measured horizontal wall deflections

下载: 全尺寸图片幻灯片

图 93 现场照片

Figure 93. Photo of excavation

下载: 全尺寸图片幻灯片

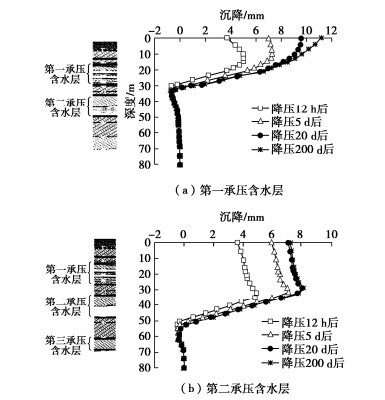
表 1 土层物理和力学指标

Table 1 Physical and mechanical parameters of soils

层号	土层	层厚/m	$\gamma$ /(kN·m^-3)	w /%	e	$\varphi$ /(°)	c /kPa
①	人工填土	3.66	17.5	—	—	10.0	8.0
②₁	淤泥质砂土	7.97	20.0	17.9	0.549	22.6	—
②₂	淤泥	8.80	15.2	77.8	2.079	1.5	2.1
②₃	黏土	3.86	18.0	32.3	0.977	17.1	21.4
②₄	淤泥质土	12.16	16.4	53.7	4.670	6.6	7.5
②₅	粗砂	8.00	20.2	15.2	0.504	29.1	—

下载: 导出CSV

参考文献(61)

[1]	郑刚, 朱合华, 刘新荣, 等. 基坑工程与地下工程安全及环境影响控制[J]. 土木工程学报, 2016, 49(6): 1–24. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201606001.htm ZHENG Gang, ZHU He-hua, LIU Xin-rong, et al. Control of safety of deep excavations and underground engineering and its impact on surrounding environment[J]. China Civil Engineering Journal, 2016, 49(6): 1–24. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC201606001.htm
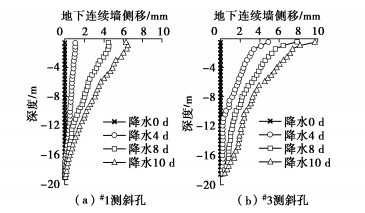
[2]	郑刚, 曾超峰. 基坑开挖前潜水降水引起的地下连续墙侧移研究[J]. 岩土工程学报, 2013, 35(12): 2153–2163. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201312002.htm ZHENG Gang, ZENG Chao-feng. Lateral displacement of diaphragm wall by dewatering of phreatic water before excavation[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(12): 2153–2163. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201312002.htm
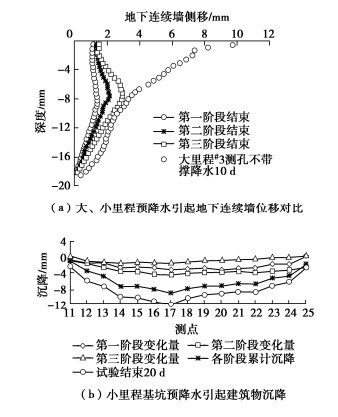
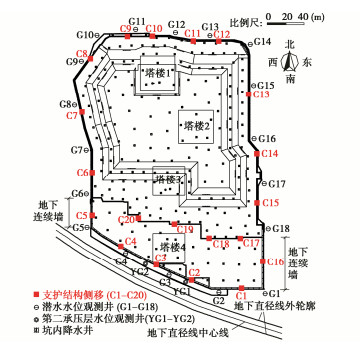
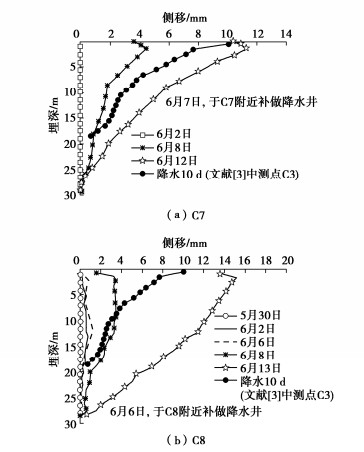
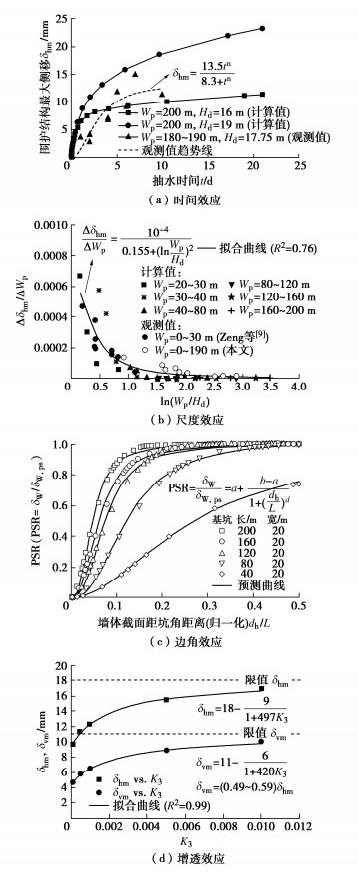
[3]	曾超峰, 郑刚, 薛秀丽. 大面积基坑开挖前预降水对支护墙变形的影响研究[J]. 岩土工程学报, 2017, 39(6): 1012–1021. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201706008.htm ZENG Chao-feng, ZHENG Gang, XUE Xiu-li. Wall deflection induced by pre-excavation dewatering in large-scale excavations[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(6): 1012–1021. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201706008.htm
[4]	曾超峰, 薛秀丽, 郑刚. 软土区基坑预降水引起支护墙侧移的典型参数影响研究[J]. 岩土力学, 2017, 38(11): 3295–3303, 3318. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201711028.htm ZENG Chao-feng, XUE Xiu-li, ZHENG Gang. A parametric study of lateral displacement of support wall induced by foundation pre-dewatering in soft ground[J]. Rock and Soil Mechanics, 2017, 38(11): 3295–3303, 3318. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201711028.htm
[5]	ZENG C F, ZHENG G, ZHOU X F, et al. Behaviours of wall and soil during pre-excavation dewatering under different foundation pit widths[J]. Computers and Geotechnics, 2019, 115: 103169. doi: 10.1016/j.compgeo.2019.103169
[6]	ZHENG G, CAO J R, CHENG X S, et al. Experimental study on the artificial recharge of semiconfined aquifers involved in deep excavation engineering[J]. Journal of Hydrology, 2018, 557: 868–877. doi: 10.1016/j.jhydrol.2018.01.020
[7]	ZENG C F, XUE X L, ZHENG G, et al. Responses of retaining wall and surrounding ground to pre-excavation dewatering in an alternated multi-aquifer-aquitard system[J]. Journal of Hydrology, 2018, 559: 609–626. doi: 10.1016/j.jhydrol.2018.02.069
[8]	郑刚, 曾超峰, 薛秀丽. 承压含水层局部降压引起土体沉降机理及参数分析[J]. 岩土工程学报, 2014, 36(5): 802–817. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405003.htm ZHENG Gang, ZENG Chao-feng, XUE Xiu-li. Settlement mechanism of soils induced by local pressure-relief of confined aquifer and parameter analysis[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 802–817. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201405003.htm
[9]	ZENG C F, ZHENG G, XUE X L, et al. Combined recharge: a method to prevent ground settlement induced by redevelopment of recharge wells[J]. Journal of Hydrology, 2019, 568: 1–11. doi: 10.1016/j.jhydrol.2018.10.051
[10]	曹剑然. 天津地区基坑工程中承压层回灌控沉理论与技术研究[D]. 天津: 天津大学, 2018. CAO Jian-ran. Study on the Theory and Technology of Recharge and Subsidence Control of Confined Layer in Excavation Engineering in Tianjin Area[D]. Tianjin: Tianjin University, 2018. (in Chinese)
[11]	郑刚, 曹剑然, 程雪松, 等. 天津第二粉土粉砂微承压含水层回灌试验研究[J]. 岩土工程学报, 2018, 40(4): 592–601. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201804004.htm ZHENG Gang, CAO Jian-ran, CHENG Xue-song, et al. Experimental study on artificial recharge of second Tianjin silt and silty sand micro-confined aquifer[J]. Chinese Journal of Geotechnical Engineering, 2018, 40(4): 592–601. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201804004.htm
[12]	哈达, 朱敢平, 李竹, 等. 天津市承压含水层条件下地下连续墙深度优化[J]. 地下空间与工程学报, 2018, 14(2): 490–499. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201802027.htm HA Da, ZHU Gan-ping, LI Zhu, et al. Underground diaphragm wall depth optimization considering the confined aquifer in Tianjin[J]. Chinese Journal of Underground Space and Engineering, 2018, 14(2): 490–499. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201802027.htm
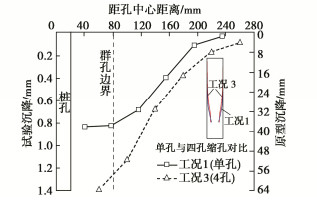
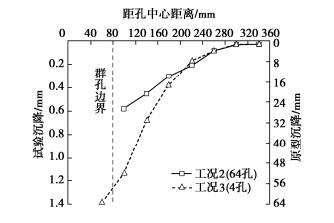
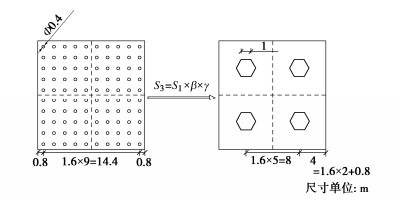
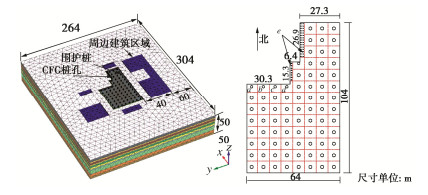
[13]	孙宏宾, 郑刚, 程雪松, 等. 软土地区CFG桩群孔效应引发周边土体变形机理研究[J]. 石家庄铁道大学学报(自然科学版), 2018, 31(1): 39–46, 54. https://www.cnki.com.cn/Article/CJFDTOTAL-SJZT201801008.htm SUN Hong-bin, ZHENG Gang, CHENG Xue-song, et al. Study on the mechanism of soil deformation caused by the borehole group effect of CFG piles in soft soil area[J]. Journal of Shijiazhuang Tiedao University (Natural Science Edition), 2018, 31(1): 39–46, 54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJZT201801008.htm
[14]	郑刚, 王若展, 程雪松, 等. 软土地区桩基施工群孔效应作用机理研究[J]. 天津大学学报(自然科学与工程技术版), 2019, 52(增刊1): 1–8. ZHENG Gang, WANG Ruo-zhan, CHENG Xue-song, et al. Mechanism of borehole group effect induced by pile foundation construction in soft soils[J]. Journal of Tianjin University (Science and Technology), 2019, 52(S1): 1–8. (in Chinese)
[15]	郑刚, 李溪源, 王若展, 等. 群孔效应对周边环境影响的控制措施研究[J]. 石家庄铁道大学学报(自然科学版), 2020, 33(2): 8–15. https://www.cnki.com.cn/Article/CJFDTOTAL-SJZT202002003.htm ZHENG Gang, LI Xi-yuan, WANG Ruo-zhan, et al. Research on control measures of influence of borehole group on surrounding environment[J]. Journal of Shijiazhuang Tiedao University (Natural Science Edition), 2020, 33(2): 8–15. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJZT202002003.htm
[16]	李姝婷. 地下连续墙施工引起的土体变形实测与数值分析研究[D]. 天津: 天津大学, 2014. LI Shu-ting. Field Monitoring and Numerical Analysis of Ground Movements due to Diaphragm Wall Installation[D]. Tianjin: Tianjin University, 2014. (in Chinese)
[17]	郑刚, 邓旭, 刘畅, 等. 不同维护结构变形模式对坑外深层土体位移场影响的对比分析[J]. 岩土工程学报, 2014, 36(2): 273–285. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201402003.htm ZHENG Gang, DENG Xu, LIU Chang, et al. Comparative analysis of influences of different deformation modes of retaining structures on displacement field of deep soils outside excavations[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(2): 273–285. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201402003.htm
[18]	龚晓南. 深基坑工程设计施工手册[M]. 北京: 中国建筑工业出版社, 1998. GONG Xiao-nan. Construction Design Manual of Deep Excavation[M]. Beijing: China Architecture & Building Press, 1998. (in Chinese)
[19]	郑刚, 李志伟. 不同围护结构变形形式的基坑开挖对邻近建筑物的影响对比分析[J]. 岩土工程学报, 2012, 34(6): 969–977. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201206003.htm ZHENG Gang, LI Zhi-wei. Comparative analysis of responses of buildings adjacent to excavations with different deformation modes of retaining walls[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(6): 969–977. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201206003.htm
[20]	郑刚, 李志伟. 基坑开挖对邻近不同楼层建筑物影响的有限元分析[J]. 天津大学学报, 2012, 45(9): 829–837. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX201209015.htm ZHENG Gang, LI Zhi-wei. Finite element analysis of response of building with different storeys adjacent to pit excavation[J]. Journal of Tianjin University, 2012, 45(9): 829–837. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX201209015.htm
[21]	郑刚, 王琦, 邓旭, 等. 不同围护结构变形模式对坑外既有隧道变形影响的对比分析[J]. 岩土工程学报, 2015, 37(7): 1181–1194. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201507004.htm ZHENG Gang, WANG Qi, DENG Xu, et al. Comparative analysis of influences of different deformation modes of retaining structures on deformation of existing tunnels outside excavations[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1181–1194. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201507004.htm
[22]	郑刚, 李志伟. 基坑开挖对邻近任意角度建筑物影响的有限元分析[J]. 岩土工程学报, 2012, 34(4): 615–624. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201204008.htm ZHENG Gang, LI Zhi-wei. Finite element analysis of response of buildings with arbitrary angle adjacent to excavations[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(4): 615–624. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201204008.htm
[23]	城市轨道交通结构安全保护技术规范: GJJ/T 202—2013[S]. 北京: 中国建筑工业出版社, 2013. Technical Specification for Structural Safety Protection of Urban Rail Transit: GJJ/T 202—2013[S]. China Architecture & Building Press, 2013. (in Chinese)
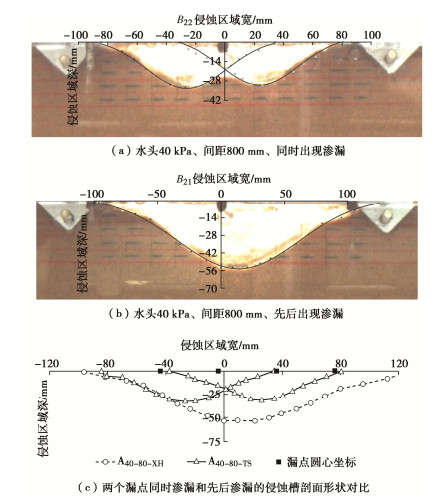
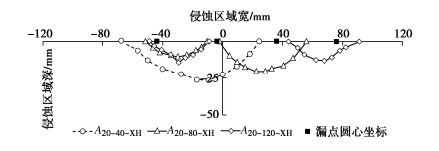
[24]	ZHENG G, TONG J B, ZHANG T Q, et al. Progression of backward erosion piping with sudden and gradual hydraulic loads[J]. Acta Geotechnica, 2021: 1–7.
[25]	VAN BEEK V M, BEZUIJEN A, SELLMEIJER J B, et al. Initiation of backward erosion piping in uniform sands[J]. Géotechnique, 2014, 64(12): 927–941. doi: 10.1680/geot.13.P.210
[26]	VAN BEEK V M, VAN ESSEN H M, VANDENBOER K, et al. Developments in modelling of backward erosion piping[J]. Géotechnique, 2015, 65(9): 740–754. doi: 10.1680/geot.14.P.119
[27]	VANDENBOER K, VAN BEEK V M, BEZUIJEN A. 3D character of backward erosion piping[J]. Géotechnique, 2018, 68(1): 86–90. doi: 10.1680/jgeot.16.P.091
[28]	郑刚, 程雪松. 长短桩组合排桩悬臂支护工作机理试验研究[J]. 岩土工程学报, 2008, 30(增刊1): 410–415. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2008S1089.htm ZHENG Gang, CHENG Xue-song. Experimental study on cantilever contiguous retaining piles with different lengths[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(S1): 410–415. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2008S1089.htm
[29]	李竹, 郑刚, 王海旭. 带水平支撑长短桩组合排桩工作性状模型试验研究[J]. 岩土工程学报, 2010, 32(增刊1): 440–446. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2010S1087.htm LI Zhu, ZHENG Gang, WANG Hai-xu. Model tests on work behaviors of retaining piles with different lengths and horizontal support[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(S1): 440–446. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2010S1087.htm
[30]	CHEN R P, MENG F Y, LI Z C, et al. Investigation of response of metro tunnels due to adjacent large excavation and protective measures in soft soils[J]. Tunnelling and Underground Space Technology, 2016, 58: 224–235. doi: 10.1016/j.tust.2016.06.002
[31]	王卫东, 沈健, 翁其平, 等. 基坑工程对邻近地铁隧道影响的分析与对策[J]. 岩土工程学报, 2006, 28(增刊1): 1340–1345. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2006S1006.htm WANG Wei-dong, SHEN Jian, WENG Qi-ping, et al. Analysis and countermeasures of influence of excavation on adjacent tunnels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(S1): 1340–1345. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2006S1006.htm
[32]	郑刚, 潘军, 程雪松, 等. 基坑开挖引起隧道水平变形的被动与注浆主动控制研究[J]. 岩土工程学报, 2019, 41(7): 1181–1190. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201907002.htm ZHENG Gang, PAN Jun, CHENG Xue-song, et al. Passive control and active grouting control of horizontal deformation of tunnels induced neighboring excavation[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(7): 1181–1190. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201907002.htm
[33]	ZHENG G, PAN J, CHENG X S, et al. Use of grouting to control horizontal tunnel deformation induced by adjacent excavation[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2020, 146(7): 05020004. doi: 10.1061/(ASCE)GT.1943-5606.0002276
[34]	秦宏亮. 钢支撑轴力伺服系统技术在基坑开挖中的应用[J]. 建筑施工, 2019, 41(7): 1195–1198. https://www.cnki.com.cn/Article/CJFDTOTAL-JZSG201907005.htm QIN Hong-liang. Application of steel support axis force servo system technology to foundation pit excavation[J]. Building Construction, 2019, 41(7): 1195–1198. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JZSG201907005.htm
[35]	DIAO Y, BI C, DU Y M, et al. Greenfield test and numerical study on grouting in silty clay to control horizontal displacement of underground facilities[J]. International Journal of Geomechanics, 2021, 21(10): 04021178. doi: 10.1061/(ASCE)GM.1943-5622.0002140
[36]	刁钰, 李光帅, 郑刚. 一种控制土体变形的单点囊式注浆装置: CN208235526U[P]. 2018-12-14. DIAO Yu, LI Guang-shuai, ZHENG Gang. Single-Point Capsule Grouting Device to Control Soil Deformation: CN208235526U[P]. 2018-12-14. (in Chinese)
[37]	刁钰, 杨超, 郑刚. 一种控制土体变形的多点囊式注浆装置及其方法: CN208235526U[P]. 2018-12-14. DIAO Yu, Yang Chao, ZHENG Gang. Multiple-Point Capsule Grouting Device to Control Soil Deformation Device: CN208235524U[P]. 2018-12-14. (in Chinese)
[38]	ZHENG G, SU Y M, DIAO Y, et al. Field measurements and analysis of real-time capsule grouting to protect existing tunnel adjacent to excavation[J]. Tunnelling and Underground Space Technology, 2021, 122: 104350.
[39]	ZHENG G, HUANG J Y, DIAO Y, et al. Formulation and performance of slow-setting cement-based grouting paste (SCGP) for capsule grouting technology using orthogonal test[J]. Construction and Building Materials, 2021, 302: 124204. doi: 10.1016/j.conbuildmat.2021.124204
[40]	曾超峰, 薛秀丽, 郑刚. 基坑工程长期地下水回灌控沉应注意的几个问题[J]. 土木工程学报, 2019, 52(增刊2): 127–131. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2019S2018.htm ZENG Chao-feng, XUE Xiu-li, ZHENG Gang. Problems needed to be noticed for artificial recharge in deep excavation for settlement control[J]. China Civil Engineering Journal, 2019, 52(S2): 127–131. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC2019S2018.htm
[41]	郑刚, 哈达, 程雪松, 等. 回灌开启时间对地层沉降与应力应变的影响[J]. 天津大学学报(自然科学与工程技术版), 2020, 53(2): 180–191. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX202002009.htm ZHENG Gang, HA Da, CHENG Xue-song, et al. Impact of recharge wells' opening time on the subsidence, stress, and strain of soil[J]. Journal of Tianjin University (Science and Technology), 2020, 53(2): 180–191. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX202002009.htm
[42]	HA D, ZHENG G, ZHOU H Z, et al. Estimation of hydraulic parameters from pumping tests in a multiaquifer system[J]. Underground Space, 2020, 5(3): 210–222. doi: 10.1016/j.undsp.2019.03.006
[43]	郑刚, 曾超峰, 刘畅, 等. 天津首例基坑工程承压含水层回灌实测研究[J]. 岩土工程学报, 2013, 35(增刊2): 491–495. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2084.htm ZHENG Gang, ZENG Chao-feng, LIU Chang, et al. Field observation of artificial recharge of confined water in first excavation case in Tianjin[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 491–495. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2084.htm
[44]	郑刚, 曹剑然, 程雪松, 等. 考虑承压含水层间越流的地下水回灌现场试验研究[J]. 岩土工程学报, 2019, 41(9): 1609–1618. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909005.htm ZHENG Gang, CAO Jian-ran, CHENG Xue-song, et al. Field tests on groundwater recharge considering leakage between semiconfined aquifers[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(9): 1609–1618. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201909005.htm
[45]	岳清瑞. 钢结构与可持续发展[J]. 建筑, 2021(13): 20–21, 23. https://www.cnki.com.cn/Article/CJFDTOTAL-JANZ202113007.htm YUE Qing-rui. Steel structure and sustainable development[J]. Construction and Architecture, 2021(13): 20–21, 23. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-JANZ202113007.htm
[46]	郑刚, 陈红庆, 雷扬, 等. 基坑开挖反压土作用机制及其简化分析方法研究[J]. 岩土力学, 2007, 28(6): 1161–1166. doi: 10.3969/j.issn.1000-7598.2007.06.018 ZHENG Gang, CHEN Hong-qing, LEI Yang, et al. A study of mechanism of earth berm and simplified analysis method for excavation[J]. Rock and Soil Mechanics, 2007, 28(6): 1161–1166. (in Chinese) doi: 10.3969/j.issn.1000-7598.2007.06.018
[47]	李顺群, 郑刚, 王英红. 反压土对悬臂式支护结构嵌固深度的影响研究[J]. 岩土力学, 2011, 32(11): 3427–3431, 3436. doi: 10.3969/j.issn.1000-7598.2011.11.037 LI Shun-qun, ZHENG Gang, WANG Ying-hong. Influence of earth berm on embedment depth of cantilever retaining structure for pit excavation[J]. Rock and Soil Mechanics, 2011, 32(11): 3427–3431, 3436. (in Chinese) doi: 10.3969/j.issn.1000-7598.2011.11.037
[48]	郑刚, 李欣, 刘畅, 等. 考虑桩土相互作用的双排桩分析[J]. 建筑结构学报, 2004, 25(1): 99–106. doi: 10.3321/j.issn:1000-6869.2004.01.014 ZHENG Gang, LI Xin, LIU Chang, et al. Analysis of double-row piles in consideration of the pile-soil interaction[J]. Journal of Building Structures, 2004, 25(1): 99–106. (in Chinese) doi: 10.3321/j.issn:1000-6869.2004.01.014
[49]	郑刚, 郭一斌, 聂东清, 等. 大面积基坑多级支护理论与工程应用实践[J]. 岩土力学, 2014, 35(增刊2): 290–298. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2014S2041.htm ZHENG Gang, GUO Yi-bin, NIE Dong-qing, et al. Theory of multi-bench retaining for large area foundation pit and its engineering application[J]. Rock and Soil Mechanics, 2014, 35(S2): 290–298. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2014S2041.htm
[50]	ZHOU H Z, ZHENG G, HE X P, et al. Numerical modelling of retaining structure displacements in multi-bench retained excavations[J]. Acta Geotechnica, 2020, 15(9): 2691–2703. doi: 10.1007/s11440-020-00947-3
[51]	郑刚, 程雪松, 刁钰. 无支撑多级支护结构稳定性与破坏机理分析[J]. 天津大学学报, 2013, 46(4): 304–314. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX201304005.htm ZHENG Gang, CHENG Xue-song, DIAO Yu. Analysis of the stability and collapse mechanism of non-prop and multi-stage retaining structure[J]. Journal of Tianjin University, 2013, 46(4): 304–314. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDX201304005.htm
[52]	任望东, 张同兴, 张大明, 等. 深基坑多级支护破坏模式及稳定性参数分析[J]. 岩土工程学报, 2013, 35(增刊2): 919–922. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2173.htm REN Wang-dong, ZHANG Tong-xing, ZHANG Da-ming, et al. Parametric analysis of failure modes and stability of muti-level retaining structure in deep excavations[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 919–922. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2173.htm
[53]	郑刚, 聂东清, 刁钰, 等. 基坑多级支护破坏模式研究[J]. 岩土力学, 2017, 38(增刊1): 313–322. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2017S1047.htm ZHENG Gang, NIE Dong-qing, DIAO Yu, et al. Failure mechanism of multi-bench retained foundation pit[J]. Rock and Soil Mechanics, 2017, 38(S1): 313–322. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2017S1047.htm
[54]	郑刚, 聂东清, 程雪松, 等. 基坑分级支护的模型试验研究[J]. 岩土工程学报, 2017, 39(5): 784–794. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201705003.htm ZHENG Gang, NIE Dong-qing, CHENG Xue-song, et al. Experimental study on multi-bench retaining foundation pit[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(5): 784–794. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201705003.htm
[55]	刘杰, 郑刚, 聂东清. 天津软土地区深基坑多级支护结构变形的参数分析[J]. 石家庄铁道大学学报(自然科学版), 2018, 31(1): 47–54. https://www.cnki.com.cn/Article/CJFDTOTAL-SJZT201801009.htm LIU Jie, ZHENG Gang, NIE Dong-qing. Parametric analysis on deformation of multi-bench retaining system of deep foundation pit in Tianjin soft ground area[J]. Journal of Shijiazhuang Tiedao University (Natural Science Edition), 2018, 31(1): 47–54. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-SJZT201801009.htm
[56]	郑刚, 白若虚. 倾斜单排桩在水平荷载作用下的性状研究[J]. 岩土工程学报, 2010, 32(增刊1): 39–45. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2010S1009.htm ZHENG Gang, BAI Ruo-xu. Behaviors study of inclined single row contiguous retaining piles under horizontal force[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(S1): 39–45. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2010S1009.htm
[57]	DIAO Y, ZHU P Y, JIA Z Y, et al. Stability analysis and safety factor prediction of excavation supported by inclined piles in clay[J]. Computers and Geotechnics, 2021, 140: 104420. doi: 10.1016/j.compgeo.2021.104420
[58]	周海祚, 郑刚, 何晓佩, 等. 基坑倾斜桩支护稳定特性及分析方法研究[J/OL]. 岩土工程学报: 1-8. [2021-12-02]. http://kns.cnki.net/kcms/detail/32.1124.tu.20210809.1654.004.html. ZHOU Hai-zuo, ZHENG Gang, HE Xiao-pei, et al. Study on stability characteristics and analysis method of inclined retaining walls in excavations[J]. Chinese Journal of Geotechnical Engineering, 2021, 1-8. [2021-12-02]. http://kns.cnki.net/kcms/detail/32.1124.tu.20210809.1654.004.html. (in Chinese)
[59]	郑刚, 王玉萍, 程雪松, 等. 基坑倾斜桩支护性能及机理大型模型试验研究[J]. 岩土工程学报, 2021, 43(9): 1581–1591. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202109003.htm ZHENG Gang, WANG Yu-ping, CHENG Xue-song, et al. Large-scale model tests on performance and mechanism of inclined retaining structures of excavations[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(9): 1581–1591. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC202109003.htm
[60]	郑刚, 何晓佩, 周海祚, 等. 基坑斜-直交替支护桩工作机理分析[J]. 岩土工程学报, 2019, 41(增刊1): 97–100. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S1026.htm ZHENG Gang, HE Xiao-pei, ZHOU Hai-zuo, et al. Working mechanism of inclined-vertical retaining piles in excavations[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(S1): 97–100. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2019S1026.htm
[61]	郑刚, 吴小波, 周海祚, 等. 基坑倾斜桩无支撑支护机理与工程应用[J]. 施工技术, 2021, 50(13): 157–162, 178. ZHENG Gang, WU Xiao-bo, ZHOU Hai-zuo, et al. Supporting method and applications of incline retaining piles in foundation excavation[J]. Construction Technology, 2021, 50(13): 157–162, 178. (in Chinese)

施引文献(15)

期刊类型引用(8)

1.	宋二祥. 饱和土不排水计算理论与方法探究. 岩土工程学报. 2025(01): 1-29 . 本站查看
2.	史元祺，曹振中，景立平，莫红艳. 基于剪切破坏面修正的地基极限承载力计算方法. 地下空间与工程学报. 2025(01): 31-41 . 百度学术
3.	杨峰，慈新航，高益康，赵炼恒. 底部刚性层限制条件下条形基础地基承载力系数N_c与破坏模式. 岩石力学与工程学报. 2023(04): 1031-1040 . 百度学术
4.	曹振中，卢秀莲，莫红艳，秦志光，史元祺. 高内摩擦角下珊瑚礁砂地基极限承载力初步分析. 岩石力学与工程学报. 2023(S1): 3609-3617 . 百度学术
5.	谢得峰，张文，杨晓林，范延彬，张秉来，王新红，袁媛，韩磊磊. 倾斜荷载盐渍土地基承载力数值计算与试验研究. 科学技术与工程. 2023(16): 7033-7043 . 百度学术
6.	刘润，宋毅然，练继建，林毅峰，汪嘉钰. 成层土中海上风电筒型基础竖向承载影响深度研究. 河北工程大学学报(自然科学版). 2023(04): 1-8+24 . 百度学术
7.	宋二祥，陈星屹，林世杰. 关于偏心荷载下地基承载力的验算方法. 岩土力学. 2022(07): 1925-1932 . 百度学术
8.	王艳坤，刘杰，宋玲，张兴疆，高斌. 土工格室加固风积沙地基模型试验研究. 公路交通科技. 2022(07): 40-48 . 百度学术