基于极限平衡原理的地震边坡浅层和深层耦合滑移分析

宋健; 陆朱汐; 谢华威; 张飞; 姬建; 高玉峰

doi:10.11779/CJGE20220035

基于极限平衡原理的地震边坡浅层和深层耦合滑移分析 English Version

宋健^{1, 2,},
陆朱汐²,
谢华威²,
张飞^{1, 2},
姬建^{1, 2},
高玉峰^{1, 2, ,}

1.
河海大学岩土力学与堤坝工程教育部重点实验室, 江苏南京 210024
2.
河海大学土木与交通学院, 江苏南京 210024

基金项目:

国家自然科学基金面上项目 52178325

国家自然科学基金面上项目 51879091

中央高校基本科研业务费专项资金项目 B210202046

详细信息

作者简介:
宋健(1988—)，男，副教授，硕士生导师，主要从事岩土地震工程、边坡工程等方面的教学和科研工作。E-mail：jiansonghh@163.com

通讯作者:
高玉峰，E-mail: yfgao66@163.com

中图分类号: TU435
计量
- 文章访问数: 454
- HTML全文浏览量: 67
- PDF下载量: 160
出版历程
- 收稿日期: 2022-01-16
- 网络出版日期: 2023-02-08
- 刊出日期: 2023-05-31

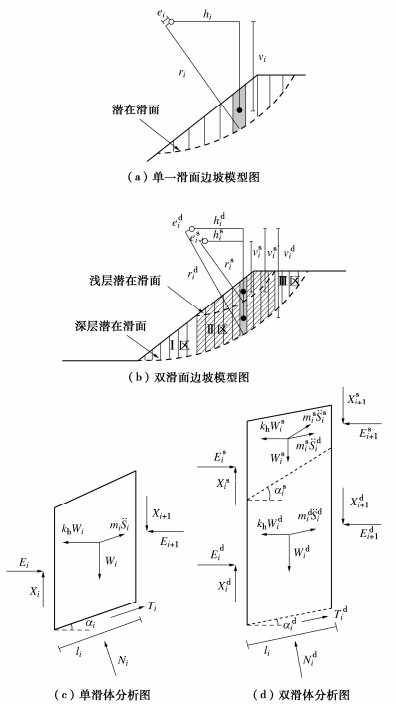
Analysis of coupled shallow and deep sliding of slopes induced by earthquake based on limit equilibrium method

SONG Jian^{1, 2,},
LU Zhuxi²,
XIE Huawei²,
ZHANG Fei^{1, 2},
JI Jian^{1, 2},
GAO Yufeng^{1, 2, ,}

1.
Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University, Nanjing 210024, China
2.
College of Civil and Transportation Engineering, Hohai University, Nanjing 210024, China

摘要

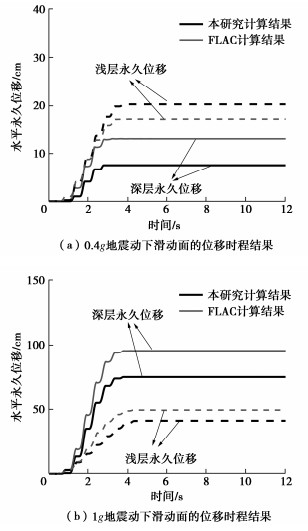
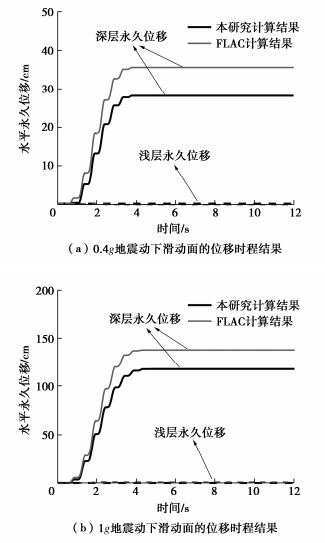
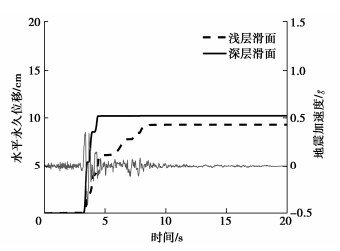
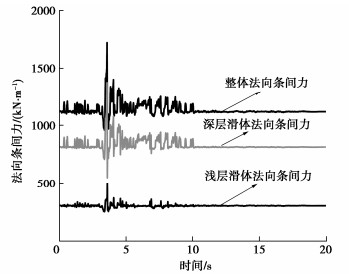
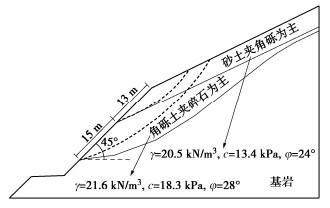
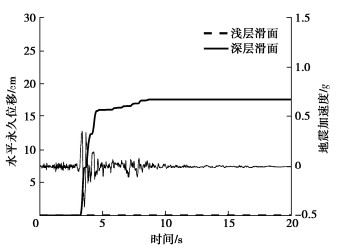
摘要: 边坡地震位移是评价边坡地震稳定性的重要指标，现有的地震位移分析方法主要针对单一滑动面边坡。基于Spencer极限平衡分析原理，提出了一种滑面为非平面的双滑面土质边坡地震位移计算方法。该方法基于考虑惯性力的极限平衡条分法建立双滑面滑块体系在地震过程中的动力平衡方程，考虑地震引起两个滑动面滑移变形过程中浅层和深层滑体之间的相互影响。将研究方法的结果与有限差分软件FLAC的数值模拟结果进行对比，证明了方法描述地震引起边坡浅层和深层耦联滑移变形模式的合理性和正确性；并将建立的方法分别用于分层土堆积层边坡以及川藏俄岗公路老折山边坡，阐明了该方法用于实际双滑面边坡地震位移计算的可行性。
- 地震边坡稳定性 /
- Newmark滑块分析 /
- 双滑动面 /
- 极限平衡条分法 /
- 动力平衡方程
Abstract: The displacement of seismic slopes is an important index to evaluate their stability. The existing seismic displacement analysis methods are mainly aimed at the slope with single sliding surface. Based on the Spencer limit equilibrium analysis principle, a method for calculating the seismic displacement of slopes with double non-planar slip surfaces is proposed. By using the limit equilibrium slice method considering the seismically inertial force, the dynamic equilibrium equations for the double-sliding block system during earthquake shaking is established, and the interaction between shallow and deep sliding bodies in the sliding process caused by earthquake is considered. The results by the proposed method are compared with the numerical results of finite difference software FLAC, which proves the rationality and correctness of the method in describing the coupled shallow and deep seismic sliding pattern of slopes. The proposed method is then applied to the layered soil accumulation slope and the Laozheshan slope of section Egang of Sichuan-Tibet Highway, respectively. The feasibility of the proposed method for calculating the seismic displacement of actual slopes with double potential slip surfaces is clarified.
- seismic slope stability /
- Newmark sliding block analysis /
- double-sliding surface /
- limit equilibrium slice method /
- dynamic equilibrium equation

HTML全文

0. 引言

岩土锚固技术因其适应性强，工程造价低的特点，被广泛用于岩体加固和支护，其中锚杆（索）锚固体-岩体界面有效黏结是锚杆（索）正常工作的基础^[1]。大量的工程实践表明，岩土体与锚固体的界面脱黏是导致锚固系统失效的重要诱因，对锚固系统的研究应该重点放在这一界面的力学性质上^[2-3]。

岩土体-工程体的界面力学性质受到两侧材料性能差异，黏结界面粗糙度等众多因素影响，相关的试验研究已经广泛开展，Ozturk等^[4]基于界面张拉试验结果，认为岩石矿物颗粒越大，则混凝土与岩体的法向黏结越强，界面粗糙度对法向黏结强度影响较小。Krounis等^[5]基于岩石-混凝土界面剪切试验，认为粗糙度对界面剪切强度的影响较为明显；Malngren等^[6]则指出，在粗糙界面条件下，岩石矿物组成对界面抗剪强度影响较大。Shen等^[7]认为岩石材料的亲疏水特性对于岩石-混凝土二元体黏结强度也有较大影响。Dong等^[8-9]从断裂力学的角度分析了岩石-混凝土界面的破坏模式，提出了一种剪切软化模型。岩土体与锚固体的界面是一种典型的岩土体-工程体界面，Kilic等^[10]认为在水泥材料中增加膨胀剂可以提高水泥锚固体与岩土体间的挤压作用，从而增加黏结强度。关于水泥锚固体与岩土体的黏结，尤春安等^[11-12]，陈昌富等^[13-14]开展了较为系统的试验研究，建立了相应的脱黏模型和松弛模型。综上所述，现有研究一般认为锚固体-岩体界面是薄弱面，而没有充分考虑其他形式破坏的可能性，尤其是对于软弱岩体，锚固体拉拔过程中岩体可能优先于黏结界面破坏。

除常规的界面剪切和锚固体拉拔试验外，数值模拟也被广泛用于二元体界面力学性能的研究，传统的有限元方法可以较好地模拟岩体和锚固体的变形，但在模拟岩体破碎、界面脱黏等非连续过程时适用性不佳。为模拟混凝土-岩体的界面脱黏，Tian等^[15]提出了一种基于平界面黏结的接触模型，Dong等^[16]则给出了界面断裂区模型。Tatone等^[17-18]采用了无厚度线性单元对锚杆加固进行了研究，刘泉声等^[19]则进行了软弱围岩锚喷-注浆加固的模拟，文献[15~19]的模拟均取得了较好的效果。可见基于界面单元的数值方法，如耦合有限-离散元^[20]（FDEM）在一定程度上解决了非连续变形问题的模拟，且该方法已被用于岩石破坏过程的模拟^[21-24]，计算效率高于离散元模型，理论上也适用于锚固体脱黏过程的模拟。

本文首先开展了黏土岩的三轴剪切试验（固结不排水）和黏土岩-砂浆的界面剪切试验，基于试验结果建立了二元体的耦合有限-离散元模型，讨论了界面模型的选择，并标定了相关模型参数；然后通过对界面形态的优化，使得界面咬合和剪胀作用得以体现，模拟了黏土岩中水泥锚固体的拉拔试验，分析了锚固体滑移脱黏过程。最后对本文模拟方法的可靠性，网格依赖性和适用性条件进行了补充讨论。

1. 试验设计

1.1 黏土岩三轴剪切试验

首先通过室内试验对黏土岩的物理力学参数进行测定。试验样品采自甘肃天水罗峪沟附近某在建穿山隧道，为新近系红层泥岩，中等风化，含少量赤铁矿，泥质结构半成岩，天然状态下为红棕色弱可塑性块体，室内试验测得其基础物理参数如表 1所示。

表 1 黏土岩基础物理参数

Table 1. Physical parameters of clay rock

干密度/(g·cm^-3)	塑限/%	液限/%	缩限/%	天然含水率/%	灵敏度	莫氏硬度
1.72	22.4	31.6	10.8	14.2	1.07	2

下载: 导出CSV

| 显示表格

将天然试样粉碎烘干后，按天然含水率重新压实，制成39.1 mm×80 mm的试样，测得重塑后的黏土岩密度为1.94~1.97 g/cm³，与原状样品一致。重塑黏土岩试样制备完成后（不饱水）直接进行三轴剪切试验。

三轴试验采用固结不排水（CU）方式进行加载，试验分为5组，围压分别为50，100，200，30，400 kPa，对应的偏应力-位移曲线如图 1所示。

图 1 黏土岩三轴固结不排水剪切试验

Figure 1. Triaxial shear (CU) tests on clay rock

下载: 全尺寸图片幻灯片

由图 1所示的三轴试验结果计算得固结不排水条件下黏土岩的内摩擦角为36.8°，黏聚力为170.4 kPa。

1.2 黏土岩-砂浆二元体界面剪切试验

黏土岩与锚固体的界面力学性能采用直接剪切试验获得。考虑到黏土岩易于模具黏连，大尺寸方形试样难以制备，本文待测试样的制备过程如图 2（a）所示，首先利用直径61.8 mm，高20 mm的环刀制作黏土岩试样，然后利用顶样器（垫块）将试样顶出10 mm，并用钢丝锯将顶出部分切除，最后在环刀内浇注10 mm水泥砂浆，待养护完成后顶出即可。制备试样所用砂浆配比为水︰水泥︰砂= 0.5︰1︰1.2，其中水泥为标号42.5的普通硅酸盐水泥，砂为洗净的级配粗砂。界面剪切试验装置为应变式电动直剪仪，剪切速度为1 mm/min，试验也分为5组，法向压力分别为50，100，200，300，400 kPa，得到得黏土岩-水泥砂浆二元体典型的破坏形态如图 2（b）所示，剪应力-剪切位移曲线如图 2（c）所示。

图 2 黏土岩-水泥砂浆界面剪切试验

Figure 2. Direct shear tests on clay rock-cement mortar (C-C) interface

下载: 全尺寸图片幻灯片

由图 2（c）中的剪应力-剪切位移曲线可知，二元体界面的破坏有明显的脆性特征，在剪应力达到峰值后出现了快速跌落，随后趋于稳定，抗剪强度和残余强度均与法向压力正相关。再结合图 2（b）中的破坏形态可知，在不同法向压力条件下黏土岩-水泥砂浆的界面破坏模式有本质性的区别，当法向压力为50，100 kPa时，破坏面位于黏土岩区域，在砂浆侧可以观察到大量的黏土岩黏连；而当法向压力大于或等于200 kPa时，破坏面均为二元体界面。分析认为，由于黏土岩的黏聚力小于黏土岩-砂浆二元体间的切向黏结强度，法向压力较小时（σ_n≤100 kPa）主要为黏土岩的剪切破坏；同时，黏土岩的内摩擦角较大，tanφ=0.75，内摩擦产生的抗剪强度大于二元体界面摩擦效应，因此随着法向压力的增加，二元体的剪切破坏由黏土岩自身的剪切破坏逐渐转变为界面的剪切脱黏，这一特点明显区别于硬岩-混凝土二元体。

2. 界面模型与参数标定

2.1 二元体的FDEM模型

数值模拟方法作为一种辅助性的研究手段，有助于定量描述二元体的抗剪性能，本文基于有限-离散元方法，建立了二元体组合结构模型，对界面破坏过程进行具体分析。

如图 3所示，有限-离散元方法（FDEM）的基本思想是采用独立节点和接触模型替代有限元的共节点模型，通过接触单元或接触关系的失效来模拟裂纹的萌生和扩展，从而实现材料由连续介质模型向非连续介质模型的过渡。

图 3 有限-离散元方法的基本思路

Figure 3. Basic theory and deformation modes of FDEM

下载: 全尺寸图片幻灯片

当接触单元未失效前，FDEM采用有限元方法（FEM）计算模型的连续变形和节点力；当接触单元达到失效条件后，虚拟裂纹被激活，FDEM将使用离散元方法（DEM）计算两侧单元的相互作用（节点的非连续位移和节点力）。

对于岩石和混凝土等准脆性材料，一般认为裂纹尖端附近区域存在如图 4所示的剪切断裂过程区（FPZ）。在宏观裂纹出现以前，这一区域应力应变曲线可以分为峰值变形前的应变硬化阶段和达到峰值应变后的应变软化阶段，而非在应力峰值点出现脆性断裂。因此，为了体现裂纹尖端附近区域力学性质的变化，在岩石和混凝土的FDEM模型中，常选择无厚度的黏聚力单元作为接触单元。

图 4 剪切断裂过程区（FPZ）

Figure 4. Shear fracture process zone (FPZ)

下载: 全尺寸图片幻灯片

根据室内试验结果，二元体的潜在破坏面位于黏结界面和黏土岩区域，而水泥砂浆部分在剪切过程中未出现破坏，同时砂浆弹性模量实测值24.7~27.5 GPa也远大于黏土岩，因此可将砂浆部简化为线弹性材料甚至刚体，采用有限元模型进行分析。对于界面和黏土岩区域，由于其力学性能的差异较大，应当分别进行建模，为此本文建立的FDEM模型如图 5所示，包括两类黏聚力单元（黏土岩黏聚力单元和界面黏聚力单元）。由于本文的研究重点关注剪切破坏，故只考虑切向损伤和对应的剪切失效模式，黏聚力单元自身没有厚度，无“应变”的概念，其本构方程为应力-位移关系（τ-δ曲线）：

$\tau =\left\{ \begin{array}{l}{K}_{\text{s}}\delta \hfill & （0\le \delta < {\delta }_{\text{ini}}）\hfill \\ {K}_{\text{s}}{\delta }_{\text{ini}}(1-D)\hfill & （{\delta }_{\text{ini}}\le \delta < {\delta }_{\text{fa}}）\hfill \end{array} \right.。$

(1)

图 5 双线性黏聚力单元本构及破坏模式（示意图）

Figure 5. Bi-linear constitutive equation for cohesive element

下载: 全尺寸图片幻灯片

式中：τ为黏聚力单元的切应力；K_s为剪切刚度，其定义为单位剪切变形产生的切应力，量纲为ML^-2T^-2；D为损伤变量；δ为对应的剪切位移； δ_ini为损伤起始位移；δ_fa为剪切失效位移。

考虑到黏土岩的塑形特征，拟采用软化型的双线性黏聚力单元进行模拟，其损伤变量可表示为

$D = \frac{{\delta - {\delta _{{\text{ini}}}}}}{{{\delta _{{\text{fa}}}} - {\delta _{{\text{ini}}}}}}\begin{array}{*{20}{c}} {}&{(\delta > {\delta _{{\text{ini}}}})} \end{array}。$

(2)

当δ < ${\delta _{{\text{ini}}}}$ 时，黏聚力单元处于无损的线弹性状态，当 ${\delta _{{\text{ini}}}}$ ≤δ < ${\delta _{{\text{fa}}}}$ ，黏聚力单元出现损伤，当δ = ${\delta _{{\text{fa}}}}$ 时，黏结失效。

由式（1）及图 5可知，黏聚力单元在剪切方向具有3个独立的参数，从直观的角度，选择损伤起始位移δ_ini，失效位移δ_fa和抗剪强度τ_max为基础参数是合适的；而从力学的角度，选择抗剪强度τ_max，剪切刚度K_s和剪切断裂能G为基础参数更具有代表性，其中剪切断裂G为图 5中剪应力-剪切位移曲线下方面积，具有MT^-2量纲，可表示为

$G = \frac{1}{2}{\delta _{{\text{fa}}}}{\tau _{\max }}。$

(3)

2.2 黏土岩参数的标定

黏土岩部分的实体单元为线弹性材料，材料参数可由无侧限试验得到，弹性模量E_c=12.7 MPa，泊松比 ${\nu _{\text{c}}}$ =0.3。而黏聚力单元的参数则需要通过三轴剪切试验进行标定，要求数值模拟得到的三轴剪切强度包络线与室内试验基本一致。标定的参数如表 2所示，所建立的数值模型及模拟的破坏形态如图 6（a）所示，对应的三轴剪切包络线如图 6（b）所示。

表 2 黏土岩黏聚力单元参数

Table 2. Parameters of cohesive element of clay rock

G/ (N·m^-1)	K_s /(Pa·m^-1)	τ_max /Pa	δ_ini /m	δ_f /m
18.9	6.30×10⁹	1.68×10⁵	3.33×10^-5	2.25×10^-4

下载: 导出CSV

| 显示表格

图 6 黏土岩黏聚力单元参数的标定过程

Figure 6. Calibration process of cohesive parameters of clay rock

下载: 全尺寸图片幻灯片

由图 4可知，表 2中的参数所模拟得到的偏应力包络线与试验值的差异较小，且破坏形态较为类似，均为斜截面的剪切破坏除100 kPa数值模型外，其余模型均由左下角起裂，并向右上延伸形成剪切带。根据数值模拟结果，笔者认为只考虑剪切失效的FDEM在模拟软岩、极软岩，甚至压实硬黏土时也是适用的。

2.3 界面参数的标定

根据图 2（c）中的界面试验结果，二元体界面剪切破坏无软化阶段，即损伤起始位移与剪切失效位移相等。假定界面为唯一潜在的脆性破坏面，仍采用式（1）中的模型，那么界面黏聚力参数理论上与宏观力学参数存在如下的对应关系：

${\tau _{\max }} = \frac{{{T_{\max }}}}{A}\text{，}$

(4)

${\delta _{{\text{fa}}}} = {\delta _{{\text{ini}}}} = \frac{{{d_{{\text{fa}}}}}}{n}。$

(5)

式中：T_max为宏观的界面抗剪力；d_fa为宏观的破坏位移；A为界面面积，对于二维模型，则表示界面长度；n为界面在剪切方向的单元数，与模型网格尺寸相关。

本文建立的界面剪切试验数值模型如图 7（a）所示，水泥砂浆和黏土岩部分尺寸均为61.8 mm×10 mm，其中砂浆部分采用有限元模型，黏土岩部分采用已标定的FDEM模型，界面部分为一层参数待标定的黏聚力单元。以法向压力300，400 kPa时的剪应力-剪切位移曲线为依据，得到界面黏聚力模型的参数如表 3所示，模拟得到法向压力为50，100 kPa时的剪应力-剪切位移曲线如图 7（b）所示。

图 7 黏土岩-砂浆二元体界面剪切模型

Figure 7. Direct shear model for C-C interface

下载: 全尺寸图片幻灯片

表 3 界面黏聚力单元参数

Table 3. Parameters of cohesive elements of C-C interface

σ_n /kPa	G/ (N·m^-1)	K_s/ (Pa·m^-1)	τ_max /Pa	$\frac{{{\delta _{{\text{ini}}}}}}{{{\delta _{{\text{fa}}}}}}{\text{/m}}$
400	11.51	1.04×10¹⁰	4.91×10⁵	4.69×10^-5
300	12.28	7.45×10⁹	4.28×10⁵	5.74×10^-5

下载: 导出CSV

| 显示表格

由图 7（b）可知，基于宏观试验得到的细观参数能够描述界面的破坏过程，且数值模拟得到的抗剪强度与试验值之差小于5%。但这一方法也存在一个明显的不足，即需要通过重复标定参数来考虑法向压力对界面抗剪强度的影响，且无法考虑界面脱黏后的残余变形阶段，模拟得到的脆性断裂与试验结果不一致，因此在理论上并不完善，也不适用复杂应力状态下的模拟。笔者认为，可以将切向黏结效应和摩擦效应分开考虑，并假设两者独立，即脱黏并不影响摩擦效应

$\tau = {\tau _{{\text{coh}}}} + {\tau _{{\text{fr}}}}。$

(6)

式中：τ_coh为切向界面黏结应力；τ_fr为界面摩擦应力。

通过对图 2（c）中的抗剪强度和残余强度的分析发现，残余强度τ_res与法向压力间存在较好的线性关系；而抗剪强度与残余强度之差(τ_max-τ_res) 随法向应力的增加无明显变化，具体如图 8（a）所示，即有

$\left. \begin{array}{l}{\tau }_{\text{res}}=k{\sigma }_{\text{n}}\text{，}\\ ({\tau }_{\mathrm{max}}-{\tau }_{\text{res}})=({{\tau }_{\text{coh}}})_{\mathrm{max}}。\end{array}\right\}$

(7)

图 8 界面摩擦效应及本构模型

Figure 8. Friction characteristics and constitutive model for interface

下载: 全尺寸图片幻灯片

式中：k为界面动摩擦系数；(τ_coh)_max为界面最大黏结应力，对于黏土岩-砂浆界面，可取0.586，248.1 kPa。

根据试验结果，黏结界面的剪切没有静摩擦阶段，因此需要对加载初期τ＜τ_res阶段（初始摩擦阶段）进行特殊处理，本文将该阶段剪应力与剪切位移的关系线性化处理，那么就有

$\tau_{\mathrm{fr}}=\left\{\begin{array}{ll} K_{\mathrm{t}} \cdot \delta & \left(0 \leqslant \delta<\delta_{\mathrm{i}}\right) \\ \tau_{\mathrm{res}}=K_{\mathrm{t}} \cdot \delta_{\mathrm{i}} & \left(\delta \geqslant \delta_{\mathrm{i}}\right) \end{array} 。\right.$

(8)

式中：δ_i为初始摩擦阶段的最大位移；K_t为初始摩擦阶段的剪切刚度。当δ≥δ_i后，界面的摩擦强度不再增加，剪应力由摩擦效应和黏结效应共同产生，其中黏结效应产生的剪应力满足：

$\tau_{\mathrm{coh}}=\left\{\begin{array}{ll} K_{\mathrm{s}} \cdot \delta & \left(\delta_{\mathrm{i}} \leqslant \delta<\delta_{\mathrm{f}}\right) \\ 0 & \left(\delta \geqslant \delta_{\mathrm{f}}, \delta \leqslant \delta_{\mathrm{i}}\right) \end{array} 。\right.$

(9)

式（7）~（9）对应的黏结摩擦模型本构如图 6（b）所示。特别地，根据图 2中的剪应力-剪切位移曲线，在峰前段的线性特征，本模型认为初始摩擦阶段和黏结变形阶段具有相同的剪切刚度，即K_t=K_s。

图 6的新模型仍有δ_f，K_s，k 3个待标定的模型参数。其中δ_f仍可按式（5）标定δ_fa的方法进行标定；k可以由图 6（a）的曲线拟合得到，K_s则可以由抗剪强度和破坏位移进行标定，

${K_{\text{s}}} = {\text{average}}\left( {\frac{{{\tau _{\max }}}}{{{\delta _{\text{f}}}}}} \right)。$

(10)

基于新的界面黏聚力模型，按式（4），（7），（10）计算得到相应模型参数如表 4所示，以200，300，400 kPa组的界面直剪试验为例，采用新模型得到的剪应力-剪切位移曲线如图 9所示。

表 4 界面黏聚力单元参数

Table 4. Parameters of cohesive element of C-C interface

k	K_s/ (Pa·m^-1)	δ_f /m
0.59	2.07×10⁸	3.86×10^-5

下载: 导出CSV

| 显示表格

图 9 较低法向压力下模拟的界面剪切破坏过程

Figure 9. Failure process of C-C interface simulated by friction- cohesive model (σ_n≥200 kPa)

下载: 全尺寸图片幻灯片

由图 9可知，采用摩擦-黏结模型后模拟得到的剪应力-剪切位移曲线与试验值得接近程度有所增加，且峰后残余变形阶段也可以较好地体现。相较于图 3中的黏结模型，图 9（b）的黏结摩擦模型更适合于界面剪切破坏的模拟。

但模型参数的选取和标定都是在界面为破坏面的预设条件下进行的，在低法向压力时是否适用，尚未验证。为此，本文采用表 2，4中的参数模拟得到法向压力为50，100 kPa时二元体直剪破坏形态和对应的剪应力-剪切位移曲线如图 10所示。

图 10 较高法向压力下模拟的界面剪切破坏过程

Figure 10. Failure process of C-C interface simulated by friction- cohesive model (σ_n=100 & 50 kPa)

下载: 全尺寸图片幻灯片

由图 10（a）可知，在低法向压力条件下，数值模拟的结果与试验结果仍较为一致，同时较高法向应力时黏土岩内产生的剪切裂纹也能够得以体现，验证了本文模拟方法在模拟二元体界面剪切破坏时的可靠性，表 2，4中的黏聚力单元参数则可用于后文水泥锚固体拉拔的数值模拟。

3. 水泥锚固体拔出试验与模拟

3.1 水泥锚固体的拉拔试验

水泥锚固体的物理模型采用直径15 cm，高30 cm的圆柱形模具制作，制作时首先铺2 cm砂垫层，随后分层填入黏土岩并压，要求压实度与室内试验试样相同；随后在黏土岩内钻直径50 mm，长150 mm的圆孔，并套上密封圈，利用注浆泵以0.6 MPa压力注入水泥砂浆，并插入直径8 mm的HRB400级钢筋。待水泥砂浆初凝后拆除密封圈，自然养护48 h。水泥锚固体的拉拔试验采用如图 11所示的试验装置进行，通过千斤顶进行位移加载，最大加载距离为5 cm，最大拉拔力为2000 kN，并配有油压表，加载过程中通过平行黏贴在钢筋外伸段的两组应变片测量拉拔力，并以千斤顶油压表读数作为参考，当3者读数差异较大时试验结果无效，并重新试验。加载位移则通过引伸计测量，位移引伸计读数每增加0.1 mm，对拉拔力进行一次记录（取两应变片的均值）。

图 11 锚固体物理模型及拉拔试验装置

Figure 11. Physical model and self-designed instrument for tensile tests on anchor solid in clay rock

下载: 全尺寸图片幻灯片

试验拔出的锚固体如图 12所示。锚固体拔出过程中钢筋未出现脱黏，水泥锚固体也保持完整，由于黏土岩本身强度较低，灌浆孔在注浆过程中不可避免的会出现轻微破坏，因此锚固体并不是规则的圆柱，侧边有明显的凹凸，不是理想的平界面。锚固体拔出后侧面有黏土岩黏连，但黏连不紧密，说明该部分黏土岩已破坏。根据锚固体最终的破坏形态，其破坏模式与低法向压力时黏土岩-砂浆二元体界面剪切基本相同，包括界面剪切脱黏和黏土岩的剪切破坏。

图 12 拔出的水泥锚固体

Figure 12. Extracted cement anchor solid

下载: 全尺寸图片幻灯片

3.2 数值模型的建立

根据室内试验的结果，锚固体在拔出后仍能保持完整，为减小计算量，锚固体采用有限元模型计算，对于黏土岩-锚固体界面和黏土岩部分，则采用FDEM模型，分别插入第2节中已标定的黏聚力单元，按实际的锚固深度，建立锚固体拉拔有限离散元模型如图 13所示。由于锚固体界面并不平整，建模时先划分网格，再根据锚固体和黏土岩区域赋予实体单元材料模型，最后插入两类黏聚力单元。

图 13 锚固体拉拔的有限-离散元模型

Figure 13. FEM-FDEM model for anchor solid in clay

下载: 全尺寸图片幻灯片

3.3 锚固体界面滑移破坏及脱黏机理

以模型3为例，数值模拟得到的锚固体拔出过程如图 14所示，拉拔过程可分为黏结变形阶段，界面脱黏阶段，剪胀摩擦阶段和滑移阶段4个阶段。

图 14 锚固体拉拔的破坏过程

Figure 14. Failure process of anchor solid in clay

下载: 全尺寸图片幻灯片

黏结变形阶段对应的拉拔位移很小（小于3 mm），界面黏聚力单元未出现破坏，锚固体与黏土岩间出现了剪应力和较小的正应力，由于锚固体与黏土岩间尚有有效黏结，整体变形是连续的，系统处于弹性状态。随着拉拔位移的增加，锚固体与黏土岩间的界面剪应力持续增加，界面黏聚力单元开始出现破坏，进入界面脱黏阶段，当拉拔位移达到6 mm后，锚固体完全脱黏，界面脱黏阶段锚固体周边黏土岩内也出现了少量的裂纹。在锚固体完全脱黏后，破坏过程进入剪胀摩擦阶段，由于界面网格间存在咬合效应，界面附近（1 cm）区域内黏土岩黏聚力单元也出现了大量的失效，并出现错动，该阶段黏土岩单元与锚固体间局部出现了较大的挤压应力，剪胀摩擦现象比较明显，其原因在于，碎屑颗粒间出现相对位移以后将不再紧密接触，而是会产生空隙，即产生剪胀效应。同时，试样的体积变形受到了较强的约束，因此颗粒间相互挤压，又会产生较大的挤压，增大了颗粒间的摩擦和咬合作用。根据数值模拟结果，此阶段摩擦和咬合作用仍能提供足够的抗拔力。随着拉拔位移的进一步增加，黏土岩内破碎的单元不断增加，黏土岩实体单元与未破坏黏土岩以及锚固体间仍存在较弱的咬合，因此黏土岩内未完全卸载，仍保留了较小的抗拔能力。最后当拉拔位移足够大时，界面附近的黏土岩被完全剪碎，咬合作用和剪胀产生的摩擦作用消失，锚固体最终出现滑移破坏。

根据数值模拟结果，黏土岩黏聚力单元的失效有局部化特征，除少量的裂纹出现了扩展，大部分裂纹均是独立的，且主要分布在界面周边2 cm范围内。

数值模拟得到拉拔过程的荷载位移曲线如图 15所示，与室内试验结果在趋势上基本一致，但在数值上存在一些差异，尤其是在峰后段差异比较明显，这是由于锚固体的最大抗拔力除了与界面黏结强度有关，也与界面形态所产生的咬合效应、剪胀效应相关，相较于岩石碎屑物，数值模拟时采用的网格尺寸较大，且随机网格与真实的界面形态存在差异，因此数值上的差异是不可避免的。

图 15 数值模拟得到的锚固体拉拔荷载-位移曲线

Figure 15. Tensile force-displacement curves of anchor solid in numerical simulation

下载: 全尺寸图片幻灯片

图 15中还给出了界面完全脱黏时对应的拉拔位移，脱黏位移受锚固体长度影响不大，为0.55~0.65 cm，对比图 14，15可知，在拉拔力达到峰值前，锚固体已经与黏土岩完全脱黏，脱黏时对应的拉拔位移约为峰值拉拔力对应位移的60%~85%，说明，锚固体的抗拔力并非完全来自于界面黏结，脱黏后的界面咬合力和剪胀作用产生的摩檫力也有助于提高锚固体的抗拔能力。

4. 讨论

对于咬合与剪胀，与网格尺寸和网格形态密切相关，根据常识判断，当剪切破碎后的碎屑较小，且球度较高时对应的剪胀和摩擦较小，而碎块尺寸大且具有棱角时剪胀、咬合和摩擦则较大。本文虽然采用了非结构化的随机Delaunay三角划分，但采用固定网格来模拟剪胀效应可能存在很大的主观性，模拟结果是否可靠，还需要专门进行讨论。

本文在图 5（a）所示模型的基础上，采用先划分网格后赋予材料，最后形成界面的方法生成了新的界面剪切模型如图 16（a）所示，界面粗糙度系数JRC=13，并采用表 2，4中的参数进行模拟，以50，400 kPa法向压力为例，得到不同模型的剪切破坏形态和剪应力-剪切位移曲线如图 16（b）所示，对应的上剪切盒纵横向位移关系如图 16（c）所示。

图 16 两类界面剪切模型的区别

Figure 16. Differences of two shear test models for interface

下载: 全尺寸图片幻灯片

由图 14可知，在小尺寸条件下，本文方法具有网格依赖性，当法向应力较大时，较粗糙的界面网格对应的峰值剪应力大于平截面，且增加幅度为29.1%，但剪胀产生的法向位移很小，上剪切盒几乎无旋转。而对于法向应力较小的情况，由界面粗糙产生的剪应力增加有所减弱，然而仍略大于平截面，且上剪切盒出现了9.2°的旋转，这是由于高法向应力条件下的剪切破坏面位于黏土岩内，受界面参数和形态影响相对较小。同时由图 14（c），8（b）的对比还可知，粗糙界面的剪切脱黏会受到界面咬合的影响而滞后于平界面，在50 kPa条件下界面裂纹甚至没有贯穿整个试件。

综上所述，界面形态也是决定剪胀效应的主要因素，在进行工程模拟时应当着重考虑。根据室内试验对参数进行标定后，本文模型对于平整界面以及脱黏前的粗糙界面的模拟，在理论上是可靠的，当由剪胀作用产生的法向应力较小时，二元体的破坏主要受黏土岩部分控制，本文的模拟结果与真实情况较为接近，因此可用于软岩内的锚固体拉拔模拟。但对于硬岩粗糙截面，本文模型虽然也能够模拟脱黏后的剪胀摩擦，但如不考虑具体的界面形态，本文模拟在数值上可能严重失真，适用性也还需要进一步验证。

5. 结论

锚固体与围岩脱黏及脱黏后的变形过程十分复杂，本文基于两类黏聚力模型，建立了黏土岩-水泥砂浆二元体的FDEM模型，基于室内试验对参数进行了标定，通过基于网格的界面识别方法模拟了水泥锚固体拉拔过程，并与模型试验进行对比，主要得到4点结论。

（1）黏土岩黏聚力为170.4 kPa，内摩擦角为36.8°，黏聚力小于黏土岩-水泥砂浆界面的切向黏结强度248.1 kPa，而内摩擦角的正切值为0.75，大于界面摩擦系数0.59，因此而随着法向压力的增加二元体的剪切破坏由黏土岩剪切破坏逐渐转变为界面脱黏。

（2）只考虑剪切失效的双线性黏聚力模型在模拟软岩或者固结硬土的破坏时也是适用的，但对于复杂应力状态下的二元体界面适用性不佳，黏结界面更适合采用黏结-摩擦型黏聚力单元模拟。

（3）水泥锚固体拉拔失效过程可分为黏结变形阶段，界面脱黏阶段，剪胀咬合阶段和滑移阶段4个阶段，锚固体-黏土岩界面完全脱黏时拉拔荷载尚未达到峰值，而剪胀咬合阶段的咬合力决定了锚固体的峰值抗拔能力，锚固体附近黏土岩的剪切破坏和界面脱黏共同导致锚固失效。

（4）本文模型在经过参数标定后，可以定量地模拟平界面的剪切破坏，也可以模拟出粗糙界面的剪胀阶段，但水泥锚固体的抗拔能力与锚固体-黏土岩的黏结界面形态密切相关，本文模型的模拟结果是否可靠，则还需进一步验证。

本文研究结果可以指导软岩地区锚固结构设计。

图 1 滑面边坡模型及分析图

Figure 1. Single- and double-slope model and analysis diagram

下载: 全尺寸图片幻灯片

图 2 FLAC网格模型

Figure 2. Grid model in FLAC

下载: 全尺寸图片幻灯片

图 3 本研究所选取的地震动

Figure 3. Ground motion used in this study

下载: 全尺寸图片幻灯片

图 4 屈服状态下不同滑体的法向条间力（算例1）

Figure 4. Inter-slice normal forces of different sliding bodies under yield state (Example 1)

下载: 全尺寸图片幻灯片

图 5 屈服状态下不同滑体的法向条间力（算例2）

Figure 5. Inter-slice normal forces of different sliding bodies under yield state (Example 2)

下载: 全尺寸图片幻灯片

图 6 不同强度地震动下的滑动面位移（算例1）

Figure 6. Sliding displacements of slip surface under ground motions with different intensities (Example 1)

下载: 全尺寸图片幻灯片

图 7 不同强度地震动下的滑动面位移（算例2）

Figure 7. Sliding displacements of slip surface under ground motions with different intensities (Example 2)

下载: 全尺寸图片幻灯片

图 8 水平成层土坡示意图

Figure 8. Schematic diagram of layered soil slope

下载: 全尺寸图片幻灯片

图 9 不同滑面的地震位移

Figure 9. Sliding displacements of different sliding surfaces

下载: 全尺寸图片幻灯片

图 10 不同滑体法向条间力

Figure 10. Inter-slice normal forces of different sliding bodies

下载: 全尺寸图片幻灯片

图 11 老折山边坡示意图

Figure 11. Schematic diagram of Laozheshan slope

下载: 全尺寸图片幻灯片

图 12 不同滑面的地震位移

Figure 12. Sliding displacements of different sliding surfaces

下载: 全尺寸图片幻灯片

图 13 滑体法向条间力

Figure 13. Inter-slice normal forces of sliding body

下载: 全尺寸图片幻灯片

表 1 土层参数信息

Table 1 Parameters of soil layers

算例	土层分类	重度 $\gamma$ / (kN·m^-3)	泊松比μ	黏聚力c/ kPa	内摩擦角φ/ (°)	剪切波速V_s/ (m·s^-1)
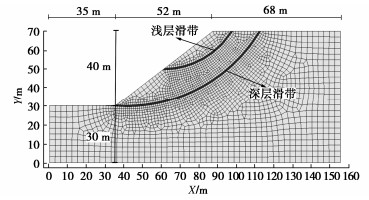
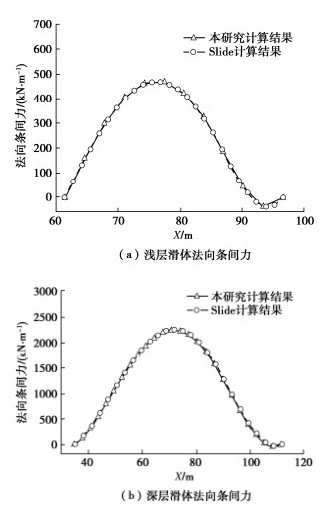
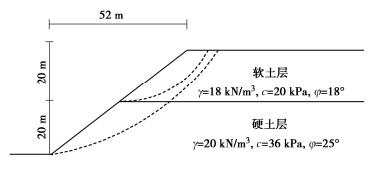
验证算例一	浅层滑带	19	0.3	22	20	300
	深层滑带	19	0.3	33	27	300
	其余部分	19	0.2	—	—	3000
验证算例二	浅层滑带	19	0.3	28	25	300
	深层滑带	19	0.3	28	23	300
	其余部分	19	0.2	—	—	3000

下载: 导出CSV

表 2 不同方法计算所得边坡安全系数与屈服系数

Table 2 Safety and yield factors of slopes by different methods

算例		${{{F}}_\text{s}}$ （浅层滑动面）	${{{F}}_\text{s}}$ （深层滑动面）	${{{k}}_\text{s}}$ (浅层滑动面)	${{{k}}_\text{d}}$ (深层滑动面)
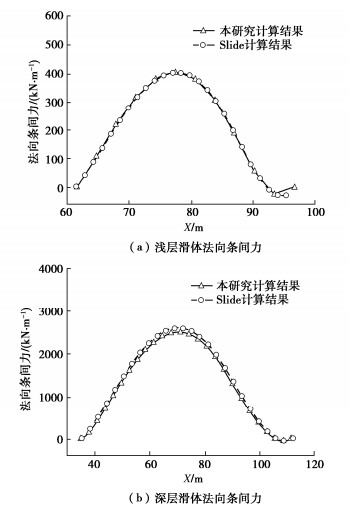
验证算例一	本研究计算结果	1.150	1.397	0.077	0.184
	Slide计算结果	1.148	1.404	0.075	0.184
	FLAC计算结果	1.120	1.348	0.078	0.129
验证算例二	本研究计算结果	1.470	1.167	0.233	0.080
	Slide计算结果	1.467	1.169	0.229	0.080
	FLAC计算结果	1.523	1.117	0.185	0.048

下载: 导出CSV

参考文献(21)

[1]	NEWMARK N M. Effects of earthquakes on dams and embankments[J]. Geotechnique, 1965, 15(2): 139-160. doi: 10.1680/geot.1965.15.2.139
[2]	MAKDISI F I, SEED H B. Simplified procedure for estimating dam and embankment earthquake-induced deformations[J]. Journal of the Geotechnical Engineering Division, 1978, 104(7): 849-867. doi: 10.1061/AJGEB6.0000668
[3]	RATHJE E M, BRAY J D. Nonlinear coupled seismic sliding analysis of earth structures[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(11): 1002-1014. doi: 10.1061/(ASCE)1090-0241(2000)126:11(1002)
[4]	秦雨樵, 汤华, 邓琴, 等. 强震作用下边坡屈服加速度计算方法的改进[J]. 岩石力学与工程学报, 2019, 38(增刊2): 3439-3447. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2019S2019.htm QIN Yuqiao, TANG Hua, DENG Qin, et al. Improvement on the calculation method of slope critical acceleration under strong earthquake[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S2): 3439-3447. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2019S2019.htm
[5]	陈春舒, 夏元友. 基于极限分析的边坡实时动态Newmark滑块位移法[J]. 岩石力学与工程学报, 2016, 35(12): 2507-2515. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201612015.htm CHEN Chunshu, XIA Yuanyou. A real-time dynamic Newmark sliding block method for slopes based on limit analysis[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(12): 2507-2515. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201612015.htm
[6]	BANDNI V, BIONDI G, CASCONE E, et al. A GLE-based model for seismic displacement analysis of slopes including strength degradation and geometry rearrangement[J]. Soil Dynamics and Earthquake Engineering, 2015, 71: 128-142. doi: 10.1016/j.soildyn.2015.01.010
[7]	JI J, ZHANG W, ZHANG F, et al. Reliability analysis on permanent displacement of earth slopes using the simplified Bishop method[J]. Computers and Geotechnics, 2020, 117: 103286. doi: 10.1016/j.compgeo.2019.103286
[8]	李明, 辛鸿博. 人工土山的地震永久变形分析[J]. 岩土工程学报, 2015, 37(11): 2128-2132. doi: 10.11779/CJGE201511027 LI Ming, XIN Hongbo. Seismic permanent deformation of earth-fill hill[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(11): 2128-2132. (in Chinese) doi: 10.11779/CJGE201511027
[9]	黄帅, 宋波, 蔡德钩, 等. 近远场地震下高陡边坡的动力响应及永久位移分析[J]. 岩土工程学报, 2013, 35(增刊2): 768-773. http://www.cgejournal.com/cn/article/id/15488 HUANG Shuai, SONG Bo, CAI Degou, et al. Dynamic response and permanent displacement of high-steep slopes under near- and far-field earthquakes[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 768-773. (in Chinese) http://www.cgejournal.com/cn/article/id/15488
[10]	宋健, 高广运. 基于速度脉冲地震动的边坡地震位移统一预测模型[J]. 岩土工程学报, 2013, 35(11): 2009-2017. http://www.cgejournal.com/cn/article/id/15330 SONG Jian, GAO Guangyun. Empirical predictive model for seismic displacement of slopes under velocity pulse-like ground motions[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 2009-2017. (in Chinese) http://www.cgejournal.com/cn/article/id/15330
[11]	杨涛, 张忠平, 马惠民. 多层复杂滑坡的稳定性分析与支护选择[J]. 岩石力学与工程学报, 2007, 26(增刊2): 4189-4194. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2007S2088.htm YANG Tao, ZHANG Zhongping, MA Huimin. Stability analysis and supporting selection of multi-layer complex landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(S2): 4189-4194. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2007S2088.htm
[12]	张俊文, 邹烨, 李玉琳. 大型多层次堆积体破坏模式及其稳定性[J]. 岩石力学与工程学报, 2016, 35(12): 2479-2489. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201612012.htm ZHANG Junwen, ZOU Ye, LI Yulin. Failure mechanism and stability analysis of big multi-layer deposit[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(12): 2479-2489. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201612012.htm
[13]	WARTMAN J, SEED R B, BRAY J D. Shaking table modeling of seismically induced deformations in slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(5): 610-622. doi: 10.1061/%28ASCE%291090-0241%282005%29131%3A5%28610%29
[14]	艾挥, 吴红刚, 冯文强, 等. 多滑动面滑坡变形破坏机理的振动台试验研究[J]. 防灾减灾工程学报, 2018, 38(1): 65-71. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201801010.htm AI Hui, WU Honggang, FENG Wenqiang, et al. Shaking table test study on deformation and failure mechanism of landslide wtih multiple slip surface[J]. Journal of Disaster Prevention and Mitigation Engineering, 2018, 38(1): 65-71. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-DZXK201801010.htm
[15]	LESHCHINSKY B A. Nested Newmark model to calculate the post-earthquake profile of slopes[J]. Engineering Geology, 2018, 233: 139-145. http://d.wanfangdata.com.cn/periodical/c7b18585b611b385c65cc9caf85cf430
[16]	SONG J, FAN Q, FENG T, et al. A multi-block sliding approach to calculate the permanent seismic displacement of slopes[J]. Engineering Geology, 2019, 255: 48-58.
[17]	SONG J, WU K, FENG T, et al. Coupled analysis of earthquake-induced permanent deformations at shallow and deep failure planes of slopes[J]. Engineering Geology, 2020, 274: 105688.
[18]	SPENCER E. A method of analysis of the stability of embankments assuming parallel inter-slice forces[J]. Géotechnique, 1967, 17(1): 11-26. http://www.onacademic.com/detail/journal_1000039588501610_c145.html
[19]	Rocscience Inc. RocScience, SLIDECP[R]. Toronto: Rocscience Inc. 2017.
[20]	Itasca Consulting Group. Fast Lagrangian Analysis of Continua in 3 Dimensions[M]// Minneapolis: Itasca Consulting Group, 2018.
[21]	黄琳. 地震作用下成层土边坡的动力稳定性分析[D]. 成都: 西南交通大学, 2017. HUANG Lin. Dynamic Stability Analysis of Layered Soil Slope Under Seismic Action[D]. Chengdu: Southwest Jiaotong University, 2017. (in Chinese)