土压平衡盾构推力简化估算方法与实测分析

杨松松; 朱湘旭; 章定文; 李顺; 禹鹏飞

doi:10.11779/CJGE2021S2056

土压平衡盾构推力简化估算方法与实测分析 English Version

杨松松^{1, 2,},
朱湘旭³,
章定文^{1, 2},
李顺³,
禹鹏飞³

1.
东南大学交通学院,江苏　南京　211189
2.
道路交通工程国家级试验教学示范中心（东南大学）,江苏　南京　211189
3.
中建八局轨道交通建设有限公司,江苏　南京　210046

基金项目:

国家重点研发计划课题 2016YFC0800201

详细信息

作者简介:
杨松松(1994— ),男,博士研究生,主要从地下工程施工与地基处理方面研究。E-mail: 18435167584@163.com

中图分类号: TU43
计量
- 文章访问数: 280
- HTML全文浏览量: 31
- PDF下载量: 136
出版历程
- 收稿日期: 2021-08-18
- 网络出版日期: 2022-12-05
- 刊出日期: 2021-10-31

Simplified estimation method and on-site analysis of thrust of EPB shield

1.
School of Transportation, Southeast University Nanjing 211189, China
2.
National Demonstration Center for Experimental Road and Traffic Engineering Education (Southeast University), Nanjing 211189, China
3.
China Construction Eighth Bureau Rail Transit Construction Co., Ltd., Nanjing 240046, China

摘要

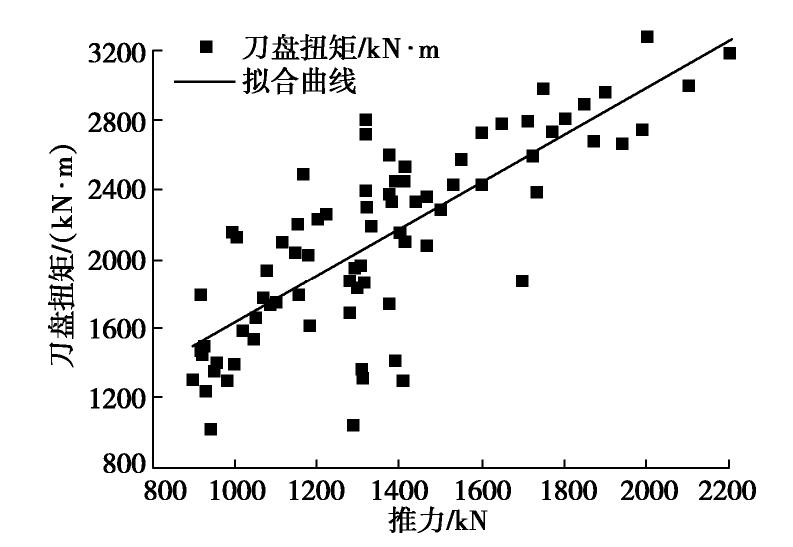
摘要: 盾构隧道掘进过程中推力是盾构施工安全的重要因素。为了能够准确地估算水位线以下盾构掘进过程中所需的推力,分析水浮力对盾构机的受力影响。推导水浮力影响下的盾构推力计算公式,基于现场实测数据分析盾构推力与扭矩之间的关系。研究结果表明推导的盾构推力计算公式可以与现场盾构推力吻合良好,推导的推力计算公式可以用于水位线以下盾构的推力计算；扭矩与盾构推力具有良好的线性关系,因此可以通过推力计算盾构扭矩。
- 盾构 /
- 推力 /
- 浮力 /
- 扭矩
Abstract: Thrust is an important factor in shield construction safety during shield tunneling. In order to accurately estimate the thrust required during shield tunneling below the water level, the influences of water buoyancy on the force of shield tunneling are analyzed. The formula for calculating the shield thrust under the influences of water buoyancy is derived, and the relationship between the shield thrust and the torque is analyzed based on field measured data. The research results show that the deduced formula for the shield thrust can be in good agreement with the on-site shield thrust, and it can be used to calculate the thrust of the shield below the water level. The torque has a good linear relationship with the shield thrust, so the shield torque can be calculated through the thrust.
- shield /
- thrust /
- buoyancy /
- torque

HTML全文

图 1 盾壳受力分析

Figure 1. Force analysis of shield shell

下载: 全尺寸图片幻灯片

图 2 盾构隧道侧穿桥桩位置图

Figure 2. Position of shield tunneling crossing a bridge

下载: 全尺寸图片幻灯片

图 3 盾构推力曲线

Figure 3. Curves of shield thrust

下载: 全尺寸图片幻灯片

图 4 盾构推力与刀盘扭矩

Figure 4. Shield thrust and cutter head torque

下载: 全尺寸图片幻灯片

图 5 盾构推力与刀盘扭矩关系曲线

Figure 5. Relationship between shield thrust and torque of cutter head

下载: 全尺寸图片幻灯片

参考文献(11)

[1]	王强, 谢雄耀, 黄钟晖, 等. 四线并行盾构隧道下穿火车站股道沉降特征研究[J]. 岩石力学与工程学报, 2017, 36(增刊2): 4235-4243. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S2058.htm WANG Qiang, XIE Xiong-yao, HUANG Zhong-hui, et al. Study of settlement troughs over quadruple-tube parallel shield tunnels crossing railway tracks[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(S2): 4235-4243. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S2058.htm
[2]	DENG K, TANG X, WANG L, et al. On the Analysis of Force Transmission Performance for the Thrust Systems of Shield Tunneling Machines[C]//International Conference on Intelligent Robotics and Applications. Springer-Verlag, 2009.
[3]	徐冲. 砂卵石地层泥水平衡盾构隧道掘进参数控制[J]. 铁道建筑, 2019, 59(2): 94-97. https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ201902023.htm XU Chong. Control of tunnel driving parameters of slurry balance shield in sandy gravel stratum[J]. Railway Engineering, 2019, 59(2): 94-97. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TDJZ201902023.htm
[4]	徐前卫. 盾构施工参数的地层适应性模型试验及其理论研究[D]. 上海: 同济大学, 2006. XU Qian-wei. Study on the Simulated Model Test of Shield Machine’s Working Parameters Applicable to Different Stratums and Its Theoretical Investigation[D]. Shanghai: Tongji University, 2006. (in Chinese)
[5]	陈仁朋, 刘源, 汤旅军, 等. 复杂地层土压平衡盾构推力和刀盘扭矩计算研究[J]. 地下空间与工程学报, 2012, 8(1): 26-32. https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201201004.htm CHEN Ren-peng, LIU Yuan, TANG Lv-jun, et al. Research on calculation of thrust and cutter head torque on shield in complex strata[J]. Chinese Journal of Underground Space and Engineering, 2012, 8(1): 26-32. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-BASE201201004.htm
[6]	朱合华, 徐前卫, 廖少明, 等. 土压平衡盾构施工的顶进推力模型试验研究[J]. 岩土力学, 2007, 28(8): 1587-1594. doi: 10.3969/j.issn.1000-7598.2007.08.011 ZHU He-hua, XU Qian-wei, LIAO Shao-ming, et al. Experimental study on thrust force during tunnel excavation with earth pressure balance shield machine[J]. Rock and Soil Mechanics, 2007, 28(8): 1587-1594. (in Chinese) doi: 10.3969/j.issn.1000-7598.2007.08.011
[7]	DENG K S, TANG X Q, WANG L P, et al. Research on characteristics of deformation in thrust system for EPB shield machines[J]. Tunnelling and Underground Space Technology, 2011, 26(1): 15-21. doi: 10.1016/j.tust.2010.06.008
[8]	王洪新. 土压平衡盾构刀盘扭矩计算及其与盾构施工参数关系研究[J]. 土木工程学报, 2009, 42(9): 109-113. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200909018.htm WANG Hong-xin. Calculation of cutterhead torque for EPB shield and the relationship between cutterhead torque and shield driving parameters[J]. China Civil Engineering Journal, 2009, 42(9): 109-113. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200909018.htm
[9]	刘铁雄. 日本隧道标准规范(盾构篇)及解释[M]. 成都: 西南交通大学出版社, 1988. LIU Tie-xiong. Japanese Tunnel Standard Specification (Shield Tunneling) and Interpretation[M]. Chengdu: Southwest Jiaotong University Press, 1988. (in Chinese)
[10]	王明年, 张晓军, 苟明中, 等. 盾构隧道掘进全过程三维模拟方法及重叠段近接分区研究[J]. 岩土力学, 2012, 33(1): 273-279. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201201045.htm WANG Ming-nian, ZHANG Xiao-jun, GOU Ming-zhong, et al. Method of three-dimensional simulation for shield tunneling process and study of adjacent partition of overlapped segment[J]. Rock and Soil Mechanics, 2012, 33(1): 273-279. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201201045.htm
[11]	王承德. 顶管施工中管壁摩阻力理论公式的商榷[J]. 特种结构, 1999, 16(3): 22-25. https://www.cnki.com.cn/Article/CJFDTOTAL-TZJG199903005.htm WANG Cheng-de. For pipe jacking construction pipe surface frictional resistance formula under discussion[J]. Special Structures, 1999, 16(3): 22-25. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TZJG199903005.htm