软土地区桩基横向抗力系数的精细化取值研究

张俊云; 张乐; 冯君

doi:10.11779/CJGE2021S2048

软土地区桩基横向抗力系数的精细化取值研究 English Version

西南交通大学土木工程学院,四川　成都　610031

基金项目:

四川省科技计划重点项目 2021YFS0321

详细信息

作者简介:
张俊云(1974— ),男,博士,副教授,主要从事土力学与基础工程方面的教学和科研。E-mail: zjy74@126.com

中图分类号: TU473.1
计量
- 文章访问数: 185
- HTML全文浏览量: 13
- PDF下载量: 88
出版历程
- 收稿日期: 2021-08-14
- 网络出版日期: 2022-12-05
- 刊出日期: 2021-10-31

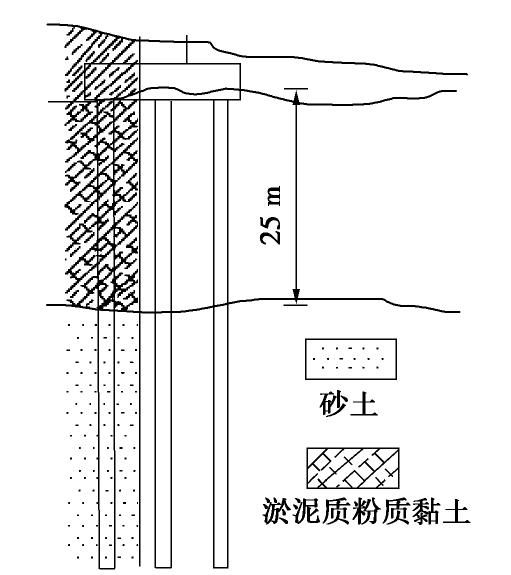
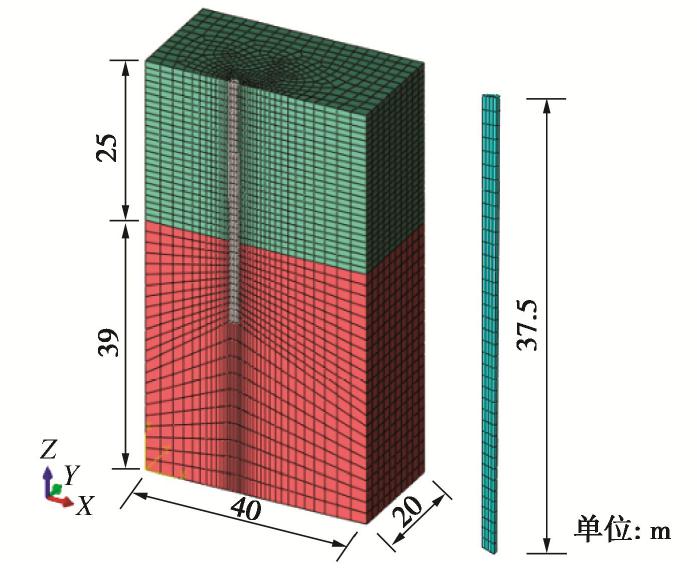
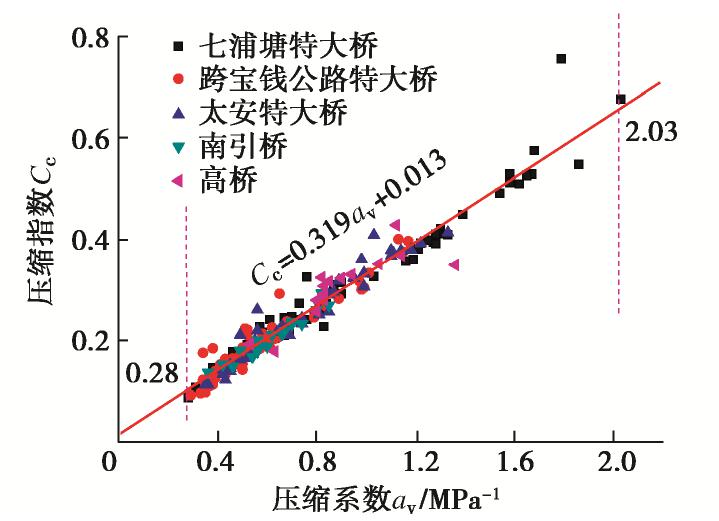
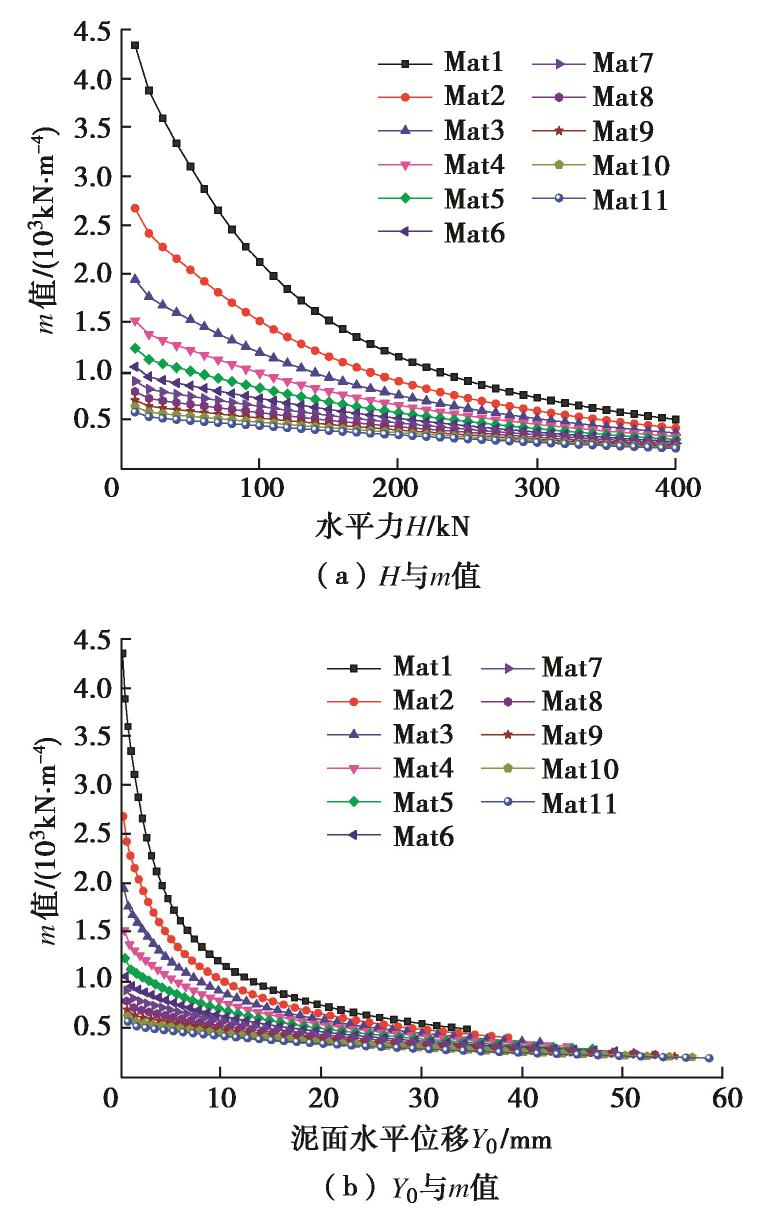
Refined value of lateral resistance coefficient of pile foundation in soft soil areas

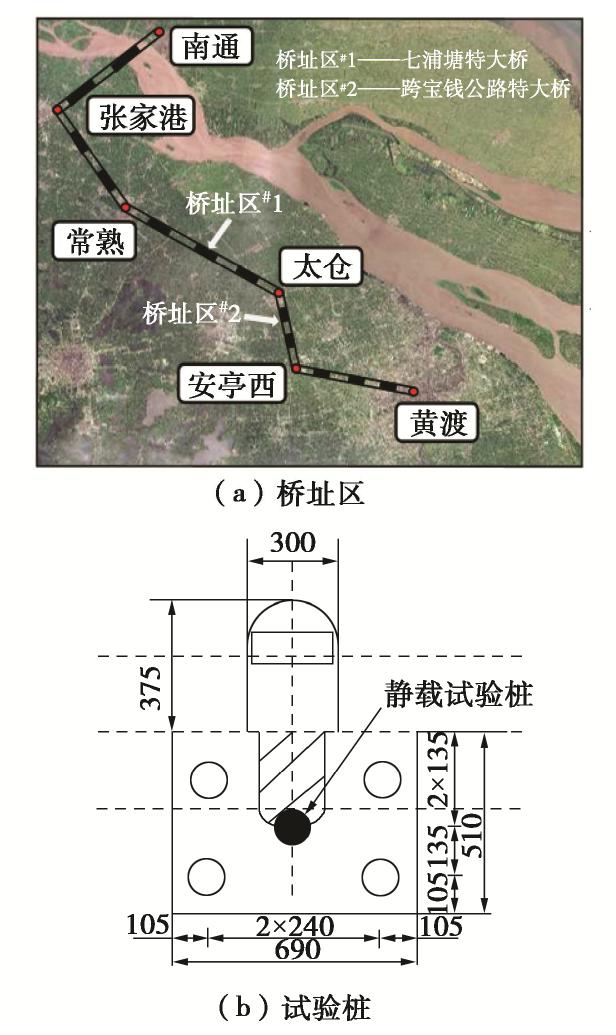
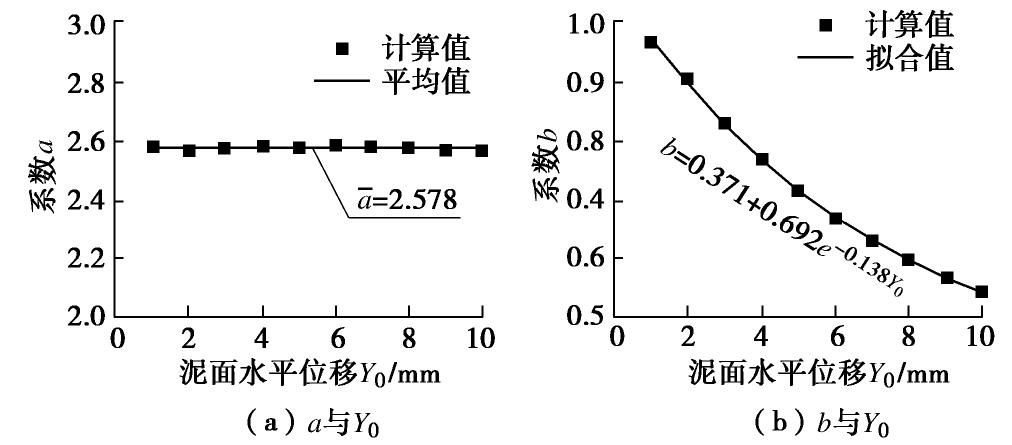
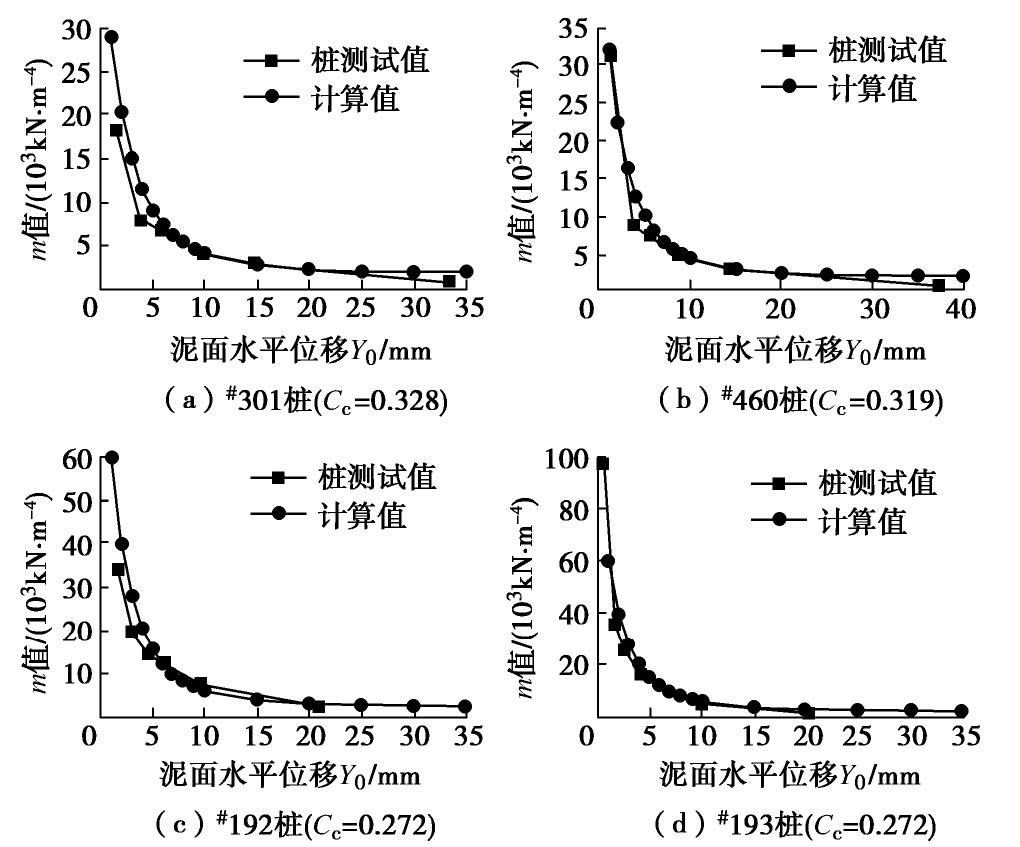
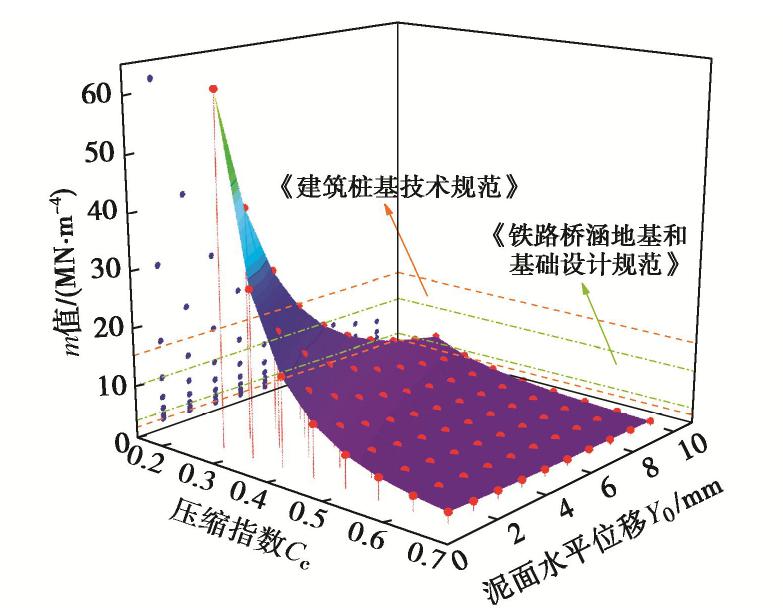
School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China

摘要

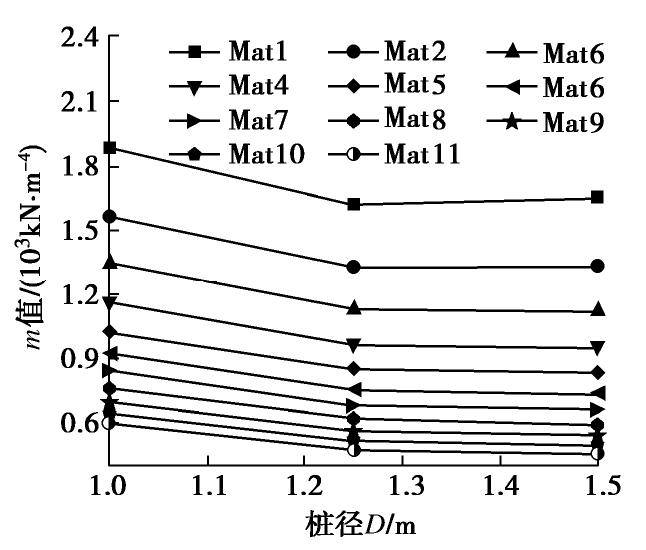
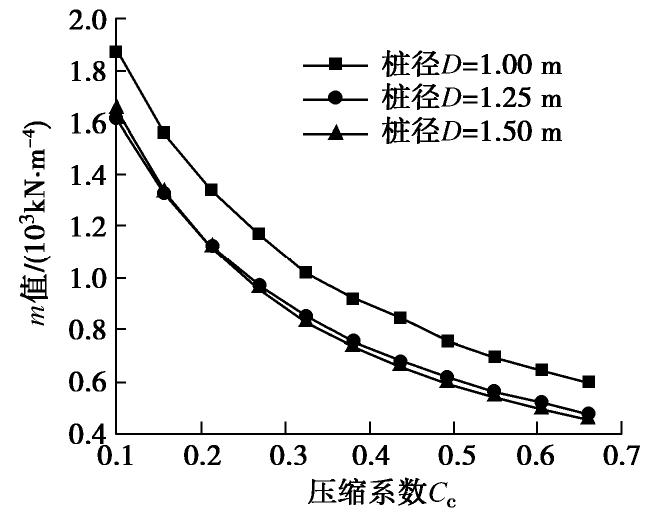
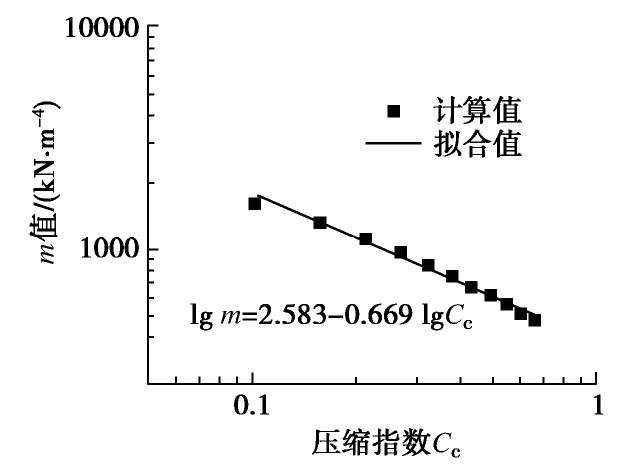
摘要: m法是横向受荷桩桩身变形和内力分析的一种常用方法。在没有试桩的条件下,m法中横向抗力系数的比例系数m值只能根据地基土的类型等从规范推荐的较大范围中取值,对工程经验依赖性强,具有较大的随机性。将沪通铁路沿线主要软土按压缩特性分为11亚类,通过有限元模拟分析了水平力H、泥面（桩顶）水平位移和土体压缩指数 $C_{c}$ 等对m值的影响作用；经统计分析建立了m值与 $Y_{0}$ , $C_{c}$ 间的拟合关系式,并以现场水平静载试验对其进行校核验证。结果表明：m值随H, $Y_{0}$ 和 $C_{c}$ 的增大而减小,且衰减速度不断减小；桩径D对m值有一定影响,现有桩径水平中D=1.25 m最佳；现场试验修正后的m值拟合关系计算可靠,且能依据土体变形参数精细化取值。
- 软土地区 /
- 桩基 /
- m值 /
- 精细化取值 /
- 拟合关系式
Abstract: The m method is a common method to analyze the deformation and internal force of laterally loaded piles. In the absence of test piles, the ratio coefficient m value of lateral resistance coefficient in the m method can only be taken from a wide range recommended by the relevant code according to the type of foundation soil, etc., highly dependent on engineering experience and random. Main soft soils along Shanghai-Nantong Railway are classified into 11 subcategories according to the compression characteristics. The influences of horizontal force H, horizontal displacement $Y_{0}$ of mud surface (pile top), pile diameter D and soil compression index $C_{c}$ on m value are analyzed through the numerical test method. The fitting relation between m and $C_{c}$ and the relation between m and $Y_{0}$ are established through statistical analysis, and are verified by the field horizontal static load tests. The results show that the m value decreases with H, $Y_{0}$ and $C_{c}$ , and the attenuation speed decreases continuously. D has a certain influence on the m value, corresponding to the best diameter of pile D=1.25 m. The fitting formula for m value corrected by the field tests is reliable and can be fine-tuned according to the deformation parameters of soils.
- soft soil area /
- pile foundation /
- m value /
- refined value /
- fitting formula

HTML全文

0.   引言

土的渗透特性是土重要的工程性质之一,影响着土木工程的施工。目前无黏性土渗透特性的试验研究,多是采用竖向圆柱体模型槽进行,试验中土体受到的水流的作用方向是由下至上的竖直方向,而对于土体承受水平向渗流时土体渗透特性的研究不多^[1],渗流方向对土体渗流变形特性的研究还尚未给予足够重视。对土渗流的研究表明,实际施工中渗流的优势方向往往是水平方向,通常土体水平向的渗透性大于竖向,而抵抗水平向渗透破坏的能力低于抵抗竖向渗透破坏的能力^[2-6]。

本文针对粉砂竖向和水平向渗透特性研究存有的不足,利用自主设计的实验装置,对粉砂开展竖向和水平向渗流试验,对比分析了两种不同方向渗流场下粉砂的渗透特性。基于室内模拟试验,建立三维离散元与计算流体力学耦合的细观力学模型,对粉砂在竖向和水平向的渗流情况进行分析和计算。通过数值计算结果,对竖向和水平向渗流作用下的粉砂内部接触力、渗流速度及流场的分布规律进行细观分析,将数值模拟与室内试验的结果进行分析、比较。

1.   不同渗流方向下粉砂渗透变形室内试验模拟

1.1   试验仪器和方法

（1）试验仪器

粉砂的竖向渗透变形试验借助实验室自主设计的圆柱形渗流试验仪进行,该装置示意图如图1所示。粉砂水平向渗流渗透变形特性的研究是在自主设计的水平渗流试验装置中进行的,见图2。模型由进水系统,装样区及排水系统3个主要部分组成。进水系统可以通过对进水水头高度的调节自由选择水头加载高度。

图 1 圆柱形渗流试验仪示意图

Figure 1. Schematic diagram of instrument for cylindrical seepage tests

下载: 全尺寸图片幻灯片

图 2 粉砂水平向渗流试验研究模型示意图

Figure 2. Schematic of model for horizontal seepage tests

下载: 全尺寸图片幻灯片

（2）试验方法及步骤

粉砂烘干并分层装样。称样烘干24 g取出装样,每10 cm分为一层进行装样；排气饱和。装样完成,分次提升水箱供水高度对试验土样进行饱和,最后一次使水头抬升至与试样顶端齐平,静置24 h；逐级调整水头进行试验。逐级抬升水头高度,对测压管水头高度读数并记录,同时量测渗流量大小,记录试验进程中的渗流现象,直至该级渗流稳定,转入下一级水头；当试验过程中,流量忽然增大,并出现明显的渗流通道,可以认定为试样发生渗透破坏,不再继续加大水头高度,试验完成。

1.2   粉砂竖向和水平向渗流试验结果分析

对粉砂在竖向渗流下的渗透流速受水力梯度影响下的变化规律进行研究,得到渗流速度随水力梯度变化的关系曲线,如图3所示。对粉砂在水平向渗流作用下的临界水力梯度进行研究,结果如图4所示。

图 3 竖向渗流下渗流速度随水力梯度变化曲线

Figure 3. Relationship between seepage velocity and vertical hydraulic gradient

下载: 全尺寸图片幻灯片

图 4 水平向渗流下渗流速度随水力梯度变化曲线

Figure 4. Relationship between seepage velocity and critical hydraulic gradient

下载: 全尺寸图片幻灯片

由图3得到,在水力梯度 $i$ <0.787时,渗流速度随水力梯度呈近似线性的变化,此时土样处于渗流稳定阶段；当水力梯度为1.1时,渗流速度忽然增大,粉砂颗粒流失量也徒增,此时土体发生渗透变形。图4粉砂在水平向渗流下的变化规律显示：水力梯度小于0.45时,粉砂土渗透流速随着水力梯度的增大呈线性增长,水流清澈,粉砂流出较少。当水力梯度增至0.52时,试样整体的流速瞬间增大,粉砂流出量明显增多且呈持续流失状态,此时粉砂土样内部颗粒运移不再规律,试样开始发生渗透破坏。

表1给出粉砂在两种渗流方向下的渗透系数、临界坡降与破坏坡降。粉砂在竖向渗流时的临界水力梯度为0.787,破坏水力梯度为1.10；而水平向渗流中,所能承受的临界水力梯度为0.45。在影响因素诸如种类、级配、密度、孔隙大小等相同的前提下,粉砂竖向渗流的临界水力梯度比水平向高出近44%。由于土体在受到水平向渗流时,平均渗透系数取决于最透水土层的厚度和渗透性；而对于竖向渗流,其平均渗透系数取决于最不透水土层的渗透性。加之,竖向渗流中重力作用与渗流方向一致,会产生对土层的压密作用,使得该渗流方向下的渗透系数小于水平向,而土体能够承受的水头高于水平向的渗流。

表 1 不同渗流方向下粉砂渗透系数、临界坡降和破坏坡降

Table 1. Datat of permeability coeffieient of silt, critical slope and failure slope under different seepage directions

渗流方向渗透系数/(10^-4 cm·s^-1) 临界水力梯度破坏水力梯度

竖向 6.13 0.787 1.10
水平 6.25 0.450 0.52

下载: 导出CSV
| 显示表格

2.   不同渗流方向下粉砂渗透变形颗粒流模拟

对于固相颗粒,通过求解运动和动量方程模拟颗粒运动,采用离散元的颗粒流理论进行模拟；对于液相介质,采用均一化流体计算技术模拟其在孔隙中的运动,也就是通过求解平均Navier-Stokes方程模拟孔隙中流体的运动^[7-9]。

2.1   数值模型

对粉砂土不同向渗流形态的模拟中,边界条件的界定也略有不同。竖向渗流下,颗粒周边的边界为固壁边界条件,上下为压力边界条件。水平向渗流下,模型的前后和上下边界为固壁边界条件,左右设置为压力边界条件和自由边界条件。生成的土体模型如图5所示。

图 5 PFC^3D颗粒模型及网格划分示意图

Figure 5. PFC^3D particle model and mesh generation

下载: 全尺寸图片幻灯片

对于竖向的渗流,按照试验中模型,上覆为自由边界,没有压重。对于水平向的渗流,试样在重力和浮力作用下保持平衡,当作用渗流力后,土中小颗粒将从模型右侧流出,因此在试样右侧设置了相互交叉垂直的线墙,如图6所示。

图 6 线墙示意图

Figure 6. Schematic of line wall

下载: 全尺寸图片幻灯片

2.2   数值计算流程

采用PFC^3D对流固耦合问题进行计算流程如图7所示。

图 7 PFC^3D流固耦合计算流程示意图

Figure 7. Flow chart of PFC^3D flow-solid coupling calculation

下载: 全尺寸图片幻灯片

2.3   数值模拟结果

（1）粉砂土竖向和水平向渗流下渗透变形情况

a）粉砂竖向渗流下的渗透变形情况

图8给出了粉砂在竖向渗流作用下,土样随水力梯度的变化情况。

图 8 竖向渗流下粉砂土随水力梯度变化情况

Figure 8. Variation of silty sand with gradient under vertical seepage

下载: 全尺寸图片幻灯片

水力梯度从0.1,0.2,0.3,...,逐级增加,水力梯度施加至0.7时,粉砂几乎无变化；当水力梯度增至0.8时,土样出现从底部被整体抬升的趋势,发生少量细小颗粒流失的现象；水力梯度继续增至1.0时,土体发生了整体的抬升,土体表面颗粒簇发生整体迁移的现象。模拟结果表明,试样的临界水力梯度在0.8左右。

b）粉砂水平向渗流下的渗透变形情况

粉砂土的水平向渗流中水力梯度也是由0.1,0.2,0.3依次逐级抬升,图9给出了粉砂土在水平向渗流下试样随水力梯度变化的情况。

图 9 水平向渗流下粉砂土随水力梯度变化情况

Figure 9. Variation of silt with gradient under horizontal seepage

下载: 全尺寸图片幻灯片

从图9中可以看出,当水力梯度增至0.3时,试样底部细小颗粒也开始发生迁移,水力梯度继续增大至0.4,此时试样发生颗粒成团的流失,土体发生了渗透变形。水力梯度加载至0.5时,土体颗粒发生了更加显著的整体性渗流破坏。根据模拟结果,得到粉砂土水平向渗流的临界水力梯度在0.4左右。

（2）粉砂土竖向和水平向渗流下配位数变化情况分析

土体的配位数表示了颗粒间的接触数,是表达土颗粒间接触情况的参数之一,总配位数是颗粒与颗粒之间以及颗粒与墙之间的平均接触数,反映出试样的压密程度；力学配位数为颗粒与颗粒之间接触数大于2时的颗粒接触数,反映额土骨架的压密程度。图10,11给出了粉砂土在竖向和水平向渗流作用下,配位数随水力梯度的变化情况。

图 10 竖向渗流下粉砂配位数随水力梯度变化

Figure 10. Variation of coordination number with gradient under vertical seepage

下载: 全尺寸图片幻灯片

图 11 水平向渗流粉砂配位数随水力梯度变化

Figure 11. Variation of coordination number with gradient under horizontal seepage

下载: 全尺寸图片幻灯片

图10,11可以看出,当竖向渗流的水力梯度为0.8,水平向渗流水力梯度为0.4时,土体的两个配位数都发生迅速的下降,说明此时的土体状态发生了较大的变化,即渗透变形发生。图中,总配位数和力学配位数都在随着水力梯度的增大而不断降低,总的配位数较力学配位数下降更快速,幅度也更大。这是由于水力梯度增大,颗粒发生了移动,颗粒的接触数减小,但在水力梯度增加至土体渗透变形前的整个过程中,总配位数下降幅度明显大于力学配位数,说明发生移动的多为小颗粒,小颗粒的运移使土体中接触数减少,随之小颗粒填充至骨架颗粒孔隙间,与大颗粒发生接触,保持了力学配位数的大小。

3.   结论

（1）粉砂在水平向能承受的渗流破坏作用一般低于竖向渗流。

（2）数值模拟结果与模拟试验过程中粉砂的渗流变化过程相符,数值方法所测得的临界水力梯度与试验测得的结果亦较为吻合。

（3）竖向和水平向渗流下,粉砂的总配位数和力学配位数均随着水力梯度的抬升而衰减,当土体发生渗透破坏,土体配位数出现迅速降低。

图 1 地层概化

Figure 1. Stratigraphic generalization

下载: 全尺寸图片幻灯片

图 2 有限元模型

Figure 2. Finite element model

下载: 全尺寸图片幻灯片

图 3 土样压缩系数 $C_{c}$ 与压缩指数 $a_{v}$ 关系

Figure 3. Relationship between compression coefficient $C_{c}$ of soil samples and compression index $a_{v}$

下载: 全尺寸图片幻灯片

图 4 数值模拟结果(D=1.25 m)

Figure 4. Results of numerical simulation (D=1.25 m)

下载: 全尺寸图片幻灯片

图 5 桩径D与m值关系

Figure 5. Relationship between pile diameter D and m value

下载: 全尺寸图片幻灯片

图 6 压缩指数 $C_{c}$ 与m值关系

Figure 6. Relationship between compression index of soil $C_{c}$ and m value

下载: 全尺寸图片幻灯片

图 7 单桩水平静载现场试验

Figure 7. Horizontal static load field tests on single pile

下载: 全尺寸图片幻灯片

图 8 现场试验结果

Figure 8. Results of field tests

下载: 全尺寸图片幻灯片

图 9 土体压缩指数 $C_{c}$ 与m值关系

Figure 9. Relationship between compression index of soil $C_{c}$ and m value

下载: 全尺寸图片幻灯片

图 10 系数a, b与 $Y_{0}$ 关系

Figure 10. Relationship among coefficient a, b and $Y_{0}$

下载: 全尺寸图片幻灯片

图 11 m值拟合关系式修正

Figure 11. Correction of modified formula for m value

下载: 全尺寸图片幻灯片

图 12 m值拟合关系式验证

Figure 12. Verification of modified formula for m value

下载: 全尺寸图片幻灯片

表 1 沿线主要软土亚类划分

Table 1 Classification of main soft soil subclasses along line

材料编号	压缩系数 $a_{v}$ /MPa^-1	压缩指数 $C_{c}$	压缩参数λ	回弹参数k
Mat1	0.280	0.102	0.044	0.0044
Mat2	0.455	0.158	0.069	0.0069
Mat3	0.630	0.214	0.093	0.0093
Mat4	0.805	0.270	0.117	0.0117
Mat5	0.980	0.326	0.142	0.0142
Mat6	1.155	0.381	0.166	0.0166
Mat7	1.330	0.437	0.190	0.0190
Mat8	1.505	0.493	0.214	0.0214
Mat9	1.680	0.549	0.239	0.0239
Mat10	1.855	0.605	0.263	0.0263
Mat11	2.030	0.661	0.287	0.0287

下载: 导出CSV

表 2 修正剑桥模型参数（软土）

Table 2 Material parameters for MCC (soft soil)

材料	重度 $γ$ /(kN·m^-3)	初始孔隙比 $e_{0}$	CSL斜率M	压缩参数 $λ$
黏土	18.5	1.07	0.566	0.044~0.287

下载: 导出CSV

表 3 中砂与桩基物理力学参数

Table 3 Physico-mechanical parameters of medium sand and pile foundation

材料	重度 $γ$ /(kN·m^-3)	模量E/MPa	泊松比 $ν$	摩擦角 $φ$ /(°)
中砂	20.5	36	0.25	35
桩基	24.0	30000	0.20	—

下载: 导出CSV

表 4 桩顶水平位移系数 $v_{y}$ 取值

Table 4 Values of coefficient of horizontal displacement of pile top $v_{y}$

$α h$	≥4.0	3.5	3.0	2.8	2.6	2.4
$v_{y}$	2.441	2.502	2.727	2.905	3.163	3.526

下载: 导出CSV

参考文献(17)

[1]	姚文娟, 吴怀睿, 程泽坤, 等. 基于p-y曲线法的超长桩非线性数值分析[J]. 岩土工程学报, 2011, 33(11): 1683-1690. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201111009.htm YAO Wen-juan, WU Huai-rui, CHENG Ze-kun, et al. Nonlinear numerical analysis of super-long piles based on p-y curves[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1683-1690. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC201111009.htm
[2]	RAO S N, RAMAKRISHNA V G S T, RAO M B. Influence of rigidity on laterally loaded pile groups in marine clay[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(6): 542-549. doi: 10.1061/(ASCE)1090-0241(1998)124:6(542)
[3]	LI Wei, CHEN Fa-bo, XU Xue-yong, et al. Comparative study of pile-soil interaction analysis methods[J]. Applied Mechanics and Materials, 2012, 170/171/172/173: 246-251.
[4]	WANG J P, SU J B, WU F, et al. Lateral dynamic load tests of offshore piles based using the m-method[J]. Ocean Engineering, 2021, 220: 108413. doi: 10.1016/j.oceaneng.2020.108413
[5]	刘陕南, 侯胜男, 蔡忠祥. m法计算单桩水平承载力在上海地区的适用性分析[J]. 岩土工程学报, 2013, 35(增刊2): 721-724. https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2132.htm LIU Shan-nan, HOU Sheng-nan, CAI Zhong-xiang. Applicability of m-method for horizontal bearing capacity of single pile in Shanghai area[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S2): 721-724. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTGC2013S2132.htm
[6]	戴自航, 陈林靖. 多层地基中水平荷载桩计算m法的两种数值解[J]. 岩土工程学报, 2007, 29(5): 690-696. doi: 10.3321/j.issn:1000-4548.2007.05.010 DAI Zi-hang, CHEN Lin-jing. Two numerical solutions of laterally loaded piles installed in multi-layered soils by m method[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(5): 690-696. (in Chinese) doi: 10.3321/j.issn:1000-4548.2007.05.010
[7]	劳伟康, 周治国, 周立运. 水平推力桩在大位移情况下m值的确定[J]. 岩土力学, 2008, 29(1): 192-196. doi: 10.3969/j.issn.1000-7598.2008.01.036 LAO Wei-kang, ZHOU Zhi-guo, ZHOU Li-yun. Analysis of m value for lateral loaded pile under large deflection[J]. Rock and Soil Mechanics, 2008, 29(1): 192-196. (in Chinese) doi: 10.3969/j.issn.1000-7598.2008.01.036
[8]	吴锋, 时蓓玲, 卓杨. 水平受荷桩非线性m法研究[J]. 岩土工程学报, 2009, 31(9): 1398-1401. doi: 10.3321/j.issn:1000-4548.2009.09.012 WU Feng, SHI Bei-ling, ZHUO Yang. Nonlinear m method for piles under lateral load[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(9): 1398-1401. (in Chinese) doi: 10.3321/j.issn:1000-4548.2009.09.012
[9]	戴自航, 王云凤, 卢才金. 水平荷载单桩计算的综合刚度和双参数法杆系有限元数值解[J]. 岩石力学与工程学报, 2016, 35(10): 2115-2123. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201610018.htm DAI Zi-hang, WANG Yun-feng, LU Cai-jin. Numerical solution of link finite element based on composite stiffness and bi-parameter method for computation of laterally loaded single pile[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(10): 2115-2123. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201610018.htm
[10]	邓涛, 林聪煜, 柳志鹏, 等. 大位移条件下水平受荷单桩的简明弹塑性计算方法[J]. 岩土力学, 2020, 41(1): 95-102. DENG Tao, LIN Cong-yu, LIU Zhi-peng, et al. A simplified elastoplastic method for laterally loaded single pile with large displacement[J]. Rock and Soil Mechanics, 2020, 41(1): 95-102. (in Chinese)
[11]	YU G M, GONG W M, LIU Y C, et al. Lateral capacity of pile with grouted upper soil: field test and numerical simulation[J]. Innovative Infrastructure Solutions, 2017, 3(1): 1-9.
[12]	冯君, 张俊云, 朱明, 等. 软土地层高承台桥梁群桩基础横向承载特性研究[J]. 岩土力学, 2016, 37(增刊2): 94-104. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S2011.htm FENG Jun, ZHANG Jun-yun, ZHU Ming, et al. Characteristic study of horizontal bearing capacity and pile group effect coefficient of laterally loaded high pile group foundation for bridge in soft soil[J]. Rock and Soil Mechanics, 2016, 37(S2): 94-104. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX2016S2011.htm
[13]	KARTHIGEYAN S, RAMAKRISHNA V V G S T, RAJAGOPAL K. Influence of vertical load on the lateral response of piles in sand[J]. Computers and Geotechnics, 2006, 33(2): 121-131. doi: 10.1016/j.compgeo.2005.12.002
[14]	KIM Y, JEONG S. Analysis of soil resistance on laterally loaded piles based on 3D soil-pile interaction[J]. Computers and Geotechnics, 2011, 38(2): 248-257. doi: 10.1016/j.compgeo.2010.12.001
[15]	陈建峰, 孙红, 石振明, 等. 修正剑桥渗流耦合模型参数的估计[J]. 同济大学学报(自然科学版), 2003, 31(5): 544-548. https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ200305008.htm CHEN Jian-feng, SUN Hong, SHI Zhen-ming, et al. Estimation of parameters of modified cam-clay model coupling Biot theory[J]. Journal of Tongji University, 2003, 31(5): 544-548. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TJDZ200305008.htm
[16]	铁路工程基桩检测技术规程：TB 10218—2008[S]. 2008. Technical Specification for Testing of Railway Piles: TB 10218—2008[S]. 2008. (in Chinese)
[17]	铁路桥涵地基和基础设计规范：TB 10093—2017[S]. 2017. Code for Design on Subsoil and Foundation of Railway Bridge and Culvert: TB 10093—2017[S]. 2017. (in Chinese)

施引文献(6)

期刊类型引用(4)

1.	应宏伟，陈雨，王阳扬，刘冠. 含碎石芯软黏土复合试样大三轴试验研究. 湖南大学学报(自然科学版). 2024(11): 104-114 . 百度学术
2.	邱俊峰，叶晨峰，陈峰，郑铖杰. 镍铁渣粉水泥固化砂土剪切强度与应力应变关系研究. 湖南文理学院学报(自然科学版). 2023(02): 78-82+95 . 百度学术
3.	殷天军，宁华宇，寇晓强. 深中通道沉管基础水下深层水泥搅拌桩应用全过程探讨. 中国港湾建设. 2022(07): 11-16 . 百度学术
4.	张振，郑文强，叶观宝，陈勇. 循环荷载下水泥土桩复合单元体变形特性及其地基长期沉降计算方法. 中国公路学报. 2022(11): 21-29 . 百度学术