考虑抗剪强度空间变异性的双层黏土边坡风险分析

易顺; 岳克栋; 陈健; 黄珏皓; 李健斌; 邱岳峰; 田宁

doi:10.11779/CJGE2021S2027

考虑抗剪强度空间变异性的双层黏土边坡风险分析 English Version

易顺^{1, 2, 3, 4,},
岳克栋⁵,
陈健^{1, 2, 3, 4, ,},
黄珏皓^{1, 2, 3, 4},
李健斌⁶,
邱岳峰⁷,
田宁^{1, 2}

1.
中国科学院武汉岩土力学研究所,岩土力学与工程国家重点实验室,湖北　武汉　430071
2.
中国科学院大学,北京　100049
3.
湖北省环境岩土工程重点实验室,湖北　武汉　430071
4.
岩土力学与工程国家重点实验室宁波工程学院工程软土实验中心,浙江　宁波　315211
5.
长江勘测规划设计研究院有限责任公司,湖北　武汉　430010
6.
广州大学土木工程学院,广东　广州　510006
7.
中国电建集团中南勘测设计研究院有限公司,湖南　长沙　410014

基金项目:

国家自然科学基金面上项目 52079135

国家自然科学基金青年基金项目 51909259

国家自然科学基金青年基金项目 52008122

宁波市公益类科技计划项目 2019C50012

湖北省建设科技计划项目 2018

中国科学院国际合作局国际伙伴计划 131551KYSB20180042

详细信息

作者简介:
易顺(1993— ),男,博士研究生,主要从事随机场理论及边坡稳定性方面的研究。E-mail: sunyee_123@163.com

通讯作者:
陈健, E-mail: jchen@whrsm.ac.cn

中图分类号: TU43
计量
- 文章访问数: 202
- HTML全文浏览量: 12
- PDF下载量: 129
出版历程
- 收稿日期: 2021-08-12
- 网络出版日期: 2022-12-05
- 刊出日期: 2021-10-31

Risk analysis of two-layer clay slopes considering spatial variability of shear strength

YI Shun^{1, 2, 3, 4,},
YUE Ke-dong⁵,
CHEN Jian^{1, 2, 3, 4, ,},
HUANG Jue-hao^{1, 2, 3, 4},
LI Jian-bin⁶,
QIU Yue-feng⁷,
TIAN Ning^{1, 2}

1.
State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
Hubei Key Laboratory of Geo-Environmental Engineering, Wuhan 430071, China
4.
The Soft Soil Research Center in Ningbo University of Technology, State Key Laboratory of Geomechanics and Geotechnical Engineering, Ningbo 315211, China
5.
Changjiang Institute of Survey, Planning Design and Research Co., Ltd., Wuhan 430010, China
6.
School of Civil Engineering, Guangzhou University, Guangzhou 510006, China
7.
Power China Zhongnan Engineering Corporation limited, Changsha 410014, China

摘要

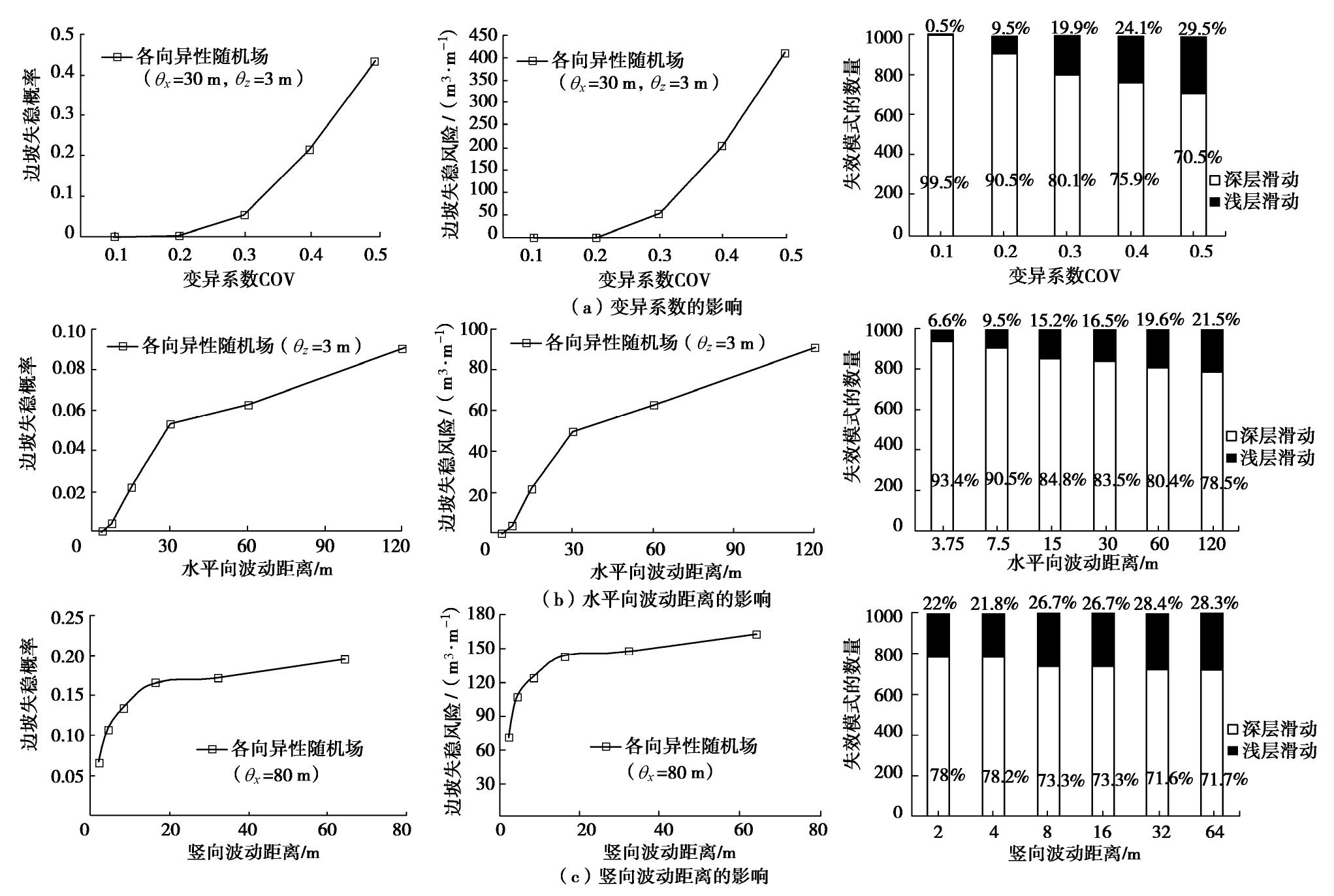
摘要: 土性参数空间变异性具有各向异性的特点,因而采用各向异性随机场来描述边坡参数空间分布的特征更为合理。针对某一双层黏土边坡,基于土体抗剪强度的各向异性随机场,研究了土体参数的竖向波动距离、水平向波动距离和变异系数对边坡失稳概率、失稳模式和风险评估的影响。主要得到的结论如下：随着COV的增大,边坡失稳风险逐步增大,在低变异性土体中,几乎没有边坡失稳风险。整体而言,边坡失稳概率和边坡失稳风险随变异系数的变化规律保持一致性。深层滑动模式占比很大,但随着COV的增大,深层滑动模式逐步向浅层滑动模式过渡；当波动距离（包括水平向和竖向）增大时,边坡失稳概率和失稳风险均相应增大,但当波动距离超过一定大小（表现与边坡尺寸相关）时,失稳概率和失稳风险受到波动距离增大的影响幅度变小。
- 各向异性 /
- 随机场 /
- 双层黏土边坡 /
- 失稳概率 /
- 失稳风险
Abstract: Anisotropy exists in the spatial variability of soil parameters. Therefore, it is rational to indicate the spatial distribution of slope parameters using anisotropy random fields. Based on the anisotropic random field of shear strength of soil for a two-layer slope, the effects of vertical scales of fluctuation, horizontal scales of fluctuation and coefficient of variation (COV) of soil parameters on the slope failure probability, instability modes and risk assessments are studied. The main conclusions are drawn as follows: with the increase of COV, the risk of slope failure gradually increases. In low-variability soils, there is almost no risks of slope failure. On the whole, the failure probability of slope is consistent with the risk of failure as COV increases. The deep-layer slop mode accounts for a large proportion, but with the increase of COV, the deep-layer slope mode gradually becomes the shallow slope one. When the scale of fluctuation (including horizontal and vertical) increases, the failure probability of slope and risks increase accordingly. However, when the scale of fluctuation exceed a particular size, which is related to the size of the slope, the increasing amplitude of failure probability and risks slows down as the scale of fluctuation increases.
- anisotropy /
- random field /
- two-layer clay slope /
- probability of failure /
- risk of failure

HTML全文

0. 引言

随着城市化进程的推进,基坑工程向更深、更复杂的趋势发展,为了保证周边环境安全,基坑变形的现场监测和预报已成为基坑工程的重要内容。传统的理论分析、数值模拟等方法虽然理论上可以实现变形的预测,但是岩土工程的变形机理复杂,涉及的影响因素众多,这类方法无法全面考虑^[1]。

近年来,基于数据分析的时间序列建模方法被逐渐应用于岩土工程领域。其中灰色预测模型对样本数据量要求低,但对于非线性序列的预测效果较差^[2]；人工神经网络具有较强的非线性映射能力,但存在网络结构难以确定、容易陷入局部最优、样本数据量要求高等缺点^[3]；遗传算法、粒子群算法等优化算法与人工神经网络结合的组合模型改善了神经网络的性能,但仍然存在数据量要求高、泛化能力差的问题^[4]。现有方法在预测时都以单测点的监测数据作为输入变量,只关注数据在时间维度上的关联性,而忽略了邻近监测点之间空间维度上的关联性。实际工程会设置大量的监测点,如何充分利用多个监测点的监测数据以提高预测精度是值得进一步研究的问题。针对上述不足,本文提出运用卷积神经网络与长短期记忆神经网络（CNN-LSTM）结合的组合模型,考虑监测数据在时间维度和空间维度上的关联性,对基坑工程多维序列进行预测。该方法在上海云岭超深基坑工程的地表沉降实际监测数据预测中取得了令人满意的效果。

1. CNN-LSTM模型

1.1 卷积神经网络（CNN）

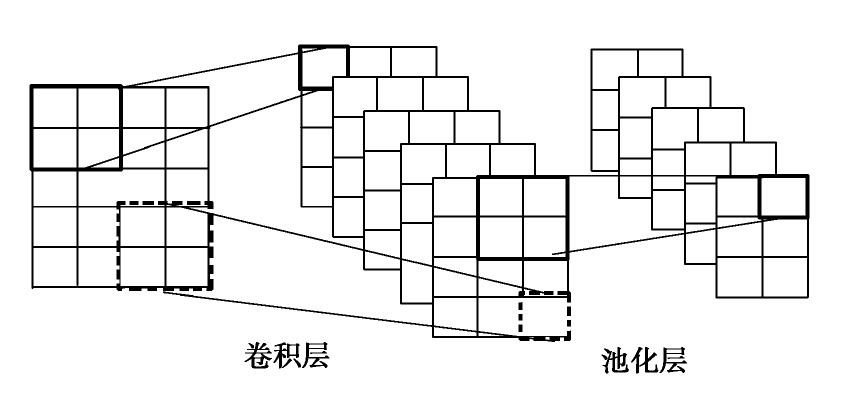
卷积神经网络（convolutional neural networks）是一类包含卷积运算的前馈神经网络。CNN通过对数据的卷积和池化操作,提取数据之间的相互关系,可以用少量参数表达数据的空间特征,具有优秀的高维特征提取能力,被广泛用于图像处理、计算机视觉等问题。CNN网络的核心结构如图1所示。卷积层通过设置卷积核,对输入数据按式（1）进行离散卷积运算,提取输入数据的空间特征。池化层通过对卷积核内的数据进行取最大值、取平均值等操作,实现数据的降采样,即去除杂余信息,保留关键特征。

$y_{i, j} = σ (W_{k} \otimes x_{i, j} + b_{k})$ ,

(1)

$W_{k} \otimes x_{i, j} = \sum_{m = 0}^{a - 1} \sum_{n = 0}^{b - 1} w_{m, n} \times x_{i + m, j + n}$ ,

(2)

图 1 CNN网络核心结构示意图

Figure 1. Structure of convolutional neural networks

下载: 全尺寸图片幻灯片

式中 x_ij为卷积层的输入数据；y_ij为卷积层的输出数据；为离散卷积运算；W_k和b_k分别为第k个卷积核的权重系数和偏置参数； $σ$ 为神经元的激活函数；a,b为卷积核的尺寸参数。

1.2 长短期记忆神经网络（LSTM）

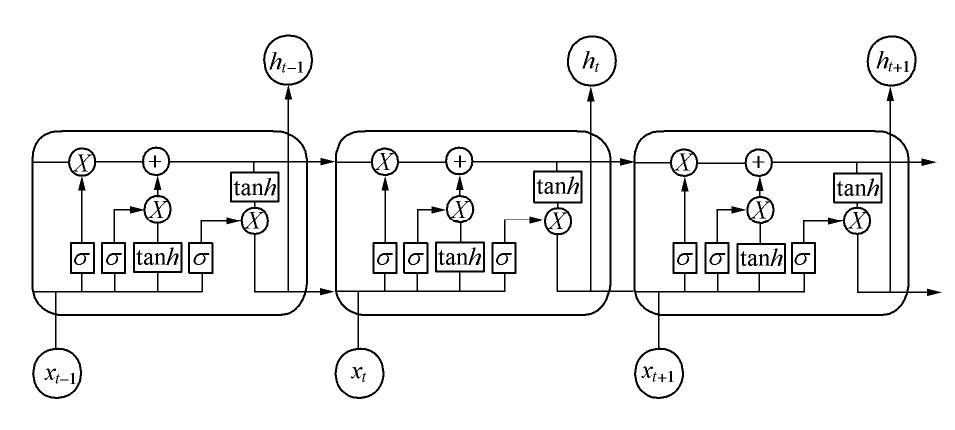
LSTM神经网络（long short-term memory neural network）是循环神经网络RNN（recurrent neural network）的一种变体。LSTM神经网络通过设置特殊的“门”结构,可以有选择性地记忆长短期信息,解决了RNN结构的长时间依赖问题,在时序数据的预测问题上表现优异。LSTM单元结构如图2所示。

图 2 LSTM结构示意图

Figure 2. Structure of LSTM

下载: 全尺寸图片幻灯片

1.3 CNN-LSTM模型

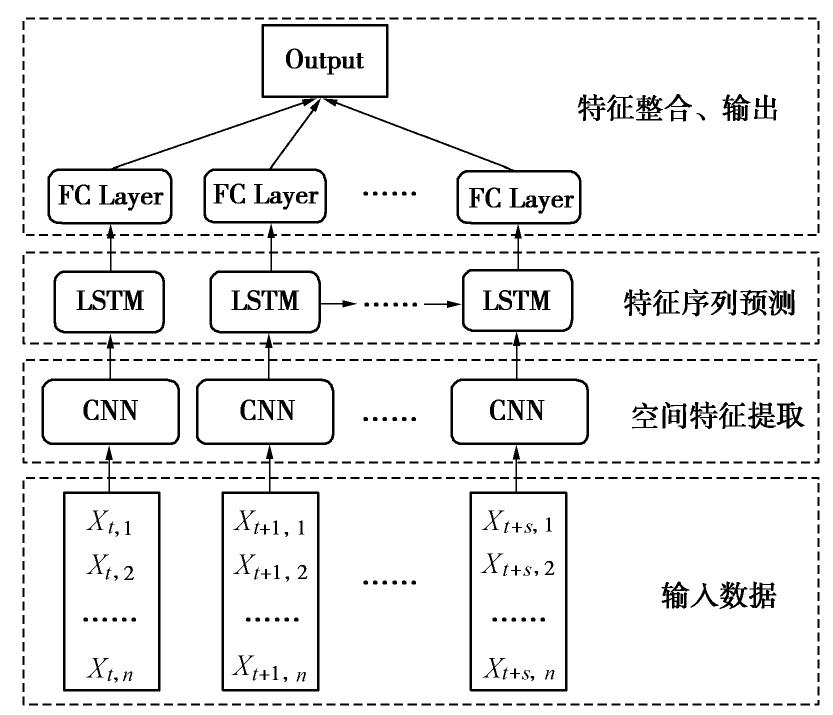
卷积神经网络CNN与循环神经网络LSTM结合的CNN-LSTM神经网络结构如图3所示。CNN部分以多个监测点的标准化后的历史数据构成的多维时间序列X_t,n作为输入数据。X_t,n是一个二维矩阵,一行表示某一时刻n个监测点的监测值,一列表示某一监测点在时间步长t内的监测值。将该序列输入CNN部分后,进行卷积运算,提取空间特征,输出多个由空间特征组成一维序列。LSTM部分以CNN网络输出的一维序列作为输入数据。LSTM对序列进行回归预测,输出多个空间特征的预测值。最后通过全连接层整合空间特征预测值,输出监测数据的预测值。

图 3 CNN-LSTM模型结构示意图

Figure 3. Structure of CNN-LSTM model

下载: 全尺寸图片幻灯片

2. 工程实例验证

2.1 工程概况

云岭竖井基坑是上海苏州河深隧工程的一部分。竖井基坑为圆形,深度约60 m,支护结构为1500 mm地下连续墙。基坑位于上海软土地区,且基坑开挖深度范围内的深层土体力学特性尚不明确,给基坑周边地表沉降的计算带来了困难。为了实时地进行动态化施工反馈,在基坑周边布置了大量监测点。基坑周边对称布置DB-1、DB-2、DB-3和DB-4四条测线,其中DB-4的监测点在施工中被破坏,监测数据不完整。

本文选取其余三条测线的第一个测点（DB1-1、DB2-1、DB3-1）从2020年7月27日至2020年12月28日,共计155组数据,前135组数据用于训练模型,后20组数据用于验证模型的精度。

2.2 监测数据建模预测

现在以DB1-1测点的监测数据作为预测目标,详细描述如何利用CNN-LSTM模型进行时序预测。

（1）数据预处理

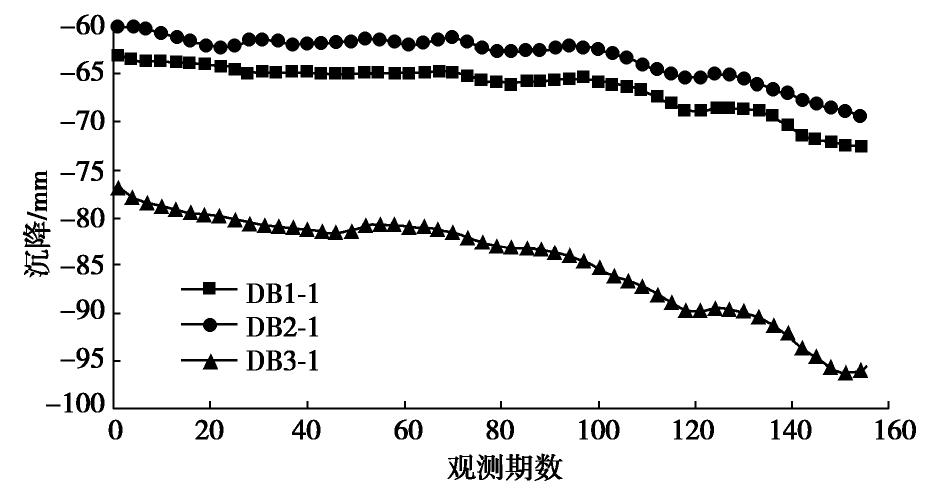
现场采集的数据受各种因素的干扰,包含大量噪声^[5]。为避免拟合噪声,在导入模型训练前,对原始数据进行降噪处理。降噪后数据如图4所示。此外,不同监测点的监测数据在绝对值上相差较大,为了避免模型训练时的梯度方向被某一监测点的数据控制,本文按式（3）标准化数据,标准化后的数据符合均值为0,方差为1的正态分布。

${x^{'}}_{t, i} = \frac{x_{t, i} - μ_{i}}{σ_{i}}$ ,

(3)

图 4 降噪后数据示意图

Figure 4. Curves of data after noise reduction

下载: 全尺寸图片幻灯片

式中,μ_i,σ_i为第i个测点全部监测数据的均值和方差。

（2）CNN-LSTM模型构建

本文基于Python的Keras库构建CNN-LSTM模型。第一层为卷积层,卷积核个数为80,即提取80个空间特征,卷积核尺寸为1×3；第二层为LSTM层,LSTM层的神经元个数对网络的性能影响最大,因此取初始值80,在训练过程中优化；第三层为Dense层。需要指出的是由于本文选取的数据集在空间维度上只有3个监测点,数据规模不大,不设置池化层可以取得更好的效果。

（3）训练样本构造与模型训练

本文采用“5+1”的样本构造模式,即以3个测点前5天的监测数据作为输入数据,输入数据为5×3的二维矩阵,第6天DB1-1测点的监测数据作为输出数据。训练集共135组监测数据构造130组训练样本。训练优化器选择Adam,迭代次数epoch取100次,损失函数为均方误差MSE,模型收敛。

（4）监测值预测

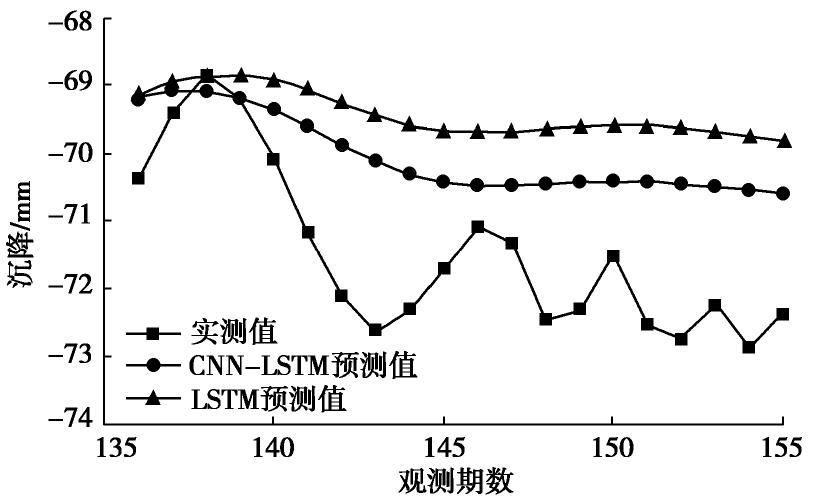
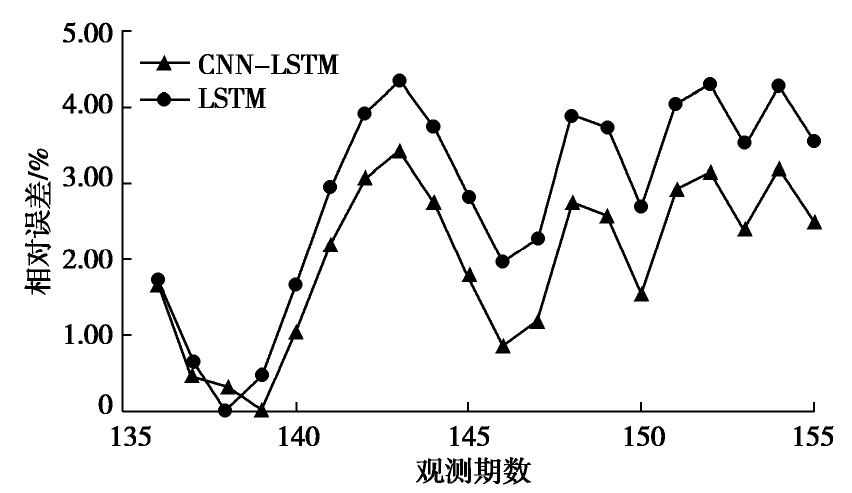
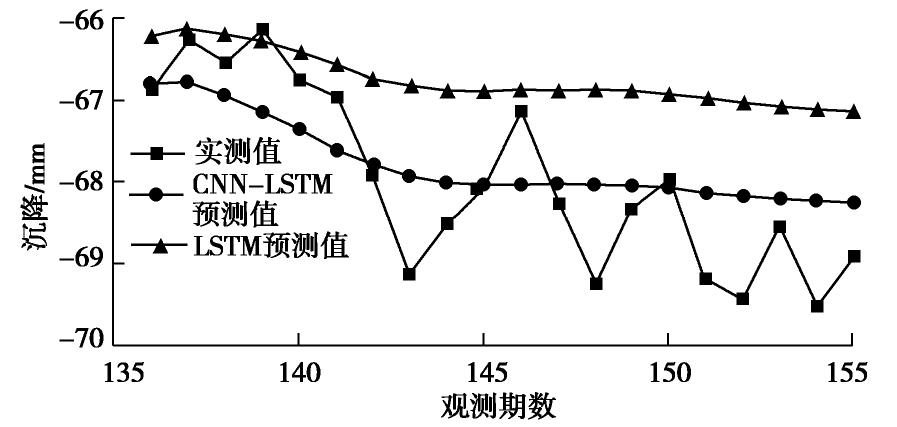
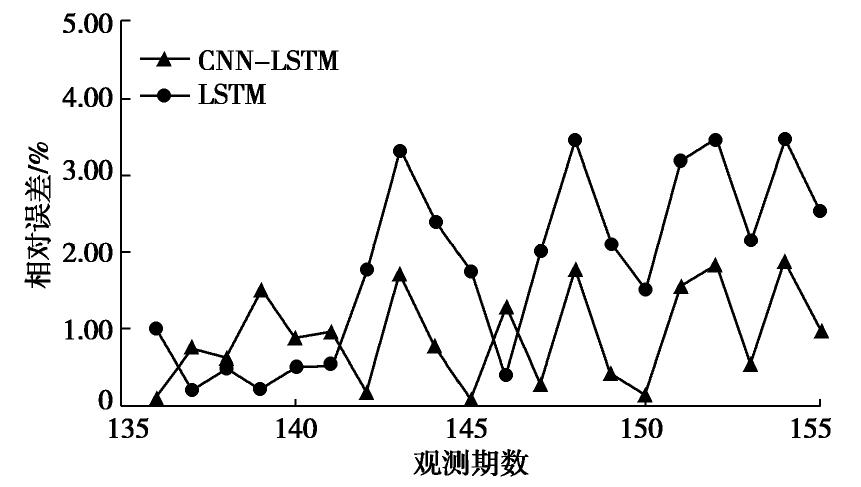
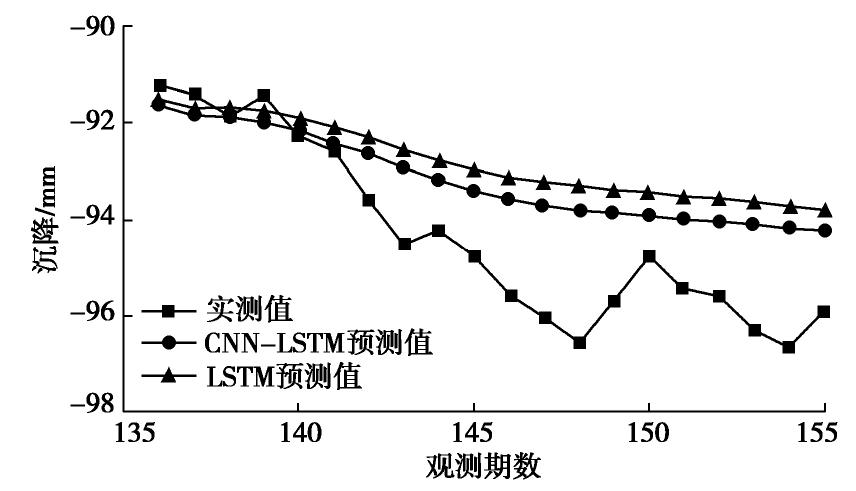
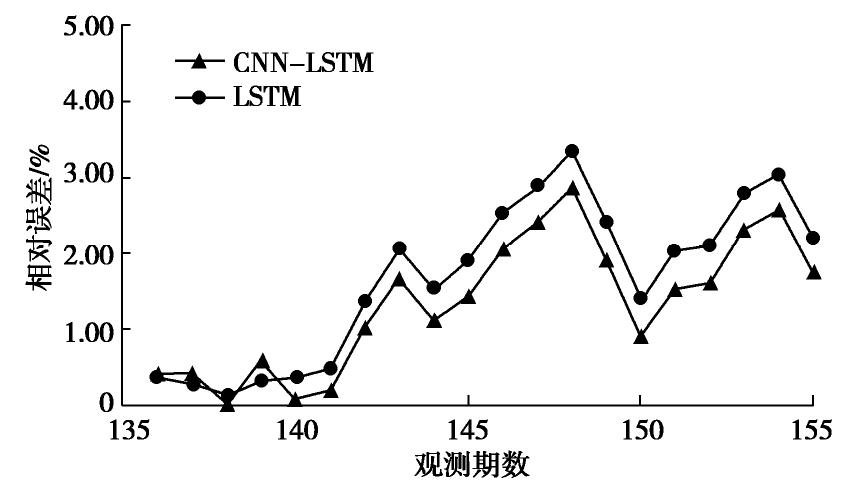
最后利用训练完毕的模型对最后20组数据进行滚动预测。考虑到前期数据的降噪预处理,本文同时对噪声采用统计学模型ARMA进行分析、预测后,与CNN-LSTM的输出结果合并,作为最终预测值。为了验证CNN-LSTM模型的预测效果,本文同时单独采用LSTM模型进行预测,两种方法的结果和预测相对误差对比如图5,6所示。对DB2-1、DB3-1测点采用同样方法的预测结果和误差如图7～10所示。

图 5 DB1-1测点监测值与预测值

Figure 5. Measured and predicted values of DB1-1

下载: 全尺寸图片幻灯片

图 6 DB1-1测点预测相对误差对比

Figure 6. Comparison of prediction relative errors of DB1-1

下载: 全尺寸图片幻灯片

图 7 DB2-1测点监测值与预测值

Figure 7. Measured and predicted values of DB2-1

下载: 全尺寸图片幻灯片

图 8 DB2-1测点预测相对误差对比

Figure 8. Comparison of prediction relative errors of DB2-1

下载: 全尺寸图片幻灯片

图 9 DB3-1测点监测值与预测值

Figure 9. Measured and predicted values of DB3-1

下载: 全尺寸图片幻灯片

图 10 DB3-1测点预测相对误差对比

Figure 10. Comparison of prediction relative errors of DB3-1

下载: 全尺寸图片幻灯片

图5和图6表明,CNN-LSTM组合模型的预测结果与单一LSTM模型相比,在所有观测时间点上都更接近实测值,但是两种模型预测结果的趋势仍然与实测值有明显不同,这是由于噪声的预测模型难以拟合本例的数据。采用CNN-LSTM模型时,预测结果的相对误差介于0.01%～3.44%之间,平均值为2.00%,而LSTM模型相对误差介于0.02%～4.36%,平均值为2.84%,说明前者预测精度更高,效果更为理想。

图7～10表明,DB2-1测点和DB3-1测点的预测结果与DB1-1测点基本一致,CNN-LSTM模型的预测结果更接近实测值。采用CNN-LSTM模型,DB2-1测点、DB3-1测点的预测平均相对误差分别为0.93%、1.35%,而采用LSTM模型的平均相对误差分别为1.84%和1.69%,综合来看,CNN-LSTM模型取得了更好的效果。

需要指出的是,CNN-LSTM的精度优化得益于测点之间的空间关联度,选择测点时可综合测点的几何分布和历史监测曲线两方面判断。本例测点对称分布于基坑周边,且历史监测曲线的趋势也具有一致性。

3. 结论

本文在已有岩土工程时间序列预测方法的基础上,提出可以考虑监测数据空间关联性的CNN-LSTM组合模型。通过基于上海云岭竖井超深基坑工程现场地表沉降监测数据的工程实例验证,得出以下结论：

（1）多个监测点的监测数据构成一个多维时间序列,不同监测点数据之间的空间关联特征可以用CNN网络中的卷积运算提取。

（2）CNN-LSTM模型采用CNN网络提取多维时间序列的空间特征,LSTM网络多空间特征序列进行回归预测。工程实例表明,该模型在预测精度上相较于基于单测点数据的LSTM模型具有更高的精度。

（3）本文预测的多维时间序列的均为地表沉降,即同一类监测数据。工程现场的不同监测项目之间,理论上也可采用CNN-LSTM模型建模预测,如何将该模型推广到任意监测项目组成的多维时间序列是值得深入研究的问题。

图 1 边坡滑体估算示意图

Figure 1. Schematic of estimating volume of slope landslide

下载: 全尺寸图片幻灯片

图 2 双层边坡的确定性计算结果图

Figure 2. Deterministic calculated results of two-layer slope

下载: 全尺寸图片幻灯片

图 3 边坡安全系数均值与随机计算次数的关系

Figure 3. Relationship between mean value of safety factor of slope and number of stochastic calculations

下载: 全尺寸图片幻灯片

图 4 参数各向异性随机场对双层边坡失稳概率、失稳风险和失稳模式的影响

Figure 4. Effects of anisotropy random field on probability of failure, risks of failure and instability modes for a two-layer slope

下载: 全尺寸图片幻灯片

参考文献(13)

[1]	MORGENSTERN N R. Performance in geotechnical practice[J]. HKIE Transactions, 2000, 7(2): 2-15. doi: 10.1080/1023697X.2000.10667819
[2]	LUMB P. The variability of natural soils[J]. Canadian Geotechnical Journal, 1966, 3(2): 74-97. doi: 10.1139/t66-009
[3]	PHOON K K, KULHAWY F H. Characterization of geotechnical variability[J]. Canadian Geotechnical Journal, 1999, 36(4): 612-624. doi: 10.1139/t99-038
[4]	ALONSO E E. Risk analysis of slopes and its application to slopes in Canadian sensitive clays[J]. Géotechnique, 1976, 26(3): 453-472. doi: 10.1680/geot.1976.26.3.453
[5]	程红战, 陈健, 王占盛, 等. 考虑旋转各向异性相关结构的黏土边坡稳定性分析[J]. 岩石力学与工程学报, 2017, 36(增刊2): 3965-3973. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S2029.htm CHENG Hong-zhan, CHEN Jian, WANG Zhan-sheng, et al. Stability analysis of a clay slope accounting for the rotated anisotropy correlation structure[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(S2): 3965-3973. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX2017S2029.htm
[6]	GRIFFITHS D V, HUANG J S, FENTON G A. Influence of spatial variability on slope reliability using 2-D random fields[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(10): 1367-1378. doi: 10.1061/(ASCE)GT.1943-5606.0000099
[7]	HUANG J, LYAMIN A V, GRIFFITHS D V, et al. Quantitative risk assessment of landslide by limit analysis and random fields[J]. Computers and Geotechnics, 2013, 53: 60-67. doi: 10.1016/j.compgeo.2013.04.009
[8]	CHENG H Z, CHEN J, CHEN R P, et al. Risk assessment of slope failure considering the variability in soil properties[J]. Computers and Geotechnics, 2018, 103: 61-72. doi: 10.1016/j.compgeo.2018.07.006
[9]	EL-RAMLY H, MORGENSTERN N R, CRUDEN D M. Probabilistic stability analysis of a tailings dyke on presheared clay shale[J]. Canadian Geotechnical Journal, 2003, 40(1): 192-208. doi: 10.1139/t02-095
[10]	DAVIS M W. Production of conditional simulations via the LU triangular decomposition of the covariance matrix[J]. Mathematical Geology, 1987, 19(2): 91-98.
[11]	GUZZETTI F. Landslide hazard and risk assessment[D]. Bonn, Germany: Universitat Bonn, 2006.
[12]	HICKS M A, SAMY K. Influence of heterogeneity on undrained clay slope stability[J]. Quarterly Journal of Engineering Geology and Hydrogeology, 2002, 35(1): 41-49. doi: 10.1144/qjegh.35.1.41
[13]	李典庆, 肖特, 曹子君, 等. 基于高效随机有限元法的边坡风险评估[J]. 岩土力学, 2016, 37(7): 1994-2003. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201607021.htm LI Dian-qing, XIAO Te, CAO Zi-jun, et al. Slope risk assessment using efficient random finite element method[J]. Rock and Soil Mechanics, 2016, 37(7): 1994-2003. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201607021.htm

施引文献(6)

期刊类型引用(3)

1.	符传邦，吴育麒，吴月磊. 水泥搅拌桩各项参数对软土路基沉降的影响. 市政技术. 2023(02): 73-77 . 百度学术
2.	赵楠. 地铁隧道基底围岩动三轴试验研究. 资源信息与工程. 2022(02): 116-120 . 百度学术
3.	魏丽，柴寿喜，张琳，李瑶. 冻融作用下三类纤维加筋固化土的抗压抗拉性能. 岩土力学. 2022(12): 3241-3248+3280 . 百度学术