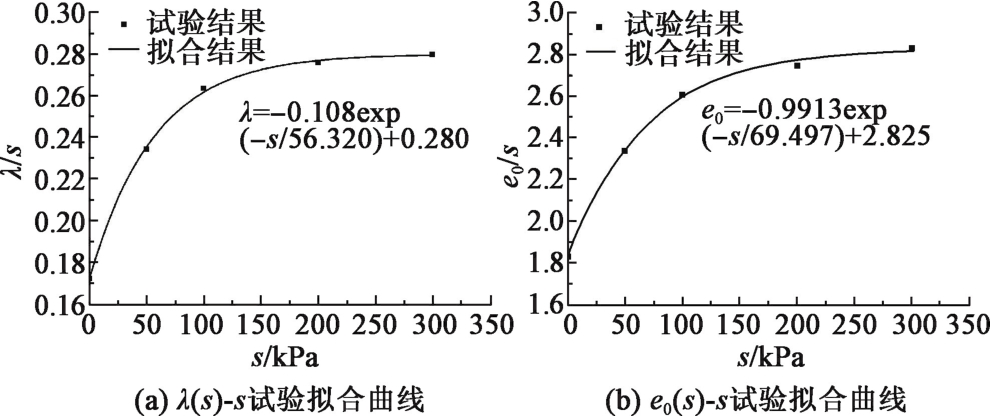
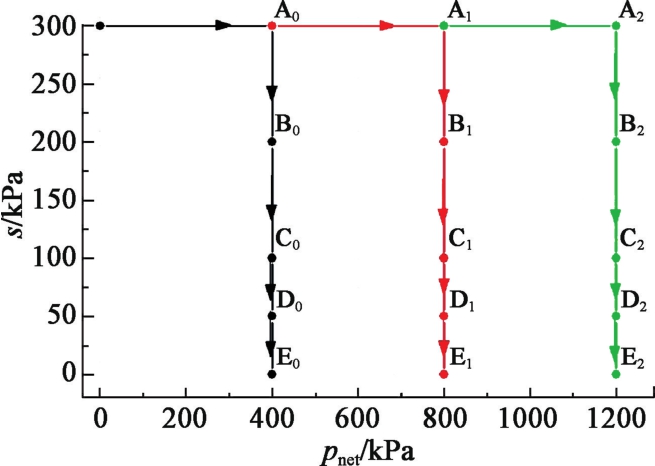
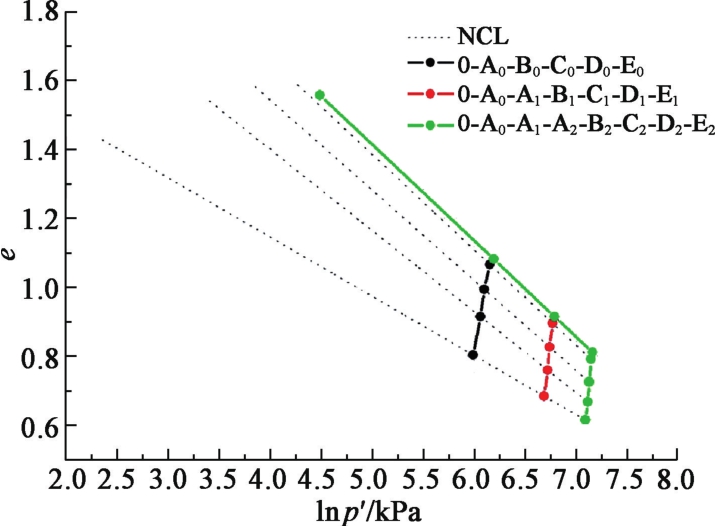
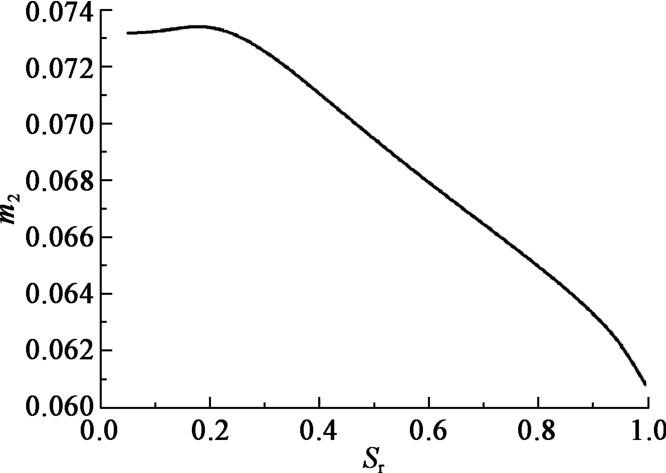
Wetting deformation properties of unsaturated collapsible loess
-
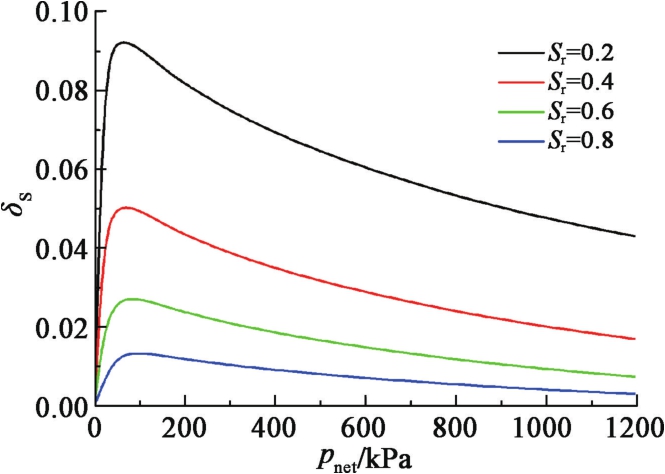
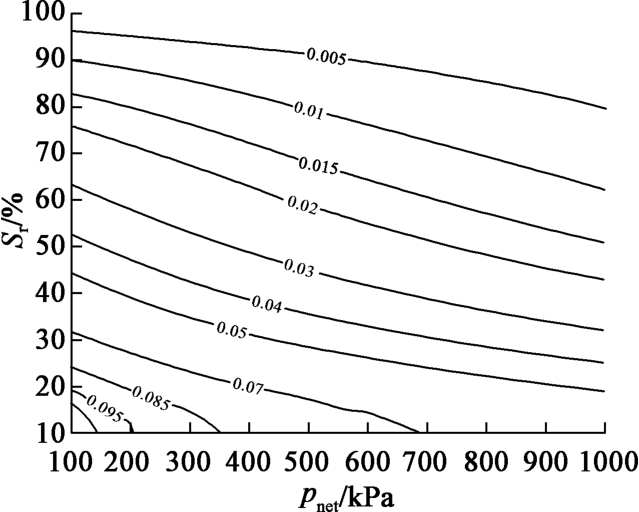
摘要: 在非饱和土力学的框架下对非饱和黄土的增湿变形行为进行了研究。基于粒间吸应力表示的非饱和土有效应力原理,建立了非饱和黄土增湿变形的本构模型,通过理论分析,给出了加载增湿屈服函数的积分表达式以及黄土湿陷性系数的显式计算公式。结合原状非饱和黄土的试验数据,分析了不同水力路径下的湿陷变形特性,并探讨了湿陷性系数的变化规律。结果表明,提出的模型能够很好地揭示非饱和黄土湿陷变形的力学机制,可为黄土增湿变形特性的研究和工程应用提供一定的参考价值。Abstract: The wetting deformation behavior of unsaturated loess is studied under the framework of unsaturated soil mechanics.Based on the principle of effective stress of unsaturated soil is expressed by intergranular attraction, a constitutive model for wettig deformation of unsaturated loess is established.Through theoretical analysis, the integral expression for the yielding function of loading-wetting and the explicit formula for collapsibility coefficient of loess are given.Combined with the experimental data of undisturbed unsaturated loess, the characteristics of collapsing deformation under different hydraulic paths are analyzed, and the variation law of collapsibility coefficient is discussed.The results show that the model can well reveal the mechanical mechanism of deformation of unsaturated collapsible loess, and can provide some reference value for the researches on wetting deformation properties of loess and engineering application.
-
0. 引言
土工离心模型试验技术是一项崭新的土工物理模型技术,通过施加在模型上的离心惯性力使模型的重度变大,从而使模型的应力与原型一致,这样就可以用模型反映、表示原型。离心模型是各类物理模型中相似性最好的模型,在国内外受到广泛重视,试验技术飞速发展与进步,研究内容涉及几乎所有的岩土工程研究领域,已成为岩土工程技术研究中的最主要、最有效、最广泛应用的研究手段[1]。
Biot动力固结方程是土力学的基本方程,包括动力平衡方程和连续方程。从连续方程出发,得到固结与孔隙水压力的扩散问题的时间比尺关系tp/tm=n2[2],这个关系的前提假设是,模型的渗透系数km是原型渗透系数kp的n倍,模型与原型的固结系数相等,这一假设存在争议,未得到试验完全证实。
Pokrovsky & Fyodorov认为离心模型的水力坡降im与原型的水力坡降ip相等,模型的渗透系数km是原型渗透系数kp的n倍,得到了tp/tm=n2的时间比尺关系;而Cargill等[3]则认为离心模型的水压力坡降im是原型的水压力坡降ip的n倍,模型的渗透系数km与原型渗透系数kp相等,令人奇怪的是,他们利用相互矛盾、相互对立的假定得到了相同的结论。
其实,Cargill等把达西定律中的“水力梯度(h/L)”用“水压力梯度(p/L)”来代替是错误的,因为水力梯度(无量纲)与水压力梯度(有量纲)并不相同。因而,模型渗透系数km与原型渗透系数kp的关系,成了问题的关键。即土的渗透系数(达西渗透系数)在高重力场下变不变?是否随加速度而增大?
从不同的研究目的出发,世界各国的离心模型试验专家进行了不懈的努力。Goodings[4]通过试验研究了灰坝的浸润线,Croce等[5]研究了土样的固结问题,Singh等[6]和Khalifa等[7]都研究过土的渗透系数随加速度的变化规律。令人不解的是,Singh等的结果表明,土的渗透系数随加速度而增大,而Khalifa等的结果却表明,在50g以下,土的渗透系数不随加速度变化。Singh等的试验装置不能防止水的蒸发,结果令人怀疑;Khalifa等的试验只进行到50g,也难以说明问题,不能令人信服。Sharma等[8]分析了离心机半径对变水头试验测得的渗透系数的影响。隋海宾等[9]总结了国外离心模型试验中土的渗透相似性研究成果,但没有自己的试验。Anderson等[10]研制了在离心机上进行土的渗透系数试验的装置,可以大大缩短试验时间。
国内外离心模型试验发展很快,离心模型试验中固结与孔隙水压力扩散问题的时间比尺问题一直未能得到有效的试验验证。固结与孔隙水压力扩散问题的时间比尺关系tp/tm=n2正确与否,归根结底就是高重力场条件下土的渗透特性与普通重力场条件下是否一致?如果不一致,土的渗透特性随离心加速度是怎样变化的?本文通过离心模型渗透试验,研究了土的渗透系数随离心加速度的变化规律,验证离心模型渗透相似理论,澄清固结与孔隙水压力扩散问题的时间比尺关系的一些模糊不清问题,对离心模型试验技术的发展具有十分重要的理论意义和应用价值。
1. 渗透相似理论
水在土体孔隙中的渗透采用达西定律描述,
v=kΔhL=ki, (1) 式中:v为渗透速度;k为渗透系数,其物理意义是当水力梯度等于1时的渗透速度;L为渗径长度;Δh为试样两端的水位差;i为水力梯度,它是沿渗透方向单位距离的水头损失,无量纲。
定义任一模型变量xm与原型变量xp的相似常数:
ηx=xp/xm。 (2) 将式(2)代入式(1),可以得到
ηvv=ηkηiki。 (3) 达西定律可以描述原型和模型,因此它对原型与模型来说都应当是正确的。只有当所有的η项系数都相等时,式(3)才与原方程式(1)相同,也就是,
ηv=ηkηi。 (4) 离心模型试验中,模型的渗透速度是原型的n倍,即ηv=1/n,而水力梯度无量纲,则ηi=1,得到
ηk=1/n。 (5) Muskat[11]、Lambe等[12]分别给出了渗透系数与流体重度的关系式:
k=Kγμ=Kρgμ。 (6) 式中:K为土体的内在渗透系数,是颗粒形状、直径和填料的函数;μ为流体的动力黏度;ρ为流体的密度;g为重力加速度。
由式(6)可以明显看出,渗透系数随土体的内在渗透系数、流体的动力黏度、流体的密度、重力加速度变化,模型和原型土体的内在渗透系数、流体的动力黏度、流体的密度相同,重力加速度为n倍,即,ηK=ημ=ηρ=1,ηg=1/n,因此,可得ηk=1/n。
2. 渗透离心模型试验
2.1 试验设备
试验在南京水利科学研究院NHRI400 g·t土工离心机上进行。该机最大半径5.5 m,吊篮平台的尺寸为1100 mm×1100 mm,最大加速度200g,最大负荷2 t,容量400 g·t。为在离心机中进行渗透试验,研制出离心机渗透仪,渗透仪装置由渗透容器、变水头管、水头测量装置等组成(图 1)。渗透容器由金属圆筒(内径100 mm、高100 mm)、透水石、上盖和下盖组成,变水头管由连接段(内径40 mm)和测量段(内径20 mm)组成,水头测量装置由激光位移传感器和浮标组成。
2.2 试验方法
试验土样为低液限黏土(CL)、低液限粉土(ML)、粉土质砂(SM)3种,其物理性质指标见表 1。
表 1 土样的物理性质指标Table 1. Physical properties of soils土名 低液限黏土 低液限粉土 粉土质砂 含水率/% 29.0 26.2 20.5 密度/(g·m-3) 1.94 2.08 2.10 试样高度/mm 40 36 69 液限/% 42.2 24.8 塑性指数 20.7 6.6 颗粒组成
/%砂粒 12.8 39.0 55.3 粉粒 44.7 41.6 38.5 黏粒 42.5 19.4 6.2 将土样制备成饱和泥浆,放入试样筒内,采用预压方法进行固结成型,固结完成后土样的含水率、密度、试样高度见表 1。将安装好的渗透仪装置放置在模型箱内,以控制下水位,从而控制渗透水头。将渗透仪装置和模型箱放入离心机吊篮,接好激光位移传感器,启动离心机到设定加速度,通过位移传感器测试上水位下降过程。每种土样的试验加速度分别1g(常规)、10g、25g、50g、75g、100g、150g,每种工况进行2组平行试验。
2.3 渗透水头修正
离心惯性加速度场是通过离心机的旋转而产生的,离心机旋转产生的离心惯性加速场是沿旋转中轴形成的一个个圆形的柱面,在每个等半径的圆柱面上,其离心惯性加速场的惯性势是相等的,离心加速度也相同,离心加速度的大小与半径成正比。这样,在模型的不同高度上,所受到的离心惯性力是不同的。那么离心模型中,上、下水位差并不是真正的渗透水头,而必须进行修正。
如图 2所示,任意旋转半径R处的水柱dR,对试样中心产生的渗透压力增量dp可表示为,
dp=ρwa0R0RdR 。 (7) 式中dp为试样中心的渗透压力增量;ρw为水的密度;a0为试样中心的加速度;R0为试样中心的旋转半径;R为任意水柱的旋转半径;dR为任意水柱的高度。
对式(7)积分,可得土样中心产生的渗透压力为
p=∫R2R1ρwa0R0RdR=12ρwa0R0(R22−R21)。 (8) 式中,p为试样中心的渗透压力;R2为下水位的旋转半径;R1为上水位的旋转半径;其他符号意义同前。
因此,渗透水头为
Δh=pρwa0=R22−R212R0, (9) 式中,Δh为试样的渗透水头,其他符号意义同前。
变水头渗透系数按式(10)计算
kT=BLA(t2−t1)lnΔh1Δh2。 (10) 式中,kT为水温为T℃时试样的渗透系数;B为测量段变水头管的断面积;L为渗径,即试样高度;A为试样的断面积;t1,t2分别为测读水头的起始和终止时间;Δh1,Δh2分别为起始和终止渗透水头。
标准温度(20℃)下的渗透系数按式(11)计算
k20=kTηTη20。 (11) 式中,k20为标准温度时试样的渗透系数;ηT为T℃时水的动力黏滞系数;η20为20℃时水的动力黏滞系数。
3. 试验结果分析
3.1 渗透系数的变化规律
表 2列出了不同加速度下3种土样的渗透系数试验结果,图 3给出了3种土样的渗透系数随加速度的变化,从图中可以看出,3种土样的渗透系数随加速度的增加而线性增大,表明渗透系数与加速度呈正线性关系。把图 3的纵坐标改为ng时渗透系数与1g时渗透系数之比km/kp,如图 4所示,可以看出,km/kp与加速度具有良好的线性变化关系,可表示为
km/kp=χn, (12) 表 2 渗透系数试验结果Table 2. Test results of permeability coefficient (cm/s)土名 加速度/g 1 10 25 50 75 100 150 低液限黏土 1.21×10-8 1.24×10-8 1.28×10-7 3.58×10-7 6.16×10-7 8.50×10-7 1.40×10-6 1.79×10-6 1.29×10-8 1.25×10-8 1.14×10-7 2.97×10-7 5.26×10-7 7.57×10-7 1.26×10-6 1.73×10-6 低液限粉土 1.21×10-7 1.37×10-7 1.21×10-6 2.92×10-6 6.06×10-6 8.48×10-6 1.07×10-5 1.73×10-5 1.26×10-7 1.18×10-7 1.17×10-6 2.67×10-6 5.77×10-6 7.91×10-6 9.97×10-6 1.52×10-5 粉土质砂 1.32×10-6 1.18×10-6 1.29×10-5 2.99×10-5 5.99×10-5 9.44×10-5 1.22×10-4 1.85×10-4 1.50×10-6 1.09×10-6 1.13×10-5 3.10×10-5 6.16×10-5 9.81×10-5 1.26×10-4 1.79×10-4 式中,χ为比例系数。试验数据拟合得出,3种土样的χ分别0.984,0.937,0.992。除去试验仪器以及固结等因素的影响,比例系数χ≅1。因此,试验证明了离心模型试验渗透系数比尺为ηk=1/n。Singh等[6]利用小离心机变水头试验,也得出了类似的试验结果。
3.2 离心模型中达西定律的适用性
进行渗透试验时,渗透水头随时间的变化直接反映了试样的渗透稳定情况,图 5给出了不同加速度条件下3种土样的渗透水头过程线。试验结果表明,3种土样的渗透水头随时间的延长而逐渐下降,且下降速率基本一致,说明试样的渗透稳定。下降速率与离心机加速度和土性有关,加速度越大,下降速率越大,土样黏粒含量越大,下降速率越慢。
图 6给出了3种土样的渗透速度随加速度与水力梯度乘积的关系曲线,从图中可以看出,3种土样的渗透速度随加速度与水力梯度乘积的增加而线性增大,且线性关系相当好,增长速率与试样的黏粒含量有关,试样黏粒含量越大,增长速率越大,增长速率即为1g条件下试样的渗透系数。表 3列出了3种土样渗透试验最大加速度与水力梯度乘积,表明在这个范围内,离心模型试验渗透符合达西定律,试样黏粒含量越大,加速度与水力梯度乘积也越大。
表 3 3种土样渗透试验最大加速度与水力梯度乘积Table 3. Products of maximum acceleration and hydraulic gradients of three soil samples in permeability tests土名 d10/mm k/(cm⋅s-1) v/(cm⋅s-1) 试验最大加速度×水力梯度 低液限黏土 0.0014 1.22×10-8 4.81×10-5 4033 低液限粉土 0.0021 1.15×10-7 3.50×10-4 3037 粉土质砂 0.0112 1.24×10-6 8.14×10-4 661 4. 结语
离心模型渗透试验结果表明,渗透系数随加速度的增加而线性增大,离心模型试验渗透符合达西定律,模型的渗透系数与原型渗透系数之比km/kp随加速度成比例线性增大,比例系数≈1,从而验证了离心模型试验渗透系数比尺为ηk=1/n。虽然国外也得出了类似的试验结果,但我们试验的渗透水头比他们的大,土样类型也多。研究成果对离心模型试验具有重大理论和应用价值。
-
-
[1] DERBYSH IRE E, D IJKSTRA T A, SMALLEY I J, et al. Failure mechanisms in loess and the effects of moisture content changes on remoulded strength[J]. Quaternary International, 1994, 24: 5-15. doi: 10.1016/1040-6182(94)90032-9
[2] LI H, ZHANG Y M, XU H, et al. A constitutive model for collapsible loess material: i analytic formulation[J]. Advanced Materials Research, 2012, 511: 117-121. doi: 10.4028/www.scientific.net/AMR.511.117
[3] 邵生俊, 于清高, 王婷, 等. 深厚湿陷性黄土地基综合整治新技术研究[J]. 土木工程学报, 2007, 40(12): 77-82. https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200712015.htm SHAO Sheng-jun, YU Qing-gao, WANG Ting. A novel comprehensive treatment technology for deep wet-collapsible loess foundations[J]. China Civil Engineering Journal, 2007, 40(12): 77-82. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-TMGC200712015.htm
[4] 邢义川, 谢定义, 李永红. 非饱和黄土湿陷过程中有效应力变化规律[J]. 岩石力学与工程学报, 2004, 23(7): 1100-1103. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200407011.htm XING Yi-chuan, XIE Ding-yi, LI Yonghong. Effective stress and collapse process of unsaturated loess[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(7): 1100-1103. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX200407011.htm
[5] LU N. Is matric suction stress variable?[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(7): 899-905. doi: 10.1061/(ASCE)1090-0241(2008)134:7(899)
[6] BISHOP A W. The effective of stress principle[J]. Teknisk Ukeblad, 1959, 39: 859-863.
[7] BLIGHT G E. Effective stress evaluation for unsaturated soils[J]. Journal of the Soil Mechanics and Foundations Division, 1967, 93(2): 125-148. doi: 10.1061/JSFEAQ.0000949
[8] FREDLUND D G, MORGENSTERN N R. Stress state variables for unsaturated soils[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1977, 103(5): 447-466.
[9] LU N, LIKOS W J. Suction Stress Characteristic Curve for Unsaturated Soil[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2006, 132(2): 131-142. doi: 10.1061/(ASCE)1090-0241(2006)132:2(131)
[10] LU N, GODT J W, WU D T. A Closed form equation for effective stress in unsaturated soil[J]. Water Resources Research, 2010, 46(5): 1-14.
[11] 王娇. 非饱和黄土土水特性与真三轴屈服及强度变形特性试验研究[D]. 西安: 西安理工大学. 2018. WANG Jiao. Research on Soil Water Characteristics and Yielding, Strength and Deformation Properties of Unsaturated Loess by the True Triaxial Test[D]. Xi'an University of Technology, 2018. (in Chinese)
[12] 陈存礼, 张登飞, 张洁, 等. 等向应力下原状黄土的压缩及增湿变形特性研究[J]. 岩石力学与工程学报, 36(7): 1736-1747. https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201707018.htm CHEN Cun-li, ZHANG Deng-fei, ZHANG Jie, et al. Compression and wetting deformation behavior of intact loess under isotropic stresses[J]. Chinese Journal of Rock Mechanics and Engineering, 36(7): 1736-1747. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YSLX201707018.htm




 下载:
下载: