Stress-strain model and deformation parameters of K0-consolidated coral sand
-
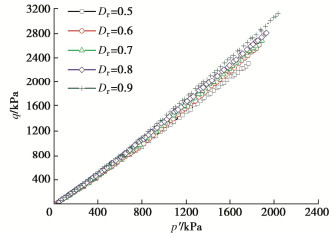
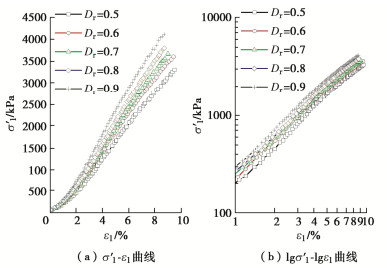
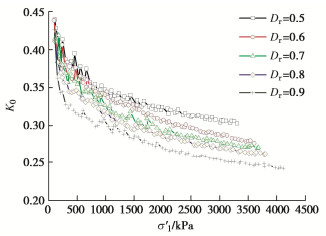
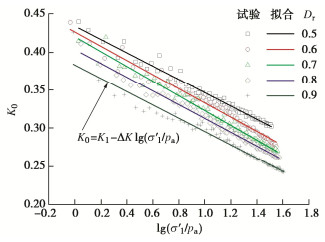
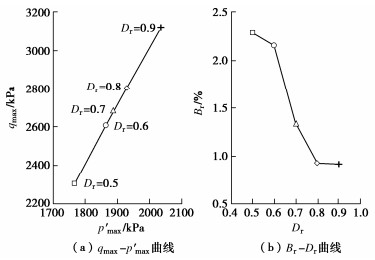
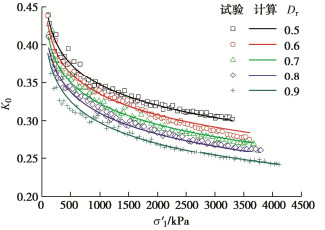
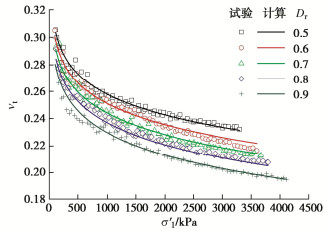
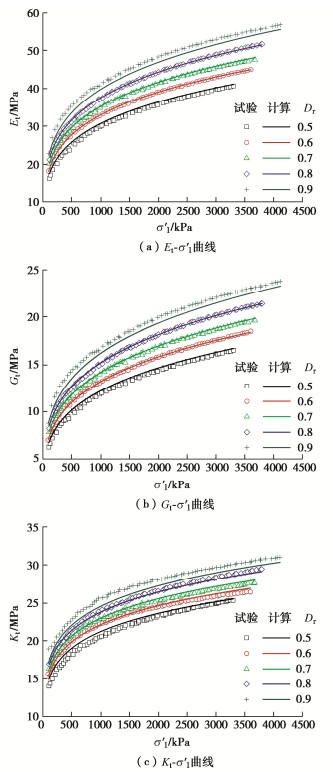
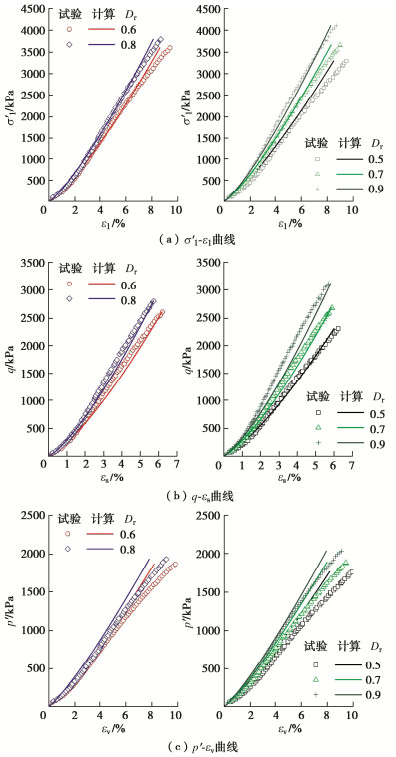
摘要: 珊瑚砂作为岛礁吹填地基的填料，在填筑期的应力路径具有K0固结的特点。利用三轴试验系统对不同初始相对密度的珊瑚砂进行了一系列的K0固结试验，研究了珊瑚砂的应力–应变特性，测试了珊瑚砂的K0系数和颗粒破碎率。基于广义虎克定律，建立了幂函数形式的非线性弹性模型来描述K0固结珊瑚砂的应力–应变关系，提出了变形参数的函数表达式，并将模型计算结果与试验曲线进行了对比。结果表明：K0固结珊瑚砂的应力-应变关系可用幂函数表示。随着轴向有效应力的增加，K0减小，颗粒破碎率增大。在相同的轴向有效应力条件下，珊瑚砂的初始相对密度越小，K0越大，颗粒破碎率越高。在K0状态下，随着轴向有效应力的增加，珊瑚砂的切线模量增加，切线泊松比减小。珊瑚砂的初始相对密度越大，相同轴向有效应力下的切线模量越大，切线泊松比越小。幂函数模型合理地预测了一定应力范围内K0固结珊瑚砂的应力–应变关系，模型及变形参数反映了K0固结的应力路径对应力–应变关系的影响。Abstract: The stress path followed by soil consolidation in the hydraulic filling site where the coral sand is used as the filling materials is characterized by K0-consolidation. In order to investigate the stress-strain behaviors of the K0-consolidated coral sand, a series of K0-consolidation tests in a triaxial cell are carried out for the coral sands with different initial relative densities. The K0-values of the coral sands are measured and their particle breakage indexes are evaluated. Based on the generalized Hooke's law, a nonlinear elastic model in the form of a power function is proposed to describe the stress-strain relationship of the K0-consolidated coral sand. The functional expressions for the deformation parameters are presented, and the calculated results of the model are compared with the test curves. The results show that the stress-strain relationship of the K0-consolidated coral sand may be expressed by a power function. With the increase of the axial effective stress, the K0-value decreases, and the particle breakage index increases. Under the same axial effective stress, a small initial relative density corresponds to a large K0-value and a large particle breakage index. As the increase of the axial effective stress in the K0-state, the tangent modulus of the coral sand increases, and the tangent Poisson's ratio decreases. Under the same axial effective stress, the larger the initial relative density, the larger the tangent modulus, and the smaller the tangent Poisson's ratio. The stress-strain relationship of the K0-consolidated coral sand with different initial relative densities within a certain stress range is reasonably predicted by the power function model. The model and deformation parameters reflect the influence of the stress path of K0-consolidation on the stress-strain relationship.
-
0. 引言
在完善综合交通网络、提升运输服务质量的过程中，传统双车道隧道已不能满足大交通量快速运输发展需求，单洞三车道、四车道的大跨度隧道已成为现阶段公路隧道修建热点工程。然而，大跨度隧道受结构跨度与扁平度制约，传统锚喷支护结构设计理念相对落后[1]，支护效果不理想，为施工安全及后期运营带来隐患。
现阶段深埋大跨度隧道施工设计多依赖收敛约束法与工程类比法。尽管传统公路隧道支护机理、支护方法已趋于成熟，但对于大跨度隧道而言，其设计原理与支护方案缺乏严谨性和规范性，设计理念落后于现场实践。由于隧道跨度大，常规台阶法很难保证隧道施工安全性，分部开挖法能够很好地适用于大跨度隧道的修建[2]。不可避免的是，复杂的开挖工序增加了岩土体自由面的暴露时间与应力释放次数，多次扰动下塑性区扩展形式、承载拱演化特征与围岩压力作用模式不明。大量工程实践表明常规系统锚杆在塑性区演化后期难以发挥有效支护作用[3-4]。早在21世纪初已经有部分学者提出了利用长深锚杆（索）实现为地下工程减跨的支护理念并进行了一定研究[5-6]。近年来，随着隧道工程逐渐向大埋深、大跨度发展，一些学者对于大跨度隧道锚固体系展开了相关研究并取得丰硕成果，但仍处于探索阶段。罗基伟等[7]将预应力锚杆-锚索协同支护体系运用于京张八达岭长城站过渡段，证实了长锚索能够调用深层围岩，提高锚杆组合拱的稳定性。孙振宇等[8]建立了大跨隧道锚固体系协同作用全过程演化机制。以上研究证明了长锚杆/锚索锚固体系在大跨度隧道修建过程中具备减跨及调动深层围岩承载等作用，但针对大跨度隧道初期支护结构受荷性能的研究尚不深入，长锚杆/锚索支护下的隧道初期支护力学行为不明。
因此，本文提出了长锚杆或锚索（后面将不加区分统称为长锚杆）联合系统锚杆的支护技术，依托自主开发的多点衬砌力学加载平台进行相似模型试验，对典型大跨度隧道初期支护受力变形特征及开裂破坏规律展开研究，并探索了相同目标荷载下长短锚杆联合支护措施对初支受力的改善效果，给出了长锚杆合理设计方案，可为大跨度隧道支护设计提供参考。
1. 试验概况
1.1 试验原理
长短锚杆联合支护机理如图 1所示，长锚杆支护主要包括两类作用：①外部主动加固围岩作用，在不改变系统锚杆设计方案的基础上，在系统锚杆施做后立即搭设长锚杆支护，通过长锚杆形成二次加固区，在一次加固区加固作用减弱或部分失效时，限制围岩塑性区增加，减少支护结构所受围岩压力；②内部调荷作用，依赖长锚杆拉力将支护结构所受部分围岩压力转移至深部锚固区岩体，抵消部分上覆围岩荷载，同时增设的支护点可等效为初支内部多点径向支座约束，即大跨结构减跨支点，可对结构受力进行改善。
1.2 试验平台与装置
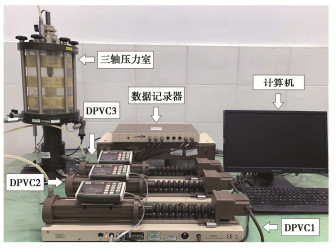
模型试验依托课题组自行研制的隧道结构力学性能测试平台[9]，见图 2。平台采用卧式加载模式，忽略隧道模型自重的影响。设计了如图 3所示的配套装置进行模型试验。将长锚杆悬吊力等效为支座反力，采用ϕ3 mm螺栓搭配7.5 mm×7.5 mm橡胶垫片与石膏模型相接触，以此模拟长锚杆对大跨度结构的支座减跨效应。设计研究范围为拱顶部120°，制作了如图 4所示的弧形辅助钢板用于固定螺栓，钢板厚15 mm，沿初期支护内轮廓轧制拼接而成。螺栓孔环向间距12.5 cm（原型环向间距2 m），纵向间距3.13 cm（原型纵向间距50 cm），呈梅花形布置。通过钢丝与焊接在外围钢支护上的吊环固定辅助弧形钢板。
1.3 试验对象
试验研究对象为位于山东省境内的盘顶山隧道，该隧道为双向六车道分离式特长隧道（4125 m），是山东省公路第一长隧，隧道最大埋深为256.6 m，典型横断面支护结构形式见图 5。隧道修建过程中初期支护结构混凝土开裂、钢架变形过大现象频发（图 6），甚至引起隧道局部坍塌，严重影响施工进度与工程质量。
![]()
图 6 施工阶段初期支护典型破坏形式Figure 6. Typical failure modes of initial supports at construction stage1.4 模型试验设计
隧道原型初期支护为C25混凝土结构，力学参数按照工程实际取值，弹性模量为29.5 GPa，极限抗压强度为19 MPa，极限抗拉强度为2 MPa；钢拱架采用I22b型钢，弹性模量为210 GPa，极限抗压强度为235 MPa，极限抗拉强度为370 MPa。隧道初期支护中的钢拱架与钢筋网的支护作用等效到喷射混凝土中，计算初支等效弹性模量为36.475 GPa，等效刚度法计算公式如下式所示：
Ec=E0+AsEsAc。 (1) 式中：Ec为折算后的初支弹性模量；E0为C25混凝土弹性模量；As为钢拱架截面积；Es为钢材弹性模量；Ac为混凝土截面积。
确定几何相似比CL=16，并以几何相似比CL=16和重度相似比Cγ=1为基础相似比，控制材料的弹性模量、强度相似，采用量纲分析法以相似第二定理（见式（2））为理论基础推导得到模型各物理量间的相似常数如表 1所示。
f(σ,ε,E,μ,L,δ,X,¯X)=1。 (2) 表 1 模型相似常数Table 1. Model similarity constants物理量 相似关系 相似比 长度L CL = 16 16 重度γ Cγ = 1 1 面荷载q Cq = CLCγ 16 弹性模量E CE = Cq 16 泊松比μ Cμ = 1 1 应力σ Cσ = CE 16 应变ε Cε = 1 1 强度R CR = CL Cγ 16 力N CN=CσC2L 1∶4096 弯矩M CM=CσC3L 1∶65536 式中：L为几何尺寸；δ为位移；X为体积力；ˉX为面力。
经室内配比试验，当石膏与水的质量比为1∶1.2时，石膏试件的弹性模量为2.3 GPa，则弹性模量相似比CE=15.86≈16，满足相似精度要求。模型几何尺寸为原型的1/16，跨度为116.4 cm，高78.5 cm，轴向长30 cm，基于结构弯曲变形相似准则[10]计算初期支护石膏模型厚度为4.4 cm，计算公式见式（3），浇筑模型及配套试验装置如图 7所示。
hm=hpn[EcEm(1−v2m)(1−v2p)]13。 (3) 式中：Em为模型弹性模量；vm，vp分别为模型、原型材料泊松比；n为相似常数。
1.5 加载方案与量测项目
本次模型试验立足于上述试验平台，对隧道模型进行全周径向加载。依托工程修建过程中，在上行线K69+335和K69+341断面（断面埋深分别为138，129 m）V级围岩与初支之间埋设有压力传感器。现场实测压力是支护体系对围岩进行加固后所得到的，即系统锚杆施作后的接触压力，无需单独考虑系统锚杆对围岩压力的影响，试验设计只需对长锚杆的支护作用进行模拟。为便于分析，试验选取相同的围岩压力作为目标荷载，对常规支护体系下初支结构力学响应规律及长短锚杆联合支护体系下的初支受力改善效果进行研究。实际工程中，长锚杆具备调整外部围岩压力的作用，同时仰拱回填等措施一定程度可改善初支受力，本试验结果相对保守。
本次试验目标荷载是将现场围岩压力实测数据与统计的所处V级围岩的相近跨度隧道围岩压力数据[11-14]（见表 2）进行归一化处理得到的，加载目标围岩压力包络图如图 8所示，为便于试验控制取与均值相近的整数值。对15个加载点进行径向加载试验，力求对隧道结构断面的实际接触压力环境进行真实模拟。试验过程中油缸法向压力为控制指标，忽略加载面板与隧道模型间剪切力的影响，沿中线对称的围岩压力加载方案也保证了隧道结构在水平方向受力平衡，最大程度上降低了切向力对试验结果的干扰。
表 2 大跨度隧道围岩压力统计数据Table 2. Statistical data of pressures on surrounding rock of long-span tunnel隧道名称 断面信息跨度/高度/m 围岩压力/kPa 拱顶 左拱肩 右拱肩 左边墙 右边墙 左拱脚 右拱脚 仰拱左 仰拱右 仰拱中 九州隧道[11] 15.6/11.2 226.7 110.9 223.7 233.4 204.9 — — — — — 黄家峪隧道[11] 16.0/13.0 104.7 118.2 150.6 117.1 204.9 — — — — — 阳宗隧道[11] 16.0/12.0 145.4 135.1 98.4 54.5 36.9 — — — — — 天恒山隧道[11] 16.8/12.0 129.2 64.2 183.8 129.7 49.5 — — — — — 勤丰隧道[14] 17.2/11.7 59.4 78.5 62.8 52.8 73.6 37.3 39.3 — — — 大东山隧道[13]（左线） 18.2/10.1 260.0 150.0 190.0 50.0 70.0 — — — — — 大东山隧道[13]（右线） 18.2/10.1 240.0 200.0 190.0 90.0 70.0 — — — — — 山冲箐隧道[11] 18.5/11.0 420.0 250.0 150.0 210.0 90.0 — — — — — 盘顶山隧道（K69+335） 18.6/12.6 233.6 147.3 115.3 89.7 93.9 139.4 128.2 65.1 89.0 103.1 盘顶山隧道（K69+341） 18.6/12.6 227.1 121.4 134.2 114.7 119.3 131.7 156.3 73.0 71.7 105.8 港沟隧道[11] 20.0/13.1 687.3 447.3 158.2 471.8 196.0 — — — — — 老虎山隧道[12] 20.0/13.4 90.0 9.0 15.0 14.0 45.0 — — — — — 戴云山隧道[11] 21.0/15.8 240.0 223.7 216.8 52.3 204.9 — — — — — 樵岭前隧道[12] 21.0/14.3 211.0 40.0 25.0 16.0 13.0 — — — — — 乐瞳隧道[12] 21.5/14.3 19.0 20.0 — 22.0 13.0 — — — — — 试验开始时，控制加载系统中液压缸的行进速度为空载0.5 mm/min，将弧形钢板与模型外表面密贴，并预施加2%的目标荷载。试验过程中采取等比例加载的方式对隧道模型进行加载，共分十级加载，每级加载后保持一段时间。加载至目标荷载后继续以等比例增大荷载的方式加载，直至结构整体失稳破坏，试验过程中加载速率控制在1 kPa·min-1。
试验量测和观察项目包括模型表面应变、关键点位移、长锚杆支护力和模型开裂情况。应变量测采用粘贴在模型内、外表面的120-5AA型免焊电阻式应变片，电阻值为120 Ω，灵敏系数为2%。位移量测采用WBD—50A型百分表式电阻应变位移传感器，量程为50 mm。6个径向位移监测点在模型的拱顶、拱肩、拱脚和仰拱中心处呈对称布设，应变与位移监测点均位于隧道结构纵向高度的中间一环。此外，在每列长锚杆中间位置的螺栓与石膏模型间加入垫片及微型压力传感器来实时测量试验过程中锚杆支护力的变化情况，试验前通过调整钢丝预紧使各传感器存在较小读数，以保证长锚杆支护点与石膏模型密贴。应变片及传感器的布设位置、编号见图 9。
![]()
图 9 应变、位移与压力监测点布置Figure 9. Arrangement of strain, displacement and pressure monitoring points2. 大跨度公路隧道初支受力特征
根据归一化所得围岩压力加载方案对常规支护体系下隧道初支结构变形破坏特征进行试验研究。为便于分析，按照相似关系将试验结果返还到原型，除已说明内容外，文章均作此处理。
2.1 受力破坏特征分析
图 10为隧道模型失稳破坏后最终的裂缝分布素描展布图，包括模型内外表面，裂缝展布图从隧道仰拱中点处开始，顺时针转动一周而得，按裂缝出现先后依次编号。模型裂缝基本沿隧道中线对称分布，主要分布于隧道拱脚、拱顶及仰拱处。试验加载过程中模型拱顶、拱脚内侧监测点位应变变化及模型开裂规律如图 11所示。结合加载过程中应变监测数据（正值为拉应变，负值为压应变）和模型开裂情况，可得到结构的破坏过程为：拱脚及边墙处外表面→拱顶内表面→拱脚内表面→仰拱内表面→拱脚及拱顶处开裂加剧形成二次开裂区→仰拱开裂加剧→结构失稳破坏。
基于结构监测点内外应变计算所得40%，70%，100%目标荷载下的隧道原型初支结构轴力和弯矩包络图见图 12，结构应变-内力换算公式如式（4），（5）所示，设衬砌的内外侧应变值分别为ε1和ε2根据材料的本构关系及平截面假定，可得
N=12Ec(ε1+ε2)bh, (4) M=112Ec(ε1−ε2)bh2。 (5) 式中：b为单位长度，取1 m；h为衬砌厚度，按设计取值；Ec为初支的等效弹性模量。
进一步分析可知，初期支护拱顶处存在最大正弯矩，拱顶内侧结构受拉，拱脚外侧存在最大负弯矩，拱脚内侧受压，结构弯矩呈“蝶状”分布；初支拱顶处有最小轴力，结构轴力由拱顶、拱肩、边墙、拱脚、仰拱逐渐增大。加载至目标荷载时，拱脚处#4监测点最大弯矩和轴力分别为：-145.14 kN·m，-2671.10 kN；拱顶处#8监测点最大弯矩和轴力分别为100.05 kN·m，-1816.12 kN。
2.2 变形破坏特征分析
常规支护条件下模型各监测点的径向位移值随荷载的变化曲线如图 13所示。模型整体呈压扁趋势，结构最大变形位于拱顶处，其次为隧道拱肩。结构整体变形过程可分为3个阶段：第一阶段（前七级加载）为弹性变形阶段，结构整体变形较小且平稳线性增长，无裂缝产生，模型拱顶径向位移为1.57 mm；第二阶段为带裂缝变形阶段，结构径向位移出现第一次突变，荷载-位移曲线出现拐点，增长速度突然加快，拱脚及拱顶附近出现裂缝并持续扩展，加载至目标荷载时，模型拱顶沉降值为3.16 mm；第三阶段为加速破坏阶段，荷载-位移曲线出现第二次突变，仰拱开裂导致拱脚及拱顶处裂缝密集区进一步发展至结构失稳，结构破坏时模型拱顶沉降为6.86 mm。
![]()
图 13 监测点荷载-位移变化曲线Figure 13. Change curves of load and displacement at monitoring points2.3 分析总结
由上述试验结果可知，大跨度隧道由于其断面形式的特殊性，初支拱脚及拱顶处结构内力较大，拱脚及拱顶处开裂情况最为严重，这也与隧道施工过程中初支变形开裂现象相吻合。值得注意的是，加载至目标荷载值时，结构处于损伤状态，带有裂缝并持续变形。可推断现场大跨度隧道初期支护结构可能处于带损伤工作状态，在多次开挖扰动下围岩塑性扩展难以控制，同时大跨度隧道开挖范围大，遇到软弱夹层等不良地质体可能性高，隧道结构很容易进入加速变形破坏阶段，产生严重施工灾害。因此应采取有效的处治措施以防止裂缝的产生及扩展。
3. 长短锚杆联合支护下初支结构响应特征
为系统探究长短锚杆联合支护措施对大跨度隧道初期支护受力的改善效果，在同等目标荷载下分别设置了如表 3所示的不同环向间距、不同布设范围共4种对比方案。
表 3 试验方案设计Table 3. Design of test conditions方案 环向间距/ m 布设范围 方案1 2 拱部120° 方案2 4 拱部120° 方案3 2 拱部60° 方案4 2 两侧拱肩各30° 3.1 环向间距
长锚杆承载能力强，在大跨度隧道支护中布设间距可适当增大，分别设置了拱部120°范围依原型2 m（方案1）、4 m（方案2）环向间距加载试验，记录并总结结构受力变形特征与长锚杆支护力变化规律。
图 14为不同环向间距下40%，70%，100%目标荷载下原型隧道初支结构内力包络图。2 m和4 m环向间距下初支结构内力分布相似，长锚杆支护点附近结构外侧由于径向支护力产生负弯矩，最大负弯矩位置均位于拱脚外侧。相比常规支护体系，拱顶处较大正弯矩被抵消，拱脚及拱顶处结构内力明显减小。加载至目标荷载时，方案1拱顶处原型初支结构轴力减小至-444.23 kN，与常规支护试验相比减小了75.67%，文后不再赘述用括号内百分比表示。拱顶处弯矩减小至-23.45 kN·m，由拱顶内侧正弯矩转变为拱顶外侧负弯矩；拱脚处轴力和弯矩分别减小至-507.94 kN（81.08%），-30.48 kN·m（79.00%）。方案2拱顶处初支结构轴力减小至-1052.24 kN（42.38%），拱顶处弯矩减小至-43.27 kN·m，由拱顶内侧正弯矩转变为支护点外侧负弯矩；拱脚处轴力和弯矩分别减小至-945.80 kN（64.76%），-60.68 kN·m（58.19%）。
![]()
图 14 不同长锚杆环向间距结构内力Figure 14. Internal forces of structures with different circumferential spacings of long anchors加载过程结构无异响及开裂，处于无裂缝线性变形阶段。加载至目标荷载时，方案1与方案2试验模型各点位监测变形量与返还至原型的计算结果如图 15所示，结构最大变形位置位于初支拱顶，相比原设计方案试验结果，加载至目标荷载时，方案1模型拱顶径向位移为1.18 mm（62.66%）；方案2模型拱顶径向位移为1.45 mm（54.11%）。
加载过程中原型长锚杆支护力变化如图 16所示。由图 16可知，不同环向间距下长锚杆支护力均呈现出由拱顶处至两侧拱肩先减小后增大的规律。加载至目标荷载时，方案1右拱肩外侧原型支护力为90.08 kN，拱顶中部原型支护力为86.72 kN；方案2右拱肩外侧原型支护力为152.32 kN，拱顶中部原型支护力为161.12 kN。
上述试验结果表明，隧道拱部长锚杆支护可有效解决大跨度隧道初期支护拱脚及拱顶受力过大问题。布设环向间距越大，单支护点所需提供的支护力越大，单根锚杆承受的拉拔力越大。锚杆的抗拔力主要取决于围岩质量、锚固长度、锚杆钢材料参数、浆液质量、孔径及孔内灌浆的饱满程度、预应力等因素[15-17]。因此，设计环向间距不应过大，同时可适当增大托盘面积以扩大长锚杆支护点处的锚板面积。
3.2 布设范围
（1）方案3
由图 17可知，初支整体内力分布相对均匀，轴力由拱顶至拱肩逐渐减小，随后由边墙、拱脚、仰拱逐渐增大，初支拱脚、拱肩处有较大负弯矩，拱顶处正弯矩由长锚杆群负弯矩效应抵消，锚杆支护点位置初支外侧存在一定负弯矩。相比常规支护体系，加载至目标荷载时，拱顶处初支结构轴力减小至-1138.42 kN（37.66%），拱顶处弯矩减小至-34.71 kN·m，由拱顶内侧正弯矩转变为拱顶外侧负弯矩；拱脚处轴力和弯矩分别减小至-1054.75 kN（60.70%），-63.48 kN·m（56.27%）。
分级加载过程中结构变形特征与长锚杆原型支护力分布情况见图 18。如图 18（a）所示，相比常规支护模型试验结果，加载至目标荷载时拱顶处径向位移减小61.08%，拱脚处径向位移减小44.09%。图 18（b）的结果表明，长锚杆支护力分布呈拱顶中间向两侧逐渐减小的分布规律。拱顶#6监测点有结构最大支护力为256.48 kN，4号监测点有最小支护力为168.32 kN。
![]()
图 18 结构变形与原型长锚杆支护力Figure 18. Structural deformations and supporting forces of prototype long anchors综上，在拱顶部60°范围内布设长锚杆，一定程度上改善了初支拱顶和拱脚处较大弯矩的问题，隧道拱顶及拱脚处结构位移明显减小。此外，为保证结构稳定各支护点均需提供较大的支护力，且相邻长锚杆间所受支护力值差异大，对隧道拱部中心位置长锚杆有效支护力要求高。
（2）方案4
由图 19所示的原型隧道初支内力变化规律可知，初支内力分布形式与常规支护初支内力分布相似，弯矩呈“蝶状”分布。初支拱顶处存在最大正弯矩，拱肩及拱脚处存在较大负弯矩，拱肩处有最大轴力。相比常规支护体系，加载至目标荷载时，拱顶处初支结构轴力减小至-1236.01 kN（32.32%），拱顶处弯矩减小至41.72 kN·m（58.30%）；拱脚处轴力和弯矩分别减小至-1119.81 kN（58.28%），-67.03 kN·m（53.82%）。
图 20展示了分级加载过程中结构变形特征与长锚杆支护力的分布情况。如图 20（a）所示，隧道拱顶沉降较大，拱肩处初支位移相对较小。相比原支护模型试验结果，加载至目标荷载时拱顶处、拱肩处、拱脚处及仰拱处径向位移同比分别减小了46.20%，63.40%，47.24%，53.07%。图 20（b）所示的长锚杆支护力分布规律表明拱顶两侧布设长锚杆支护力呈由拱肩向拱顶侧逐渐减小的变化规律，加载至目标荷载时，拱肩#1监测点有最大监测值，原型支护力为201.44 kN，最小监测值位于#3监测点，原型支护力为174.88 kN，支护力分布相对均匀。
![]()
图 20 结构变形与原型长锚杆支护力Figure 20. Structural deformations and supporting forces of prototype long anchors3.3 支护效果对比
根据上述试验结果，采用《公路隧道设计细则：JTG/T D70—2010》[18]中综合安全系数法确定不同方案初期支护不利位置混凝土受压安全系数，结合结构变形、长锚杆支护力等因素综合表征各方案的加固效果。I22b型钢拱架计算面积0.00465 m2，验算截面抗弯刚度0.000325 m3，其他计算参数如1.4节所述，试验结果与安全系数计算结果如表 4所示。
表 4 不同方案支护效果对比Table 4. Comparison of support effects of different schemes工况 不利位置 弯矩/(kN·m) 轴力/kN 混凝土受压强度安全系数 长锚杆支护力/kN 拱顶沉降量/mm 均值 极差 原设计 拱顶 100.05 -1816.12 1.35 — — 50.56 拱脚 -145.14 -2671.10 0.92 方案1 拱顶 -23.45 -444.23 6.20 75.07 28.96 18.88 拱脚 -30.48 -507.94 4.81 方案2 拱顶 -43.27 -1052.24 2.86 139.33 45.12 23.20 拱脚 -60.68 -945.80 2.58 方案3 拱顶 -34.71 -1138.42 2.64 208.67 88.16 19.68 拱脚 -63.48 -1054.75 2.15 方案4 拱顶 41.72 -1236.01 2.43 188.91 26.56 27.20 拱脚 -67.03 -1119.81 2.18 综合分析试验结果可知，各方案初支结构内力与变形明显减小，安全系数显著增大，说明长锚杆有效改善了初期支护结构受力状态，限制了结构过大变形。相比原设计方案，方案1布设支护点最多，结构内力改善效果最好，大跨度拱形结构在多个减跨支点作用下分为多段微拱，拱顶处安全系数从1.35增加至6.20，拱脚处安全系数由0.92增加至4.81，长锚杆支护力均值最小且分布较为均匀；方案2支护机理与方案1相同，减跨支点与微拱数量减半，结构内力改善效果下降但加载至目标荷载模型无开裂，拱顶与拱脚处安全系数分别为原设计方案下的2.12倍、2.80倍，满足设计需求；方案3在隧道拱部60°形成长锚杆密集加固区，可将初期支护等效为拱顶被长锚杆悬吊的高次超静定结构，通过长锚杆群轴向强拉力产生的局部负弯矩组合效应抵消拱顶处较大正弯矩，拱顶与拱脚处安全系数分别为原设计方案下的1.96，2.34倍，此方案长锚杆支护力有各方案中最大值，且极差最大；方案4在两侧拱肩30°范围以2 m环向间距布设长锚杆而形成了有效的斜拉力集中区段，进而改善了初期支护结构内力状态，拱顶沉降为4类优化方案最大值，拱顶与拱脚处安全系数分别为原设计方案下的1.80，2.37倍，长锚杆支护力分布相对均匀。现场应用可结合现场围岩条件，适当减少长锚杆布设数量，以提高经济性。
4. 结论
（1）常规支护体系下，拱脚及拱顶处是初期支护集中受力的薄弱部位，结构首先起裂于拱脚及边墙附近外表面区域，拱顶内表面随之开裂，仰拱内侧拉裂后模型加速变形进而引起结构整体失稳破坏。加载至目标荷载时，初期支护处于带裂缝稳定变形阶段。
（2）不同长锚杆支护方案加载试验结果均表明，长锚杆支护可有效改善初支结构内力。加载至目标荷载时，方案1至方案4初支拱顶处结构安全系数分别为原设计方案的4.59，2.12，1.96，1.80倍，拱脚处结构安全系数分别为原设计方案的5.23，2.80，2.34，2.37倍。
（3）支护力监测结果表明，不同部位长锚杆支护力存在差异，拱顶与拱肩为关键支护区域。拱顶120°范围内长锚杆支护力均呈现出从拱顶处至拱肩侧先减小后增大的规律；仅支护拱顶60°范围，支护力由两侧向拱顶中心急剧增大，拱顶中心处长锚杆支护力最大；加固隧道两侧拱肩30°范围，长锚杆支护力由拱肩侧向拱顶侧小幅减小，分布相对均匀。
（4）综合试验结果可得，隧道拱部120°范围以2 m环向间距布设长锚杆支护效果最佳，局部增设长锚杆可有效解决初支拱脚及拱顶处混凝土开裂、拱架变形过大问题，所得结果能够为大跨度隧道支护设计提供科学参考。
-
![]()
图 7 K0试验结束时q-p′平面内的有效应力和颗粒破碎率
Figure 7. Effective stresses in q-p′plane and particle breakage indexes at end of K0-tests
![]()
图 8 参数A，K1的试验回归值与Dr的关系曲线
Figure 8. Curves of test regression values A, K1 versus Dr values
![]()
图 10 切线泊松比的计算与试验结果的比较
Figure 10. Comparison between calculated and measured tangent Poisson's ratio
![]()
图 11 切线模量的计算与试验结果的比较
Figure 11. Comparison between calculated and measured tangent moduli
![]()
图 12 应力-应变曲线的预测与试验结果的比较
Figure 12. Comparison between predicted and measured stress-strain curves
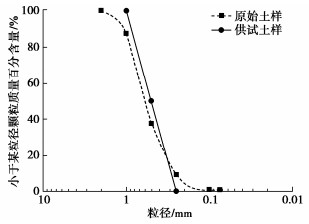
表 1 珊瑚砂的基本物理指标
Table 1 Physical parameters of coral sand
土粒相对质量密度Gs 平均粒径d50/mm 不均匀系数Cu 最大孔隙比emax 最小孔隙比emin 2.78 0.50 1.93 1.196 0.829 
下载: 导出CSV
表 2 式（1）参数A，B的试验回归值
Table 2 Test regression values for parameters A and B of Eq. (1)
Dr A B R2 0.5 718.94 1.281 0.9960 0.6 732.40 1.242 0.9961 0.7 779.94 1.245 0.9969 0.8 870.28 1.261 0.9976 0.9 906.65 1.237 0.9965
下载: 导出CSV
表 3 式（2）参数K1，ΔK的试验回归值
Table 3 Test regression values for parameters K1 and ΔK of Eq. (2)
Dr K1 ΔK R2 0.5 0.434 0.087 0.9777 0.6 0.426 0.093 0.9739 0.7 0.420 0.097 0.9800 0.8 0.403 0.090 0.9903 0.9 0.383 0.087 0.9589
下载: 导出CSV
表 4 试验参数回归值的计算公式
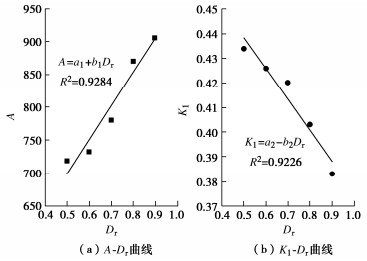
Table 4 Formulas for test parameter regression value
试验参数 回归值计算公式 相关参数 R2 A A=a1+b1Dr a1 =442.33, b1=513.30 0.9284 B B=c1 c1= 1.253 K1 K1=a2−b2Dr a2 =0.501, b2=0.125 0.9226 ΔK ΔK=c2 c2=0.091
下载: 导出CSV
表 5 试验参数的计算回归值
Table 5 Calculated regression values of test parameters
Dr A B K1 ΔK 0.5 698.98 1.253 0.439 0.091 0.6 750.31 1.253 0.426 0.091 0.7 801.64 1.253 0.414 0.091 0.8 852.97 1.253 0.401 0.091 0.9 904.30 1.253 0.389 0.091
下载: 导出CSV
-
[1] 刘祖德, 陆士强, 杨天林, 等. 应力路径对填土应力应变关系的影响及其应用[J]. 岩土工程学报, 1982, 4(4): 45-55. http://cge.nhri.cn/cn/article/id/8692 LIU Zude, LU Shiqiang, YANG Tianlin, et al. The influence of stress path on the stress-strain behavior of earthfills and its application[J]. Chinese Journal of Geotechnical Engineering, 1982, 4(4): 45-55. (in Chinese) http://cge.nhri.cn/cn/article/id/8692
[2] 孙岳崧, 濮家骝, 李广信. 不同应力路径对砂土应力-应变关系影响[J]. 岩土工程学报, 1987, 9(6): 78-88. http://cge.nhri.cn/cn/article/id/9112 SUN Yuesong, PU Jialiu, LI Guangxin. Influence of different stress path on stress-strain relationship of sandy soil[J]. Chinese Journal of Geotechnical Engineering, 1987, 9(6): 78-88. (in Chinese) http://cge.nhri.cn/cn/article/id/9112
[3] 姚仰平, 刘林, 罗汀. 砂土的UH模型[J]. 岩土工程学报, 2016, 38(12): 2147-2153. doi: 10.11779/CJGE201612002 YAO Yangping, LIU Lin, LUO Ting. UH model for sands[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(12): 2147-2153. (in Chinese) doi: 10.11779/CJGE201612002
[4] DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Journal of the Soil Mechanics and Foundations Division, 1970, 96(5): 1629-1653. doi: 10.1061/JSFEAQ.0001458
[5] DUNCAN J M, BYRNE P, WONG K S, et al. Strength, Stress-Strain, and Bulk Modulus Parameters for Finite Element Analyses of Stresses and Movements in Soil Masses[R]. Berkeley, California: College of Engineering, University of California, 1980.
[6] DOMASCHUK L, VALLIAPPAN P. Nonlinear settlement analysis by finite element[J]. Journal of the Geotechnical Engineering Division, 1975, 101(7): 601-614. doi: 10.1061/AJGEB6.0000175
[7] 柳志平, 刘泉声, 程勇, 等. 卸荷土体本构模型选用及其参数的确定——以港珠澳大桥拱北隧道明挖段基坑为例[J]. 岩土工程学报, 2012, 34(增刊1): 197-202. http://cge.nhri.cn/cn/article/id/14746 LIU Zhiping, LIU Quansheng, CHENG Yong, et al. Selection and parametric determination of constitutive model for unloading soil—Case study of foundation pit at open excavation section of Gongbei tunnel of Hongkong- Zhuhai-Macau Bridge[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(S1): 197-202. (in Chinese) http://cge.nhri.cn/cn/article/id/14746
[8] 邵晓泉, 迟世春. 堆石料变形参数的粒径尺寸相关性研究[J]. 岩土工程学报, 2020, 42(9): 1715-1722. doi: 10.11779/CJGE202009016 SHAO Xiaoquan, CHI Shichun. Particle size correlation of deformation parameters for rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(9): 1715-1722. (in Chinese) doi: 10.11779/CJGE202009016
[9] MIHAI L A, GORIELY A. How to characterize a nonlinear elastic material? A review on nonlinear constitutive parameters in isotropic finite elasticity[J]. Proceedings Mathematical, Physical, and Engineering Sciences, 2017, 473(2207): 20170607.
[10] 张季如, 罗明星, 彭伟珂, 等. 不同应力路径下钙质砂力学特性的排水三轴试验研究[J]. 岩土工程学报, 2021, 43(4): 593-602. doi: 10.11779/CJGE202104001 ZHANG Jiru, LUO Mingxing, PENG Weike, et al. Drained triaxial tests on mechanical properties of calcareous sand under various stress paths[J]. Chinese Journal of Geotechnical Engineering, 2021, 43(4): 593-602. (in Chinese) doi: 10.11779/CJGE202104001
[11] 胡利文, 刘志军. 真空预压加固土体变形机制分析[J]. 岩土力学, 2021, 42(3): 790-799, 812. https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103022.htm HU Liwen, LIU Zhijun. Analysis on deformation mechanism of soft soil reinforcement by vacuum preloading[J]. Rock and Soil Mechanics, 2021, 42(3): 790-799, 812. (in Chinese) https://www.cnki.com.cn/Article/CJFDTOTAL-YTLX202103022.htm
[12] 王立忠, 沈恺伦. K0固结结构性软黏土的本构模型[J]. 岩土工程学报, 2007, 29(4): 496-504. http://cge.nhri.cn/cn/article/id/12452 WANG Lizhong, SHEN Kailun. A constitutive model of K0 consolided structured soft clays[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(4): 496-504. (in Chinese) http://cge.nhri.cn/cn/article/id/12452
[13] HARDIN B O. Crushing of soil particles[J]. Journal of Geotechnical Engineering, 1985, 111(10): 1177-1192.
[14] CHU J, GAN C L. Effect of void ratio on K0 of loose sand[J]. Géotechnique, 2004, 54(4): 285-288.
[15] XIAO Y, LIU H L, CHEN Q S, et al. Particle breakage and deformation of carbonate sands with wide range of densities during compression loading process[J]. Acta Geotechnica, 2017, 12(5): 1177-1184.
[16] WANG C Y, DING X M, XIAO Y, et al. Effects of relative densities on particle breaking behaviour of non-uniform grading coral sand[J]. Powder Technology, 2021, 382: 524-531.
[17] 相彪, 张宗亮, 迟世春. 堆石料等应力比路径三模量增量非线性模型[J]. 岩土工程学报, 2008, 30(9): 1322-1326. http://cge.nhri.cn/cn/article/id/12969 XIANG Biao, ZHANG Zongliang, CHI Shichun. Three-modulus incremental nonlinear model of rockfill under paths of constant stress ratio[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(9): 1322-1326. (in Chinese) http://cge.nhri.cn/cn/article/id/12969
-
期刊类型引用(2)
1. 罗正良，李凡，赵亮，董思军，刘几上. 大直径深孔采场破碎顶板支护方案优化研究. 云南冶金. 2025(01): 28-33 . 
百度学术
2. 肖明清，徐晨，崔岚，盛谦，陈健，谢壁婷，吴鹏. 基于总安全系数法的喷锚组合支护承载能力试验研究. 岩石力学与工程学报. 2024(10): 2381-2395 . 百度学术
其他类型引用(0)
-
其他相关附件
计量
- 文章访问数: 337
- HTML全文浏览量: 93
- PDF下载量: 95
- 被引次数: 2
