0.   引言

西南地区高速铁路建设是西部开发战略的重要交通保障，路基基床变形控制则是保证高速铁路线路平顺性的关键因素之一。西南地区分布有大量红层地质，面积占全国红层总面积30%以上。一些学者提出利用红层泥岩作为高速铁路路基填料以解决西南地区沿线AB组填料不足且填料运输成本高等因素的限制。蒋关鲁等^[1-2]在达成线和遂渝线^[3]开展了现场试验及相应室内试验^[4]，初步证明了红层泥岩在最优含水率下碾压密实后作为高速铁路路基填料的可行性。

路基状态受环境影响，尤其是西南地区具有降雨丰富且集中的环境特征，连续降雨可能导致路基填料的从最优含水率状态转化为饱和状态。红层泥岩具有遇水软化崩解的不良工程特征，饱和强度不足最优含水率的40%^[5]。因此，在研究最优含水率下红层泥岩填料动力特性的基础上，还应对饱和状态下红层泥岩填料的动力特性进行研究。不少学者研究了动载作用下无黏性颗粒材料的累积变形^[6-7]、应变速率^[8]和动模量^[9-10]等基本动力特性，但红层泥岩及其他低液限黏土的动力特性与无黏性颗粒材料明显不同。如周文权等^[11]和Bian等^[12]的试验结果表明无黏性颗粒材料的动模量随振次增加而增加，而黏性土的试验结果则表明动模量则随振次增加而呈现逐渐减小的趋势^[13-15]。无黏性颗粒材料和黏性土在动载下的变形机制也不尽相同。对于无黏性材料，常用颗粒破碎效应解释相应的动力特性^[16-17]；而黏性土由于颗粒成团作用，单独的颗粒破碎效应有限，团聚体和胶结材料在动载下的损伤和结构劣化被认为是黏性土变形的主要成因之一^[18]。近年来，部分文献尝试从能量角度对土体动力响应进行解释。如Tao等^[19]对多种无黏性颗粒材料的耗散能和应变速率特征进行了研究，结果表明耗散能和应变速率之间具有相关性，曲线形状可以作为累积变形的分类标准。Rojo等^[20]也得到了同样的结论。既有研究结果表明了采用能量方法分析无黏性颗粒材料动力响应的适用性，而动载下饱和红层泥岩填料动力响应和能量耗散特性相关报道则值得补充。

针对这一问题，本文开展了不同围压和动应力下和红层泥岩填料的动三轴试验，研究了饱和红层泥岩填料累积变形、应变速率和动模量特性，并阐明了三者之间的相关性和极限状态。从能量角度出发，揭示了饱和红层泥岩填料动力响应的能量相关性和状态边界面。最后，基于能量随动应力的发展规律对红层泥岩的能量水平区间进行了划分。成果可为红层泥岩路基稳定性分析及变形控制提供参考。

1.   试验材料与方案

1.1   试验材料

试验材料取自成都南部，岩块分布均匀，外观呈褐红色，内部部分呈灰绿色。由于红层泥岩具有崩解特性，作路基填料时常用预崩解和预碾压的方法破碎较大岩块以防止填料遇水产生不可控的崩解变形。文献[1]也指出，较小粒径的红层泥岩具有更好的水稳性，改良效果也更好，更适宜作路基填料。岩样取回后，将岩块风干破碎并过1 mm筛，得到的泥岩颗粒即为本次试验所用材料。一系列基本物理试验结果表明，所用红层泥岩以粉粒为主，占比92.10%，相对质量密度为2.69，液限含水率为32.5%，塑限含水率为18.2%，自由膨胀率为34%。重型击实试验结果表明，红层泥岩填料击实的最大干密度为2.01 g/cm³，最优含水率为8.7%。XRD结果表明，所用红层泥岩矿物成分主要是石英，占比超过80%，含少量膨胀矿物（蒙脱石），占比2%~3%，其余为非膨胀矿物。红层泥岩详细物理指标见表 1。

表  1  试验所用红层泥岩基本物理指标

Table  1.  Basic properties of test red mudstone

液限/ %	塑限/ %	塑性指数/ %	相对质量密度	自由膨胀率/%	颗粒组成/mm			石英含 量/%	蒙脱石含量/ %
					砂粒 2~0.075	粉粒 0.075~0.002	黏粒 < 0.002
32.5	18.2	14.3	2.69	34	4.30%	92.10%	3.60%	81	2-3

下载: 导出CSV 

| 显示表格

1.2   试验方案

试验在GDS动三轴仪上进行，试样为圆柱样，高度为76 mm，直径为38 mm。首先在最优含水率8.7%下进行击实，使试样干密度达到1.91 g/cm³（压实度K=95%）。制样后，装袋密封3 d使试样内部水分分布均匀。对试样进行7 d真空抽气饱和，用于模拟连续降雨对红层泥岩路基的影响。饱和完成后再次测定试样含水率并进行B检测（B=$\Delta u/\Delta {\sigma _3}$，其中$\Delta u/\Delta {\sigma _3}$为孔隙水压增量与围压增量的比值），结果表明试样含水率为15.6%~15.8%，与现场人工降雨的结果一致^[1]，试样B值均大于0.95。

试验条件为排水，围压设置为25，50，100，150，200 kPa，前3组围压对应路基0~3 m的深度，后二者是为了探究更高应力水平下饱和红层泥岩填料的动力响应。围压为25~100 kPa时，设置${\sigma _{\text{s}}}/{\sigma _3}$=2模拟车辆轴重的影响，其中${\sigma _{\text{s}}}$表示轴向偏应力；围压为25 kPa时，在${\sigma _{\text{s}}}/{\sigma _3}$=2情况下未观察到试样破坏，因而设置了更高的固结应力比和动应力以获取填料完整的变形规律。当围压为150，200 kPa时，对应路基的深度大于3 m，交通荷载传递随深度增加而衰减，此时的固结应力比将小于2，试样变形较小。为了研究更高围压水平下红层泥岩填料的破坏规律，在围压为150 kPa时设置${\sigma _{\text{s}}}/{\sigma _3}$=1.5，围压为200 kPa时设置${\sigma _{\text{s}}}/{\sigma _3}$=1.4，使试样的偏应力与静强度比值在50%左右，与围压为25~100 kPa的情况一致。试验首先按照设定的应力比进行非等向固结，固结完成后按照预设动应力${\sigma _{\text{d}}}$加载。波形为正弦波，频率为5 Hz，振次为5万次。详细试验方案见表 2。

表  2  饱和红层泥岩填料动三轴试验方案

Table  2.  Cyclic triaxial test programs for SRMF

测试组名	围压${\sigma _3}$/kPa	静强度${q_{\text{s}}}$/kPa	偏应力比${\sigma _{\text{s}}}/{\sigma _3}$	动应力${\sigma _{\text{d}}}$/kPa
C25	25	202	2	15, 30, 40, 50
	25	202	2.5	62.5
	25	202	3	75
	25	202	4	100
C50	50	249	2	20, 30, 40, 50, 60, 80
C100	100	347	2	30, 40, 50, 60, 70, 85
C150	150	448	1.5	45, 65, 80, 90, 100, 110, 130
C200	200	546	1.4	65, 85, 100, 110, 120, 130

下载: 导出CSV 

| 显示表格

2.   累积变形及动模量特性分析

2.1   累积变形、等效模量及耗散能的定义

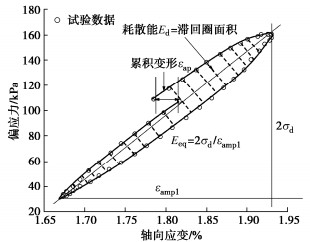
外部动荷载做功将引起试样内部变形，并进行能量耗散。填料的累积变形、变形速率和等效模量是填料的内部动力响应，而耗散能则是结合外部荷载与内部变形的综合评价指标。图 1是饱和红层泥岩填料典型动力加载的应力-应变滞回圈，试样的在某一振次下的累积变形${\varepsilon _{{\text{ap}}}}$定义为该振次结束时试样的应变与初始应变之差；等效模量E_eq定义为动应力振幅$2{\sigma _{\text{d}}}$与应变振幅${\varepsilon _{{\text{ampl}}}}$的比值；耗散能E_d则通过滞回圈面积计算。图 1的定义及计算方法与文献[21，22]一致。

图  1  典型饱和红层泥岩填料的应力-应变滞回圈

Figure  1.  Typical stress-strain loops for SRMF

下载: 全尺寸图片 幻灯片

2.2   累积变形、变形速率及等效模量的边界状态面

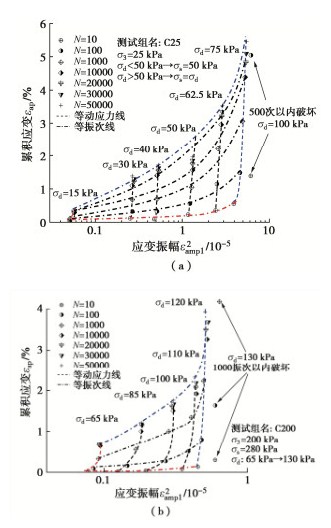
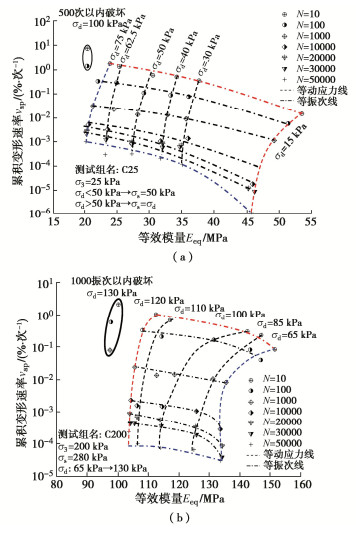
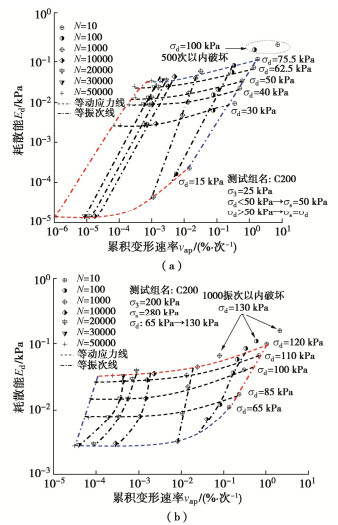
图 2是应变振幅随累积应变的等振次图。对于GDS动三轴仪而言，当加载频率较高时，仪器加载系统在前几振次内存在一定系统记录误差（不超过4%）。为最小化初始振动时的机器误差，取前10振次内累积应变和应变振幅的平均值作为第10振次的累积应变和应变振幅^[23]。图 2中只绘制了围压为25 kPa（低围压）和200 kPa（高围压）的结果进行例证，在汇总图中给出了全部结果，其他图处理方式相同。Wichtmann等^[23]的试验结果表明，对于无黏性砂粒类材料，${\varepsilon _{{\text{ap}}}}$和$\varepsilon _{{\text{ampl}}}^2$呈直线关系。而图 2则表明，饱和红层泥岩填料的${\varepsilon _{{\text{ap}}}}$与$\varepsilon _{{\text{ampl}}}^2$形成一个等振次曲面，说明饱和红层泥岩的变形特性与无黏性砂粒类材料有所不同。从图 2还可以看出，饱和红层泥岩填料的应变振幅具有动应力相关性。随动应力增大，填料的应变振幅和累积应变均显著增加；当动应力超过极限水平时，填料也将出现极限振幅，并在较少振次内破坏（极少振次内填料累积变形接近甚至超过低一级动应力振动50000次产生的变形）。因此图 2可认为是饱和红层泥岩填料的应变振幅状态边界面。本文所有试验均观察到了试样的累积变形，通过试验只确定了填料的极限状态边界，并未确定弹性边界。对于饱和红层泥岩填料，即使动应力非常小（15 kPa，图 2（a）），也观察到了累积变形的产生。因此，相应的状态边界面已经能够代表工程上饱和红层泥岩填料所承受的动应力及动力响应，后续着重讨论饱和红层泥岩填料的累积变形特性。

图  2  累积应变随振幅的边界状态面

Figure  2.  State boundary surfaces of axial strain amplitude with permanent axial strain

下载: 全尺寸图片 幻灯片

状态边界面描述了填料能承受的极限动力状态，即填料在某一应力状态下进行振动，动力响应如累积应变、应变振幅等将落在相应的状态面之内。如果超出状态面，将导致填料在较短振次内破坏，边界点则代表了填料的能承受的极限应力水平。需要指出，填料的极限状态并非临界状态。根据文献[4]，当动应力超过某一水平后，填料累积变形无法稳定，而是随振次增加不断发展，该动应力水平定义为临界动应力。以图 2（b）为例，围压为200 kPa时，填料在${\sigma _{\text{d}}}$ < 85 kPa时变形随振次发展首先增加，随后达到稳定状态；${\sigma _{\text{d}}}$ > 85 kPa后变形随振次增加不断发展且无法稳定，而极限状态则大于85 kPa（图 2（b）中为120 kPa）。

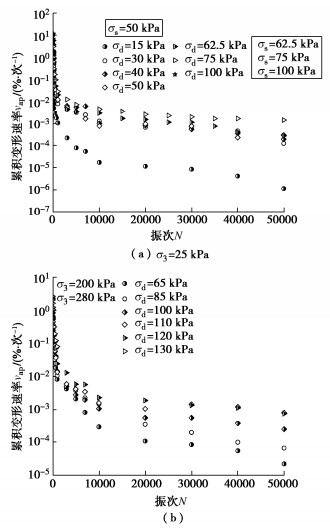
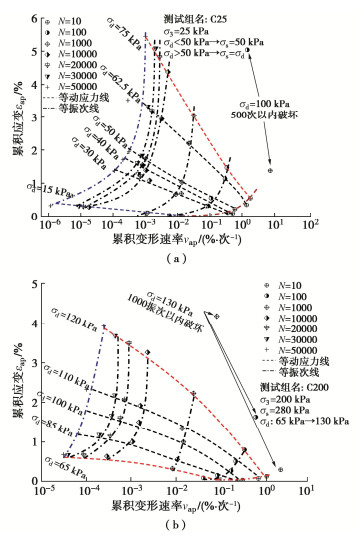
应变速率v_ap也是分析填料动力特性的一项重要指标，常定义为应变增量与振次增量的比值（${v_{{\text{ap}}}} =$ $\Delta {\varepsilon _{{\text{ap}}}}/\Delta N$）^[19]。图 3是应变速率随振次N的变化规律，图 4是饱和红层泥岩填料累积变形和应变速率的状态边界面。

图  3  累积变形速率随振次的变化关系

Figure  3.  axial strain rate versus loading cycles

下载: 全尺寸图片 幻灯片

图  4  累积应变随应变速率的状态边界面

Figure  4.  State boundary surfaces of axial strain rate with permanent axial strain

下载: 全尺寸图片 幻灯片

从图 3，4可以看出，填料的应变速率随振次增加而明显减小，随动应力增大而显著增大。这说明循环加载下填料内部结构调整逐渐适应外部荷载。但对于较高的动应力，如围压25 kPa，动应力为100 kPa时，填料的变形速率随振次衰减的幅度很小，这说明该级荷载引起填料变形在极短振次内迅速累积，产生破坏。而对于不同的动应力，虽然变形速率随振次衰减，但在高振次时填料的变形速率也有非常大的差距。以围压25 kPa为例，在第50000振次时，动应力75 kPa对应的变形速率明显高于动应力15 kPa，这说明即使高振次下，较大的动应力引起的变形速率也更高，动应力水平增加对所有振次下填料的累积变形和变形速率均有不利影响。

图 5是饱和红层泥岩填料应变速率和等效模量的状态边界面。可以看出，应变速率和等效模量具有良好的相关性。相同振次下，等效模量越大，填料的应变速率就越小。围压也是影响填料等效模量和应变速率的关键因素之一。以动应力65 kPa为例，围压25 kPa时填料在第50000振次的等效模量在25 MPa左右，应变速率在10^-4%/次~10^-3%/次；而当围压为200 kPa，填料的等效模量在135 MPa左右，远高于围压25 kPa的情况，应变速率接近10^-5%/次，也明显低于围压25 kPa的情况。增加路基侧向约束能够有效提升路基抗变形能力。常规路基变形分析时，动模量取值多对应弹性状态，且为常数^[24]。而图 5的结果表明，饱和红层泥岩填料的等效模量具有振次和应力状态相关性。等效模量随振次增加而衰减，当振次超过10000次以后，填料等效模量呈现稳定状态。因此红层泥岩路基变形分析应根据列车轴重进行模量取值，且应取高振次对应的等效模量，避免低估路基的累积变形量。

图  5  累积变形速率随等效模量的状态边界面

Figure  5.  State boundary surfaces of axial strain rate with equivalent Young's modulus

下载: 全尺寸图片 幻灯片

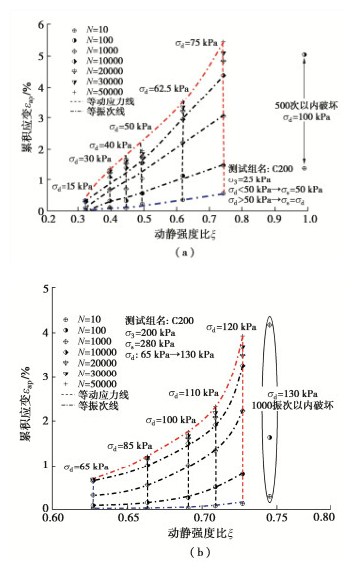
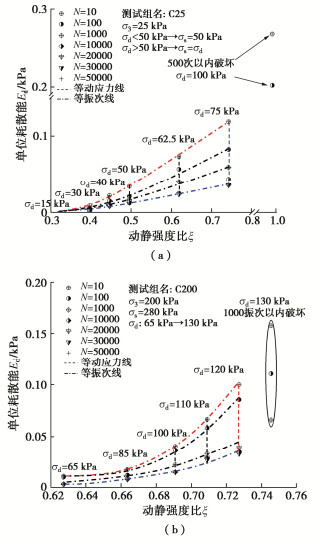
定义动静强度比$\xi = ({\sigma _{\text{s}}} + {\sigma _{\text{d}}})/{q_{\text{s}}}$，其中${q_{\text{s}}}$是试样的静强度值。图 6绘出了累积应变与$\xi$的状态边界面。由图 6可知，饱和红层泥岩填料动静强度比极限值约为0.7~0.75，相比无黏性类砂粒材料也有所不同。无黏性类砂粒材料的动力极限状态与静强度非常相近^[25]，说明饱和状态下，黏土矿物尤其是膨胀矿物的存在降低了红层泥岩填料的动强度。

图  6  累积变形随$\xi$的状态边界面

Figure  6.  State boundary surfaces of permanent axial strain with $\xi$

下载: 全尺寸图片 幻灯片

图 2~6阐明了动载作用下饱和红层泥岩填料从稳定状态到破坏状态的内部响应特征，归纳为：饱和红层泥岩填料的累积变形、变形速率和等效模量具有内在相关性，相应极限由状态边界面表征。状态边界面的存在说明动荷载下饱和红层泥岩填料的变形响应非常复杂，常规的静强度分析方法不适用于高速铁路路基的动力分析。围压变化将引起状态边界面形状和大小的改变，动应力大小则决定了填料内部响应在状态边界面中所处的位置。当动应力超过极限值时，填料累积变形及应变速率响应点将落在状态边界面外。通过状态边界面可以直接确定填料在指定动应力下的累积变形、应变速率和等效模量随振次的变化规律，从而进行路基的变形分析。

3.   耗散能演变特性分析

3.1   耗散能随振次的演化规律

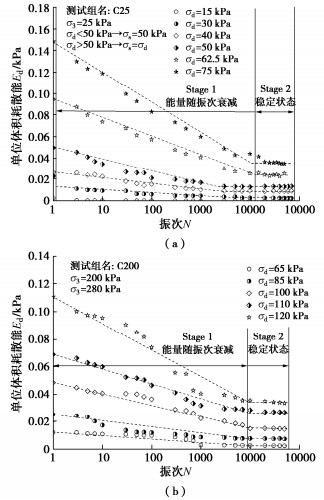
耗散能的大小直接决定了土体内部结构的变化程度。耗散能越大，土体内部微结构演变程度就越剧烈，相同振次内的累积变形越多，应变速率也越大，从而导致土体向破坏方向发展。图 7绘出了不同围压和动应力下耗散能随振次的演变规律。由图 7可知，饱和红层泥岩填料耗散能演变分为两个阶段。第一阶段（N < 10000），耗散能随振次增加而迅速衰减；第二阶段（N > 10000）耗散能趋于稳定状态。第一阶段反映了填料的初始动力响应，即填料在初始振动阶段的内部结构劣化更为剧烈，累积变形和速率也越大。第二阶段则揭示了填料在高振次的动力响应，耗散能趋于稳定说明第二阶段每振次的填料内部结构调整程度基本相同，当第二阶段能量较小时，填料的结构调整大部分是可恢复的，所产生的变形基本为弹性变形，因此填料的累积变形速率将迅速降低，累积应变则逐渐趋于稳定状态。而当第二阶段能量逐渐增加，土体结构劣化程度加剧，所产生的变形大部分是塑性变形。此时填料的累积变形速率明显高于低能量的情况，且应变在高振次也不断发展，即填料最终无法到达稳定状态。能量演变的第一阶段与文献[26]所观察到的动载下土体“再压实”现象相对应，而能量演变的第二阶段则可用于解释和判断填料的长期稳定性。

图  7  耗散能随振次的演化规律

Figure  7.  Relationship between dissipated energy and loading cycles

下载: 全尺寸图片 幻灯片

3.2   耗散能、等效模量、累积变形的边界状态面

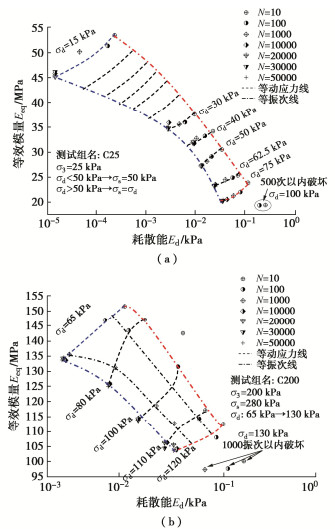
由前述，耗散能大小是填料结构变化程度的表征。因此，耗散能与填料的累积变形和等效模量之间必然具有相关性。图 8是等效模量与耗散能的状态边界面，可以看出，能量大小显著影响填料的等效模量。当E_d > 10^-1 kPa，填料内部无法耗散该级别的能量，从而在极短振次内破坏；当能量水平为10^-3 kPa < E_d < 10^-2 kPa时，填料的等效模量随能量减小而逐渐增加，在这一能量水平下填料具有一定的抗变形能力。而当E_d < 10^-3 kPa时，填料的等效模量显著增加，表明此时填料具有较高的抗变形能力。图 8的状态边界面大小随围压变化而不同，说明填料耗散能的状态边界面同样具有围压相关性。

图  8  等效模量随耗散能的状态边界面

Figure  8.  State boundary surfaces of equivalent Young's modulus with dissipated energy

下载: 全尺寸图片 幻灯片

图 9为应变速率与耗散能的状态边界面，图 9的应变速率和耗散能与图 7的两阶段能量演变规律相对应。首先，在第一阶段内填料能量迅速下降导致速率急剧降低，在图 9中表现为向左下方发展的曲线；此后在第二阶段，根据能量水平决定速率的下降程度。能量越低，填料在第二阶段的应变速率下降就越明显；而能量越高，填料速率在第10000振次和第50000振次的速率差也就越小，填料在高振次下应变累积更加显著。

图  9  应变速率随耗散能的状态边界面

Figure  9.  State boundary surface of axial strain rate with dissipated energy

下载: 全尺寸图片 幻灯片

图 10是耗散能与动静强度比的状态边界面。低动静强度比下，填料内部耗散能较小，累积变形速率将迅速降低，变形将最终达到稳定。这一阶段，动应力的增长引起的能量增加相对有限，在图 10中由能量曲线较为平缓的一段表征。而高动静强度比引起的能量也较高，填料无法承受该能量水平，从而导致结构不断劣化甚至往破坏的趋势发展，在图 10中由能量曲线随动应力增加而变“陡峭”的一段表征。

图  10  耗散能-动静强度比状态边界面

Figure  10.  State boundary surfaces of E_d with $\xi$

下载: 全尺寸图片 幻灯片

图 7~10阐明了动载作用下饱和红层泥岩填料从稳定状态到破坏状态的能量耗散特性，归纳为：能量随振次变化具有明显的两阶段特征，饱和红层泥岩填料的累积变形、变形速率和等效模量由相应的耗散能大小决定，而能量大小则由所受外部动应力水平影响。因此，能量随动应力的增长规律反映了相应累积变形和应变速率受动应力水平的影响特性，填料在动载下的稳定性也可通过这一规律进行判定。

3.3   变形稳定性的能量判定方法

累积变形和长期稳定性是高速铁路路基设计时主要关注的问题。对于前者，可以从相应的状态边界面（图 2~5）进行判断，而对于后者，则可从第二阶段的能量特征进行判定。定义相对能量水平${E_{\text{L}}} =$ ${E_{d2}}/{E_{\text{s}}}$，其中${E_{{\text{d2}}}}$是指填料在第二阶段（即稳定阶段）的能量大小，${E_{\text{s}}}$是指定围压下土体能够承受的极限能量，具体数值可通过能量状态边界面确定。从图 6可以看出，稳定阶段的能量也有少许波动。为最小化这一影响，取第二阶段能量的平均值作为${E_{{\text{d2}}}}$，即

式中：${N_2}$是填料进入第二阶段时的振次，${N_{\text{s}}}$是试验结束时填料经历的振次。能量大小决定了填料内部结构的调整程度，从而决定了填料累积变形速率的大小。当第二阶段能量（${E_{{\text{d2}}}}$）产生突增时，说明填料内部结构劣化程度增加，从而导致高振次下填料应变速率相应增加，填料的长期稳定性就无法保证。填料能量突增点的确定方法与确定超固结黏土先期固结应力的方法类似，具体见文献[15]。

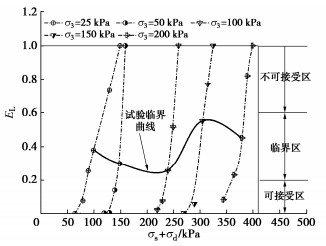
将5个围压下饱和红层泥岩填料相对能量水平随动应力的变化规律绘制于图 11，根据文献[4]对临界动应力的定义，将${E_{\text{L}}}$开始突增时对应的动应力标记为临界动应力，最终在相对能量水平和动应力平面绘出临界曲线。称临界曲线的所处的能量区间为临界区，低于临界曲线的能量区间为可接收区，高于临界曲线的能量区间则为不可接受区。可以看出，当动应力引起的能量低于极限能量的20%时（${E_{\text{L}}}$ < 0.2），填料处于动力稳定状态，相对能量水平在可接受区。在路基设计时，应尽量使动应力引起的能量水平处在可接受区内。当动应力引起的能量为极限能量的20%~60%时（0.2 < ${E_{\text{L}}}$ < 0.6），填料处于动力临界状态，相对能量水平在临界区，填料稳定性对动应力非常敏感，极小的动应力增加都会导致填料变形处于不稳定状态。路基设计时，应根据路基设计年限和容许变形量，结合相应累积变形和应变速率的能量状态边界面，判定该临界状态是否可以接受。而当动应力引起的能量超过极限能量的60%（${E_{\text{L}}}$ > 0.6）时，填料处于动力失稳状态，相对能量水平位于不可接受区，过高的能量水平将导致填料长期稳定性无法保证，甚至可能在较少振次（较短运营年限）内产生超过限度的累积变形，路基设计中必须避免这一情况发生。

图  11  能量水平区间划分

Figure  11.  Identification of dissipated energy ranges

下载: 全尺寸图片 幻灯片

4.   结论

本文通过不同围压和动应力下饱和红层泥岩填料的动三轴试验，阐述了饱和红层泥岩填料的累积变形、应变速率、等效模量的自相关性以及与耗散能的相关性，根据相对能量水平划分了饱和红层泥岩填料的动力状态，得到以下4点结论。

（1）饱和红层泥岩填料的累积变形、应变速率和等效模量具有内在相关性，相应特征和极限由状态边界面表征。围压变化将引起状态边界面形状和大小的改变。动应力大小则决定了填料内部响应在状态边界面中所处的位置。动应力超过极限值后，响应点将落在状态边界面外，填料将在较短振次内破坏。

（2）饱和红层泥岩填料的能量随振次的演化具有两阶段特征，第一阶段（振次N < 10000）能量随振次迅速衰减，第二阶段（N > 10000）耗散能趋于稳定状态。能量演变的第一阶段动载下对应土体“再压实”现象，反映了填料的初始动力响应。而能量演变的第二阶段揭示了填料在高振次作用下的动力响应，可用于解释和判断填料的长期稳定性。

（3）饱和红层泥岩填料的累积变形、变形速率和等效模量由相应的耗散能大小决定，相关性同样通过状态边界面表征。而能量大小则由所受外部动应力水平影响，能量随动应力的增长规律反映了累积变形和应变速率受动应力的影响规律。

（4）当动应力引起的能量低于极限能量的20%时（${E_{\text{L}}}$ < 0.2），饱和红层泥岩填料处于动力稳定状态；当动应力引起的能量为极限能量的20%~60%时（0.2 < ${E_{\text{L}}}$ < 0.6），填料处于动力临界状态；而当动应力引起的能量超过极限能量的60%（${E_{\text{L}}}$ > 0.6）时，填料处于动力失稳状态。路基设计时应使能量水平处于可接受区间，而必须避免处于不可接受区间。