Mechanism and control of progressive collapse caused by failure of local anchors in multiple-level anchored pile excavation
-
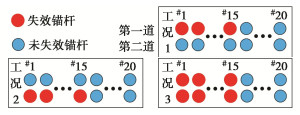
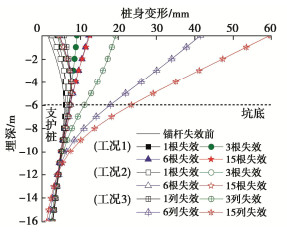
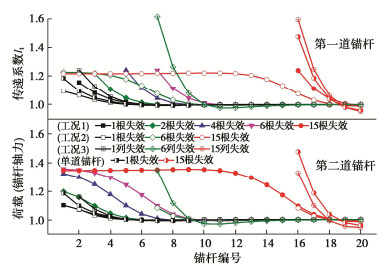
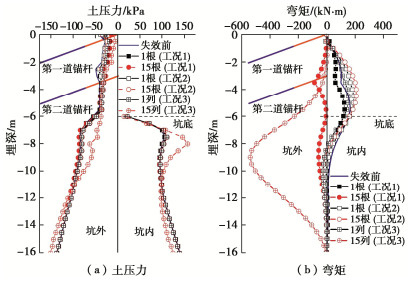
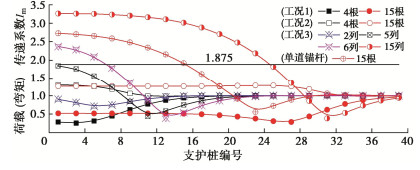
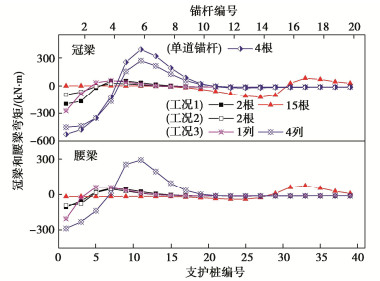
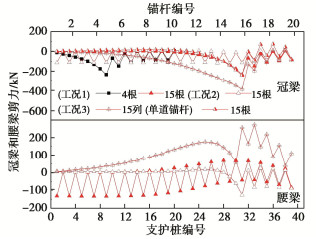
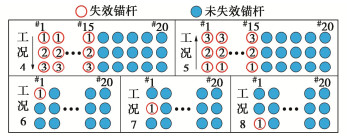
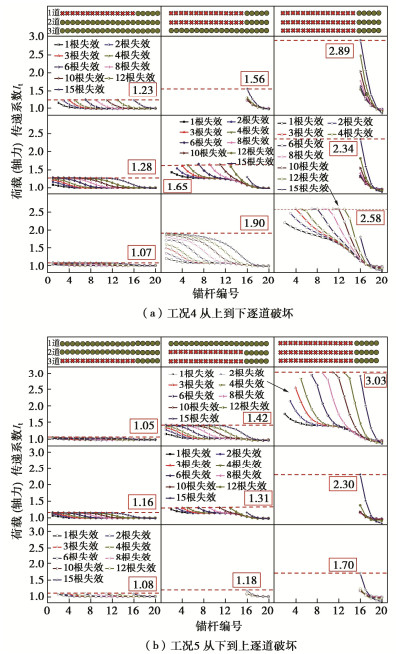
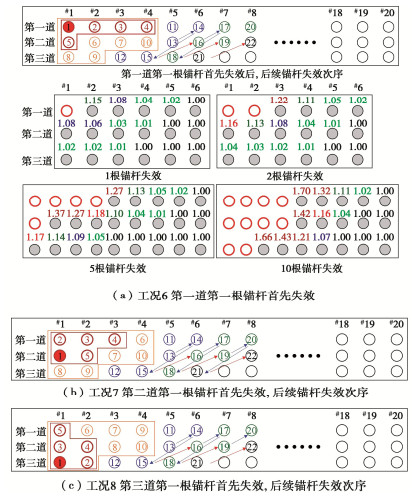
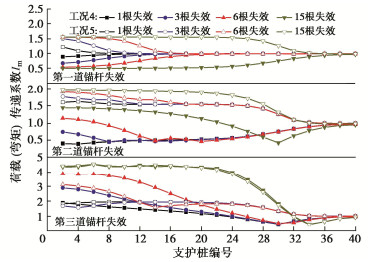
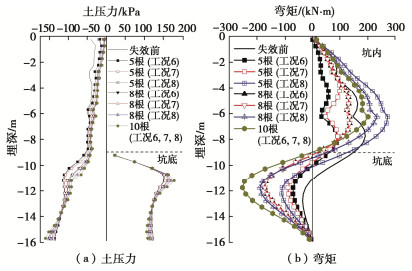
摘要: 多道锚杆支护体系具有节约施工空间、变形控制效果好等优点,广泛应用于深基坑支护中。然而局部锚杆失效引发的基坑连续破坏事故时有发生。针对此问题,采用有限差分法研究了多道锚杆支护体系中局部锚杆失效引发的土压力与支护结构内力变化及结构连续失效规律,初步揭示了局部锚杆失效后的荷载传递路径及其引发基坑连续破坏的机理。多道锚杆支护体系中,首道锚杆局部失效对邻近未失效锚杆影响大,但会引起支护桩弯矩下降,最下道锚杆局部失效则相反,但仅一道锚杆局部失效影响相对较小,均小于基坑深度相同的单道锚杆支护体系,然而多道锚杆整列同时局部失效影响显著大于单道锚杆支护体系,更易引发连续破坏,因此应采用隔道加强等设计或施工措施将局部锚杆失效控制在一道内。局部若干根锚杆失效导致邻近受影响最大的锚杆依次失效时,锚杆失效数量较多后,初始锚杆失效位置对连续破坏发展传递路径不再产生影响,锚杆连续破坏接近于整列失效,且呈倒梯形水平向扩展。多道锚杆支护体系中发生整列锚杆失效时,冠梁或腰梁极易发生破坏,造成支护桩弯曲破坏,加快基坑连续垮塌过程,因此应对冠(腰)梁进行局部锚杆失效工况下的设计,以提高基坑防连续破坏整体安全性能。Abstract: Collapse of tied-back excavations occurs frequently. In this study, the finite difference method is used to simulate failure of anchors. In a multi-level anchored pile excavation, the failure of the first-level anchors has a great impact on the adjacent anchors and causes the bending moments of piles to decrease, while the failure of the lowest-level anchors has the opposite effects. The impact of failure of column anchors in a multi-level anchored-pile system is significantly greater than that of a single-level anchored-pile system, which easily leads to progressive collapse. Therefore, the construction or design methods, such as interval-level anchor strengthening, should be adopted to limit the failure at a certain level. When the failure of anchors causes the most affected adjacent anchors to fail progressively and even many anchors to fail, the failure position of the initial anchors does not affect the transmission path development of failure of anchors. Accordingly, the progressive failure of anchors is close to the failure of column anchors, and shows an inverted trapezoidal horizontal expansion. The failure of column anchors in a multi-level anchored pile system easily leads to damage to the beam. Then it will cause pile failure and accelerate the process of excavation collapse. Therefore, the capping (waler) beams should be designed under the failure of column anchors to improve the overall safety performance of the retaining system.
-
0. 引言
近年来中国开展了南海岛礁工程建设,以适应海上生产活动、交通运输和国防战略的需要。岛礁工程因远离大陆,通常就地取材,利用珊瑚礁沉积物吹填形成岛礁工程的地基。这些沉积物以珊瑚砂为主,具有颗粒强度低、易破碎的特点。静止土压力系数K0(K0=σ′h/σ′v,其中σ′h,σ′v分别为水平向和竖向有效应力)是土力学的一个基本参数,吹填地基固结期的应力变化符合K0固结的应力路径[1],而砂土应力-应变关系具有明显的应力路径依附性的特性[2],因此有必要深入认识K0固结珊瑚砂的应力-应变特性,并在此基础上建立一个能考虑实际应力路径影响的、简单和实用的变形计算模型,以准确预估吹填地基的固结变形量,提高岛礁吹填工程的设计和施工质量。
描述土的应力-应变关系的数学模型分为弹性和弹塑性两大类,其中弹塑性模型较好地反映了土体的硬化、软化和剪胀特性[3],但是模型比较复杂,参数求取相对困难。而弹性类的非线性弹性模型,例如Duncan-Chang的双曲线E-μ模型[4]及改进的E-B模型[5]、K-G模型[6]等,能较好地模拟土的非线性变形特性,并具有形式简洁和参数少的特点,因而在土的变形计算中被广泛采用[7-8]。然而非线性弹性模型在描述土的剪胀特性方面存在局限性,但是考虑到K0固结土体变形主要表现为压缩性质,剪胀特性并不明显。因此采用非线性弹性模型来描述K0固结珊瑚砂的应力–应变关系,在工程应用上仍具有明显的优势。
非线性弹性模型的应力-应变关系不能用常数表示,而是用应力或变形的函数参数来描述。由于有多种方法可以定义非线性变形中的应力和应变,因此对应于同一种模型参数,可以存在多个非线性函数[9],而这些函数的选择往往取决于特定的应力路径试验。珊瑚砂具有应力路径依附性的特性,其应力-应变关系与应力路径有关[10]。土体K0固结的应力-应变关系不同于常规三轴试验的双曲线关系,因此采用双曲线的非线性弹性模型计算变形误差较大。有关K0固结变形计算的研究,迄今为止多针对的是软黏土[11-12],珊瑚砂的研究资料不多,对变形参数的变化规律和取值知之甚少,需要通过K0试验模拟珊瑚砂地基固结的应力路径实况,以求得能够反映实际应力路径影响的变形参数。另外,对于常应力下就能产生颗粒破碎的珊瑚砂,也需要查明K0固结过程中的颗粒破碎状况。
鉴于此,本文利用计算机控制的三轴试验系统对不同初始相对密度的珊瑚砂进行K0试验,研究珊瑚砂的应力-应变关系和颗粒破碎状况。在此基础上,建立描述K0固结珊瑚砂应力-应变关系的非线性弹性模型,提出非线性弹性变形参数的表达式并确定模型参数,最后利用模型预测K0固结珊瑚砂的应力-应变关系,可为珊瑚砂吹填地基的设计与施工提供参考。
1. 土样与试验方法
1.1 土样
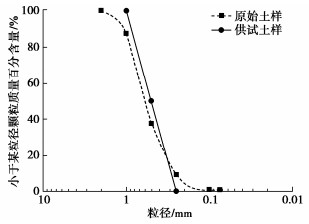
珊瑚砂取自中国南海岛礁,采用筛分法制备粒径范围为1~0.5 mm和0.5~0.25 mm两个粒组的土样,颗粒的质量百分比各占50%,供试土样占珊瑚砂原始土样的质量百分比超过80%。土样的粒径分布曲线见图 1,基本物理性质指标见表 1。
表 1 珊瑚砂的基本物理指标Table 1. Physical parameters of coral sand土粒相对质量密度Gs 平均粒径d50/mm 不均匀系数Cu 最大孔隙比emax 最小孔隙比emin 2.78 0.50 1.93 1.196 0.829 1.2 试验仪器
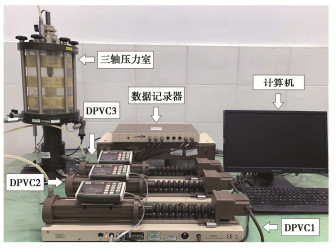
本文采用三轴仪法进行K0试验。如图 2所示,试验设备为英国GDS公司生产的全自动三轴试验系统,主要由三轴压力室、数据记录器、计算机、3个数字压力/体积控制器(DPVC1~3)等组成。其中DPVC1控制轴向荷载,DPVC3控制围压,DPVC2控制反压(或孔压)并测量体变,可以对试样施加指定的压力或强制执行所需的体积变化,试样底部的孔压由压力传感器测量。
1.3 试验方法
试样为圆柱形,直径39.1 mm,高80 mm。在圆柱形底座上包裹橡皮膜,称取所需质量的烘干砂样, 采用砂雨法分三等分在膜内撒干砂制备试样,制成试样的初始相对密度Dr=0.5,0.6,0.7,0.8,0.9,为中密至密实状态。试样饱和采用水头饱和与反压饱和法,水头饱和前,先从试样底部通入CO2气体置换孔隙中的空气,完毕后利用排水管从试样底部注入无气水饱和,最后再利用三轴试验系统反压饱和,方法是先对试样施加20 kPa的围压进行预压,再分级施加反压饱和,此时需同步施加围压,并始终保持围压比反压大20 kPa。每级反压施加后检测孔压系数B值,当检测到B > 0.95时可认为试样完全饱和。由于K0固结开始前所有试验都施加了20 kPa的初始有效围压,意味着K0试验并非从零应力状态开始,而是存在着一个初始等向固结应力,试验从各向同性应力状态开始施加应力。
本文采用的应力和应变的符号意义如下:轴向有效应力σ′1,有效围压σ′3,偏应力q=σ′1−σ′3,平均有效应力p′=(σ′1+2σ′3)/3,轴向应变ε1,径向应变ε3,体应变εv,剪应变εs。K0试验为应力式控制,试验过程中同时施加轴向有效应力σ′1和有效围压σ′3,加载速率dσ′3=5 kPa/min,DPVC根据轴向应变调节试样的体积变化,以保持试样的体应变与轴向应变的变化相等(dεv/dεvdε1dε1=1),径向应变保持不变(dε3=0)。当到达预设的有效围压σ′3=1000 kPa后试验终止。K0值由K0=σ′3/σ′3σ′1σ′1计算获得。
对试验后的各试样,利用筛分试验获得粒径分布曲线,采用Hardin[13]提出的相对破碎率Br来量化珊瑚砂的颗粒破碎程度,即分别将试验前和试验后的粒径分布曲线与0.075 mm粒径截断线所围成的面积,定义为试验前和试验后的破碎势。再将试验前和试验后的破碎势之差定义为破碎量,则Br为破碎量与试验前破碎势的比值。
2. 结果与分析
2.1 应力-应变曲线
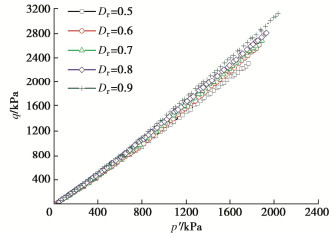
图 3为K0试验在q-p′平面内的应力路径,从中可以发现,K0固结珊瑚砂的初始相对密度Dr不同,有效应力路径表现出一定的差异性,Dr越小,有效应力路径越低。考虑到珊瑚砂具有应力路径依附性的特点,珊瑚砂的Dr不同,应力路径也不同,故对应力–应变关系会产生一定的影响。
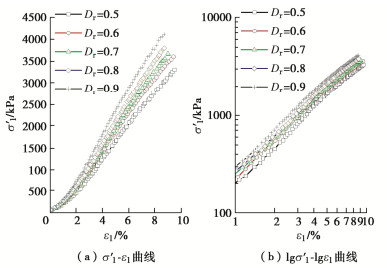
图 4为K0固结珊瑚砂的轴向有效应力σ′1与轴向应变ε1的关系曲线。从图 4(a)可以发现,σ′1-ε1曲线的坡度随初始相对密度的增大而逐渐变陡。Dr越大,相同轴向应变时的轴向有效应力越大。将图 4(a)中的σ′1-ε1曲线绘制在双对数坐标图上,见图 4(b),从中可以发现,在双对数坐标轴上的σ′1与ε1近似成线性关系,说明σ′1-ε1曲线为幂函数型,可表示为
σ′1pa=AεB1。 (1) 式中:A,B为试验参数;pa=101.33 kPa,为标准大气压力。引入pa目的是使试验参数变成无量纲量,以适应不同计量单位。
基于K0试验结果,利用式(1)对σ′1-ε1曲线回归分析,参数A,B的试验回归值及拟合度见表 2,显示了拟合度R2均大于0.996,表明回归分析的显著性水平较高,σ′1-ε1曲线可采用式(1)的幂函数模型来描述。由K0条件下的σ′3=K0σ′1,εv=ε1,可推得q=(1−K0)σ′1,p′=(1+2K0)σ′1/3,εs=2ε1/2ε133,说明K0固结珊瑚砂的q-εs曲线、p′-εv曲线也可以用幂函数模型来描述。
表 2 式(1)参数A,B的试验回归值Table 2. Test regression values for parameters A and B of Eq. (1)Dr A B R2 0.5 718.94 1.281 0.9960 0.6 732.40 1.242 0.9961 0.7 779.94 1.245 0.9969 0.8 870.28 1.261 0.9976 0.9 906.65 1.237 0.9965 2.2 K0系数
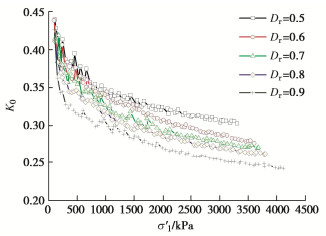
图 5为珊瑚砂的静止土压力系数随轴向有效应力的变化曲线,从中可以发现,在K0试验的开始阶段,K0先急剧减小,然后变缓。Chu等[14]采用三轴仪法对硅质砂的K0试验中也观察到类似的现象。究其原因,是因为在三轴仪里进行的K0试验,开始于各向同性的应力状态,因此存在着一个从各向同性向K0状态转变的过程。一旦跨过这个过渡期,K0的变化趋于平缓。图 5还显示,随着σ′1的增加,K0逐渐减小。Dr对K0的影响较为明显,在相同σ′1条件下,Dr越小,K0越大。
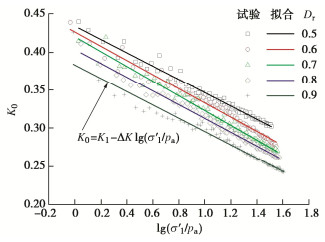
将K0和轴向有效应力的对数值lg(σ′1/pa)进行线性回归分析,结果绘于图 6,回归参数值及拟合度R2见表 3,显示线性回归的显著性水平较高,说明K0与lg(σ′1/pa)之间具有良好的直线关系,即
K0=K1−ΔKlgσ′1pa。 (2) 表 3 式(2)参数K1,ΔK的试验回归值Table 3. Test regression values for parameters K1 and ΔK of Eq. (2)Dr K1 ΔK R2 0.5 0.434 0.087 0.9777 0.6 0.426 0.093 0.9739 0.7 0.420 0.097 0.9800 0.8 0.403 0.090 0.9903 0.9 0.383 0.087 0.9589 式中:K1为一个标准大气压下的K0取值;ΔK为随轴向有效应力增加的K0减小值。
2.3 颗粒破碎特性
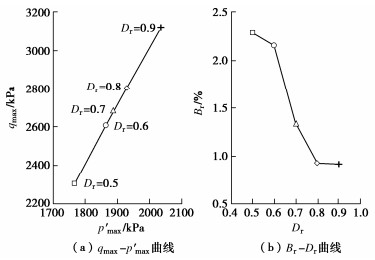
图 7为K0试验结束时不同初始相对密度珊瑚砂在q-p′平面内的应力和相对破碎率Br。图 7(a)显示,珊瑚砂的Dr越小,K0试验结束时的平均有效应力p′max和偏应力qmax越小,然而Br越大,见图 7(b)。一些学者在钙质砂的侧限压缩试验中,也得到相同的结论[15-16]。对该现象可解释为:单位体积内松砂颗粒较少、密砂颗粒较多,因此松砂颗粒之间的接触点相对较少,密砂颗粒间的接触点较多。尽管作用于密砂试样上总的有效应力更大,但是传递到颗粒间接触点的平均有效应力,松砂的较大,密砂的较小,因此松砂较密砂更容易产生颗粒破碎。
从图 7(b)还可以发现,在本文的试验应力范围内,珊瑚砂的颗粒破碎量非常小,中密状态珊瑚砂(Dr=0.5~0.6)的Br小于2.3%,密实状态珊瑚砂(Dr=0.7~0.9)的Br不到1.4%,因此可以认为珊瑚砂的颗粒破碎对K0固结的影响不大。
3. 变形参数
式(1)描述的幂函数非线性弹性模型,其理论基础仍是弹性理论,因此应力–应变关系可以用应力和应变增量形式表征的切线模量和切线泊松比来联系,并可由广义虎克定律导出。
3.1 切线泊松比
轴对称条件下,轴向应变ε1和径向应变ε3分别为
ε1=1E(σ′1−2νσ′3), (3) ε3=1E[σ′3−ν(σ′1+σ′3)]。 (4) 式中:E为弹性模量;ν为泊松比。
将式(3),(4)相除,可得
ε1ε3=σ′1−2νσ′3σ′3−ν(σ′1+σ′3)。 (5) 将K0状态下的σ′3=K0σ′1代入式(5),移项整理,并写成应变增量的形式,可得切线泊松比
νt=K0−dε3/dε3dε1dε11+K0−2K0⋅dε3/dε3dε1dε1。 (6) 考虑K0状态时的dε3=0,式(6)可简化为
νt=K01+K0。 (7) 3.2 切线模量
将K0状态下的σ′3=K0σ′1代入式(3),并写成应力和应变增量的形式,可得
dε1=(1−2νtK0)Etdσ′1。 (8) 式中:Et为切线弹性模量。
将式(1),(7)代入式(8)并移项整理,可得用轴向应变的函数表示的切线弹性模量:
Etpa=ABεB−11(1−2K201+K0)。 (9) 对式(1)变形可得ε1=(1/A)1/1BB⋅(σ′1/pa)1/1BB,代入式(9)并整理,可得用轴向有效应力的函数表示的切
线弹性模量:
Etpa=BA1B(1−2K201+K0)⋅(σ′1pa)B−1B。 (10) 在非线性弹性模型中,以增量形式表征的q-εs,p′-εv关系,可分别用切线剪切模量Gt和切线体积模量Kt来联系,即
dεs=13Gtdq, (11) dεv=1Ktdp′。 (12) 按照弹性理论,非线性弹性模型中的其他弹性参数可以从Et,νt二个参数获得。由广义虎克定律可知,Gt,Kt与Et,νt的关系为
Gt=Et2(1+νt) (13) Kt=Et3(1−2νt) (14) 将式(13),(14)分别代入式(10),再代入式(7)并移项整理,可得
Gtpa=BA1B⋅1−K02⋅(σ′1pa)B−1B (15) Ktpa=BA1B⋅1+2K03⋅(σ′1pa)B−1B (16) 式(10),(15),(16)表明,幂函数模型的3个切线模量Et,Gt,Kt都可表示为轴向有效应力的函数,并通过K0和参数A,B来描述。
3.3 模型参数的确定
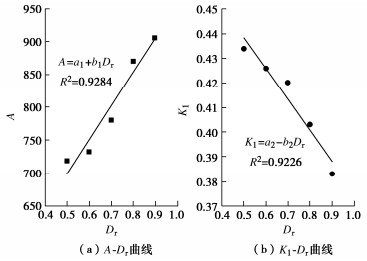
考察表 2中参数A,B的试验回归值随Dr的变化规律,可建立它们之间的相关关系。分析表明,参数A随Dr的增大而增大,并与Dr大致成线性关系,回归分析结果见图 8(a);参数B是一个与lgσ′1-lgε1线性关系的斜率有关的量,由于不同Dr的lgσ′1-lgε1直线大致平行,见图 4(b),因此B可近似为常数。有关回归值的计算公式及相关参数见表 4,可见参数A,B的计算回归值可以用a1,b1,c1 3个参数表示。
表 4 试验参数回归值的计算公式Table 4. Formulas for test parameter regression value试验参数 回归值计算公式 相关参数 R2 A A=a1+b1Dr a1 =442.33, b1=513.30 0.9284 B B=c1 c1= 1.253 K1 K1=a2−b2Dr a2 =0.501, b2=0.125 0.9226 ΔK ΔK=c2 c2=0.091 同理,建立表 3中参数K1,ΔK的试验回归值与Dr的相关关系。表 3显示,参数K1随Dr的增大而减小,与Dr大致满足直线关系,线性回归结果见图 8(b)。参数ΔK是K0-lg(σ′1/σ′1papa)线性关系的斜率,不同Dr的拟合直线大致保持平行,见图 6,因此ΔK也近似为常数。回归值计算公式及相关参数见表 4,参数K1,ΔK的计算回归值可以用a2,b2,c2 3个参数表示。
从上述分析可知,幂函数模型通过表 4中的a1,b1,c1,a2,b2,c2等6个参数,表达了K0,νt和3个切线模量Et,Gt,Kt,完成了对一定范围Dr值的K0固结珊瑚砂的应力–应变–体变关系曲线的描述。
4. 模型计算与试验曲线的比较
将本文模型的计算结果与试验曲线进行比较,以验证描述K0固结珊瑚砂的应力–应变关系的幂函数模型及其参数的适用性。模型计算的具体步骤如下:
(1)将K0固结珊瑚砂预备比较的初始相对密度Dr代入表 4中的回归值计算公式,求得试验参数A,B,K1,ΔK的计算回归值,结果如表 5所示。
表 5 试验参数的计算回归值Table 5. Calculated regression values of test parametersDr A B K1 ΔK 0.5 698.98 1.253 0.439 0.091 0.6 750.31 1.253 0.426 0.091 0.7 801.64 1.253 0.414 0.091 0.8 852.97 1.253 0.401 0.091 0.9 904.30 1.253 0.389 0.091 (2)将K1,ΔK的计算回归值代入式(2)确定K0,再将K0和参数A,B的计算回归值代入式(7),(10),(15),(16),以确定νt,Et,Gt,Kt。
(3)先给定一个较小的有效应力增量步dσ′1、dq=(1−K0)dσ′1或dp′=(1+2K0)dσ′1/3,再将计算得到的K0,νt,Et,Gt,Kt分别代入式(8),(11),(12),计算出相应的应变增量值dε1,dεs,dεv。最后分别累加各应力增量、应变增量值,得到全量的σ′1-ε1、q-εs、p′-εv关系曲线。
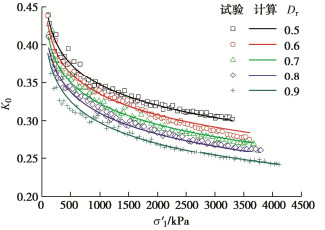
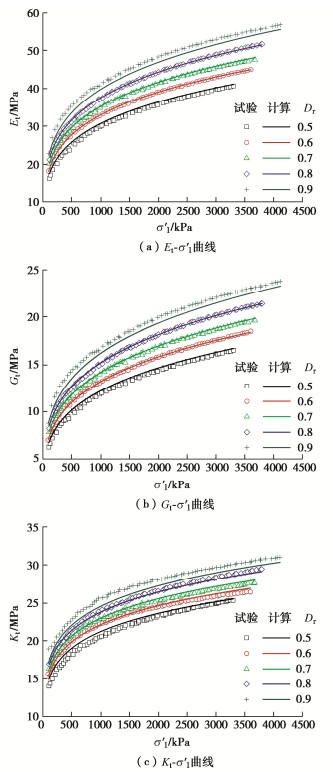
图 9为K0的式(2)计算结果与试验曲线的比较,显示K0的计算值与试验值吻合较好。将试验参数的计算回归值和试验回归值分别代入式(7),(10),(15),(16),计算出对应的νt,Et,Gt,Kt并相互比较,结果如图 10~11所示。从中可以发现,无论是νt,还是Et,Gt,Kt,采用计算与试验回归值算得的变形参数都吻合较好,说明幂函数模型对K0固结珊瑚砂的各种变形参数都能够合理预测。
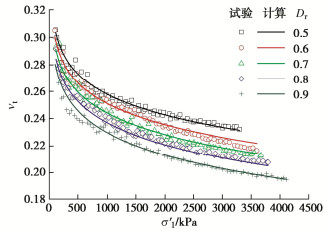
图 10显示,切线泊松比νt并非是一个常量,而是随着σ′1的增加而逐渐减小。在相同的σ′1条件下,Dr越大,νt越小。图 11显示,切线模量Et,Gt,Kt随着σ′1的增加而逐渐增大。在相同的σ′1条件下,Dr越大,Et,Gt,Kt越大。在本文Dr范围内,珊瑚砂变形参数的取值范围:νt为0.2~0.3,Et为16~56 MPa,Gt为6~24 MPa,Kt为14~31 MPa。
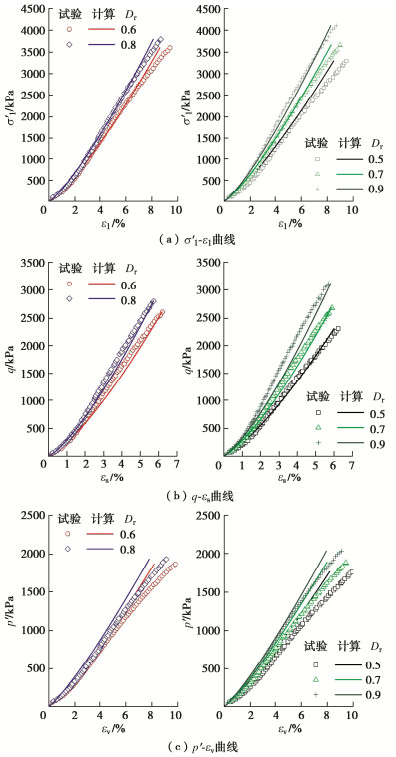
将模型计算得到的σ′1-ε1,q-εs,p′-εv曲线与试验曲线进行比较,结果如图 12所示。从图 12(a),(b)可以发现,σ′1-ε1,q-εs曲线的计算与试验结果较为吻合,说明幂函数模型对轴向应变和剪应变都能合理预测。其中σ′1-ε1曲线的计算与试验结果在大部分的试验应力范围内都极为吻合,只有当σ′1超出了某个临界应力值之后,ε1的计算值开始偏离试验结果。
σ′1-ε1曲线计算与试验结果相吻合的应力范围,与珊瑚砂的初始相对密度有关。Dr越小,对应的σ′1范围也越小,在本文试验条件下,不同Dr对应的临界σ′1:Dr=0.5约2500 kPa,Dr=0.6,0.7约3000 kPa,Dr=0.8约3500 kPa,Dr=0.9约4000 kPa,见图 12(a)。由此可见,σ′1-ε1计算与试验曲线相吻合的应力范围比较宽泛,涵盖了K0固结珊瑚砂正常的工程应力范围。
图 12(c)显示,与σ′1-ε1曲线相比较,p′-εv曲线计算结果与试验曲线的误差稍显偏大,但在p′≤1000 kPa的应力范围内吻合较好,说明在实际的工程应力范围内,模型计算与试验结果的误差都可以接受。与σ′1-ε1曲线的计算结果相似,随着p′的增加,εv的计算值略小于试验结果,误差值与珊瑚砂的初始相对密度有关。相同p′条件下,Dr越小,εv计算与试验结果的误差越大。初步分析原因,是因为式(12)只能描述dp′产生的dεv,没有考虑dq产生的dεv,而珊瑚砂具有剪胀特性,因此存在剪应力与体应变的交叉效应[17],即剪应力也能产生体变,从而导致体应变的模型计算值比试验结果偏小。
图 12给出的对比结果验证了采用幂函数模型描述一定应力范围内K0固结珊瑚砂应力–应变关系的合理性,同时也表明了模型对各种应力–应变关系的预测效果在不同程度上受到应力范围的影响,应力范围的大小与珊瑚砂的初始相对密度有关。幂函数模型和变形参数不仅能够反映K0固结的应力路径对珊瑚砂应力–应变关系的影响,而且模型的本构关系式概念清楚、简单易懂,模型参数易于求取、便于应用,因此可以将本文模型结合有限元程序,对珊瑚砂吹填地基的固结变形进行计算分析,具有一定的实用性。
5. 结论
本文利用三轴试验系统对5种不同初始相对密度的珊瑚砂进行K0固结试验,研究了珊瑚砂的应力–应变关系和颗粒破碎状况。在此基础上,建立了幂函数非线性弹性模型,描述了K0固结珊瑚砂的应力-应变关系。得到以下5点结论。
(1)K0固结珊瑚砂的轴向有效应力与轴向应变、偏应力与剪应变、平均有效应力与体应变之间的关系曲线都可以用幂函数表示,这些应力–应变曲线受到珊瑚砂初始相对密度的影响。
(2)珊瑚砂的静止土压力系数随轴向有效应力的增加而减小,初始相对密度对其影响较为明显。在相同的轴向有效应力条件下,初始相对密度越小,静止土压力系数越大。
(3)K0固结珊瑚砂的初始相对密度越小,颗粒破碎率越大。在本文的试验应力范围内,由于颗粒破碎量很小,对珊瑚砂K0固结特性的影响不大。
(4)K0固结珊瑚砂的变形参数受到应力状态和初始相对密度的影响。随着轴向有效应力的增加,切线模量增加,切线泊松比减小。初始相对密度越大,相同轴向有效应力下的切线模量越大,切线泊松比越小。
(5)幂函数模型能够合理预测一定应力范围内K0固结珊瑚砂的应力–应变关系,并能反映K0固结的应力路径对应力–应变关系的影响,而且具有形式简单,参数易于求取,实用性强的优点。
-
-
[1] OU C Y. Deep Excavation: Theory and Practice[M]. London: Taylor & Francis/Balkema, 2006.
[2] HSU S T. Behavior of pressure-grouted anchors in gravel[J]. Canadian Geotechnical Journal, 2012, 49(6): 719-728. doi: 10.1139/t2012-032
[3] ITOH K, KIKKAWA N, TOYOSAWA Y, et al. Failure mechanism of anchored retaining wall due to the breakage of anchor head[M]// Developments in Geotechnical Engineering. New Delhi: Springer India, 2015: 175-186.
[4] ÖSER C, SAYIN B. Geotechnical assessment and rehabilitation of retaining structures collapsed partially due to environmental effects[J]. Engineering Failure Analysis, 2021, 119: 104998. doi: 10.1016/j.engfailanal.2020.104998
[5] BILGIN Ö. Numerical studies of anchored sheet pile wall behavior constructed in cut and fill conditions[J]. Computers and Geotechnics, 2010, 37(3): 399-407. doi: 10.1016/j.compgeo.2010.01.002
[6] 黄雪峰, 马龙, 陈帅强, 等. 预应力锚杆内力传递分布规律与时空效应[J]. 岩土工程学报, 2014, 36(8): 1521-1525. doi: 10.11779/CJGE201408019 HUANG Xuefeng, MA Long, CHEN Shuaiqiang, et al. Distribution characteristics and time-space effects of internal force of prestressed anchor rod[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(8): 1521-1525. (in Chinese) doi: 10.11779/CJGE201408019
[7] SHU J C, ZHANG D W. A case study: observed deformation characteristics and internal force of pile-anchor retaining excavation[C]// Geotechnical Frontiers 2017. Reston, VA, USA: American Society of Civil Engineers, 2017: 136-148.
[8] WEERASINGHE R B, LITTLEJOHN G S. Uplift capacity of shallow anchorages in weak mudstone[J]. Thomas Telford, 1997, 3: 23-33.
[9] LITTLEJOHN G S. Ground anchorages: corrosion performance[J]. Proceedings of the Institution of Civil Engineers, 1987, 82(3): 645-662. doi: 10.1680/iicep.1987.328
[10] STILLE H, BROMS, B. B. Load redistribution caused by anchor failures in sheet pile walls[C]// Proceedings of the 6th European Conference on Soil Mechanics and Foundation Engineering, Vienna, 1976: 197-200.
[11] ANDERSON PECCIN D S, LUCAS F, JOAO RICARDO M. A new methodology to assess the structural safety of anchored retaining walls[J]. Thin-Walled Structures, 2017, 117: 343-355. doi: 10.1016/j.tws.2017.04.022
[12] ZHAO W, HAN J Y, CHEN Y, et al. A numerical study on the influence of anchorage failure for a deep excavation retained by anchored pile walls[J]. Advances in Mechanical Engineering, 2018, 10(2): 168781401875677. doi: 10.1177/1687814018756775
[13] 郑刚, 雷亚伟, 程雪松, 等. 局部锚杆失效对桩锚基坑支护体系的影响及其机理研究[J]. 岩土工程学报, 2020, 42(3): 421-429. doi: 10.11779/CJGE202003003 ZHENG Gang, LEI Yawei, CHENG Xuesong, et al. Influences and mechanisms of anchor failure on anchored pile retaining system of deep excavations[J]. Chinese Journal of Geotechnical Engineering, 2020, 42(3): 421-429. (in Chinese) doi: 10.11779/CJGE202003003
[14] 土木智库. 南宁深基坑坍塌事故原因初步确定, 设计图纸公布![EB/OL]. [2019-06-12) https://baijiahao.baidu.com/s?id=1636099866858085864&wfr=spider&for=pc. Civil Engineering Think Tank. The Cause of the Collapse of A Deep Excavation in Nanning Has Been Initially Determined, and the Design Drawings Have Been Announced! [EB/OL]. (2019-06-12) https://baijiahao.baidu.com/s?id=1636099866858085864&wfr=spider&for=pc. (in Chinese)
[15] CHENG X S, ZHENG G, DIAO Y, et al. Study of the progressive collapse mechanism of excavations retained by cantilever contiguous piles[J]. Engineering Failure Analysis, 2017, 71: 72-89. doi: 10.1016/j.engfailanal.2016.06.011
[16] 郑刚, 雷亚伟, 程雪松, 等. 局部破坏对钢支撑排桩基坑支护体系影响的试验研究[J]. 岩土工程学报, 2019, 41(8): 1390-1399. doi: 10.11779/CJGE201908002 ZHENG Gang, LEI Yawei, CHENG Xuesong, et al. Experimental study on influences of local failure on steel-strutted pile retaining system of deep excavations[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(8): 1390-1399. (in Chinese) doi: 10.11779/CJGE201908002
[17] 程雪松, 郑刚, 邓楚涵, 等. 基坑悬臂排桩支护局部失效引发连续破坏机理研究[J]. 岩土工程学报, 2015, 37(7): 1249-1263. doi: 10.11779/CJGE201507011 CHENG Xuesong, ZHENG Gang, DENG Chuhan, et al. Mechanism of progressive collapse induced by partial failure of cantilever contiguous retaining piles[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(7): 1249-1263. (in Chinese) doi: 10.11779/CJGE201507011
[18] 冯永. 光大银行基坑支护方法的比较与数值模拟[D]. 长春: 吉林大学, 2015. FENG Yong. The Comparision and Numericial Simulation of Foundation Pit Supporting for the Everbright Bank[D]. Changchun: Jilin University, 2015. (in Chinese)
-
期刊类型引用(2)
1. 张季如,郑颜军,彭伟珂,王磊,陈敬鑫. 填土应力路径下珊瑚砂幂律应力-应变模型的适用性研究. 岩土力学. 2023(05): 1309-1318 .  百度学术
百度学术
2. 熊雪梅,郑宇轩,黄俊宇,周风华. 粒径和围压对珊瑚砂侧限压缩性能的影响. 硅酸盐通报. 2023(06): 2037-2046 .  百度学术
百度学术
其他类型引用(0)



 下载:
下载: